2. 中国水利水电科学研究院, 北京 100038
2. Inst. of Water Resource and Hydraulic Research, Beijing 100038, China
汛限水位是汛期水库允许兴利蓄水的上限水位,在中国具有合法的地位[1]。汛限水位控制理论发展主要经历了整个汛期单一固定控制阶段、分期固定控制阶段[2-3]和汛限水位的动态控制[4-5]3个阶段。汛限水位动态控制的关键是确定一个安全经济的动态控制域。
汛限水位动态控制本质上是风险调度的范畴。水库汛限水位动态控制最重要的风险源来自于入库径流不确定性。文献[6-8]考虑入库径流的不确定性,在不增加防洪风险的情况下推求了单库情况下的汛限水位动态控制域。梯级水库的入库径流一部分来源于经上游水库调蓄影响后的出库径流,一部分来自于区间流域的天然径流。当下游水库取某一标准的设计洪水时,其上游来水和区间来水可能出现各种组成情况,导致受上游水库调蓄的水量具有不确定性,因而下游水库的设计洪水具有不确定性。《水利水电工程设计洪水计算规范》[9]规定设计洪水的地区组成采用典型洪水组成法和同频率组成法,原则是以对防洪不利为原则确定上游和区间的地区组成方案。但是,由于梯级水库防洪调度受到多种因素的制约,不仅与水库自身的库容状态、下泄能力以及下游防洪控制点的安全流量约束等有关,还受上游水库的调蓄作用和区间来水影响。梯级水库防洪调度是一个复杂的非线性问题,实际操作中要找出偏不利的组合方式往往并不容易。而且,实际应用中还可能由于考虑到不符合水文规律的地区组成情况,过于保守而造成弃水和投资浪费。因此,考虑梯级水库设计洪水不确定性的关键是合理设置梯级水库设计洪水的地区组成。需要解决以下两个问题:
1) 确定一个上游来水量的可能变化范围,该区间需要把对防洪不利的组成方式都考虑进去,以期确定一个不增加防洪风险的汛限水位动态控制域。
2) 避免将不符合水文规律,不可能发生的组成方式考虑在内,科学合理地确定地区组成方案,以最大限度的利用水库的防洪库容抬升汛限水位,增加发电效益。
Copula函数由于能反映变量间的内在联系,且计算简单,已被越来越多的学者引入到径流随机模拟[10-12]、丰枯遭遇分析[13]以及洪水地区组成[14-15]的研究中。本文以Copula函数为工具,解决汛限水位动态控制域计算面临的以上两个问题。首先通过Copula函数建立上游天然来水和区间天然来水的联合密度函数,求出给定显著性水平下的上游来水的置信区间,以此将上游和区间的各种不利的地区组成方式考虑在内,并且排除不符合水文规律的地区组成方式。在此基础上推求下游水库汛限水位动态控制域求解的不确定性设计洪水输入,以调洪高水位不超过水库允许的最高水位为风险约束条件,求解满足风险约束的汛限水位上限值。并将该方法应用于考虑潘口水库补偿调节的黄龙滩水库汛限水位动态控制域研究中。
1 研究方法考虑梯级水库库容补偿和设计洪水不确定性的汛限水位动态控制域计算模型主要包括库容补偿模块、风险控制模块以及梯级水库模拟运行模块。库容补偿模块主要是根据上下游的水力联系,在不考虑径流不确定性的情况下,推求下游水库的极限汛限水位值。风险控制模块主要是为了控制防洪风险不增加而为汛限水位动态控制域的求解添加风险约束。梯级水库模拟运行模块主要是根据各个水库的防洪调度规程,模拟水库的调度过程,通过反复模拟寻找水库最合理的汛限水位上限值。
1.1 库容补偿模块当上游水库(简称上库)起调水位低于设计汛限水位(或者上游水库在汛限水位以上为下游水库预留了防洪库容)时,上库存在一定的富余库容为下游水库(简称下库)分担防洪压力,上库可以在涨水阶段减小出库流量,使得下库的入库洪水总量减小,下库可在不改变调洪高水位的情况下,适当的抬升汛限水位。
图 1直观表述了库容补偿提高下库汛限水位的原理:QA, in(t)、QA, out(t)、QA, out′(t)分别表示上库A的设计洪水过程、设计调度规则下的出库过程和为下游预留防洪库容后的出库过程。QB, in(t)、QB, in′(t)、QB, out(t)分别表示下库B的设计洪水过程、利用上库补偿调节的入库过程和设计调度规则下的出库过程。
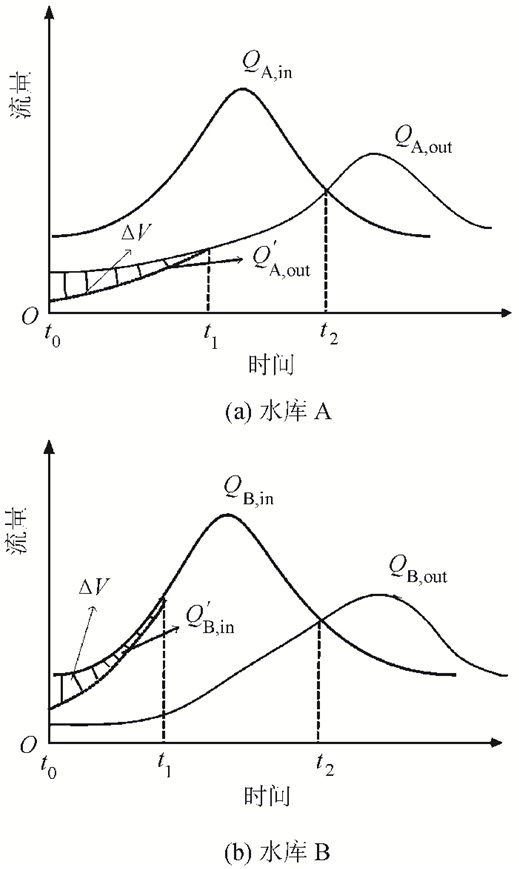 |
| 图1 出入库变化示意图 Fig. 1 Sketch of changes in the inflow and outflow hydrographs of the reservoir A and B |
洪水来临时,上库A尽快使用富余库容ΔV,尽量减少上库涨水期间出库流量。假设上库A在t0~t1之间减小出库以利用富余库容ΔV,t1时刻之后两种调度方式的入库流量和库水位均相同,两者的出库过程完全重合。所以,在整个调度期内出库过程变为:
| $ {Q_{{\rm{A}},{\rm{out}}}}^{'} = \left\{ \begin{array}{l} {Q_{{\rm{A}},{\rm{out}}}} - k\left( t \right),t = {t_0} + 1,{t_0} + 2, \ldots ,{t_1};\\ {Q_{{\rm{A}},{\rm{out}}}},t = {t_1} + 1,{t_1} + 2, \ldots ,n \end{array} \right. $ | (1) |
式中,
下库B的入库流量由QB, in(t)变为了QB, in′(t):
| $ \left\{ \begin{array}{l} {Q_{{\rm{B,in}}}}\left( t \right) = {Q_{{\rm{A,out}}}}\left( {t - \tau } \right) + QJ\left( t \right),\\ t = {t_0} + 1,{t_0} + 2, \ldots ,n \end{array} \right. $ | (2) |
| $ {Q_{{\rm{B,in}}}}^{'} \left( t \right) = \left\{ \begin{array}{l} {Q_{{\rm{A,out}}}}\left( {t - \tau } \right) - k\left( t \right) + QJ\left( t \right),\\ \;\;\;\;\;\;\;\;t = {t_0} + 1,{t_0} + 2, \ldots ,{t_1};\\ {Q_{{\rm{A,out}}}}\left( {t - \tau } \right) + QJ\left( t \right),\\ \;\;\;\;\;\;\;\;t = {t_1} + 1,{t_1} + 2, \ldots ,n \end{array} \right. $ | (3) |
其中,τ为上库至下库与区间来水至下库的洪水传播时间之差,QJ(t)为区间流量。下库B原汛限水位的调洪高水位为ZB, max,利用下库涨水阶段的入库流量减小,将汛限水位从ZB, 0提高到ZB, 0′,提高后的调洪高水位为ZB, max′。若保持下游出库流量和调洪高水位不变:
| $ \begin{array}{l} {Z_{{\rm{B,max}}}} = V({Z_{{\rm{B}},0}}) + \sum\limits_{t = {t_0}}^{{t_2}} {{Q_{{\rm{B,in}}}}\left( t \right)} \times \Delta t - \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{t = {t_0}}^{{t_2}} {{Q_{{\rm{B,out}}}}\left( t \right)} \times \Delta t \end{array} $ | (4) |
| $ \begin{array}{*{20}{l}} {{Z_{{\rm{B}},{\rm{max}}}}^{'} = V({Z_{{\rm{B}},{\rm{0}}}}^{'}) + \sum\limits_{t = {t_0}}^{{t_2}} {{Q_{{\rm{B}},{\rm{in}}}}^{'}\left( t \right)} \times \Delta t - }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{t = {t_0}}^{{t_2}} {{Q_{{\rm{B}},{\rm{out}}}}\left( t \right)} \times \Delta t} \end{array} $ | (5) |
| $ {Z_{{\rm{B}},{\rm{max}}}} = {Z_{{\rm{B}},{\rm{max}}}}^{'} $ | (6) |
联立式(1)~(6)可以得到,提高后的汛限水位:
| $ {Z_{{\rm{B}},0}}^{'} = Z(V({Z_{{\rm{B}},0}}) + \Delta V) $ | (7) |
式中,V(·)表示由水位计算库容的函数,Z(·)表示由库容计算水位的函数。从式(7)可以看出,若保持区间径流不变,上库有多少富余的防洪库容,就可将下库的汛限水位抬升多少的水量。
考虑到下库的汛限水位不能无限制的增加,本文定义极限汛限水位值为:
| $ Z_{{\rm{B}},0}^{{\rm{max}}} = {\rm{min}}[Z(V({Z_{{\rm{B}},0}}) + \Delta V),{Z_{{\rm{p,max}}}}] $ | (8) |
式中:ZB, 0max为不考虑入库径流等不确定性因素,单独分析库容补偿和水库允许最高水位约束得到的水库极限汛限水位值; Zp, max为水库允许最高水位,一般为校核洪水位(或坝顶高程)。
1.2 风险控制模块水库防洪调度的风险主要指水库的调洪高水位高于水库的校核水位(或坝顶高程),使坝体安全受到危险而带来的溃坝的风险[7]。图 2为最常见的梯级水库串联示意图。图 2中:A表示上游水库, 天然来水量为X;B为下游水库,未经上游水库调蓄的天然来水量为Z;区间天然来水量为Y。下游水库B的天然来水量由上游天然来水量X和区间天然来水量Y共同组成。
| $ Z = X + Y $ | (9) |
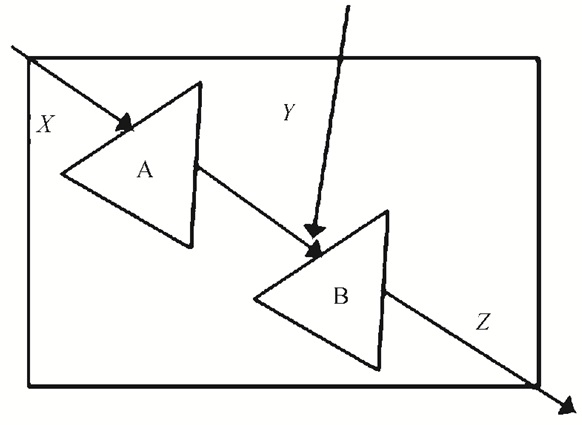 |
| 图2 梯级水库串联示意图 Fig. 2 Sketch of cascade reservoirs |
水库汛限水位动态控制的风险主要来自于入库径流的不确定性。对于下库B的入库径流的不确定性主要来自于两个方面:一是实时调度中由于预报不确定性带来的风险;二是设计阶段对于洪水地区组成的不确定性考虑不周,实时调度中出现了设计之外对防洪不利的地区组成方式,导致水库可能存在超校核水位的风险。本文尝试在设计阶段将防洪风险控制在一定范围内确定汛限水位上限值。考虑洪水地区组成不确定性的防洪风险约束可以表示为:
| $ \left\{ \begin{array}{l} \forall X = {x_i},{x_i} \in \left[ {{x_{\rm{l}}},{x_{\rm{u}}}} \right],{Z_{i,{\rm{max}}}} \le {Z_{p,{\rm{max}}}};\\ {z_{\rm{p}}} = {x_i} + {y_i},{\rm{ }}{x_i} > 0,{y_i} > 0 \end{array} \right. $ | (10) |
式中,zp为下库校核标准洪水,xi和yi表示第i种分配方式下的上游天然来水量和区间天然来水量,Zi, max为第i种分配方式下的调洪高水位,Zp, max为水库允许最高水位, xl、xu分别为上游来水量的最小值和最大值。
为了保证大坝安全,在下库遭遇校核洪水zp时,不管上游来水和区间来水怎么分配,经过梯级水库调洪之后的下库调洪高水位都应当小于水库允许最高水位。虽然理论上上游来水量的取值范围为xi∈[0, zp],但是并不是所有的取值xi都服从水文现象的物理规律。[xl, xu]即为剔除不符合水文规律以后的上游来水量的取值范围。要进行防洪风险分析,首先需要确定上游天然来水量的合理取值区间。
由于水文现象的随机性,当下库遭遇某一标准的洪水时,上游和区间的各种组成情况都有可能发生,只是各种组成情况发生的概率不一样而已。Copula函数的出现使作者能建立起上游洪水和区间洪水的联合分布,可求得下游遭遇某种洪水时,各种不同组成情况出现的概率。Archimedean Copula是一种重要的Copula函数,其中,Gumbel-Hugaard Copula在构造洪水联合分布FX, Y(x, y)中应用最为广泛[16],2维的Gumbel-Hugaard Copula函数的表达式为:
| $ \begin{array}{l} {F_{X,Y}}\left( {x,y} \right) = P\left( {X \le x,Y \le y} \right) = C\left( {u,v} \right) = \\ {\rm{exp}}\{ - {[( - {\rm{ln}}\;u)\theta + {( - {\rm{ln}}\;v)^\theta }]^{1/\theta }}\} ,\theta \in \left[ {1,\infty } \right) \end{array} $ | (11) |
式中,u=FX(x)、v=FY(y)分别为随机变量X、Y的边缘分布函数,θ为Copula函数的结构参数。可通过Kendall秩相关系数法[17]估计Copula函数的参数θ。
Copula函数相应的密度函数为:
| $ \begin{array}{l} {c_\theta }\left( {u,v} \right) = {C_\theta }\left( {u,v} \right)\frac{{{{({\rm{ln}}\;u{\rm{ln}}\;v)}^{\theta - 1}}}}{{uv}}\{ \left( {\theta - 1} \right) \times \\ {\left[ { - {\rm{ln}}\;{C_\theta }\left( {u,v} \right)\left] {^{1 - 2\theta } + } \right[ - {\rm{ln}}\;{C_\theta }\left( {u,v} \right)} \right]^{2 - 2\theta }}\} \end{array} $ | (12) |
根据《水利水电工程设计洪水计算规范》规定,洪水要素X和Y均服从P-Ⅲ型分布。X和Y的概率密度函数fX(x)、fY(y)分别为:
| $ {f_X}\left( x \right) = \frac{{{\beta _x}^{{\alpha _x}}}}{{\Gamma ({\alpha _x})}}{(x - {\gamma _x})^{{\alpha _x} - 1}}{{\rm{e}}^{ - {\beta _x}(x - {\gamma _x})}} $ | (13) |
| $ {f_Y}\left( y \right) = \frac{{{\beta _y}^{{\alpha _y}}}}{{\Gamma ({\alpha _y})}}{(y - {\gamma _y})^{{\alpha _y} - 1}}{{\rm{e}}^{ - {\beta _y}(x - {\gamma _y})}} $ | (14) |
式中,αx、βx、γx和αy、βy、γy分别为随机变量X、Y的P-Ⅲ型分布参数,Γ(·)为伽马函数。随机变量X与Y的联合密度函数fX, Y(x, y)可以表示为:
| $ \begin{array}{l} {f_{X,Y}}\left( {x,y} \right) = {f_{X,Y}}(x,{z_{\rm{p}}} - x) = {f_X}\left( x \right) \times \\ \;\;\;\;\;\;{f_Y}\left( {{z_{\rm{p}}} - x} \right) \times {c_\theta }\left( {{F_X}\left( x \right),{F_y}\left( {{z_{\rm{p}}} - x} \right)} \right) \end{array} $ | (15) |
归一化后的概率密度函数为:
| $ \begin{array}{l} g\left( x \right) = \\ \frac{{{c_\theta }({F_X}\left( x \right),{F_y}({z_{\rm{p}}} - x)) \times {f_X}\left( x \right) \times {f_Y}({z_{\rm{p}}} - x)}}{{\int\limits_0^{{z_{\rm{p}}}} {{c_\theta }} ({F_X}\left( x \right),{F_y}({z_{\rm{p}}} - x)) \times {f_X}\left( x \right) \times {f_Y}({z_{\rm{p}}} - x){\rm{d}}x}} \end{array} $ | (16) |
图 3为g(x)的示意图,g(x)随x有先增大后减小的趋势,可以借助g(x)求出X落在不同区间的概率值。
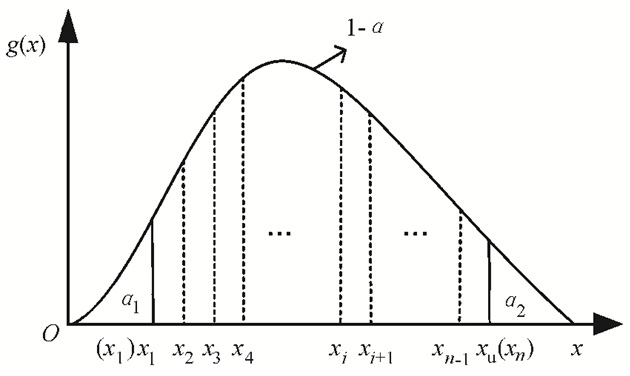 |
| 图3 联合概率密度函数示意图 Fig. 3 Sketch of the normalized joint density function g(x) |
假定上游天然来水落在[0, xl]区间的概率为α1, 落在[xu, zp]区间的概率为α2,α=α1+α2为显著性水平。即:
| $ \int\limits_0^{{x_{\rm{l}}}} {g\left( x \right){\rm{d}}x} = {\alpha _1} $ | (17) |
| $ \int\limits_{{x_{\rm{u}}}}^{{z_{\rm{p}}}} {g\left( x \right){\rm{d}}x} = {\alpha _2} $ | (18) |
| $ P({x_{\rm{l}}} \le X \le {x_{\rm{u}}}) = 1 - \alpha $ | (19) |
则可以通过式(20)的流程计算下库的汛限水位上限值。即给定显著性水平α,求出显著性水平α下的X取值上下限[xl, xu]α,将区间[xl, xu]α离散为x1, x2, …, xn共n个状态,然后以式(10)为风险约束条件,得出满足风险约束的汛限水位上限值Zu。
| $ \alpha \to [{x_{\rm{l}}},{x_{\rm{u}}}]\alpha \to {Z_{\rm{u}}} $ | (20) |
考虑库容补偿和洪水地区组成不确定性的梯级水库模拟流程如图 4所示,具体操作步骤如下:
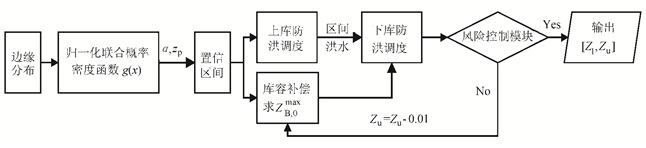 |
| 图4 梯级水库模拟运行流程 Fig. 4 Framework of the simulation operation for cascade reservoirs |
1) 求出上游入库洪水X和区间洪水Y的边缘分布u、v,并通过Copula函数建立两者的联合概率密度函数fX, Y(x, y), 并通过归一化求出g(x)。
2) 给定下游校核标准洪水zp和显著性水平α,且令α1=α2,求出X的置信区间[xl, xu]。将X取值离散为n个状态,xi, i=1, 2, …, n, xi∈[xl, xu]。
3) 假定下库汛限水位动态控制域为[Zl, Zu], 汛限水位动态控制域的下限Zl保持原设计不变,通过库容补偿模块求出极限汛限水位值ZB, 0max作为Zu的初始值。
4) 按上库A的汛期防洪调度规程计算入库洪水X=xi,i=1, 2, …, n的出库过程。
5) 上库出库过程考虑滞时与区间洪水叠加得到下库B的入库洪水,并以[Zl, Zu]为下库B的汛限水位动态控制域,按下库的防洪调度规程调度,得到下库B的调洪高水位Zi, max, i=1, 2, …, n。
6) 若调洪高水位Zi, max, i=1, 2, …, n满足风险约束条件,则输出[Zl, Zu]。若不满足风险约束条件,则Zu=Zu-0.01,转入第3)步重新计算,直到满足风险约束为止。
2 实例研究 2.1 流域概况潘口和黄龙滩水库是汉江支流堵河上的梯级水库,下游黄龙滩水库于1976年建成,控制流域面积11 892 km2,约占堵河总流域面积的95.1%。上游潘口水库,2011年9月下闸蓄水,控制流域面积8 950 km2,占堵河全流域面积的71.6%。两库坝址相距约108 km,洪水传播时间约6 h,区间集水面积3 008 km2,约占黄龙滩坝址以上集水面积的24.9%。区间洪水占比大,对黄龙滩的防洪形势有较大影响。两水库的设计特征参数如表 1所示。
| 表1 潘口和黄龙滩水库设计特征参数 Tab. 1 Basic characteristics of reservoirs PK and HLT |
 |
黄龙滩采用的是预报预泄的调度规则,实行预报预泄调度的库水位区间为[40, 247] m。汛期调度方式为:在涨水段,当预报洪峰流量在6 000 m3/s以下,按出入库平衡控制,控制水位在汛限水位247 m。当预报洪峰流量在6 000~11 000 m3/s,库水位高于240 m时,按最大预报流量的85%作为出库开闸预泄;如果当前入库流量大于最大预报流量85%时,可按当前入库作为出库泄洪。由预报误差产生的调度误差由下一时段修正。当预报洪峰流量大于11 000 m3/s时,水库应该敞泄,以降低库水位腾空库容。洪峰过后,逐步关闭闸门,控制库水位在247 m。
潘口水库汛限水位347.60~353.20 m之间的3.0×108 m3防洪库容为配合丹江口水库对汉江中下游防洪运用而预留,353.20~358.40 m之间的3.11×108 m3防洪库容为提高黄龙滩水库防洪标准而预留,358.40 m以上按保坝方式运用。潘口水库分担黄龙滩水库防洪压力的洪水调度方式为:从353.20 m起调,当入库流量小于353.20 m对应泄流能力时,逐步开启泄洪设施,保持泄量等于来流量,库水位保持353.20 m运用;当入库流量超过353.20 m对应泄流能力,水库水位雍高后,控制下泄流量不超过10 700 m3/s;当水库水位超过358.40 m后,按保坝方式运用,闸门全开敞泄。调洪时考虑机组参与泄流,根据潘口水电站可行性研究阶段设计成果,发电流量按500 m3/s计(约为全厂额定流量的2/3),但当入库流量大于厂房设计标准200年一遇洪水洪峰流量14 300 m3/s后,不计发电流量。
2.2 计算结果潘口建库后,黄龙滩水库利用潘口水库预留的防洪库容提高黄龙滩水库的汛限水位上限值。通过建立上游潘口和潘黄区间洪水的联合概率密度函数,给定显著性水平α=0.05推求潘口洪水的置信区间。考虑到潘口和潘黄区间洪水地区组成的不确定性,将置信区间离散为200个状态,相应的得到了200种洪水地区组成方式。对200种地区组成方式分别进行梯级模拟调度,推求了满足风险约束条件的黄龙滩汛限水位上限值。
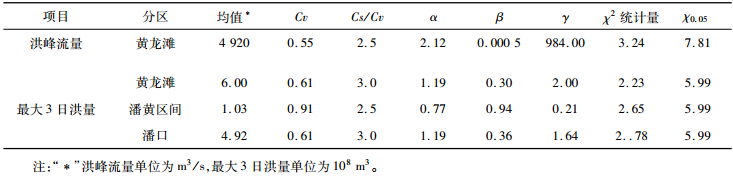
2.2.1 边缘分布和归一化联合概率密度函数黄龙滩水库为季调节水库,潘口为年调节水库,对于大水库选取3 d为有效控制时段。研究采用潘口和黄龙滩1959—2009年的3 h时段径流资料。由于潘黄区间没有实测资料,区间流量资料通过将黄龙滩坝址洪水减去潘口坝址经马斯京根河道演算至黄龙滩坝址的洪水得到。令Qm为最大洪峰流量,W3d为最大3 d洪量,各变量的统计参数如表 2所示。利用χ2检验法进行假设检验,在5%的显著性水平下,自由度为k-r-1(r为参数个数,k为χ2检验的分组数)的χ2检验的接受域为小于等于临界值,表中χ0.05为临界值,从表 2可以看出4个随机变量的P-Ⅲ型分布均通过了检验。将潘口和潘黄区间的α、β、γ分别带入到式(13)和(14)中可得到两者的密度函数。
| 表2 各分区的洪水统计参数 Tab. 2 Flood statistical parameters of each subarea |
 |
通过Gumbel-Hugaard Copula函数建立潘口和潘黄区间W3d之间的2维联合分布。秩相关法求出的Copula函数的结构参数θ为1.91。采用Kolmogorov-Simirnov (K-S)检验法对Copula函数进行拟合检验, K-S检验统计量D:
| $ D = \mathop {\max }\limits_{1 \le k \le n} \left\{ {\left| {{C_k} - \frac{{{m_k}}}{n}} \right|,\left| {{C_k} - \frac{{{m_k} - 1}}{n}} \right|} \right\}。$ |
式中:Ck为联合观测值样本(xk, yk)的Copula值;mk为联合观测值样本中满足条件x≤xk, y≤yk的联合观测值的个数;n为样本长度。K-S检验的显著性水平为α=0.05, n=53(实测期51 a加1867年和1900年调查期)对应的分位数近似为
| $ \begin{array}{l} {F_{X,Y}}\left( {x,y} \right) = P\left( {X \le x,Y \le y} \right) = C\left( {u,v} \right) = \\ \;\;\;\;{\rm{exp}}\left\{ { - {{\left[ {{{\left( { - {\rm{ln}}\;u} \right)}^{1.91}} + {{\left( { - {\rm{ln}}\;v} \right)}^{1.91}}} \right]}^{1/1.91}}} \right\}。\end{array} $ |
结合式(12)~(16)可以计算出归一化的概率密度函数g(x)。
2.2.2 置信区间计算黄龙滩500年一遇洪水的最大3日洪量为24.4×108 m3。图 5为黄龙滩遭遇500年一遇洪水时,潘口和潘黄区间归一化的联合概率密度函数g(x)随潘口天然来水x的变化曲线。取显著性水平α=0.05得上游来水量x的置信区间为[16.48, 20.23]。即当黄龙滩遭遇500年一遇的洪水时,上游潘口来水量有95%的可能性处于区间[16.48, 20.23]。
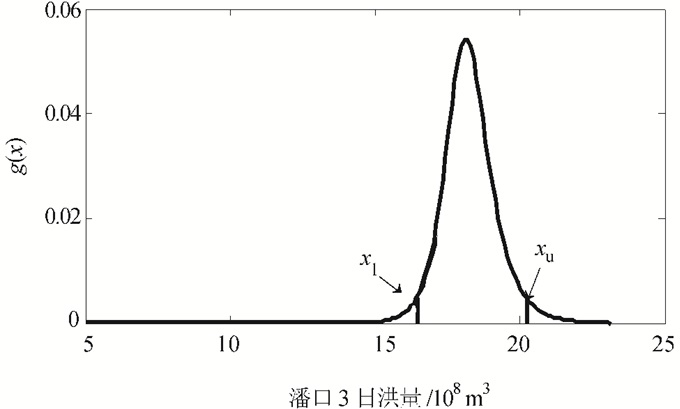 |
| 图5 g(x)随潘口最大3日洪量的变化曲线 Fig. 5 Changing process of g(x) with the maximal three-day flood volume of PK |
2.2.3 汛限水位动态控制域计算结果
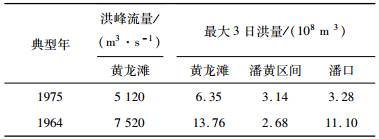
潘黄区间暴雨主要分为锋面雨和台风雨两大类。锋面雨影响范围大,一般可影响到黄龙滩以上的全流域,潘口上游、潘黄区间、黄龙滩洪水的相应性好。这类暴雨一般历时较长,洪水峰型一般较胖,且多为复峰。台风类暴雨一般仅影响到潘口水库以下地区,此类暴雨降雨历史短、强度大、峰型一般为单峰、且尖瘦。本次研究分别选择了1964年锋面雨和1975年台风雨两场典型洪水。1964年双峰型洪水实测3日洪量为历史最大,1975年单峰型洪水实测区间来水为历史最大。两场典型洪水的分区来水特征值如表 3所示。500年一遇设计洪水按同倍比放大法推求。
| 表3 典型洪水特征特征值 Tab. 3 Characteristics of the typical floods |
 |
本次研究设定了4种地区组成方案:①潘黄同频率地区组成;②区黄同频率地区组成;③典型年地区组成(1964型设计洪水按以上游来水为主的1964年典型分配和1975型设计洪水按以区间来水为主的1975年典型分配);④显著性水平为0.05,将置信区间离散为200种状态,考虑200种可能出现的地区组成方式。
最终得到4种方案的汛限水位上限值如表 4所示。
| 表4 汛限水位上限值计算结果表 Tab. 4 Upper FLWL of the four kinds of flood spatial pattern |
 |
从表 4中可以看出,按照传统的同频率法和典型年法计算的汛限水位上限值偏大,这主要是因为传统方法仅考虑了地区组成的某几种情况,而这几种情况并不能包含所有对防洪偏不利的地区组成方式,而导致计算的汛限水位上限值偏大。而本文提出的方法,考虑了洪水地区组成的不确定性,包含的地区组成情况更全面,能将最不利的地区组成方式考虑在内,因而求出的汛限水位上限值相对偏安全。图 6和7分别是黄龙滩遭遇1964型和1975型500年一遇设计洪水时,上游潘口取不同W3d时,分别设定黄龙滩汛限水位上限值为247、249、251 m时的调洪高水位值。
 |
| 图6 黄龙滩调洪高水位随潘口洪量变化图(1964年典型) Fig. 6 Changing process of the highest water level of HLT during flood operation with the maximum three-day flood volume of PK (1964 typical year) |
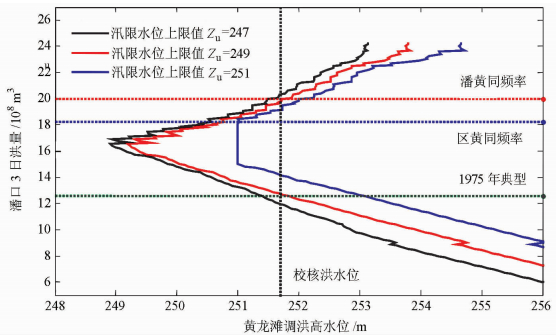 |
| 图7 黄龙滩调洪高水位随潘口洪量变化图(1975年典型) Fig. 7 Changing process of the highest water level of HLT during flood operation with the maximum three-day flood volume of PK (1975 typical year) |
从图 6中可以看出,α=0.05时,置信区间能包含传统的3种地区组成情况,但是传统的3种组成方式并不能包含对防洪不利的所有形式。
从图 7中可以看出,按潘黄同频率地区组成求出的汛限水位上限值相对偏安全。按区黄同频率求出的汛限水位上限值为251.53 m,当实际应用中出现其他的地区组成情况时很可能有漫坝的风险。而按1975年典型年地区组成计算的汛限水位上限值为248.21 m。考虑到500年一遇的洪水一般是全流域性的大洪水,来水量应该大致跟流域面积呈正比,基本不可能出现1975年型的地区组成方式。α=0.05时的置信区间能事先排除这种不符合水文规律的地区组成方式,充分利用防洪库容提高汛限水位以增加发电效益。
从图 6和7还可以看出,对于某一个起调水位,黄龙滩的调洪高水位随潘口洪量的增加整体有先减小后增加的趋势。这主要是因为上库有削减洪峰的作用,随着潘口洪量的增加,而使得不受潘口调蓄作用的区间洪量减少。随着潘口洪量的增加,潘口水库对黄龙滩入流的削峰作用不断增强,而使得调洪高水位降低。但是,从潘口的防洪调度规则也可以看出,潘口的削峰作用并不是无限制的,当其入库流量太大,为了保证潘口水库自身的安全,水库将按敞泄方式运用,所以之后再增加潘口的洪量,黄龙滩的调洪高水位反倒会增加。所以,实际运用中,建议按以下两种思路设定偏不利的地区组成:1) 洪量大都来自上游地区;2) 洪量大都来自于区间流域。
从1964型设计洪水的调度结果还可以看出,由于梯级水库防洪调度是一个复杂的非线性问题,调洪高水位往往存在不规则变化的现象,所以设计阶段应当尽可能多的考虑可能出现的所有情况,尽可能地减小由于设计阶段洪水地区组成考虑不周而给汛限水位实时动态控制带来的风险。
图 8给出了4中地区组成方式在联合概率密度函数上的位置。
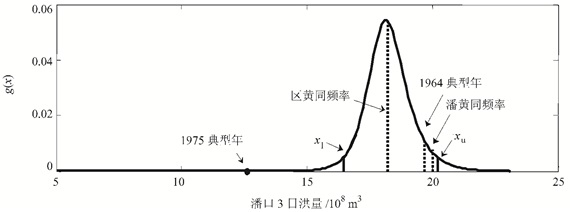 |
| 图8 不同地区组成方式在联合概率密度函数上的位置 Fig. 8 Allocation of the different spatial patterns on the normalized joint density function |
由图 8可以看出:1) 同频率地区组成并不一定是最可能出现的地区组成方式。结合图 6和7也可以看出,同频率地区组成方式也不一定是对防洪不利的地区组成方式。
2) 典型年分配方式受典型年影响较大,具有很大的随机性,而且可能出现置信区间之外的分配方式,如1975典型年分配方式。
2.2.4 效益计算通过计算,利用潘口水库预留的防洪库容,能将黄龙滩的汛限水位上限值提升到248.21 m。即汛限水位动态控制域由[240, 247] m变为[240, 248.21] m。分别选取汛期来水较丰的2000年和汛期来水较枯的1994年计算发电效益,相比于原始的动态控制域[240, 247] m, 增大动态控制域后1994年汛期发电量从4.70×108增加至4.81×108 kW·h,增加了0.11×108 kW·h。2000年汛期发电量从6.60×108增加至6.73×108 kW·h,增加了0.13×108 kW·h。按当地最低电价0.58元/(kW·h)计算, 1994年能提高经济效益638万元,2000年能提高经济效益754万元。
3 结论从上游天然来水和区间天然来水的边缘分布出发,以Copula函数为工具建立上游天然来水和区间来水特征的联合概率密度函数,以此作为设定上游和区间来水各种地区组成方式的依据。以不同的地区组成方式作为下游水库汛限水位动态控制域求解的不确定性径流输入,求解满足风险约束的汛限水位上限值。结合该方法在堵河流域潘口-黄龙滩梯级水库的应用结果,得到以下结论:
1) 所提方法能够考虑梯级水库设计洪水的不确定性。通过设置多种地区组成方式,推求考虑梯级水库调蓄作用的不确定性设计洪水,显著控制了防洪风险,相对于同频率法和典型年法,所求汛限水位动态控制域更加的安全。
2) 由于利用了历史统计信息,给定显著性水平确定了一个合理的置信区间,为地区组成方式设定提供参考信息。避免了洪水地区组成设定的盲目性,也避免了考虑置信区间之外,不符合水文规律的地区组成情况。
3) 黄龙滩水库的汛限水位动态控制域能从[240, 247] m增加至[240, 248.21] m,能将汛期来水较丰的2000年发电量增加0.13×108 kW·h,汛期来水较枯的1994年发电量增加0.11×108 kW·h。分别增加经济效益754、638万元。
4) 考虑到典型洪水的不确定性,设计阶段还可以多选几组典型洪水,从而计算出最安全的汛限水位上限值。
5) 该研究属于实施汛限水位动态控制规划设计阶段的内容,实际应用中可以根据面临时段的水情、雨情、工情以及水雨情预报信息,在动态控制域范围内,合理的选择汛期运行水位。
| [1] |
邬福肇. 中华人民共和国防洪法释义[M]. 北京: 法律出版社, 1999.
|
| [2] |
Liu Pan, Guo Shenglian, Xiao Yi, et al. Study on the optimal reservoir seasonal flood control water level[J]. Journal of Hydroelectric Engineering, 2007, 26(3): 5-10. [刘攀, 郭生练, 肖义, 等. 水库分期汛限水位的优化设计研究[J]. 水力发电学报, 2007, 26(3): 5-10.] |
| [3] |
Yun R, Singh V P. Multiple duration limited water level and dynamic limited water level for flood control, with implications on water supply[J]. Journal of Hydrology, 2008, 354(1/2/3/4): 160-170. |
| [4] |
Zhou Yanlai, Guo Shenglian, Liu Pan, et al. Joint operation and dynamic control of flood limiting water levels for mixed cascade reservoir systems[J]. Journal of Hydrology, 2014, 519(3): 248-257. |
| [5] |
Li Wei, Guo Shenglian, Liu Pan. A reservoir dynamic flood limited water level control method based on real-time forecasting information[J]. Water Power, 2005, 31(1): 66-70. |
| [6] |
Liu Pan, Guo Shenglian, Li Xiang, et al. Deriving the interval of reservoir dynamic flood control water levels based on risk analysis[J]. China Hydrology, 2009, 29(4): 1-5. [刘攀, 郭生练, 李响, 等. 基于风险分析确定水库汛限水位动态控制约束域研究[J]. 水文, 2009, 29(4): 1-5.] |
| [7] |
Li Xiang, Guo Shenglian, Liu Pan, et al. The dynamic control bound of flood limited water level considering inflow uncertainty in Three Gorges Reservoir[J]. Journal of Sichuan University (Engineering Science Edition), 2010, 42(3): 49-55. [李响, 郭生练, 刘攀, 等. 考虑入库洪水不确定性的三峡水库汛限水位动态控制域研究[J]. 四川大学学报(工程科学版), 2010, 42(3): 49-55.] |
| [8] |
Yan Baowei, Guo Shenglian. Risk estimation of reservoir flood operation in consideration of inflow hydrograph forecasting error[J]. Journal of Hydraulic Engineering, 2012, 43(7): 803-807. [闫宝伟, 郭生练. 考虑洪水过程预报误差的水库防洪调度风险分析[J]. 水利学报, 2012, 43(7): 803-807.] |
| [9] |
水利水电工程设计洪水计算规范SL44—2006[S].北京:中国水利水电出版社, 2006.
|
| [10] |
Xiao Yi, Guo Shenglian, Xiong Lihua, et al. A new random simulation method for constructing synthetic flood hydrographs[J]. Journal of Sichuan University (Engineering Science Edition), 2007, 39(2): 55-60. [肖义, 郭生练, 熊立华, 等. 一种新的洪水过程随机模拟方法研究[J]. 四川大学学报(工程科学版), 2007, 39(2): 55-60.] |
| [11] |
Yan Baowei, Guo Shenglian, Liu Pan, et al. Streamflow simulation based on Copula function[J]. Journal of Sichuan University (Engineering Science Edition), 2010, 42(1): 5-9. [闫宝伟, 郭生练, 刘攀, 等. 基于Copula函数的径流随机模拟[J]. 四川大学学报(工程科学版), 2010, 42(1): 5-9.] |
| [12] |
Li Yu, Guo Shenglian, Zhou Yanlai, et al. Optimal flood control operation for the cascade reservoirs considering stochastic reservoir inflow hydrograph[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 13-20. [李雨, 郭生练, 周研来, 等. 考虑入库洪水随机过程的梯级水库防洪优化调度[J]. 四川大学学报(工程科学版), 2012, 44(6): 13-20.] |
| [13] |
Xie Hua, Luo Qiang, Huang Jiesheng. Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3D copula function[J]. Advances in Water Science, 2012, 23(2): 186-193. [谢华, 罗强, 黄介生. 基于三维copula函数的多水文区丰枯遭遇分析[J]. 水科学进展, 2012, 23(2): 186-193.] |
| [14] |
Li Tianyuan, Guo Shenglian, Liu Zhangjun, et al. Design flood estimation methods for cascade reservoirs[J]. Journal of Hydraulic Engineering, 2014, 45(6): 641-648. [李天元, 郭生练, 刘章君, 等. 梯级水库下游设计洪水计算方法研究[J]. 水利学报, 2014, 45(6): 641-648.] |
| [15] |
Liu Zhangjun, Guo Shegnlian, Li Tianyuan, et al. Interval estimation method for design flood region composition[J]. Journal of Hydraulic Engineering, 2015(5): 543-550. [刘章君, 郭生练, 李天元, 等. 设计洪水地区组成的区间估计方法研究[J]. 水利学报, 2015(5): 543-550.] |
| [16] |
Guo Shenglian, Yan Baowei, Xiao Yi, et al. Multivariate hydrological analysis and estimation[J]. Journal of China Hydrology, 2008, 28(3): 1-7. [郭生练, 闫宝伟, 肖义, 等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3): 1-7.] |
| [17] |
Nelson R B. An Introduction to Copulas[M]. New York: Springer, 1999.
|
 2017, Vol. 49
2017, Vol. 49


