风电叶片作为风力发电机组的关键部件之一,其使用寿命对发电效率至关重要,所以对它进行疲劳性能测试是投入使用的必需环节之一[1-4]。在疲劳性能试验中,常用的激振方法是采用单点驱动模式(液压激振法、偏心轮激振法和凸轮轴法)[5-6],使叶片持续上下振动,以此来验证结构设计的可靠性。
但是随着叶片逐渐向大功率方向发展,单点激励方式不仅在试验精度上达不到要求,激振能力更有待于提高[7],因此作者提出基于激振源联振的新型疲劳测试方法,即采用双激振源对风电叶片进行合力驱动。但是两激振源之间固存着耦合现象,为了提高解耦控制系统的动态性能和鲁棒性,研究人员提出了若干控制方法应用于风电叶片全尺寸结构测试试验。廖高华等[8]将模糊自整定PID算法应用于风电叶片全尺寸疲劳试验,完成了频率搜索和载荷谱测试过程,减小了试验误差。文献[9-10]设计了激光测距位移反馈的风电叶片结构测试闭环控制系统,并提出了趋势二分法快速定位共振频率,提高了叶片测试精度。孙宜标等[11]将定量反馈理论(QFT)与交叉耦合相结合,有效解决了外界干扰对控制精度的影响问题,取得了很好的解耦控制效果。文献[12-13]设计了基于控制器的风电叶片多节点加载系统,采用模糊控制理论研究了模糊PID控制算法,并通过联合仿真试验验证了该算法应用于叶片加载试验具有良好的解耦性和控制精度。
针对作者提出的两激振源联振耦合问题,首先对某大型风电叶片进行非控制激振试验,获得激振源联振耦合特性。然后设计了滑模变结构控制算法,并从理论上验证了其渐近稳定性。最后搭建了大型测试平台,利用该控制算法对风电叶片进行两点激振试验。试验表明,该算法能有效提高同步激振精度,从而获得很好的试验效果。
1 激振系统耦合特性试验研究 1.1 试验方案为了验证联振过程中激振源的耦合特性,首先进行风电叶片非控制激振试验。2个激振源安装在沿叶片展向相应位置的夹具上,初始转速通过变频器设定。激振系统的动力源为三相异步电机,电机驱动偏心质量块旋转从而产生离心力,带动叶片做上下振动。电机输出转轴上串联一个测速齿轮(共180个平齿),在齿顶旁边安装2个高速脉冲输出传感器,分别用于测量激振源的转速和相位,具体结果如图 1所示。参数测量原理如图 2和3所示,单位时间内通过采集齿轮脉冲个数来计算偏心质量块的转速和相位,地面固定1个激光测距仪,激光点打在叶片下表面,即叶片振幅采用激光测距仪非接触实现。
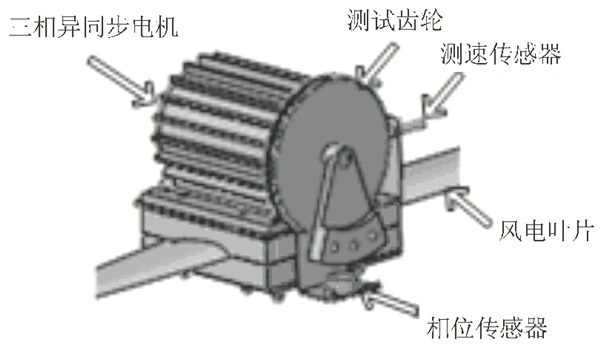 |
| 图1 激振源结构 Fig. 1 Excitation source structure |
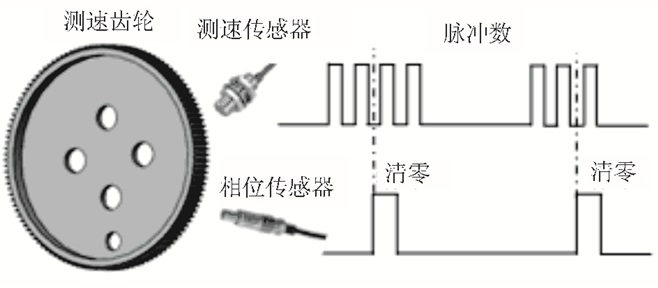 |
| 图2 激振源转速、相位与叶片振幅的测量方案 Fig. 2 Measuring program of speed, phase and amplitude of blade |
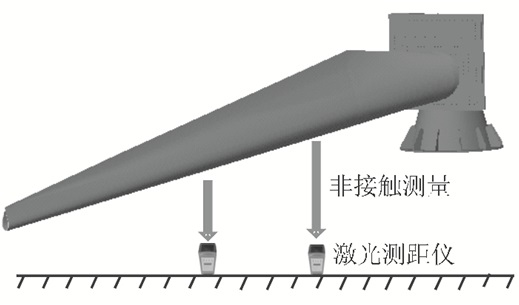 |
| 图3 叶片振幅的非接触测量方案 Fig. 3 Amplitude non-contact measurement of wind turbine blade |
1.2 耦合特性分析
理想条件(激振源几何尺寸、性能和结构等参数一致)试验时,通过变频器设定两激振源的输出轴转速均为35 r/min,初始相位差为零,2个激振源之间控制上互相独立,测试得出转速差、相位差和叶片振幅如图 4~6所示。
 |
| 图4 转速差变化曲线 Fig. 4 Speed difference variable curve |
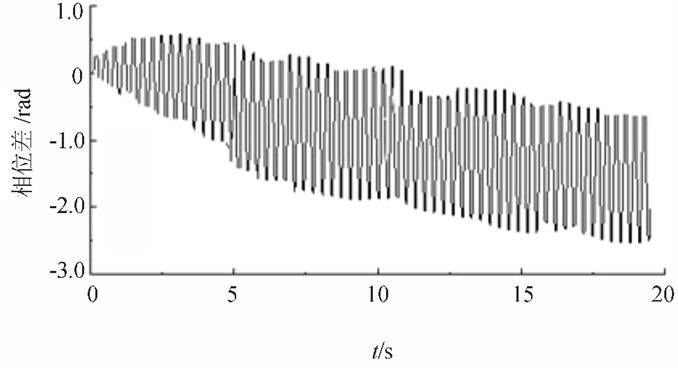 |
| 图5 相位差变化曲线 Fig. 5 Phase difference variable curve |
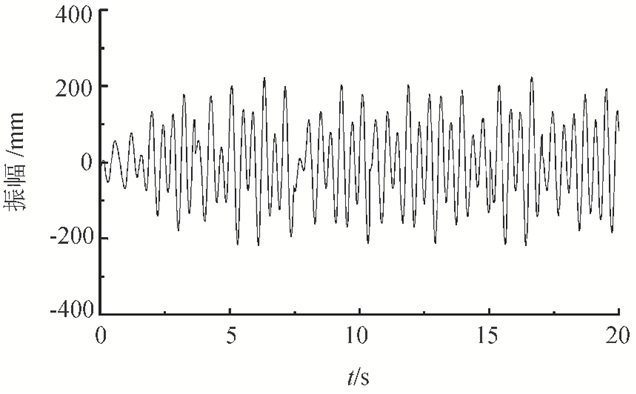 |
| 图6 叶片振幅变化曲线 Fig. 6 Amplitude variable curve of wind turbine blade |
由试验结果可知,虽然两激振源初始转速相同,但由于两激振源联振时固存着耦合特性,因此导致了2个激振源转速不一致,转速差和相位差均出现比较大的波动,转速差在±5 r/min左右波动,相位差也波动很大,最终导致叶片振幅发生紊乱,说明两激振源与叶片之间难以达到共振,影响疲劳试验的顺利进行。
2 控制策略研究 2.1 控制原理从上述非控制激振试验得出,两激振源在振动时固存着空间耦合,难以与叶片共振,达不到理想的激振效果。为了消除该耦合现象,需要设计一种解耦控制算法实现对激振系统的同步控制,从而提高疲劳试验精度。目前,同步控制方法主要有虚拟主轴控制、等同控制和偏差耦合控制等[14-15]。由于并联交叉耦合控制适用于两电机驱动,而滑模变结构控制方法在非线性耦合系统上非常有效,因此拟采用并联交叉耦合控制架构,并结合滑模变结构控制理论设计跟随误差同步控制器,控制原理如图 7所示。
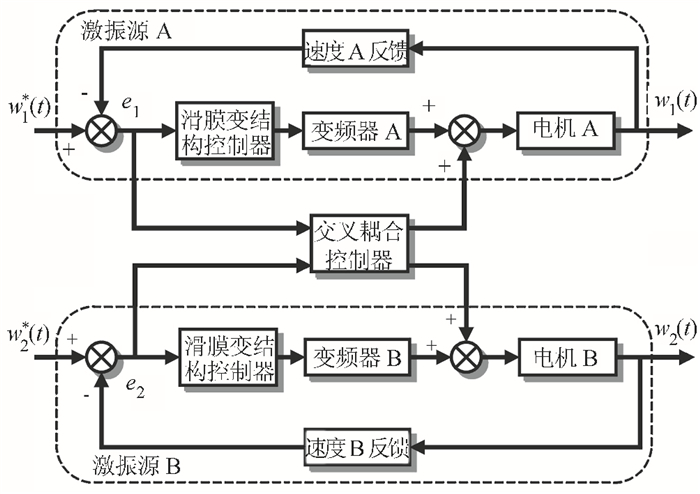 |
| 图7 滑模变结构控制系统结构 Fig. 7 Sliding-mode control system structure |
由图 7可知,wi*(t)(i=1, 2)为两激振源的设定转速, 支路上的滑模变结构控制器通过变频器实时调整激振源转速。滑膜变结构控制器以两激振源的跟踪误差ei(t)(i=1, 2)作为输入,由ei(t)(i=1, 2)的转速误差模型经过控制算法后获得误差分配模型,以误差分配模型按比例添加到激振源上的控制量作为输出,因此该控制器能够减小2个激振源的同步误差,从而实现对叶片合力激振。
2.2 滑模变结构控制算法设计在并联交叉耦合控制结构基础上,设计了滑模变结构跟随误差同步控制算法,激振源的每个控制支路均有1个跟随误差控制器,能有效地将滑动模态与干扰、参数扰动等隔离,从而使激振源的当前转速更接近设定值,从而保证同步控制精度。
三相异步电动机的运动表达式为:
| $ \dot w\left( t \right) = \frac{{n_{\rm{p}}^2{L_{\rm{m}}}}}{{J{L_{\rm{r}}}}}{i_{{\rm{sq}}}}{\psi _{\rm{r}}} - \frac{{{n_{\rm{p}}}}}{J}{T_{\rm{L}}} $ | (1) |
式中, J为转动惯量,w(t)为转子角速度,TL负载转矩,Lm为定子与转子同轴等效互感,Lr为转子等效自感,np为极对数,isq为dq坐标系下定子电流在q轴上的分量,ψr为转子磁链。
若
| $ \dot w\left( t \right) = au\left( t \right) + b{T_{\rm{L}}} $ | (2) |
考虑外干扰及参数摄动,式(2)修改为:
| $ \dot w\left( t \right) = au\left( t \right) + b{T_{\rm{L}}} + d\left( t \right) $ | (3) |
式中, d(t)为干扰项。设定d(t)有界,且|d(t)|≤D, D>0,D为常数。
跟随误差ei(t)为:
| $ {e_i}\left( t \right) = w_i^*\left( t \right) - {w_i}\left( t \right),{\rm{ }}i = 1,2 $ | (4) |
式中, wi*(t)、wi(t)(i=1, 2)分别为两激振源的设定转速与实际转速。
跟随误差的滑模面Si(t)可表示为:
| $ {S_i}\left( t \right) = {e_i}\left( t \right) + \alpha \int_0^t {{e_i}\left( \tau \right){\rm{d}}\tau } ,\alpha > 0 $ | (5) |
对式(4)求导,并将式(2)代入其中,得:
| $ {{\dot e}_i}\left( t \right) = \dot w_i^*\left( t \right) - {a_i}u\left( t \right) - {b_i}{T_L} $ | (6) |
对式(5)求导,并将式(6)代入其中,得:
| $ {{\dot S}_i}\left( t \right) = {{\dot e}_i}\left( t \right) + \alpha {e_i}\left( t \right) = \dot w_i^*\left( t \right) - {a_i}u\left( t \right) - {b_i}{T_L} + \alpha {e_i}\left( t \right) $ | (7) |
令
| $ {u_{{\rm{EQ}}i}}\left( t \right) = {({a_i})^{ - 1}}[\dot w_i^*\left( t \right) - {b_i}{T_L} + \alpha {e_i}\left( t \right)] $ | (8) |
上述等效控制函数主要为无干扰设计,若负载转矩发生变化,则采用切换控制函数实现对外负载的鲁棒控制。跟随误差导数和切换函数分别表示为:
| $ {{\dot e}_i}\left( t \right) = \dot w_i^*\left( t \right) - {a_i}u\left( t \right) - {b_i}{T_L} - {d_i}\left( t \right) $ | (9) |
| $ {u_{{\rm{SW}}i}}\left( t \right) = {({a_i})^{ - 1}}{k_i}\left( t \right){\rm{sign}}[{S_i}\left( t \right)] $ | (10) |
式中,ki(t)为控制增益函数,且ki(t)=Di+ζ, ζ>0。
式(8)和(10)构建了跟随控制器,其输出表示为:
| $ \begin{array}{l} {u_{Fi}}\left( t \right) = {u_{{\rm{EQ}}i}}\left( t \right) + {u_{{\rm{SW}}i}}\left( t \right) = \\ {({a_i})^{ - 1}}\left[ {\dot w_i^*\left( t \right) - {b_i}{T_L} + \alpha {e_i}\left( t \right) + {k_i}\left( t \right){\rm{sign}}\left[ {{S_i}\left( t \right)} \right]} \right] \end{array} $ | (11) |
对滑模面函数Si(t)求导, 可得:
| $ {{\dot S}_i}\left( t \right) = - {d_i}\left( t \right) - {k_i}\left( t \right){\rm{sign}}[{S_i}\left( t \right)] $ | (12) |
构造李雅普诺夫函数:
| $ \begin{array}{l} {V_i} = {S_i}\left( t \right){{\dot S}_i}\left( t \right) = \\ \;\;\;\;\;\;{S_i}\left( t \right)\left\{ { - {d_i}\left( t \right) - {k_i}\left( t \right){\rm{sign}}\left[ {{S_i}\left( t \right)} \right]} \right\} = \\ \;\;\;\;\;\; - {d_i}\left( t \right){S_i}\left( t \right) - {k_i}\left( t \right){S_i}\left( t \right) \le \\ \;\;\;\;\;\;{D_i}\left| {{S_i}\left( t \right)} \right| - {k_i}\left( t \right)\left| {{S_i}\left( t \right)} \right| = \\ \;\;\;\;\;\;\left( { - {k_i}\left( t \right) + D} \right)\left| {{S_i}\left( t \right)} \right| = - \zeta \left| {{S_i}\left( t \right)} \right| < 0。\end{array} $ |
因此该控制系统渐近稳定。
3 试验及结果分析 3.1 试验平台搭建为了验证滑模变结构同步控制算法的解耦有效性,对某型风电叶片(LZ2.0-54.38)进行激振控制试验。控制系统采用分布式主从网络总线构架,控制算法在主控制器采用C语言完成,从控制器控制变频器输出频率来修改电机转速,主/从控制器之间采用CAN-Bus总线实现数据双向交换。转速、相位等参数均通过从控制器的高速计数单元采集完成,激光测距仪与从控制器、主控制器与监控界面均通过RS485总线进行数据双向交互。
搭建了一套大型风电叶片全尺寸结构测试平台,用该试验平台能完成10 MW及以上的大型风电叶片静力+疲劳试验,试验参数如表 1所示。通过设定同步和异步初始转速两种工况,检验该算法对激振系统的同步控制效果。
| 表1 试验参数 Tab. 1 Test parameters |
 |
3.2 试验结果分析
在理想状态下(初始转速相同,相位差为零)进行激振试验,设定2个激振源转速均为35 r/min,初始相位差为零。激振源A的转速、两激振源相位差及叶片振幅的试验变化曲线分别如图 8~10所示。
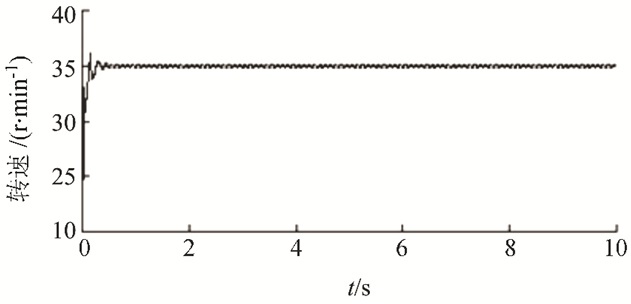 |
| 图8 激振源A转速测量曲线 Fig. 8 Speed measuring curve of excitation source A |
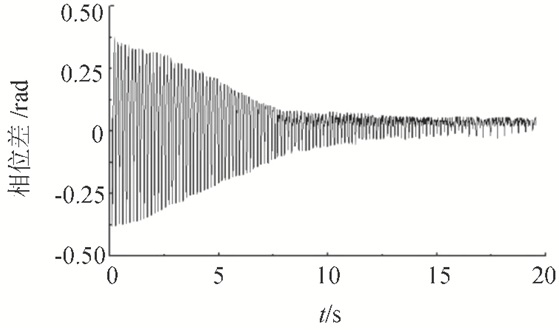 |
| 图9 相位差测量曲线 Fig. 9 Phase difference measuring curve |
 |
| 图10 振幅变化曲线 Fig. 10 Amplitude variable curve |
由图 8~10可知,在滑模变结构同步算法作用下,两激振源转速均能很好地稳定在35 r/min左右,相位基本保持同步,相位差也逐渐趋向于零,此时叶片振幅不仅最大,而且非常稳定,说明该算法的同步控制精度较高,很好地消除了两激振源固存着耦合特性,使两激振源的步调(速度和相位)一致,合力激振,所以使叶片上下的振幅最大,此时最适合进行风电叶片疲劳加载试验。
当2个激振源的初始转速分别设定为40和30 r/min,即检验两激振源在不同初始转速时控制算法的健壮性。两激振源的转速、叶片振幅测试结果如图 11~12所示。
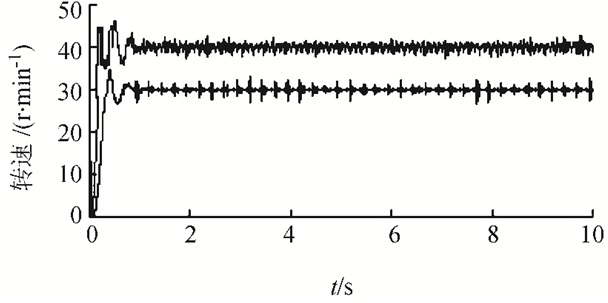 |
| 图11 设定异步转速时两激振源转速曲线 Fig. 11 Speed curve with different initial setting speed |
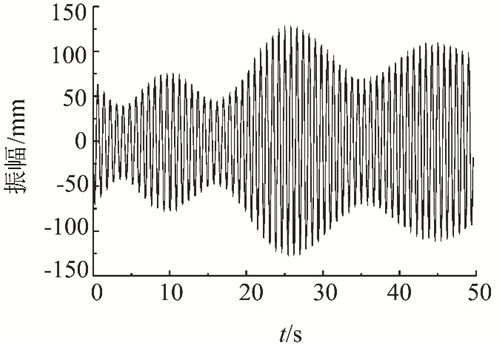 |
| 图12 设定异步转速时叶片振幅曲线 Fig. 12 Amplitude curve with different initial setting speed |
由图 11~12可知,当两激振源初始转速相差10 r/min时,虽然激振系统固存着耦合特性,但是在控制算法作用下,2个激振源的转速也能快速跟随并保持。另外,由于两个激振源与叶片不同时处于共振状态,所以叶片振幅表现为不同程度的波动,也完全符合实际试验工况。
4 结论针对风电叶片疲劳试验两点激振的非线性强耦合特性,本文采用并联交叉耦合架构,设计了滑模变结构跟随误差同步控制算法,并将该算法成功应用于两点激振试验,得出结论如下:
1) 对于非控制条件下的联振系统,试验结果表明耦合现象是固有存在着,严重影响着两激振源速度和相位的同步性,导致叶片振幅絮乱,不利于风电叶片疲劳加载试验的顺利进行。
2) 为了获得良好的同步激振效果,控制结构采用并联交叉耦合架构,设计了滑模变结构跟随误差同步控制器,并利用李雅普诺夫函数从理论上证明了该控制算法的渐近稳定性。
3) 搭建了一套10 MW级风电叶片全尺寸结构测试平台,并将设计的解耦控制算法对2种不同工况进行同步性能测试。试验结果表明该算法具有良好的同步控制效果,能很好地使2个激振源步调一致,保证了风电叶片疲劳试验的顺利进行。
| [1] |
Chen Xiao, Zhao Wei, Zhao Xiaolu, et al. Failure test and finite element simulation of a large wind turbine composite blade under static loading[J]. Energy, 2014, 7(4): 2274-2297. |
| [2] |
Zhang Leian, Wu Jianzhong. Frequency capture characteristics in wind turbine blade fatigue loading process[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(6): 248-252. [张磊安, 乌建中. 风电叶片疲劳加载过程频率俘获特性[J]. 四川大学学报(工程科学版), 2011, 43(6): 248-252.] |
| [3] |
Shi Kezhong, Zhao Xiaolu, Xu Jianzhong. Research on fatigue test of large horizontal axis wind turbine blade[J]. Acta Energiae Solaris Sinica, 2011, 32(8): 1264-1268. [石可重, 赵晓路, 徐建中. 大型风电机组叶片疲劳试验研究[J]. 太阳能学报, 2011, 32(8): 1264-1268.] |
| [4] |
Liu Deshun, Dai Juchuan, Hu Yanping, et al. Status and development trends of modern large-scale wind turbines[J]. China Mechanical Engineering, 2013, 24(1): 125-135. [刘德顺, 戴巨川, 胡燕平, 等. 现代大型风电机组现状与发展趋势[J]. 中国机械工程, 2013, 24(1): 125-135.] |
| [5] |
Liao Gaohua, Wu Jianzhong, Wang Yichun. System property analysis on chordwise fatigue loading for wind turbine blades[J]. Chinese Journal of Construction Machinery, 2014, 12(5): 450-453. [廖高华, 乌建中, 王亦春. 风机叶片弦向疲劳加载系统特性研究[J]. 中国工程机械学报, 2014, 12(5): 450-453.] |
| [6] |
Zhang Leian, Huang Xuemei. Design, modeling and test of MW wind turbine blade single-point fatigue loading system[J]. Acta Energiae Solaris Sinica, 2013, 9(34): 1556-1560. [张磊安, 黄雪梅. MW级风机叶片单点疲劳加载系统设计、建模及试验[J]. 太阳能学报, 2013, 9(34): 1556-1560.] |
| [7] |
Zhang Leian, Huang Xuemei, Yuan Guangming. Vibration coupling features for a dual-point fatigue loading system of wind turbine blade[J]. Journal of Vibration and Shock, 2015, 34(17): 83-88. [张磊安, 黄雪梅, 袁光明. 风电叶片两点疲劳加载试验振动耦合特性[J]. 振动与冲击, 2015, 34(17): 83-88.] |
| [8] |
Liao Gaohua, Wu Jianzhong, Wang Yichun. Design and experiment of fatigue loading system for full scale wind turbine blade[J]. Mechanical Science and Technology, 2016, 35(8): 1227-1232. [廖高华, 乌建中, 王亦春. 全尺寸风机叶片疲劳加载系统设计及试验研究[J]. 机械科学与技术, 2016, 35(8): 1227-1232.] |
| [9] |
Le Yunfei, Cheng Gengyong, Zhu Bilin. Study on the key parameters of wind turbine blade fatigue loading device[J]. Mechatronics, 2013, 19(1): 26-29. [乐韵斐, 成更勇, 朱碧琳. 风电叶片疲劳加载装置关键参数研究[J]. 机电一体化, 2013, 19(1): 26-29.] |
| [10] |
Wu Jianzhong, Zhou Wen, Zhou Zhijian, et al. Study on close-loop control system of wind turbine resonance rotating fatigue loading system[J]. Mechatronics, 2013, 19(11): 30-33. [乌建中, 周文, 周智健, 等. 摆锤共振型风电叶片疲劳加载系统研究[J]. 机电一体化, 2013, 19(11): 30-33. DOI:10.3969/j.issn.1007-080x.2013.11.005] |
| [11] |
Sun Yibiao, Li Mengmeng, Guo Qingding. Robust synchronization control for dual linear motors based on QFT[J]. Journal of Shenyang University of Technology, 2008, 30(3): 249-252. [孙宜标, 李萌萌, 郭庆鼎. 基于QFT的双直线电机鲁邦同步控制[J]. 沈阳工业大学学报, 2008, 30(3): 249-252.] |
| [12] |
Liao Gaohua, Jiang Shichun. Wind turbine blade static loading system and control study[J]. Machine Tool & Hydraulics, 2015, 44(5): 98-100. [廖高华, 蒋时春. 风电机组叶片静力加载系统及控制研究[J]. 机床与液压, 2015, 44(5): 98-100.] |
| [13] |
Zhang Leian, Huang Xuemei. Loading coordination control algorithm of full-scale static test for wind turbine blade[J]. Acta Energiae Solaris Sinica, 2015, 36(6): 1418-1422. [张磊安, 黄雪梅. 风电叶片全尺寸静力试验加载力协调控制算法[J]. 太阳能学报, 2015, 36(6): 1418-1422.] |
| [14] |
Zhu Shuping, Liu Dejun. Control for synchronous drive of dual linear motors based on single neural PID[J]. Micro-computer Information, 2007, 23(6): 84-85. [祝淑萍, 刘德君. 单神经元PID双主线电机同步控制[J]. 微计算机信息, 2007, 23(6): 84-85.] |
| [15] |
Wei Jianhua, Guo Kai, Xiong Yi. Synchronized motion control for multi-axis electro-hydraulic system of large equipment[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(5): 755-760. [魏建华, 国凯, 熊义. 大型装备多轴电液执行器同步控制[J]. 浙江大学学报(工学版), 2013, 47(5): 755-760.] |
 2017, Vol. 49
2017, Vol. 49

