2. 武汉大学 水工岩石力学教育部重点实验室, 湖北 武汉 430072
2. Key Lab. of Rock Mechanics in Hydraulic Structural Eng. of Ministry of Education, Wuhan Univ., Wuhan 430072, China
中国水资源空间分布极不均衡,供需矛盾突出,长距离区域调水和引水发电逐渐成为水利和水电工程建设的一个重要方向。长距离引水隧洞常常要穿越高地震烈度区,面临抗震稳定问题[1-4],特别是位于西南地区的工程,其面临的抗震问题尤为突出。此外,随着经济建设的蓬勃发展,出现了越来越多的高水头、大直径引水隧洞工程,在地震作用下会出现高内压、大质量的液体晃动,给隧洞抗震稳定带来极大的挑战。因此,研究水工隧洞的抗震问题对保证工程的安全稳定运行具有重要意义。
水工隧洞抗震稳定分析的关键在于混凝土衬砌的动态响应,因而建立科学实用的混凝土动态本构模型显得尤为重要。目前的混凝土动力本构主要有非线性弹性动力本构[5]、弹塑性动力本构[6]、黏塑性动力本构[7-8]以及动力损伤本构[9-10]等,但这些本构模型多建立在试验研究的基础上,往往因参数众多无法确定, 未能考虑动力循环加卸载作用下材料疲劳损伤特性, 迭代计算复杂严重影响计算速度和精度等原因而无法推广应用,且缺乏对衬砌结构动态损伤开裂过程的有效模拟。此外,分析水工隧洞混凝土衬砌在地震激励下的反应,需要考虑与之相互作用的水体的存在。国内外隧洞设计规范中均提出对水工隧洞的抗震设计需要考虑地震引起的动水压力,然而目前对地震作用下隧洞衬砌与流体之间的动力相互作用研究较少,对动水压力的计算和取值尚不明确。内水与衬砌的相互作用属于典型的流-固界面耦合问题[11-12],20世纪80年代以来,流-固耦合问题的研究在水工、海洋等领域内得到了发展,诸如, 储液容器中的液体晃动[13-14]、堤坝的库水波动[15-16]以及深埋海底隧洞的结构震动[17-18]等。尽管如此,将流-固耦合运用于高水头、大直径输水隧洞则少有研究,多采用附加质量的方法对水体的影响简单加以考虑,并未体现隧洞结构和流体的相互作用,对结构与流体的地震动响应特性尚不清楚。
本文在以上研究的基础上,提出了一种水工隧洞衬砌与内水耦合作用的动力显式有限元分析方法,对地震作用下混凝土衬砌结构的动力损伤演化过程进行了分析。研究成果对解决跨流域调水、水力发电、油气输送等工程领域的管道抗震安全问题, 以及提高水工隧洞的抗震设计水平具有重要参考价值。
1 混凝土衬砌动力响应分析模型混凝土作为一种非均质的预先有微裂缝的材料,在地震循环加载条件下,逐渐产生宏观缺陷,并扩展累积,表现出材料性质的劣化。本文在理论研究的基础上,结合大量室内外试验,基于静力损伤本构的基本思路,建立了混凝土材料动力损伤本构模型[19-20],并基于单元损伤状态,对其动态开裂过程进行了分析。
1.1 混凝土动力损伤演化规律基于应变空间的混凝土静力损伤本构关系为:
| $ {\sigma _{\text{s}}} = {E_{\text{s}}}\varepsilon \left( {1-{D_{\text{s}}}} \right) $ | (1) |
式中, Es为混凝土静态弹性模量,Ds为静态损伤变量。
根据大量的室内外试验[21-22],可以得到混凝土静动力本构曲线示意图如图 1所示,其中,曲线①为静力情形,②为动力情形,有关试验成果证明两者具有较高的相似性,满足几何关系式:
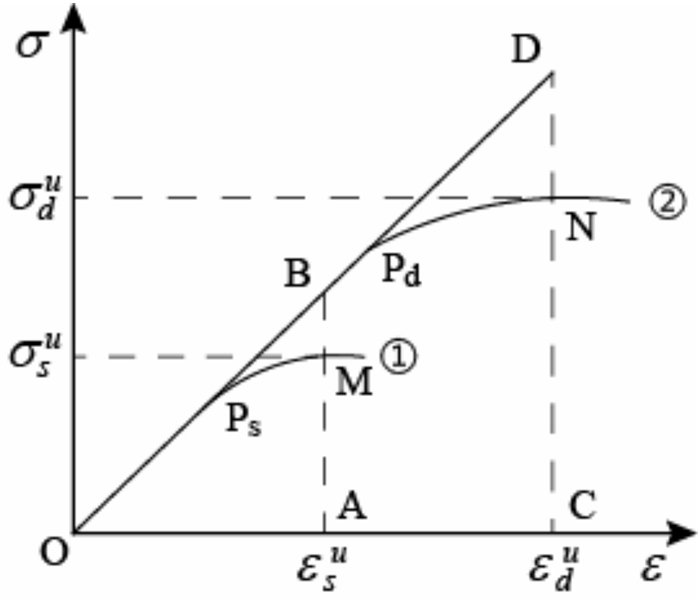 |
| 图1 混凝土静动力本构曲线 Fig. 1 Static and dynamic constitutive curves of concrete |
| $ AB/CD = OA/OC $ | (2) |
参照静力损伤本构关系式,假设动力荷载作用下混凝土本构关系为:
| $ {\sigma _{\text{d}}} = {E_{\text{d}}}\varepsilon \left( {1-{D_{\text{d}}}} \right) $ | (3) |
式中:Ed为混凝土动态弹性模量,在没有专门试验情况下,从工程偏安全角度出发,可取静态弹性模量;Dd为动态损伤变量。
根据相似关系可以得到:
| $ \left[{1-{D_{\text{d}}}\left( {\varepsilon _{\text{d}}^u} \right)} \right] = \frac{{{f_\sigma }\left( {\dot \varepsilon } \right)}}{{{f_\varepsilon }\left( {\dot \varepsilon } \right)}}\left[{1-{D_{\text{s}}}\left( {\varepsilon _{\text{s}}^u} \right)} \right] $ | (4) |
式中,
实际上,对应于静力曲线和动力曲线上每一对对应点上式均成立,但
| $ \left[{1-{D_{\text{d}}}\left( {{\varepsilon ^{\text{d}}}} \right)} \right] = \frac{{{f_\sigma }\left( {\dot \varepsilon, \varepsilon } \right)}}{{{f_\varepsilon }\left( {\dot \varepsilon, \varepsilon } \right)}}\left[{1-{D_{\text{s}}}\left( {\frac{{{\varepsilon ^{\text{d}}}}}{{{f_\varepsilon }\left( {\dot \varepsilon, \varepsilon } \right)}}} \right)} \right] $ | (5) |
为了简单近似地描述
| $ {f_\sigma }\left( {\dot \varepsilon, \varepsilon } \right) = {f_\sigma }\left( {\dot \varepsilon } \right), {f_\varepsilon }\left( {\dot \varepsilon, \varepsilon } \right) = {f_\varepsilon }\left( {\dot \varepsilon } \right) $ | (6) |
欧洲国际混凝土委员会 (CEB) 在统计众多混凝土动力加载试验结果的基础上,给出的混凝土动态拉、压应力和应变放大系数计算公式[23]:
| $ \left\{ \begin{gathered} f_\sigma ^l\left( {\dot \varepsilon } \right) = {\left( {{{\dot \varepsilon }_{\text{d}}}/{{\dot \varepsilon }_{\text{s}}}} \right)^{1.016\alpha }}, \hfill \\ f_\sigma ^y\left( {\dot \varepsilon } \right) = {\left( {{{\dot \varepsilon }_{\text{d}}}/{{\dot \varepsilon }_{\text{s}}}} \right)^{1.026\beta }}, \hfill \\ {f_\varepsilon }\left( {\dot \varepsilon } \right) = {\left( {{{\dot \varepsilon }_{\text{d}}}/{{\dot \varepsilon }_{\text{s}}}} \right)^{0.020}} \hfill \\ \end{gathered} \right. $ | (7) |
式中:
根据基本假定2) 可得到混凝土动力损伤阈值:
| $ \varepsilon _{\text{d}}^0 = {f_\varepsilon }\left( {\dot \varepsilon } \right)\varepsilon _{\text{s}}^0 $ | (8) |
由此可见:混凝土动力损伤阈值应变与静力损伤阈值应变成正比,其中静力情况的损伤阈值应变εs0分别为极限拉应变εt0和极限压应变εc0。
可以得到混凝土动力损伤本构方程:
| $ \left\{ \begin{gathered} {\sigma _{\text{d}}} = {E_{\text{d}}}\varepsilon, \varepsilon \leqslant \varepsilon _{\text{d}}^0; \hfill \\ {\sigma _{\text{d}}} = {E_{\text{d}}}\varepsilon \frac{{{f_\sigma }\left( {\dot \varepsilon } \right)}}{{{f_\varepsilon }\left( {\dot \varepsilon } \right)}}\left[{1-{D_{\text{s}}}\left( {\frac{\varepsilon }{{{f_\varepsilon }\left( {\dot \varepsilon } \right)}}} \right)} \right], \varepsilon > \varepsilon _{\text{d}}^0 \hfill \\ \end{gathered} \right. $ | (9) |
衬砌损伤开裂后,可根据非线性迭代计算得到的单元最大主应变值ε以及动力损伤系数D按式 (10) 估算衬砌单元的可能最大裂缝宽度[24]:
| $ {W_{{\text{max}}}} = \frac{{2.9\;\sqrt[3]{{bA}}\left( {1 -\rho + n\rho } \right)D\varepsilon }}{{\left( {\eta -\eta \rho + n\rho D} \right)}} $ | (10) |
式中:Wmax为裂缝宽度;A=2br,b为混凝土保护层厚度,r为钢筋间距;n=Er/Ed为钢筋和混凝土的弹性模量比值;ρ为配筋率。
1.3 混凝土静力损伤变量求解由前面的推导过程可以看出,要完善混凝土动力损伤本构模型,需要对其静力损伤变量进行合理定义和求解,下面以单轴拉伸和压缩的弹性损伤本构关系为基础,并推广到3维应力状态,给出复杂应力状态下混凝土弹性损伤本构关系表达式[25]。其中,以拉应力 (应变) 为正,压应力 (应变) 为负。
在单轴受拉应力状态下,混凝土损伤变量可以表示为:
| $ D_{\text{s}}^{\text{t}} = \left\{ \begin{gathered} 0, 0 \leqslant \varepsilon < {\varepsilon _{{\text{t0}}}}; \hfill \\ 1-\frac{{\eta {\varepsilon _{{\text{t0}}}}}}{\varepsilon }, {\varepsilon _{{\text{t0}}}} \leqslant \varepsilon < {\varepsilon _{{\text{u0}}}}; \hfill \\ 1, \varepsilon \geqslant {\varepsilon _{{\text{u0}}}} \hfill \\ \end{gathered} \right. $ | (11) |
式中:εt0为弹性极限拉应变,即拉伸损伤应变阈值;εu0为极限拉伸应变,当单轴拉伸应变达到极限值时,单元将完全损伤,达到拉伸断裂状态,一般情况下,εu0=(2~5)εt0;η(0 < η≤1) 为残余强度系数。
假定在3维应力状态下混凝土单元损伤为各向同性的,当单元满足最大拉应变准则而产生拉损时,按照文献[26]的方法,将损伤变量计算式扩展至3维,用等效应变ε代替式 (11) 中的ε,即可得到3维应力状态下的受拉损伤变量表达式。其中,等效应变可以定义为:
| $ \bar \varepsilon = \sqrt {{{\left\langle {{\varepsilon _1}} \right\rangle }^2} + {{\left\langle {{\varepsilon _2}} \right\rangle }^2} + {{\left\langle {{\varepsilon _3}} \right\rangle }^2}} $ | (12) |
式中:ε1、ε2、ε3分别为单元的3个主应变; 〈〉是一个函数式,其定义为:
| $ \left\langle x \right\rangle = \left\{ \begin{gathered} x, x \geqslant 0; \hfill \\ 0, x < 0 \hfill \\ \end{gathered} \right. $ | (13) |
类似地,在单轴压缩应力状态下,混凝土损伤变量可以表示为:
| $ D_{\text{s}}^{\text{c}} = \left\{ \begin{gathered} 0, \varepsilon > {\varepsilon _{{\text{c0}}}}; \hfill \\ 1-\frac{{\eta {\varepsilon _{{\text{c0}}}}}}{\varepsilon }, \varepsilon \leqslant {\varepsilon _{{\text{c0}}}} \hfill \\ \end{gathered} \right. $ | (14) |
式中:εc0为弹性极限压应变,即压缩损伤应变阈值;η同样为单元残余强度系数。
当混凝土单元处于复杂3维应力状态,并满足Mohr-Coulomb准则时,其弹性极限压应变εc0可以表示为[27]:
| $ {\varepsilon _{{\text{c0}}}} = \frac{1}{{{E_{\text{s}}}}}\left[{-{f_{\text{c}}} + \frac{{1 + \sin \;\varphi }}{{1-\sin \;\varphi }}{\sigma _1}-\nu \left( {{\sigma _2} + {\sigma _3}} \right)} \right] $ | (15) |
式中, fc为混凝土单轴抗压强度,φ为摩擦角,ν为泊松比。
此时,用最大压缩应变ε3来代替式 (14) 中单轴压应变ε,可以得到3维应力状态下的受压损伤变量表达式。需要指出的是:本文分别依据不同的损伤准则,提出了拉、压损伤变量的求解方法。在数值计算过程中,应保证拉伸准则具有更高地优先级。若单元满足拉伸准则,产生拉损,则不需再判断该单元是否满足摩尔-库仑准则;只有未满足拉伸准则的单元,才判定其是否满足摩尔-库仑准则。
2 内水与衬砌耦合作用分析模型根据结构受力特性,可以将水工隧洞的地震响应过程分解为两种介质有条件地震动响应过程的叠加,如图 2所示。其中,图 2(a)为水工隧洞地震动响应示意图,图 2(b)、(c)分别为衬砌与围岩结构以及内水的地震动响应示意图,f1、f2为流-固耦合界面相互作用力,F、R2为地震波输入荷载。
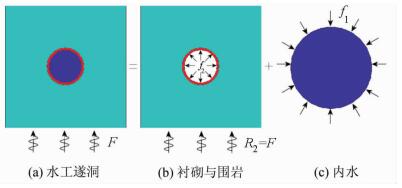 |
| 图2 水工隧洞动力响应分析模型 Fig. 2 Seismic response analysis model of hydraulic tunnel |
根据2种介质的动力有限元离散方程,结合耦合界面的应力和位移边界条件,即可推导出水工隧洞各介质的时域有限元逐步积分格式。
2.1 流体介质动力显式有限元方法本文研究针对地震波横向激励展开,因而对水工隧洞内水与衬砌结构相互作用体系进行有限元分析时,可假定有限计算区域内隧洞流体为恒定均匀流,且主要考虑流体与结构的法向相互作用, 则流体满足基于位移的流体单元基本假定。可以得到无黏性可压缩流体 (理想流体) 动力方程:
| $ {\rho _1}{{\ddot u}_{1i}} = {K_1}{u_{1j, ij}} $ | (16) |
式中, 1为流体介质,ρ1和K1分别为流体密度和体积模量,
当显式方法与多次透射边界相结合时,为了消除多次透射边界高频震荡失稳问题[28],这里引入很小的与刚度矩阵成正比的阻尼,得到无黏性可压缩流体动力方程的有限元离散方程:
| $ {{\mathit{\boldsymbol{m}}}_{1}}\ {{{\mathit{\boldsymbol{\ddot{u}}}}}_{1}}\ +{{\mathit{\boldsymbol{c}}}_{1}}\ {{{\mathit{\boldsymbol{\dot{u}}}}}_{1}}\ +{{\mathit{\boldsymbol{k}}}_{1}}{{\mathit{\boldsymbol{u}}}_{1}}\ ={{\mathit{\boldsymbol{f}}}_{1}} $ | (17) |
式中, m1、c1、k1分别为流体质量、阻尼和刚度矩阵,f1为指流-固耦合界面流体外荷载矩阵,
从稳定性和计算工作量的角度综合考虑,采用基于时域加权残数的显式逐步积分格式[29]进行求解,可以得到无黏性可压缩流体动力方程:
| $ \begin{gathered} u_{1li}^{n + 1} = u_{1li}^n + \Delta t\dot u_{1li}^n-\frac{1}{2}\Delta tm_{1l}^{-1}{c_{1li}}\left( {2\Delta t\dot u_1^n-u_1^n + } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\left. {u_1^{n - 1}} \right) - \frac{1}{2}\Delta {t^2}m_{1l}^{ - 1}\left( {{k_{1li}}u_1^n - f_{1li}^n} \right) \hfill \\ \end{gathered} $ | (18) |
| $ \begin{gathered} \dot u_{1li}^{n + 1} = \frac{1}{{\Delta t}}\left( {u_{1li}^{n + 1}-u_{1li}^n} \right)-\frac{1}{2}m_{1l}^{-1}{c_{1li}}\left( {u_1^{n + 1} - u_1^n} \right) - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\Delta tm_{1l}^{ - 1}\left( {{k_{1li}}u_1^n - f_{1li}^{n + 1}} \right) \hfill \\ \end{gathered} $ | (19) |
| $ \begin{gathered} f_{1li}^{n + 1} = \frac{2}{{\Delta t}}{m_{1l}}\left[{\dot u_{1li}^{n + 1}-\frac{1}{{\Delta t}}\left( {u_{1li}^{n + 1}-u_{1li}^n} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{\Delta t}}{c_{1li}}\left( {u_1^{n + 1} -u_1^n} \right) + {k_{1li}}u_1^{n + 1} \hfill \\ \end{gathered} $ | (20) |
式中, l为流体节点编号,i为节点坐标轴方向。
2.2 固体介质动力显式有限元方法对于固体介质,根据经典线性弹性动力学理论,在不考虑体力的情况下,得到线弹性固体介质动力学方程:
| $ \left( {\lambda + \mu } \right){{\ddot u}_{2j, ij}} + \mu {u_{2j, ij}} = {\rho _2}{{\ddot u}_{2i}} $ | (21) |
式中, 2为固体介质,λ和μ为拉梅常数,ρ2为固体密度。
根据Galerkin法,将连续介质动力学方程空间离散化,并采用Rayleigh阻尼假定,得到固体介质3维有限元运动方程:
| $ {\mathit{\boldsymbol{m}}_2}\;{{\mathit{\boldsymbol{\ddot u}}}_2} + {\mathit{\boldsymbol{c}}_2}\;{{\mathit{\boldsymbol{\dot u}}}_2}\; + {\mathit{\boldsymbol{k}}_2}{\mathit{\boldsymbol{u}}_2}\; = {\mathit{\boldsymbol{f}}_2} + {\mathit{\boldsymbol{R}}_2} $ | (22) |
式中,m2、c2、k2分别为固体质量、阻尼和刚度矩阵,f2、R2分别为流-固耦合界面固体外荷载矩阵和地震波输入荷载矩阵。
同样采用基于时域加权残数的显式逐步积分格式进行求解,得到:
| $ \begin{gathered} u_{2li}^{n + 1} = u_{2li}^n + \Delta t\dot u_{2li}^n-\frac{1}{2}\Delta tm_{2l}^{-1}{c_{2li}}\left( {2\Delta t\dot u_2^n-u_2^n + u_2^{n - 1}} \right) - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\Delta {t^2}m_{2l}^{ - 1}\left( {{k_{2li}}u_2^n - f_{2li}^n - R_{2li}^n} \right)\; \hfill \\ \end{gathered} $ | (23) |
| $ \begin{gathered} \dot u_{2li}^{n + 1} = \;\frac{1}{{\Delta t}}\left( {u_{2li}^{n + 1}-u_{2li}^n} \right)-\frac{1}{2}m_{2l}^{-1}{c_{2li}}\left( {u_2^{n + 1} - u_2^n} \right) - \hfill \\ \;\;\;\;\;\;\;\frac{1}{2}\Delta tm_{2l}^{ - 1}\left( {{k_{2li}}u_2^n - f_{2li}^{n + 1} - R_{2li}^{n + 1}} \right) \hfill \\ \end{gathered} $ | (24) |
| $ \begin{gathered} f_{2li}^{n + 1} = \frac{2}{{\Delta t}}{m_{2l}}\left[{\dot u_{2li}^{n + 1}-\frac{1}{{\Delta t}}\left( {u_{2li}^{n + 1}-u_{2li}^n} \right)} \right] + \hfill \\ \;\;\;\;\;\;\frac{1}{{\Delta t}}{c_{2li}}\left( {u_2^{n + 1} -u_2^n} \right) + {k_{2li}}u_2^{n + 1} -R_{2li}^{n + 1} \hfill \\ \end{gathered} $ | (25) |
对于流体介质和固体介质,均可引入如下初始条件:
| $ {u^0} = {{\dot u}^0} = 0, \ddot u_{li}^0 = m_l^{-1}\left( {f_{li}^0-{c_{li}}{{\dot u}^0}-{k_{li}}{u^0}} \right) $ | (26) |
| $ u_{li}^{-1} = u_{li}^0-\Delta t\dot u_{li}^0 + \frac{1}{2}\Delta {t^2}\ddot u_{li}^0 $ | (27) |
理想流体介质和衬砌介质交界面边界条件可以表述如下:
1) 交界面法向运动连续,即:
| $ {u_{1rz}}\; = {u_{2rz}}, {{\dot u}_{1rz}} = \;{{\dot u}_{2rz}} $ | (28) |
2) 交界面法向应力连续,即:
| $ {f_{1rz}} + {f_{2rz}} = 0 $ | (29) |
3) 交界面切向应力为零,即:
| $ {f_{1rk}} = {f_{2rk}} = 0 $ | (30) |
式中, r为交界面节点编号,z为交界面节点法向,k为交界面节点切向。
将交界面边界条件式 (28)~(30) 代入流体和固体介质位移、速度表达式 (18)~(19) 及 (23)~(24),得到n+1时刻流体介质和衬砌介质交界面节点的法向位移和速度:
| $ \left\{ \begin{align} & u_{1rz}^{n+1}=u_{1rz}^{n}+\Delta t\dot{u}_{1rz}^{n}-\frac{1}{2}\Delta {{t}^{2}}{{\left( {{m}_{1r}}+{{m}_{2r}} \right)}^{-1}}. \\ & \ \ \ \ \ \ \ \ \left( {{k}_{1r}}u_{1}^{n}+{{k}_{2r}}u_{2}^{n} \right)-\frac{1}{2}\Delta t{{\left( {{m}_{1r}}+{{m}_{2r}} \right)}^{-1}}. \\ & \ \ \ \left[ {{c}_{1r}}\left( 2\Delta t\dot{u}_{1}^{n}-u_{1}^{n}+u_{1}^{n-1} \right)+{{c}_{2r}}\left( 2\Delta t\dot{u}_{2}^{n}-u_{2}^{n}+u_{2}^{n-1} \right) \right], \\ & u_{2rz}^{n+1}=u_{1rz}^{n+1} \\ \end{align} \right. $ | (31) |
| $ \left\{ \begin{gathered} \dot u_{1rz}^{n + 1} = \frac{1}{{\Delta t}}\left( {u_{1rz}^{n + 1}- u_{1rz}^n} \right)- \frac{1}{2}\Delta t{\left( {{m_{1r}} + {m_{2r}}} \right)^{- 1}}. \hfill \\ \;\;\;\;\;\;\;\;\;\left( {{k_{1r}}u_1^{n + 1} + {k_{2r}}u_2^{n + 1}} \right) - \frac{1}{2}{\left( {{m_{1r}} + {m_{2r}}} \right)^{ - 1}}. \hfill \\ \;\;\;\;\;\;\;\;\;\left[{{c_{1r}}\left( {u_1^{n + 1}-u_1^n} \right) + {c_{2r}}\left( {u_2^{n + 1}-u_2^n} \right)} \right], \hfill \\ \dot u_{2rz}^{n + 1} = \dot u_{1rz}^{n + 1} \hfill \\ \end{gathered} \right. $ | (32) |
根据交界面节点的法向位移和速度分别带入式 (20) 和 (25) 即可求解下一时步交界面节点荷载。需要指出的是,本文只考虑结构与内水相互作用的法向荷载,忽略切向荷载作用,且初始时刻交界面法向荷载为静态条件下的内水压力值。
3 工程实例 3.1 工程概况某水电站位于云南省西部澜沧江流域,其引水发电系统全长7 126 m,沿线地面波状起伏,经过不同的地质构造区,本文选取2+500.00 m~2+680.00 m段进行隧洞结构地震动响应分析。该隧洞段位于引水系统中部, 地震烈度为Ⅶ,采用圆形断面结构,开挖洞径10.2 m,衬砌后过水洞径9.0 m,隧洞中心高程为32.00 m,洞室埋深241.67 m,最大内水水头135.24 m,采用钢筋混凝土结构,其中衬砌厚度为0.6 m,采用C25混凝土。
水工隧洞3维有限元模型均采用八节点六面体单元,共剖分了59 584个等参单元,64 003个节点。其中, 混凝土衬砌单元2 688个,流体单元5 264个,内水与衬砌接触面为流-固耦合界面,共696个节点。模型范围及坐标系:X方向从-90.0 m到90.0 m,与洞轴线垂直;Y方向从-90.0 m到90.0 m,与洞轴线重合,顺水流为正;Z方向从-48.0 m到273.67 m,与大地坐标系平行。水工隧洞整体3维有限元模型如图 3所示,隧洞结构局部有限元模型和监测点布置如图 4所示。其中,选取Y=0平面为监测断面,选取了该断面上衬砌结构半周的顶拱、腰拱以及底拱部位的A、B、C 3个监测点。
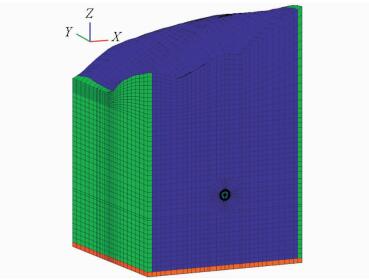 |
| 图3 水工隧洞整体有限元模型 Fig. 3 Completefinite element model of hydraulic tunnel |
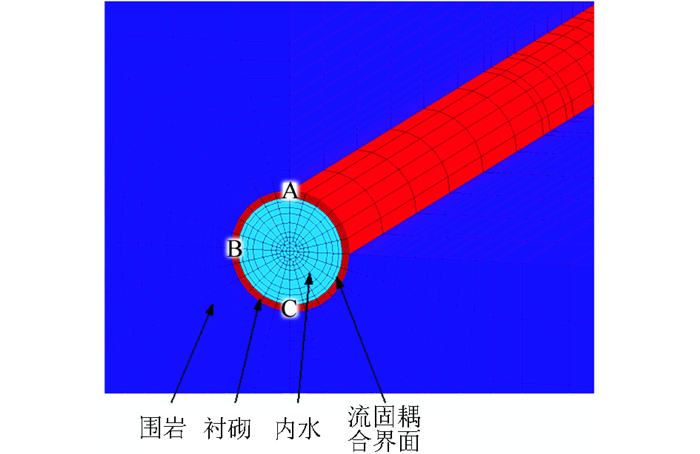 |
| 图4 局部有限元模型和监测点 Fig. 4 Local finite element model and monitoring points |
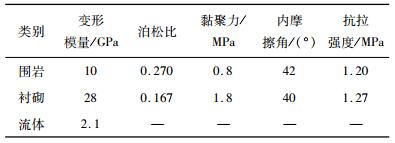
初始地应力场通过实测地应力反演获得,隧洞区域应力在-5~-7 MPa范围内,属于偏低地应力场。水工隧洞区域岩体以Ⅲ类为主,材料力学参数取值见表 1。
| 表1 材料力学参数取值 Tab. 1 Mechanical parameters of materials |
 |
需要指出的是,在进行水工隧洞地震响应分析前,应先进行隧洞的开挖以及衬砌支护工况的3维有限元静力计算。
3.2 计算条件计算程序采用课题组自主开发的3维弹塑性损伤动力有限元程序[30],并在此基础上进行改进。模型边界材料本构与岩体保持一致,并在左右采用自由场边界条件以减少地震波在模型边界上的反射,底部采用黏弹性人工边界条件以吸收边界上的入射波,具体设置方式参考文献[31]。
地震波输入选用EI-Centro SN加速度时程 (最大加速度为3.417 m/s2),在进行水工隧洞地震反应分析时,根据场地抗震设防烈度将地震峰值加速度调整为0.17g,地震持时取前20 s,其中考虑地震沿隧洞横向 (X轴方向) 激振。经处理后得到模型底部输入波 (X向) 加速度时程曲线如图 5所示。
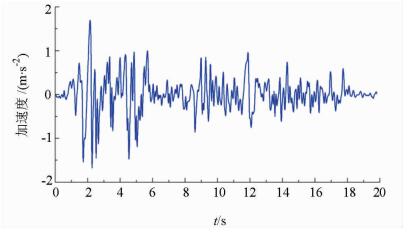 |
| 图5 输入地震波X向加速度时程曲线 Fig. 5 X-acceleration-time history curve of input seismic wave |
3.3 计算结果分析 3.3.1 衬砌结构位移时程分析
衬砌结构监测点X向位移时程曲线如图 6所示。
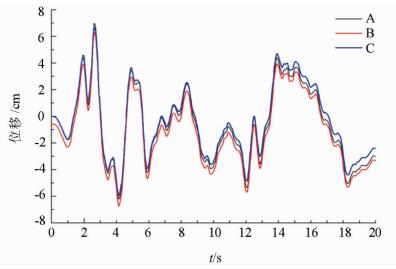 |
| 图6 监测点X向位移时程曲线 Fig. 6 X-displacement-time history curves of monitoring points |
由图 6可以看出:1) 顶拱、底拱和腰拱的动力时程曲线基本一致;2) 监测点X向位移最大值出现在2.56 s,最大值为7.08 cm,最小值出现在4.12 s,最小值为-6.88 cm;3) 监测点位移同时出现峰值和谷值,表明水工隧洞各部位处于同步震动状态。
对比各监测点的位移时程曲线可以看出,考虑动水压力作用时,腰拱部位位移明显小于顶拱和底拱,最大位移差值达到10 mm,该部分位移差值正好表征隧洞衬砌结构的相对变形,对结构受力产生重要影响。同时,表明隧洞腰部受动水压力影响较大,动水压力阻碍了衬砌结构的变形。
3.3.2 衬砌结构应力时程分析由于混凝土的抗压强度远大于抗拉强度,地震作用下衬砌结构的损伤破坏主要为拉裂破坏。本文主要分析地震作用下衬砌结构的最大主应力变化规律,得到衬砌结构监测点最大主应力时程曲线如图 7所示。
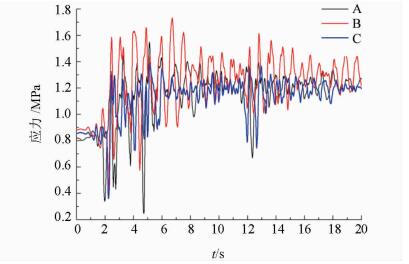 |
| 图7 监测点最大主应力时程曲线 Fig. 7 Maximum principal stress-time curves of monitoring points |
由各监测点最大主应力时程曲线 (图 7) 可以看出:1) 在初始静水压力作用下,衬砌结构的最大主应力达0.8~0.9 MPa;2) 衬砌结构的最大主应力迅速增大,并逐渐超过混凝土抗拉强度,其中,隧洞腰拱部位受动水压力影响较大,衬砌应力增加较大,损伤破坏严重;3) 动水压力对衬砌结构的受力影响较大,考虑地震作用下水工隧洞内水与结构的耦合作用对隧道抗震设计具有重要意义。
3.3.3 衬砌结构损伤与开裂分析采用本文提出的混凝土动力响应分析模型, 模拟地震作用下衬砌结构的损伤开裂过程, 得到地震完成后衬砌结构损伤系数分布 (图 8) 以及内外层衬砌最大裂缝宽度包络图 (图 9)。
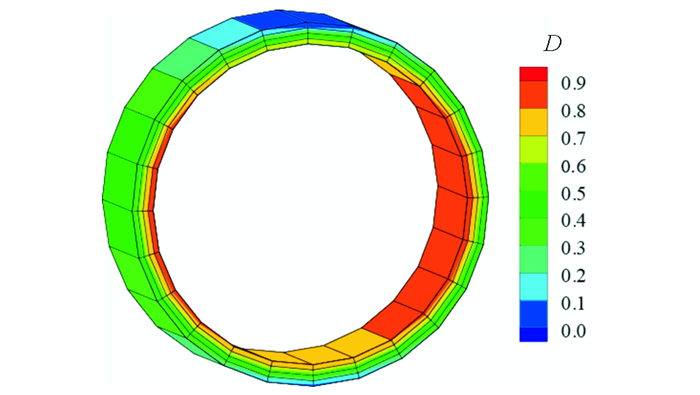 |
| 图8 监测断面衬砌结构损伤系数 Fig. 8 Damage coefficient distribution of lining structure at the monitoring section |
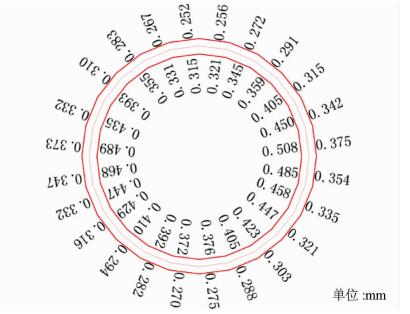 |
| 图9 监测断面衬砌结构开裂图 Fig. 9 Crack width distribution of lining structure at the monitoring section |
由图 8可以看出,在地震和动水压力共同作用下,衬砌结构最大主应力基本均超过混凝土的抗拉强度,进入损伤阶段,且衬砌结构破坏区逐渐由腰拱向顶部和底部扩展。由于地震作用下结构以弹性变形为主,动水压力成为影响衬砌损伤破坏的关键。其中,腰拱部位受动水压力影响,损伤程度最大,部分区域进入损伤断裂阶段,并逐渐向腰拱两端扩展。
由图 9可以看出,随着衬砌结构进入损伤演化阶段,开裂破坏随之产生,其最大裂缝宽度分布规律与损伤系数一致。监测断面衬砌裂缝宽度在0.25~0.5 mm范围内,其中, 腰拱部位裂缝宽度最大,达到0.5 mm,并逐渐向顶部和底部扩展。对比内外层衬砌结构裂缝宽度可以看出,内层衬砌受内水作用影响较大,明显大于外层衬砌,表明衬砌结构与内水直接作用部位破坏严重,是抗震设计的薄弱环节。
4 结论基于水工隧洞混凝土衬砌结构地震动响应力学机制,提出了一种考虑内水与衬砌耦合作用的混凝土衬砌动力响应分析模型,结合某水电站引水隧洞工程实例,对地震作用下混凝土衬砌结构的动力损伤开裂过程进行了分析,可以得出如下结论:
1) 地震作用下监测点的位移时程曲线与输入地震波位移时程曲线相类似,水工隧洞各部位处于同步震动状态。考虑动水压力作用时,腰拱部位位移明显小于顶拱和底拱部位,产生较大的相对变形,对结构受力产生重要影响。
2) 在地震和动水压力作用下,衬砌结构的最大主应力迅速增大,逐渐超过混凝土抗拉强度,其中,腰拱部位受动水压力影响较大,衬砌应力增加明显,损伤破坏严重。
3) 隧洞腰拱部位损伤与开裂破坏严重,并逐渐向两端扩展,与内水直接作用的内层衬砌结构是抗震设计的薄弱环节。
| [1] |
Yashiro K, Kojima Y, Shimizu M. Historical earthquake damage to tunnels in Japan and case studies of railway tunnels in the 2004 Niigataken-Chuetsu earthquake[J]. Quarterly Report of RTRI, 2007, 48(3): 136-141. DOI:10.2219/rtriqr.48.136 |
| [2] |
Wang W L, Wang T T, Su J J, et al. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi earthquake[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 133-150. DOI:10.1016/S0886-7798(01)00047-5 |
| [3] |
Li Tianbin. Damage to mountain tunnels related to the Wenchuan earthquake and some suggestions for a seismic tunnel construction[J]. Bulletin of Engineering Geology and the Environment, 2012, 71(2): 297-308. DOI:10.1007/s10064-011-0367-6 |
| [4] |
Wang Zhengzheng, Gao Bo, Jiang Yuanjun, et al. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan earthquake[J]. Science in China (Technological Sciences), 2009, 52(2): 546-558. DOI:10.1007/s11431-009-0054-z |
| [5] |
Tedesco J W, Powell J C, Ross C A, et al. A strain-rate-dependent concrete material model for ADINA[J]. Computers and Structures, 1997, 64(5/6): 1053-1067. |
| [6] |
Winnicki A, Cichon C. Plastic model for concrete in plane stress state[J]. Journal of Engineering Mechanics, 1998, 124(6): 591-602. DOI:10.1061/(ASCE)0733-9399(1998)124:6(591) |
| [7] |
Xiao Shiyun, Li Hongnan, Du Rongqiang, et al. Four-parameter dynamic constitutive model of concrete[J]. Journal of Harbin Institute of Technology, 2006, 38(10): 1754-1757. [肖诗云, 李宏男, 杜荣强, 等. 混凝土四参数动态本构模型[J]. 哈尔滨工业大学学报, 2006, 38(10): 1754-1757.] |
| [8] |
Pandey A K, Kumar R, Paul D K, et al. Strain rate model for dynamic analysis of reinforced concrete structures[J]. Journal of Structural Engineering, 2006, 132(9): 1393-1401. DOI:10.1061/(ASCE)0733-9445(2006)132:9(1393) |
| [9] |
Shkolnik I E. Influence of high strain rates on stress-strain relationship, strength and elastic modulus of concrete[J]. Cement and Concrete Composites, 2008, 30(10): 1000-1012. DOI:10.1016/j.cemconcomp.2007.10.001 |
| [10] |
Li Qingbin, Zhang Chuhan, Wang Guanglun. Dynamic damage constitutive model of concrete in uniaxial tension and compression[J]. Journal of Hydraulic Engineering, 1994, 12: 55-60. [李庆斌, 张楚汉, 王光纶. 单轴状态下混凝土的动力损伤本构模型[J]. 水利学报, 1994, 12: 55-60.] |
| [11] |
Wang Jinting, Du Xiuli, Zhao Chenggang, et al. Explicit finite element scheme for dynamic analyses of wave propagation in multi-layered media[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 75-79. [王进廷, 杜修力, 赵成刚, 等. 分层介质中波动传播分析的显式有限元法[J]. 岩石力学与工程学报, 2003, 22(1): 75-79.] |
| [12] |
Wang Jinting, Du Xiuli, Zhao Chenggang. Explicit finite element method for dynamic analyses of fluid-saturated porous solid[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(8): 1199-1204. [王进廷, 杜修力, 赵成刚. 液固两相饱和介质动力分析的一种显式有限元法[J]. 岩石力学与工程学报, 2002, 21(8): 1199-1204.] |
| [13] |
Wang Tongtao, Yang Chunhe, Yan Xiangzhen, et al. Dynamic response of underground gas storage salt cavern under seismic loads[J]. Tunnelling and Underground Space Technology, 2014, 43(7): 241-252. |
| [14] |
Hashemi S, Saadatpour M M, Kianoush M R. Dynamic behavior of flexible rectangular fluid containers[J]. Thin-Walled Structures, 2013, 66(3): 23-38. |
| [15] |
Du Xiuli, Wang Jinting. Seismic response analysis of arch dam-water-rock foundation systems[J]. Earthquake Engineering and Engineering Vibration, 2004, 3(2): 283-288. DOI:10.1007/BF02858242 |
| [16] |
Bouaanani N, Renaud S. Effects of fluid-structure interaction modeling assumptions on seismic floor acceleration demands within gravity dams[J]. Engineering Structure, 2014, 67: 1-18. DOI:10.1016/j.engstruct.2014.02.004 |
| [17] |
Nateghi R, Kiany M, Gholipouri O. Control negative effects of blasting waves on concrete of the structures by analyzing of parameters of ground vibration[J]. Tunnelling and Underground Space Technology, 2009, 24(6): 608-616. DOI:10.1016/j.tust.2009.04.004 |
| [18] |
Cheng Xuansheng, Xu Weiwei, Yue Caiquan, et al. Seismic response of fluid-structure interaction of undersea tunnel during bidirectional earthquake[J]. Ocean Engineering, 2014, 75(1): 64-70. |
| [19] |
宋玉普. 混凝土的动力本构关系和破坏准则[M]. 北京: 科学出版社, 2013.
|
| [20] |
Zhou X Q, Hao H. Modelling of compressivebehaviour of concrete-like materials at high strain rate[J]. International Journal of Solids and Structures, 2008, 45(17): 4648-4661. DOI:10.1016/j.ijsolstr.2008.04.002 |
| [21] |
Bischoff P H, Perry S H. Compressive behavior of concrete at high strain rates[J]. Materials and Structures, 1991, 24(6): 425-450. DOI:10.1007/BF02472016 |
| [22] |
Brooks J J, Samaraie N H. Influence of rate of stressing on tensile stress-strain behavior of concrete[M]. Essex, England: Elsevier Science Publisher, 1989.
|
| [23] |
Chen Jianyun, Lin Gao, Hu Zhiqiang. Seismic analysis of arch dam with joints based on a new strain-rate-dependant plastic damage model[J]. Chinese Journal of Computational Mechanics, 2004, 21(1): 45-49. [陈建云, 林皋, 胡志强. 考虑混凝土应变率变化的高拱坝非线性动力响应研究[J]. 计算力学学报, 2004, 21(1): 45-49.] |
| [24] |
Yuan Jinliang, Xiao Ming, Fu Zhihao. Numerical analysis on lining structure of restricted cylindric surge chamber in rock masses with steep obliquity[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1296-1300. [袁金亮, 肖明, 傅志浩. 陡倾角岩体中阻抗式圆形调压井衬砌结构数值分析[J]. 岩石力学与工程学报, 2004, 23(8): 1296-1300.] |
| [25] |
Wang S Y, Sun L, Yang C, et al. Numerical study on static and dynamic fracture evolution around rock cavities[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(4): 262-276. DOI:10.1016/j.jrmge.2012.10.003 |
| [26] |
Tang C A, Kaiser P K. Numerical simulation of cumulative damage and seismic energy release during brittle rock failure—Part Ⅰ:Fundamentals[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 113-121. DOI:10.1016/S0148-9062(97)00009-0 |
| [27] |
Zhu Wancheng, Tang Chun'an. Micromechanical model for simulating the fracture process of rock[J]. Rock Mechanics and Rock Engineering, 2004, 37(1): 25-56. DOI:10.1007/s00603-003-0014-z |
| [28] |
廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002.
|
| [29] |
Wang Jinting, Du Xiuli. An explicit difference method for dynamic analysis of a structure system with damping[J]. Engineering Mechanics, 2002, 19(3): 109-111. [王进廷, 杜修力. 有阻尼体系动力分析的一种显式差分法[J]. 工程力学, 2002, 19(3): 109-111.] |
| [30] |
Zhang Zhiguo, Xiao Ming, Chen Juntao. Simulation of earthquake disaster process of large-scale underground caverns using three-dimensional dynamic finite element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 510-523. [张志国, 肖明, 陈俊涛. 大型地下洞室地震灾变过程三维动力有限元模拟[J]. 岩石力学与工程学报, 2011, 30(3): 510-523.] |
| [31] |
Zhang Zhiguo, Chen Juntao, Xiao Ming. Artificial boundary setting for dynamic time-history analysis of deep buried underground caverns in earthquake disaster[J]. Disaster Advances, 2012, 5(4): 1136-1142. |
 2017, Vol. 49
2017, Vol. 49

