磁瓦是永磁电机中产生恒定磁势源的核心组成部件,其品质对电机的性能和使用寿命均有至关重要的影响。目前,中国国内磁瓦表面缺陷的检测工作均由人工视觉完成。由于磁瓦表面加工精度低,生产批量大等原因,人工检测存在稳定性差,效率低和成本高等问题,这对提高磁瓦产品品质,降低生产成本造成了不利影响[1]。因此,磁瓦表面缺陷检测工序的自动化势在必行。
近年来,国内外学者提出了大量基于机器视觉的表面缺陷检测方法。Koch等[2]将机器视觉应用于沥青路面缺陷的自动检测中。通过基于直方图的阈值法将原始路面图像分为潜在缺陷区域和正常区域,再比较两者纹理特征以确定缺陷区域。该方法适合于路面状况评估,但无法有效捕捉图像细节。Li等[3]提出了将下包络线韦伯对比度检测法应用于钢棒表面凹坑缺陷的检测。该方法可准确地检测出是否存在凹坑缺陷,但无法对凹坑进行定量检测,且不适用于其他类型的缺陷。贺振东等[4]通过建立钢轨表面图像背景模型,提出了基于背景差分的高铁钢轨表面缺陷检测方法。该方法克服了铁轨表面缺陷检测过程中光照变化,反射不均匀和特征少等困难,但要求原始钢轨表面图像具备较高的一致性。关于磁瓦表面缺陷检测,余永维等[5]设计了一种新的自适应形态学滤波器,通过逐行自适应形态学滤波模拟出背景,进而使用背景差分得到缺陷。该方法可快速检测出磁瓦表面缺陷,但未考虑垂直于扫描线方向的邻域关系,有可能将孤立噪声点误检测为缺陷。Li等[6]将快速离散曲线波变换和纹理分析应用到磁瓦表面裂纹缺陷的检测中,有效地抑制了磁瓦图像中的磨削纹理,并对长于0.8 mm的裂纹取得了理想的检测效果,但该方法对图像获取环节的光照条件要求严格。Xie等[7]提出了结合Shearlet变换和自适应阈值面的磁瓦表面缺陷检测方法,有效地去除了原始磁瓦图像中的不均匀背景,增强了缺陷和正常区域之间的对比度。但该方法未对噪声进行针对性处理,降低了检测结果的准确性。
针对以上算法中存在的问题,作者提出了一种基于非下采样Shearlet变换 (non-subsampled Shearlet transform,NSST) 的磁瓦表面缺陷检测方法。利用NSST的多尺度多方向分解特性和对细节良好的表达能力,对图像背景、噪声和目标缺陷等特征的分布进行了分析,进而提出了基于自适应阈值面的非均匀背景校正方法和基于Shearlet系数方差和能量的缺陷识别方法。通过与现有算法进行实验对比,验证了本文方法的优势,为实现磁瓦表面缺陷检测的自动化提供了有价值的参考。
1 非下采样Shearlet变换原理Shearlet是一种在传统仿射系统的基础上,对函数进行伸缩、剪切和平移操作生成基函数,从而实现多分辨率和多方向分析的图像表示方法[8]。在2维情况下,具有合成膨胀的仿射构造系统构造如下[9-10]:
| $ \{{{\psi }_{j, l, k}}\left( x \right)=|det~\mathit{\boldsymbol{A}}{{|}^{j/2}}\psi ({{\mathit{\boldsymbol{S}}}^{l}}{{\mathit{\boldsymbol{A}}}^{j}}x-k):j, l\in \mathbb{Z}, k\in {{\mathbb{Z}}^{2}}\} $ | (1) |
式中: ψ为基函数,且满足ψ∈L2(ℝ2); j、l和k分别表示变换的尺度因子、方向因子和平移因子;A和S均为2×2可逆矩阵;A为各向异性膨胀矩阵,决定分解尺度;S为剪切矩阵,决定分解方向,且满足|det S|=1。A和S取值如下:
| $ \mathit{\boldsymbol{A}}=\left[\begin{matrix} 4 & 0 \\ 0 & 2 \\ \end{matrix} \right], \mathit{\boldsymbol{S}}=\left[\begin{matrix} 1 & 1 \\ 0 & 1 \\ \end{matrix} \right] $ | (2) |
对于任意ξ=(ξ1, ξ2)∈2,ξ1≠0,令
| $ {{{\hat{\psi }}}^{(0)}}(\xi )={{{\hat{\psi }}}^{(0)}}({{\xi }_{1}}, {{\xi }_{2}})={{{\hat{\psi }}}_{1}}({{\xi }_{1}}){{{\hat{\psi }}}_{2}}({{\xi }_{2}}/{{\xi }_{1}}) $ | (3) |
式中,
| $ \left\{ \begin{align} &\text{supp}\ {{{\hat{\psi }}}_{1}}\ \subset \left[-1/2, -1/16 \right]\ \cup \ \left[1/16.1/2 \right]; \\ &\text{supp}\ {{{\hat{\psi }}}_{2}}\ \subset \ \left[-1, 1 \right] \\ \end{align} \right. $ | (4) |
| $ \left\{ \begin{align} &\sum\limits_{j\ge 0}{|{{{\hat{\psi }}}_{1}}\left( {{2}^{-2j}}\omega \right){{|}^{2}}=1}, |\omega |\ge 1/8; \\ &\sum\limits_{l=-2j}^{2j-1}{|{{{\hat{\psi }}}_{2}}\left( {{2}^{j}}\omega-l \right){{|}^{2}}=1}, |\omega |\le 1 \\ \end{align} \right. $ | (5) |
则函数ψj, l, k的频域支撑如下:
| $ \begin{align} &\text{supp}\ j, l, {{k}^{\left( 0 \right)}}\ \subset \ \{\left( {{\xi }_{1}}, {{\xi }_{2}} \right):{{\xi }_{1}}\in \left[-{{2}^{2j-1}}, -{{2}^{2j-4}} \right]\ \cup \ \\ &\left[{{2}^{2j-4}}, {{2}^{2j-1}} \right], |{{\xi }_{2}}/{{\xi }_{1}}+l{{2}^{-j}}|\le {{2}^{-j}}\} \\ \end{align} $ | (6) |
即
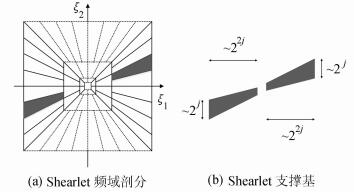 |
| 图1 Shearlet频域剖分和支撑基 Fig. 1 Shearlet frequency subdivision and frequency support bases |
离散NSST由两部分实现[11]:多尺度分解和多方向分解。多尺度分解主要由非下采样拉普拉斯金字塔 (non-subsampled Laplacian pyramid,NSLP) 完成,原始图像经过j级NSLP分解,得到j+1个大小与原始图像相同的子带图像,包括1个低频子带和j个高频子带。多方向分解由改进的剪切滤波器 (improved shear filter,ISF) 完成,由于ISF去除了临界取样操作,高频子带图像经过l级多方向分解得到2l个大小与原图像相同的多方向子带。2层NSST的分解过程如图 2所示。相较于其他传统多尺度分析方法,NSST不仅具备多尺度和多方向等特点,而且具备各向异性、平移不变性和最优稀疏等特性[12-13]。
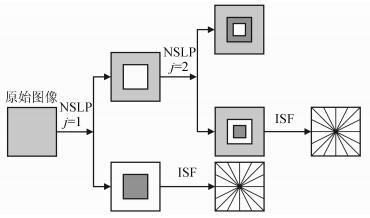 |
| 图2 2层NSST分解示意图 Fig. 2 Diagram of two levels NSST |
2 基于NSST的磁瓦表面缺陷检测算法 2.1 缺陷特征提取
图 3为一幅磁瓦表面缺陷图像。
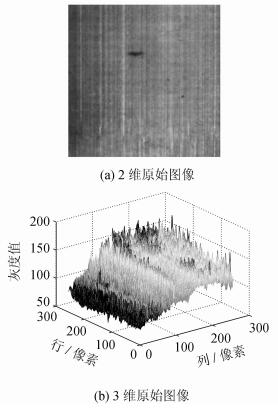 |
| 图3 原始磁瓦缺陷图像 Fig. 3 Original magnetic tile defect image |
从图 3中可以看出:该类型磁瓦磨削精度低,表面分布有深浅不一的磨削纹理;磁瓦图像背景不均匀;图像中存在强烈的噪声干扰。所以,本文的任务为去除磨削纹理和噪声对缺陷检测的干扰,并进行非均匀背景校正,从而准确地提取出缺陷区域。基于以上分析,本文提出了一种在NSST域中去除复合干扰的缺陷提取方法,具体步骤如下:
步骤1:对原始图像进行多尺度多方向NSST分解,尺度系数和方向系数均取为3。
步骤2:在低频子带中完成基于自适应阈值面的非均匀背景校正。
步骤3:在高频子带中完成基于Shearlet系数能量和方差的噪声和背景干扰的去除,及磨削纹理细节抑制。
步骤4:对重建图像进行自适应阈值分割,提取出缺陷区域。
本文算法流程如图 4所示。
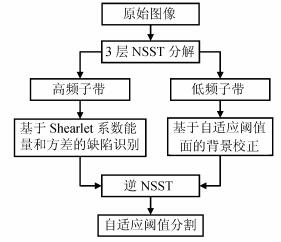 |
| 图4 本文算法流程 Fig. 4 Flowchart of the proposed method |
2.2 基于自适应阈值面的非均匀背景校正
磁瓦表面呈空间分布,导致图像背景不均匀,部分背景区域灰度与低对比度缺陷区域很接近,这对低对比度缺陷区域的判别造成严重的干扰。与此同时,由NSST的分解原理可知,磁瓦图像经NSST分解后,背景成分主要集中在低频子带中,图 3中图像分解所得低频子带如图 5所示。
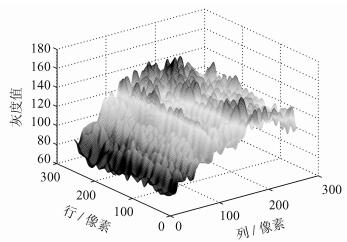 |
| 图5 原始低频子带系数 Fig. 5 Original low frequency subband coefficients |
为了便于提取缺陷,在低频子带中完成非均匀背景校正。观察图 5可知,低频子带中不仅包含了由光照不一致造成的非均匀背景,还包含了磨削纹理的低频成分,并且磨削纹理严格沿垂直方向分布。因此,为了在背景校正过程中有效地避免磨削纹理的干扰,采用一种基于均值的自适应阈值面方法,具体步骤如下:
步骤1:计算低频子带A(x, y) 每行均值,得到线图像R(x)。
步骤2:计算A(x, y) 每列均值,得到线图像C(x)。
步骤3:将C(x) 沿R(x) 扩展,得到自适应阈值面T(x, y)。
步骤4:求A(x, y) 和T(x, y) 之差,得到背景均匀且磨削纹理得到有效抑制的新低频子带M(x, y)。
通过以上步骤, 图 5中图像得到的阈值面和阈值校正结果如图 6所示。
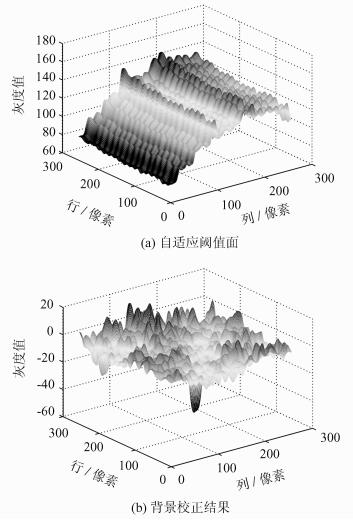 |
| 图6 非均匀背景校正结果 Fig. 6 Uneven background correction |
由图 6可以看出,背景得到了有效的校正,其与缺陷区域之间的对比度得到了明显的增强,粗糙的磨削纹理成分得到了显著的抑制。
2.3 基于高频系数方差和能量的缺陷识别图 3中磁瓦图像NSST分解所得第1层8个高频子带如图 7所示。结合NSST原理,可以得出高频子带的主要成分包括:磨削纹理细节、缺陷区域细节和大量噪声。
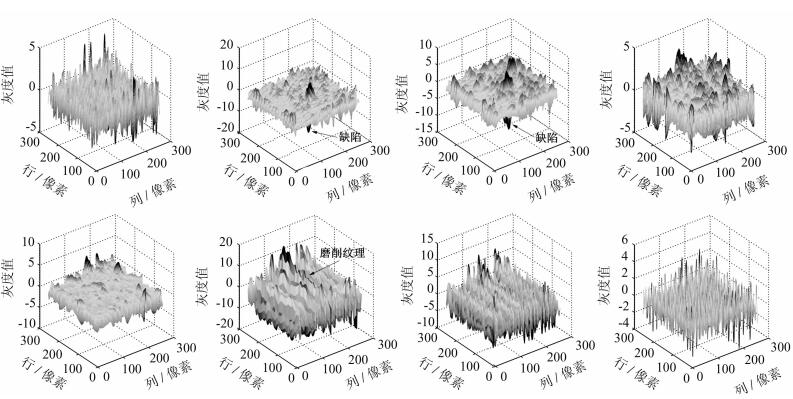 |
| 图7 原始第1层高频子带系数 Fig. 7 Distribution of original shearlet coefficient at the first level |
从图 7可以看出,磨削纹理严格分布在垂直方向上。因此,将各层垂直方向高频子带置零可有效地抑制高频磨削纹理。在NSST高频域,微弱缺陷和噪声对应分解系数的模值均明显小于显著缺陷对应分解系数的模值,即从能量的角度考虑,显著缺陷对应分解系数的能量较大,微弱缺陷和噪声对应分解系数的能量明显偏小。从几何结构的角度考虑,显著缺陷和微弱缺陷均为连续的几何结构,而噪声通常是孤立的像素点[14]。同时注意到各向异性的特性使NSST能够捕捉到图像中2维几何信息。因此,显著缺陷对应的分解系数在各个方向的高频子带中均表现出较大的模值;微弱缺陷仅在与其方向接近的高频子带中才表现出较大模值,在其余方向中均表现出较小模值[15];噪声对应的分解系数在各个方向子带中均表现出较小模值。因此,在同一分解尺度下的各方向子带中,微弱信号对应的分解系数之间的方差较大,显著信号和噪声对应的分解系数之间的方差较小。根据以上的分析,提出基于Shearlet系数方差和能量的缺陷识别算子,计算过程如下:
步骤1:将各尺度垂直方向高频子带置零,计算像素点 (x, y) 在j尺度下的Shearlet系数平均能量Ej, x, y,定义如下:
| $ {{E}_{j, x, y}}=\frac{1}{{{L}_{j}}}\sum\limits_{l=1}^{{{L}_{j}}}{c_{_{j, l, x, y}}^{^{2}}} $ | (7) |
式中,cj, l, x, y为j尺度下第l个方向子带中坐标为 (x, y) 的分解系数, Lj为j尺度下方向子带数量。
步骤2:计算像素点 (x, y) 在j尺度下的系数方差σj, x, y,定义如下:
| $ {{\sigma }_{j, x, y}}=\frac{1}{{{L}_{j}}}\sum\limits_{l=1}^{{{L}_{j}}}{{{({{c}_{j, l, x, y}}-mea{{n}_{j, x, y}})}^{2}}} $ | (8) |
式中,meanj, x, y为j尺度下像素点 (x, y) 的各方向子带系数均值,定义如下:
| $ mea{{n}_{j, x, y}}=\frac{1}{{{L}_{j}}}\sum\limits_{l=1}^{{{L}_{j}}}{{{c}_{j, l, x, y}}} $ | (9) |
步骤3:对噪声和背景干扰进行判别,即:
| $ {{{\hat{c}}}_{j, l, x, y}}=\left\{ \begin{align} &{{c}_{j, l, x, y}}, {{E}_{j, x, y}}+{{\sigma }_{j, x, y}}>T; \\ &0, 其他 \\ \end{align} \right. $ | (10) |
式中,T为预置阈值参数。干扰抑制后的第1层高频系数如图 8所示。
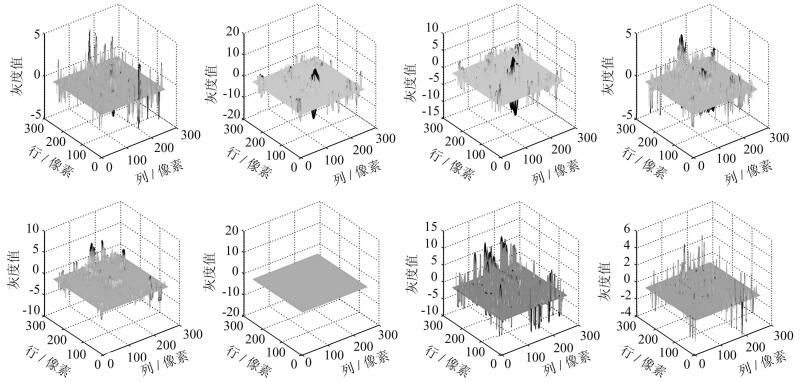 |
| 图8 干扰抑制后的第1层高频子带系数 Fig. 8 Distribution of shearlet coefficient at the first level after interference suppression |
2.4 缺陷提取
对修改后的分解系数进行逆NSST重建,可以得到背景均匀的无噪重建图像。对重建图像进行自适应阈值处理,得到二值化检测结果R(x, y), 阈值公式定义如下:
| $ \boldsymbol{R}\left( x, y \right)=\left\{ \begin{align} &1, \text{ }\left| f\left( x, y \right)-\mu \right|>K\sigma ; \\ &0, 其他 \\ \end{align} \right. $ | (11) |
式中,μ和σ分别为重建图像像素均值和标准差,K为阈值控制参数。图 3中缺陷图像的检测结果如图 9所示。
 |
| 图9 缺陷检测结果 Fig. 9 Defect detection results |
3 实验结果与分析
本文的实验测试环境如下:CPU为Inter quad-core 3.3 GHz,8 G内存;测试软件为MATLAB 2012a;全部测试图像大小均为256×256。为了验证本文算法的有效性和对比现有算法的优越性,本文分别进行了定性和定量对比实验。在定性对比实验中,采用了4幅典型的磁瓦表面缺陷图像和1幅合格磁瓦图像测试本文算法效果,并与文献[5-7]中算法鲜果进行了对比,对比结果如图 10所示。
 |
| 图10 4种检测算法检测结果对比 Fig. 10 Comparison of detecton results for the four methods |
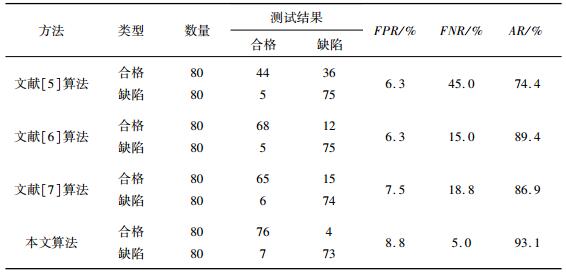
从图 10可以看出:文献[5]中算法对显著缺陷的检测效果较好,但无法消除磨削纹理和噪声,导致了大量的误判,在合格磁瓦图像的检测中尤为明显。文献[6]中的算法,有效地消除了噪声的影响,准确地提取了缺陷区域边缘。但是,Canny算子将显著的磨削纹理误检测为缺陷,使该算法将存在显著纹理的合格磁瓦误判为缺陷品,严重影响了该算法的精度。文献[7]中算法成功地去除了磁瓦图像的非均匀背景,并准确地分割出显著缺陷区域。但该算法未考虑噪声的影响,导致检测结果中大量噪声被误测检为缺陷。相比之下,本文提出的算法有效地消除了干扰,对缺陷磁瓦和合格磁瓦均取得了准确的分割结果,缺陷分割精度明显高于上述3种方法。与此同时,本文还进行了定量对比实验,实验选取了160片样品磁瓦进行测试,包括80片合格磁瓦和80片缺陷磁瓦,测试算法的准确性和效率。检测准确性指标包括假阳性率 (false positive rate,FPR)、假阴性率 (false negative rate,FNR) 和准确率 (accuracy rate,AR),计算公式分别如下:
| $ FPR=\frac{FP}{FP+TN}\times 100\% $ | (12) |
| $ FNR=\frac{FN}{FN+TP}\times 100\% $ | (13) |
| $ AR=\frac{TP+TN}{P+N}\times 100\% $ | (14) |
式中:P为合格磁瓦总数,N为缺陷磁瓦总数,TP为被检测为合格的合格磁瓦数量,TN为被检测为缺陷的缺陷磁瓦数量,FP为被检测为合格的缺陷磁瓦数量,FN为被检测为缺陷的合格磁瓦数量。测试结果如表 1所示。本文算法FPR为8.8%,主要原因为部分缺陷与磨削纹理重合,导致被误检测为纹理。本文算法FNR为5.0%,主要原因为部分磁瓦表面精度低,导致显著的纹理和杂质被误检测为缺陷。最终,本文算法测试准确率为93.1%,明显高于其余3种参考算法的准确率。
| 表1 4种算法检测准确性对比 Tab. 1 Results of detection accuracy for the four methods |
 |
此外,实验还对本文算法的执行效率进行了测试,并与参考算法进行了对比,对比结果如表 2所示。从表 2中可以看出,本文算法在MATLAB中的平均运行时间为0.629 s,完全满足当前磁瓦企业在线检测效率要求,如果算法改由C语言编程实现,效率将进一步提高。
| 表2 4种算法检测平均耗时对比 Tab. 2 Results of the average computational time (ACT) for the four methods |
 |
上述结果表明:本文算法可以有效地去除不均匀背景、噪声和磨削纹理的干扰,准确地检测出磁瓦表面缺陷,且执行效率满足在线检测需求。相较于现有算法,本文的算法在缺陷分割效果和检测准确率两方面有明显的优势。
4 结论提出了一种基于NSST的磁瓦表面缺陷检测算法。该算法利用NSST多尺度分解的优势,将磁瓦图像中的不同成分分解到不同频率子带中进行处理。在低频近似子带中,利用基于均值的自适应阈值面去除了不均匀背景。在高频方向子带中,利用NSST多方向分解性质及对细节良好的捕捉能力,构造了基于Shearlet系数方差和能量的缺陷识别算子,成功区分了缺陷信号、噪声及背景干扰,并通过将垂直方向Shearlet系数置零,有效地抑制了磨削纹理干扰,最终准确地提取出缺陷区域。实验结果表明,本文算法可有效抑制磁瓦图像中的强烈干扰,并准确地提取出磁瓦表面缺陷区域,检测准确率为93.1%,平均运行时间为0.629 s,完全满足当前磁瓦企业在线检测要求。与现有算法相比,本文算法的准确性和鲁棒性有明显的优势。本文算法存在的问题是无法有效地区分垂直方向上的磨削纹理和缺陷,从而导致部分缺陷磁瓦的漏检,下一步将针对这一情况对算法做出改进。
| [1] |
Jiang Honghai, Yin Guofu, Liu Peiyong, et al. Defect detection on magnetic tile surfaces based on fast discrete curvelet transform and support vector machine[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(3): 147-152. [蒋红海, 殷国富, 刘培勇, 等. 基于Curvelet变换和支持向量机的磁瓦表面缺陷识别方法[J]. 四川大学学报 (工程科学版), 2012, 44(3): 147-152.] |
| [2] |
Koch C, Brilakis I. Pothole detection in asphalt pavement images[J]. Advanced Engineering Informatics, 2011, 25(3): 507-515. DOI:10.1016/j.aei.2011.01.002 |
| [3] |
Li Wubin, Lu Changhou, Zhang Jianchuan. A lower envelope Weber contrast detection algorithm for steel bar surface pit defects[J]. Optics & Laser Technology, 2013, 45: 654-659. |
| [4] |
He Zhendong, Wang Yaonan, Liu Jie, et al. Background differencing-based high-speed rail surface defect image segmentation[J]. Chinese Journal of Scientific Instrument, 2016, 37(3): 640-649. [贺振东, 王耀南, 刘洁, 等. 基于背景差分的高铁钢轨表面缺陷图像分割[J]. 仪器仪表学报, 2016, 37(3): 640-649.] |
| [5] |
Yu Yongwei, Yin Guofu, Jiang Honghai, et al. Defect extraction method of arc magnet surface images based on adaptive morphological filtering[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(3): 351-356. [余永维, 殷国富, 蒋红海, 等. 磁瓦表面图像的自适应形态学滤波缺陷提取方法[J]. 计算机辅助设计与图形学学报, 2012, 24(3): 351-356.] |
| [6] |
Li Xueqin, Jiang Honghai, Yin Gguofu. Detection of surface crack defects on ferrite magnetic tile[J]. NDT & E International, 2014, 62: 6-13. |
| [7] |
Xie Luofeng, Lin Lijun, Yin Ming, et al. A novel surface defect inspection algorithm for magnetic tile[J]. Applied Surface Science, 2016, 375: 118-126. DOI:10.1016/j.apsusc.2016.03.013 |
| [8] |
Liu Jian, Lei Yingjie, Xing Yaqiong, et al. Fusion technique for SAR and gray visible image based on hidden Markov model in non-subsample shearlet transform domain[J]. Control and Decision, 2016, 31(3): 453-457. [刘健, 雷英杰, 邢雅琼, 等. 基于NSST域隐马尔可夫树模型的SAR和灰度可见光图像融合[J]. 控制与决策, 2016, 31(3): 453-457.] |
| [9] |
Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25-46. DOI:10.1016/j.acha.2007.09.003 |
| [10] |
Lim W Q. The discrete shearlet transform:A new directional transform and compactly supported Shearlet frames[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1166-1180. DOI:10.1109/TIP.2010.2041410 |
| [11] |
Singh S, Gupta D, Anand R S, et al. Nonsubsampled Shearlet based CT and MR medical image fusion using biologically inspired spiking neural network[J]. Biomedical Signal Processing and Control, 2015, 18: 91-101. DOI:10.1016/j.bspc.2014.11.009 |
| [12] |
Tao Feixiang, Wu Yiquan. Remote sensing image enhancement based on non-subsampled Shearlet transform and parameterized logarithmic image processing mode[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 884-892. [陶飞翔, 吴一全. 非下采样Shearlet变换与参数化对数图像处理相结合的遥感图像增强[J]. 测绘学报, 2015, 44(8): 884-892.] |
| [13] |
Kong Weiwei, Lei Yang, Zhao Huaixun. Adaptive fusion method of visible light and infrared images based on non-subsampled Shearlet transform and fast non-negative matrix factorization[J]. Infrared Physics & Technology, 2014, 67: 161-172. |
| [14] |
Da Cunha A L, Zhou J, Do M N. The nonsubsampled contourlet transform:Theory, design, and applications[J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101. DOI:10.1109/TIP.2006.877507 |
| [15] |
Imani E, Pourreza H R, Banaee T. Fully automated diabetic retinopathy screening using morphological component analysis[J]. Computerized Medical Imaging and Graphics, 2015, 43: 78-88. DOI:10.1016/j.compmedimag.2015.03.004 |
 2017, Vol. 49
2017, Vol. 49


