围岩分级是开展岩土工程建设的重要技术指标,对工序工法、支护设计具有重要指导意义。围岩分级中,围岩自稳时间属于单一的综合岩性指标[1],能够整体上表征岩体质量,影响开挖方法的选择、开挖循环时间的计算、支护方法的选取及支护时机的确定。对于特殊地质环境隧道,自稳时间不仅是反映岩体质量好坏的指标,更是一种开挖技术的体现[2]。
自稳时间最早应用于Lauffer的岩体质量的分级。Lauffer发现在任意给定的条件下,自稳时间会随着活跃跨度的增长而明显减小[3]。Barton等[4]通过隧道最大无支护跨度与自稳时间关系对岩体质量进行评价。Bieniawski[5]根据RMR体系,研究了平均自稳时间与无支护跨度的关系。Myer等[6]研究了掘进工作面的尺寸及开挖速度对自稳时间的影响。Nguyen等[7]基于流变变形模型,建立与开挖跨度相关的隧道围岩自稳时间解析解,该解析法计算简单,且仍能考虑岩体性质。
隧道施工过程中,经常遇到具有明显软化性的岩石,如石膏岩、泥岩、泥质砂岩等。这类岩体遇地下水后,其强度和自稳能力显著降低,且岩质越软弱,节理越发育,受地下水的影响越显著[8–9]。藤宏伟等[10]采用声波探测与单轴抗压试验相结合的方法,对共和隧道页岩遇水软化性进行研究,得到页岩动弹模量及强度随遇水时间增加而衰减的软化方程。周翠英等[11–12]进行软岩(粉砂质泥岩、泥质粉砂岩)力学性质软化的试验研究,发现软岩与水相互作用后,其抗压强度、抗拉强度及抗剪强度变化的定量表征关系服从指数变化规律,各力学参数将随着饱水时间的延长而不断弱化。目前关于这类岩石受水软化的试验方法比较成熟,结果也比较明确,力学参数随浸水时间增长而逐渐弱化。
地下水能显著弱化这类岩石的力学参数,进而影响该类岩体的自稳能力。Nguyen的自稳时间解析法没有考虑地下水的软化作用,所以并不适用于这类岩石。针对此,以重庆梁忠高速公路礼让隧道工程为背景,对工程中遇到的具有典型软化性的石膏岩,通过软化试验建立其力学参数与浸水时间之间的定量关系。基于此定量关系及经典的圆形轴对称隧道弹性解,建立考虑软化效应的隧道围岩自稳时间解析模型,用以解决上述问题。通过把该模型应用于评价礼让隧道石膏围岩的自稳时间,验证其实用性。通过自洽分析,验证该模型的自洽性。基于实际情况中地下水分布具有动态不均匀性,对后续研究进行了探讨。
1 软化试验 1.1 试验条件及方法试验用石膏岩取自重庆市梁平县礼让隧道。该地层石膏岩属于三叠系下统嘉陵江组。通过X射线衍射定性分析法,确定所取岩样的矿物成份:CaSO4·2H2O、CaSO4、SiO2和CaCO3。基于定性分析结果,采用内标法确定重要成份的比例(CaSO4·2H2O和CaSO4),见表1。
| 表1 石膏岩矿物成分 Tab. 1 Mineral compositions of gypsum |
 |
石膏岩亲水软化试验步骤包括:
1)岩样加工成直径50 mm、高100 mm的圆柱形试件(图1)。在40 ℃烘干箱内烘至质量不变,记录烘干后质量M1。
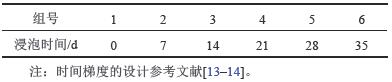
2)浸泡烘干后的试件于蒸馏水中,浸水时间方案见表2,每组时间梯度下重复3个试件。
3)完成浸泡后,擦干表面,保证表面无明显水迹,记录试件质量M2。进行单轴压缩试验:采用位移加载方法,加载速率为0.1 mm/min,直至试件完全破坏。
| 表2 软化试验方案 Tab. 2 Softening test scheme |
 |
 |
| 图1 试件 Fig. 1 Test samples |
1.2 试验结果及分析
根据国际岩石力学试验通行标准,计算出不同浸水时间下的石膏岩吸水率、弹性模量和泊松比的平均值,见表3。
| 表3 试验结果 Tab. 3 Test results |
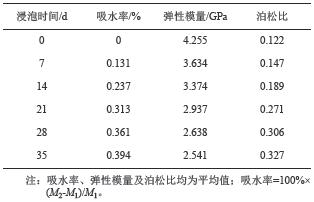 |
图2为吸水率随时间的变化。石膏岩的吸水率随浸水时间呈增加趋势,且初期增加快,后期速率逐渐减缓。为定量描述试验结果,且兼顾实际情况,吸水率最终达到饱和含水率[16],用式(1)对试验数据拟合:
| ${w_t} = \frac{t}{{\alpha t + \beta }}$ | (1) |
式中,t为浸水时间,wt为t时刻的吸水率,α和β为与岩石水理性有关的参数。当t=0时,wt=0,对应岩石未吸水;随着浸水时间增加,吸水率逐渐增大。β为材料的疏水系数,越小则吸水率增加越快。当t趋向于无穷时,wt=1/α,α为岩石饱和含水率的倒数。
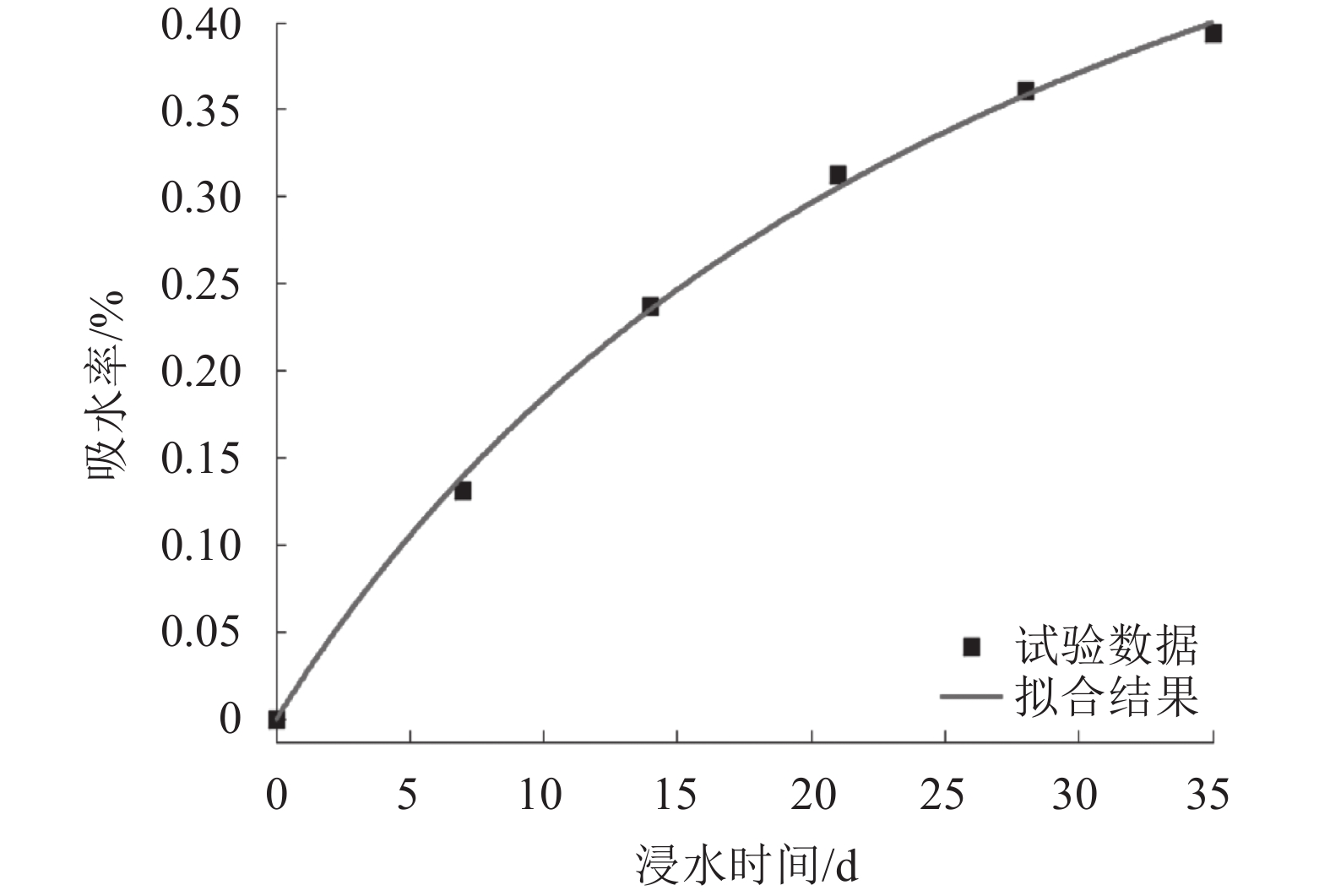 |
| 图2 石膏岩吸水率随浸水时间变化 Fig. 2 Water absorption of gypsum changes over soaking time |
图3为弹性模量随时间的变化。石膏岩弹性模量随浸水时间呈下降趋势。浸水35 d后,其降至2.541 GPa,降幅达40.28%。可见,水对石膏岩弹性模量衰减作用显著。为定量表征弹性模量随浸水时间衰减这一过程,且兼顾合理性:完全软化后弹性模量趋近于0[15],引用式(2)[16]对图3 的数据拟合:
| ${E_t} = E{\text{e}^{ - mt}}$ | (2) |
式中:Et为t时刻的弹性模量,E为初始弹性模量,当t=0时,Et=E,对应岩石未被软化,t趋向于无穷时,Et趋向于0,对应岩石被完全软化;m为岩石软化特性参数,m越大,弹性模量衰减越快,表明该岩石软化特性越明显。
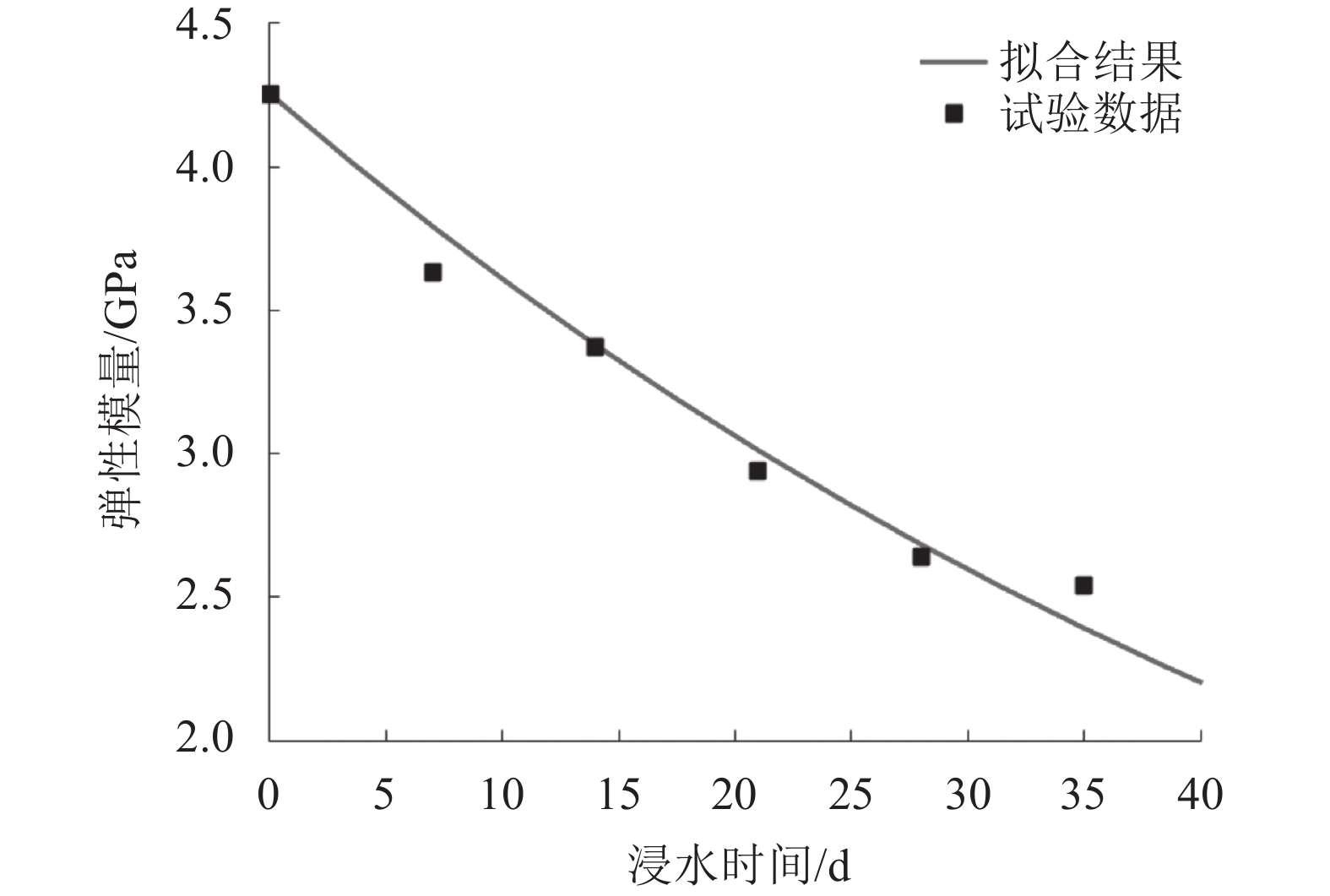 |
| 图3 石膏岩弹性模量随浸水时间变化 Fig. 3 Elasticity modulus of gypsum changes over soaking time |
图4为泊松比随时间的变化。石膏岩的泊松比随浸泡时间呈增大趋势。文献[15]指出岩石的泊松比不会无限增大。为兼顾上述特征,较好地表征泊松比和浸水时间的定量关系,用式(3)拟合试验数据:
| ${\textit{υ} _{\rm{t}}} = \frac{t}{{t + n}} + \textit{υ} $ | (3) |
式中,υt为t时刻的泊松比,υ为初始泊松比,n为软化特性参数。当t=0时,υt=υ,表示岩石没有被软化。随着浸水时间增长,泊松比逐渐增大,n越小,泊松比增加得越快,对应的岩石软化特性越明显。
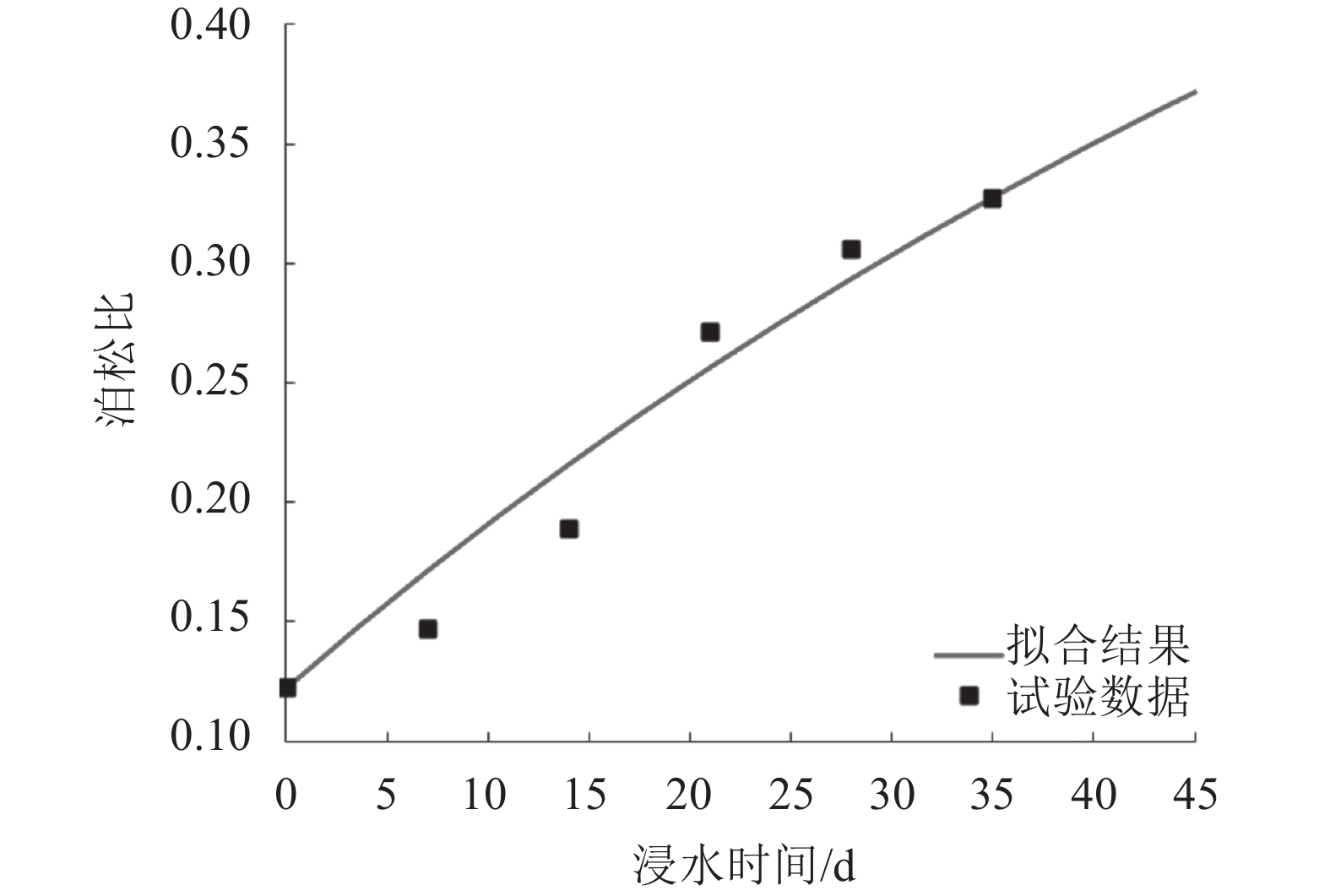 |
| 图4 石膏岩泊松比随浸水时间变化曲线 Fig. 4 Poisson ratio of gypsum changes over soaking time |
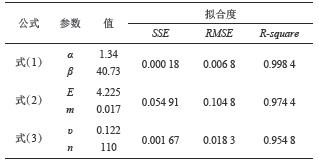
表4列举出各式的参数值及拟合度。其中,最大误差平方和(SSE)小于0.055,最大标准差(RMSE)小于0.11,最小确定系数(R-square)大于0.95。表明式(1)~(3)能很好地反映试验结果。
| 表4 参数值及拟合度 Tab. 4 Values of parameters and goodness of fit |
 |
2 自稳时间解析模型
由于圆形结构在数学上的简单性,且具有一定的代表性,基于圆形轴对称隧道弹性解及软化试验获得的定量关系,建立考虑软化效应的隧道围岩自稳时间解析模型。
2.1 模型建立为建立解析模型,基于经典的圆形轴对称隧道模型的假设条件,增加如下假设:
1)实际工程中围岩变形随时间增加,且变形速率及大小受岩体力学性能的影响[17]。研究侧重隧道在时间尺度上的稳定性,因此,假设浸水软化对岩体的影响集中表现为由力学参数下降而导致的围岩变形随时间增加。
2)工程应用中,为简化问题,通常用一个影响系数概括地下水对工程的影响效果[18]。基于此,视地下水对围岩的软化具有一个整体效果,建模中暂不考虑地下水的分布特征。
3)实际施工中,通常用位移管理法判断岩体是否失稳[19–20]。基于此方法的原理,认为当围岩变形量达到一个临界值时即失稳。
根据圆形轴对称隧道弹性解[15],隧道任意一点的位移:
| $u = \frac{{({\sigma _0} - {p_0}){R^2}}}{{2Gr}}$ | (4) |
式中,u为位移,σ0为地应力,p0为支护力,R为隧道开挖半径,G为剪切模量,r为围岩内一点到隧道中心的距离。为研究自稳时间,不考虑支护力的作用,即p0=0。研究关注隧洞临空面的位移,取r=R。地应力与埋藏深度有关,取σ0=γH[15],γ为岩体容重。以上参数代入式(4)得:
| $u = \frac{{\gamma HR}}{{2G}}$ | (5) |
基于假设1)、2),通过在式(2)和(3)中引用系数K、s,定量描述水对岩体的软化作用:
| $E(t) = KE{\text{e}^{ - mst}}$ | (6) |
| $\textit{υ} (t) = \frac{{st}}{{t + n}} + \textit{υ}$ | (7) |
式中:E(t)、
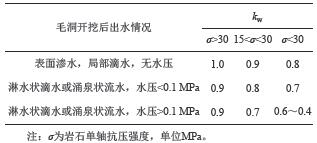
地下水对工程围岩的影响,一般按其水量多少、岩石软硬及节理多少加以评价。现行的隧道设计规范中,给出地下水影响系数kw的取值[2],见表5。基于s和kw具有相同的工程作用,建立如下的对应关系:
| $s = 1 - {k_{\rm{w}}}$ | (8) |
| 表5 kw的取值依据 Tab. 5 Basis for assigning value to kw |
 |
根据岩石剪切模量的定义及式(6)~(7),可得岩体剪切模量受地下水软化作用的表达式:
| $G(t) = \frac{{E(t)}}{{2[1 + \textit{υ} (t)]}} = \frac{{(t + n)KE{\text{e}^{ - mst}}}}{{2[st + (\textit{υ} + 1)(t + n)]}}$ | (9) |
式(9)代入式(5):
| $u = \frac{{\gamma HR}}{{2G}} = \frac{{\gamma HR[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}}$ | (10) |
式(10)为考虑了软化效应的圆形轴对称隧道的临空面位移模型。实际工程中,临空面位移量存在空间效应,即受掌子面的影响[21]:
若临空面上点到掌子面距离为l,隧道宽度为B,掌子面的影响范围为l0(l0一般为3到5倍的B[7])。当l>l0时,位移不受掌子面影响,可用式(10)描述;当l≤l0时,位移与掌子面关系可用式(11)描述[21]:
| ${u_{\rm{l}}} = u(1 - {\text{e}^{\frac{{ - al}}{R}}})\;\;\left( {l \le {l_0}} \right)$ | (11) |
式中,u1为距离掌子面l处的隧道临空面位移,a为经验常数。
联立式(10)和(11)可得临空面上任一点的位移表达式,即式 (12)。由位移连续性可知:当l=l0时,u1≈u。根据此条件,可确定式中a的取值:基于实际隧道监测中,收敛尺可分辨0.01 mm的围岩变形这一事实,在边界l=l0处,假设
| $\left\{ {\begin{array}{*{20}{l}}{u = \displaystyle\frac{{\gamma HR[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}}{\kern 1pt} ,l > {l_0}\text{;}}\\[10pt]{{u_{\rm{l}}} = \displaystyle\frac{{\gamma HR[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}}(1 - {\text{e}^{\frac{{ - al}}{R}}}),l \le {l_0}\;}\end{array}} \right.$ | (12) |
| 表6 参数a的取值依据 Tab. 6 Basis for selecting parameter a |
 |
Lauffer定义了活跃跨度Las(图5)[7]:当l≤B时,Las=l;l > B时,Las=B=2R。据此,把Las代入式(12)中得:
| $\left\{ {\begin{array}{*{20}{l}}{u = \displaystyle\frac{{{\rm{0}}{\rm{.5}}\gamma {L_{{\rm{as}}}}H[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}} ,l > {l_0};}\\[10pt]{{u_{\rm{l}}} = \displaystyle\frac{{{\rm{0}}{\rm{.5}}\gamma {L_{{\rm{as}}}}H[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}} (1 - {\text{e}^{\frac{{ - al}}{{0.5{L_{{\rm{as}}}}}}}}) ,B < l \le {l_0};}\\[10pt]{{u_{\rm{l}}} = \displaystyle\frac{{\gamma HR[st + (\textit{υ} + 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}}{\kern 1pt} (1 - {\text{e}^{\frac{{ - a{L_{{\rm{as}}}}}}{R}}}),{\rm{0}} < l \le {\rm{B}}}\end{array}} \right.$ | (13) |
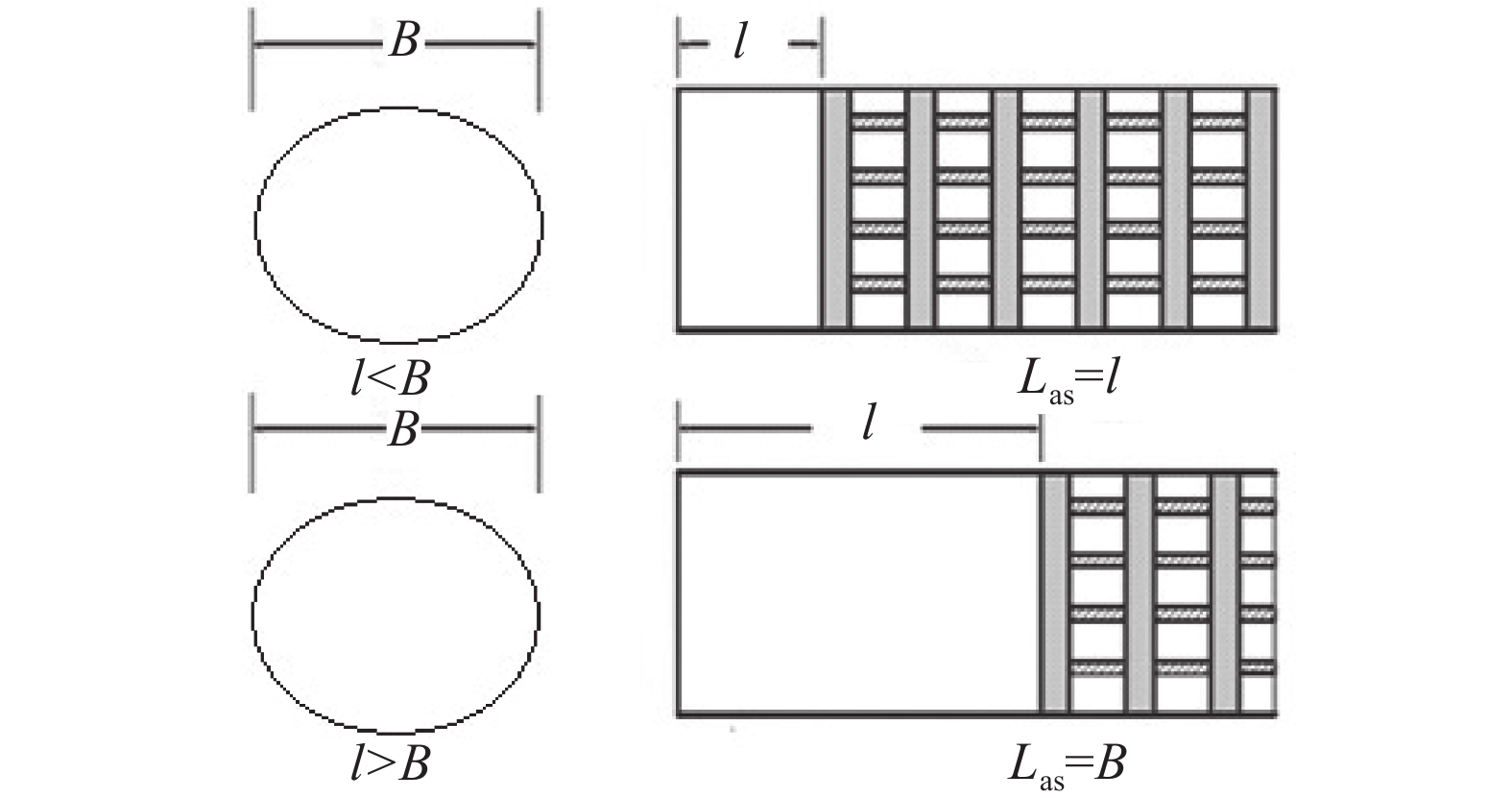 |
| 图5 Las的定义 Fig. 5 Definition of Las |
隧道工程中,当围岩位移量超过临界值时,就会出现失稳、垮塌现象。不同岩性围岩的临界位移值不同,李文江等[20]对此做了大量研究。定义ucv为围岩的临界位移,在无支护作用下,开挖后的围岩能够保持稳定的条件为u≤ucv,u1≤ucv。用ucv替换式(13)中的u和u1,可得临界状态下的各参数关系如式(14)。其中:当B<l≤l0时,
| $\left\{ {\begin{array}{*{20}{l}}{{u_{{\rm{cv}}}} = \displaystyle\frac{{{\rm{0}}{\rm{.5}}\gamma {L_{{\rm{as}}}}H[st + (\textit{υ}+ 1)(t + n)]}}{{(t + n)KE{\text{e}^{ - mst}}}}{\kern 1pt} {\kern 1pt} ,l > {{B;}}}\\[10pt]\! {{u_{{\rm{cv}}}} \! = \! \displaystyle\frac{{\gamma HR[st \! + \! (\textit{υ} \! + \! 1)(t \! + \! n)]}}{{(t \! + \! n)KE{\text{e}^{ \! - \! mst}}}} (1 \! - \! {\text{e}^{\frac{{ - a{L_{{\rm{as}}}}}}{R}}}),0 \! < \! l \! \le \! B}\! \end{array}} \right.\! \! $ | (14) |
在0<l≤B区间,
| $(1 - {\text{e}^{\frac{{ - a{L_{{\rm{as}}}}}}{R}}})\quad {\rm{ = }}\frac{{a{L_{{\rm{as}}}}}}{R} - \frac{1}{2}{(\frac{{a{L_{{\rm{as}}}}}}{R})^2} + \cdots $ | (15) |
取
| $\left\{ {\begin{array}{*{20}{l}}{{L_{{\rm{as}}}} = \displaystyle\frac{{{u_{{\rm{cv}}}}(t + n)KE{\text{e}^{ - mst}}}}{{{\rm{0}}{\rm{.5}}\gamma H[st + (\textit{υ} + 1)(t + n)]}} ,l > {{B;}}}\\[10pt]{{L_{{\rm{as}}}} = \displaystyle\frac{{{u_{{\rm{cv}}}}(t + n)KE{\text{e}^{ - mst}}}}{{a\gamma H[st + (\textit{υ} + 1)(t + n)]}},0 < l \le B}\end{array}} \right.$ | (16) |
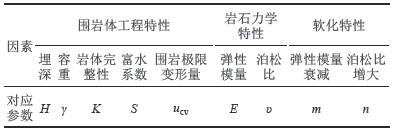
式(16)即为所建立的自稳时间解析模型,描述了活跃跨度、自稳时间及各参数之间的关系。模型涉及多种因素,见表7。
模型中参数m和n体现了围岩的软化性。通过试验,可获得其相应的值。因此,本模型对具有类似浸水软化性质的其他围岩有一定的参考意义。
2.2 模型应用研究为重庆梁忠高速公路礼让隧道项目的一部分。模型用于计算该隧道石膏段自稳时间。计算结果可为围岩分级提供依据,进而达到指导支护设计和现场施工的目的。
基于地勘资料、施工资料及软化试验结果,确定模型中各参数的取值,见表8。各参数取值的依据简述如下:
1)地勘资料显示:石膏岩段上部为平均厚度120 m的灰岩,H=120 m,γ=25.5 kN/m3;石膏段岩体较破碎,完整性系数K=0.4。
2)石膏段最大单位涌水量0.028 6 L/(s·m),地下水状态属于经常渗水级别,水压介于0.2~0.71 MPa,石膏岩的单轴抗压强度介于11~25 MPa。对照表5,确定kw=0.7,s=0.3。
3)根据文献[20]中的软弱围岩隧道稳定位移管理基准,取ucv=100 mm。
4)E、υ、m、n的值通过软化试验获得,列于表8。隧道在施工过程中及时支护,隧洞开挖长度小于隧洞宽度,取a=0.77。
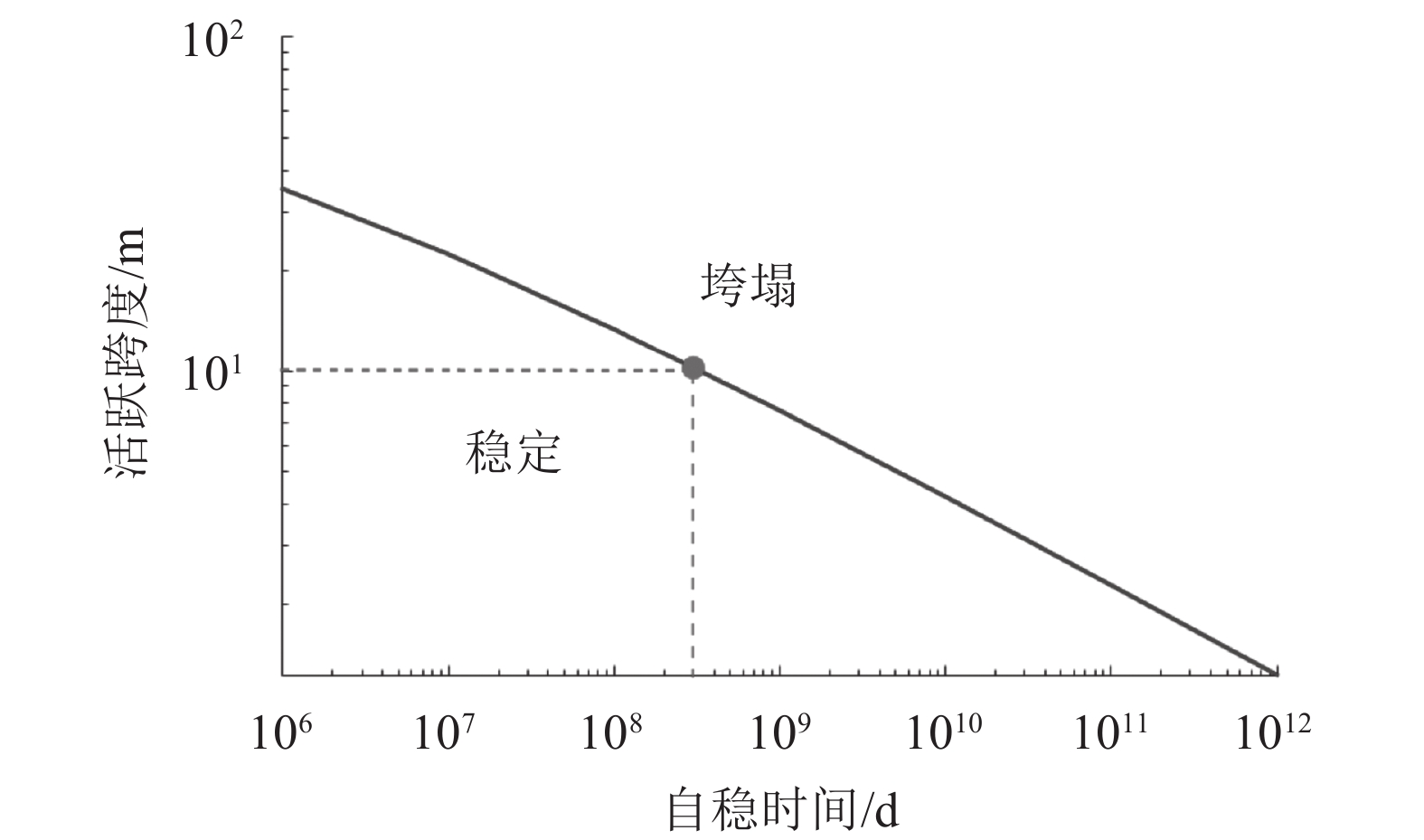
代入各参数值,得自稳时间与活跃跨度关系,见图6。可看出两者呈指数型关系,活跃跨度越大,自稳时间越短。
| 表7 模型中涉及的影响因素 Tab. 7 Factors included in this model |
 |
| 表8 参数取值 Tab. 8 Values of parameters |
 |
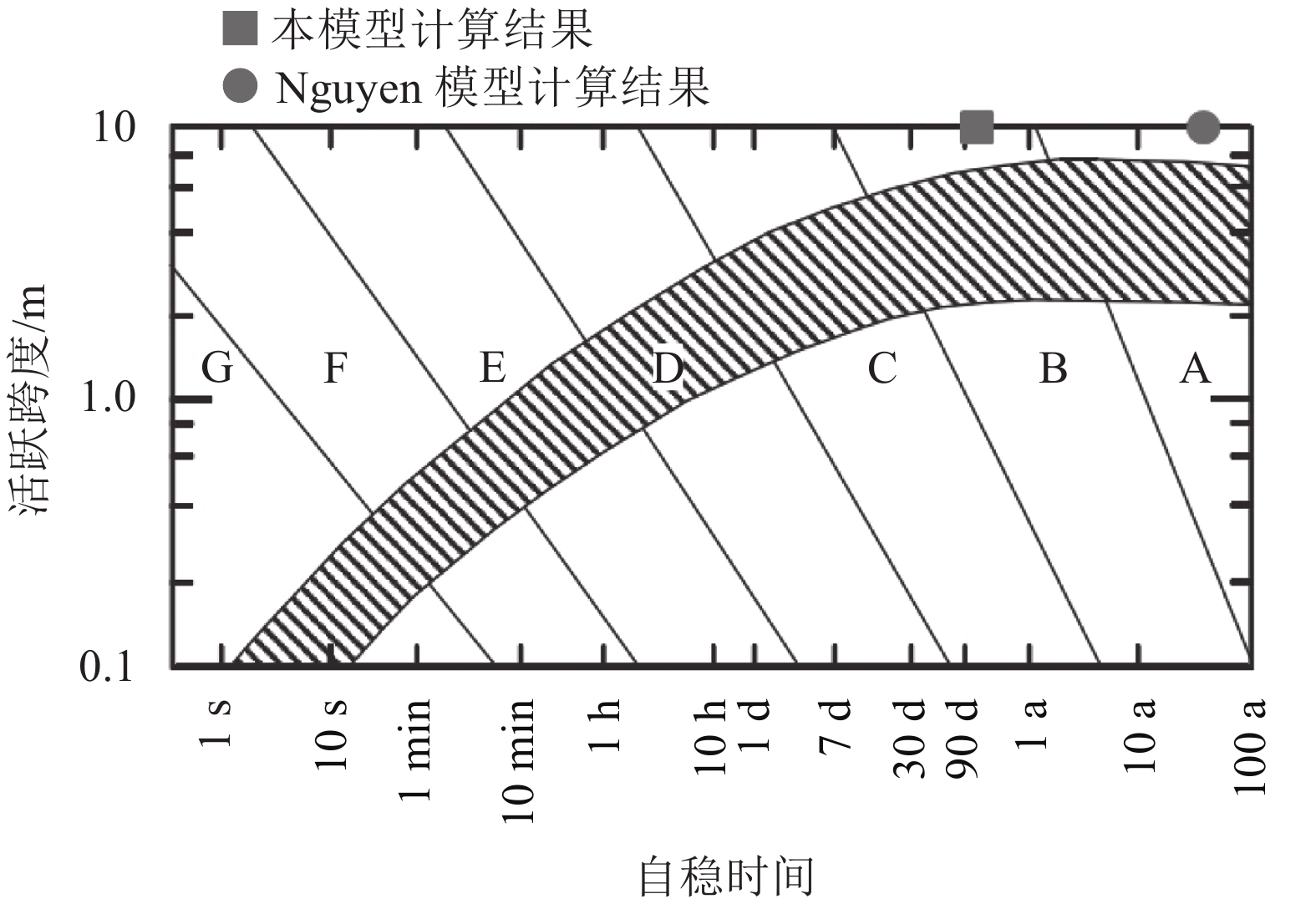
为对比分析,在此给出Nguyen模型对本问题的计算结果,见图7。计算参数来自表8中的部分参数,以及文献[7]中的流变参数。
Lauffer根据活跃跨度与时间关系对围岩分级[5],是一种较为合理的分级方法,见图8。图8中A级围岩质量最好,G级围岩质量最差。是否考虑软化效应会影响分级结果:隧道活跃跨度为10 m;图6中,其对应自稳时间达到375 d;图7中,相同跨度对应的自稳时间能达到1×108 d。依据图8中的分级方法,文中模型所得结果属B级,Nguyen结果属A级。两者定量结果相差之大,以至于导致定性的差别。
基于本文模型的评价结果,现场试验段按照B级围岩进行施工,主要采取如下措施:
1)用上下台阶法,台阶长度为8 m。
2)洞身开挖后,立即施作初期支护锚杆、钢筋网、钢架、喷射混凝土,及时封闭围岩。初期支护采用C30高性能混凝土。
3)初期支护基本稳定后及时施作二衬,二衬距掌子面70 m。
上述措施已经应用于试验阶段,取得了满意的结果。综合现场施工情况及后期监控量测结果来看,参照B级围岩进行施工和管理是合适的。
 |
| 图6 本文模型计算出的自稳时间与活跃跨度关系曲线 Fig. 6 Curve of stand-up time and active span predicted by model developed in this paper |
 |
| 图7 由Nguyen模型计算出的自稳时间与活跃跨度关系曲线 Fig. 7 Curve of stand-up time and active span predicted by Nguyen model |
 |
| 图8 不同等级岩体的活跃跨度与自稳时间关系(Lauffer,1958) Fig. 8 Active span versus stand-up time for different classes of rock mass (Lauffer,1958) |
2.3 模型参数自洽分析
模型计算出的自稳时间值,很难通过现场试验直接验证。所幸,在围岩分级中并不需要精确的自稳时间值,因为其定量的结果通常是用于更好地、定性地评估围岩质量。在此,通过对模型中的关键参数自洽分析,验证模型自洽性。
基于表8中参数,代入不同的H值,得到埋深对自稳时间的影响,如图9所示。
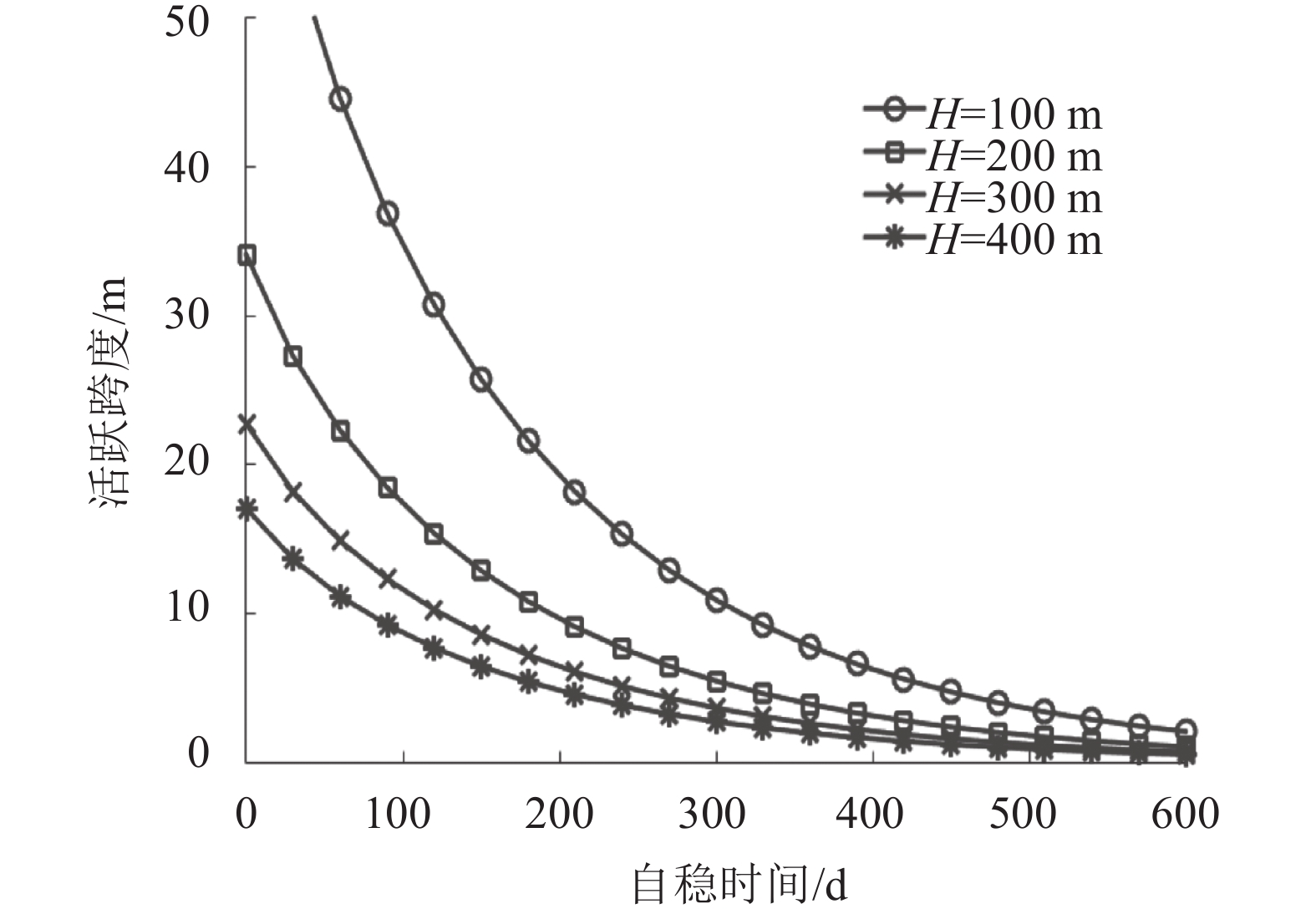 |
| 图9 隧道埋深对自稳时间的影响 Fig. 9 Influence of tunnel depth on stand-up time |
由图9可知,在相同的跨度下,自稳时间随着埋深的增大而减小。这与实际情况一致:通常情况下,深埋隧道的自稳时间要小于浅埋隧道的自稳时间。
基于表8,代入不同的K值,得岩体完整性系数对自稳时间的影响,如图10所示。可知,在相同跨度下,自稳时间随着完整性系数的增大而增加。这是合理的,因为岩体裂隙和结构面越少,围岩越稳定,自稳时间也就越长。
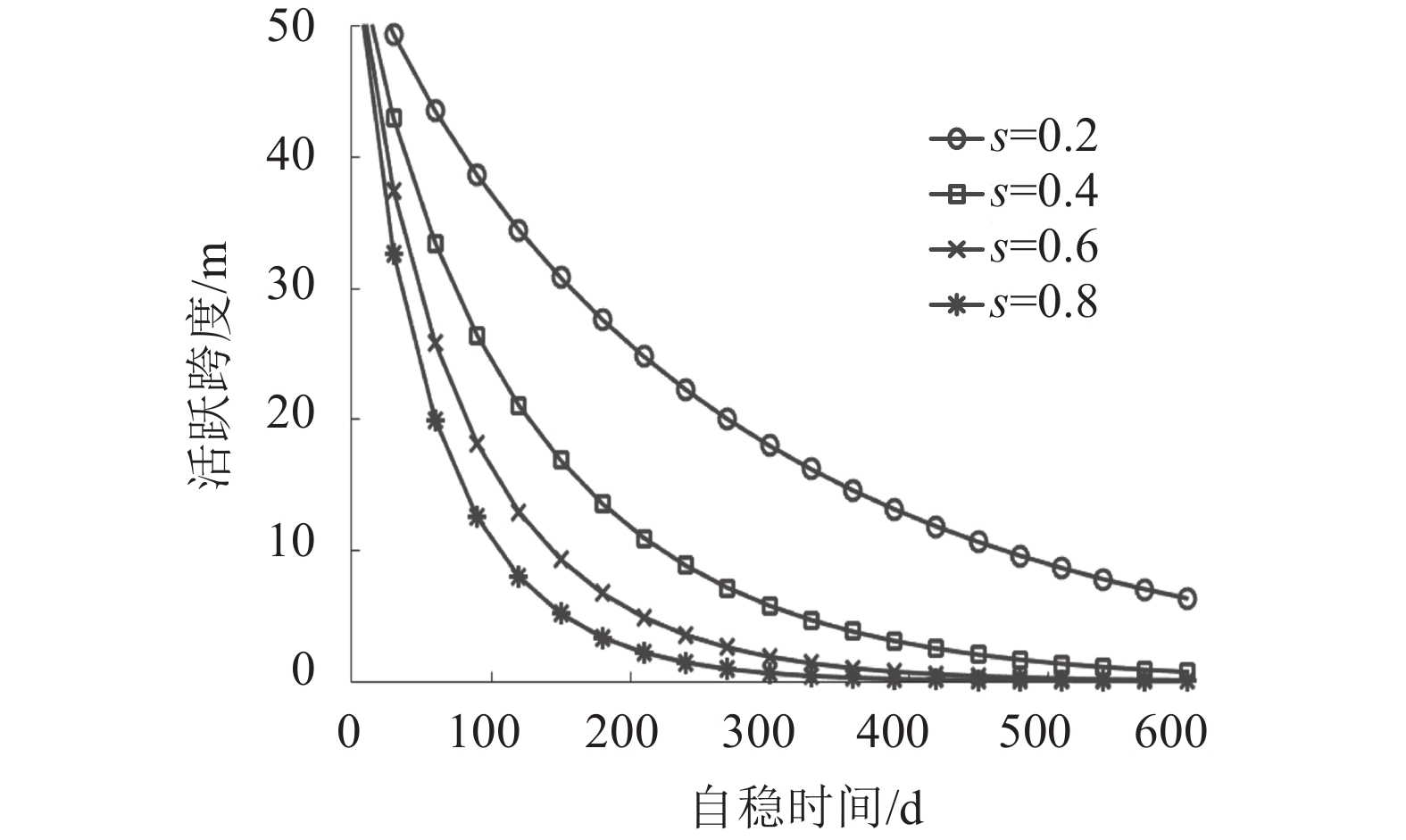
同样的方法分别分析富水系数s和弹性模量对自稳时间的影响,分别见图11和12。由图11可知,s越大,相同跨度下自稳时间越短,说明地下水越丰富,围岩越易垮塌。由图12可知,弹性模量越大,自稳时间越长,说明硬质围岩比软弱围岩更稳定。
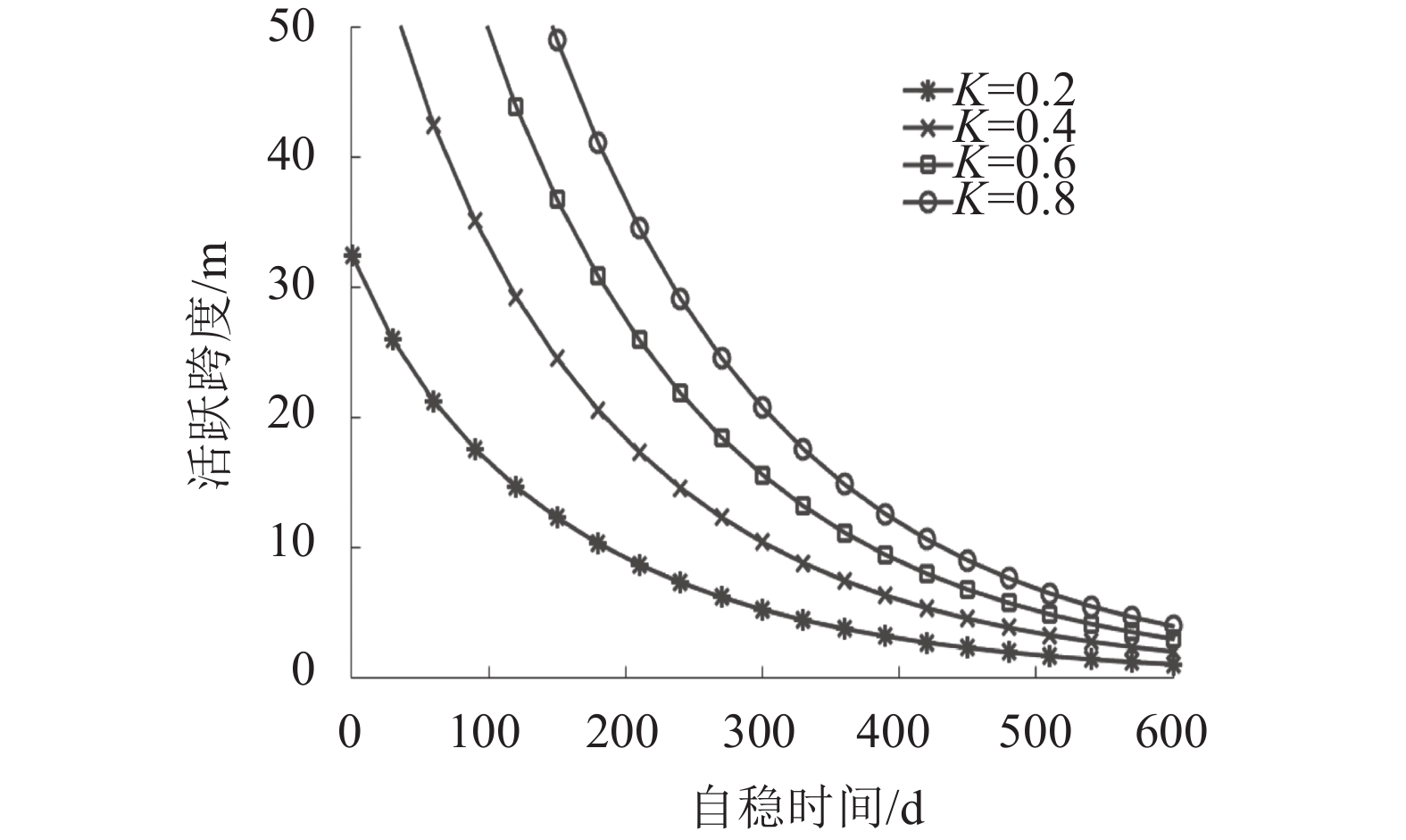 |
| 图10 岩体完整性系数对自稳时间的影响 Fig. 10 Influence of rock-mass integrity index on stand-up time |
 |
| 图11 系数s对自稳时间的影响 Fig. 11 Influence of coefficient s on stand-up time |
 |
| 图12 弹性模量对自稳时间的影响 Fig. 12 Influence of elasticity modulus on stand-up time |
上述自稳时间随各参数的变化规律与实际情况相符,这表明本模型具有自洽性。
3 讨 论在建模过程中,基于假设2),通过引用富水系数s反映水对整个围岩体的软化效果。这样能简化问题,但与实际情况有一定的差异。事实上,隧道不同点处围岩体的浸水程度并不相同,且地下水量会随时间变化,即地下水分布的动态不均匀性;这会导致围岩的动态非均匀软化。本节讨论如何在力学参数中考虑这种软化,这对后续的围岩软化研究和本模型的改进具有重要意义。
可用体积含水率量化浸水程度。在到掌子面距离大于l0处有一断面,该断面上各点的体积含水率受空间位置和时间影响,假设表示为:
| ${W_{\rm{n}}} = w(r,\theta ,t)$ | (17) |
式中,Wn为该点处的体积含水率。以圆形隧道中心为原点建立极坐标系,r和θ为该点极坐标。水是导致软化的根本原因,因此体积含水率和力学参数之间应该存在定量的关系,设为:
| ${E_{\rm{n}}} = g({W_{\rm{n}}})$ | (18) |
| ${\textit{υ} _{\rm{n}}} = h({W_{\rm{n}}})$ | (19) |
式中,En和υn分别为该点的弹性模量和泊松比。将式(17)代入式(18)和(19),可得到力学参数的动态非均匀变化关系。
对于本文模型,岩体力学参数可用表示为:
| $E(t) = \frac{{\iint\limits_D {g[w(r,\theta ,t)]} r{\rm{d}}r{\rm{d}}\theta }}{D}$ | (20) |
| $\textit{υ} (t) = \frac{{\iint\limits_D {h[w(r,\theta ,t)]} r{\rm{d}}r{\rm{d}}\theta }}{D}$ | (21) |
| $D = \left\{ {r,\theta |{R_{\rm{0}}} < r < {R_{\rm{m}}},0 \le \theta \le 2{\rm{\text{π}}}} \right\}$ | (22) |
式中:E(t)和υ(t)为围岩体t时刻的弹性模量和泊松比;R0为隧道开挖半径;Rm为隧道受地下水影响范围的半径,如图13所示。分别用式(20)和(21)代替式(6)和(7),可达到改进模型的目的。
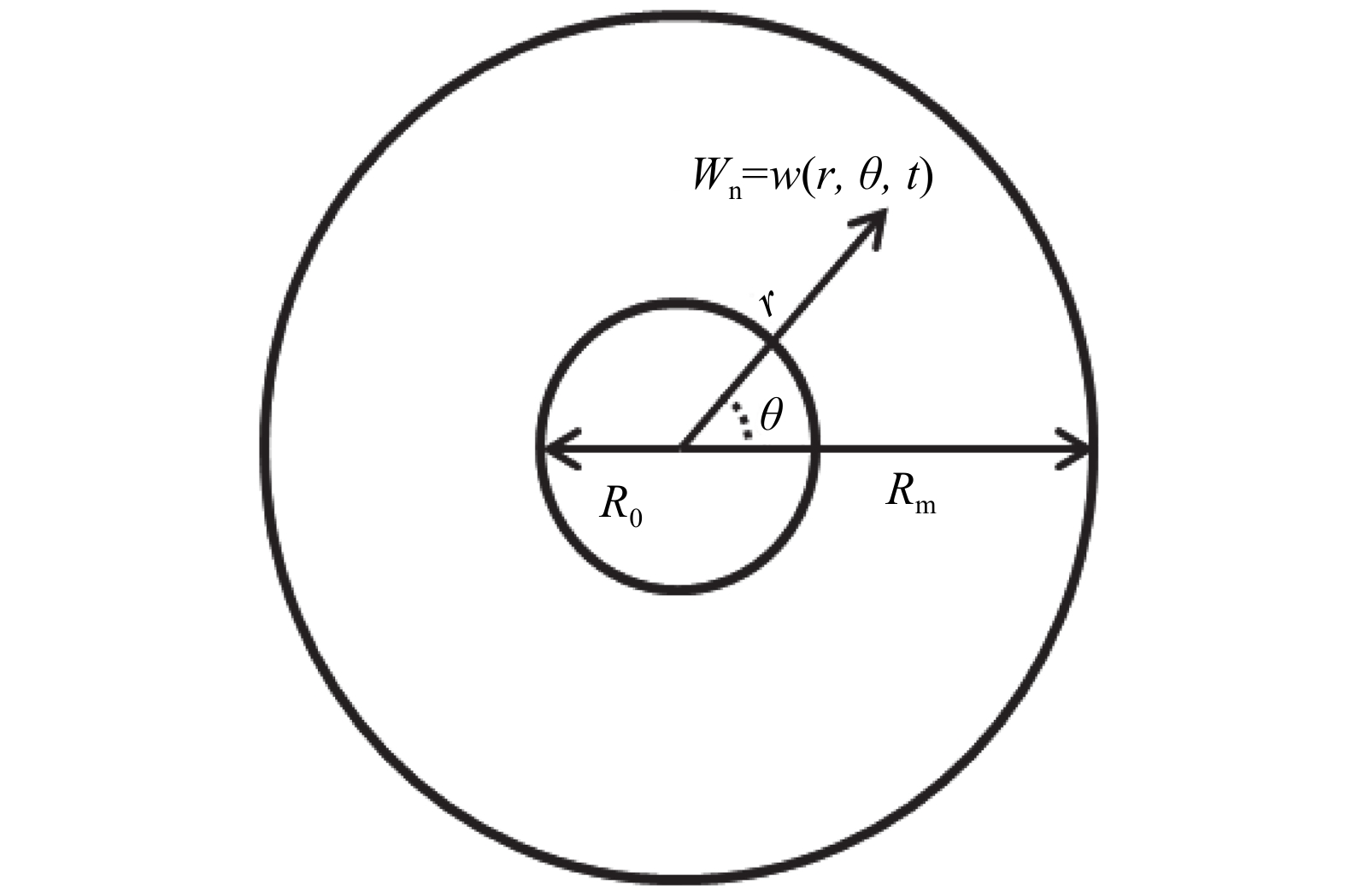 |
| 图13 轴对称圆形隧道模型 Fig. 13 Model of axisymmetric circular tunnel |
由上述讨论可知,后续研究的关键在于获得
进行了石膏岩的软化试验,结果表明:石膏岩的吸水率和泊松比随浸水时间增大,弹性模量随浸水时间衰减;水对石膏岩软化作用明显。基于试验结果,建立了吸水率、弹性模量和泊松比分别与浸水时间之间的定量关系。
建立了考虑软化效应的隧道围岩自稳时间解析模型。模型中考虑了岩体工程特性、岩石力学特性及岩石软化特性。
模型用于礼让隧道石膏段围岩分级。基于该模型的分级结果,提出有效的措施应用于现场。
对模型进行了参数自洽分析。自稳时间随各参数的变化规律与实际情况相符,验证了本文模型的自洽性。
| [1] |
高谦,乔兰,吴顺川,等.地下工程系统分析与设计[M].北京:中国建材工业出版社,2005.
|
| [2] |
刘卫丰.隧道工程[M].北京:北京交通大学出版社,2012.
|
| [3] |
Li P, Zhang Z, Tao L. Stability ranking system of rockmass surrounding a large-scale underground cavern group[J]. Journal of Engineering Geology, 2004, 12(1): 25-29. |
| [4] |
Barton N,Lien R,Lunde J.Estimation of support requirements for underground excavations[C]//The 16th US Symposium on Rock Mechanics (USRMS).American Rock Mechanics Association,1975.
|
| [5] |
Bieniawski Z T.Classification of rock masses for engineering[M]//Rock Testing and Site Characterization.London:Pergamon Press,1973.
|
| [6] |
Myer L R,Brekke T L,Dare C T,et al.An investigation of stand-up time of tunnels in squeezing ground[C]//Rapid Excavation and Tunnelling Conference,San Francisco,1981:1415–1433.
|
| [7] |
Nguyen V M, Nguyen Q P. Analytical solution for estimating the stand-up time of the rock mass surrounding tunnel[J]. Tunnelling and Underground Space Technology, 2015, 47: 10-15. DOI:10.1016/j.tust.2014.12.003 |
| [8] |
朱汉华,孙红月,杨建辉.公路隧道围岩稳定性与支护技术[M].北京:科学出版社,2007.
|
| [9] |
Marchetti M E, Capra A J C. Analysis of circular tunnels in soft ground[J]. Tunnels and Tunnelling, 1986, 18: 45-48. |
| [10] |
Teng Hongwei, Ren Song, Jiang Deyi. Experimental study of mechanical properties of water-saturated weaken shale in gonghetunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 2657-2662. [藤宏伟, 任松, 姜德义. 共和隧道页岩饱水软化试验研究[J]. 岩石力学与工程学报, 2010, 29(1): 2657-2662.] |
| [11] |
Zhou Cuiying, Tan Xiangshao, Deng Yimei, et al. Research on softening micro-mechanism of special soft rock[J]. Journal of Rock Mechanics and Engineering, 2005, 24(3): 394-400. [周翠英, 谭祥韶, 邓毅梅. 特殊软岩软化的微观机制研究[J]. 岩石力学与工程学报, 2005, 24(3): 394-400.] |
| [12] |
Zhou Cuiying, Zhu Fengxian, Zhang Lei. Research on saturation test and softening critical phenomena of soft rocks[J]. Rock and Soil Mechanics, 2010, 31(6): 1709-1715. [周翠英, 朱凤贤, 张磊. 软岩饱水试验与软化临界现象研究[J]. 岩土力学, 2010, 31(6): 1709-1715.] |
| [13] |
Ren Song, Wen Yongjiang, Jiang Deyi. Experimental research on softening in mudstone interlayer[J]. Rock and Soil Mechanics, 2013, 34(11): 3110-3116. [任松, 文永江, 姜德义. 泥岩夹层软化试验研究[J]. 岩土力学, 2013, 34(11): 3110-3116.] |
| [14] |
Liang Weiguo, Zhang Chuanda, Gao Hongbo. Experimental study of mechanical properties of gypsum saturated in brine[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1156-1162. [梁卫国, 张传达, 高红波. 盐水浸泡作用下石膏岩力学特性试验研究[J]. 岩石力学与工程学报, 2010, 29(6): 1156-1162.] |
| [15] |
蔡美峰.岩石力学与工程[M].北京:科学出版社,2002.
|
| [16] |
Chen Jie.Catastrophic mechanism induced by damaged surrounding rock and mitigation principle during bedded salt cavern construction period[D].Chongqing :Chongqing University,2012. [陈结.含夹层盐穴建腔期围岩损伤灾变诱发机理及减灾原理研究[D].重庆:重庆大学,2012.]
|
| [17] |
Wood A M M. Development of tunnel support philosophy[J]. Excavation,Support and Monitoring, 2016, 4: 349. |
| [18] |
Angel M L, Johnston S, O’steen K. Groundwater control issues in transportation engineering:A short review of dewatering methods and lessons learned[J]. Journal of Engineering Science and Technology Review, 2015, 8(3): 8-13. |
| [19] |
Wu Q D, Yan B, Zhang C. Displacement prediction of tunnel surrounding rock:A comparison of support vector machine and artificial neural network[J]. Mathematical Problems in Engineering, 2014, 1-6. |
| [20] |
李文江,朱永全.隧道力学[M].上海:机械工业出版社,2013.
|
| [21] |
Turymbetov T, Azhikhanov N, Zhunisov N, et al. Stress-strain state of two diagonal cavities weighty inclining layered massif system with slots in terms of elastic-creep deformations ☆[J]. Procedia-Social and Behavioral Sciences, 2015, 195:2263–2271.
|
 2017, Vol. 49
2017, Vol. 49


