2. 中国科学院大学,北京 100049
2. Chinese Academy of Sciences Univ., Beijing 100049, China
随着移动互联网和大数据的快速发展,数据存储量呈现爆炸式的增长,致使存储系统的规模日益扩大,进而导致了越来越多磁盘和扇区同时出错的概率。存储系统的可靠性和可用性受到了极大的挑战。为保障数据的可靠性,存储容灾技术成为目前存储系统研究的重点课题之一。
复制备份的存储容灾策略由于操作简单,实施方便,成为当前常用的一种存储容灾技术,但是,其不超过50%的存储空间利用率造成了极大的空间浪费,特别是在大规模存储系统中,导致了高昂的存储成本开销。因此,编码存储容灾技术应运而生,受到越来越多的关注。
现有编码存储容灾技术可以划分为两大类:一类是确定性存储容灾技术,另一类是概率性存储容灾技术。确定性存储容灾技术一般采用固定的编译码参数,并具有严格的存储结构布局,能百分之百实现其容灾能力之内失效数据的译码恢复,通常具有最大距离可分(maximum distance separable,MDS)性质。进一步地,确定性存储容灾技术又可以划分为两类:一类是基于XOR运算的阵列码方案,典型的如EVENODD码[1]、X-Code[2]、RDP码[3]、D-Code[4]等,它们基于XOR运算,具有较高的编译码速率和更新效率,并具有MDS性质等优点,同时,也具有编码参数受到素数的限制,冗灾能力不超过3,存储结构难以线性扩展等缺点,致使其在大规模存储系统中的应用受到了极大的限制。另一类是基于有限域运算的纠删码方案,典型的如RS[5](Reed-Solomon)码、CRS[6](Cauchy Reed-Solomon)码等,其编译码参数在有限域范围内可灵活设置,具有一定的扩展能力和灵活性,从而其冗灾能力也可在有限域范围内灵活设置,同时也具有MDS性质。但是,由于有限域上的运算复杂度随着有限域规模的增大呈指数级增长,因此,在较大规模存储系统中,有限域运算效率严重影响了编译码速率,进而影响了存储系统的整体性能。对此,Luo等[7–8]进行了有限域运算算法及CPU缓存利用上的改进;Plank等[9]进行了一些指令集上的优化,但在较大规模参数下的运算效率依然不高。此外,为了应对实际存储系统中频发的扇区错,Blaum和Plank[10]提出了SD码;作为SD码的改进,Li等[11]提出了Stair码,进一步加强了存储系统的可靠性,但是它们仍然需要面对大规模有限域运算复杂度高这一难题。
概率性存储容灾技术完全基于XOR运算,同时编译码参数不受素数限制,具有很高的灵活性和扩展能力,并以可控的概率实现译码恢复,逐渐受到越来越多的关注,典型的如LDPC码[12](low-density parity-check)、Tornado码[13]、LT码[14]、Raptor码[15]等。1962年,Gallager提出了LDPC码,鉴于其稀疏性及基于XOR运算具有很高的编译码速率,引起了学者们极大的兴趣。1997年,提出的Tornado码是一种级联的构造方式;2002年,提出的LT码实现了一种无码率构造方式;2006年,提出的Raptor码是一种对LT码的改进。目前,Tornado码已经应用在OceanStore[16]存储系统,LT码应用在Robustore[17]中。采用概率性存储容灾方案的优势在于:1)因为现实环境中的数据容灾系统的可靠性多以概率指标来衡量,符合事物的本性;2)由此途径有希望进一步寻求容灾性能(比如系统的可扩展性能、更高的容灾指标等)的突破。其缺点在于译码成功的概率性,但可以将其限制在一个可控的范围内。
针对大数据时代高容灾易扩展存储系统的要求,作者提出了一种基于随机矩阵的RAID容灾存储方法—随机阵列码(random RAID,R-RAID)。通过增加随机冗余δ,可保证很高的译码成功率,此外,随机阵列码还具有编译码参数可灵活设置,编译码效率较高以及近似MDS性质等特点。因此,适用于当前大规模RAID阵列存储容灾系统。
1 RAID存储模型RAID存储系统通常采用条带化技术实现数据的高效容灾存储,各条带在编译码关系上是相互独立的,因此,本文提出的随机阵列码聚焦于RAID存储系统中的一个条带进行编码容灾存储的研究。
图1为RAID存储系统中的一个条带(stripe)。该条带由N个磁盘中处于相同位置的一段连续存储空间组成,称为N个组块(chunk或strip),每个组块由r个块(block)构成,从而,可将该条带看做一个r×N的块阵列。在这N个组块中,T个组块被专门用来存储编码数据。另外,剩余的(N–T)个组块中,δ个块也被用来进行编码,称之为随机冗余,这些块可以在(N–T)个组块中均匀地分布。图1所示的条带中白色部分存储原始数据,阴影部分存储编码冗余数据。
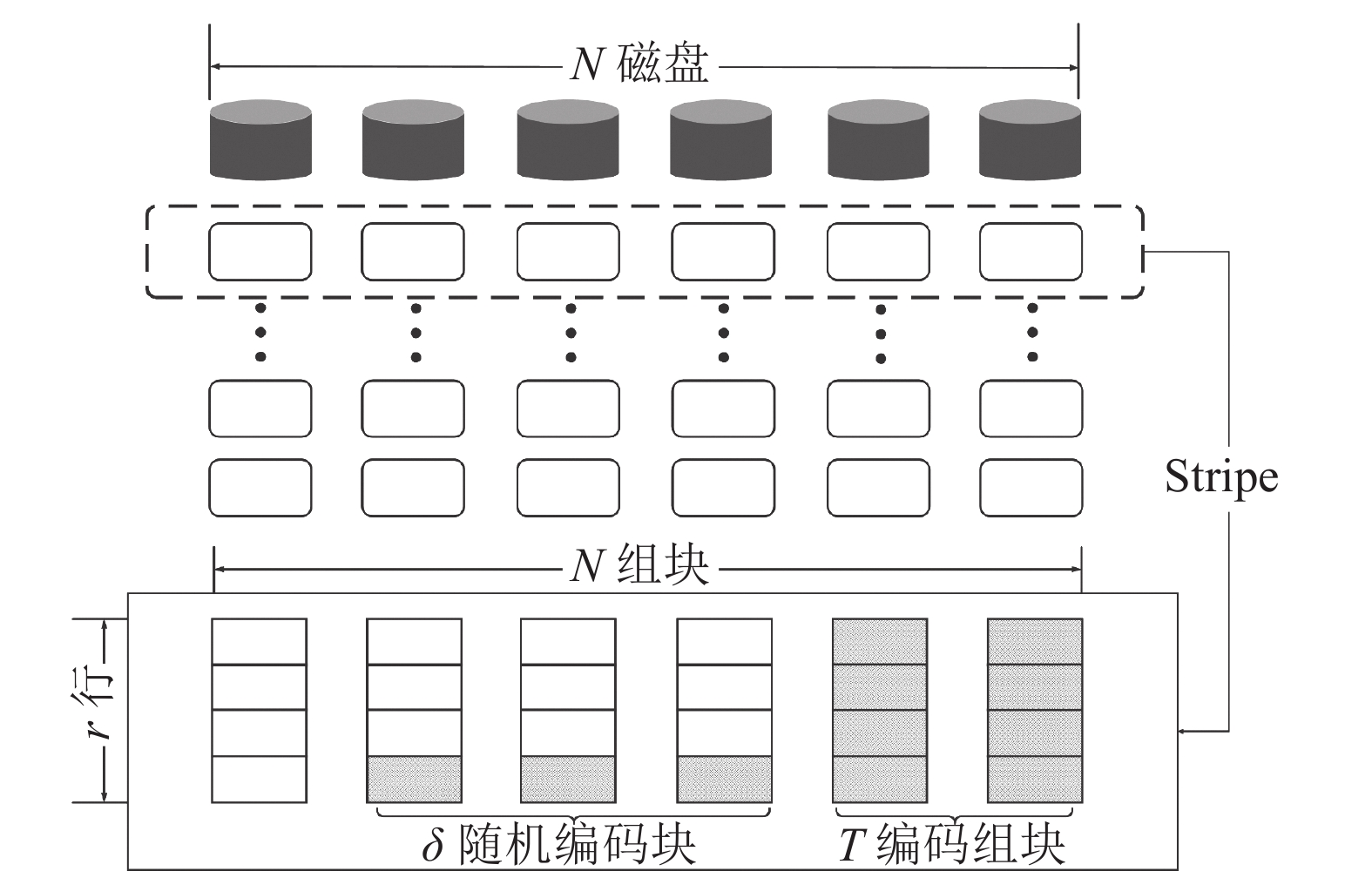 |
| 图1 RAID存储系统中的条带结构 Fig. 1 A stripe in a RAID storage system |
作为RAID中的基本单元——块,既可以是一个扇区,也可以是多个扇区的组合,因此,块、扇区在本文中是通用的。
RAID存储系统经常遭受磁盘失效和扇区失效的情况。磁盘失效的情况可以被映射为条带中对应磁盘上组块的失效,而扇区失效则可以被映射为对应磁盘中块的失效。目前,纠删编码技术已经被用于实际存储系统中以预防数据的丢失。随机阵列码是一类具有近似最优存储空间利用率的高容灾易扩展的纠删编码方案,可以有两种层面的表述方式:1)从宏观磁盘上来看,它是一种MDS编码方案。(n,k)MDS码具有特点为,k个原始数据编码生成n个编码数据,其中,任意k个数据均可由剩余的(n–k)个数据恢复出来。对于随机阵列码而言,其任意T个组块失效,均可由剩余的(N–T)个组块恢复,因此,宏观上随机阵列码是一种MDS编码方案,可表示为(
此外,参数T作为可容灾的盘数,是随机阵列码容灾能力的一种体现。一般地,定义RAID存储系统的容灾能力(Fault tolerance,F)为存储系统中最大可删除的盘数或块数占整个存储区域的比例。对于随机阵列码有F=T/N。相对于传统阵列码,随机阵列码的编码参数不再受到素数的限制,因此其容灾能力可以超过3,实现更高的容灾能力。同时,由于随机阵列码中编码冗余分块的产生与RAID存储布局方式无关,其容灾只与失效块所占比例有关,因此它既可以实现传统阵列码磁盘模式的容灾,也可实现扇区–磁盘模式的容灾。而参数δ作为随机阵列码的随机冗余,是保证随机阵列码能够高概率译码的关键因素。
2 随机阵列码的编译码方案 2.1 编码过程随机阵列码是一类线性分组码,其每个编码数据块均可看作原始数据块的线性组合。通常线性分组码的编码过程可以表示为:
聚焦于存储系统中的一个条带,假设其实施者已经给出了存储系统的设计参数N、r,可根据RAID存储系统容灾需求得到T,根据译码成功率需求得到随机冗余δ。从而,随机阵列码的编码冗余数据可以按照算法1产生。
算法1 随机阵列码编码流程
输入:该条带含N个磁盘,T个编码盘,随机冗余δ,条带的行数为r。
输出:编码冗余数据。
1. 计算
//构造编码矩阵
2. 构造
3. if
4. goto步骤2;
5. end if
6. 利用初等矩阵变换将
7. 编码矩阵
//产生编码冗余
8. 将原始数据平均分为k个块,不足的位补零;
9. 在(N–T)个数据盘中依次选取k个块存放原始数据块;
10. 利用公式
11. 将编码数据
12. 编码结束。
根据算法1可知,随机阵列码的编码效率重点在于G下半部分的矩阵D中元素为“1”的个数。特别地,当随机矩阵为均匀分布时,G矩阵下半部分矩阵D中元素“1”的平均数目约为
图2为存储系统中某条带参数为
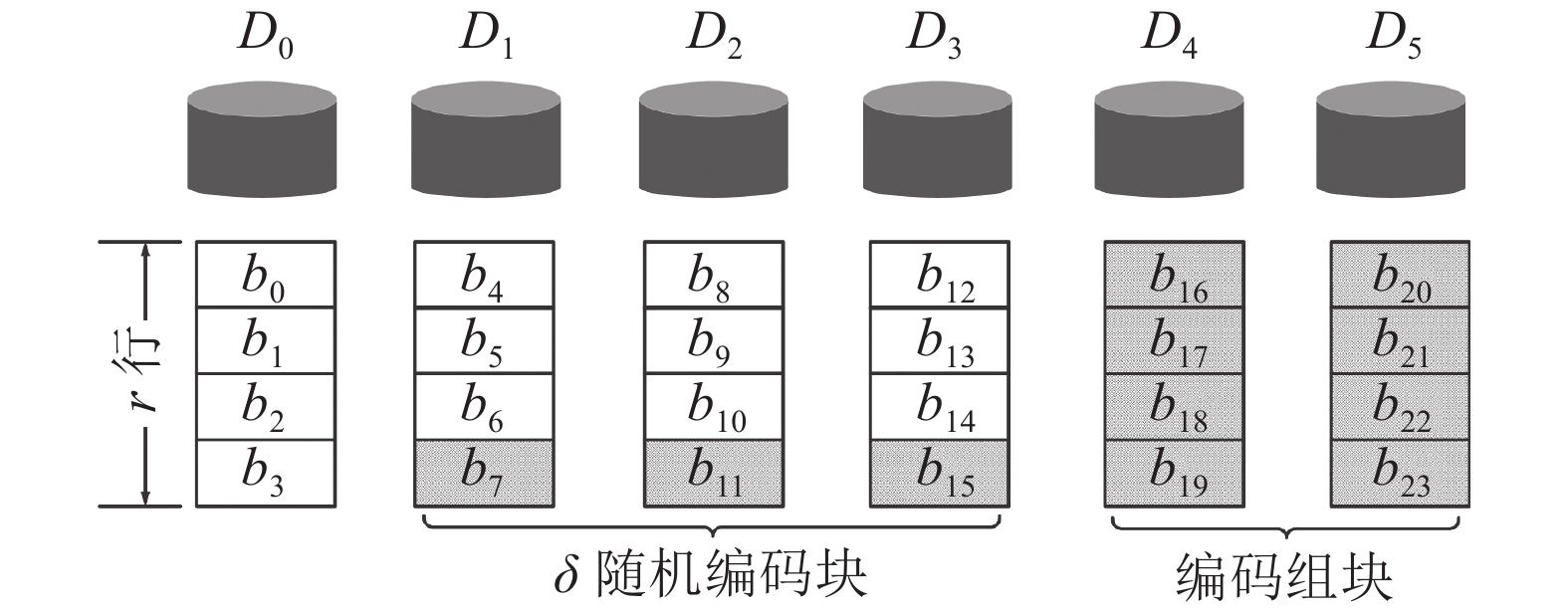 |
| 图2 (6, 4)随机阵列码存储示意图 Fig. 2 (6, 4)Random RAID code |
2.2 译码过程
当RAID存储系统中由于磁盘损毁或扇区损坏等原因导致编码数据丢失时,也即条带中对应的组块或块失效时,可根据损毁程度进行失效数据的译码恢复。
定义条带上的失效率s为条带中失效编码块数或磁盘数占整个条带中编码块数或编码盘数的比例。
线性分组码通常利用校验矩阵进行译码恢复:
算法2 随机阵列码译码流程
输入:编码矩阵G,容灾能力F。
输出:失效数据块数据。
1. 统计存储条带中的失效块数;
2. 计算该条带的失效率s;
3. if
4. 失效数据块过多,超过容灾能力F,无法恢复失效数据,重构失败;
5. return
6. end if
7. 标记失效编码块上的数据为未知;
8. 根据生成矩阵G产生校验矩阵H;
9. 提取H中失效数据块对应的行构建子矩阵
10.将未失效数据块信息代入译码方程组中,得到数据块向量B;
11. 化简
12. 求出子矩阵
13. 由
14. 方程的解即为失效数据块的数据,并将其依次放入失效数据块中;
15. 重构成功,译码结束。
由随机阵列码的译码过程可知,通过对校验矩阵子矩阵构造的译码矩阵广义逆矩阵的求解,可以减少因直接使用高斯消去法而产生的大规模数据块的频繁异或。特别地,当数据块规模较大时,数据块间的异或产生的译码开销也是非常大的,因此利用译码矩阵的广义逆进行失效数据块数据的求解。
由随机阵列码的译码方案可以看出,相对于确定性的阵列码,随机阵列码的译码只考虑整个条带的失效率,而对失效块的分布情况不用关心。特别地,假定条带中第1行的数据全部失效,传统阵列码方案如EVENODD码是无法恢复的;随机阵列码只要失效率低于其容灾能力,就可以恢复,从而具有更广的容错模式。
2.3 可行性分析随机阵列码的构造使用了
定理1 二元域
逐列增加随机矩阵的秩,显然定理1易证。
定理2 随机高矩阵
由定理1以及相关数学推导,定理2易证。
定理3
证明:假设
记
1)
2)记
根据已知条件,
| $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\; \text{证毕。}$ |
推 论 当
由定理3可知,若G中删除任意t行仍然列满秩,则H中对应的t行线性无关,也即译码矩阵有唯一解。从而,随机阵列能够成功译码的概率等价于G中删除任意t行仍然列满秩的概率。根据定理1、定理2可知,当
实验运行环境:测试所用计算机CPU为Intel(R)Core(TM)i3,3.07 GHz;内存4.0 GB;64位Ubuntu 15.10操作系统。
3.1 可行性分析选取
由图3可见,当δ ≥15时,对于任意的k,随机高矩阵
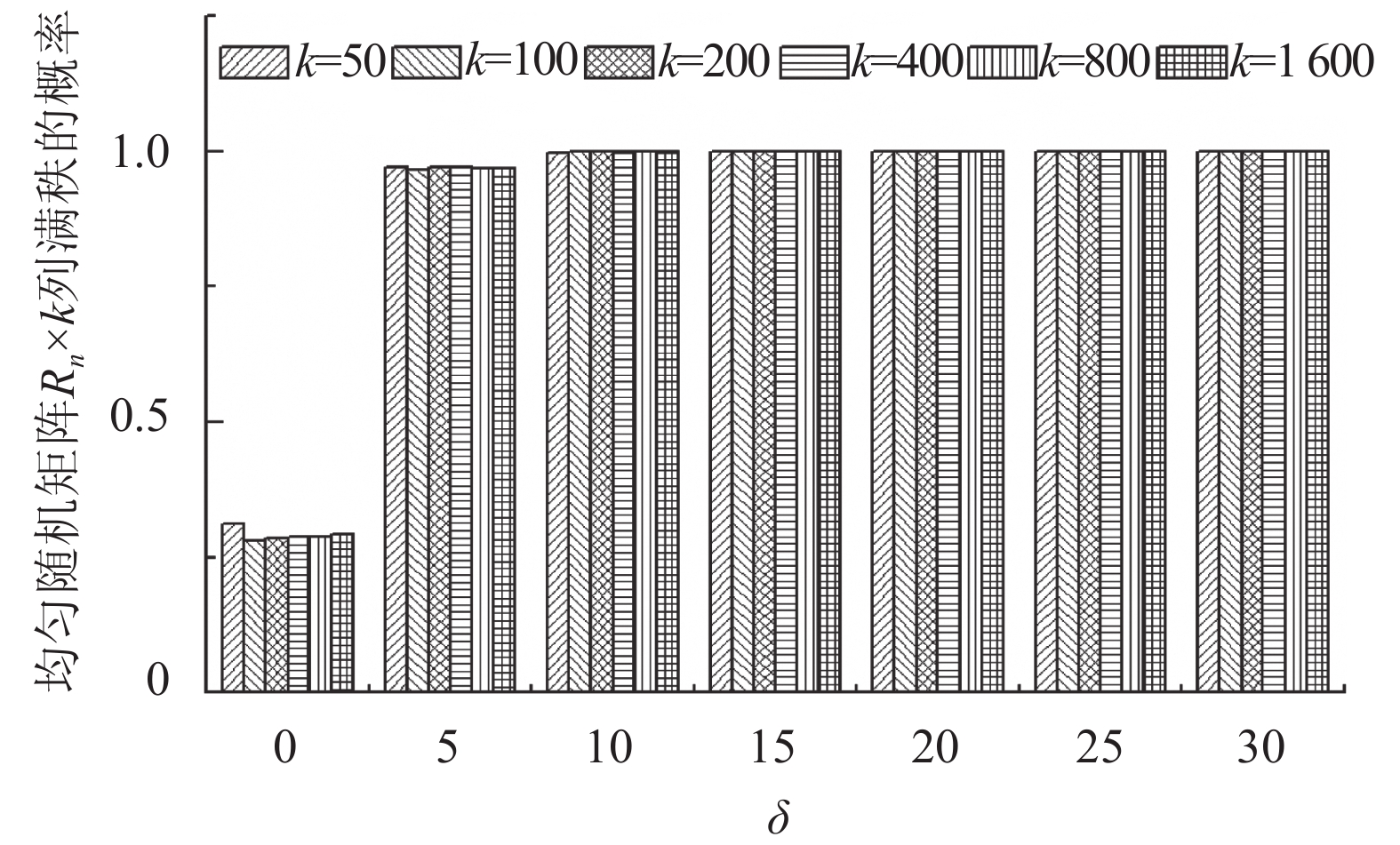 |
| 图3 不同规模均匀随机矩阵列满秩概率图 Fig. 3 Full column rank probability of different uniform random matrices |
3.2 编码参数及容灾能力
随机阵列码与部分现有的确定性存储容灾技术和概率性存储容灾技术在编码参数上的对比如表1所示。
| 表1 编码参数对比 Tab. 1 Comparison of coding variables |
 |
由表1可知:对于确定性存储容灾技术之基于XOR的传统阵列码方案,如EVENODD、X-Code、RDP等,编码参数u(u>2)受限于素数的影响,只能产生一些固定结构的编码方案,相应地,其容灾能力也受到影响,一般只为2~3。而其优势在于具有MDS性质并基于XOR运算,因此具有最优的存储空间利用率和较高编译码速率。对于基于有限域上的编码方案,如RS码、CRS码等,其编码参数可以在有限域范围内灵活设置,相应的容灾能力也可以灵活设置,且均为MDS码,因此其存储空间利用率也可以达到最优。但是,由于有限域上的运算随着有限域规模的增大,计算复杂度呈指数级增长,因此,在较大规模的有限域中,其编译码速率很低(详见第3.3节)。对于概率性存储容灾技术,如LDPC、Tornado码、LT码,其编码参数可以灵活设置,其容灾能力也可以灵活设置。此外,它们基于XOR运算,具有较高编译码效率。但是,由于其概率性译码和非MDS特性,为了保证高概率译码通常需要较多的编码冗余块,因此其存储空间利用率一般较低。而随机阵列码吸取各方所长,既基于XOR运算,又可达到近似MDS性质,从而,其编译码效率较有限域方式较高,而存储空间利用率较LT码等方式也较高,同时还具有容灾扩展性。因此,具有很好的研究和应用价值。
3.3 性能分析假定原始文件大小为256 MB,存储系统的容灾能力F=20%,随机冗余δ=20,随机概率p=0.5。不同码长下,构造随机阵列码方案与Plank提供的Jerasure2.0库中经过SIMD指令集优化的相应RS码及CRS码方案,并进行编译码效率比较。
1)编码速率比较
选取码长n=100~1 000,间隔100,根据存储系统的容灾能力设置相应的编译码参数,构造编码方案进行编码速率比较。
由图4可见,在相同码长下,随机阵列码方案较相应的RS码、CRS码方案,其编码速率更快。这主要是由于基于XOR运算的随机阵列码较使用有限域运算的RS码在运算效率上更高。尽管CRS码本质上采用了XOR运算,但由于其是在有限域
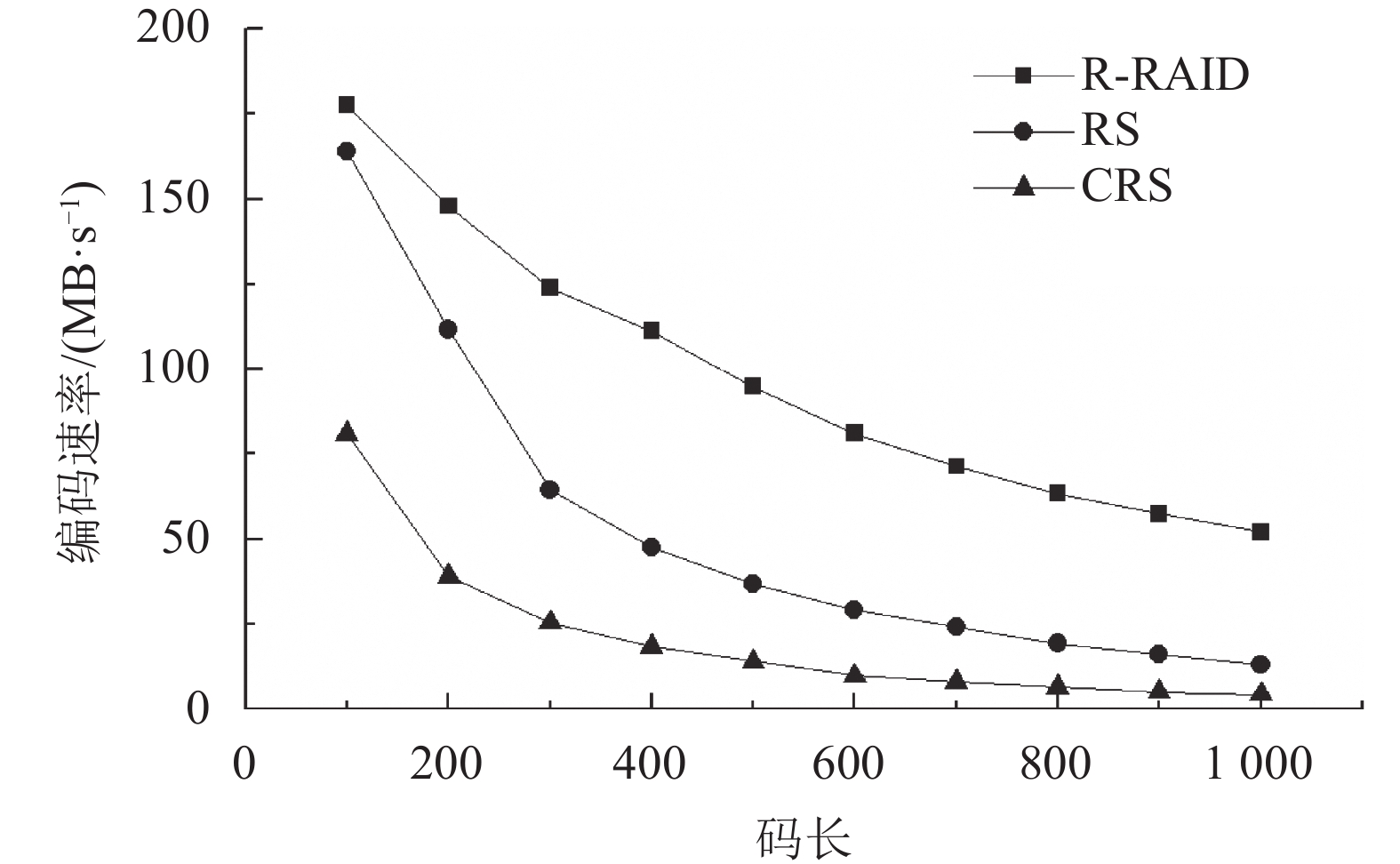 |
| 图4 编码速率比较 Fig. 4 Comparison of encoding speeds |
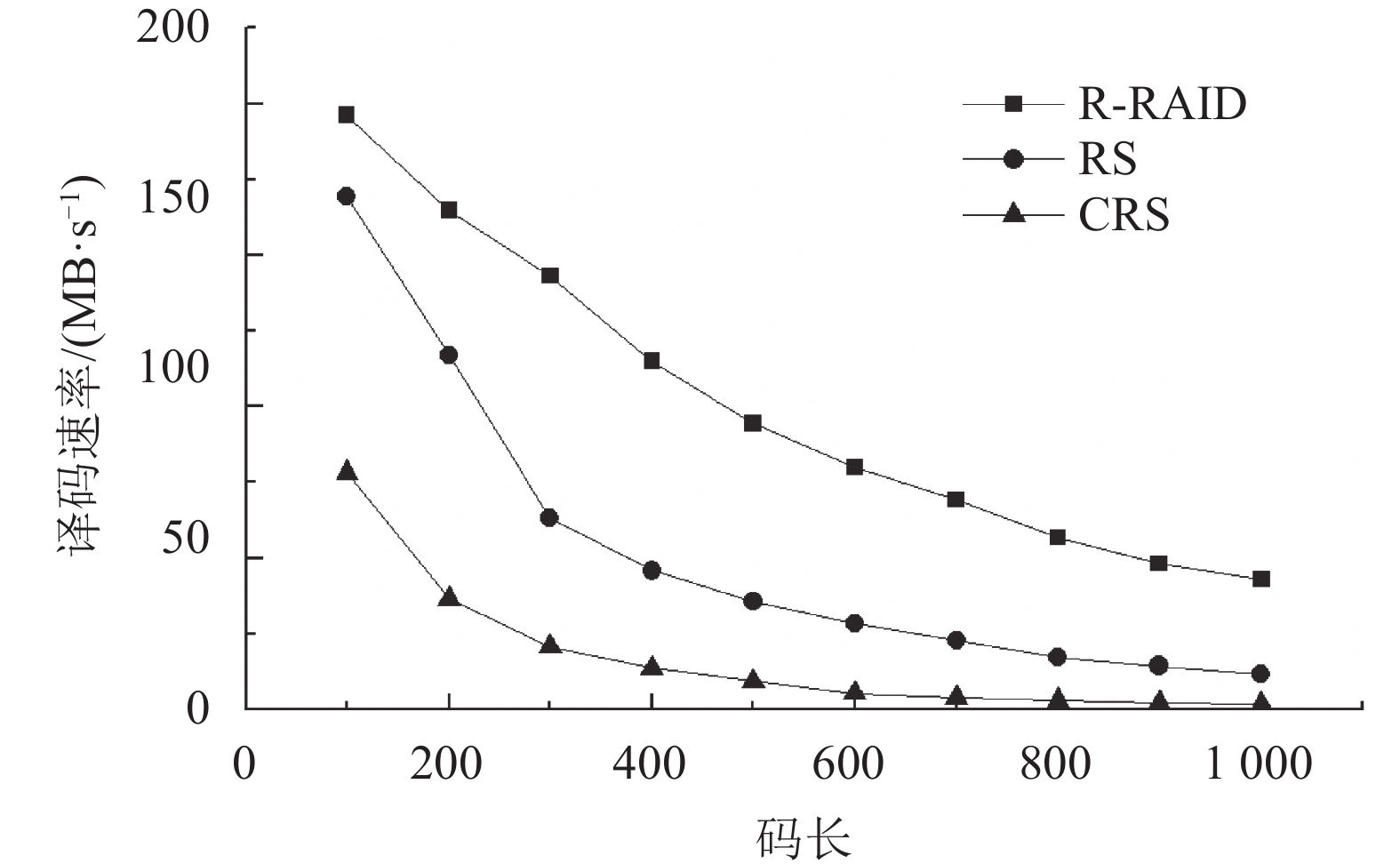 |
| 图5 译码速率比较 Fig. 5 Comparison of decoding speeds |
2)译码速率比较
当条带中存在容灾能力允许下最大可删除的块数丢失时,也即t个删除块时,可利用该条带中剩余的块进行译码恢复。
由图5可见,在相同码长及删除块数下,随机阵列码方案较相应的RS码、CRS码方案,其译码速率更快。这进一步说明采用XOR运算较有限域运算具有巨大优势。另外,随着码长的增大,三者的译码速率均呈下降趋势,但是随机阵列码的译码速率下降速度更慢。
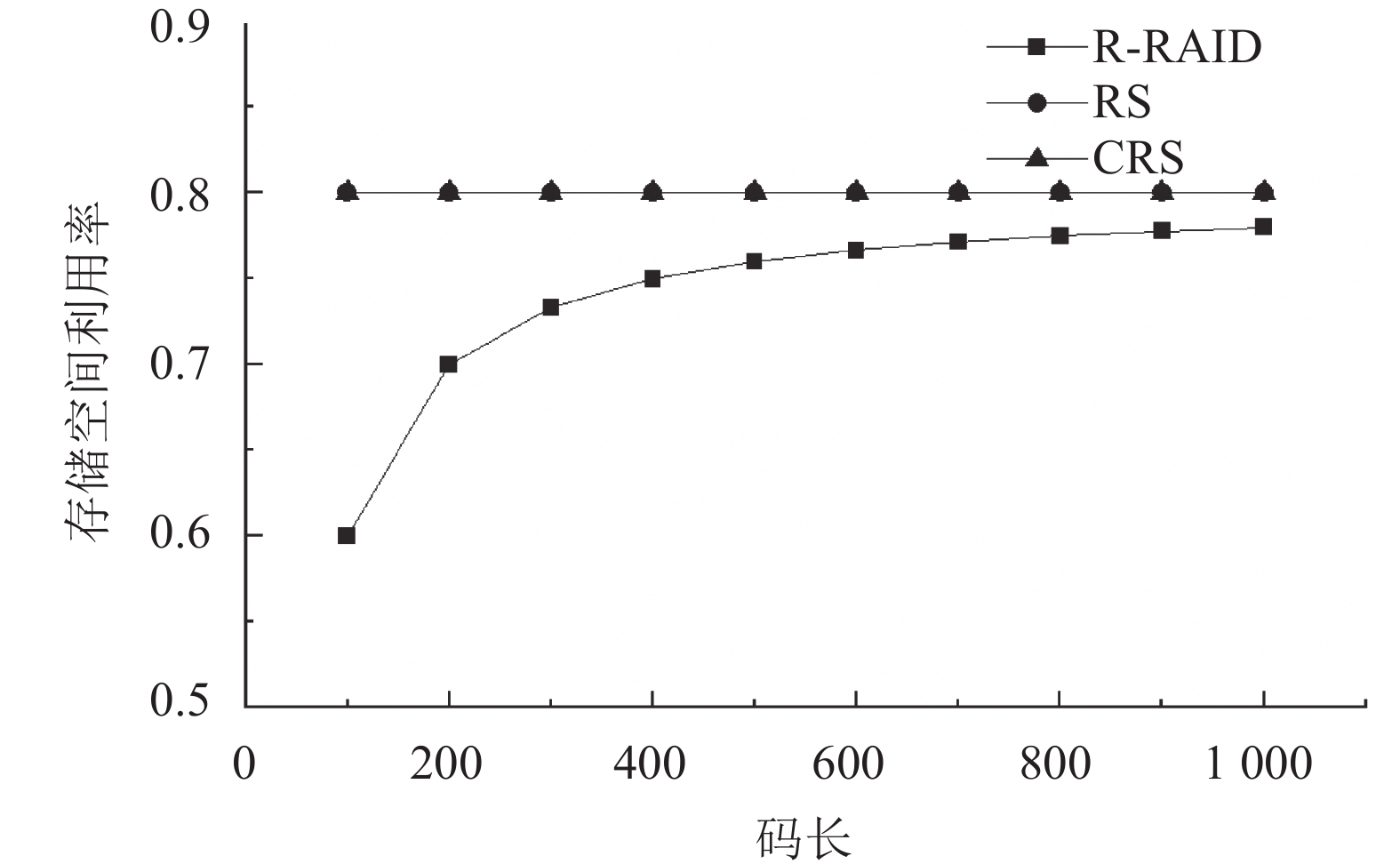 |
| 图6 存储空间利用率比较 Fig. 6 Comparison of storage efficiency |
3)存储空间利用率比较
当前大规模存储系统中,存储空间利用率是一个很重要衡量标准,也是纠删码方案替代复制方案的重要驱动之一。存储空间利用率反映了在保证存储容灾能力的情况下,存储容灾技术对存储空间的使用情况有两种表达方式:可利用原始数据量占整个存储区域的比例进行描述;也可利用恢复k个数据块,所需要的编码块数量衡量。根据后一种表述方式,对于随机阵列码,高概率恢复k个数据块需要
由图6可见,随着码长的不断增加,随机阵列的存储空间利用率越来越接近RS和CRS方案。由于RS和CRS方案具有MDS性质,因此,随机阵列码在较大码长时可具有近似MDS性质。
综上所述,随机阵列码随着k的增长,恢复k个数据块所需的编码块数量将越来越接近k,而Tornado码和LT码所需的编码块数量均呈k的倍数级增长。显然,随机阵列码相较于Tornado码和LT码具有更优的存储空间利用率。
4)更新效率比较
根据随机阵列码的构造方案可知,在一个条带中对于k个原始数据块,需要m个编码块进行容灾,因此,根据随机阵列码的随机性特点,每更新一个原始数据块,最坏情况下m个编码块均要更新。特别地,对于均匀随机矩阵,由于矩阵中每行每列中为“1”的元素比较均匀,因此,每更新一个原始数据块,平均需要更新m/2个编码冗余块;对于稀疏随机矩阵,平均需要更新的编码冗余块数将更少。对于RS码来讲,每更新一个原始数据块,则条带中所有的编码块都要更新一遍,因此其更新次数也为编码块的数目m。对于LT码来讲,根据文献[14],要覆盖所有k个输入块,编码块的度和约为
依据随机高矩阵高概率列满秩的特性,提出了一种随机阵列码编译码方案。与确定性存储容灾技术之传统阵列码如EVENODD码、X码等相比,随机阵列码具有编码参数不受素数限制,容灾能力随规模扩展可灵活扩展等优势。与确定性存储容灾技术之基于有限域运算的编码方案如RS码、CRS码相比,随机阵列码采用XOR运算,避免了有限域上高昂的计算开销,具有较高的编译码速率。与概率性存储容灾技术如Tornado码、LT码比较,随机阵列码又具有较高的存储空间利用率,因此,具有良好的研究价值和广阔的应用前景。
本文提出的随机阵列码为RAID存储容灾系统的概率性存储容灾技术提供了一种新的思路和解决方案。该方案还有需要进一步解决的问题,例如,如何构建更稀疏的编译码矩阵,以及编译码效率的改进提升等问题,都将成为下一步的研究工作。
| [1] |
Blaum M, Brady J, Bruck J. EVENODD:An efficient scheme for tolerating double disk failures in RAID architectures[J]. IEEE Transactions on Computers, 1995, 44(2): 192-202. DOI:10.1109/12.364531 |
| [2] |
Xu L, Bruck J. X-code:MDS array codes with optimal encoding[J]. IEEE Transactions on Information Theory, 1999, 45(1): 272-276. DOI:10.1109/18.746809 |
| [3] |
Corbett P,English B,Goel A,et al.Row-diagonal parity for double disk failure correction[C]//Proceedings of the 3rd USENIX Conference on File and Storage Technologies.San Francisco:USENIX Association,2004:1–14.
|
| [4] |
Fu Y,Shu J.D-Code:An efficient RAID-6 code to optimize I/O loads and read performance[C]//Proceedings of the 2015 IEEE International Parallel and Distributed Processing Symposium (IPDPS).Hyderabad:IEEE,2015:603–612.
|
| [5] |
Reed I S, Solomon G. Polynomial codes over certain finite fields[J]. Journal of the Society for Industrial & Applied Mathematics, 1960, 8(2): 300-304. |
| [6] |
Plank J S,Xu L.Optimizing Cauchy Reed-Solomon codes for fault-tolerant network storage applications[C]//Proceedings of the 2006 Fifth IEEE International Symposium on Network Computing and Applications.Massachusetts:IEEE,2006:173–180.
|
| [7] |
Luo J, Bowers K D, Oprea A. Efficient software implementations of large finite fields GF (2n) for secure storage applications
[J]. ACM Transactions on Storage, 2012, 8(1): 2. |
| [8] |
Luo J, Shrestha M, Xu L. Efficient encoding schedules for XOR-based erasure codes[J]. IEEE Transactions on Computers, 2014, 63(9): 2259-2272. DOI:10.1109/TC.2013.23 |
| [9] |
Plank J S,Greenan K M,Miller E L.Screaming fast Galois Field arithmetic using Intel SIMD instructions[C]//Proceedings of the FAST-2013:11th Usenix Conference on File and Storage Technologies.San Jose:USENIX,2013:299–306.
|
| [10] |
Plank J S, Blaum M. Sector-disk (SD) erasure codes for mixed failure modes in RAID systems[J]. ACM Transactions on Storage, 2014, 10(1): 4-20. |
| [11] |
Li M,Lee P P.STAIR codes:a general family of erasure codes for tolerating device and sector failures in practical storage systems[C]//Proceedings of the FAST-2014:12th USENIX conference on File and Storage Technologies.Santa Clara:USENIX,2014:147–162.
|
| [12] |
Gallager R G. Low-density parity-check codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21-28. DOI:10.1109/TIT.1962.1057683 |
| [13] |
Luby M G,Mitzenmacher M,Shokrollahi M A,et al.Practical loss-resilient codes[C]//Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing.El Paso:ACM,1997:150–159.
|
| [14] |
Luby M.LT codes[C]//Proceedings of the 43rd Symposium on Foundations of Computer Science.Washington,DC: IEEE,2002:271–280.
|
| [15] |
Shokrollahi A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551-2567. DOI:10.1109/TIT.2006.874390 |
| [16] |
Kubiatowicz J, Bindel D, Chen Y. Oceanstore:An architecture for global-scale persistent storage[J]. ACM Sigplan Notices, 2000, 35(11): 190-201. DOI:10.1145/356989 |
| [17] |
Xia H,Chien A A.RobuSTore:A distributed storage architecture with robust and high performance[C]//Proceedings of the 2007 ACM/IEEE Conference on Supercomputing.New York:ACM,2007:44.
|
 2017, Vol. 49
2017, Vol. 49


