2. 咸阳师范学院 数学与信息科学学院,陕西 咸阳 712000
2. College of Mathematics and Info. Sci., Xianyang Normal Univ., Xianyang 712000, China
1971年,忆阻(memristor)(记忆(memory)和电阻(resistor)的缩写)首次由Chua[1]从理论上提出,他在研究物理电路时推断,除了电阻、电容、电感器3个基本电路元件外,还存在第4个元件即忆阻,它表示磁通与电荷的关系。尽管电阻和忆阻有相同的量纲和许多相同的性质,但电阻的阻值是由流经它的电流决定的,忆阻的阻值即忆阻值(memristance)是由流经它的电荷确定的,满足函数关系式
另一方面,耗散是物理系统的一种重要性质,耗散理论为控制系统的分析和设计提供了一个基于能量的输入–输出的描述性框架[7]。Wu等[7]指出:虽然耗散性与系统的稳定性存在紧密的关系,但是前者揭示系统的性能比后者多,比如,无源性、几乎扰动解耦、H∞控制等性能。而且无源理论、Kalman-Yakubovich引理、有界实引理等理论均可看作是耗散理论的特殊情况。随着线性矩阵不等式方法的发展,对各种动力系统的耗散问题进行了研究[8–14]。Zhang等[8]研究了随机混杂系统的可靠耗散问题。Wu等[9]考虑了离散随机神经网络的耗散问题。文献[10–14]研究了带有不同时滞的神经网络的耗散问题。Wu等[10]运用Jensen积分不等式来估计所构造KLF微分的上界,得到了较大保守性的耗散条件。Zeng等[11] 估计积分项上界时仅仅考虑了时滞上界d,而未考虑时滞d(t),这势必会带来一定的保守性。正如文献[15]所指出的,从数学角度看,基于自由权矩阵不等式[12]与Wirtinger积分不等式[16]在减少保守性方面的作用是相同的。而且与结合Wirtinger积分不等式和倒凸技术方法相比,它在处理时变时滞系统时,会引入更多的未知变量,这将带来较大的计算量。作为耗散的特例,文献[17–21]研究了时滞神经网络的无源问题。不同于文献[13,17–21],本文中的激活函数具有更一般的形式。
为了得到更弱保守性的耗散条件,本文从两方面进行了改进。
1)LKF的构造。本文构造的LKF中除了有目前常见的状态向量2次项、1重积分项和2重积分项外,还增加了时滞系数的状态向量2次项和3重积分项,这样的构造方法能更充分地考虑时滞d(t)、时滞上界d以及时滞微分
2)倒凸技术和Wirtinger积分不等式结合。用Wirtinger积分不等式处理积分项时,常常出现时滞项在分母上的情况,针对这种情况,常见的凸组合技术很难处理,然而倒凸技术能较好地消除这种情况,仅需增加少量的未知变量。
1 问题阐述和准备 1.1 模型描述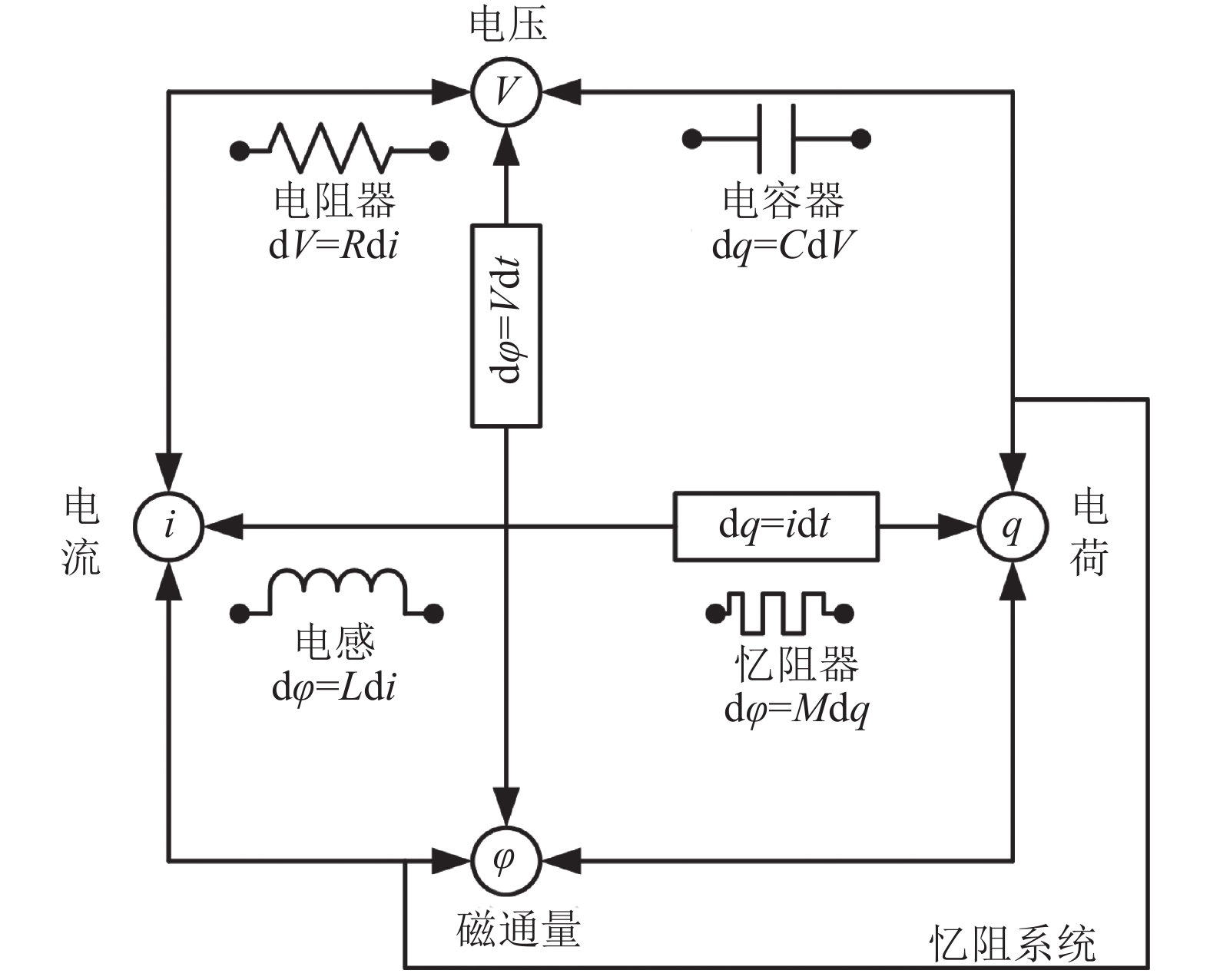 |
| 图1 4个基本二端电路元件关系图 Fig. 1 Four fundamental two-terminal circuit elements |
4个基本二端电路元件之间关系见图1。
正如文献[14]所述,由Krichoff电流定律,一类时滞神经网络第i个子系统为:
| $\left\{ {\begin{array}{*{20}{l}}\displaystyle\!\!\!{{{\dot x}_i}(t) = - {a_i}({x_i}(t)){x_i}(t) + }\\[3pt]\qquad \;\;\; \displaystyle{\sum\limits_{j = 1}^n {{w_{{{ij}}}}} ({x_i}(t)){f_j}({x_j}(t)) + }\\[5pt]\qquad \;\;\; \displaystyle{\sum\limits_{j = 1}^n {w_{ij}^{\left( 1 \right)}} ({{{x}}_i}(t)){f_j}({{{x}}_j}(t - {d_j}(t))) + {J_i}(t)}\text{;}\\\displaystyle\!\!\!{{{{y}}_i}(t) = {f_i}({{{x}}_i}(t)),t \ge {\rm{0, }}{\mathop{i}\nolimits} = 1,2, \cdots ,n}\text{;}\\[4pt]\displaystyle\!\!\!{{{{x}}_i}(t) = {\varphi _i}(t),t \in \left[ { - d,0} \right]}\end{array}} \right.$ | (1) |
式中:
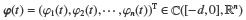
| $\begin{array}{l}\displaystyle{a_{{i}}}({{{x}}_i}(t)) = \frac{1}{{{C_i}}}[\sum\limits_{j = 1}^n {{\rm{sign}}_{ij}({M_{ij}} + {N_{ij}})} + {{\overline{R}}_i}],\\[10pt]\displaystyle{w_{ij}}({{{x}}_i}(t)) = \frac{{{\rm{sign}}_{ij}{M_{ij}}}}{{{C_i}}},w_{ij}^{{\rm{(1)}}}({x_i}(t)) = \frac{{{\rm{sign}}_{ij}{N_{ij}}}}{{{C_i}}}\text{。}\end{array}$ |
其中:符号函数
| $\begin{array}{l}{a_i}({x_i}(t)) = \left\{ \begin{array}{l}{\! \! \! {\hat a}_i},\;\left| {{x_i}(t)} \right| \le {I_i}\text{;}\\{\! \! \!{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_i},\;\left| {{x_i}(t)} \right| > {I_i}\text{。}\end{array} \right.\\[10pt]{w_{ij}}({x_i}(t)) = \left\{ \begin{array}{l}{\! \! \!{\hat w}_{ij}},\;\left| {{x_i}(t)} \right| \le {I_i}\text{;}\\[4pt]{\! \! \!{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} }_{ij}},\;\left| {{x_i}(t)} \right| > {I_i}\text{。}\end{array} \right.\\[10pt]w_{{\rm{ij}}}^{{\rm{(1)}}}({x_i}(t)) = \left\{ \begin{array}{l}\! \! \! \hat w_{ij}^{{\rm{(1)}}},\;\left| {{x_i}(t)} \right| \le {I_i}\text{;}\\[6pt]\! \! \!\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} _{ij}^{{\rm{(1)}}},\;\left| {{x_i}(t)} \right| > {I_i}\text{。}\end{array} \right.\end{array}$ |
其中,切换界值
由于系统(1)中的
| $\left\{ {\begin{aligned}& {{{\dot x}_i}(t) \in - {\rm{co}}\{ {{\hat a}_i},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_i}\} {x_i}(t) + \sum\limits_{j = 1}^n {{\rm{co}}\{ {{\hat w}_{{ij}}},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} }_{ij}}\} {f_j}({x_j}(t))} }+\\[-4pt]& \quad \quad \;\;\; { \sum\limits_{j = 1}^n {{\rm{co}}\{ \hat w_{ij}^{(1)},\mathord{\buildrel{\lower1pt\hbox{$\scriptscriptstyle\smile$}} \over w} _{ij}^{(1)}\} {f_j}({x_j}(t - {d_{\mathop{\rm j}\nolimits} }(t))) + {J_i}(t)} }\text{;}\\[-2pt]& {{y_i}(t) = {f_i}({x_i}(t)),t \ge {{0},i} = {\rm{1,2,}} \cdots ,n}\text{;}\\& {{x_i}(t) = {\varphi _i}(t),t \in \left[ { - d,0} \right]}\end{aligned}} \right.$ | (2) |
根据文献[6,13]的描述方式,
| $\left\{ \begin{aligned}& {{\dot x}_i}(t) = - {a_i}{x_i}(t) + \sum\limits_{j = 1}^n {{w_{ij}}} {f_j}({x_j}(t))+\\[-3pt]& \qquad \; \; \displaystyle\sum\limits_{j = 1}^n {w_{ij}^{\left( 1 \right)}} {f_j}({x_j}(t - {d_j}(t))) + {J_i}(t)\text{;}\\[-2pt]& \; {y_i}(t) = {f_i}({x_i}(t)),t \ge 0,i = 1,2, \cdots ,n\text{;}\\& \; {x_i}(t) = {\varphi _i}(t),t \in \left[ { - d,0} \right]\end{aligned} \right.$ | (3) |
其中:
满足系统(1)的初始条件
| $\begin{aligned}{{\dot x}_{\rm{i}}}(t) \in & - {\rm{co}}\{ {{\hat a}_i},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_i}\} {x_i}(t) + \sum\limits_{j = 1}^n {{\rm{co}}\{ {{\hat w}_{ij}},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} }_{ij}}\} } {f_j}({x_j}(t)) + \\& \sum\limits_{j = 1}^n{{\rm{co}}\{ \hat w_{ij}^{{\rm{(1)}}},\mathord{\buildrel{\lower1pt\hbox{$\scriptscriptstyle\smile$}} \over w} _{ij}^{{\rm{(1)}}}\} } {f_j}({x_{{j}}}(t - {d_j}(t))) + {J_i}(t)\text{。}\end{aligned}$ |
为了方便,式(3)也可写成向量形式:
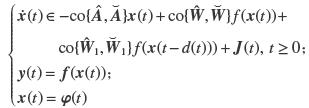
|
(4) |
或
式(4)中,矩阵区间
式(4)等价于:
| $\left\{ \begin{aligned}\dot {x}(t) = & - {\mathit{\boldsymbol{Ax}}}(t) + {\mathit{\boldsymbol{Wf}}}({\mathit{\boldsymbol{x}}}(t)) + \\& {{\mathit{\boldsymbol{W}}}_1}{\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{x}}}(t - d(t))) + {\mathit{\boldsymbol{J}}}(t),t \ge 0\text{;}\\{\mathit{\boldsymbol{y}}}(t) = & {\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{x}}}(t))\text{;}\\{\mathit{\boldsymbol{x}}}(t) = & {\mathit{\boldsymbol{\varphi }}}(t)\end{aligned} \right.$ | (5) |
显然
| $\begin{aligned}& {\text{co }}\{{{\hat {\mathit{\boldsymbol{A}}}}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\mathit{\boldsymbol{A}}} }}{\text{\} }} = [\underline {\mathit{\boldsymbol{A}}} ,{{\overline {\mathit{\boldsymbol{A}}}}}],{\rm{co}}\{ {\hat {\mathit{\boldsymbol{W}}}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\mathit{\boldsymbol{W}}} }}\} = [\underline {\mathit{\boldsymbol{W}}} ,{\overline {\mathit{\boldsymbol{W}}}}], \\& \hfill {\rm{co}}\{ {{\hat {\mathit{\boldsymbol{W}}}}_1},{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\mathit{\boldsymbol{W}}} }}}_1}\} = [{\underline {\mathit{\boldsymbol{W}}} _1},{{\overline {\mathit{\boldsymbol{W}}}}_1}] \text{。}\hfill \\ \end{aligned}$ |
其中:
| $\begin{array}{l}\;\;\;\; {\hat {\mathit{\boldsymbol{A}}}} = {({{\hat a}_i})_{{{n{\rm x}n}}}},{{\hat {\mathit{\boldsymbol{W}}}}} = {({{\hat w}_{ij}})_{{{n{\rm x}n}}}},{{{{\hat {\mathit{\boldsymbol{W}}}}}}_1} = {(\hat w_{ij}^{{{(1)}}})_{{{n{\rm x}n}}}},{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over {\mathit{\boldsymbol{A}}}} } = {({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_i})_{{{n{\rm x}n}}}},\\\;\;\; {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over {\mathit{\boldsymbol{W}}}} }} = {({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} }_{ij}})_{{{n{\rm x}n}}}},{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over {\mathit{\boldsymbol{W}}}} }}}_1} = {(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over w} _{ij}^{{{(1)}}})_{{{n{\rm x}n}}}},{\overline {\mathit{\boldsymbol{A}}}} = {({{\overline a}_i})_{{{n{\rm x}n}}}},{{ }}\underline {\mathit{\boldsymbol{A}}} = {({\underline a _i})_{{{n{\rm x}n}}}},\\[5pt]{\overline {\mathit{\boldsymbol{W}}}} = {({{\overline w}_{ij}})_{{{n{\rm x}n}}}},\underline {\mathit{\boldsymbol{W}}} = {({\underline w _{ij}})_{{{n{\rm x}n}}}},{{\overline {\mathit{\boldsymbol{W}}}}_1} = {(\overline w_{ij}^{\left( {{1}} \right)})_{{{n{\rm x}n}}}},{\underline {\mathit{\boldsymbol{W}}} _1} = {(\underline w _{ij}^{\left( {{1}} \right)})_{{{n{\rm x}n}}}},\\[5pt]\qquad \quad \;\;{\mathit{\boldsymbol{x}}}(t) = {\left[ {{x_1}(t),{x_2}(t), \cdots ,{x_{{n}}}(t)} \right]^{{\rm T}}} \in {{\mathbb{R}}^{{n}}},\\[5pt]{\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{x}}}(t)) = {[{f_1}({x_1}(t)),{f_2}({x_2}(t)), \cdots ,{f_{{n}}}({x_{{n}}}(t))]^{{\rm T}}} \in {{\mathbb{R}}^n},\\[5pt]{\mathit{\boldsymbol{f}}}({x}(t - d(t))) = [{f_1}({x_1}(t - d(t))),{f_2}({x_2}(t - d(t))),\\[5pt]\qquad \qquad \qquad \; \cdots ,{f_{{n}}}({x_{{n}}}(t - d(t))){]^{{\rm T}}} \in {{\mathbb{R}}^{{n}}},\\[5pt]\quad\quad\quad{\mathit{\boldsymbol{y}}}(t) = {[{y_1}(t),{y_2}(t), \cdots ,{y_{{n}}}(t),]^{{\rm T}}} \in {{\mathbb{R}}^{{n}}},\\[5pt]\quad\quad\quad{\mathit{\boldsymbol{J}}}(t) = {[{J_1}(t),{J_2}(t), \cdots ,{J_{{n}}}(t)]^{{\rm T}}} \in {{\mathbb{R}}^{{n}}}\text{。}\end{array}$ |
假 设 连续有界激活函数
| $l_j^{ - } \le \frac{{{f_j}(a) - {f_j}(b)}}{{a - b}} \le l_j^{ + }, j = 1, 2,\cdots ,n$ | (6) |
式中:
若b=0时,
| $l_j^{\rm{ - }} \le \frac{{{f_j}(a)}}{a} \le l_j^{\rm{ + }}$ | (7) |
下面介绍严格
定 义 给定对称矩阵G,T和矩阵S,对所有
引理1[16] 设
| $\begin{array}{l} - (b - a)\int\limits_a^b {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s)} {\mathit{\boldsymbol{R\dot x}}}(s){\rm{d}}s\le\\\quad \;\; - {[{\mathit{\boldsymbol{x}}}(b) - {\mathit{\boldsymbol{x}}}(a)]^{\rm{T}}}{\mathit{\boldsymbol{R}}}[{\mathit{\boldsymbol{x}}}(b) - {\mathit{\boldsymbol{x}}}(a)] - 3{{\mathit{\boldsymbol{\varOmega }}}^{\rm{T}}}{\mathit{\boldsymbol{R\varOmega }}}\text{。}\end{array}$ |
其中:
引理2[24] 对任意向量α1、α2,对称矩阵R和任意矩阵S,满足
| $\frac{1}{\beta }{\mathit{\boldsymbol{\alpha }}}_1^{\rm{T}}{\mathit{\boldsymbol{R}}}{{\mathit{\boldsymbol{\alpha }}}_1} + \frac{1}{{1 - \beta }}{\mathit{\boldsymbol{\alpha }}}_2^{\rm{T}}{\mathit{\boldsymbol{R}}}{{\mathit{\boldsymbol{\alpha }}}_2} \ge {{\mathit{\boldsymbol{\eta }}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}}{\mathit{\boldsymbol{R}}} & {\mathit{\boldsymbol{S}}}\\{\mathit{\boldsymbol{*}}} & {\mathit{\boldsymbol{R}}}\end{array}} \right]{\mathit{\boldsymbol{\eta }}}\text{。}$ |
其中,*表示对称矩阵的对称部分,
引理3[25] 对矩阵
| $\begin{array}{l}\displaystyle\frac{{{{(b - a)}^2}}}{2}\int\limits_a^b {\int\limits_\theta ^b {{{\mathit{\boldsymbol{\omega }}}^{\rm T}}(s){\mathit{\boldsymbol{R\omega }}}(s){\rm{d}}s{\rm{d}}\theta } } \ge \\\qquad \quad \displaystyle(\int\limits_a^b {\int\limits_\theta ^b {{\mathit{\boldsymbol{\omega }}}(s){\rm{d}}s{\rm{d}}\theta {)^{\rm{T}}}{\mathit{\boldsymbol{R}}}} } (\int\limits_a^b {\int\limits_\theta ^b {{\mathit{\boldsymbol{\omega }}}(s){\rm{d}}s{\rm{d}}\theta )} } \text{。}\end{array}$ |
给出保证时滞神经网络系统严格耗散的时滞依赖稳定性条件。
定 理 给定d>0,μ;如果存在2n×2n维正定矩阵
| ${\mathit{\boldsymbol{\varXi}}} < 0$ | (8) |
| ${\mathit{\boldsymbol{\varGamma }}} = \left[ {\begin{array}{*{20}{c}}{{{{{\overline {\mathit{\boldsymbol{Z}}}}}}_{\rm{2}}}} & {\mathit{\boldsymbol{X}}}\\{\rm{*}} & {{{{{\overline {\mathit{\boldsymbol{Z}}}}}}_{\rm{2}}}}\end{array}} \right] \ge 0$ | (9) |
则系统(5)为严格
| $\begin{aligned}&\text{其中:} {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t) = [{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t)\quad {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t - d(t))\quad {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t - d)\quad {{\mathit{\boldsymbol{f}}}^{\rm{T}}}({\mathit{\boldsymbol{x}}}(t))\\& \qquad \qquad \quad \;\;\; {{\mathit{\boldsymbol{f}}}^{\rm{T}}}({\mathit{\boldsymbol{x}}}(t - d(t)))\quad {{\mathit{\boldsymbol{f}}}^{\rm{T}}}({\mathit{\boldsymbol{x}}}(t - d))\quad {\mathit{\boldsymbol{\varepsilon }}}_{\rm{1}}^{\rm{T}}(t)\quad {\mathit{\boldsymbol{\varepsilon }}}_{\rm{2}}^{\rm{T}}(t)\\& \qquad \qquad \quad \;\;\;{{\mathit{\boldsymbol{J}}}^{\rm{T}}}(t){]^{\rm{T}}}\text{;}\\& \quad \quad \;\;{{\mathit{\boldsymbol{e}}}_i} = [{0_{n \times (i - 1)n}} \quad {{\mathit{\boldsymbol{I}}}_{{n}}} \quad {0_{n \times (9 - i)n}}]\text{,}i = 1,2, \cdots ,9\text{;}\\& \quad \;\;{{\mathit{\boldsymbol{{\varSigma}}}}_1} = {\rm{diag}}\{ l_1^ + ,l_2^ + , \cdots ,l_n^+\} \text{,}{{\mathit{\boldsymbol{{\varSigma}}}}_2} = {\mathop{\rm diag}\nolimits} \{ l_1^ - ,l_2^ - , \cdots ,l_{{n}}^- \}\text{,}\\& {\rm{diag}}\{ \cdot \} \text{表示对角矩阵;} {{\mathit{\boldsymbol{\varPi }}}_1} = {[{\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}\;\;d(t){\mathit{\boldsymbol{e}}}_7^{\rm{T}} + (d - d(t)){\mathit{\boldsymbol{e}}}_8^{\rm{T}}]^{\rm{T}}}\text{;}\\& \qquad \qquad {{\mathit{\boldsymbol{\varPi }}}_2} = {[ - {\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}{{\mathit{\boldsymbol{A}}}^{\rm{T}}} + {\mathit{\boldsymbol{e}}}_{\rm{4}}^{\rm{T}}{{\mathit{\boldsymbol{W}}}^{\rm{T}}} + {\mathit{\boldsymbol{e}}}_{\rm{5}}^{\rm{T}}{\mathit{\boldsymbol{W}}}_{\rm{1}}^{\rm{T}} + {\mathit{\boldsymbol{e}}}_{\rm{9}}^{\rm{T}}]^{\rm{T}}}\text{;}\\& \quad {{\mathit{\boldsymbol{\varPi }}}_3} = {[{{\mathit{\boldsymbol{\varPi }}}_2} \quad {\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}} - {\mathit{\boldsymbol{e}}}_3^{\rm{T}}]^{\rm{T}}}\text{;}{{\mathit{\boldsymbol{\varPi }}}_{i + 3}} = {[{\mathit{\boldsymbol{e}}}_i^{\rm{T}}\;\;{\mathit{\boldsymbol{e}}}_{{i + 3}}^{\rm{T}}]^{\rm{{\rm{T}}}}}\text{,}i = 1,2,3\text{;}\\& \qquad \quad {{\mathit{\boldsymbol{\varPi }}}_i} = {[{\mathit{\boldsymbol{e}}}_{i - 6}^{\rm{{\rm{T}}}} - {\mathit{\boldsymbol{e}}}_{i - 5}^{\rm{T}} \quad {\mathit{\boldsymbol{e}}}_{i - 6}^{\rm{T}} + {\mathit{\boldsymbol{e}}}_{i - 5}^{\rm{T}} - 2{\mathit{\boldsymbol{e}}}_i^{\rm{T}}{\rm{]}}^{\rm{T}}},i = {\rm{7,8}}\text{;}\\& \qquad \qquad \;\;{{\mathit{\boldsymbol{\varPi }}}_9} = {[{{\mathit{\boldsymbol{\varPi }}}_7}\;\;{{\mathit{\boldsymbol{\varPi }}}_8}]^{\rm{T}}}\text{;}{{\mathit{\boldsymbol{\varPi }}}_{10}} = {[{\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}} - {\mathit{\boldsymbol{e}}}_7^{\rm{T}}]^{\rm{T}}}\text{;}\\& \qquad \qquad \qquad \quad{{\mathit{\boldsymbol{\varPi }}}_{11}} = {\left[ {{\mathit{\boldsymbol{e}}}_{\rm{2}}^{\rm{T}} \quad - {\mathit{\boldsymbol{e}}}_{\rm{8}}^{\rm{T}}} \right]^{\rm{T}}}\text{;}\\[-3pt]& {{\mathit{\boldsymbol{\varPi }}}_{{\rm{1}}j}} = {\left[ {{\mathit{\boldsymbol{\varSigma}} _{(3 + {{( - 1)}^j})/2}}{\mathit{\boldsymbol{e}}}_{{\rm{(2}}j - 3 - {{( - 1)}^j}{\rm{)/4}}}^{\rm{T}} + {{( - 1)}^j}{\mathit{\boldsymbol{e}}}_{{\rm{(2}}j + 9 - {{( - 1)}^j}{\rm{)/4}}}^{\rm{T}}} \right]^{\rm{T}}}\text{,}\\& \qquad \;\;(j = 3,4, \cdots ,8)\text{;}\\& \;\;\,{{\mathit{\boldsymbol{\varPi }}}_i} = {[{\mathit{\boldsymbol{e}}}_{(i - 11)/2}^{\rm{T}}{\rm{ - }}{\mathit{\boldsymbol{e}}}_{(i - 9)/2}^{\rm{T}}{\rm{ - }}{\mathit{\boldsymbol{e}}}_{(i - 17)/2}^{\rm{T}}{{\varSigma} _2} + {\mathit{\boldsymbol{e}}}_{(i - 15)/2}^{\rm{T}}{{\varSigma} _2}]^{\rm{T}}},\,\, i = 19,21\text{;}\\& {{\mathit{\boldsymbol{\varPi }}}_i} = {\rm{ - }}{[{\mathit{\boldsymbol{e}}}_{(i - 12)/2}^{\rm{T}}{\rm{ - }}{\mathit{\boldsymbol{e}}}_{(i - 10)/2}^{\rm{T}}{\rm{ - }}{\mathit{\boldsymbol{e}}}_{(i - 18)/2}^{\rm{T}}{{\varSigma} _1} + {\mathit{\boldsymbol{e}}}_{(i - 16)/2}^{\rm{T}}{{\varSigma} _1}]^{\rm{T}}},\,\, i = 20,22\text{;}\end{aligned}$ |
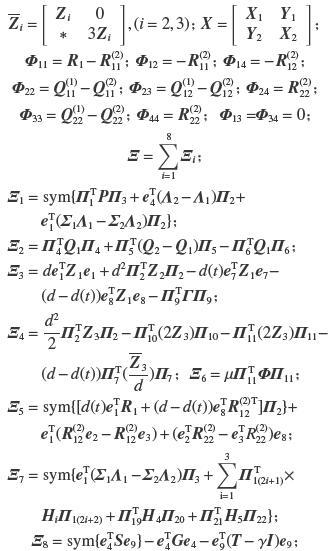
|
| ${\rm{sym}}({\mathit{\boldsymbol{A}}}) = {\mathit{\boldsymbol{A}}} + {{\mathit{\boldsymbol{A}}}^{\rm{T}}}\text{。}$ |
证明:构造如下的Lyapunov-Krasovskii泛函
| $V(t) = \sum\limits_{i = 1}^5 {{V_i}(t)} $ | (10) |
式中:
| $\begin{aligned}[b]\!\!\!\!\!\!{ V_1}(t) \!=\! & 2\sum\limits_{i = 1}^{{n}} {\int_0^{{x_i}} {[{\lambda _{1i}}(l_{{i}}^ + s - {f_i}(s))} + {\lambda _{{{2i}}}}({f_{{i}}}(s) - }l_i^ - s)]{\rm{d}}s + \\& \qquad {\mathit{\boldsymbol{\eta }}}_1^{\rm{T}}(t){\mathit{\boldsymbol{P}}}{{\mathit{\boldsymbol{\eta }}}_1}(t)\end{aligned}$ | (11) |
| ${{V}_2}(t) = \int\limits_{t - d(t)}^t {{\mathit{\boldsymbol{\eta }}}_{\rm{2}}^{\rm{T}}(s){{\mathit{\boldsymbol{Q}}}_1}{{\mathit{\boldsymbol{\eta }}}_2}(s){\rm{d}}s + } \int\limits_{t - d}^{t - d(t)} {{\mathit{\boldsymbol{\eta }}}_{\rm{2}}^{\rm{T}}(s){{\mathit{\boldsymbol{Q}}}_2}{{\mathit{\boldsymbol{\eta }}}_2}(s){\rm{d}}}s$ | (12) |
| $\begin{aligned}{{V}_3}(t) = & \int\limits_{ - d}^0 {\int\limits_{t + \theta }^t {{{\mathit{\boldsymbol{x}}}^{\rm T}}(s){{\mathit{\boldsymbol{Z}}}_1}{\mathit{\boldsymbol{x}}}(s){\rm{d}}s{\rm{d}}\theta } } + d\int\limits_{ - d}^0 {\int\limits_{t + \theta }^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_2}{\mathit{\boldsymbol{\dot x}}}(s){\rm{d}}s{\rm{d}}\theta } } \end{aligned}$ | (13) |
| ${{V}_4}(t) = \int\limits_{ - d}^0 {\int\limits_\rho ^0 {\int\limits_{t + \beta }^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_3}{\mathit{\boldsymbol{\dot x}}}(s){\rm{d}}s{\rm{d}}\beta {\rm{d}}\rho } } } $ | (14) |
| ${{V}_5}(t) = d(t){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){{\mathit{\boldsymbol{R}}}_1}{\mathit{\boldsymbol{x}}}(t) + (d - d(t)){\mathit{\boldsymbol{\eta }}}_{\rm{3}}^{\rm{T}}(t){{\mathit{\boldsymbol{R}}}_2}{{\mathit{\boldsymbol{\eta }}}_3}(t)\text{。}$ | (15) |
| $\begin{aligned}& \text{且}\,\,{{\mathit{\boldsymbol{\eta }}}_1}(t) = {[{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t)\quad {\rm{ (}}\int\limits_{t - d}^t {{\mathit{\boldsymbol{x}}}(s)} {\rm{d}}s{)^{\rm{T}}}]^{\rm{T}}},\\& \qquad \;\;{{\mathit{\boldsymbol{\eta }}}_2}(s) = {[{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(s) \quad {{\mathit{\boldsymbol{f}}}^{\rm{T}}}{\rm{(}}{\mathit{\boldsymbol{x}}}(s))]^{\rm{T}}},\\& {{\mathit{\boldsymbol{\varepsilon }}}_1}(t) = \int\limits_{t - d(t)}^t {\frac{{{\mathit{\boldsymbol{x}}}(s)}}{{d(t)}}} {\rm{d}}s,{{\varepsilon} _2}(t) = \int\limits_{t - d}^{t - d(t)} {\frac{{{\mathit{\boldsymbol{x}}}(s)}}{{d - d(t)}}} {\rm{d}}s,{\rm{ }}\\& \qquad \quad {{\mathit{\boldsymbol{\eta }}}_3}(s) = {[{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(s){\rm{ }}\quad {\mathit{\boldsymbol{\varepsilon }}}_{\rm{2}}^{\rm{T}}(t)]^{\rm{T}}}\text{。}\end{aligned}$ |
| $\begin{aligned}[b]& {{\dot {V}}_1}(t) = 2{\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{x}}}(t)}\\{d(t){{\mathit{\boldsymbol{\varepsilon }}}_1}(t) + (d - d(t)){{\mathit{\boldsymbol{\varepsilon }}}_2}(t)}\end{array}} \right]^{\rm{T}}}{\mathit{\boldsymbol{P}}} \;\cdot \\& \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{\dot x}}}(t)}\\{{\mathit{\boldsymbol{x}}}(t) - {\mathit{\boldsymbol{x}}}(t - d)}\end{array}} \right] + 2{\rm{\{ [}}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){\varSigma}_{1} - {{\mathit{\boldsymbol{f}}}^{\rm{T}}}{\rm{(}}{\mathit{\boldsymbol{x}}}(t){\rm{)]}}{{\mathit{\boldsymbol{\varLambda }}}_{\rm{1}}} + \\& \qquad \;\;{\rm{[}}{{\mathit{\boldsymbol{f}}}^{\rm{T}}}{\rm{(}}{\mathit{\boldsymbol{x}}}(t){\rm{)}} - {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){\displaystyle{\varSigma}_2}{\rm{]}}{{\mathit{\boldsymbol{\varLambda }}}_2}{\rm{\} }}{\mathit{\boldsymbol{\dot x}}}(t) = {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){{\varXi} _1}{\mathit{\boldsymbol{\xi }}}(t)\end{aligned}$ | (16) |
| ${\dot {V}_2}(t) = {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t)({{\mathit{\boldsymbol{\varXi }}}_2} + \dot d(t)({\mathit{\boldsymbol{\varPi }}}_5^{\rm{T}}({{\mathit{\boldsymbol{Q}}}_1} - {{\mathit{\boldsymbol{Q}}}_2}){{\mathit{\boldsymbol{\varPi }}}_5})){\mathit{\boldsymbol{\xi }}}(t)$ | (17) |
| $\begin{aligned}[b]{{\dot {V}}_3}(t) = {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t)(d{\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}{{\mathit{\boldsymbol{Z}}}_1}{{\mathit{\boldsymbol{e}}}_1} + {d^2}{\mathit{\boldsymbol{\varPi }}}_{\rm{3}}^{\rm{T}}{{Z}_2}{{\mathit{\boldsymbol{\varPi }}}_3}){\mathit{\boldsymbol{\xi }}}(t) - \\[-2pt]\int\limits_{t - d}^t {{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_1}{\mathit{\boldsymbol{x}}}(s){\rm{d}}s - d\int\limits_{t - d}^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_2}{\mathit{\boldsymbol{\dot x}}}(s){\rm{d}}s} } \end{aligned}$ | (18) |
对式(18)的第1个积分项应用Jensen积分不等式得:
| $\begin{aligned}[b]& - \int\limits_{t - d}^t {{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_1}{\mathit{\boldsymbol{x}}}(s){\rm{d}}s = - \int\limits_{t - d(t)}^t {{{x}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_1}{\mathit{\boldsymbol{x}}}(s){\rm{d}}s} } - \\& \qquad \qquad \quad \int\limits_{t - d}^{t - d(t)} {{{\mathit{\boldsymbol{x}}}^{\rm{T}}}\left( s \right){{\mathit{\boldsymbol{Z}}}_1}{\mathit{\boldsymbol{x}}}\left( s \right){\rm{d}}s \le } \\&\qquad {{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t)( - d(t){\mathit{\boldsymbol{e}}}_7^{\rm{T}}{{\mathit{\boldsymbol{Z}}}_1}{{\mathit{\boldsymbol{e}}}_7} - }(d - d(t)){\mathit{\boldsymbol{e}}}_8^{\rm{T}}{{\mathit{\boldsymbol{Z}}}_1}{{\mathit{\boldsymbol{e}}}_8}){\mathit{\boldsymbol{\xi }}}(t)\end{aligned}$ | (19) |
对式(18)的第2个积分项应用引理1和2得:
| $\begin{aligned}[b]& - d\int\limits_{t - d}^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_2}{\mathit{\boldsymbol{\dot x}}}(s){\rm{d}}s} = - d\int\limits_{t - d(t)}^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_2}{{\dot {x}}}(s){\rm{d}}s} - \\[-2pt]& d\int\limits_{t - d}^{t - d(t)} {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_2}{\mathit{\boldsymbol{\dot x}}}(s){\rm{d}}s} \le - \frac{d}{{d(t)}}{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{\rm{7}}^{\rm{T}}{{\overline {\mathit{\boldsymbol{Z}}}}_2}{{\mathit{\boldsymbol{\varPi }}}_7}{\mathit{\boldsymbol{\xi }}}(t) + \\[-2pt]& \frac{d}{{d - d(t)}}{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{\rm{8}}^{\rm{T}}{{\overline {\mathit{\boldsymbol{Z}}}}_2}{{\mathit{\boldsymbol{\varPi }}}_8}{\mathit{\boldsymbol{\xi }}}(t) \le - {{\mathit{\boldsymbol{\xi }}}^{\rm T}}(t)({\mathit{\boldsymbol{\varPi }}}_9^{\rm T}{\mathit{\boldsymbol{\varGamma }}}{{\mathit{\boldsymbol{\varPi }}}_9}){\mathit{\boldsymbol{\xi }}}(t)\end{aligned}$ | (20) |
将式(19)~(20)代入式(18)中,可以得到:
| ${\dot V_3}(t) \le {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){{\mathit{\boldsymbol{\varXi }}}_3}{\mathit{\boldsymbol{\xi }}}(t)$ | (21) |
| $\begin{aligned}[b]{{\dot {V}}_4}(t) = \frac{{{d^2}}}{2}{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_3^{\rm{T}}{{Z}_3}{{\mathit{\boldsymbol{\varPi}}} _3}{\xi} (t) - {{\mathit{\boldsymbol{\varepsilon }}}_3}(t) - \\[-2pt]{{\mathit{\boldsymbol{\varepsilon}}} _4}(t) - (d - d(t))\int\limits_{t - d(t)}^t {{{{\mathit{\boldsymbol{\dot x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_3}{{\dot {x}}}(s){\rm{d}}s} \end{aligned}$ | (22) |
式中,
| $\begin{aligned}{{\mathit{\boldsymbol{\varepsilon }}}_3}(t) = - \int\limits_{ - d(t)}^0 {\int\limits_{t + \beta }^t {{{{{\dot {x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_3}{{\dot {x}}}(s){\rm{d}}s{\rm{d}}\beta } }\text{,}\\{{\mathit{\boldsymbol{\varepsilon }}}_4}(t) = - \int\limits_{ - d}^{ - d(t)} {\int\limits_{t + \beta }^{t - d(t)} {{{{{\dot {x}}}}^{\rm T}}(s){{\mathit{\boldsymbol{Z}}}_3}{{\dot{x}}}(s){\rm{d}}s{\rm{d}}\beta } }\text{。} \end{aligned}$ |
用引理3估计
| ${{\mathit{\boldsymbol{\varepsilon }}}_3}(t) \le - 2{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{{\rm{10}}}^{\rm{T}}{{\mathit{\boldsymbol{Z}}}_3}{{\mathit{\boldsymbol{\varPi }}}_{10}}{\mathit{\boldsymbol{\xi }}}(t)$ | (23) |
相似地
| ${{\mathit{\boldsymbol{\varepsilon }}}_4}(t) \le - 2{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{{\rm{11}}}^{\rm{T}}{{\mathit{\boldsymbol{Z}}}_3}{{\mathit{\boldsymbol{\varPi }}}_{11}}{\mathit{\boldsymbol{\xi }}}(t)$ | (24) |
由引理1得:
| $\begin{aligned}[b]& \displaystyle - (d - d(t))\int\limits_{t - d(t)}^t {{{{{\dot {x}}}}^{\rm{T}}}(s){{\mathit{\boldsymbol{Z}}}_3}{{\dot{x}}}(s){\rm{d}}s} \le \\ & \qquad \displaystyle - (d - d(t)){{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{\rm{7}}^{\rm{T}}\left(\frac{{{{{\mathit{\boldsymbol{\overline{{Z}}}}}}_3}}}{d}\right){{\mathit{\boldsymbol{\varPi }}}_7}{\mathit{\boldsymbol{\xi }}}(t)\end{aligned}$ | (25) |
将式(23)~(25)代入式(22)有:
| ${\dot {V}_4}(t) \le {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){{\mathit{\boldsymbol{\varXi }}}_4}{\mathit{\boldsymbol{\xi }}}(t)$ | (26) |
| $\begin{aligned}[b]{{\dot {V}}_5}(t) \le & \;{{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t)[{{\mathit{\boldsymbol{\varXi }}}_5} \! + \! \dot d(t)({\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}({{\mathit{\boldsymbol{R}}}_1} \! - \! {\mathit{\boldsymbol{R}}}_{11}^{(2)}){{\mathit{\boldsymbol{e}}}_1} \! - \! {\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}{\mathit{\boldsymbol{R}}}_{12}^{(2)}{{\mathit{\boldsymbol{e}}}_2}\! \\[4pt]& - {\mathit{\boldsymbol{e}}}_{\rm{1}}^{\rm{T}}{\mathit{\boldsymbol{R}}}_{12}^{(2)}{{\mathit{\boldsymbol{e}}}_4} + {\mathit{\boldsymbol{e}}}_{\rm{2}}^{\rm{T}}{\mathit{\boldsymbol{R}}}_{22}^{(2)}{{\mathit{\boldsymbol{e}}}_4} + {\mathit{\boldsymbol{e}}}_{\rm{4}}^{\rm{T}}{\mathit{\boldsymbol{R}}}_{22}^{(2)}{{\mathit{\boldsymbol{e}}}_4})]{\mathit{\boldsymbol{\xi}}} (t)\end{aligned}$ | (27) |
在
| $\qquad \qquad \; \dot d(t){{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varPi }}}_{{\rm{11}}}^{\rm{T}}{\mathit{\boldsymbol{\varPhi}}}{{\mathit{\boldsymbol{\varPi }}}_{11}}{\mathit{\boldsymbol{\xi }}}(t) \le {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){{\mathit{\boldsymbol{\varXi }}}_6}{\mathit{\boldsymbol{\xi }}}(t)$ | (28) |
由式(6)~(7)知,存在对角阵
| $\begin{aligned}[b]\! \! 0 \! \le \! & {\varpi _i}(s)\! : = \! \! 2{[{\mathit{\boldsymbol{\varSigma }}}\! _1{\mathit{\boldsymbol{x}}}\! (s) \! - \! {\mathit{\boldsymbol{f}}}\! ({\mathit{\boldsymbol{x}}} (s))]^{\rm{T}}}\! {{\mathit{\boldsymbol{H}}}\! _{{i}}}[{\mathit{\boldsymbol{f}}}\! ({\mathit{\boldsymbol{x}}} (s)) \! \! - \! \! {\mathit{\boldsymbol{\varSigma }}}\! _2{\mathit{\boldsymbol{x}}}(s){]^{\rm{T}}},\!\\ & \qquad \qquad \qquad \quad ({{i}} = 1,2,3)\end{aligned}$ | (29) |
| $\begin{aligned}0 \le & {\varpi _i}(s): = 2[{\mathit{\boldsymbol{\varSigma }}}{}_1({\mathit{\boldsymbol{x}}}({s_1}) - {\mathit{\boldsymbol{x}}}({s_2})) - ({\mathit{\boldsymbol{f}}}({{\mathit{\boldsymbol{x}}}(s_1)}) - {\mathit{\boldsymbol{f}}}({{\mathit{\boldsymbol{x}}}(s_2)})){]^{\rm{T}}}\\& {{H}_{{i}}}[({\mathit{\boldsymbol{f}}}({{\mathit{\boldsymbol{x}}}(s_1)}) - {\mathit{\boldsymbol{f}}}({{\mathit{\boldsymbol{x}}}(s_2)})) - {\mathit{\boldsymbol{\varSigma }}}{}_2({\mathit{\boldsymbol{x}}}({s_1}) - {\mathit{\boldsymbol{x}}}({s_2})){]^{\rm{T}}},{\rm{ }}({{i}} = 4,5)\end{aligned}$ | (30) |
于是,下列不等式成立:
| ${\varpi _1}(t) + {\varpi _2}(t - d(t)) + {\varpi _3}(t - d) \ge 0$ | (31) |
| $\qquad \quad \quad \;\;{\varpi _4}(t,t - d(t)) + {\varpi _5}(t - d(t),t - d) \ge 0$ | (32) |
将式(31)~(32)加起来得:
| ${{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){{\mathit{\boldsymbol{\varXi }}}_7}{\mathit{\boldsymbol{\xi }}}(t) \ge 0$ | (33) |
由式(16)~(33)得:
| $\begin{aligned}[b]\dot {V}(t) - & {{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{Gy}}}(t) - 2{{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{SJ}}}(t) - {{\mathit{\boldsymbol{J}}}^{\rm{T}}}(t) \times \\[3pt]& ({\mathit{\boldsymbol{T}}} - \gamma {\mathit{\boldsymbol{I}}}){\mathit{\boldsymbol{J}}}(t) \le {{\mathit{\boldsymbol{\xi }}}^{\rm{T}}}(t){\mathit{\boldsymbol{\varXi \xi }}}(t)\end{aligned}$ | (34) |
因此,由式(8)可知,对任意
| $\begin{aligned}[b]{{\dot {V}}}(t) - & {{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{Gy}}}(t) - 2{{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{SJ}}}(t) - {{\mathit{\boldsymbol{J}}}^{\rm{T}}}(t) \times \\& ({\mathit{\boldsymbol{T}}} - \gamma {\mathit{\boldsymbol{I}}}){\mathit{\boldsymbol{J}}}(t) \le 0\end{aligned}$ | (35) |
对式(35)两边从0到
| $\begin{aligned}[b]\int_0^{{t_p}} & {[{{\dot {V}}}(t) - {{\mathit{\boldsymbol{y}}}^{\rm T}}(t){\mathit{\boldsymbol{Gy}}}(t) - 2{{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{SJ}}}(t)} - \\& {{\mathit{\boldsymbol{J}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{T}}} - \gamma {\mathit{\boldsymbol{I}}}){\mathit{\boldsymbol{J}}}(t)]{\rm{d}}t \le 0\end{aligned}$ | (36) |
式(36)表明,在零初始状态下有式(37)成立。
| $\begin{aligned}[b]\int_0^{{t_p}} & {[ - {{\mathit{\boldsymbol{y}}}^{\rm T}}(t){\mathit{\boldsymbol{Gy}}}(t) - 2{{\mathit{\boldsymbol{y}}}^{\rm{T}}}(t){\mathit{\boldsymbol{SJ}}}(t)} \! - \! \\ & {{\mathit{\boldsymbol{J}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{T}}} \! - \! \gamma {\mathit{\boldsymbol{I}}}){\mathit{\boldsymbol{J}}}(t)]{\rm{d}}t \le - {V}({t_p}) \le 0\end{aligned}$ | (37) |
故由定义知,若式(8)~(9)满足,系统(5)为严格
注意:1)在上述正文中,在许多电路中,放大器的输入–输出函数既不是单调递增的也不是连续可微的。因此,在设计和实现人工神经网络时,非单调函数可能更适合于描述神经元的激活函数。本文假设自2006年由Wang等[26]第一次提出以来,关于它的研究引起了许多学者[15–17]的关注。本文假设中的
2)不同于文献[10–14,17–21],在
作为耗散的一种特殊情况,时滞神经网络的无源分析也受到一些学者的关注[18–21]。若设定理中
推 论 给定d>0,μ;如果存在2n×2n维数矩阵
| $\sum\limits_{i = 1}^7 {{{\mathit{\boldsymbol{\varXi}}} _i}} + {\overline {\mathit{\boldsymbol{\varXi}}} _8} < 0$ | (38) |
则系统(5)为无源的。
式中:
下面给出求解最优耗散性能指标的优化模型:
对给定d、μ,设
则得到最优耗散指标
将给出两个例子和仿真来验证所提方法的有效性。
例1:考虑一个二阶基于忆阻时滞神经网络(1),其参数矩阵为:
| $\begin{aligned}& {\mathit{\boldsymbol{A}}}({\mathit{\boldsymbol{x}}}(t)) = {\rm{diag}}\{ {a_1}({x_1}(t)),{a_2}({x_2}(t))\} ,\\& {\mathit{\boldsymbol{W}}}({\mathit{\boldsymbol{x}}}(t)) = \left[ {\begin{array}{*{20}{c}}{{w_{11}}({x_1}(t))} & {{w_{12}}({x_1}(t))}\\{{w_{21}}({x_2}(t))} & {{w_{22}}({x_2}(t))}\end{array}} \right],\\[2pt]& {{\mathit{\boldsymbol{W}}}_1}({\mathit{\boldsymbol{x}}}(t)) = \left[ {\begin{array}{*{20}{c}}{w_{11}^{(1)}({x_1}(t))} & {w_{12}^{(1)}({x_1}(t))}\\{w_{21}^{(1)}({x_2}(t))} & {w_{22}^{(1)}({x_2}(t))}\end{array}} \right]\text{。}\end{aligned}$ |
其中:
| $\begin{aligned}{a_1}({x_1}(t))\!\! =\!\! \left\{ \begin{array}{l}\!\!\!\!\!2.1\text{,}\left| {{x_1}(t)} \right| \!\le\! {\rm{1}}\text{;}\\\!\!\!\!\!1.9\text{,}\left| {{x_1}(t)} \right| \!>\! {\rm{1}}\text{。}\end{array} \right.{a_2}({x_2}(t)) \!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!1.6\text{,}\left| {{x_2}(t)} \right| \!\le\! {\rm{1}}\text{;}\\\!\!\!\!\!1.4\text{,}\left| {{x_2}(t)} \right| \!>\! {\rm{1}}\text{。}\end{array} \right.\end{aligned}$ |
| $\begin{aligned}& {w_{11}}({x_1}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\! - 1.2\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\! - 0.9\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right. \!\!\!{w_{12}}({x_1}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!1.1\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\!0.9\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right.\\[2pt]& {w_{21}}({x_2}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!0.6\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\!0.4\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right. \!\!\!{w_{22}}({x_2}(t)) \!\!=\!\! \left\{ \begin{array}{l} \!\!\!\!\!- 1.2\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\ \!\!\!\!\!- 0.9\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right.\\[2pt]& w_{11}^{(1)}({x_1}(t)) \!\!=\!\! \left\{ \begin{array}{l} \!\!\!\!\!- 0.6\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\ \!\!\!\!\!- 0.4\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right. \!\!\!w_{12}^{(1)}({x_1}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!0.7\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\!0.5\text{,}\!\!\!\left| {{x_1}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right.\\[2pt]& w_{21}^{(1)}({x_2}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!0.8\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\!0.6\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right. \!\!\!w_{22}^{(1)}({x_2}(t)) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\!0.9\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!\le\!\! {\rm{1}}\text{;}\\\!\!\!\!\!0.7\text{,}\!\!\!\left| {{x_2}(t)} \right| \!\!>\!\! {\rm{1}}\text{。}\end{array} \right.\end{aligned}$ |
应用微分包含和集值映射理论得:
| $\begin{array}{l}{\mathit{\boldsymbol{A}}} ={\rm{diag}}\{ 2,1.5\} ,{\mathit{\boldsymbol{W}}} = \left[ {\begin{array}{*{20}{c}}{ - 1} \;\;\; 1\\{0.5} \;\;\; { - 1}\end{array}} \right],{{\mathit{\boldsymbol{W}}}_1} = \left[ {\begin{array}{*{20}{c}}{ - 0.5} \;\;\; {0.6}\\{0.7}\;\;\; {0.8}\end{array}} \right],\end{array}$ |
且
取
当d=0.4,对不同μ,由定理得出最优耗散性能γ*。表1为本文方法(定理)的结果和文献[10–12]结果的对照。
| 表1 不同μ时,最优耗散性能γ* Tab. 1 Optimal dissipativity performance γ* for various μ |
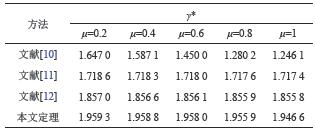 |
从表1可以看出,定理所得结果比文献[12]的结果提高了5%,这说明本文方法能更有效地减少严格耗散条件的保守性。
例2:考虑一个2阶基于忆阻时滞神经网络(1)[13,17–21],其系数矩阵为:
| $\begin{array}{l}{A} \! = \! \left[{\begin{array}{*{20}{c}}{ 1.4} \;\;\; \! 0\\0 \;\;\;\;\; {\! 1.5}\end{array}}\right],\;{W} \! = \! \left[{\begin{array}{*{20}{c}}\! {1.2} \;\;\; \! 1.0\\\! { - 1.2} \;\;\; \! {1.3}\end{array}}\right],{{W}_1} \! = \! \left[{\begin{array}{*{20}{c}}\! \!{ - 0.2} \;\;\; {0.5}\\ {0.3} \;\;\;\;\; { - 0.8}\end{array}}\right]\text{。}\end{array}$ |
激活函数
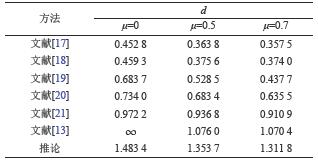
针对不同的μ,表2为由本文推论和文献[13,17–21]获得的保证系统(1)无源的最大允许时滞上界d。从表2可以看出,提出的方法大大地减少了文献[13,17–21]方法的保守性。
| 表2 不同μ时,最大允许时滞上界d Tab. 2 Maximum allowable upper bounds d for various μ |
 |
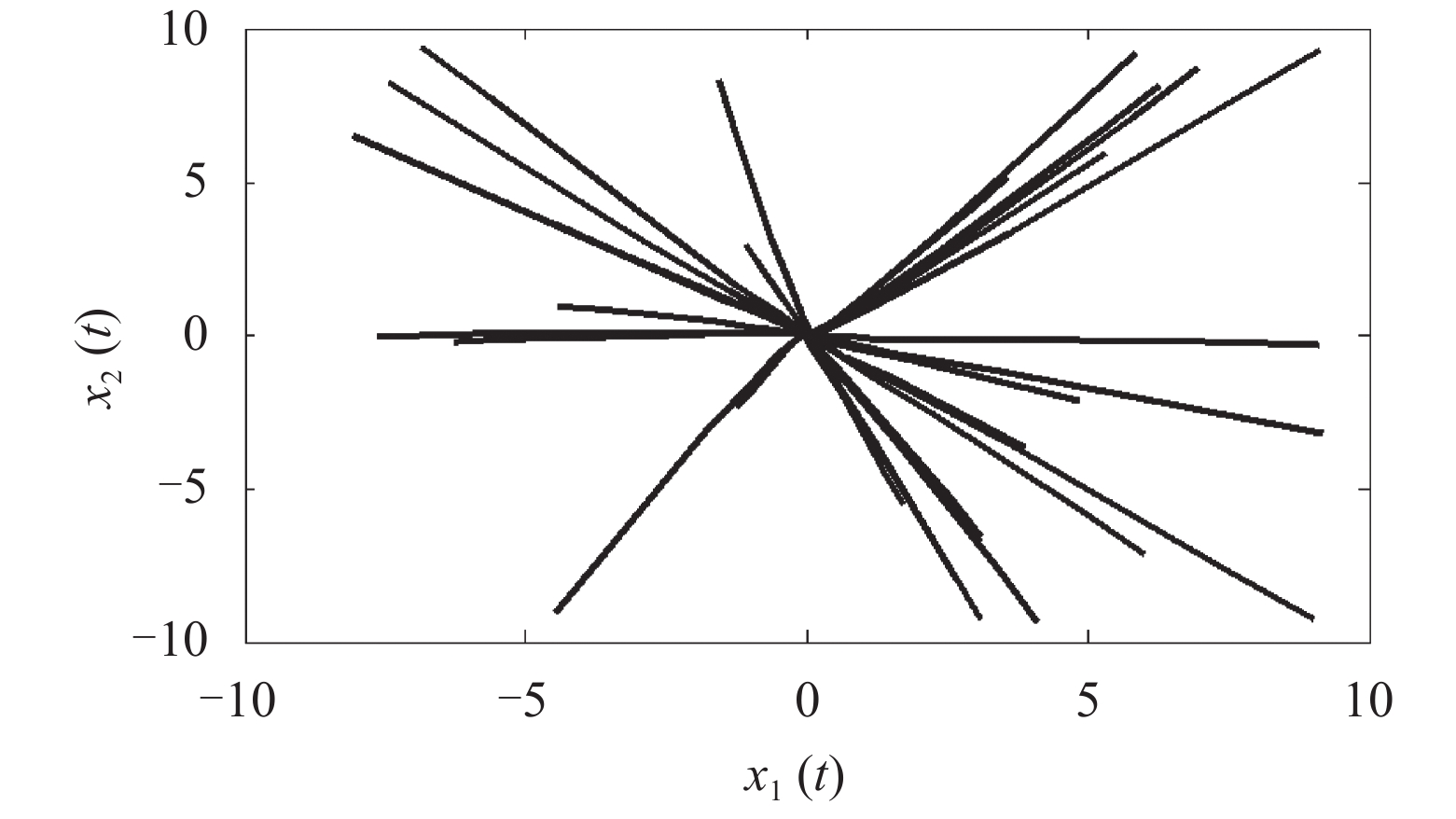
特别地,当
 |
|
图2 神经网络(1)不含
|
 |
|
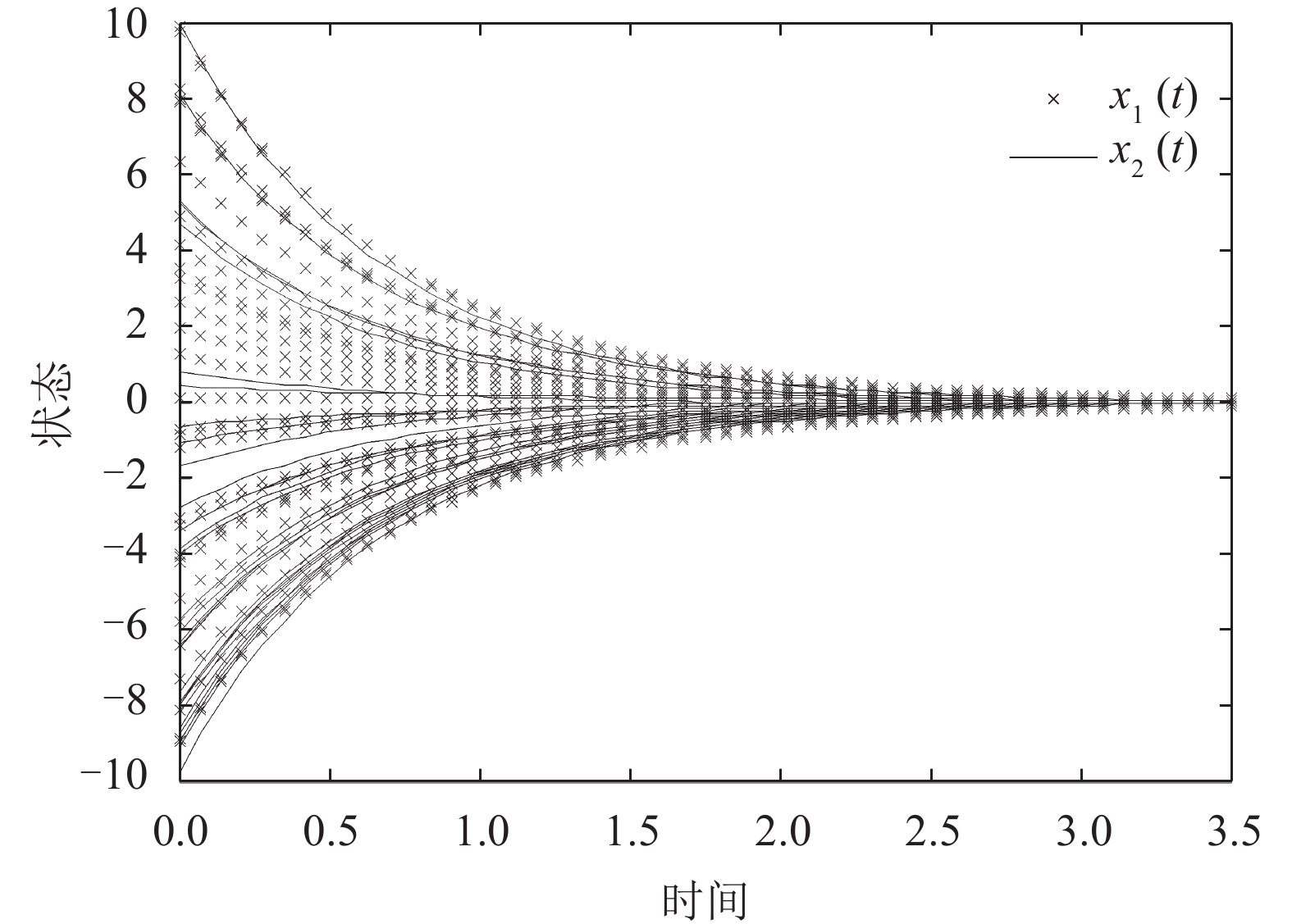
图3 神经网络(1)不含
|
 |
|
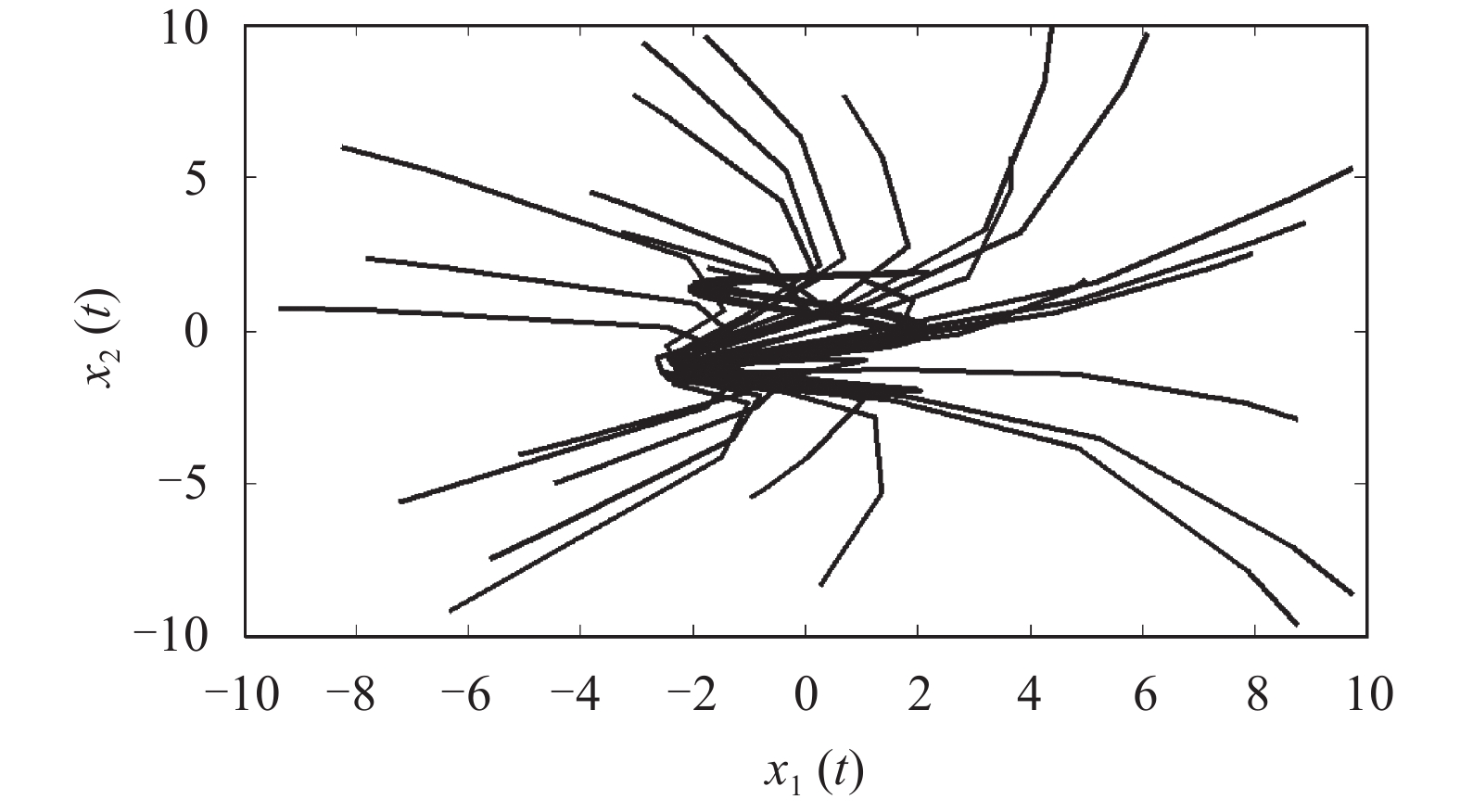
图4 神经网络(1)含有
|
 |
|
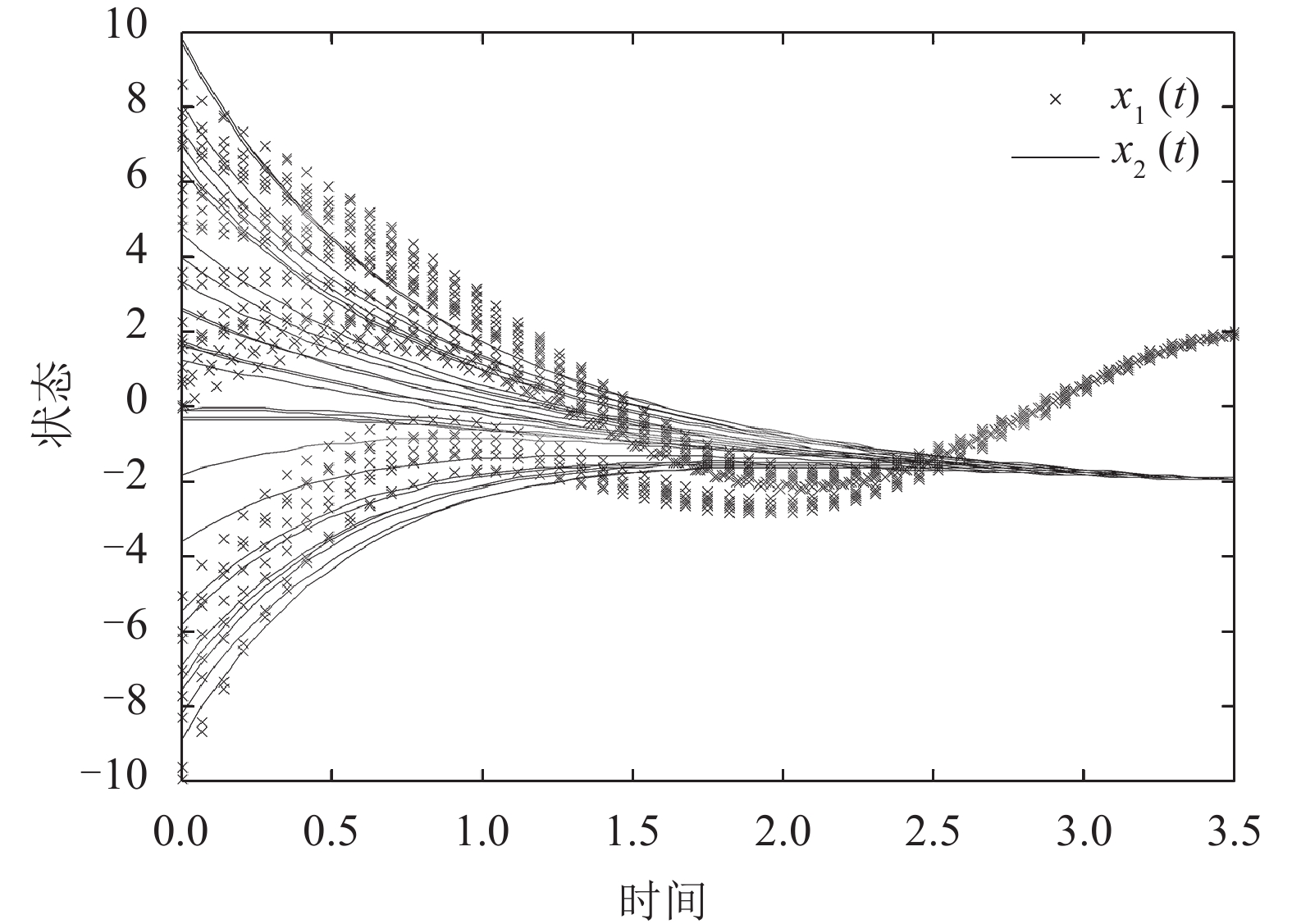
图5 神经网络(1)含有
|
4 结 论
应用微分包含和集值映射理论,结合Wirtinger积分不等式和倒凸技术,得到了较弱保守性的时滞依赖的耗散条件,数值例子表明,与现有文献相比,所得到的耗散条件有较弱的保守性。仿真结果验证了耗散条件的有效性。在接下来的研究工作中,考虑把本文方法推广到忆阻时滞神经网络的状态估计、有限时间稳定等其他动力行为中。
| [1] |
Chua L. Memristor-the missing circuit element[J]. IEEE Transaction on Circuit Theory, 1971, 18(5): 507-519. DOI:10.1109/TCT.1971.1083337 |
| [2] |
Strukov D, Snider G, Stewart D. The missing memristor found[J]. Nature, 2008, 453(191): 80-83. |
| [3] |
Hu Jin,Wang Jun.Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays[C]//Proceedings of the 2010 International Joint Conference on Neural Networks.New York:IEEE,2010:1–8.
|
| [4] |
Hu Jin, Song Qiankun. Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays[J]. Applied Mathematics and Mechanics, 2013, 34(7): 724-735. [胡进, 宋乾坤. 基于忆阻的时滞神经网络的全局稳定性[J]. 应用数学和力学, 2013, 34(7): 724-735.] |
| [5] |
Zhang Guodong, Shen Yi, Wang Leimin. Global anti-synchronization of a class of chaotic memristive neural networks with time-varying delays[J]. Neural Networks, 2013, 46(11): 1-8. |
| [6] |
Mathiyalagan K, Anbuvithya R, Sakthivel R. Reliable stabilization for memristor-based recurrent neural networks with time-varying delays[J]. Neurocomputing, 2015, 153(4): 140-147. |
| [7] |
Wu Zhaojing, Karimi H R. A novel framework of theory on dissipative system[J]. International Journal of Innovative Computing,Information and Control, 2013, 9(7): 2755-2769. |
| [8] |
Zhang Hao, Guang Zhihong, Feng Gang. Reliable dissipative control for stochastic impulsive system[J]. Automatica, 2008, 44(4): 1004-1010. DOI:10.1016/j.automatica.2007.08.018 |
| [9] |
Wu Zengguang, Shi Peng, Su Hongye. Dissipativity analysis for discrete-time stochastic neural networks with time-varying delays[J]. IEEE Transactions on Neural Network Learn Systems, 2013, 24(3): 345-355. DOI:10.1109/TNNLS.2012.2232938 |
| [10] |
Wu Zengguang, Park J H, Su Hongye. Robust dissipativity analysis of neural networks with time-varying delay and randomly occurring uncertainties[J]. Nonlinear Dynamics, 2012, 69(3): 1323-1332. DOI:10.1007/s11071-012-0350-1 |
| [11] |
Zeng Hongbing, Park J H, Xia Jianwei. Further results on dissipativity analysis of neural networks with time-varying delay and randomly occurring uncertainties[J]. Nonlinear Dynamics, 2015, 79(1): 83-91. DOI:10.1007/s11071-014-1646-0 |
| [12] |
Zeng Hongbing, He Yong, Shi Peng. Dissipativity analysis of neural networks with time-varying delays[J]. Neurocomputing, 2015, 168(11): 741-746. |
| [13] |
Xiao Jianying, Zhong Shouming, Li Yongtao. Relaxed dissipativity criteria for memristive neural networks with leakage and time-varying delays[J]. Neurocomputing, 2016, 171(1): 708-718. |
| [14] |
Wen Shiping, Zeng Zhigang, Huang Tingwen. Exponential stability analysis of memristor-based recurrent neural networks with time-varying delays[J]. Neurocomputing, 2012, 97(1): 233-240. |
| [15] |
Gyurkovics É. A note on Wirtinger-type integral inequalities for time-delay systems[J]. Automatica, 2015, 61(11): 44-46. |
| [16] |
Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: application to time-delay systems[J]. Automatica, 2013, 49(9): 2860-2866. DOI:10.1016/j.automatica.2013.05.030 |
| [17] |
Zeng Hongbing, He Yong, Shi Peng. Passivity analysis for neural networks with a time-varying delay[J]. Neurocomputing, 2011, 74(5): 730-734. DOI:10.1016/j.neucom.2010.09.020 |
| [18] |
Zhang Zexu, Mou Shaoshuai, Lam J. New passivity criteria for neural networks with time-varying delay[J]. Neural Networks, 2009, 22(7): 864-868. DOI:10.1016/j.neunet.2009.05.012 |
| [19] |
Xu Shengyuan, Zheng Weixing, Zou Yun. Passivity analysis of neural networks with time-varying delays[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2009, 56(4): 325-329. DOI:10.1109/TCSII.2009.2015399 |
| [20] |
Zhang Baoyong, Xu Shengyuan, Lam J. Relaxed passivity conditions for neural networks with time-varying delays[J]. Neurocomputing, 2014, 142(10): 299-306. |
| [21] |
Li Yuanyuan, Zhong Shouming, Cheng Jun. New passivity criteria for uncertain neural networks with time-varying delay[J]. Neurocomputing, 2016, 171(1): 1003-1012. |
| [22] |
Filippov A F.Differential equations with Discontinuous Right-Hand Sides[M].Dordrecht:Kluwer,1988.
|
| [23] |
Aubin J,Frankowsha,H.Set-valued Analysis[M].Boston:Springer,2009.
|
| [24] |
Park P, Ko J W, Jeong C K. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235-238. DOI:10.1016/j.automatica.2010.10.014 |
| [25] |
Sun Jian, Liu Guanping, Chen Jie. Improved delay-range-dependent stability criteria for linear systems with time-varying delay[J]. Automatica, 2010, 46(2): 466-470. DOI:10.1016/j.automatica.2009.11.002 |
| [26] |
Wang Zidong, Shu Huisheng, Liu Yurong. Robust stability analysis of generalized neural networks with discrete and distributed time delays[J]. Choas Solitons & Fractals, 2006, 30(4): 886-896. |
 2017, Vol. 49
2017, Vol. 49


