2. 江苏建筑节能与建造技术协同创新中心,江苏 徐州 221116;
3. 国网上海市电力公司 经济技术研究院,上海 200080
2. Jiangsu Collaborative Innovation Center of Building Energy Saving and Construction Technol., Xuzhou 221116, China;
3. State Grid Shanghai Economic Research Inst, Shanghai 200080, China
钢桁架结构具有轻质、高强、延性好等优点,在大跨结构中得到广泛应用。拼接节点作为钢桁架结构重要的连接部位,其承载力和刚度是影响钢桁架整体结构安全性和稳定性的重要因素[1],对拼接节点的设计应满足两项基本要求[2]:一是,强节点弱构件;二是,节点弯矩–转角关系,即刚度问题。作者结合大直径筒仓施工支撑平台设计项目提出两种角钢–双T型纵横梁拼接节点,该节点具有施工速度快,强度高,易于拼接,可实现装配化等优点,在实际工程中已有应用。
国内外学者对钢结构拼接节点方面的研究已经相当广泛。夏军武等[3–5]结合试验及ANSYS软件,对钢框架带悬臂梁段拼接节点进行了承载特性和弹塑性分析,提出“强焊弱栓”等设计建议。赵楠等[6]对2组1:4缩尺空间桁架相交焊接节点进行静力单调加载试验,分析节点在静力加载过程中应变与转角变化的特点,揭示了节点破坏模式。李明等[7]对两种不同形式下的全T型桁架节点进行承载力试验研究,同时借助ANSYS软件对桁架节点进行应力分析,得到节点的受力性能特征,为T型钢在桁架中的应用提供了参考。刘克勋等[8–9]对T型钢桁架节点进行分析,研究了弦杆节点受力状态及节点的极限承载力。焦遹烽等[10–11]对新型带悬臂梁段栓–焊拼接节点进行试验研究,分析了节点的极限承载力、破坏模式、各部件应力分布及塑性区的扩展问题。戴绍斌等[12–14]研究了钢框架T型钢连接节点受力性能、破坏模式等,得出T型钢连接节点具有较好的延性和滞回性能。这些研究主要集中在钢框架梁柱螺栓拼接节点、钢桁架弦杆节点板焊接节点承载性能方面的研究,但采用螺栓将角钢拼接成双T型纵横梁,以实现可装配化施工的大跨度空间钢桁架施工支撑平台,这类研究尚不充分。
为此,作者对这两种角钢–双T型纵横梁拼接节点足尺试件进行静力加载试验及数值模拟,研究角钢–双T型纵横梁拼接节点的承载性能、抗弯刚度、极限荷载及破坏模式,以确定较合理的角钢–双T型纵横梁节点拼接形式,为钢桁架筒仓施工支撑平台整体结构性能的研究及设计提供理论依据。
1 试验概况 1.1 试件设计及制作两种角钢–双T型纵横梁拼接节点单元试件均由角钢拼接而成的T型截面纵梁、T型截面横梁、拼接盖板、腹板连接板及腹板端板、填板组成。为了使2个角钢拼接而成的T型截面纵梁和T型截面横梁能起整体作用,在两角钢并肢之间焊上填板,填板宽度为60 mm,长度比角钢肢宽大14 mm,即填板长度为174 mm,以便于与角钢焊接,T型纵梁两端焊接端板以实现约束控制。根据构造要求,T型截面纵梁设置5个填板,横梁设置3个填板,填板均匀布置,其各部件尺寸及截面相应参数如表1所示。
| 表1 拼接节点试件尺寸及截面参数 Tab. 1 Specimen size and section parameters of the splicing joint |
 |
本试验共设计2个试件,带腹板连接板拼接节点编号为SJ–1,带腹板端板拼接节点编号为SJ–2,两试件整体设计轮廓如图1所示。节点域腹板连接板、腹板端板及填板均采用角焊缝焊接,采用E43焊条,焊角尺寸hf=7 mm,腹板连接板、腹板端板与梁腹板及拼接盖板与梁翼缘均采用M20–10.9级摩擦型高强螺栓连接,试验测得高强螺栓抗滑移系数为0.33。节点域构造详图如图2所示。
 |
| 图1 试件整体轮廓 Fig. 1 Overall outline of specimens |
 |
| 图2 节点域构造详图 Fig. 2 Detail construction of Panel Zone |
两试件的T型截面纵梁和T型截面横梁所用角钢、拼接盖板、腹板连接板及腹板端板、填板均采用Q235钢材加工制作而成,根据《金属材料室温单轴拉伸试验方法》(GB/T228—2002)对钢材进行材性试验,试验测得钢材的屈服强度为241 MPa,极限强度为382 MPa,伸长率为22.65%,弹性模量为2.05×105 MPa,泊松比为0.3。
1.2 试件的静力加载布置试件SJ–1和试件SJ–2的焊接工作在工厂完成,试件的拼接工作及试件的静力加载试验在中国矿业大学深部岩土力学与地下工程国家重点实验室完成。为了测定试件SJ–1和试件SJ–2的承载力和抗弯性能,每个试件均采用两种加载方式。
第1种加载方式是将T型纵梁两端通过焊接端板与龙门架固定,T型横梁梁端用反力架进行竖向约束,在距T型纵梁两端0.375 m处各设置一个30 t千斤顶,以施加2个集中荷载,T型横梁中点处设置1个30 t千斤顶以施加1个集中荷载,3个集中力同步加载,以研究角钢–双T型纵横梁拼接节点的承载力。试件SJ–1在第1种加载方式下的约束条件、加载简图及现场布置图如图3所示。
 |
| 图3 第1种加载方式加载简图及现场布置图 Fig. 3 Diagram and scene under the first loading |
第2种加载方式是将T型纵梁两端通过焊接端板与龙门架固定,横梁梁端悬臂,仅采用1个30 t千斤顶在T型横梁中点处施加1个集中荷载,以研究角钢–双T型纵横梁拼接节点荷载作用下的抗弯性能。第2种加载方式下的约束条件、加载简图及现场布置如图4所示。
 |
| 图4 第2种加载方式加载简图及现场布置图 Fig. 4 Diagram and scene under the second loading |
由于两种拼接节点的加载方式、约束条件及现场布置均相同,仅节点的拼接形式不同,此处不再赘述。
1.3 加载制度两试件均采用分级加载制度,对于第1种加载方式,试件SJ–1和试件SJ–2设计荷载150 kN,初次加载20 kN,每级增加20 kN,当荷载达到120 kN时,荷载增量降为10 kN,共分9级加载完成。当荷载达到设计值150 kN时,为避免节点发生塑性变形而影响对构件荷载作用下抗弯性能的研究,停止加载并观察实验现象。对于第2种加载方式,试件SJ–1和试件SJ–2施加的最大荷载设定为60 kN,根据T型横梁加载点距节点拼接中心的长度为0.4 m,由此可知两试件的等效弯矩Mbn=60×0.4=24 kN·m,剪力Vbn=60 kN。同样采用分级加载制度,以10 kN为一个等级,分6级加载完成,观察试验现象。每级荷载持续2 min,记录各仪器仪表读数。
1.4 量测方案角钢–双T型纵横梁拼接节点静力加载试验主要测定:1)拼接节点及加载点处的位移;2)拼接节点在正常使用条件下的承载力;3)拼接节点的主要控制截面应力;4)拼接节点处的弯矩–转角关系。
拼接盖板主要作用是防止横向弦杆发生翘曲变形,应力不是很大,腹板连接板、腹板端板应力变化较大,所以主要分析腹板连接板、腹板端板处的受力情况。两试件位移计布置及腹板连接板、腹板端板应变测点布置详见图5和6。
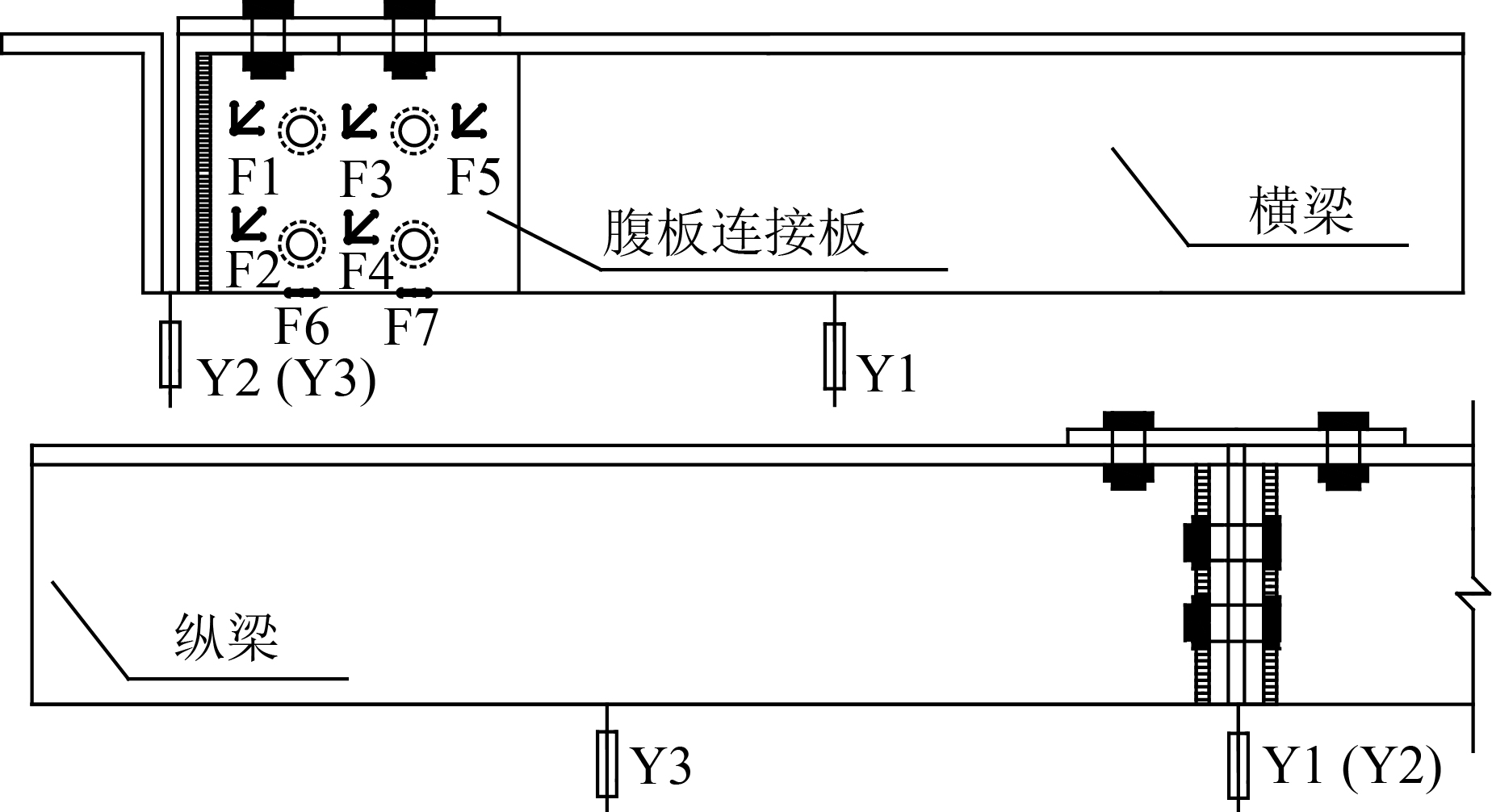 |
| 图5 试件SJ–1测点布置图 Fig. 5 Arrangement of measuring joints of specimen SJ–1 |
 |
| 图6 试件SJ–2测点布置图 Fig. 6 Arrangement of measuring joints of specimen SJ–2 |
位移计Y1用于测量横梁加载点处的变形,Y2测量拼接节点处的位移,Y3用来测量纵梁加载处的位移。F1~F7表示对应位置的应变片编号,以测量荷载作用下,腹板连接板和腹板端板各测点处的应变变化情况。
2 实验结果及其分析 2.1 测点应力变化曲线第1种加载方式是在保证两种节点在弹性变化范围内进行,以保证对节点抗弯性能进一步研究。设定荷载150 kN,分9级加载完成。试件加载后纵横梁的变形情况如图7所示。
 |
| 图7 第1种加载结束后梁的变化 Fig. 7 Change of beams after the first loading method |
图7中试件变形微小,卸载后,试件变形基本可以恢复原状,这说明试件处于弹性变形阶段,该阶段,节点的应力应变关系满足:σ=Eε(其中,E表示钢材的弹性模量)。根据各测点得出的应变数据,经处理后得出拼接节点各测点的应力变化情况如图8和9所示。
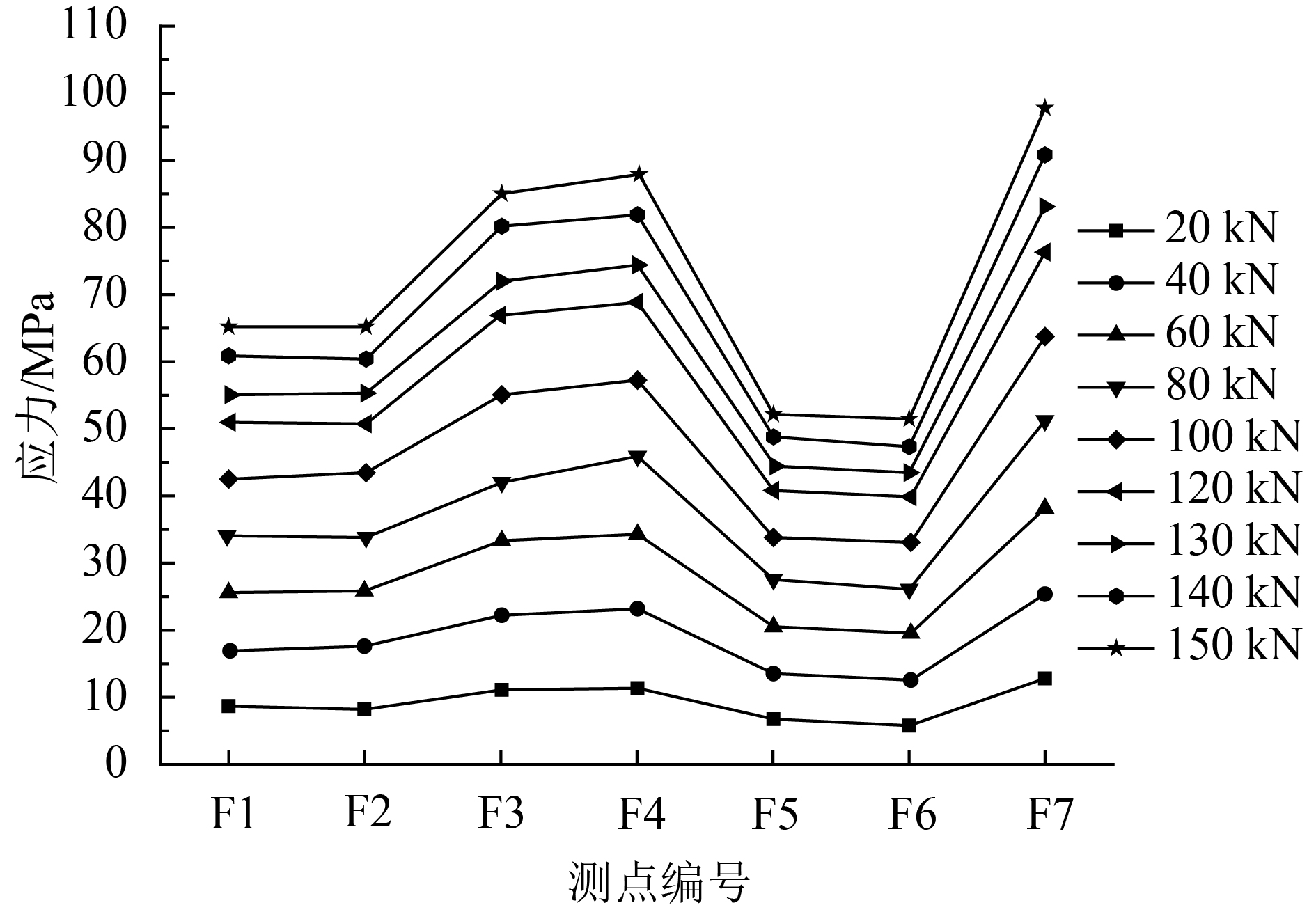 |
| 图8 试件SJ–1在第1种加载方式下各测点应力变化曲线 Fig. 8 Load-equivalent stress of specimen SJ–1 under the first loading |
 |
| 图9 试件SJ–2在第1种加载方式下各测点应力变化曲线 Fig. 9 Load-equivalent stress of specimen SJ–2 under the first loading |
图8反映了带腹板连接板拼接节点腹板连接板各处应力变化情况。由图8可见,腹板连接板各处应力变化不是很大,随着荷载的增大,应力基本呈均匀变化,最大的应力出现在拼接端板F7应变片处,当荷载达到设定值150 kN时,其应力为96 MPa,腹板连接板未达到屈服。
带腹板端板拼接节点腹板端板各处应力变化情况如图9所示。
图9中随着荷载的增大,F1、F3、F4应变片处应力呈均匀变化,F5、F6应变片处应力变化较为明显,这是由于靠近横向弦杆的拼接部位受力较大,所以应力比较大,且越往两边应力越小,特别是最外排螺栓的外侧,这说明腹板端板上中间4个螺栓为主要受力螺栓。腹板端板上远离翼缘部分,在施加荷载过程中,荷载先传递到弦杆,然后传递到拼接板上的螺栓,再由螺栓传递给腹板端板,最大应力高达246 MPa。因为腹板端板会受到2个方向的荷载传递,使得拼接节点中间位置应变较大而应力较小,特别是螺栓孔壁处,由于对中间螺栓施加了预紧力,使得螺栓孔壁和螺栓杆的接触部位应力和应变均比较大。
2.2 荷载–位移曲线图10为试件SJ–1和试件SJ–2在第1种加载方式下竖向荷载与拼接节点处位移之间的关系曲线。
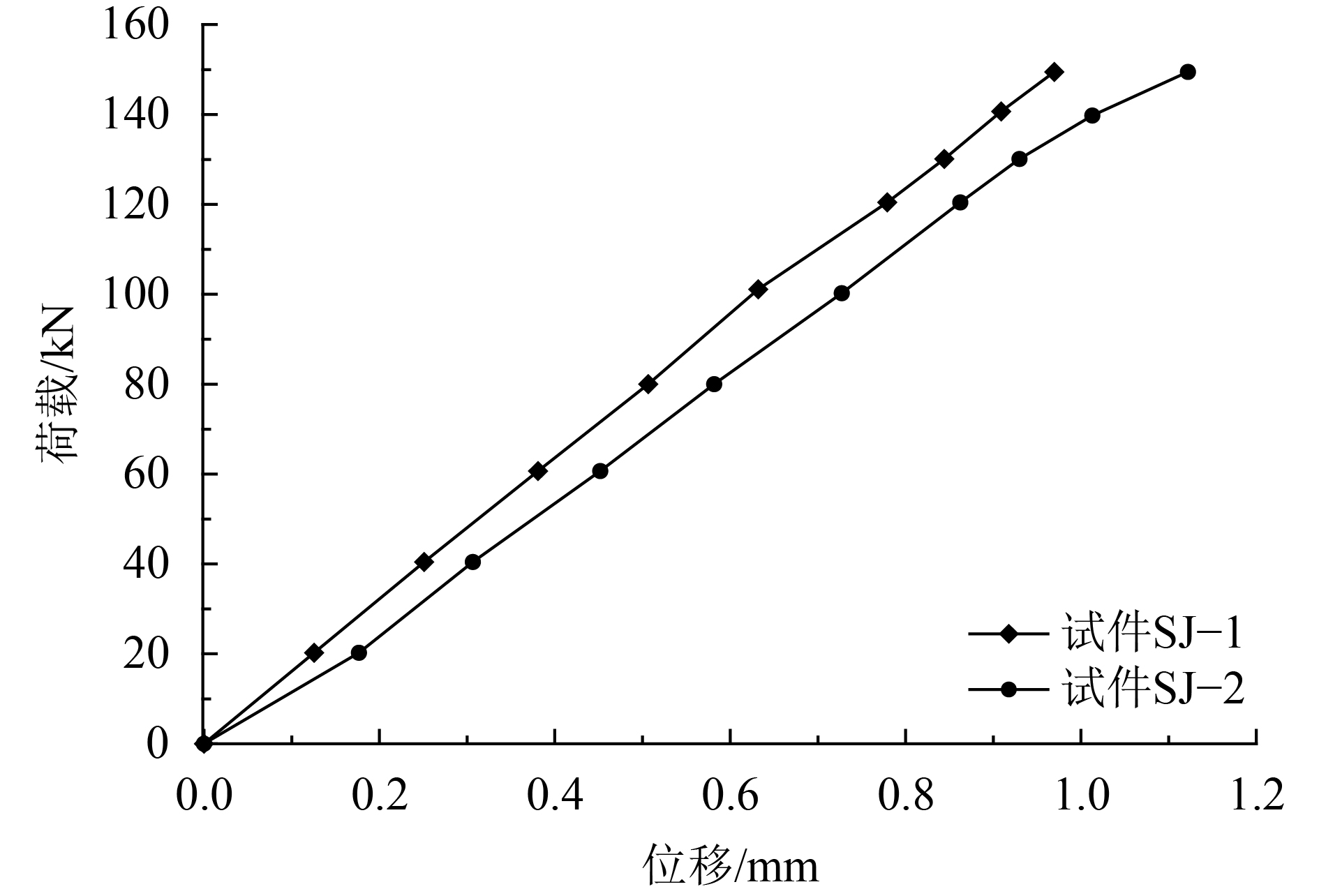 |
| 图10 两种拼接节点在第1种加载方式下的荷载–位移曲线 Fig. 10 Load-displacement curve of two kinds of the splicing joint under the first loading |
从图10中可以发现,拼接节点处竖向位移随着竖向荷载的增大呈现增大趋势,试件SJ–1拼接节点处的荷载–位移曲线基本呈线性关系,这表明,试件SJ–1在荷载小于150 kN时处于弹性阶段,这和试验现象基本一致。对于试件SJ–2,荷载小于140 kN时,荷载–位移曲线呈线性关系,但荷载达到140 kN后,位移增大略有变快,这是由于试件SJ–2腹板端板上的最大应力达到了腹板端板的屈服强度。通过对比分析试件SJ–1和试件SJ–2拼接节点处的荷载–位移曲线可知,相同荷载作用下,试件SJ–1拼接节点处的位移比试件SJ–2拼接节点处的位移小。当荷载为150 kN时,试件SJ–2位移值1.13 mm比试件SJ–1的位移值0.934 mm高20.99%,且试件SJ–2即将进入弹塑性阶段。
第2种加载方式是在第1种加载方式完成且弹性变形完全恢复的基础上进行的。图11为试件SJ–1和试件SJ–2竖向荷载与横梁加载点处变形之间的关系曲线。
图11中,试件SJ–1和试件SJ–2的竖向荷载与横梁加载点处变形之间的关系曲线变化情况基本一致,当荷载达到45 kN之前,试件SJ–1和试件SJ–2均随着竖向荷载的增大,变形呈线性增加,当荷载超过45 kN时,试件SJ–1和试件SJ–2的变形增加变快,试件进入弹塑性阶段。当荷载达到60 kN时,试件SJ–2的变形29.43 mm比试件SJ–1的变形26.46 mm高11.22%。
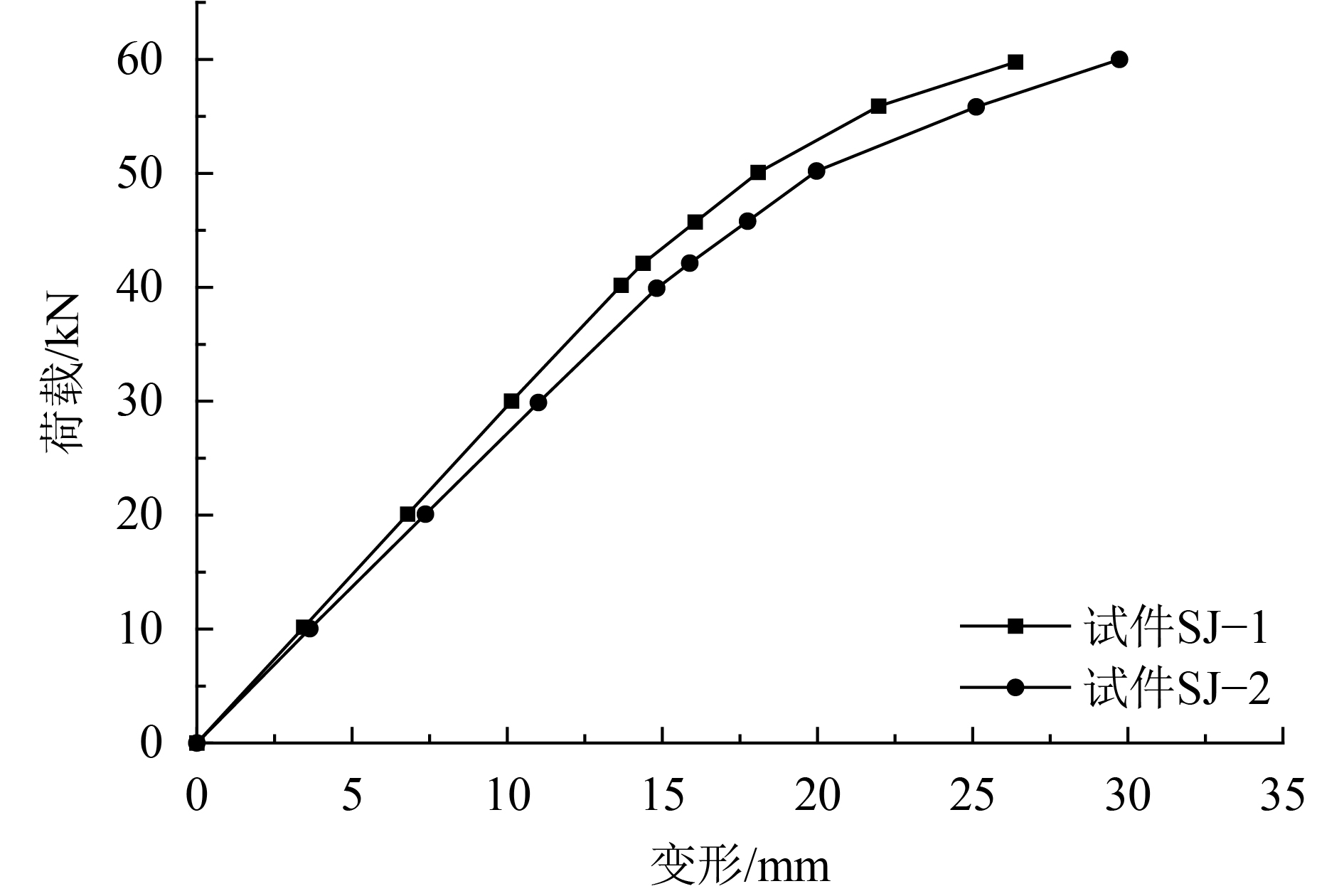 |
| 图11 两种拼接节点在第2种加载方式下的荷载-变形曲线 Fig. 11 Load-deflection curve of two kinds of the splicing joint under the second loading |
2.3 弯矩–转角曲线
节点的弯矩–转角曲线是反映节点抗弯承载力和转动能力的一项重要参数,直接影响钢桁架体系变形、极限承载力与整体性能,它表征节点传递弯矩与构件之间相对转角的关系。在不考虑T型梁扭转的前提下,考虑到拼接节点处存在一定的位移,定义节点转角θ为(横梁加载点处竖向位移–拼接节点处的竖向位移)/加载点至拼接节点中心的距离。图12给出了试件SJ–1和试件SJ–2在第2种加载方式下拼接节点的弯矩–转角曲线。
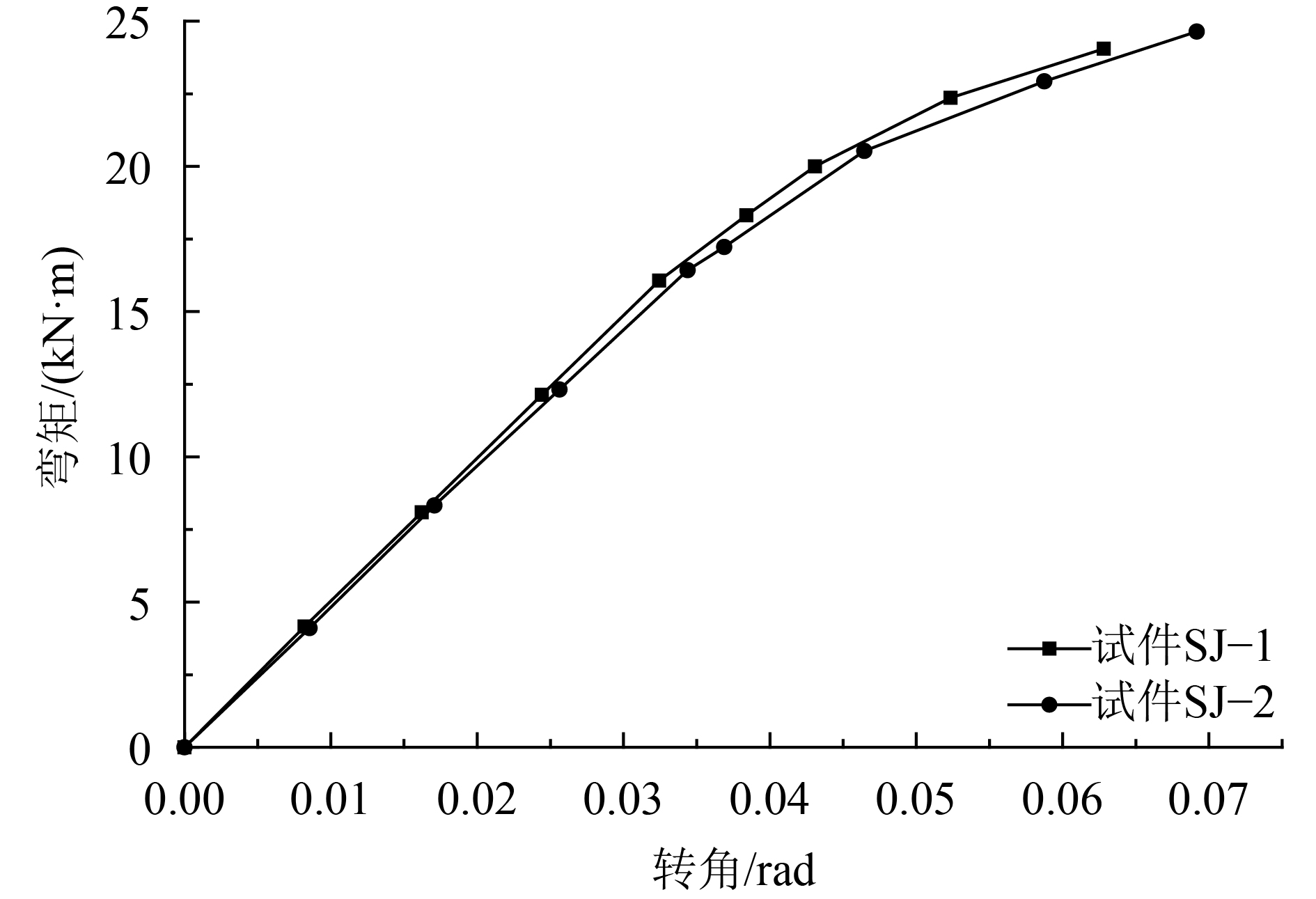 |
| 图12 两种拼接节点在第2种加载方式下的弯矩–转角曲线 Fig. 12 Moment-rotation curve of two kinds of the splicing joints under the second loading |
由图12可见,两种拼接节点的转角均随着弯矩的增大而增大,当弯矩超过17.5 kN·m时,转角增大较快,这是因为拼接节点处抗弯刚度存在一定的衰减,且横梁端部拼接位置存在滑移变形,使得两者曲线存在差异,但差别不是很大。从弯矩–转角曲线中,亦可以得出试件SJ–1和试件SJ–2的最大转角分别为0.063 rad和0.0693 rad,曲线斜率即为节点的抗弯刚度,由此可得出试件SJ–1和试件SJ–2的抗弯刚度分别为5.09×108 N·mm和4.68×108 N·mm。就竖向抗弯刚度而言,试件SJ–1的抗弯刚度比试件SJ–2的抗弯刚度高8.76%,试件SJ–1承载性能略高于试件SJ–2。
3 有限元数值模拟 3.1 模型建立结合试验中试件的几何尺寸、截面等相应参数以及钢材材性试验测得的材料属性,使用ANSYS有限元软件建立模型。对于试件中所用钢材,采用线弹性强化模型和Von Mises屈服准则。有限元模型中,采用实体SOLID95单元模拟M20–10.9级摩擦型高强螺栓、拼接盖板、腹板连接板和腹板端板以及角钢和填板;高强螺栓预紧力采用PRETS179单元模拟;拼接盖板、腹板连接板及腹板端板与角钢的接触选用3维面–面接触单元TARGE170和CONTA174分别模拟目标面和接触面。模型采用与试验相同的边界约束条件和试件加载方式。建立如图13所示有限元模型。
 |
| 图13 拼接节点有限元模型及网格划分 Fig. 13 Finite Element Model and Meshing of the splicing joint |
网格划分的精度与应力复杂程度相关[3],这两种拼接节点的网格划分比较均匀,由于拼接节点中腹板连接板、腹板端板及高强螺栓受力较大,网格划分比较密。
3.2 数值模拟与实验结果对比相同加载方式下,根据试验加载方式,对带腹板连接板拼接节点和带腹板端板拼接节点进行有限元数值模拟,分析带腹板连接板拼接节点和带腹板端板拼接节点的内力及变形等变化规律,并与实验结果进行对比分析。
图14为两试件在第1种加载方式下,有限元和试验测得拼接节点处的荷载–位移对比曲线。由图可知有限元分析所得试件SJ–1和试件SJ–2在150 kN荷载作用下的位移分别为0.976 mm和1.08 mm,试验测得试件SJ–1和SJ–2在150 kN荷载作用下的位移分别为0.934 mm和1.13 mm,两者分别相差4.50%和–4.42%。
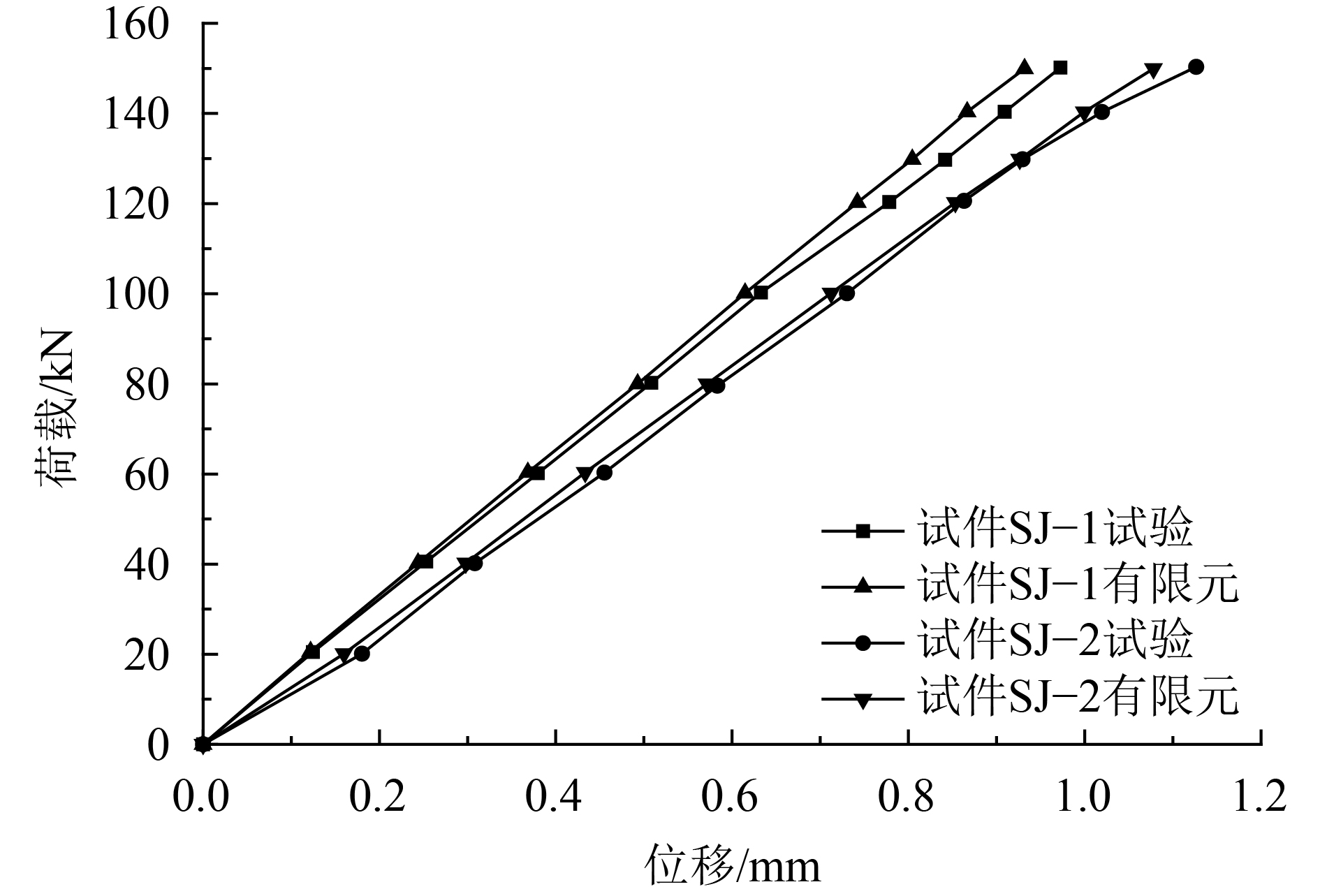 |
| 图14 第1种加载方式下两试件的荷载–位移对比曲线 Fig. 14 Load-deformation curve of two kinds of the splicing joint under the first loading |
第2种加载方式,试验和有限元测得横梁加载点处的荷载–变形对比曲线及拼接节点处的弯矩–转角对比曲线如图15和16所示。
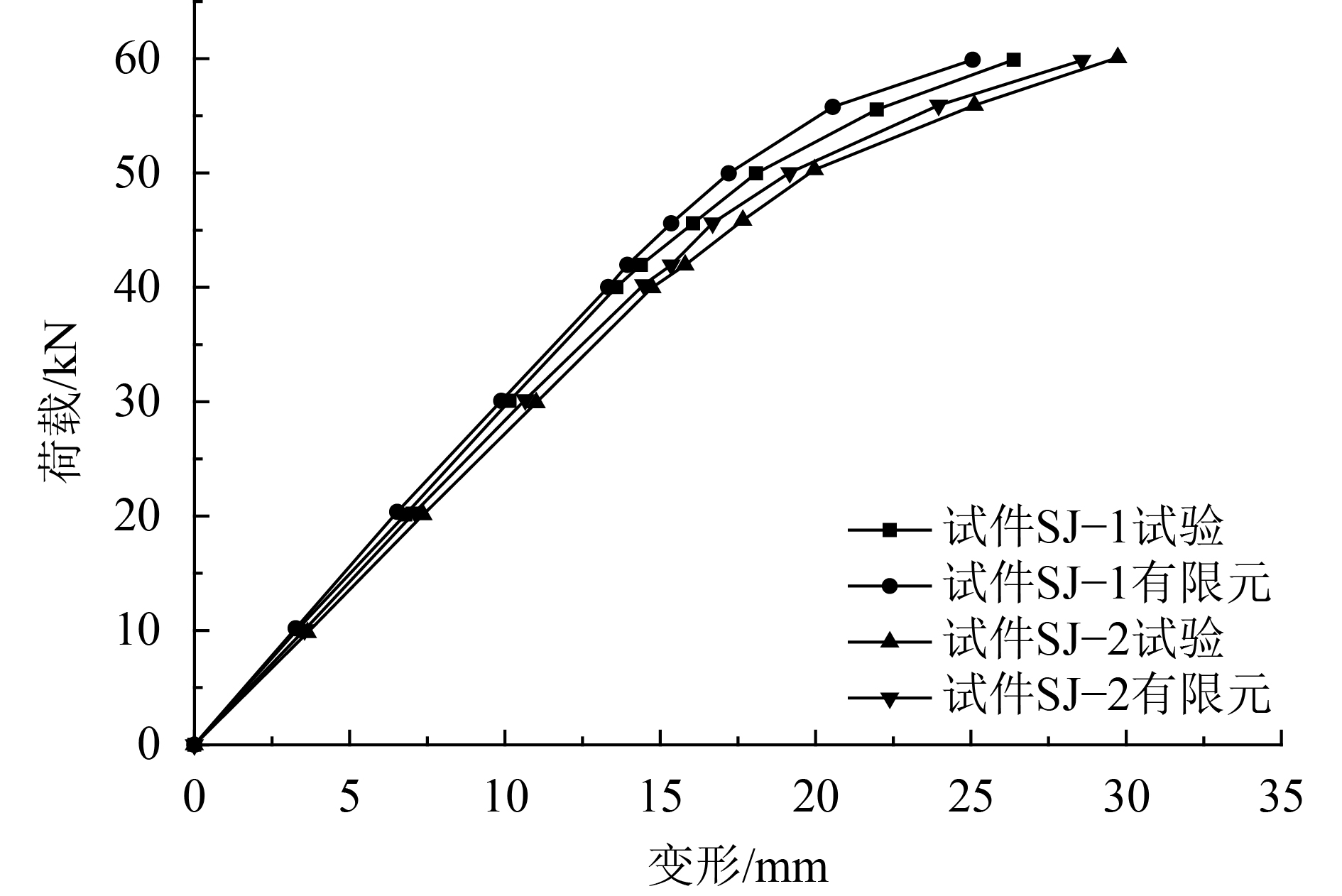 |
| 图15 第2种加载方式下两试件的荷载–变形对比曲线 Fig. 15 Load-deflection curve of two kinds of the splicing Joint under the second loading |
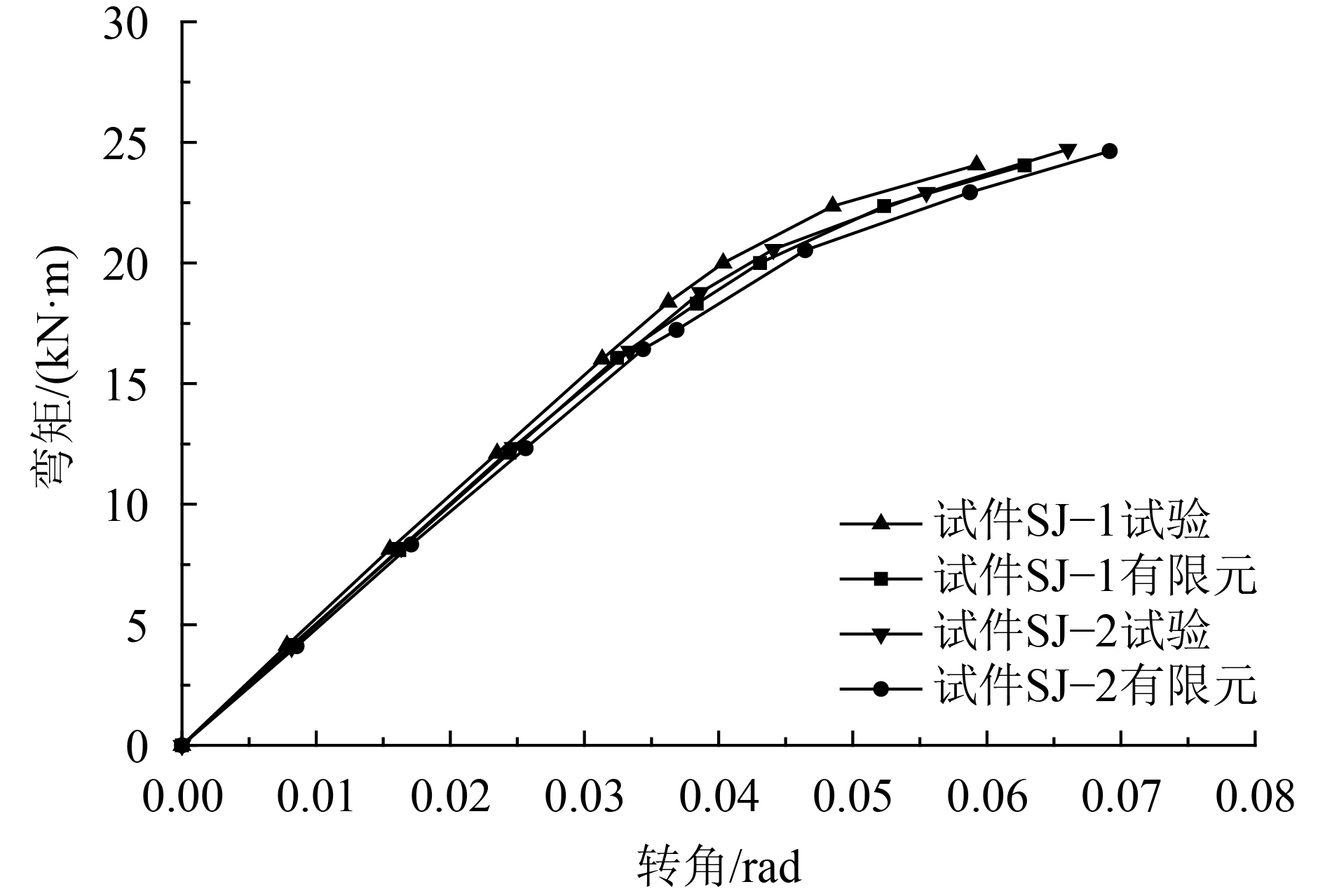 |
| 图16 第2种加载方式下两试件的弯矩-转角对比曲线 Fig. 16 Moment-rotation curve of two kinds of the splicing joint under the second loading |
由图15可知,当荷载加载至60 kN时,试验测得试件SJ–1和试件SJ–2的变形分别为26.46 mm和29.83 mm,有限元测得变形分别为25.12 mm和28.60 mm,有限元测得的变形比试验测得的变形分别相差–5.06%和–4.12%;同时通过图16弯矩–转角对比曲线分析可知,试验测得试件SJ–1和试件SJ–2的最大转角分别为0.063和0.069 rad,相应的试件SJ–1和试件SJ–2的抗弯刚度分别为4.94×108和4.68×108 N·mm,有限元测得最大转角分别为0.059和0.066 rad,相应的试件SJ–1和SJ–2的抗弯刚度分别为5.09×108和4.89×108 N·mm,有限元测得的抗弯刚度比试验测得的抗弯刚度分别相差3.04%和4.49%。
从荷载–位移、荷载–变形及弯矩–转角对比曲线分析发现,有限元分析得出的数据和试验结果存在一定的偏差,但偏差不是很大,总体上可说明有限元模拟的正确性及可靠性,因此可使用ANSYS软件对两种角钢–双T型纵横梁拼接节点极限承载力等进行模拟。
3.3 极限承载力及破坏模式分析在有限元软件计算结果与实验结果对比分析的基础上,利用有限元软件对两种试件进行极限承载力及破坏模式分析。图17为试件SJ–1和试件SJ–2在第1种加载方式下拼接节点处极限荷载作用下的变形曲线。
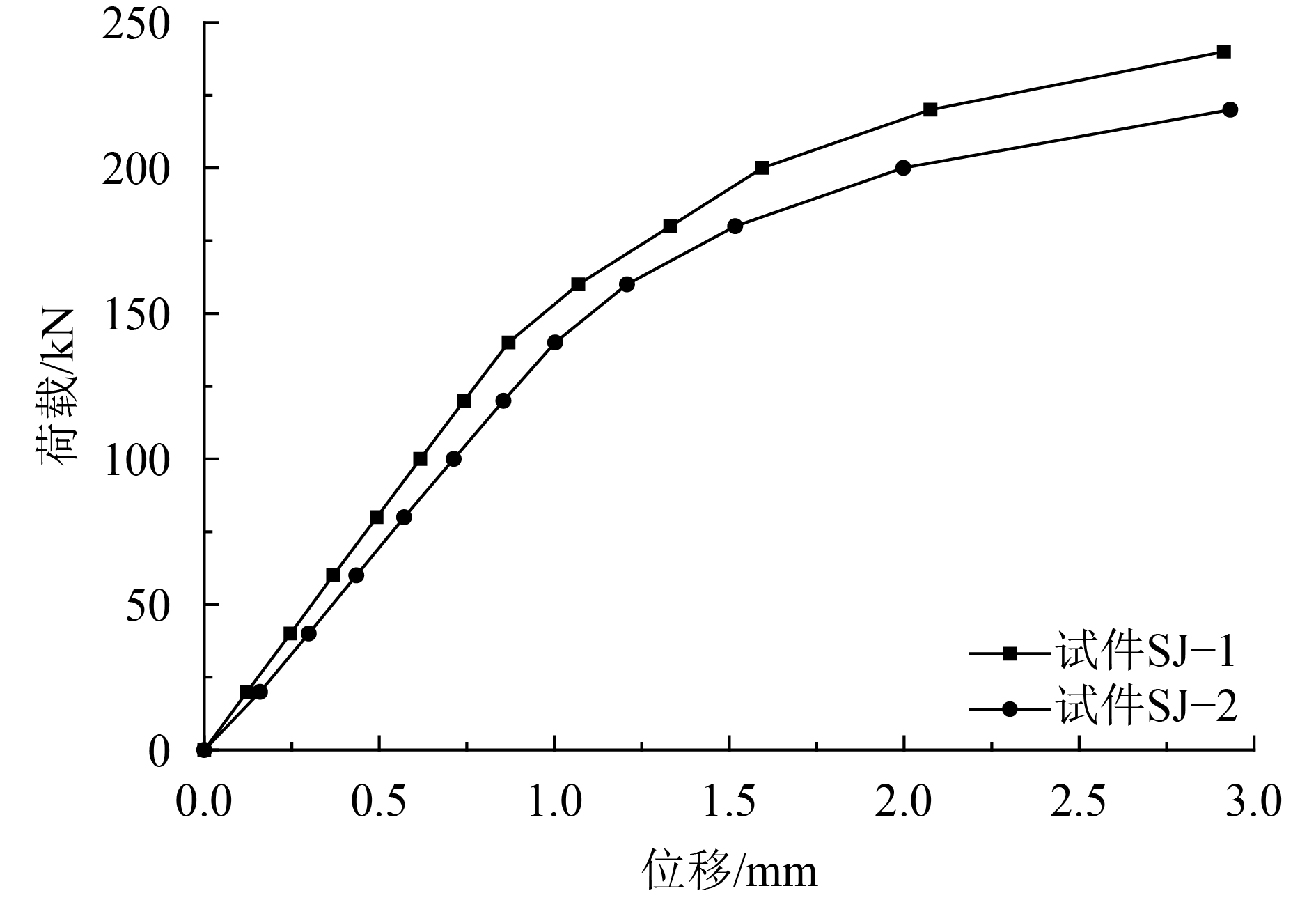 |
| 图17 两种试件在极限荷载作用下的变形曲线 Fig. 17 Deformation curve of two specimens under limit load |
对图17中试件SJ–1荷载–位移曲线分析可知,当荷载为200 kN时,除纵梁端部出现屈服,其它部位均未达到屈服,此时拼接节点位移1.595 mm,当荷载为220 kN时,拼接节点下部和横梁中间下部板件达到屈服,出现塑性变形,拼接节点处位移为2.075 mm,拼接节点位移增大0.48 mm,但当荷载为240 kN时,拼接节点位移达到2.914 mm,位移增量为0.839 mm,是位移增量0.48 mm的1.748倍,说明试件SJ–1已经产生较大塑性变形,最大位移超过试件容许最大位移,最后构件先于带腹板连接板拼接节点发生压屈破坏。由此可知,试件SJ–1的极限荷载为220 kN。图18为试件SJ–1在极限荷载220 kN作用下的应力云图。
 |
| 图18 试件SJ–1加载至220 kN时的应力分布图 Fig. 18 Stress cloud of the SJ–1 when the load is 220 kN |
对图17中试件SJ–2荷载–位移曲线进行分析,当荷载为180 kN时,拼接节点位移为1.517 mm,当荷载达到200 kN时,拼接节点位移达到1.998 mm,位移增加0.481 mm,但当荷载达到220 kN时,拼接节点最大位移达到2.932 mm,位移增量为0.934 mm,是0.481 mm的1.942倍,且最大位移超过试件容许位移,最后带腹板端板拼接节点先于构件发生剪切破坏。由此可知,试件SJ–2的极限荷载为200 kN。图19为试件SJ–2在极限荷载200 kN时的应力云图。
 |
| 图19 试件SJ–2加载至200 kN时应力分布图 Fig. 19 Stress cloud of the SJ–2 when the load is 200 kN |
带腹板连接板拼接节点的极限荷载比带腹板端板拼接节点高10%,且带腹板拼接节点不符合“强节点弱构件”的节点设计原则,带腹板连接板节点拼接形式可为设计者提供参考,其性能参数可作为钢桁架整体性能的研究提供理论依据,带腹板端板拼接节点拼接形式不宜用于实际工程中。
4 结 论提出两种角钢–双T型纵横梁拼接节点,分别采用两种加载方式对两种拼接节点进行静力加载试验研究和有限元数值模拟,分析节点抗弯刚度、极限承载力及破坏模式,得到如下主要结论:
1)带腹板连接板拼接节点抗弯刚度比带腹板端板拼接节点抗弯刚度高8.76%,带腹板连接板接节点抵抗竖向变形的能力高于带腹板端板拼接节点。
2)带腹板连接板拼接节点的极限承载力220 kN,比带腹板端板拼接节点极限承载力200 kN高10%,带腹板连接板拼接节点腹板连接板处仅螺栓孔附近应力较大,且应力扩散区域小,承载性能高于带腹板端板拼接节点。
3)带腹板连接板拼接节点构件先于拼接节点发生压屈破坏,满足“强节点弱构件”节点设计原则,符合节点拼接要求;而带腹板端板拼接节点是拼接节点先于构件发生剪切破坏,不满足节点设计要求,不宜用于实际工程中。
4)对带腹板连接板拼接节点性能的进一步研究,以试验和有限元分析所获得的节点承载特性参数可为以后对钢桁架筒仓施工支撑平台整体性能的研究提供关键节点的力学参数。
| [1] |
Li Haiwang, Lian Jianzhong. Design of the large-scale steel structure coal tower and research of complex joint[J]. Steel Structure, 2009, 24(2): 53-57. [李海旺, 廉建中. 某大型钢框架煤塔复杂节点设计和分析[J]. 钢结构, 2009, 24(2): 53-57.] |
| [2] |
Guo Bing, Wang Lei, Wang Ying. Experimental study on rotational stiffness of steel frame beam-column connec-tions[J]. Journal of Building Structures, 2011, 32(10): 82-89. [郭兵, 王磊, 王颖. 钢框架梁柱连接节点转动刚度试验研究[J]. 建筑结构学报, 2011, 32(10): 82-89.] |
| [3] |
Xia Junwu, Chang Hongfei. Elastoplastic analysis on splice joints with cantilever beam of steel frame column[J]. Journal of China University of Mining & Technology, 2006, 35(5): 596-601. [夏军武, 常鸿飞. 钢框架柱带悬臂梁段拼接节点的弹塑性分析[J]. 中国矿业大学学报, 2006, 35(5): 596-601.] |
| [4] |
Chang Hongfei, Xia Junwu. Bearing capacity analysis of steel frame joints with cantilever beam splicing[J]. Progress in Steel Building Structures, 2008, 6(10): 47-53. [常鸿飞, 夏军武. 钢框架带悬臂梁段拼接节点的承载特性分析[J]. 建筑钢结构进展, 2008, 6(10): 47-53.] |
| [5] |
Li Qicai, Su Mingzhou, Chen Aiguo. Experimental analysis of steel beam-to-column connection with cantilever beam splicing[J]. Industrial Construction, 2004, 36(6): 74-76. [李启才, 苏明周, 陈爱国. 带悬臂梁段拼接的梁柱连接节点试验分析[J]. 工业建筑, 2004, 36(6): 74-76.] |
| [6] |
Zhao Nan, Li Ting. Experimental study on intersection of large-span space truss nodes[J]. Building Structure, 2009, 39(12): 103-105. [赵楠, 李婷. 大跨度双向桁架相交节点的试验研究[J]. 建筑结构, 2009, 39(12): 103-105.] |
| [7] |
Li Ming, Li Xiaoming, Sun Qi. Experimental study on capacity and joint performance of Full T-Type steel truss[J]. Steel Structure, 2010, 25(10): 18-23. [李明, 李小明, 孙琦. 全T型钢桁架承载力及节点性能的试验研究[J]. 钢结构, 2010, 25(10): 18-23. DOI:10.3969/j.issn.1007-9963.2010.10.005] |
| [8] |
刘克勋, 余沁, 王昊. T型钢桁架连接节点分析[J]. 结构工程师, 2008, 24(2): 35-38. |
| [9] |
Wang Wanzhen, Zhang Zhentao, Jia Ziwen, Zhu Guangxin. Study on T-section steel struss joints[J]. Jaurnal of Xi'an University of Architecture and Technology, 2000, 32(4): 338-341. [王万祯, 张振涛, 贾子文, 朱广新. T型钢桁架节点研究[J]. 西安建筑科技大学学报, 2000, 32(4): 338-341.] |
| [10] |
Jiao Yufeng, He Minjuan, Ma Renle. Study on a newcantilever beam joint with bolted-welded spliced connection[J]. Progress in Steel Building Structures, 2015, 17(4): 10-18. [焦遹烽, 何敏娟, 马人乐. 新型带悬臂梁段栓–焊拼接节点力学性能研究[J]. 建筑钢结构进展, 2015, 17(4): 10-18.] |
| [11] |
He Minjuan, Jiao Yufeng, Ma renle. Experimental study on flange bolted-welted connection for steel column beam[J]. Journal of Tongji University(Natural Science), 2013, 4(2): 1787-1792. [何敏娟, 焦遹烽, 马人乐. 钢梁栓–焊混合连接节点性能试验[J]. 同济大学学报(自然科学版), 2013, 4(2): 1787-1792.] |
| [12] |
Dai Shaobin, HuangJun Jian, Zhu. Research on mechanical performance of T-joint of steel frame[J]. Industrial architecture, 2005, 35(9): 90-93. [戴绍斌, 黄俊, 朱健. 钢框架T 型钢连接节点的受力性能研究[J]. 工业建筑, 2005, 35(9): 90-93.] |
| [13] |
Song Xiaoguang, Shen Chengjun, Guo Bing. Hysteretic behavior study of steel beam-to-column T-stub Connections[J]. Progress in Steel Building Structures, 2008, 10(4): 18-25. [宋晓光, 申成军, 郭兵. 钢框架梁柱T型钢连接滞回性能的研究[J]. 建筑钢结构进展, 2008, 10(4): 18-25.] |
| [14] |
Elie G. Modified stiffness model for thick flange in built-up T-stub connections[J]. Journal of Constructional Steel Research, 2013, 81(2): 76-85. |
 2017, Vol. 49
2017, Vol. 49


