圆形深基础是工程上最常用的深基础类型之一,其地基承载力的计算一直备受学术界的关注。受基础埋深和地基轴对称破坏模式等方面的影响,该问题也一直是深基础工程承载力设计上的难点。为提高地基的承载力设计水平,国内外学者在这方面做了大量研究,并给出一系列圆形深基础地基承载力计算方法,例如Meyerhof等[1–3]通过将条形深基础地基极限承载力公式乘以某一形状修正系数,间接给出了圆形深基础的地基极限承载力计算公式;由于这些解均为假定在地基土平面应变条件下得到的,因而其不能准确地反映地基在轴对称受载时的承载能力。Terzaghi[4]根据圆形浅基础地基极限承载力计算公式,提出圆形墩式深基础极限承载力的计算方法,然而因为该方法实际上也是基于假定在地基平面应变的条件下得到的,所以不能真实反映圆形基础下地基的承载能力。
Berezantzev[5]从地基轴对称变形的角度出发,给出圆形深基础下砂土地基的极限承载力计算公式,但由于其所采用的地基破坏模式中的地基土剪切破裂面为无埋深(或特浅埋深)基础时的破坏情况,因而该公式确定的地基土水平塑性变形范围偏大,计算出的地基极限承载力偏大。Hanna等[6]在考虑地基刺入剪切破坏的基础上,结合地基轴对称变形破坏的特点,给出计算单桩极限承载力的方法,显然该方法仅适用于计算相对埋深很大的桩基础极限承载力。Vesic、陈从春等[7–8]根据孔的扩张理论给出圆形深基础极限承载力的理论解,但是受变形土体应力边界条件的限制,其也只能用于求解相对埋深很大的触探贯入阻力和桩基承载力问题。为此,根据从Berezantzev深基础承载理论中得到的启发,通过分析土颗粒移动、地基压密和土体剪切3者的关系,并考虑基础埋深、地基土相对密度等因素的影响,构建当基础埋深不太大(2≤H/b≤5)时的深基础下砂土地基破坏模式,同时结合地基轴对称破坏的特点,对圆形深基础下砂土地基的破坏模式和极限承载力进行研究。
1 圆形深基础下砂土地基破坏模式分析 1.1 深基础下砂土地基破坏模式1)深基础下砂土地基的破坏过程
对于深基础下的砂土地基,Berezantzev认为地基的破坏不是因为地基土的挤出,而是因为地基中过大压力的影响,使地基土得到了压密,从而为基础沉降提供了所需的空间,此时地基中的剪切滑动面通常不会延伸到地面,仅发展至基础周围或基底水平面以下的某一区域[9],表现为局部剪切破坏。
砂土地基中的某个区域在发生剪切破坏前,首先出现的是该处地基土体的不断压密,表现为该处地基土颗粒的移动。在此过程中,土中附加应力不断增大,当附加应力增大到恰好能使该处地基达到极限状态时即发生剪切,该处地基产生塑性区。地基中的塑性区首先是从基底两侧的边缘处产生,然后分别向两侧和压密土楔顶点方向发展[9],如图1所示。
 |
| 图1 地基塑性区发展方向示意 Fig. 1 Developing trend of the plastic zone |
如图2所示,当塑性区向两侧发展时,假设地基中①、②区域内的地基土颗粒开始分别向两侧的斜下方移动,随后,③、④内的土颗粒在①、②区域内的地基土颗粒的推动下发生移动;同理,⑤、⑥内也可发生移动。沿土颗粒移动的方向上,地基土体压密所需的土中附加应力通过土颗粒的接触逐渐向前传递。由于受到土颗粒间摩擦等因素的影响,土中附加应力在传递的过程中应逐渐减小,因此上述区域内的附加应力大小顺序应为①>③>⑤,②>④>⑥;同时,地基压密后的密实程度为①>③>⑤,②>④>⑥。
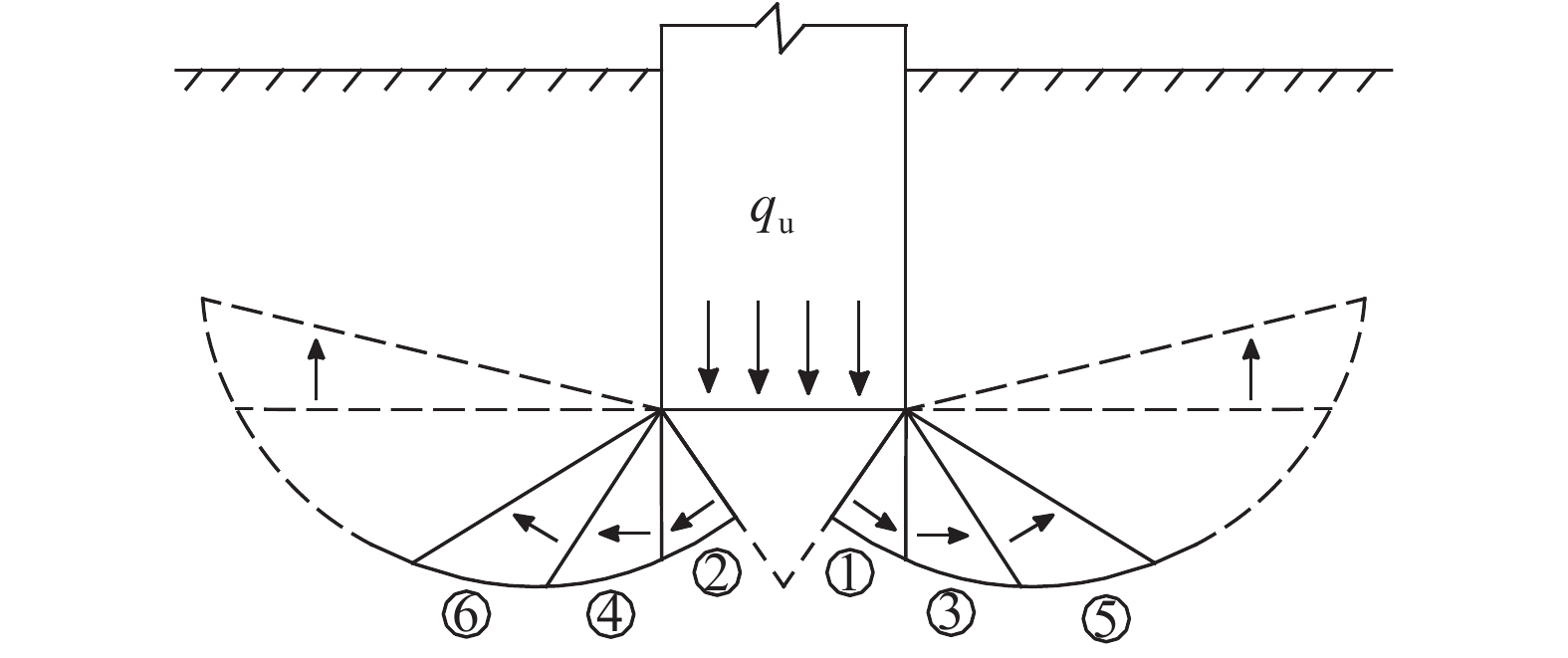 |
| 图2 砂土地基破坏过程 Fig. 2 Failure process of sand ground |
随着基底压力的增加,①、②区域最先发生剪切,③和⑤、④和⑥继续压密,随后依次(③→⑤、④→⑥)发生剪切。如此,地基中不同区域的土颗粒依次开始发生移动,地基依次发生压密,之后的土体剪切也依次不断发生,最终形成连续的剪切破裂面。当地基破坏时,地基破坏土体由此可划分为3个区域,即基底以下的楔形压密区Ⅰ、剪切区Ⅱ和出现土颗粒移动但未发生剪切的压密区Ⅲ,如图3所示。
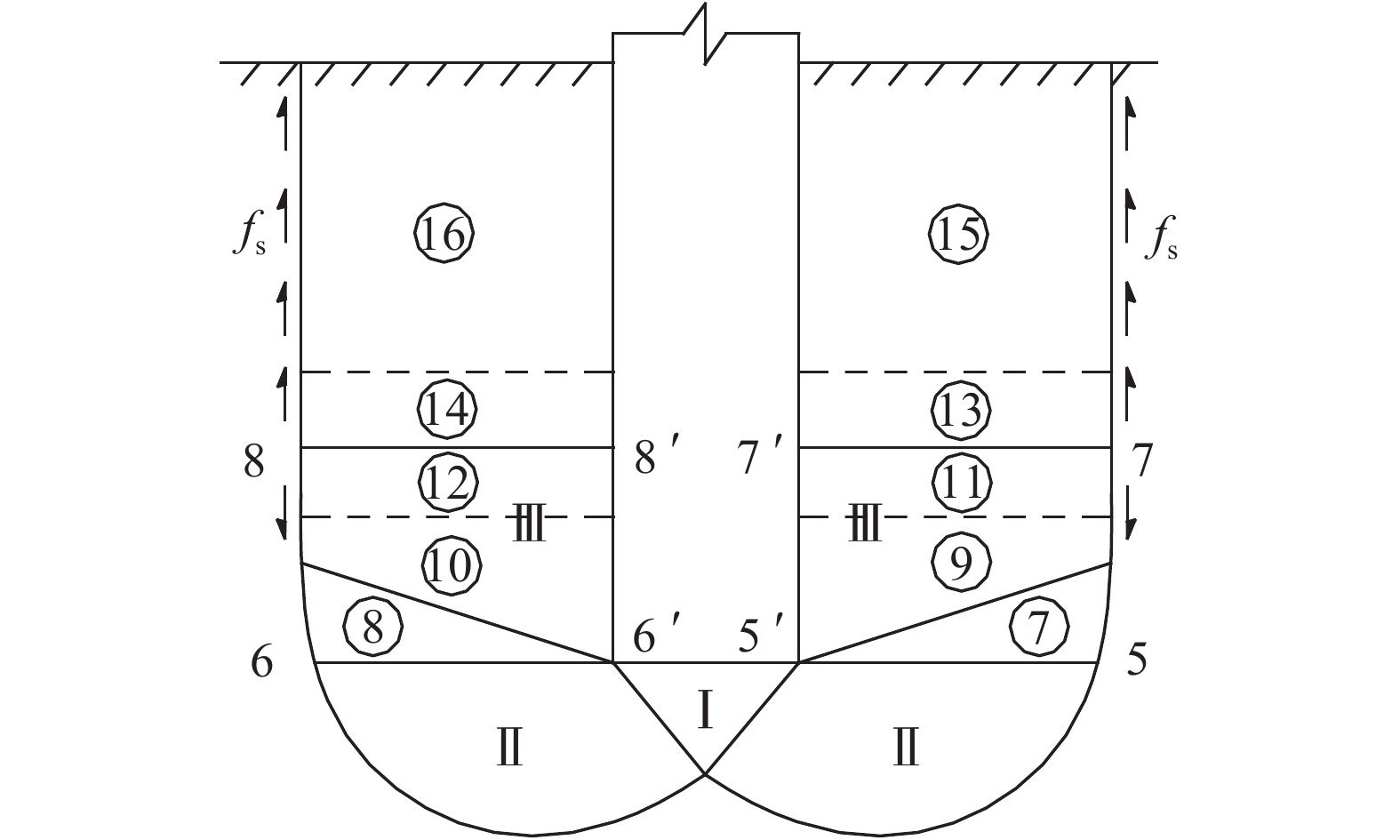 |
| 图3 基础周围土中不同土颗粒运动状态分区 Fig. 3 Partition of soil around the foundation based on the particle motion state |
需要说明的是,当①、②区域发生剪切后,③和⑤、④和⑥内土颗粒的移动方向应发生改变,根据经验的地基剪切破坏面线走向可以判断,其移动方向应发生向上的倾斜。随着土体剪切的不断发生,土颗粒的移动方向也不断地向上倾斜,直至地基破坏,如图2所示。
2)基础周围土的运动状态确定
如图4所示,在地基压密的过程中,基础出现沉降;同时,基础周围土也会因为基底水平面(3-3'和4-4')以下地基土的压密而出现下移或下移的趋势。这里所指的地基压密既包括地基中塑性区出现之前的,也包括塑性区出现之后的。对于基础周围土的下移来说,以基底水平面上土的下移为例,其位置最终分别由面3-3'和4-4'下移到面1-1'和2-2'。基础周围土体的下移要受到向上的摩擦力的影响,故此时基础周围土中各点处的竖向压力qT的数值应小于该处的自重应力γH1,其减小的数值为1-1'和2-2'面以上基础周围土体外侧面上所受的摩阻力fs,即负摩阻力。
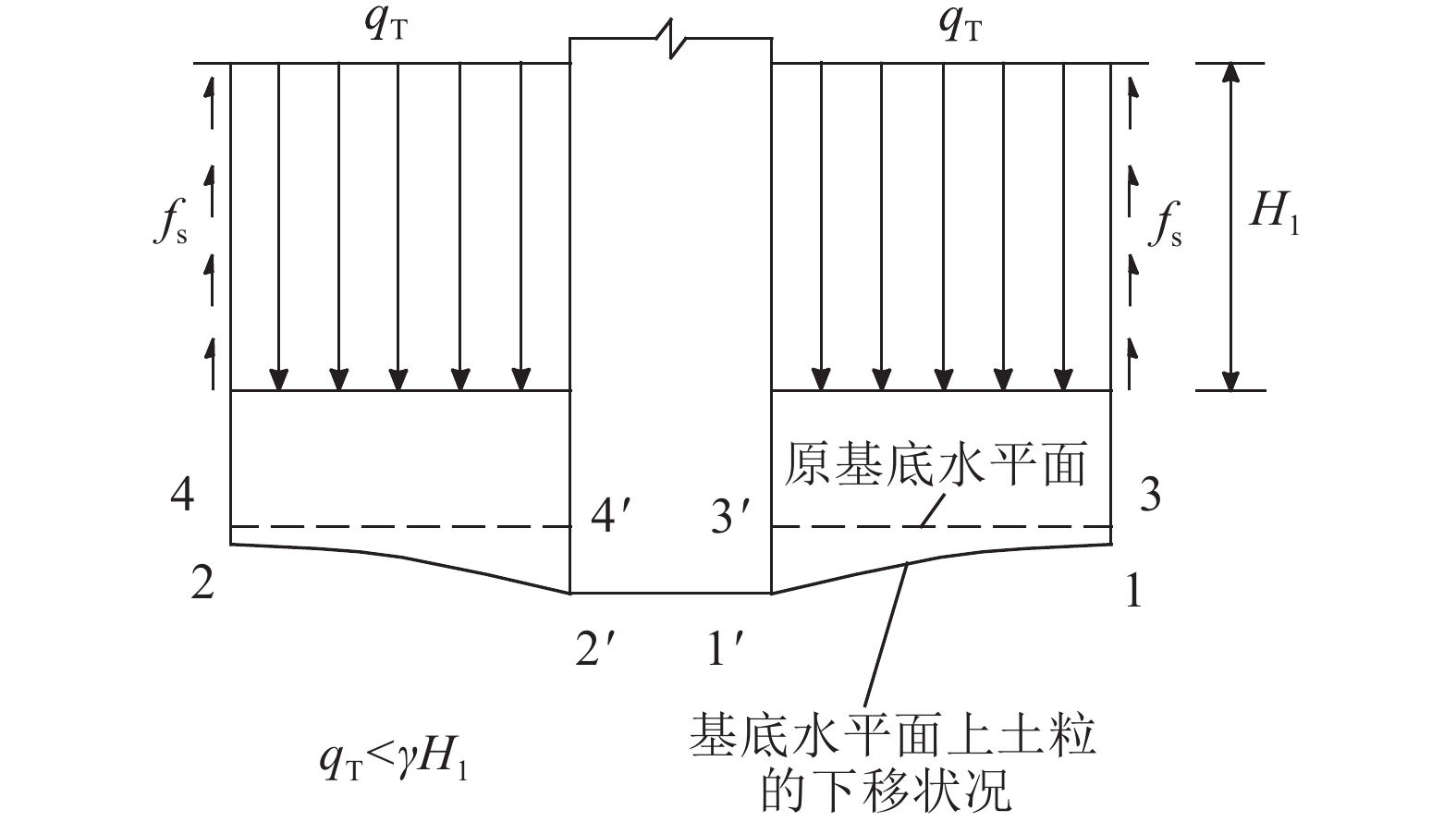 |
| 图4 基础周围土的下移 Fig. 4 Downward movement of soil around the foundation |
地基中出现塑性区以后,如前所述,沿地基剪切破坏面走向的方向上,不同区域的地基土颗粒依次开始发生移动。当位于临界基底水平面(图3中面5-5'和6-6')以上区域的土颗粒发生移动时,据上文分析可知,由于其移动的方向为沿基础底面向上或者斜向上(图2),基础周围部分土体的下移现象或下移趋势将被此时自下而上的土颗粒移动抵消;在靠近基底面处,基础周围土还可能发生自下而上的压密变形,甚至剪切(图3中右侧⑦~鰰 、左侧⑧~鰱 )。
如前所述,地基土颗粒在土中附加应力的作用下依次发生移动,土中附加应力也同时在土颗粒间传递时逐渐减小。结合图3,假定当地基达到极限状态时,基底面标高以上的部分土体也产生了向上的移动,故基底面标高以上各区域内的附加应力大小应为沿⑦→鰴 和⑧→鰵 逐渐地减小;关于此时基底面以上各区域内土颗粒的运动状态和区域外侧面上的摩阻力状况可假设如表1所示。
| 表1 基底面以上区域内土体运动状态及摩阻力状况 Tab. 1 Soil particle motion and the friction on the outer surface in regions above the level |
 |
当地基达到极限状态时,假定破坏土体的Ⅰ、Ⅱ、Ⅲ区域均为刚体,通过确定地基土中剪切破裂面的长度,即可进行地基极限承载力的计算。对于右侧⑨~鰴 、左侧⑩~鰵 区域外侧面上所受的摩擦力,为计算方便,均按滑动摩擦进行计算。在地基极限承载力计算时,鰲 和鰴 、鰳 和鰵 区域外侧面上的负摩阻力,以对作用于压密区Ⅲ上界面的自重应力进行折减的方式体现,折减方式见下文均布压力
3)地基中剪切破裂面线长度的确定
分析Berezantzev等[9–10]在试验中得到的成果可知,深基础下的地基发生破坏时,土中剪切破裂面线(图5中粗线)的长度是由基础埋深(H/b)和地基土相对密度(Dr)两个因素共同决定的:当H/b一定时,Dr越大,地基破坏时形成的剪切破裂面长度越大;当Dr一定时,H/b越大,地基破坏时的剪切破裂面长度越小。
总结Durgunoglu、Nguyen等的研究成果[3,9–11]可知,当基础的相对埋深为2≤H/b≤5时,多数情况下的地基土剪切破裂面均可发展至基底面以上,类似于Hu提出的深基础下地基破坏模式[2]。只有当Dr较大,H/b接近于2时,地基土的剪切破裂面才会发展至地表面处,形成贯通于地表的破裂面[9],如图5(a)所示;当Dr较小,H/b等于5时,地基土的剪切破裂面发展至基底面或基底面以下的某部分区域,形成很小的剪切破裂面[10] ,如图5(c)所示。由于这两种破坏模式在上述彼此对应的H/b条件下还没有定量的结果,为计算方便,假定这两种剪切破裂面也均发展至基底面以上,如图5(b)所示。此时,半径最大的对数螺旋线与基底平面的夹角为
常用的Berezantzev公式[5]在计算深基础地基极限承载力时,对于1.5~2≤H/b≤3~4情况,建议的剪切破裂面为基础无埋深(或特浅埋深)时的破裂面,类似于Terzaghi地基破坏模式。显然,用该公式确定的地基土水平塑性变形范围偏大,计算出的地基极限承载力也偏大。
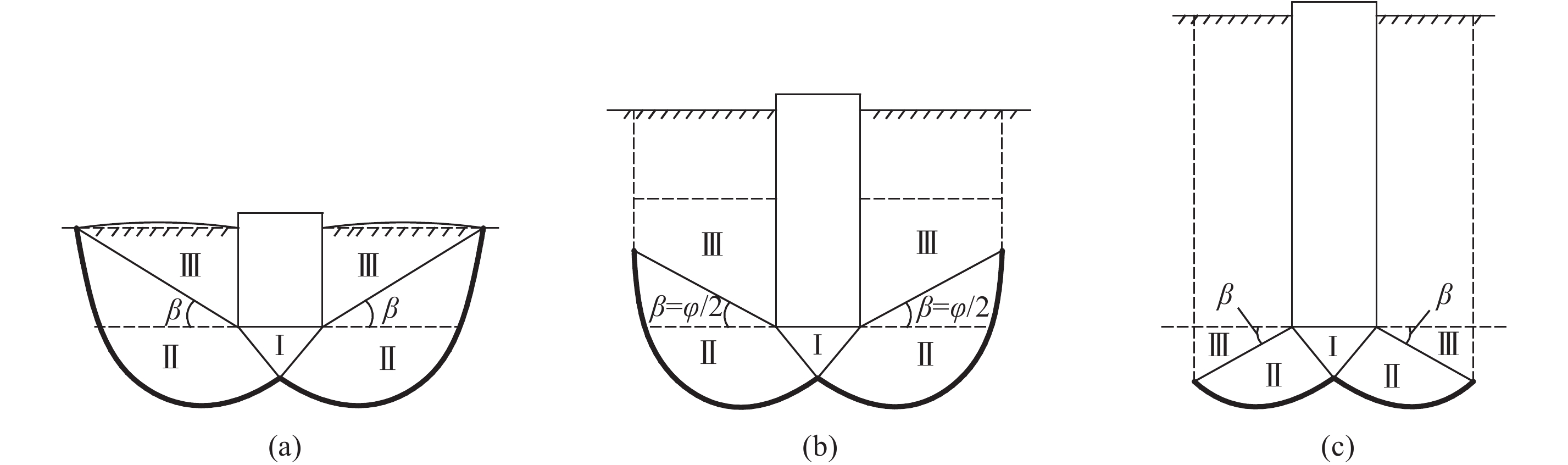 |
| 图5 地基中剪切破裂面长度 Fig. 5 Shear failure surface length in the ground |
1.2 圆形基础下砂土地基破坏模式
圆形基础下地基变形是轴对称的,地基土的水平变形区域要小于平面应变条件下[1,4],因此用条形基础下地基破坏时的对数螺旋包络线描述圆形基础下地基土体的塑性变形范围不合适。Berezantzev在试验的基础上,给出轴对称应变条件下砂土地基破坏的剪切区包络线方程[12],可表示为:
| $r = \frac{{{r_0}}}{{\cos (\varphi /2)}}{{\rm{e}}^{(\theta - \frac{\varphi }{2})\tan \frac{\varphi }{2}}}$ | (1) |
由于通常情况下基础底面并非完全光滑,因此必须考虑基底粗糙条件对地基极限承载力的影响。根据Terzaghi的研究可知[4,13],当基底完全光滑(δ=0)时,基底面上的剪应力为0,滑动土楔侧面与基底面的夹角为
综上所述,对于相对埋深为2≤H/b≤5的圆形深基础,基底下砂土地基在达到极限状态时可做出如下假定:
1)基础底面粗糙,基底下压密土楔侧面与基底面的夹角ψ=45°;
2)地基发生破坏时,如图6所示,破坏土体分为压密区Ⅰ、剪切区Ⅱ和压密区Ⅲ这3部分,剪切区Ⅱ的外包络线用式(1)的对数螺旋线表示,半径最大的对数螺旋线与基底平面的夹角为
3)地基土在压密变形前后的单位重度无变化。
如图7所示,取以ACF为中心面,绕圆形深基础中心轴O1O2左右各旋转dα后所得破坏土体隔离体作为研究对象,极限承载力的推导按以下进行:1)取图7中压密区Ⅲ的隔离体agf-a1g1f1进行受力分析;2)取剪切区Ⅱ的隔离体afCf1a1进行受力分析;3)取压密区Ⅰ的隔离体OCaa1进行受力分析,同时联立1)、2)求得的力或力矩平衡式,最终求出基底的极限承载力qu;4)将基底的极限承载力和基础侧壁的极限摩阻力相加,得到圆形深基础的地基极限承载力Q。
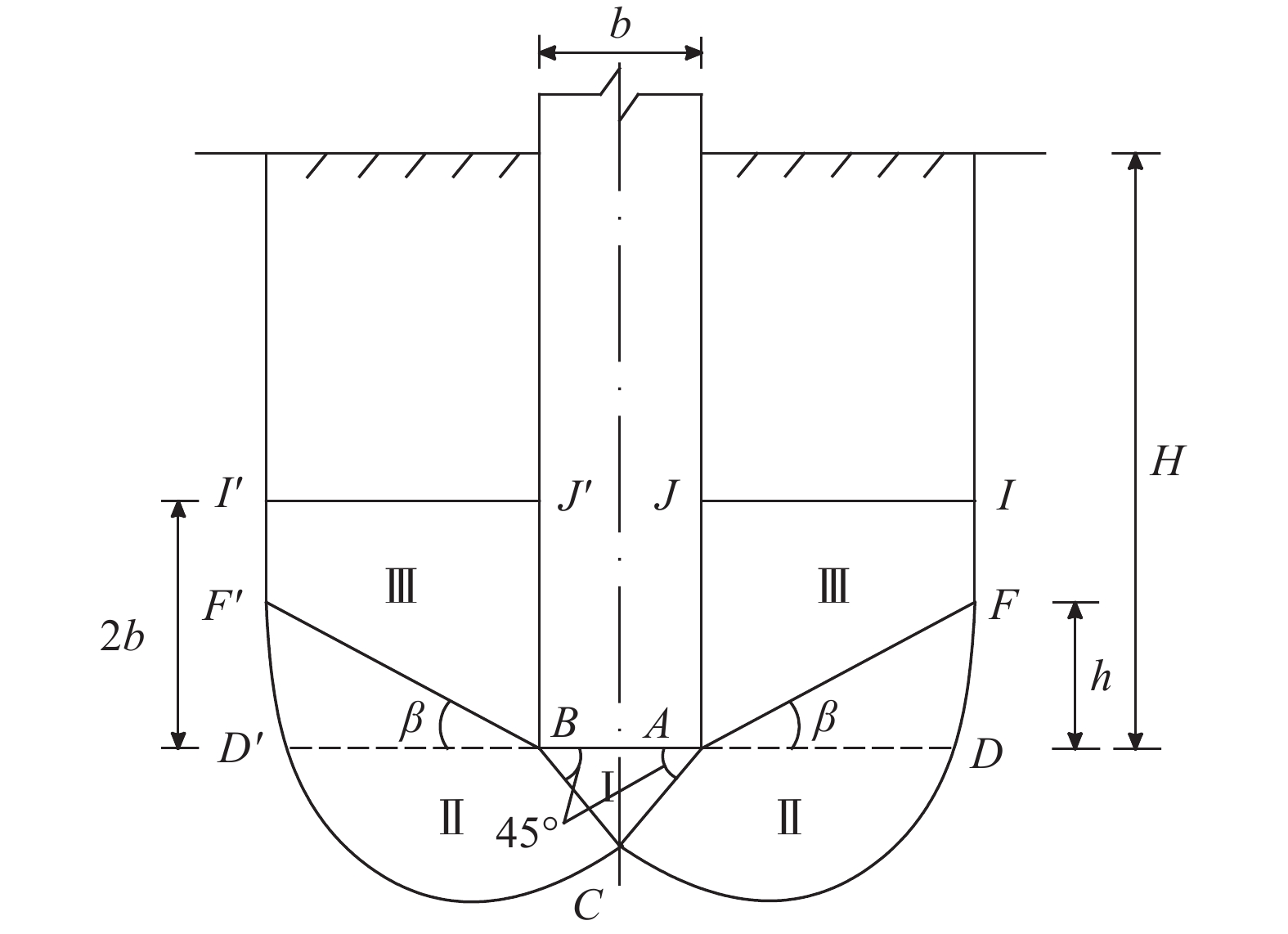 |
| 图6 圆形深基础下地基破坏剖面 Fig. 6 Failure sectional drawing of sand ground under deep circular foundation |
 |
| 图7 地基破坏隔离体 Fig. 7 Isolation body of damaged ground |
2.1 剪切区侧面aff1a1上法向压力σa的求解
如图8所示,对隔离体agf-a1g1f1进行受力分析,母线AF与水平面的夹角为β,作用在隔离体上的诸力为隔离体顶面gff1g1上的竖向压力qT1、侧表面aff1a1上的法向应力σa、切向应力τa、基础侧面agg1a1上的法向应力σ0、切向应力τ0、环向应力R1和隔离体内土体自重W1。令基础的直径为b,在静力平衡条件下对侧表面aff1a1上的法向应力σa进行推导。
如图9所示,直角边HI在基础的中心轴O1O2上,中心面AGF绕HI左右各旋转dα后可得到隔离体agf-a1g1f1,计算可得该隔离体内土体自重为:
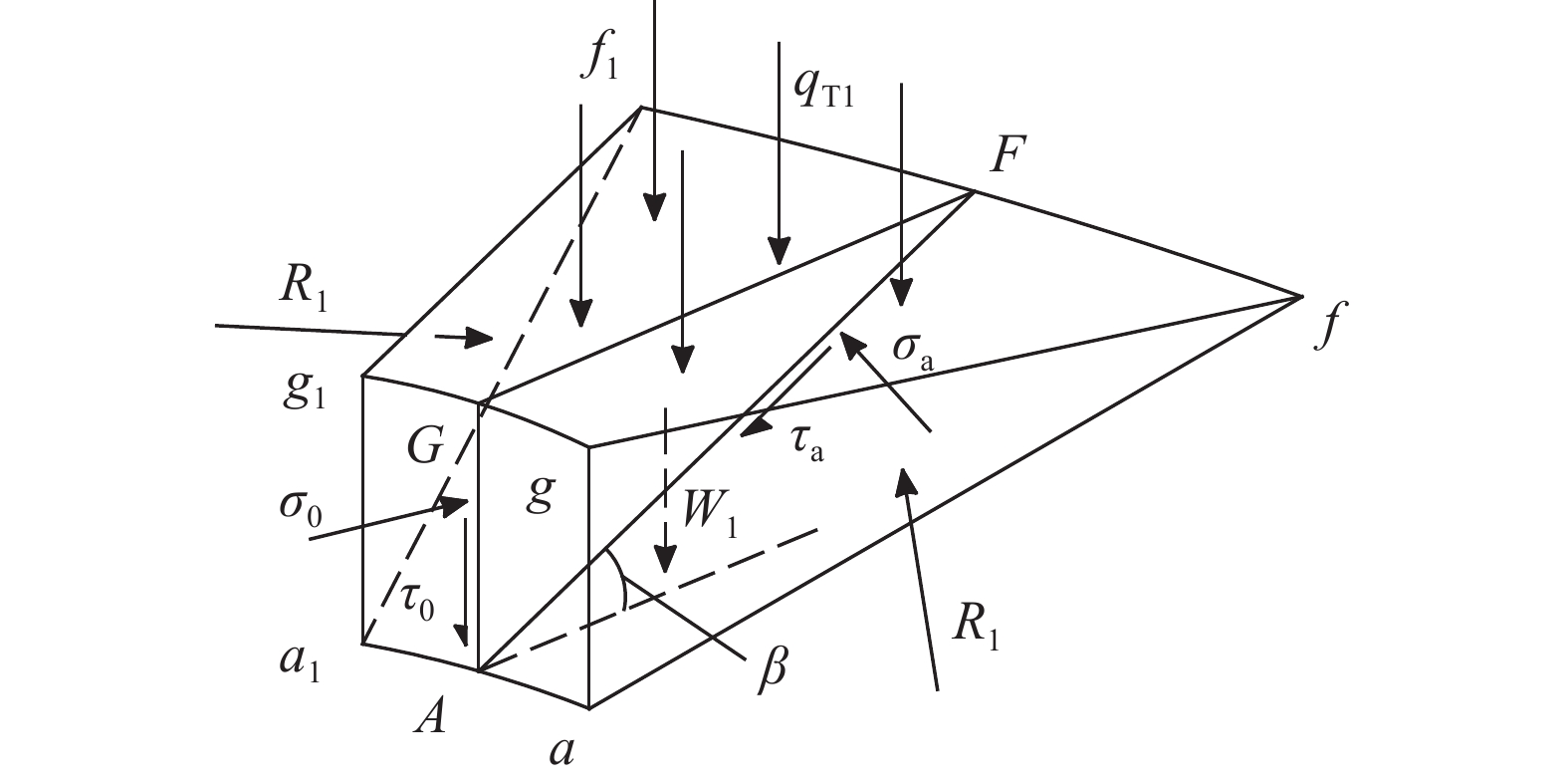 |
| 图8 隔离体agf-a1g1f1受力 Fig. 8 Force analysis of agf-a1g1f1 |
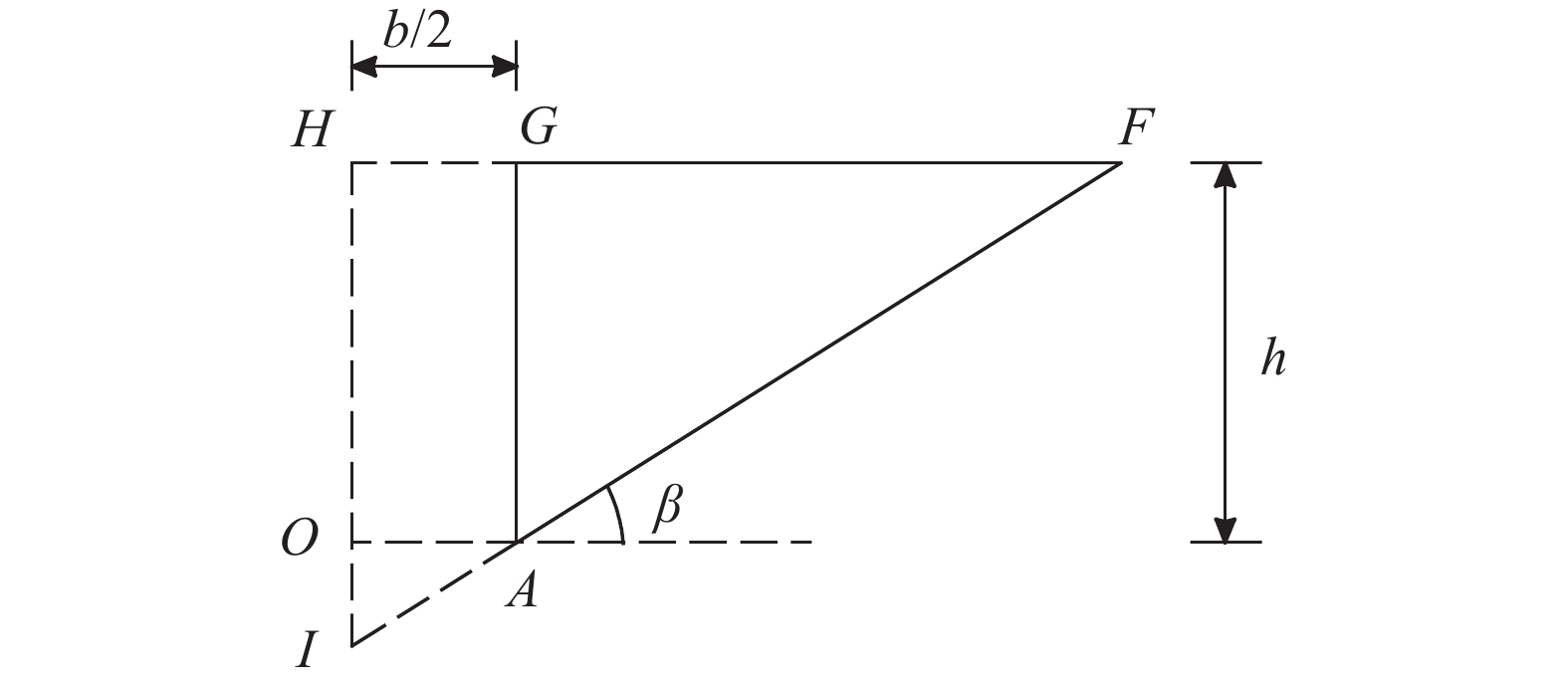 |
| 图9 中心面AGF的面积 Fig. 9 Area of center plane AGF |
| $\begin{aligned}[b]{W_1} \! = \! \gamma {V_3} & \! = \! \gamma \cdot \frac{{{\rm{d}}\alpha }}{4}{\Big{[}}\frac{1}{3}{\left(b \! + \! 2h\cot \; \beta \right)^2}\left(\frac{1}{2}b\tan \; \beta \! + \! h \right) \! - \! \! \\& \quad \frac{1}{3}{b^2} \cdot \frac{1}{2}b\tan \; \beta - {b^2}h{\Big{]}}\end{aligned}$ | (2) |
顶面gff1g1的面积为:
| ${S_{\!\!1}} = \frac{{{\rm{d}}\alpha }}{4}[{(b + 2h\cot \; \beta )^2} - {b^2}]$ | (3) |
因此,侧表面aff1a1的面积为:
| ${S_{\!\!2}} = {S_{\!\!1}}/\cos \;\beta $ | (4) |
σ0按ag或a1g1中点处所受的单位主动土压力计算,具体计算类似于下文的ea。为了推导方便,假定侧壁agg1a1各处的法向压力均等于σ0。
关于隔离体顶面gff1g1上竖向压力qT1,可以借助对地基破坏剖面的受力分析进行求解。如图10所示,面FGG'F'上所受的竖向压力即为
如前所述,
| ${q_{\rm{T}}\,'} = {\alpha _{\rm{T}}}\gamma (H - 2b)$ | (5) |
式中,αT为竖向荷载折减系数,其计算表达式可参考文献[14]。
| $h' = 2b - h$ | (6) |
式中,h为剪切滑动面在基底面以上发展的最大高度,
| ${f_{\rm{s}}}^\prime = \frac{\displaystyle{\left(2h + b\tan \; \frac{\varphi }{2}\right)\tan \;\varphi \int_{H-2b}^{H - h} {{e_{\rm{a}}}{\rm{d}}{\textit{z}}} }}{\displaystyle{{h^2}\cot \; \frac{\varphi }{2}+ bh}}$ | (7) |
式中,ea为压密区Ⅲ外侧面上所受单位主动土压力,计算可参考文献[12]。
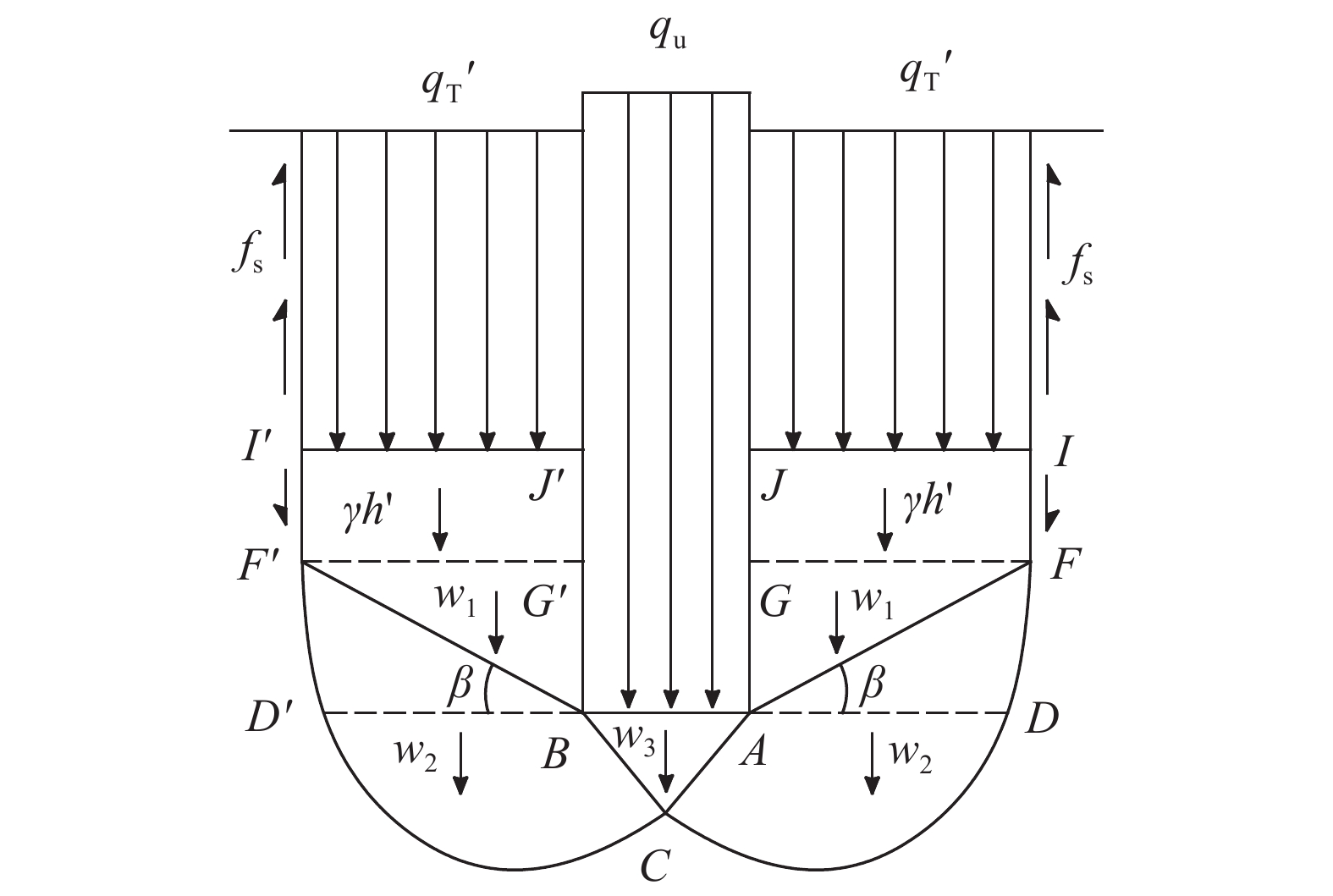 |
| 图10 地基破坏剖面受力 Fig. 10 Force analysis of failure soil section |
地基在发生轴对称破坏时,地基破坏土体显然要受到环向应力的作用。根据地基中不同区域的应力分析可知,环向应力可分为3种,即压密区Ⅲ内的环向应力R1(图8)、剪切区内除基底正下方以外部分的R2和基底正下方内的R3(图11)。
如前所述,地基土颗粒在土中附加应力的作用下发生移动,在压密区Ⅲ内,土颗粒的移动方向为在径向不断靠近基础向内移动,因此在环向上,土体处于被挤压的状态,压密土体侧面agf和a1g1f1上的压力状态为被动状态。为计算方便,压密区Ⅲ内环向应力R1可近似取为被动土压力。如图12所示,以面gf和面g1f1所受的环向应力为例,令dE1为面gf和面g1f1上由环向应力R1引起的单位水平分力,从图12中的几何关系可得:
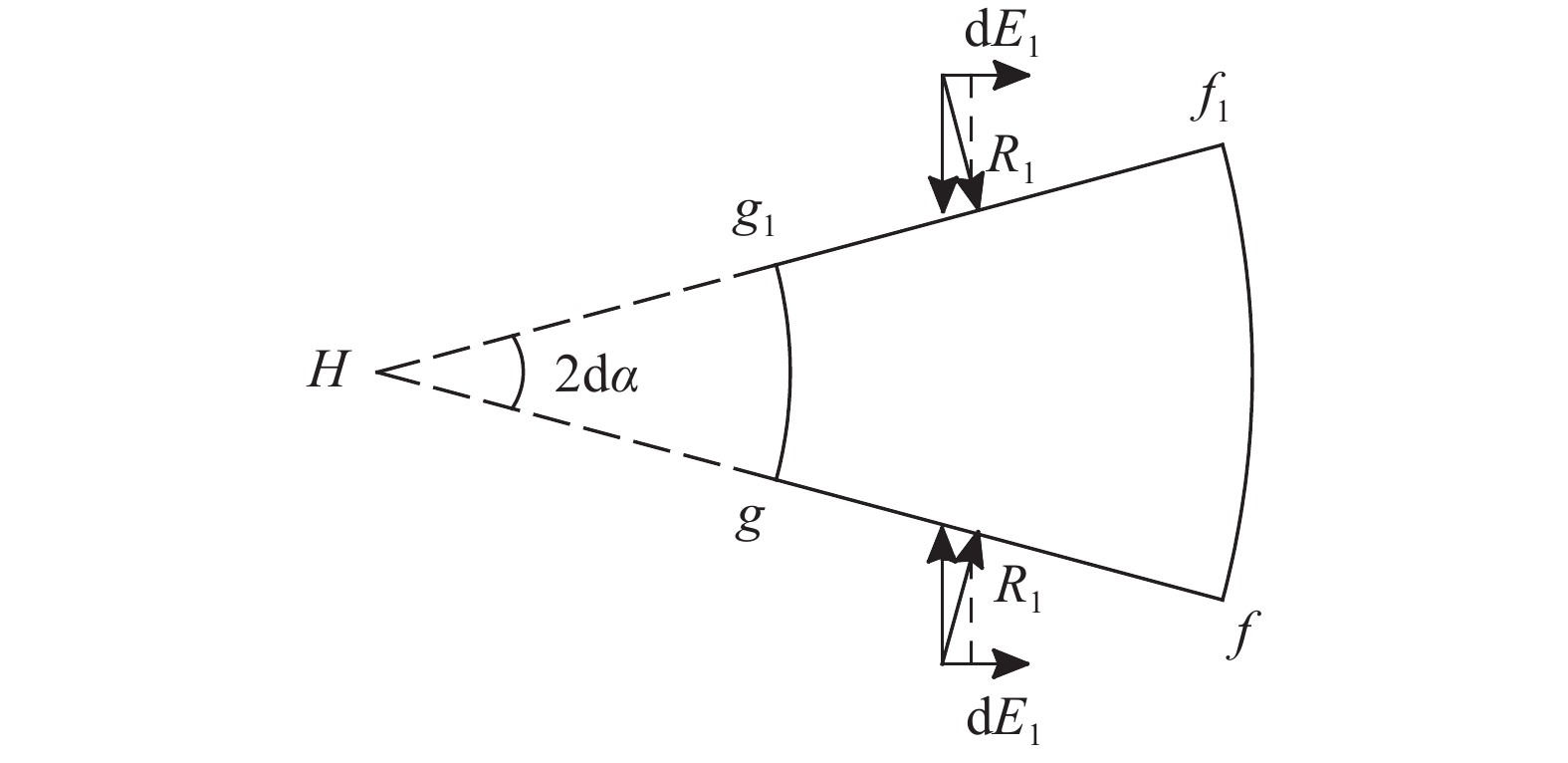 |
| 图12 水平分力dE1计算示意图 Fig. 12 Calculation of horizontal component dE1 |
| ${\rm{d}}{E_1} = {R_1}\sin ({\rm{d}}\alpha ) = ({q_{{\rm{T1}}}} + \gamma {\textit{z}}){K_{\rm{p}}}\sin ({\rm{d}}\alpha )$ | (8) |
式中:Kp为被动土压力系数,
因此,由环向应力R1引起的总的水平分力为:
| ${E_1} = {h^2}\cot \; \varphi {\rm{d}}{E_1} = {h^2}\cot \; \varphi ({q_{{\rm{T1}}}} + \gamma h/3){K_{\rm{p}}}\sin ({\rm{d}}\alpha )$ | (9) |
由隔离体侧表面aff1a1上法线方向上所有力的平衡得:
| $\begin{aligned}[b]{\sigma _{\rm{a}}}{S_2} & \! = \! {q_{{\rm{T}}1}}{S_1} \! + \! {\sigma _0}bh\left( \sin \; \beta \! + \! \cos \; \beta \; \tan \; \delta \right] \sin ({\rm{d}}\alpha ) \! + \! \! \\& \quad {W_1}\cos \; \beta + {E_1}\sin \; \beta\end{aligned}$ | (10) |
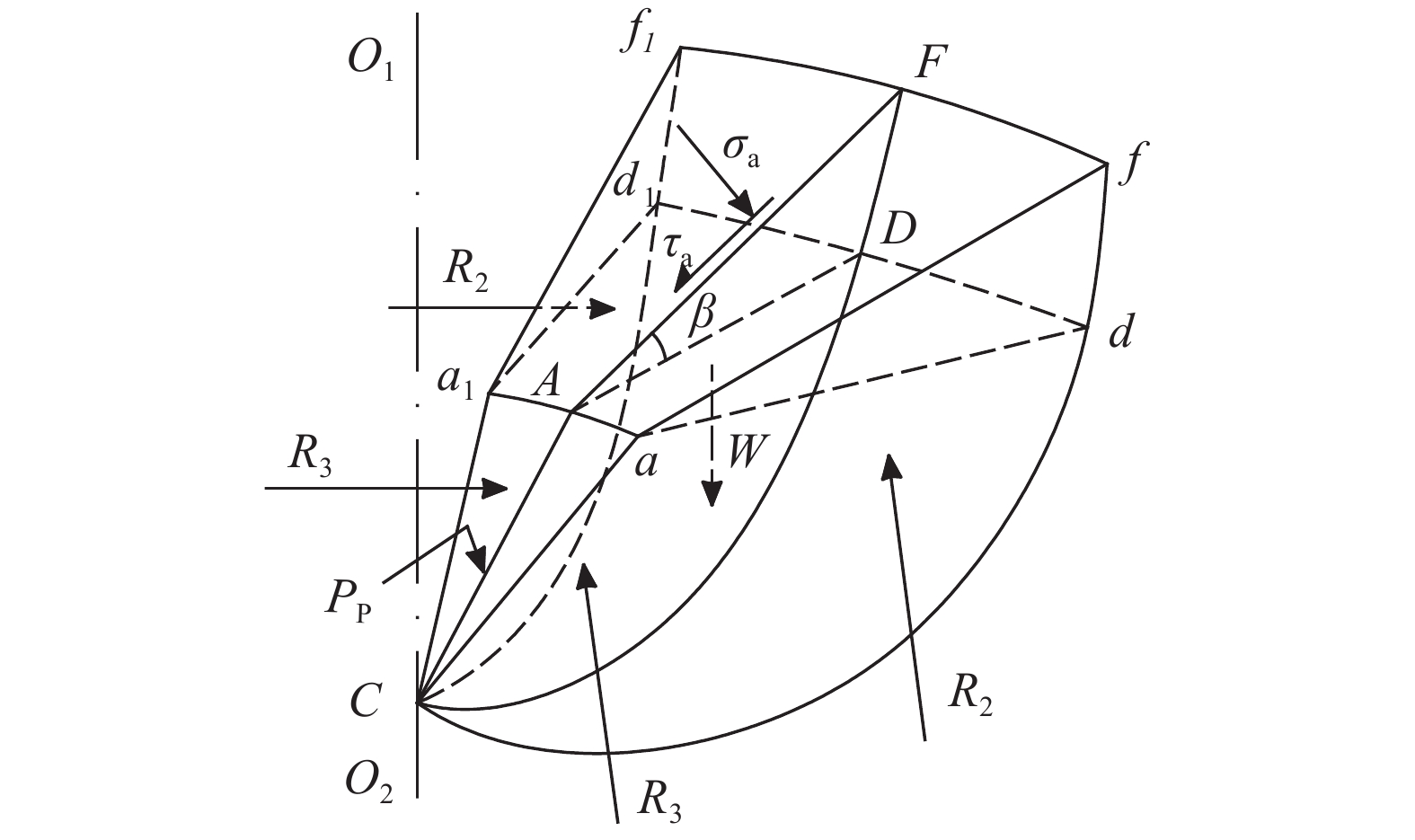
如图11所示,取剪切区Ⅱ的隔离体afCf1a1进行研究,假定作用在该隔离体上的诸力为汇交力系,在计算时,将
计算可得aff1a1面上的法向应力σa对A点的力矩为:
| $\begin{aligned}[b]M{\sigma _{\rm{\! a}}} & = {\sigma _{\rm{\! a}}}{r_2}^2(b/2 \! + \! 2{r_2}\cos \; \beta /3) \; \cdot \\& \quad [1 - {\cos ^2}\beta {\sin ^2}({\rm{d}}\alpha )]\sin ({\rm{d}}\alpha )\end{aligned}$ | (11) |
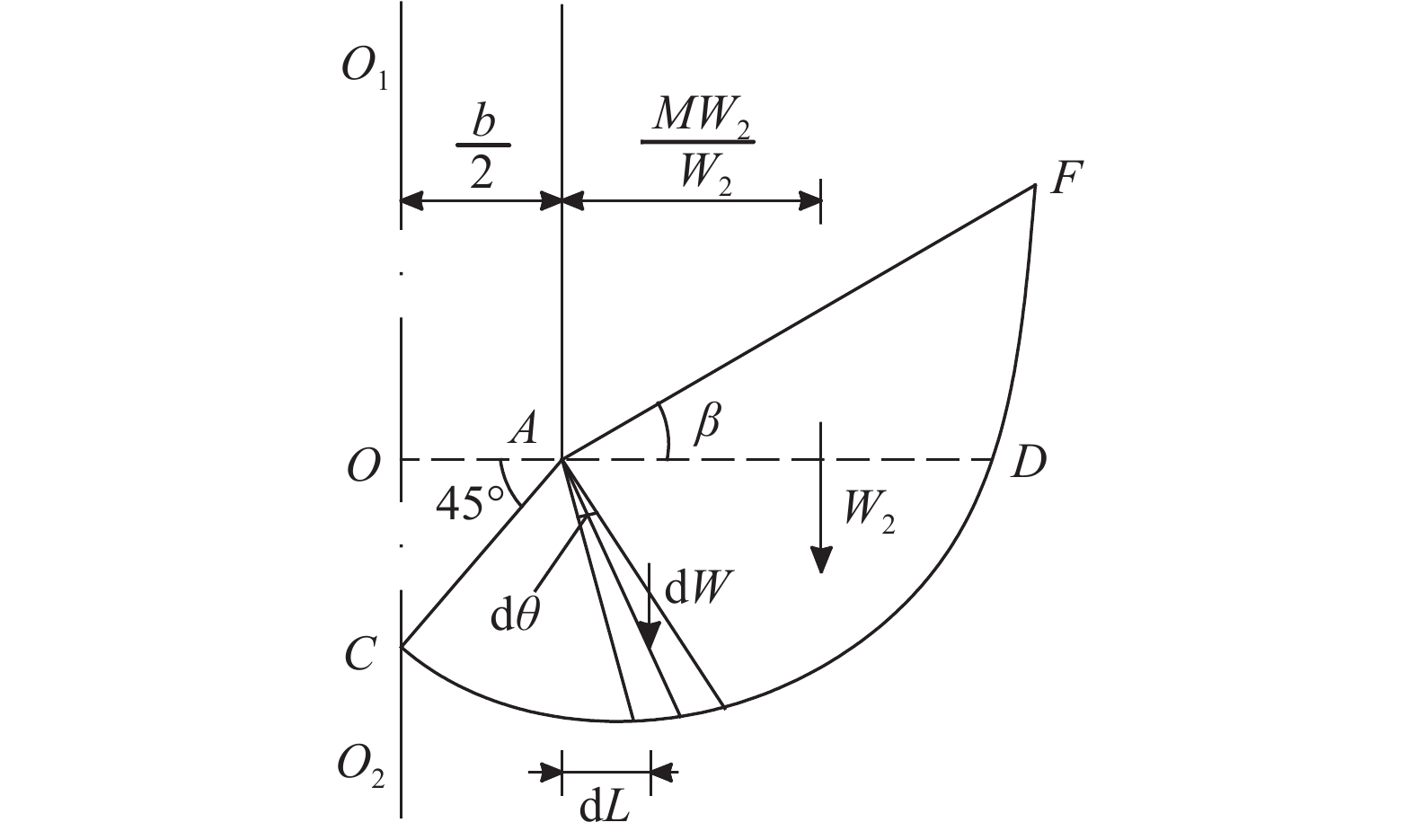
如图13所示,令W2为中心面ACF内土体的重力,L1为其到A点的力臂。面ACF内土体自重为:
| ${W_2} \! = \! \int_0^{\frac{3}{4}\text{π} \! + \! \beta } {{\rm{d}}W{\rm{d}}} L \! = \! \int_0^{\frac{3}{4}\text{π} {\rm{ + }}\beta } {\frac{1}{2}\gamma {r_0}^2{{\sec }^2}\frac{\varphi }{2}} {{\rm{e}}^{2(\theta - \frac{\varphi }{2})\tan \frac{\varphi }{2}}}{\rm{d}}\theta $ | (12) |
面ACF内土体自重对A点的力矩为:
| $\begin{aligned}[b]\! \!\!\,M{W_2} \! = \! & \int_{\frac{\text{π} }{4}}^{\frac{3}{4}\text{π} + \beta } {\frac{2}{3}{\rm{d}}M{{\left( {{\rm{d}}L} \right)}^2}} \! - \! \int_0^{\frac{\text{π} }{4}} {\frac{2}{3}{\rm{d}}M{{\left( {{\rm{d}}L} \right)}^2}} = \\& \int_0^{\frac{3}{4}\text{π} {\rm{ + }}\beta } {\frac{1}{3}\gamma {r_0}^3{{\sec }^3}\frac{\varphi }{2}} {{\rm{e}}^{3(\theta - \frac{\varphi }{2})\tan \frac{\varphi }{2}}}\cos \left(\frac{3}{4}\text{π} - \theta \right){\rm{d}}\theta\end{aligned}$ | (13) |
绕中心O对W2进行积分,得到隔离体afCf1a1内土体自重对A点的力矩为:
| $MW = 2 \! \int_0^{{\rm{d}}\alpha } \left[ {\frac{{M{W_2}}}{{{W_2}}} + \frac{1}{2}b} \right]M{W_2}\cos \eta {\rm{d}}\eta $ | (14) |
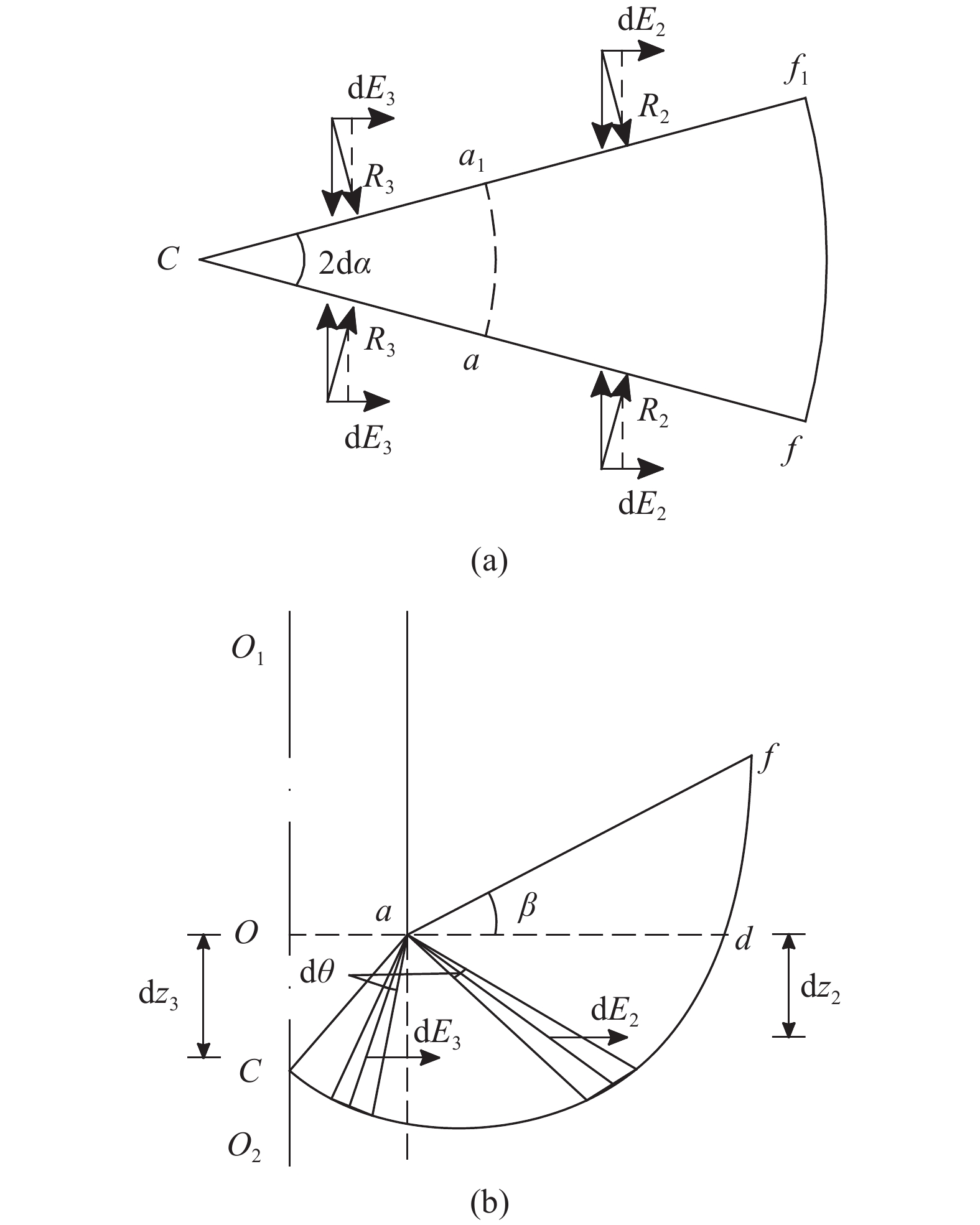
环向应力R2和R3的求解与R1类似,在剪切区Ⅱ内,土体的移动方向在径向为不断地背离基础向外移动。因此在环向上,土体处于被拉裂的状态,压密土体侧面aCf和a1Cf1上的应力为主动状态,R2和R3可近似取为主动土压力。
 |
| 图11 剪切区受力 Fig. 11 Force analysis of shear zone |
 |
| 图13 中心面ACF内土重对A点力矩 Fig. 13 Moment caused by soil gravity in the center plane ACF |
如图14所示,令dE2为在面aCf上由R2引起的单位水平分力,dE3为面aCf上由R3引起的单位水平分力,dz2和dz3分别为dE2和dE3对A点求矩时的力臂。面a1Cf1上的情况与面aCf上的相同。在
| $\begin{aligned}[b]\! \! M{E_2} \! = \! & \int {{\rm{2d}}{E_2}} {\rm{d}}{{\textit{z}}_2} \! = \! \int_{\frac{\text{π} }{4}}^{\frac{3}{4}\text{π} + \beta } {\frac{2}{3}{r_0}^3{K_{\rm{a}}}\sin ({\rm{d}}\alpha )} \cdot \\& [{q_{\rm{T1}}} \! + \! \gamma h \! + \! \gamma {{\textit{z}}_0}] {\sec ^3}\frac{\varphi }{2}{{\rm{e}}^{3(\theta - \frac{\varphi }{2})\tan \frac{\varphi }{2}}}\sin \left(\frac{3}{4}\text{π} - \theta \right){\rm{d}}\theta \!\!\!\!\!\end{aligned}$ | (15) |
在θ = 0到π/4上对2dE3dz3进行积分,可得剪切区隔离体afCf1a1上由R3引起水平分力对A点的力矩为:
| $\begin{aligned}[b]M{E_3} = & \int {2{\rm{d}}{E_3}} {\rm{d}}{{\textit{z}}_3} = \int_0^{\frac{\text{π} }{4}} {\frac{2}{3}{r_0}^3{K_{\rm{a}}}\sin ({\rm{d}}\alpha )} \cdot \\& [{q_{\rm{u}}} + \gamma {{\textit{z}}_0}] {\sec ^3}\frac{\varphi }{2}{{\rm{e}}^{3(\theta - \frac{\varphi }{2})\tan \frac{\varphi }{2}}}\sin \left(\frac{3}{4}\text{π} - \theta \right){\rm{d}}\theta \end{aligned}$ | (16) |
式中,
 |
| 图14 环向应力E2、E3引起力矩的计算 Fig. 14 Moment caused by lateral earth pressure E2, E3 |
如图15所示,面Caa1上的被动土压力Pp与法线方向夹角为φ,可得到面Caa1上的被动土压力Pp对aa1中点A的力矩为:
| ${M \! P_{\rm{p}}} = \frac{1}{4}{P_{\rm{\! p}}}b\cos \; \varphi \sqrt {2 - {{\sin }^2}({\rm{d}}\alpha )} $ | (17) |
由力矩平衡得:
| $M{\sigma _{\rm{a}}} + MW - M\! {E_2} - M\! {E_3} - M\! {P_{\rm{p}}} = 0$ | (18) |
 |
| 图15 压密区Ⅰ受力 Fig. 15 Force analysis of compaction zoneⅠ |
2.3 基底极限承载力qu的求解
由图15中三棱锥OCaa1内竖向力的静力平衡得:
| ${P_{\rm{\! p}}}\cos \left(\frac{\text{π} }{4} - \varphi \right) = {q_{\rm{u}}}{S_{\!\! 0}} + \gamma {V_{OCaa_1}}$ | (19) |
式中,
联立式(10)、(18)、(19)可得:
| ${q_{\rm{u}}} = {q_{{\rm{T}}1}}{N_{\rm{q}}} + \gamma b{N_{{\rm{\gamma }}1}} + {\sigma _0}{N_{{\rm{\gamma }}2}}$ | (20) |
其中,
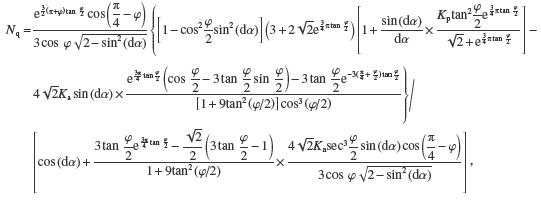
|

|
将Nq、Nγ1、Nγ2合并为系数Nγq,圆形深基础基底的极限承载力可表示为:
| ${Q_{\rm{u}}} = \frac{\text{π} }{4}{b^2}{q_{\rm{u}}} = \frac{\text{π} }{4}{b^2}\gamma H{N_{\gamma q}}$ | (21) |
式中,
另外,对于具有一定黏聚强度胶结砂地基,还应考虑黏聚力对地基承载力的贡献。根据土体抗剪强度相等的原理,用等效内摩擦角的方法可以将胶结砂土的黏聚力折算成内摩擦角,并以此时的等效内摩擦角φD计算地基的极限承载力,折算方法为:
| ${\varphi _{\rm{D}}} = \arctan \left( {\tan \; \varphi + c/{\sigma _{\rm{t}}}} \right)$ | (22) |
式中:φ为胶结砂的内摩擦角;c为黏聚力;σt为剪切破裂面上的法向应力,综合考虑可近似取为γH。
用φD替换承载力参数Nq、Nγ1、Nγ2中的φ,并将此时的Nq、Nγ1、Nγ2代入式(21),即可计算出胶结砂地基基底的极限承载力。
2.4 圆形深基础地基极限承载力的计算圆形深基础侧壁上作用的法向应力为轴对称状态下主动土压力,结合钱家欢等[2]对Hu深基础承载理论的研究可知,圆形深基础侧壁的摩阻力可按式(23)~(24)进行计算:
| ${Q_{\rm{s}}} = \sum\limits_1^n {{A_{0i}}{f_{{\rm{s}}i}} = \sum\limits_1^n {{A_{0i}}({E_{{\rm{a}}i}}\tan {\delta _i} + {c_{{\rm{a}}i}})} } $ | (23) |
| ${E_{{\rm{a}}i}} = \int_0^{{h_i}} {{{\rm{e}}_{{\rm{a}}i}}} {\rm{d}}h$ | (24) |
式中:A0i为基础埋入第i层土的周长;fsi为第i层土与基础侧壁之间的单位极限摩阻力;Eai为hi上的主动土压力;δi为第i层土与基础侧壁之间的摩擦角,取值方法同δ;cai为第i层土与基础侧壁之间的黏聚力,可根据文献[2]中确定桩侧面黏聚力的方法确定;eai为hi上的单位主动土压力,计算方法可参考文献[14];hi为第i层土层厚。
当深基础的埋深大于2b时,侧壁摩阻力的最大计算埋深取为H–2b。
将式(21)、(23)相加,可得圆形深基础地基极限承载力为:
| $Q = {Q_{\rm{u}}} + {Q_{\rm{s}}}$ | (25) |
算例1:假定土为均质砂土,深基础直径b=3,土体重度γ=18 kN/m3,黏聚力c=0,即不考虑黏聚力对承载力的贡献,基础的相对埋深H/b取为2、3、4、5,中心面ACF的水平旋转角度dα取为π/100。将所得的承载力系数Nγq与Terzaghi等的半经验公式解在砂土内摩擦角为28°~40°范围内进行对比,得到各相对埋深条件下承载力系数Nγq随地基土内摩擦角的变化规律,如图16所示;本文解得的Nγq在不同相对埋深条件下的变化规律,如图17所示。其中,Terzaghi、Durgunoglu解为假定在地基土平面变形条件下的修正解,本文解和Berezantzev解为假定在地基土轴对称变形条件下的直接解。
由图16可知,4种方法所得的圆形深基础的地基极限承载力系数Nγq均随内摩擦角的增大而增大,但本文所得Nγq随内摩擦角增大的增幅要小些。当地基土的内摩擦角一定时,本文所得Nγq值在不同的H/b条件下均小于上述3位学者的半经验公式解,且随着H/b的增加,差值不断增大。
本文解得的Nγq值小于Berezantzev解,主要是因为本文在分析深基础下砂土地基的破坏模式时,考虑了基础埋深和地基土相对密度对地基剪切区发展范围的影响,以至于本文得出的地基土水平塑性变形范围更小。小于Terzaghi解和Durgunoglu解可能是由于本文考虑了地基轴对称破坏与平面破坏时的不同,从而得出地基的水平塑性变形范围更小;同时,本文解在推导时考虑了地基中环向应力的作用,因此使得Nγq值又进一步减小。
 |
| 图16 承载力系数Nγq与内摩擦角的关系曲线 Fig. 16 Relationship between Nγq and φ |
由图17可知,对于不同的地基土内摩擦角水平,Nγq随基础相对埋深的增加不断减小;对于不同的H/b,Nγq随内摩擦角增大的增幅接近。
 |
| 图17 承载力系数Nγq与内摩擦角的关系曲线(不同H/b) Fig. 17 Relationship between Nγq and φ (different H/b) |
算例2:地基土内摩擦角φ取为28°、34°、40°,H/b取为2、3、4、5,其他参数同算例1。利用本文方法和Terzaghi、Durgunoglu、Berezantzev的半经验公式法分别对深基础的地基极限承载力、地基容许承载力进行计算,并将结果与规范法所得值对比。为方便叙述,文中所用的《建筑桩基技术规范》、《公路桥涵地基与基础设计规范》和《建筑地基基础设计规范》[15–17]分别简称规范1、规范2和规范3。其中,规范法1的计算值为单桩极限承载力标准值,即实测的单桩极限承载力;规范法2的计算值为地基承载力容许值;规范法3的计算值为P1/4临塑荷载时的地基承载力特征值,但在规范中也被当作是地基承载力容许值使用[18]。用规范法计算时承载力的取值均为所用规范中的经验值,Berezantzev方法和规范法1的基础侧摩阻力按桩基础的极限侧摩阻力取值[15],规范法1的桩端阻力按大直径干作业挖孔桩取值,砂土泊松比取为0.3;规范法2、3的基础侧摩阻力按沉井基础的侧摩阻力取值[16]。计算所得的地基极限承载力如表2所示,地基承载力容许值如表3所示。
由表2可知,本文方法和半经验公式方法计算出的地基极限承载力值均比规范法1的结果要大,但本文方法与规范法1的差异最小。由表3可知,本文方法和半经验公式方法计算出的地基承载力容许值均大于规范法2,但本文方法与规范法2的差异仍最小;本文方法与规范法3比较接近,半经验公式所得值均大于规范法3,且差异随内摩擦角的增大而增大。
综合分析可得:本文方法所得地基极限承载力比Terzaghi解、Berezantzev解和Durgunoglu解更接近于规范值。当安全系数取为3时,本文方法所得地基承载力容许值接近于规范值,而通过Terzaghi等其他3位学者的半经验公式法计算出的地基极限承载力需除以一个更大的安全系数才能接近于规范值。
| 表2 地基极限承载力对比 Tab. 2 Comparison of the ultimate bearing capacity |
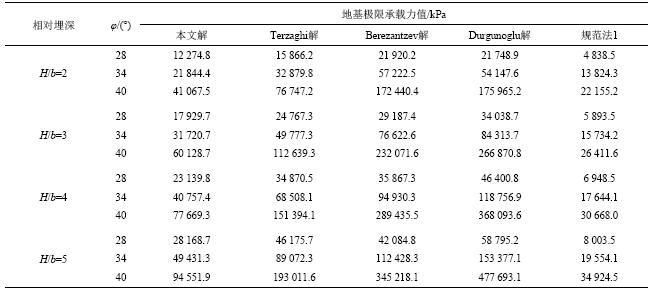 |
| 表3 地基承载力容许值对比 Tab. 3 Comparison of the allowable bearing capacity |
 |
4 结 论
深基础下砂土地基的破坏,是地基中的不同区域依次连续发生压密变形,进而发生土体剪切的结果;地基破坏时的土中剪切破裂面线长度是由基础埋深和地基土相对密度决定的;同时对于轴对称受载下的地基土,其变形破坏的规模也应小于条形受载时。在考虑以上因素的基础上,计算得到了圆形深基础下砂土地基的极限承载力,并结合算例,与Terzaghi、Durgunoglu和Berezantzev的解进行对比,得出如下结论:
1)当H/b一定时,本文所得圆形深基础地基极限承载力系数Nγq随地基土内摩擦角的增大而增大,且对于不同的H/b,其增幅几乎相同;当地基土的内摩擦角一定时,Nγq随H/b的增加而减小。
2)当地基土的内摩擦角一定时,对于不同的H/b,本文得到的Nγq值均小于以上3位学者的结果,其原因主要是作者得出的圆形深基础下砂土地基水平塑性变形范围更小。
3)本文方法所得的地基极限承载力比以上3位学者方法的结果更接近于规范值。当安全系数取为3时,本文方法所得地基承载力容许值接近于规范值,而用以上3位学者方法计算出的地基极限承载力需除以一个更大的安全系数才能接近于规范值。
4)本文结果可直接应用于沉井基础及大直径桩基础的承载力计算。
| [1] |
Meyerhof G G. The ultimate bearing capacity of foundations[J]. Geotechnique, 1951, 2(4): 301-332. DOI:10.1680/geot.1951.2.4.301 |
| [2] |
钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,1996:351–395.
|
| [3] |
Durgunglu H T,Mitchrll J K.Static penetration resistance of soils:I-analysis[C]//In Situ Measurement of Soil Properties.ASCE,1975:151–171.
|
| [4] |
K 太沙基.理论土力学[M].徐志英,译.北京:地质出版社,1960:125–145.
|
| [5] |
郑大同.地基极限承载力的计算[M].北京:中国建筑工业出版社,1979:45–55.
|
| [6] |
Hanna A M, Nguyen T Q. An axisymmetric model for ultimate capacity of a single pile in sand[J]. Journal of the Japanese Geotechnical Society Soils & Foundation, 2002, 42(2): 47-58. |
| [7] |
Vesic A S. Expansion of cavities in infinite soil mass[J]. Primary Care, 1973, 33(1): 265-290. |
| [8] |
Chen Congchun, Zhang Jiru, Xiao Ruchcng. Analysis for the ultimate bearing capacity of deep foundations in sands[J]. China Civil Engineering Journal, 2005, 38(8): 102-106. [陈从春, 张季如, 肖汝诚. 砂土中深基基底极限承载力分析[J]. 土木工程学报, 2005, 38(8): 102-106.] |
| [9] |
别列赞策夫.结构物地基强度的计算[M].张士文,译.北京:中国工业出版社,1965:64–74.
|
| [10] |
Nguyen T Q.A three dimensional model for vertical piles in sand[D].Montreal:Concordia University,1991:170–200.
|
| [11] |
Huang A B, Ma M Y. An analytical study of cone penetration tests in granular material[J]. Canadian Geotechnical Journal, 1994, 31(1): 91-103. DOI:10.1139/t94-010 |
| [12] |
别列赞策夫.松散体(土壤)极限平衡的轴对称问题[M].谢宗梁,黄贻吉,译.北京:建筑工程出版社,1956:70–84.
|
| [13] |
陈仲颐,周景星,王洪瑾.土力学[M].北京:清华大学出版社,1994:287–291.
|
| [14] |
Liu Guanfei, Lei Shengyou, Dong Xin. Analysis of ultimate bearing capacity for open-end pipe pile considering the influence of internal friction angle of bearing stratum soil[J]. China Sciencepaper, 2015, 10(13): 1516-1521. [刘贯飞, 雷胜友, 董昕. 考虑内摩擦角影响的开口管桩极限承载力理论分析[J]. 中国科技论文, 2015, 10(13): 1516-1521. DOI:10.3969/j.issn.2095-2783.2015.13.008] |
| [15] |
中华人民共和国建设部.建筑桩基技术规范: JGJ94—2008[S].北京:中国建筑工业出版社,2008.
|
| [16] |
中交公路规划设计院有限公司.公路桥涵地基与基础设计规范: JTG D63—2007[S].北京:人民交通出版社,2007.
|
| [17] |
中华人民共和国住房与城乡建设部.建筑地基基础设计规范: GB50007—2011[S].北京: 中国建筑工业出版社,2011.
|
| [18] |
建筑地基基础设计规范理解与应用[M].2版.北京:中国建筑工业出版社,2012:499–510.
|
 2017, Vol. 49
2017, Vol. 49


