2. 长春工业大学 机电工程学院, 吉林 长春 130012
2. School of Mechatronic Eng.,Changchun Univ. of Technol.,Changchun 130012,China
Huang等[1]于1998年提出了希尔伯特–黄变换(Hilbert-Huang transform,HHT)理论,该方法已成为近年来发展十分迅速的一种处理非线性、非平稳信号的重要方法。由于HHT方法能够根据信号的自身特性,有效地提取出信号的本质特征,同时Hilbert谱可以突显信号的局部特性,具有良好的时频分辨能力[2],因此,该方法被广泛应用于机械工程[3]、生物医学[4]、地理科学[5]、电力电子[6]等众多领域。
经验模态分解(empirical mode decomposition,EMD)是HHT方法的核心,其分解结果的优劣直接影响HHT分析的准确性。虽然该方法在诸多领域取得了一定研究成果,但由于EMD方法忽略了信号所拟合的包络线在端点处的约束[7],导致样条曲线在信号端点处出现发散现象,随着筛分过程的进行,这种发散现象会逐渐向内影响整个信号序列,使分解出的模态分量严重失真,并得到一些毫无意义的虚假分量或迭代误差分量[8]。此外,在该方法应用于故障诊断领域时,通常只有少数固有模态函数(intrinsic mode function,IMF)能够有效表征故障特征,反映故障特性,而其他IMF为分解误差或噪声干扰成分[9]。若对含有虚假模态分量的IMF进行Hilbert变换所得的总体Hilbert谱进行分析,其信号特征不明显,分析准确性低。
针对上述问题,提出一种基于边界极值均值延拓和虚假IMF分量剔除相结合的改进HHT方法。边界极值均值延拓方法能够根据信号端点与其相邻近极值点的特性,对端点处的信号值加以约束,从而避免端点效应问题的产生;虚假IMF分量剔除算法能够剔除EMD分解过程中所产生的迭代误差和信号中的干扰成分,突显信号自身特征,提高HHT分析的精准度。并通过仿真和工程实际应用验证了该方法的有效性。
1 经验模态分解方法EMD方法用于将非线性、非平稳信号分解为有限个IMF分量,是HHT方法中最具创新性的部分。该方法的具体步骤如下:
1)确定信号x(t)的所有极值点。
2)采用3次样条函数对所有极值点进行插值,拟合形成上、下包络线。
3)计算上、下包络线均值m1(t),并求出h1(t):
| ${h_1}(t) = x(t) - {m_1}(t)$ | (1) |
4)判断h1(t)是否符合IMF的条件[1]。若符合,则h1(t)即为第1阶IMF分量;若不符合,则重复步骤1)~3),直到分解得到
5)将c1(t)从x(t)中分离,得到残余信号r1(t),将r1(t)作为待分解信号,重复步骤1)~4),直到rn(t)为一单调函数时分解停止,则有:
| $x(t) = \sum\limits_{i = 1}^n {{c_i}(t)} + {r_n}(t)$ | (2) |
式中,rn(t)为信号平均趋势的残余项,ci(t)为频率由高到低包含不同时间尺度的IMF分量。
2 改进的HHT 2.1 边界极值均值延拓方法由EMD算法可知,采用3次样条函数拟合求得信号的包络均值是该方法的基础。但由于所分析的信号通常长度有限,在采用3次样条函数拟合包络线时,信号端点处的数据缺少相关约束,必然导致所拟合的包络线在端点附近产生较大的拟合误差,出现端点发散现象,即产生端点效应问题。若该问题处理不当,将会严重影响EMD分解效果,造成IMF分量失去实际的物理意义[1]。因此,信号的包络线在端点处缺少相关约束是EMD产生端点效应的根本原因[7]。若在求取信号包络线前对信号端点处的数据进行相应处理,则可有效抑制端点效应问题的产生。针对该问题,国内外研究人员进行了深入研究,并提出一些改进方法[10–12],但由于除信号端点处外再无数据,各种延拓均为人为预测,所以各种改进方法仍具有其自身的局限性[13]。
通常,波动信号中包含许多不同时间尺度的基本波动模式,而基于极值点信息的时间尺度具有一定规律性[14],因此,参考端点附近极值点变化趋势对于信号端点的影响,可有效实现对信号端点进行约束的目的。
鉴于上述分析,并针对端点效应产生的根本原因,本文提出一种基于边界极值均值延拓的端点效应抑制方法。该方法主要分为2步:
1)利用信号两侧端点和其临近极值点的特征,对包络线在信号两端点处的值进行估计,并将估计值添加到极值序列中。
设
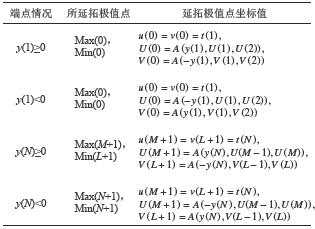
| 表1 所延拓极值点的坐标值 Tab. 1 Extended extreme point coordinates |
 |
2)考虑端点值是否应作为延拓的极值点添加到极值序列。
当原信号序列的端点值大于(小于)所延拓极大值(极小值)点时,这将导致包络线在拟合过程中出现较大的拟合误差,产生端点漂移现象[15],降低分解的准确性。因此,对于由表1延拓后的极值点,应再次判断延拓极值点和信号端点值的大小,以免上述情况的产生。具体判断过程,如表2所示。
| 表2 更改延拓极值点的坐标值 Tab. 2 Change of the coordinate values of extreme points |
 |
将所延拓的4个极值点加入原极值序列中,得到新的极值点序列
边界极值均值延拓法的步骤简单,易于实现。该方法充分考虑了端点附近极值点的变化趋势和自身端点信息对所延拓极值的影响,同时充分利用了已知极值点和端点的信息,具有较强的自适应性,可有效抑制包络拟合过程中的误差向内传播,从而达到解决端点效应问题的目的。
2.2 虚假IMF分量剔除算法由于IMF分量是对信号的一种近似正交的表达,那些真实存在的IMF分量和原信号间应具有较大的相似性[16],且相关系数是通用的相似度计算方法,所以,目前研究人员常用各IMF分量与原信号间的相关系数作为评价指标,用其去除虚假IMF分量,并且选取的给出阈值为相关系数序列中最大值的0.1倍[16–17],在一定程度上促进了HHT方法在故障诊断领域的应用。
但传统基于信号相似性的IMF判别算法并未考虑正常信息对于信号故障信息的影响,这在一定程度上削弱了信号中的故障信息,增加了选取包含正常状态信息的虚假IMF分量的可能性,降低分析的准确性。
为此,本文提出一种基于信号相似性的虚假IMF剔除方法。该算法的流程见图1。
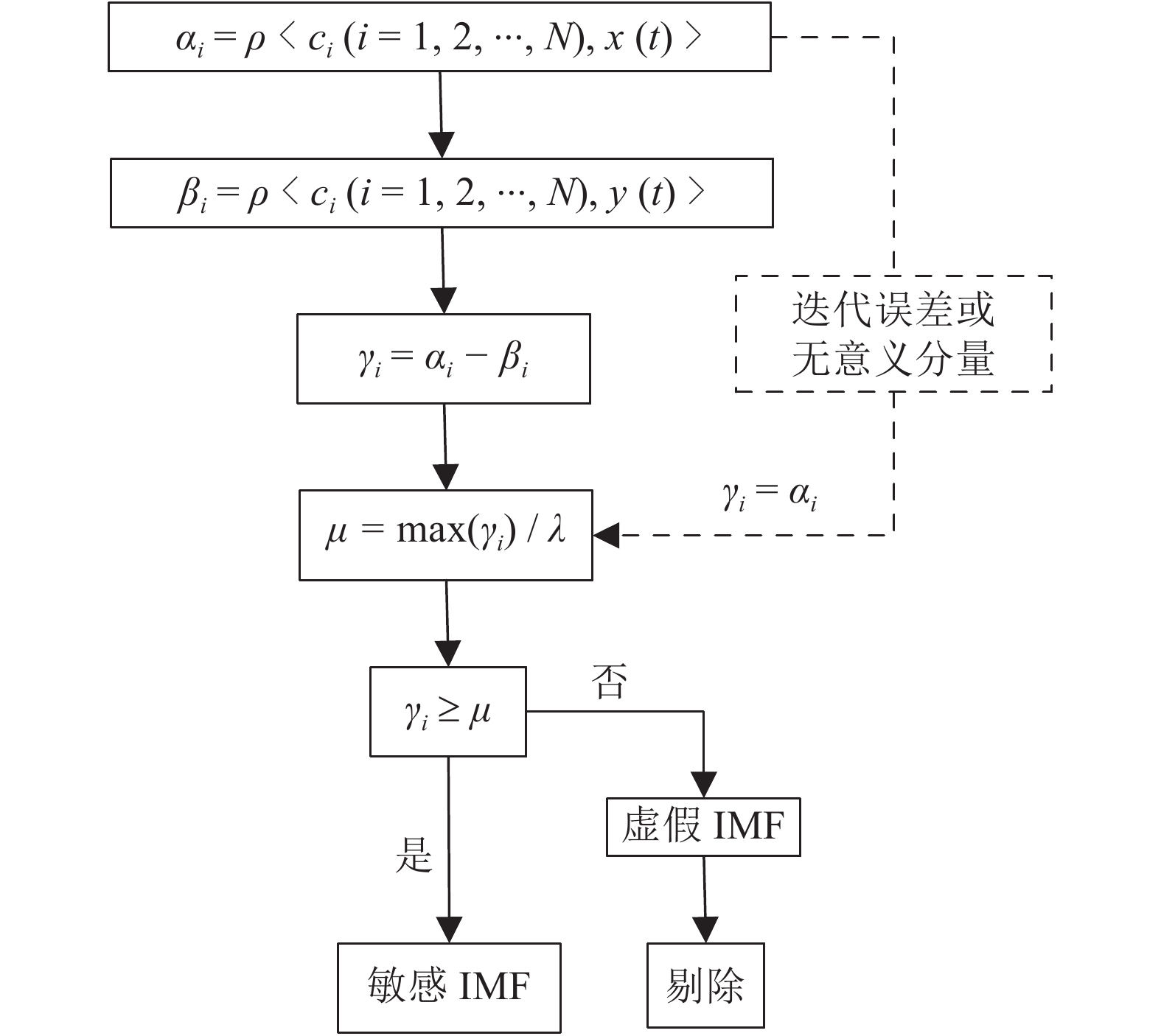 |
| 图1 算法流程图 Fig. 1 Flow chart of algorithm |
其中:算子
1)当要消除EMD分解过程中所产生的迭代误差或无意义的虚假分量时,直接求解信号x(t)的各IMF分量
2)当采用HHT方法进行故障诊断时,除计算αi外,还要计算故障信号x(t)的各IMF分量
为避免一些真实IMF分量由于振幅过低而被剔除,在进行相关系数求解前,将原信号和各IMF分量进行归一化处理。
该方法的主要原理是:与故障信号x(t)相关系数越大的IMF分量,所包含信号x(t)的故障信息越多;计算与正常状态信号y(t)的相关系数βi,可知每个IMF分量中与故障信息无关的正常信息。敏感IMF判别方法将各IMF与故障信号的相关性同正常信号的相关性相结合,配合所选取的敏感阈值,突显出故障信息,削弱正常信息的影响。
3 仿真试验当旋转机械正常工作时,其振动信号往往表现出周期性的运动,此时可以用谐波分量代表设备的旋转振动信号。对于旋转机械的异响故障,通常可以用谐波分量与高斯白噪声的叠加来模拟[18],即:
| ${\textit{z}}(t) = s(t) + rand(n)$ | (3) |
式中:z(t)表示旋转机械的异响故障信号,s(t)为包含异响故障信息的谐波分量,rand(n)为环境噪声。为更加真实地模拟旋转机械多频率故障信号,仿真包括低频20 Hz表示正常信息的谐波分量c1、高频70 Hz表示故障信息的谐波分量c2及高斯白噪声c3等3个成分的旋转机械异响故障信号Z,图2为该仿真信号的时域波形图。
 |
| 图2 仿真信号 Fig. 2 Simulation signal |
由图2可以看出,信号中的谐波分量完全淹没在背景噪声中,故障特征难以提取。因此,对仿真信号采用快速独立分量分析(fast independent component analysis,FastICA)法进行降噪处理,该方法在去除噪声方面的优越性已得到许多研究人员的证实[19]。图3为降噪后信号,由图3可知,环境噪声等因素对于信号的干扰已得到明显抑制。大部分的无用高频分量被滤去,降噪信号的波形更加突显出原信号的信息。
 |
| 图3 经FastICA法降噪信号 Fig. 3 De-noising signal with FastICA method |
对降噪后的信号分别采用本文方法和不经端点处理的原始EMD方法分解,信号的包络线如图4所示。
由图4可以看出,由于未对信号端点进行约束,原始EMD方法所拟合的包络线在信号两端出现了较大的单向偏差;随着分解的进行,端点效应将“污染”整个信号序列,使包络线无法完全将信号的各点包络其中,此时的包络线已不能准确反映信号的真实情况,必将造成分解出的IMF分量失真。采用基于边界极值均值延拓的EMD方法所构造的包络线有效地抑制了信号端点处的发散现象,包络线在整个信号序列内十分平滑,能够有效地反映出信号端点处的变化趋势;并且该方法步骤简单,计算速度快,较好地实现了对信号序列的上、下限控制。
 |
| 图4 不同方法所得包络线 Fig. 4 Envelope line of different methods |
使用原始EMD分解该仿真信号,得到6阶IMF分量,如图5所示。从图5不难看出,由于忽略了信号端点的约束问题,原始EMD分解出的IMF分量与对应的理想信号分量间存在较大差别,前2阶谐波分量IMF1和IMF2在0.1~0.15 s时间区域内产生畸变现象,IMF2靠近左侧端点处振动明显、存在异动,并且低频分量的发散现象非常严重。
 |
| 图5 原始EMD方法分解结果 Fig. 5 Decomposition results of traditional EMD |
改进EMD的分解结果如图6所示,由图6可以看出:各IMF分量的端点处并未出现异动,并且畸变现象也得到明显抑制,波形更加对称、均匀。分解得到的前2阶IMF分别为70和20 Hz的谐波分量;由于噪声因素并未完全去除,因此,IMF3为包含背景噪声和分解误差的虚假分量。采用基于边界极值均值延拓的EMD方法所获得的虚假IMF分量的个数也明显少于原始EMD方法,说明该方法在分解过程中的误差积累量较小,具有较高的分解准确性。
 |
| 图6 改进EMD方法分解结果 Fig. 6 Decomposition results of improved EMD |
采用本文所提出的虚假IMF分量剔除算法得出改进EMD分解后各IMF分量的相关系数和敏感因子,如表3所示。
| 表3 剔除算法计算结果 Tab. 3 Results of the selecting algorithm |
 |
由表3可知,IMF1的敏感阈值 μ=0.094 4,因此IMF1是敏感IMF,IMF1正是含有故障信息的谐波分量。若采用如文献[16–17]中只计算各IMF分量与故障信号间相关系数的方法,则IMF2也应为敏感IMF分量。但是,对于仿真信号,IMF2为包含正常状态信息的干扰成分,若对包含IMF2分量的信号进行后续分析,这将严重影响分析结果的准确性。
采用本文所提出的虚假IMF剔除算法能够有效剔除EMD分解过程中所产生的迭代误差分量和与故障无关的IMF分量,并削弱正常状态信息对于分析准确性的影响,突显信号的故障特征。
4 应用实例相对于其他旋转机械而言,发动机故障信号是一种典型的非线性、非平稳信号[2]。针对目前发动机振动信号在故障诊断方面存在的不足[20],以某型柴油发动机运行时缸盖表面声音信号为研究对象,采用改进HHT方法对其进行故障诊断研究。
试验装置组成如图7所示,包括信号源、信号采集系统和分析系统。其中:信号采集系统为B&K LAN–XI型声学振动分析仪,由声学传感器、前置放大器、4299型声源转换器、3050–A–060型数据采集器组成;分析系统由计算机、PLUSE12.0和MATLAB分析软件组成。试验过程中,同步采样,精度16 bit,发动机转速为900 r/min,采样频率为6 000 Hz,采样点数为8 200。
 |
| 图7 试验装置组成 Fig. 7 Composition of test equipment |
图8(a)为发动机正常状态下所测的声振信号,图8(b)和8(c)为发动机气门响和活塞销响两种常见异响故障的声振信号。
图9为不同工况下采用FastICA降噪后信号。将降噪后发动机正常状态信号作为改进HHT方法的参考信号。通过对比可知,由于环境噪声等因素影响,使信号的信噪比降低,这将影响HHT分析准确性并增加故障检测难度。经降噪处理后,大部分高频干扰成分被滤去,信号波形更加突显出原信号的信息。虽然不同工况下发动机的时域信号存在差异,但以此为依据不能准确区分故障类型。
 |
| 图8 发动机不同工况下声振信号 Fig. 8 Acoustic vibration signal of engine under different working conditions |
 |
| 图9 发动机不同工况下降噪信号 Fig. 9 De-noising signal of engine under different working conditions |
图10为正常与异响故障信号的频谱。
由图10可以发现,发动机正常状态下其工作频率主要为240 Hz,两种异响故障的频谱中,频率成分几乎一样,难以判别故障类型,原因在于各种异响故障的频率成分只能反映时域信号频率成分的总体构成,无法表示出频率与时间两者的变化规律。
 |
| 图10 发动机不同工况下频谱 Fig. 10 Spectrums of engine under different working conditions |
为找出故障信号的内在规律特征,利用改进的HHT方法对图9中的发动机声振信号进行分析,发动机正常状态和气门响故障信号经改进EMD分解得到5阶IMF分量,而活塞销响故障信号经EMD分解得到4阶IMF分量。各IMF分量对应的相关系数αi或敏感因子γi如图11所示。
通过虚假IMF剔除算法,选择正常状态信号和气门响故障信号的c1和c2为敏感IMF;选择活塞销响故障信号的c1为敏感IMF。而其他未选择的IMF中所包含的是正常信号与故障信号的共同信息或不含任何故障信息的迭代误差,所以被剔除。分别对各敏感IMF分量进行Hilbert变换,相应局部的Hilbert的3维谱和边际谱如图12和13所示。
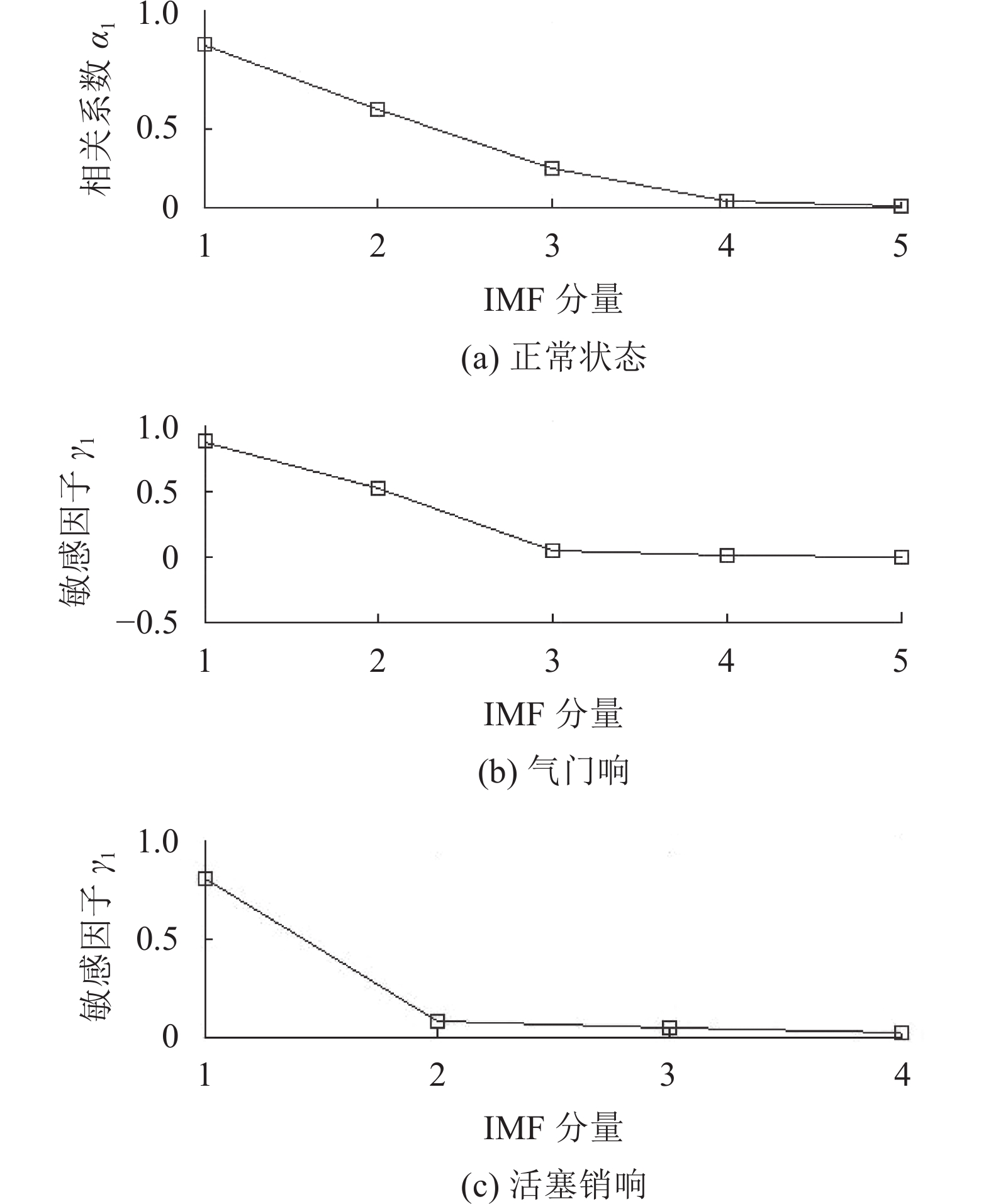 |
| 图11 虚假IMF剔除算法结果 Fig. 11 Results of the false IMF selecting method |
 |
| 图12 基于改进HHT的Hilbert谱 Fig. 12 Hilbert spectra based on improved HHT method |
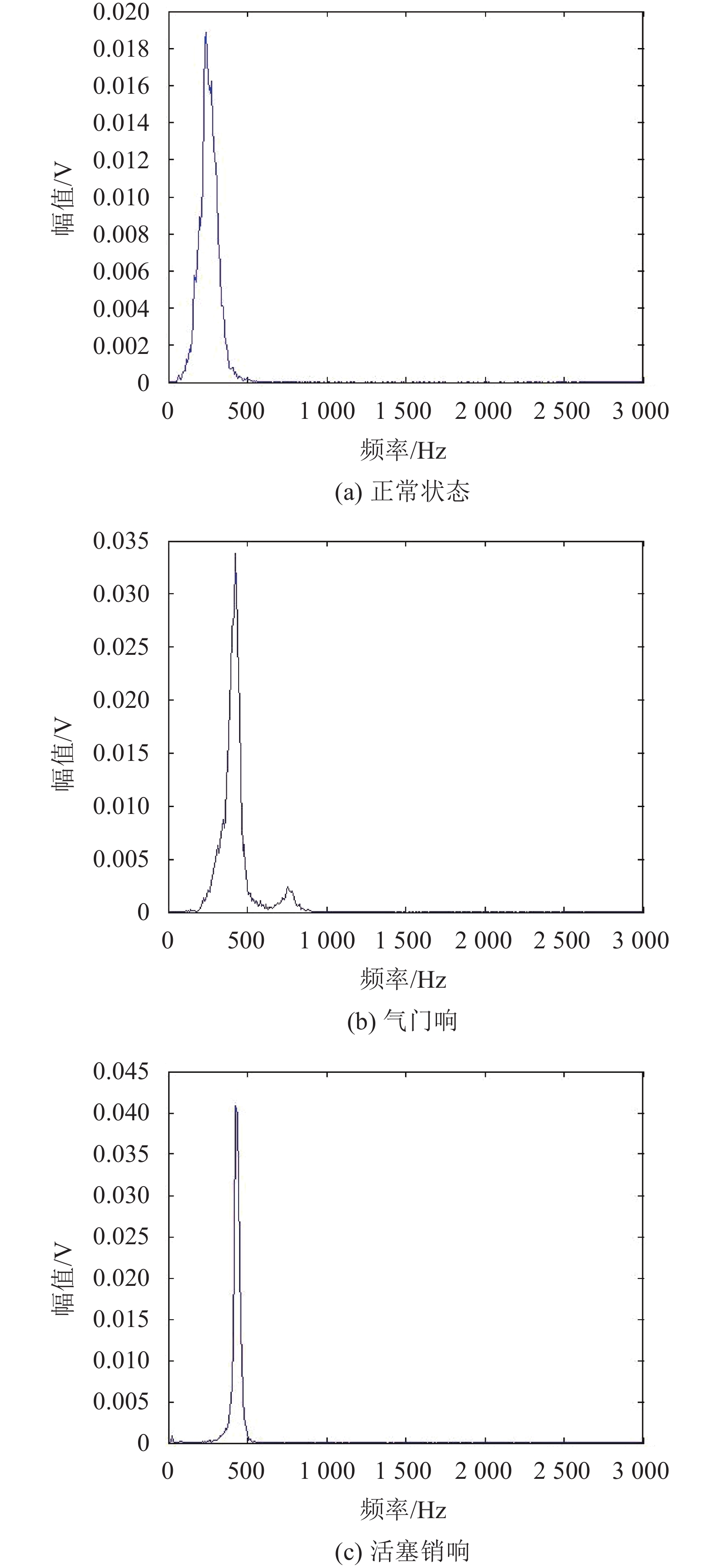 |
| 图13 基于改进HHT的边际谱 Fig. 13 Local marginal spectra based on improved HHT method |
对比图12和13可知,发动机正常信号的能量稳定地呈线条状均匀分布在低频区域,单线条的大能量周期性出现,能量主要集中在40~500 Hz频带范围内,边际谱的峰值频率为240 Hz,时域持续时间约为36 ms。
气门响信号的能量比正常情况明显增大;能量主要分布在200~500 Hz的低频段和600~800 Hz的高频段内,主要频率为408和786 Hz;频带比正常情况宽;主要能量在低频部分呈线条状分布于时间轴上;高频部分周期性分布着单根大线条能量。低频段在时域内持续时间比较长,约为41 ms;而高频段在时域内持续时间短,约为25 ms。
活塞销响故障的能量比正常情况有所增加;频带比较窄;能量主要集中在300~500 Hz频率段内,主要频率为428 Hz;在时域持续时间比较短,约为33 ms;主要能量呈单线条状周期性地分布在时间轴上,高频部分无能量分布。不同异响信号故障特征明显,如表4所示。
| 表4 不同状态下发动机信号的特征 Tab. 4 Characteristics of engine signals under different conditions |
 |
依据发动机声振诊断机理,当发动机出现异响故障时,异响声音信号表现为高频特性,其能量由低频向高频转移,故障原因不同,异响频率也不同[18]。由表4可以看出,不同状态下发动机声振信号的主要特征具有明显差别。局部Hilbert谱和边际谱反映了各种异响故障信号在时域和频域的细微特征,所得到的信息是单独时域或频域信号无法得到的。同时,不同异响故障特征信号的局部Hilbert谱和局部边际谱差别很大。一方面,可以利用它们在时域和频域具有良好分辨率的特点对各种异响特征做出进一步的解释;另一方面,可以采用它们实现对不同异响故障的诊断识别。
为了便于比较,采用基于EMD和所有IMF的原始HHT方法对活塞销异响故障信号进行分析。原始HHT方法所得的Hilbert谱和边际谱分别如图14、15所示,由于端点效应和虚假模态问题的抑制效果不理想,原始EMD分解得到的Hilbert谱中存在很多干扰成分,其中低频区域尤为明显,很难从中总结Hilbert谱的特征;而且从边际谱中难以准确找到故障状态下的主要频带和频率,从而降低故障诊断的准确性。因此,原始的HHT不能有效提取信号的故障特征。
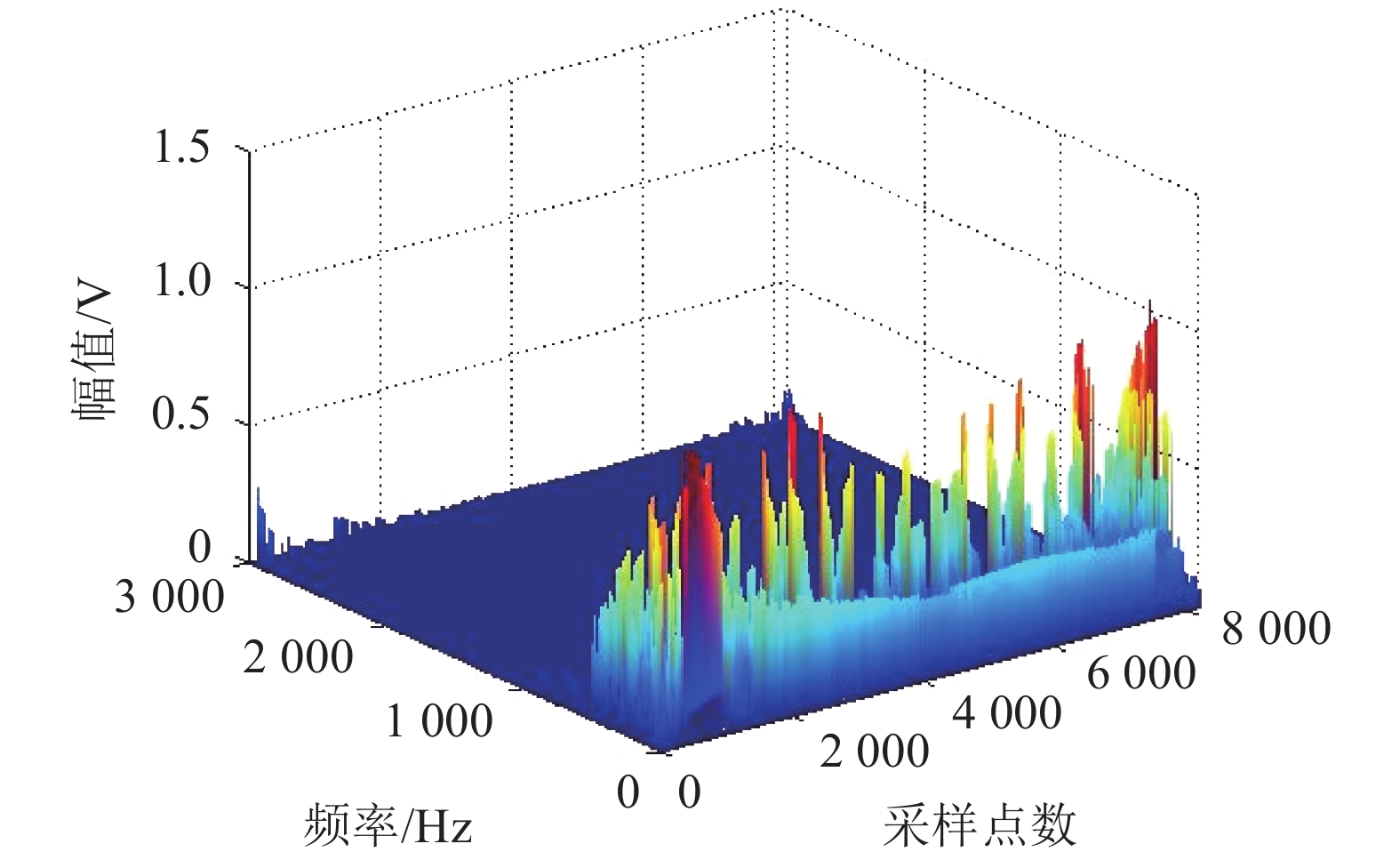 |
| 图14 基于原始HHT的活塞销异响故障Hilbert谱 Fig. 14 Hilbert spectrum of piston pin abnormal sound signal based on traditional HHT |
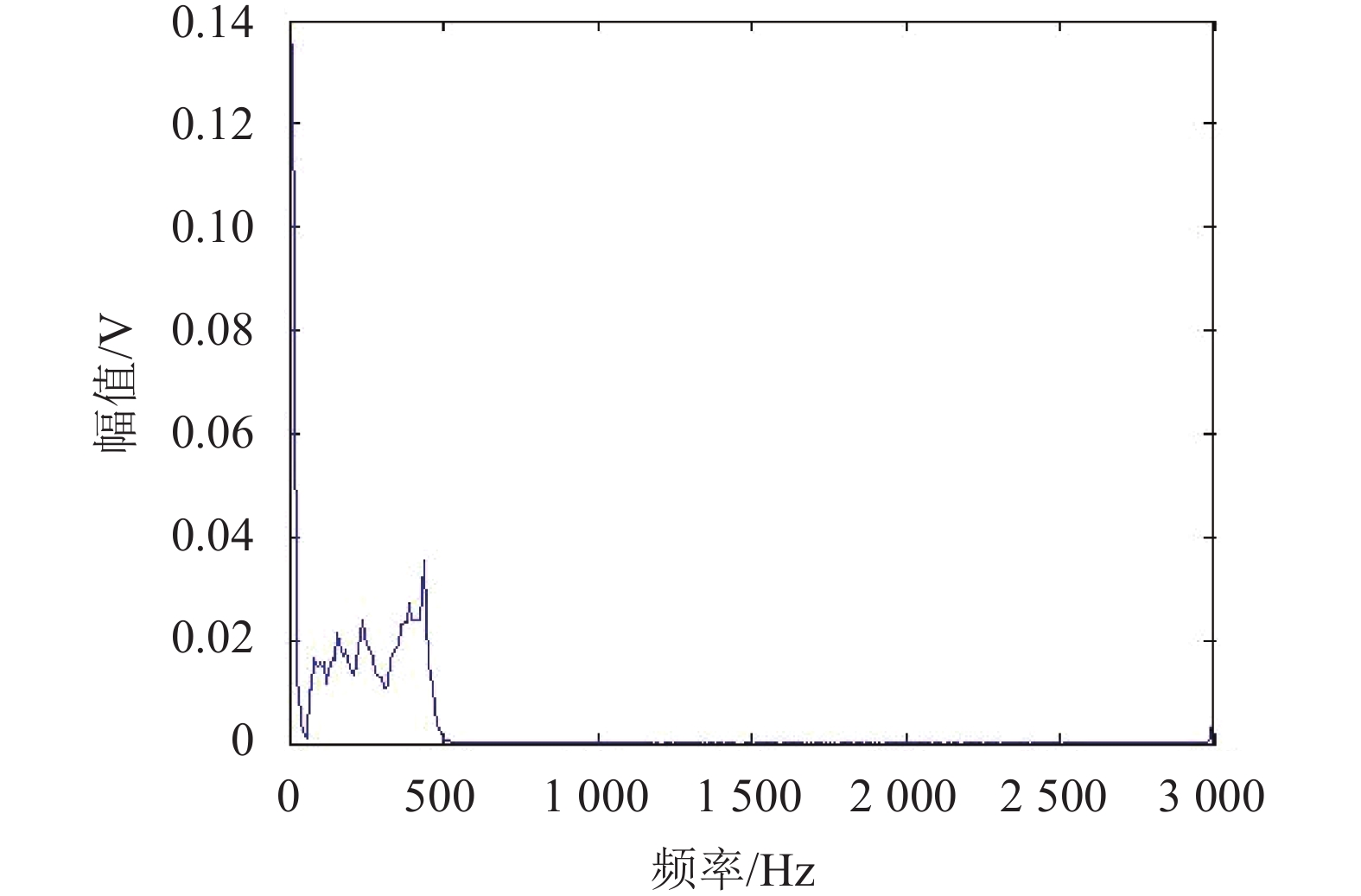 |
| 图15 基于原始HHT的活塞销异响故障边际谱 Fig. 15 Local marginal spectrum of piston pin abnormal sound signal based on traditional HHT |
5 结 论
基于边界极值均值延拓的改进EMD方法,充分考虑了信号端点缺少约束的问题,利用信号自身端点及其临近极值点的特性,有效地抑制了EMD分解过程中产生的端点效应。
采用基于正交性原理的虚假IMF剔除算法能够有效解决EMD分解过程中由于分解误差所产生的虚假模态问题,同时在故障诊断过程中可以选择包含故障特征的敏感IMF分量,强化故障信息。
通过仿真试验和发动机异响故障诊断实例的验证,证明该方法提升了HHT的性能,可以有效提取信号的故障特征信息。
| [1] |
Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society of London-Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [2] |
Zhou Xiaolong.Hilbert-Huang transform applied in fault diagnosis[D].Changchun:Changchun University of Technology,2014. [周小龙.希尔伯特–黄变换在故障诊断中的应用[D].长春:长春工业大学,2014.]
|
| [3] |
Wan Haibo, Yang Shixi. Development of HHT-based vibration monitoring system for NC spindle[J]. Journal of Vibration and Shock, 2014, 33(6): 48-52. [万海波, 杨世锡. 基于HHT的数控机床主轴振动监测系统的研制[J]. 振动与冲击, 2014, 33(6): 48-52.] |
| [4] |
Bai F, Zhang J, Zheng J. Similarity analysis of DNA sequences based on the EMD method[J]. Applied Mathematics Letters, 2011, 24: 323-237. |
| [5] |
Zhang Z, Zhang Y, Zhu Y. A new approach to analysis of surface topography[J]. Precision Engineering, 2010, 34: 807-810. DOI:10.1016/j.precisioneng.2010.05.002 |
| [6] |
Wang X, Cai J, He K. EMD copula based value at risk estimates for electricity markets[J]. Procedia Computer Science, 2015, 55: 1318-1324. DOI:10.1016/j.procs.2015.07.115 |
| [7] |
Zhu Sai, Shang Wei. Analysis and study of envelope algorithm in EMD[J]. Fire Control & Command Control, 2012, 37(9): 125-128. [朱赛, 尚伟. 经验模态分解中包络线算法[J]. 火力与指挥控制, 2012, 37(9): 125-128.] |
| [8] |
Shao Chenxi, Wang Jian, Fan Jinfeng. A self-adaptive method dealing with the end issue of EMD[J]. Acta Electronica Sinica, 2007, 35(10): 1943-1948. [邵晨曦, 王剑, 范金锋. 一种自适应的EMD端点延拓方[J]. 电子学报, 2007, 35(10): 1943-1948.] |
| [9] |
Lei Yaguo. Machinery fault diagnosis based on improved Hilbert-Huang transform[J]. Journal of Mechanical Engineering, 2011, 47(5): 71-77. [雷亚国. 基于改进Hilbert-Huang 变换的机械故障诊断[J]. 机械工程学报, 2011, 47(5): 71-77.] |
| [10] |
Zhao J P, Huang D J. Mirror extending and circular spline function for empirical mode decomposition method[J]. Journal of Zhejiang University (Science), 2001, 2(3): 247-252. DOI:10.1631/jzus.2001.0247 |
| [11] |
Cheng Junsheng, Yu Dejie, Yang Yu. Disscussion of the end effects in Hilbert-Huang transform[J]. Journal of Vibration and Shock, 2005, 24(6): 40-42. [程军圣, 于德介, 杨宇. Hilbert-Huang变换端点效应问题探讨[J]. 振动与冲击, 2005, 24(6): 40-42.] |
| [12] |
Hu Aijun, Tang Guiji, An Liansuo. Research on boundary process technique in Hilbert-Huang transform[J]. Journal of Mechnical Strength, 2008, 30(5): 739-743. [胡爱军, 唐贵基, 安连锁. Hilbert-Huang变换边界问题处理方法研究[J]. 机械强度, 2008, 30(5): 739-743.] |
| [13] |
Li Yong, Fang Zhaoben, Wei Yongfeng. Suppressing end effect of EMD based on local polynomial regressing[J]. Journal of University of Scence and Technology of China, 2014, 44(9): 786-792. [李勇, 方兆本, 韦勇凤. 基于局部多项式回归的EMD端点效应抑[J]. 中国科学技术大学学报, 2014, 44(9): 786-792.] |
| [14] |
Guo Mingwei, Ni Shihong, Zhu Jiahai. HHT/EMD end extension method in vibration signal analysis[J]. Journal of Vibration and Shock, 2012, 31(8): 62-66. [郭明威, 倪世宏, 朱家海. 振动信号中HHT/EMD端点延拓方法研究[J]. 振动与冲击, 2012, 31(8): 62-66.] |
| [15] |
Shu Zhongping, Yang Zhichun. A better method for effectively suppressing end effect of empirical mode decomposition (EMD)[J]. Journal of Northwestern Ploytechnical University, 2006, 24(6): 639-643. [舒忠平, 杨智春. 抑制经验模态分解边缘效应的极值点对称延拓法[J]. 西北工业大学学报, 2006, 24(6): 639-643.] |
| [16] |
褚福磊,彭志科,冯志鹏,等.机械故障诊断中的现代信号处理方法[M].北京:科学技术出版社,2009:122–124.
|
| [17] |
Peng Z K, Tse P W, Chu F L. An improved Hilbert-Huang transform and its application in vibration signal analysis[J]. Journal of Shound and Vibration, 2005, 286(1/2): 187-205. |
| [18] |
Zang Yuping, Zhang Dejiang, Wang Weizheng. Fault diagnosis of engine abnormal sound based on wavelet transform technique[J]. Journal of Mechanical Engineering, 2009, 45(6): 239-244. [臧玉萍, 张德江, 王维正. 基于小波变换技术的发动机异响故障诊断[J]. 机械工程学报, 2009, 45(6): 239-244.] |
| [19] |
Li Hong, Sun Yunlian, Xu Changbao. Noise Elimination of PD signals by independent component analysis[J]. Journal of Sichuan University(Engineering Science Edition), 2007, 39(6): 143-148. [李洪, 孙云莲, 徐长宝. 基于独立分量分析算法的局部放电信号去噪方法研究[J]. 四川大学学报(工程科学版), 2007, 39(6): 143-148.] |
| [20] |
Dong Xiaogang, Chang Donghui, Zheng Zhongqiang. Simulation study on impact fault of reciprocating machinery induced by piston slap based on ADAMS[J]. Journal of Machine Design, 2013, 30(5): 28-31. [董晓刚, 常东辉, 郑中强. 基于ADAMS的往复发动机敲缸故障仿真研究[J]. 机械设计, 2013, 30(5): 28-31.] |
 2017, Vol. 49
2017, Vol. 49


