2. 成都理工大学 博物馆,四川 成都 610059
2. Museum,Chengdu Univ. of Technol.,Chengdu 610059,China
地质力学模型试验是研究高坝工程稳定安全性的一种重要方法,该方法是依据一定的相似原理对工程与地质问题进行缩尺研究。通过试验可以了解坝体在正常工况下的工作性态,获得大坝在超载或降强情况下的破坏模式及破坏机理,揭示大坝与地基的薄弱部位,研究大坝的整体稳定安全性[1]。地质力学模型的特点是:通过真实模拟岩体中断层、节理裂隙等软弱结构的结构特征,以及岩体的非均匀性、非弹性、非连续性及多裂隙的岩石力学特征,研究坝与地基整体在外荷载特别是在渐增荷载作用下,或在岩体结构面力学参数降低的情况下,超出弹性范围以外的变形和破坏特性及其破坏失稳的整个变化过程,直观地揭示其破坏机理,为工程的设计、施工及加固处理提供科学依据[2–4]。目前在地质力学模型试验研究过程中,通常采用模拟坝体及坝肩(坝基)岩体超载变位曲线的波动、拐点、增长幅度、转向等特征、模型开裂以及裂缝贯通等方法来综合推断各破坏阶段[5–8],但位移曲线的变位特征与敏感测点的选择关系密切,模型开裂的观测又受模型比尺、设备精度和人为因素影响,因此具有一定的主观意识,因此在地质力学模型试验中怎样准确的通过测试结果建立大坝失稳判据,判断坝与地基的失稳破坏过程,得到综合稳定安全系数,是地质力学模型试验的关键技术问题。
非线性科学理论,如耗散结构理论、非线性动力学以及突变论等是研究非线性系统问题的有力工具[9]。突变理论注重研究系统状态发生突变时外界的控制条件,阐述系统中某些变量为何从连续逐渐变化导致系统状态的突然变化[9]。尖点突变理论已被广泛应用于地下工程洞室围岩稳定和边坡稳定的研究工作中,并且取得了较为理想的成果[10–12]。付成华等[10]基于突变理论,根据围岩失稳的直观判别条件,建立了位移模突变判据、洞周屈服区面积突变判据和广义黏塑性剪应变突变判据,并将其与能量突变判据和熵突变判据一道应用于某地下洞室断面,根据系统的突变条件从不同方面判别围岩系统失稳的可能性。刘会波等[11]借助突变理论,建立了岩体地下工程局部围岩系统开挖失稳的能量耗散突变判据,通过表征突变特征值判断系统失稳状态。黄润秋等[12]通过实例介绍了尖点突变理论在工程地质中的应用现状,包括用突变理论评价层状结构斜坡、地下洞室的顶板冒落及活断层的稳定性,以及斜坡失稳的时间预报等问题。目前,在地质力学模型试验研究过程中,对于采用尖点突变理论进行坝与地基整体稳定失稳判据的应用研究仍较少报道。
本文的研究思路及研究内容如下:
1)尖点突变模型的建立
引入法国数学家托姆创立的突变理论,建立其中应用最广泛,对具有代表性的尖点突变模型,得出其标准势函数的形式,并根据相关数学基础知识推导出相应的突变判别式。
2)在有限元算例中应用尖点突变模型,印证其可靠性和适用性。
选取一重力坝段进行ANSYS有限元分析,提取其典型高程点的位移随超载系数增加的变化曲线,并依据此计算成果建立位移与超载系数变化曲线的尖点突变模型失稳判据,并将判别结果与ANSYS计算中的塑性区发展及贯通,计算不收敛等失稳判据进行对比分析,印证尖点突变模型的可靠性和适用性。
3)尖点突变模型应用于地质力学模型破坏试验。
选取深厚覆盖层上丹巴水电站闸坝进行大坝稳定3维地质力学模型综合法试验,基于尖点突变理论,建立典型测点位移与超载系数关系曲线的地质力学模型试验失稳判据,并与基于变位特征和破坏过程的常规地质力学模型失稳判据对比分析,论证尖点突变模型失稳判据在地质力学模型试验中应用的可靠性和适用性,从而为其在以后的应用中奠定基础。
1 突变理论及尖点突变模型 1.1 突变理论一些事物从性状的一种形式突然跳跃到根本不同的另一种形式的不连续变化,称之为突变,在这样的时代背景下,突变理论应运而生。突变理论首先由托姆(1972年)提出,是非线性理论的一个分支,它利用数学模型讨论了动力学系统中状态发生跳跃性变化的普通规律,其主要出发点是分叉理论和奇异性理论,以及结构稳定性概念[13]。发生在3维空间和1维时间的4个因子控制下的初等突变,概括起来只有7种性质不同的基本类型,这7种类型的初等突变,按其几何形状分别被称为折迭型、尖点型、燕尾型、蝴蝶型、双曲型、椭圆型和抛物型,其中尖点型突变是其中应用最广的,并且已经成功的运用到很多与突变相关的问题中。
1.2 尖点突变模型尖点突变模型标准势函数为:
| $V(x) = {x^4} + u{x^2} + vx$ | (1) |
式中:
 |
| 图1 尖点突变模型 Fig. 1 Cusp catastrophe model |
以上比较直观地了解了系统的状态与分叉集之间的决定性关系,那么也就可以用分叉集
鉴于分析,可以将分叉集
选取了某重力坝典型坝段进行了有限元ANSYS计算,该坝段坝高为102.34 m,坝底高程为559.0 m,上游坝面垂直,下游坝坡坡比为1∶0.75;该坝段坝基中地质条件极为复杂,主要存在有层间错动带、缓倾角结构面、断层破碎带等地质构造缺陷;计算模拟范围为上游取1.5倍坝高,下游取2倍坝高,坝基深度取1.0坝高;约束条件为上下游边界为法向约束,底面为三向约束,强度破坏准则采用Drucker-Prager(D-P)屈服准则,离散中坝体采用solid65 单元,坝基及各软弱结构面采用solid45 单元。该坝段计算模型共计离散为37 350个节点和36 159个单元。计算工况为上游正常蓄水位658.0 m,下游无水,不考虑泥沙压力的影响。计算采用超载法,先加至1倍水荷载,然后在以0.2的步长超载,逐步加至计算模型破坏。有限元计算模型如图2所示。
 |
| 图2 有限元计算模型 Fig. 2 Finite element calculation model |
2.2 计算成果分析
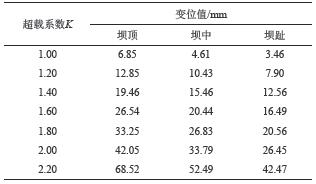
重力坝在外荷载作用下主要发生顺河向的位移,所以本文着重提取了坝体下游面的3个典型高程(坝顶、1/2坝高、坝趾)的顺河向位移,并规定顺河向位移以向下游为正。变位值见表1,不同超载系数下的变位曲线如图3所示。
| 表1 不同坝体位置变位值 Tab. 1 Displacement values for different dam area |
 |
 |
| 图3 不同坝体位置顺河向位移与超载系数关系曲线 Fig. 3 Relationship curves of displacement along the river and overloading coefficient of different dam body area |
有限元超载法计算中可以提取坝与地基在外荷载作用下的变位数值,建立不同超载系数下的变位过程的尖点突变模型的势函数:
| $k = f(\delta )$ | (2) |
式中,
采用最小二乘法的原理,对尖点突变模型势函数进行多项式拟合,因为尖点突变模型标准势函数为4次,所以拟合多项式采用四次式:
| $k = {a_0} + {a_1}\delta + {a_2}{\delta ^2} + {a_3}{\delta ^3} + {a_4}{\delta ^4}$ | (3) |
式中,
为了将式(3)转换为尖点突变模型标准势函数形式,所以采用切森豪斯变化,令
| $\delta = {b_0} + {b_1}Y + {b_2}{Y^2} + {b_4}{Y^4}$ | (4) |
其中,
| $\left( {\begin{array}{*{20}{c}}{{b_0}}\\{{b_1}}\\{{b_2}}\\{{b_4}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{L^4}}&{ - {L^3}}&{{L^2}}&{ - L}&1\\{ - 4{L^3}}&{3{L^2}}&{ - 2L}&1&0\\{6{L^2}}&{ - 3L}&1&0&0\\1&0&0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{a_4}}\\{{a_3}}\\{{a_2}}\\{{a_1}}\\{{a_0}}\end{array}} \right)$ |
令
| $V = {r^4} + u{r^2} + vr$ | (5) |
1)坝顶测点:
当超载系数Kp=2.0时,对Kp=1.0~2.0共5级超载系数下的
| $k \! = \! 0.681\;8 \! + \! 5.7 \! \times \! {10^{ - 2}}\delta \! - \! 1.9 \! \times \! {10^{ - 3}}{\delta ^2} \! + \! 6 \! \times \! {10^{ - 5}}{\delta ^3} \! - \! 8 \! \times \! {10^{ - 7}}{\delta ^4}\text{。}\!\!\!$ |
其中相应的多项式系数为
| $V = {r^4} - 0.237\;6{r^2} + 0.934\;1r\text{。}$ |
所以可得:
代入判别式
当超载系数Kp=2.2时,对Kp=1.0~2.2共6级超载系数下的
| $k \! = \! 0.764\;9 \! + \! 3.6 \! \times \! {10^{ - 2}}\delta \! - \! 6.2 \! \times \! {10^{ - 4}}{\delta ^2} \! + \! 2 \! \times \! {10^{ - 6}}{\delta ^3} \! - \! 8 \! \times \! {10^{ - 8}}{\delta ^4}\text{。}\!\!\!$ |
其中相应的多项式系数为
所以可得:
代入判别式
2)坝中测点
与上述计算过程相同,当超载系数Kp=2.0时,
3)坝趾测点
与上述计算过程相同,当超载系数Kp=2.0时,
综上所述,基于突变理论建立的坝与地基的失稳判据计算结果可得,当Kp=2.2时,坝与地基出现整体失稳状态。综合依据有限元计算结果,当Kp=2.2时,塑性区沿断层也基本贯通,等效塑性区图见图4,且当Kp=2.4时,有限元计算不收敛,所以综合来说,尖点突变模型失稳判据是与有限元计算结果是相符合的,从而印证了尖点突变模型失稳判据的可靠性和适用性。
 |
| 图4 Kp=2.2时等效塑性区 Fig. 4 Figure of equivalent plastic zone when Kp =2.2 |
3 闸坝地质力学模型试验 3.1 工程概况及地质特征
丹巴水电站工程为大渡河干流22级梯级开发中的第8级梯级电站。工程采用混合方式开发,正常蓄水位1 997.00 m,装机容量约为1 196.60 MW。枢纽建筑物主要由拦河闸坝、引水系统、发电厂房及开关站等组成,混凝土闸坝基础覆盖层深厚,结构及组成复杂,且筑坝规模超出了目前国内已建同类工程。
通过综合分析闸址河床覆盖层的形成年代、形成原因、组成物质、空间分布等方面的差异,最终将其自上而下分为以下5层。
第⑤层:混合土卵石,厚度一般2.00~5.00 m,分布于河漫滩一带。
第④层:低液限粉土层,厚度一般4.00~18.00 m,中等压缩性,具相对隔水性。
第③层:按成因和组成又细分为2个亚层,即③-2亚层混合土漂(块)石,厚度在2.50~19.25 m之间,河床部位多有分布;第③-1亚层混合土卵石,厚度变化大,在13.50~74.90 m之间,呈中间厚、两岸薄。
第②层:低液限粉土,厚度在5.39~22.60 m之间,多分布于左河岸。
第①层:混合土卵(碎)石,厚度变化大,在6.21~53.60 m之间,分布于河谷底部一带。
3.2 相似系数及模型模拟范围本次3维模型试验采用以下相似关系:
容重比:Cγ=1.0;几何比:CL=100;变模比:CE=100;位移比:Cδ=100;应力比:Cσ=100;集中力比:CF=1003。
根据丹巴水电站工程特点及试验任务要求,结合试验场地规模及试验精度要求等综合分析,确定模型几何比CL=100。确定模型模拟范围为横河向(横向)模拟左1#坝段、闸1#~闸8#、右1#坝段、鱼道、右2#~右4#坝段,总宽236 m;顺河向(纵向)边界为坝轴线上游至上游防渗墙处(闸上0-018.5),防渗墙与底板相连接;坝轴线下游至下游防冲墙下游处(闸下0+150.0),则顺河向模拟总长度为168 m;模型基底高程确定为1 892.00 m,闸室底板底面高程确定为1 961.00 m,则坝基以下模拟深度为69 m,坝顶高程为1 999.5 m,总模拟原型高度达107.5 m,相应模型高度1.075 m。综上定出模型尺寸为1.68 m×2.36 m×1.075 m(顺河向×横河向×高度),相当于原型工程168 m×236 m×107.5 m范围。
3.3 模型相似材料闸段和坝体原型材料由混凝土浇筑而成,容重γp为2.4 g/cm3,闸墩和坝体的变形模量分别为25.5和28 GPa,由相似关系Cγ=1,CE=100,可得闸坝模型材料容重γm为2.4 g/cm3,闸墩和坝体模型材料的变形模量分别为255和280 MPa。根据模型材料试验结果,混凝土模型材料采用重晶石粉为加重剂,少量石膏粉为胶凝剂,水为稀释剂,按模型材料的物理力学指标选定配合比,最后按体型要求浇制而成。
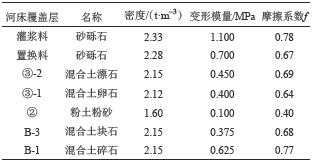
坝址区各类坝基模型材料力学参数如表2所示。
| 表2 坝址区不同模型材料力学参数 Tab. 2 Mechanical parameters for different model materials at dam site zone |
 |
3.4 地质力学模型试验方法及程序
本次试验采用综合法测试,即以超载为主、降强为辅进行模型破坏试验。对河床开挖置换层及置换灌浆层进行降强试验,以考虑开挖置换后坝基受到水的侵蚀或渗透的影响可能出现的强度弱化现象,试验中置换层及置换灌浆层的强度降低幅度约为15%。
模型试验的程序:首先对模型进行预压,然后加载至1倍正常荷载,在1倍正常荷载基础上进行降强试验,降强过程通过加热埋设在坝基材料中的电阻丝来完成,根据标定的抗剪强度与温度关系,达到预设温度后,在保持降低后的强度参数条件下进行超载阶段试验,对上游水荷载及坝基渗水压力分级进行超载,超载按0.2P0(P0为正常工况下的水荷载)的步长加载至3.6P0,此时闸坝与地基出现整体失稳的趋势。整体地质力学模型如图5所示。
 |
| 图5 整体地质力学模型试验照片 Fig. 5 Photo of integral geo-mechanical model test |
4 不同失稳判据在试验成果中的应用
通过试验测试获得以下主要数据:
1)闸坝与坝基表面测点顺河向变位δx、竖直向变位δy与超载系数KP发展过程图,即δ-KP关系曲线;
2)闸坝应变测点应变με与超载系数KP变化发展过程图,即με–KP关系曲线;
3)闸坝与坝基的破坏过程及破坏形态。
4.1 地质力学模型失稳判据应用 4.1.1 闸段变位特征1)顺河向变位:典型闸段测点顺河向变位δx与超载系数KP关系曲线如图6所示图中编号如“26”表示测点编号,下同。从测点变位与超载系数关系曲线来看,闸室各测点变位曲线总体在KP=1.6~1.8时出现拐点,在拐点前曲线斜率较大,变位值增幅较小;KP=1.8以后,变位曲线斜率减缓,变化幅度明显,逐步出现大变形,直至KP=3.6时部分测点变位值出现不稳定现象,闸坝与地基出现整体失稳趋势,超载结束。
 |
| 图6 1#闸段顺河向δx~Kp关系曲线 Fig. 6 Relationship between displacement δx along the river and overloading coefficient Kp for 1# gate section |
2)竖直向变位:在超载初期闸室均先发生竖直向下的变位,但变位值较小,随超载系数的增加,闸室逐渐出现上抬现象。从测点变位数值上看,在同一超载系数下,闸室底部变位大于顶部变位,上游变位大于下游变位,且相对于顺河向变位值,竖直向变位值较小,典型闸段测点竖直向变位与超载系数关系曲线如图7所示。
 |
| 图7 1#闸段竖直向δy~Kp关系曲线 Fig. 7 Relationship between vertical displacement δy and overloading coefficient Kp for 1# gate section |
4.1.2 坝段变位特征
1)顺河向变位:典型坝段测点顺河向变位与超载系数关系曲线如图8所示。从测点变位与超载系数关系曲线来看,坝体测点变位曲线总体在KP=1.8~2.0时出现拐点,在KP=2.0以后,变位曲线斜率变缓,变位值开始明显增大,在KP=3.6时部分测点表现不稳定,坝与地基出现整体失稳趋势。
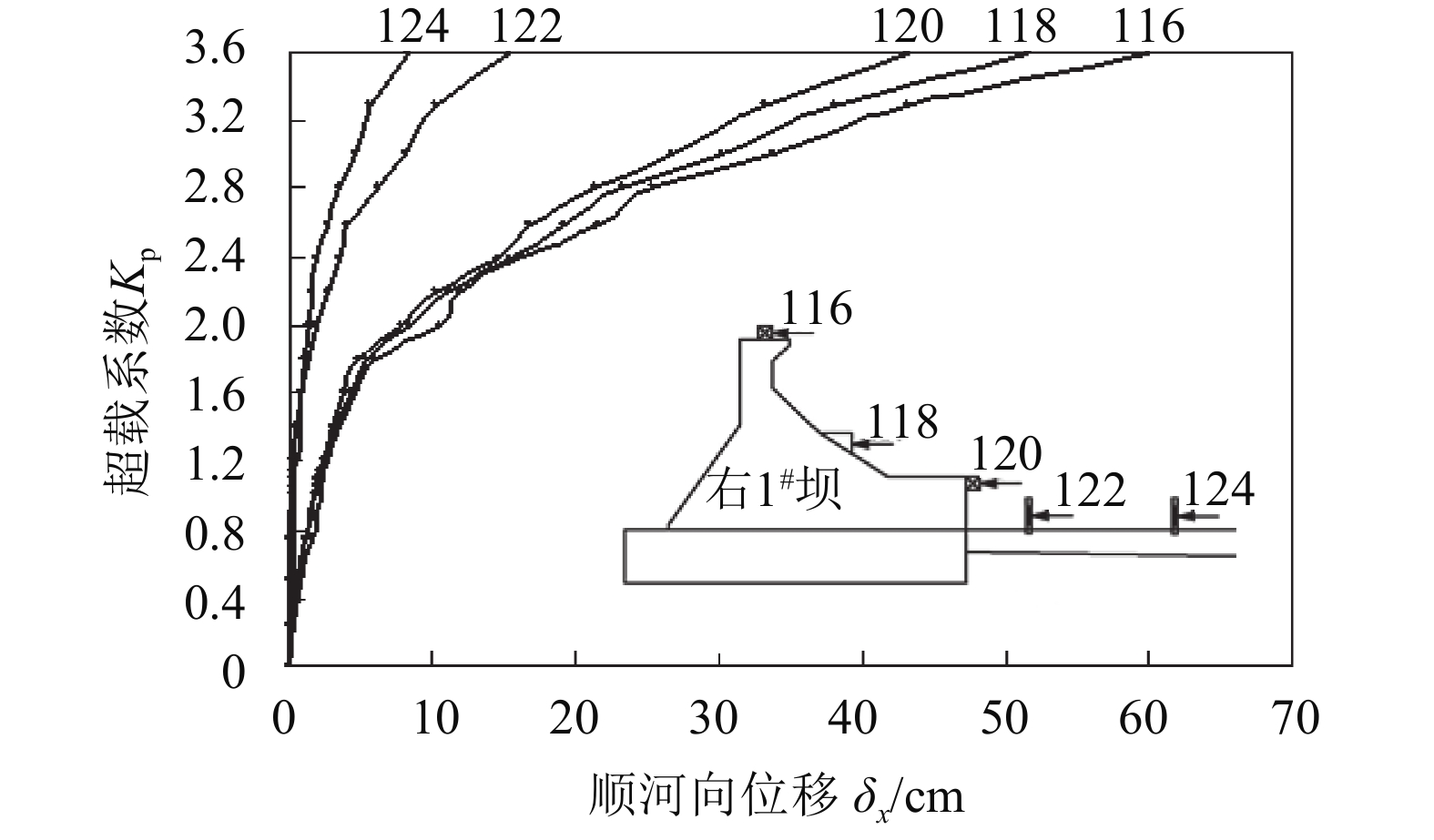 |
| 图8 右1#坝段顺河向δx~Kp关系曲线 Fig. 8 Relationship between displacement δx along the river and overloading coefficient Kp for right 1# dam section |
2)竖直向变位:在超载阶段各重力坝段在竖直方向表现出先下沉后上抬的现象。从测点数值上看,在同一超载系数下,坝顶竖直向变位最大,坝趾变位最小,相对于顺河向变位值,竖直向变位值较小。典型坝段测点竖直向变位值与超载系数关系曲线如图9所示。
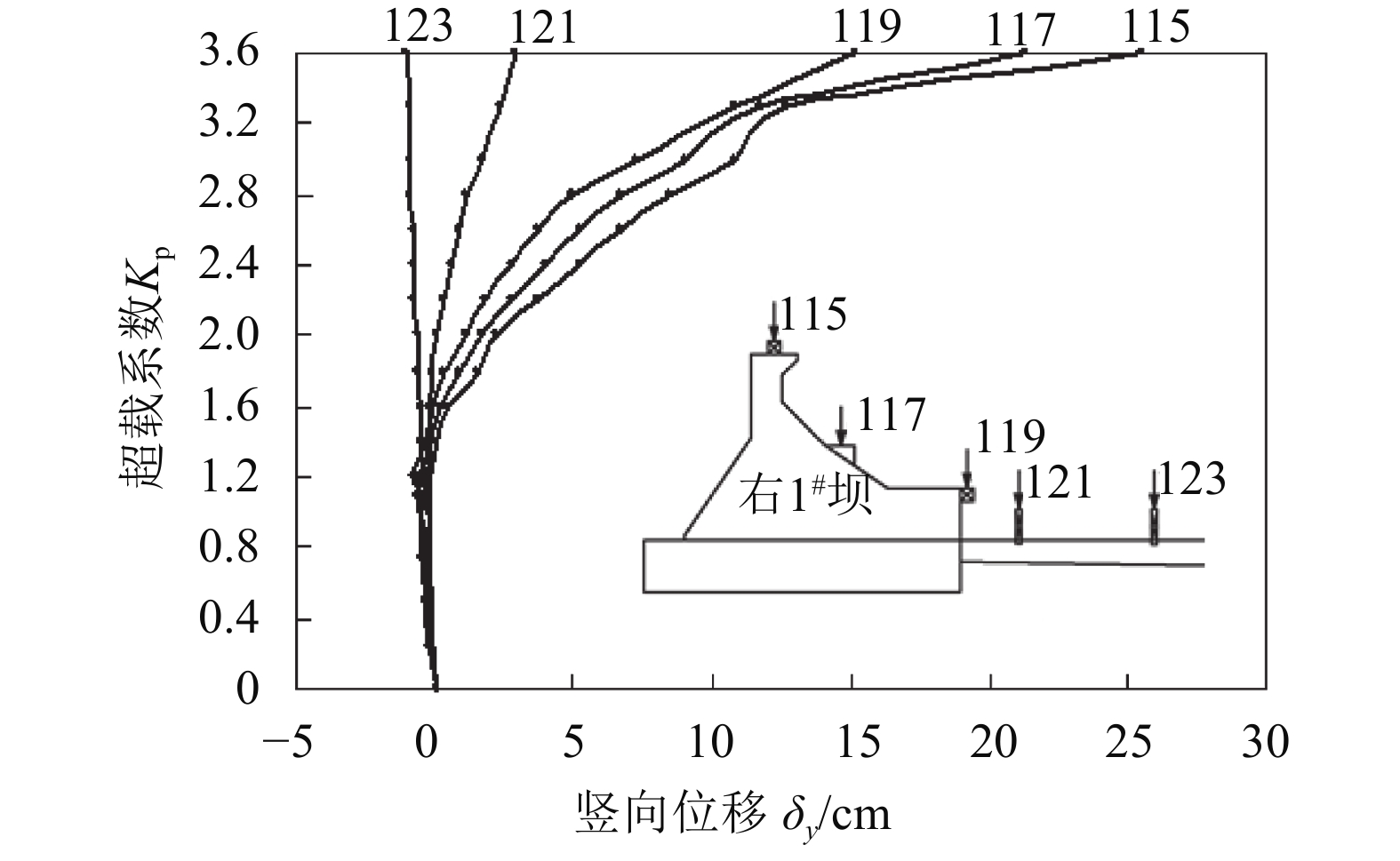 |
| 图9 右1#坝段竖直向δy~Kp关系曲线 Fig. 9 Relationship between vertical displacement δy and overloading coefficient Kp for right 1# dam section |
4.1.3 基于模型试验失稳判据的稳定安全系数
1)在正常荷载下进行降强试验,此时闸坝表面位移测试数据波动较小,闸坝应变测试数据有微小波动,闸坝与坝基仍处于正常工作状态,无开裂破坏迹象,降强系数
2)通过分析各关系曲线的超载特征,如曲线的波动、拐点、增长幅度、转向等特征,以及现场观测各阶段的破坏过程,提出超载系数KP。保持降强幅度约为15% 的条件进行超载试验,当超载系数KP=1.6~2.0时,闸坝应变与变位曲线大部分测点出现反向,发生转折,变位幅度加大,变位增长明显;由现场观测可得,闸底板上游侧相继发生开裂,闸底板与下游护坦连接处有挤压破坏,右1#坝和鱼道坝段坝踵部位出现裂缝,下游坝趾处出现挤压裂缝,并不断扩展,可综合判断,闸坝与地基出现大变形失稳。
3)当超载系数KP=3.0~3.6时,变位值较大,变位发展迅速,应变曲线频繁波动;各闸室段相对错动明显,重力坝段下游面、顶部横缝出现贯通裂缝,闸坝与地基逐渐呈现出整体失稳的趋势。
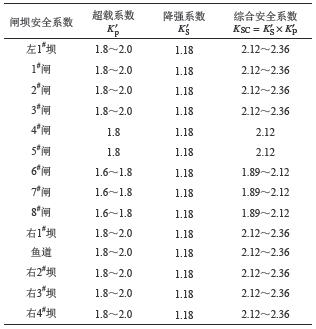
综合分析,本次试验各闸坝段的稳定安全系数表3所示,从表中可以看出,各闸段的安全系数范围为1.89~2.36,各坝段及鱼道段安全系数范围为2.12~2.36。
| 表3 不同闸坝段安全系数 Tab. 3 Safety coefficient of different gate and dam section |
 |
4.2 基于突变理论失稳判据的综合稳定安全系数
1)1#闸段闸顶12#测点变位分析
当Kp=2.0时,由
所以可得:
代入判别式
当Kp=2.2时,对Kp=1.0~2.2共6级超载系数下的
所以可得:
代入判别式
2)右1#坝段坝顶116#测点变位分析
当Kp=1.8时,对Kp=1.0~1.8共4级超载系数下的
所以可得:
代入判别式
当Kp=2.0时,由
所以可得:
代入判别式
依据尖点突变模型计算结果可得,当超载系数KP=1.8~2.2时,各闸段相继出现
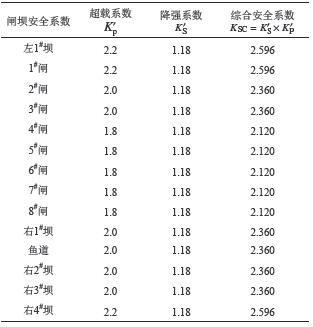
经尖点突变模型计算结果综合分析可得,本次试验各闸坝的安全系数见表4所示,可以看出,各闸段的安全系数范围为2.12~2.60,各坝段及鱼道段安全系数范围为2.36~2.60。
| 表4 基于突变理论的不同闸坝段安全系数 Tab. 4 Safety coefficient of different gate and dam section according to catastrophe theory |
 |
4.3 不同失稳判据应用成果对比分析
通过二者成果对比分析可得,基于尖点突变理论失稳判据所得的稳定安全系数略大于基于变位特征及破坏过程的常规地质力学模型试验失稳判据的稳定安全系数,但是结果相差不大,破坏阶段几乎相同。
5 结 语本文通过分析大坝地质力学模型试验成果,基于突变理论,建立试验中位移–超载载倍数尖点突变模型失稳判据,判断坝与地基的失稳破坏阶段,得出稳定安全系数,并与基于变位特征及破坏过程的常规地质力学模型失稳判据进行对比分析,印证了突变理论在大坝地质力学模型试验失稳判据应用中的可靠性和适用性。以尖点突变模型此作为判别坝与地基出现失稳状态的判别依据,将地质力学模型试验失稳判别这一过程进行了定量分析,一定程度上避免了人为因素的影响,但地质力学模型试验中,破坏过程的观测也是一个很重要的失稳判据及成果,所以可将基于尖点突变理论失稳判据与基于试验现场观测的破坏过程失稳判据结合一起应用,得出的结果将会更为准确。
| [1] |
富马利加.静力学与地力学模型[M].北京:水利电力出版社,1979.
|
| [2] |
张林,陈媛.水工大坝与地基模型试验及工程应用[M].北京:科学出版社,2015.
|
| [3] |
Dong Jianhua, Xie Heping, Zhang Lin. Experimental study of 3D geomechanical model on global stability of dagangshan double curvature arch dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2027-2033. [董建华, 谢和平, 张林. 大岗山双曲拱坝整体稳定三维地质力学模型试验研究[J]. 岩石力学与工程学报, 2007, 26(10): 2027-2033. DOI:10.3321/j.issn:1000-6915.2007.10.010] |
| [4] |
Chen Jianye, Zhang Lin, Chen Yuan. Failure model test on deep anti-sliding stability of wudu RCC gravity dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2097-2103. [陈建叶, 张林, 陈媛. 武都碾压混凝土重力坝深层抗滑稳定破坏试验研究[J]. 岩石力学与工程学报, 2007, 26(10): 2097-2103. DOI:10.3321/j.issn:1000-6915.2007.10.020] |
| [5] |
Li Meirong,Chen Yuan,Zhang Lin,et al.Impacts of multi-structural planes on gravity dam foundation stability and treatment under complex geological conditions[J].Rock and Soil Mechanics,2014,35(Supp1):334–339. [李美蓉,陈媛,张林,等.复杂地质条件下多结构面对重力坝坝基稳定性的影响及处理[J].岩土力学,2014,35(增刊1):334–339.]
|
| [6] |
Chen Yuan,Zhang Lin,Yang Baoquan,et al.Geomechanical model experiment of global stability of Lizhou arch dam on muli river[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(Supp2):475–482. [陈媛,张林,杨宝全,等.木里河立洲拱坝整体稳定地质力学模型试验研究[J].岩石力学与工程学报,2012,31(增刊2):475–482.]
|
| [7] |
Yang Baoquan, Chen Yuan, Zhang Lin. Research on dam abutment reinforcement effect of Jinping arch dam based on geomechanical model test[J]. Rock and Soil Mechanics, 2015, 36(3): 216-223. [杨宝全, 陈媛, 张林. 基于地质力学模型试验的锦屏拱坝坝肩加固效果研究[J]. 岩土力学, 2015, 36(3): 216-223.] |
| [8] |
Liu Jian, Feng Xiating, Ding Xiuli. Stability assessment of the Three-Gorges Dam foundation,China,using physical and numerical modeling—Part I:Physical model tests[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(5): 609-631. |
| [9] |
Zheng Yingren, Liu Xinghua. Modern nonlinear science and problem of rock mechanics[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 691-696. [郑颖人, 刘兴华. 近代非线性科学与岩石力学问题[J]. 岩土工程学报, 1996, 18(1): 691-696.] |
| [10] |
Fu Chenghua, Chen Shenghong. Study on instability criteria of surrounding rock of underground engineering cavern based on catastrophe theory[J]. Rock and Soil Mechanics, 2008, 29(1): 167-172. [付成华, 陈胜宏. 基于突变理论的地下工程洞室围岩失稳判据研究[J]. 岩土力学, 2008, 29(1): 167-172.] |
| [11] |
Liu Huibo, Xiao Ming, Chen Juntao. Instability criterion for judging energy dissipation catastrophe of local rock mass system of underground engineering[J]. Engineering Journal of Wuhan University, 2011, 44(2): 202-206. [刘会波, 肖明, 陈俊涛. 岩体地下工程局部围岩失稳的能量耗散突变判据[J]. 武汉大学学报:工学版, 2011, 44(2): 202-206.] |
| [12] |
Huang Runqiu, Xu Qiang. Application of catastrophe theory to engineering geology[J]. Journal of Engineering Geology, 1993, 1(1): 65-73. [黄润秋, 许强. 突变理论在工程地质中的应用[J]. 工程地质学报, 1993, 1(1): 65-73.] |
| [13] |
凌复华.突变理论及其应用[M].上海:上海交通大学出版社,1987.
|
 2017, Vol. 49
2017, Vol. 49


