2. 中国电建集团 成都勘测设计研究院有限公司,四川 成都 610072
2. Chengdu Eng. Corp. Ltd.,PowerChina,Chengdu 610072,China
众所周知,心墙堆石坝由于其投资省、便于就地取材、对地形地质条件适应性好、施工简单、抗震性好等优点,在国内外坝工建设中占有重要地位[1]。随着筑坝经验的积累和施工机械的发展,将有一批高心墙堆石坝工程投入建设和运行。由于高坝大库水电工程所处的地形地质环境复杂,坝体与地基载荷大、应力水平高,其大坝与基础变形机理复杂,变形预测难度大,是高土石坝工程建设和运行中需要解决的关键科学与技术问题之一[2–4]。高心墙堆石坝在自重和水荷载作用下将产生大量的变形,包括沉降变形、顺河向水平变形、横河向水平变形。这些变形在施工填筑、初期蓄水和运行阶段随筑坝材料的压缩、湿化和流变发展而变化,其变形过程、量值与大坝安全密切相关。施工阶段,可基于变形监测序列,通过数学和力学的方法建立数理统计模型预测坝体变形的发展,其预测模型中的因子主要有以下3种构建方法:其一是根据坝工理论,采用确定性函数考察因子的形式;其二是根据物理推断法判断因子的组成及其形式;其三是根据统计相关法检查因子及其拟合程度[5]。
这3种方法中,统计回归法简单实用,拟合效果较好,但其仅为单点预测,且需要较长的样本序列[6–7]。为此,部分学者引入灰色理论、神经网络理论等减小预测模型对监测数据样本的需求[8–9],但单纯从监测数据出发建立的变形预测模型难以从物理力学成因上解释堆石坝的变形规律;且实际工程中,大坝变形监测的可靠性受地形、测点数量和施工作业干扰或其他因素的综合影响,单点时间序列模型也难以反映这一问题[10];在时空模型研究方面开展的工作较少,特别是关于高心墙堆石坝变形时空模型的研究鲜见。因此,开展高心墙堆石坝变形时空模型研究,实时把控其整体变形规律和趋势,不仅对高心墙堆石坝变形调控与设计反馈具有重要意义,且对其运行安全管理具有重要的应用价值。
变形时空模型的构建主要可采用两种方式,即基于时序列实施空间拟合[11]和空间插值[12]。整体上来看,时空序列模型虽然能克服单点序列模型的某些缺点,但在构造上往往比较困难。因此,基于单点时间序列模型研究的经验,在单点模型的基础上进行空间拓展是构建变形时空模型的一种便捷、有效的途径。
1 模型构建 1.1 概述高心墙堆石坝变形是一个多因素综合作用的复杂系统,如果坝体填筑材料一定,根据荷载作用的叠加原理[13–14],坝体变形与环境量之间时空对应关系可表示为:
| $\delta = \small\sum\limits_{j = 1}^n {{\delta _i}} (x,y,{\textit{z}},{f_j},t)$ | (1) |
式中,
由式(1)可知,建立高心墙堆石坝变形时空模型最关键的问题在于确定时空变异函数,以反映采样点变形在时间尺度上的延伸和空间尺度上的相互联系。时空变异函数主要有可分离型和不可分离型[6],两者在插值处理上均以数理统计理论为基础。其中,可分离型模型通过分割时间和空间的相关信息构造,通常能得到较满意的效果[12,14–16]。
基于高心墙堆石坝变形物理力学成因,参考分离型模型的构建方式,采用单点拟合与空间插值的思路构建高心墙堆石坝变形时空模型,其模型架构形式可表达为:
| $\tilde \delta (h,t) = \delta (\tilde \delta ({h_i},t),{\lambda _i})$ | (2) |
式中:
| $\tilde \delta ({h_i},t) = \small\sum\limits_{j = 1}^n {{\delta _j}} ({f_j},t)$ | (3) |
| $\tilde \delta ( \cdot ,\lambda ) = \small\sum\limits_{i = 1}^N {{\lambda _i}} \tilde \delta ({h_i},{t_j})$ | (4) |
式中,
因此,时空模型构建的关键在于建立兼顾力学成因的单点变形时间序列预测模型
高心墙堆石坝施工填筑阶段坝体沉降变形的主要来源为填筑产生的瞬时压缩变形和随时间变化的蠕变变形。基于现有的粗粒土变形计算理论,坝体任意一点的瞬时压缩变形,由该点上覆土层对该点以下坝体产生的压缩变形和坝基压缩产生的牵连变形组成:
| ${S_{\! {\text{s}}}} = {S_{\! {\rm{d}}}} + {S_{\! {\rm{l}} }}$ | (5) |
式中,
设坝体填筑高度为H,坝基覆盖层深度为HL,坝内任意点i与坝高H和覆盖层深度HL之间的位置关系如图1所示,图中z为监测点离基准面的距离。
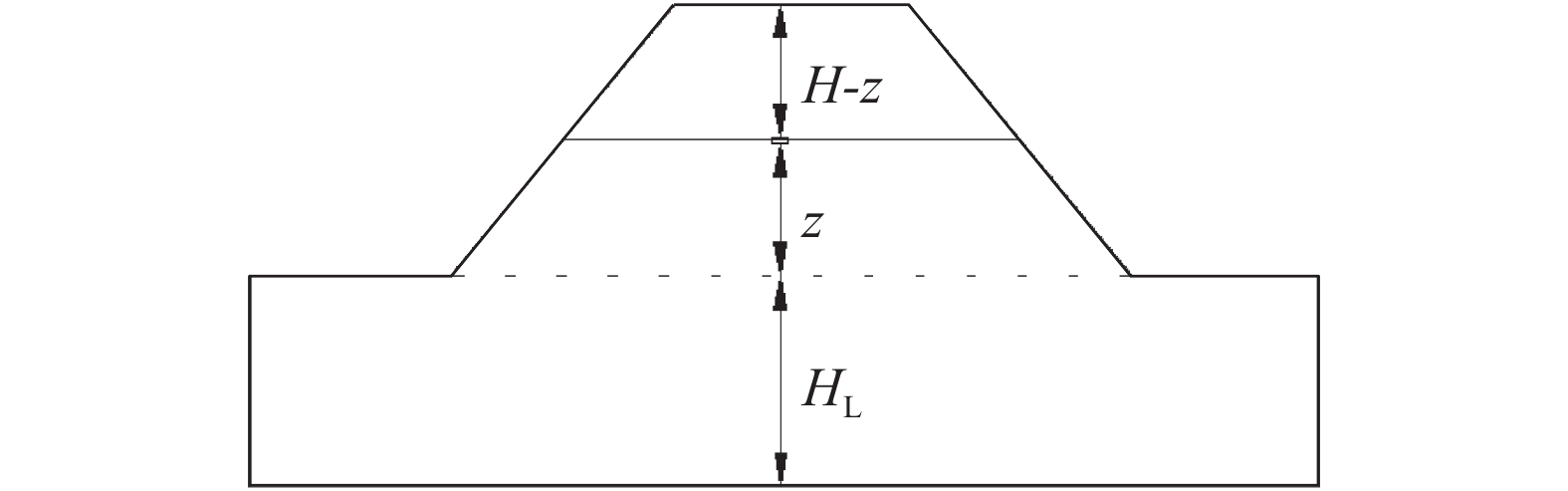 |
| 图1 坝内任意点与坝高、覆盖层深度的位置关系 Fig. 1 Position relationship between any point of the dam and the height of dam,the depth of cover |
坝内任意一点由坝体产生的压缩变形可由式(6)进行计算(以坝底为基准平面,向上为坐标正向):
| ${S_{\! {\rm{d}}}} = \int_0^{H - {\textit{z}}} {\int_0^{\textit{z}} {\frac{{\alpha \gamma }}{{{E_{\rm{s}}}}}} } {\rm{d}}{{\textit{z}}_1}{\rm{d}}{{\textit{z}}_2}$ | (6) |
式中:α为压应力修正系数,与材料、坝体结构和河谷地形有关,但修正系数对同一工程具体点可近似为常数;γ为填筑料的容重;z为监测点离基准面的距离;z1、z2为积分变量;Es为填筑料的压缩模量,该模量随应力状态而改变,若采用邓肯-张模型进行坝体变形计算,压缩模量可按式(7)计算:
| ${E_{\rm{s}}} = {k_{\rm{e}}}P_{\! \rm{a}}{(\frac{{{\sigma _3}}}{P_{\rm{a}}})^n}{(1 - {R_{\! \rm{f}}}\frac{{({\sigma _1} - {\sigma _3})(1 - \sin \; \phi )}}{{2c\cos \; \phi + 2{\sigma _3}\sin \; \phi }})^2}$ | (7) |
其中,Pa为大气压强,Rf、ke为试验常数,c为土体黏聚力,
为简化分析,点主应力可近似用竖向压应力表示:
| ${\sigma _1} = \beta \gamma {\textit{z}}$ | (8) |
| ${\sigma _3} = \eta \gamma {\textit{z}}$ | (9) |
式中:β、η为主应力系数,该系数也与材料、坝体结构、河谷地形等相关,具体点的主应力修正系数也可近似考虑为常数;其他符号意义同前。
将式(8)和(9)代入式(7),可得:
| ${E_{\rm{s}}} = {k_{\rm{e}}}P_{\! \rm{a}}{(\frac{{\eta \gamma {\textit{z}}}}{P_{\! \rm{a}}})^n}[1 - {R_{\rm{f}}}\frac{{(\beta - \eta )(1 - \sin \; \phi )}}{{2\eta \sin \; \phi }}]^2$ | (10) |
将式(10)代入式(6)中,令
| ${S_{{\rm{d}}}} = {\int_0^{H - {\textit{z}}} {\int_0^{\textit{z}} {B({{\textit{z}}_1} + {{\textit{z}}_2})} } ^{ - n}}{{\rm d}{\textit{z}}_1}{{\rm d}{\textit{z}}_2}$ | (11) |
因此,因坝体压缩产生的沉降变形为:
| ${S_{{\rm{d}}}} = \frac{{\textit{B}}}{{(1 - n)(2 - n)}}[{H^{2 - n}} - {{\textit{z}}^{2 - n}} - {(H - {\textit{z}})^{2 - n}}]$ | (12) |
式中,z为坝体变形监测点离基准面的距离,H为测点位置基准面到坝表面的距离,n为材料的邓肯-张模型参数,B为系数,其他符号意义同前。
从式(12)揭示的变形规律可知,施工填筑期单点的沉降变形与该点对应的坝高呈幂函数关系。在此,令
对于坝基覆盖层的影响,若应力在坝基内的扩散系数为φ(系数取值与荷载的分布及扩散点的位置有关,不考虑附加应力在坝基内的扩散时取1.0),由覆盖层变形引起的坝体的牵连变形可表示为:
| ${S_{\! 1}} = \int_0^{H - {\textit{z}}} {\int_0^{\textit{z}} {\frac{{\alpha \gamma }}{{{E_{\rm{s}}}}}} } {\rm{d}}{{\textit{z}}_1}{\rm{d}}{{\textit{z}}_2}$ | (13) |
同样,设坝基内的主应力修正系数分别为β1、η1,坝基内的应压力修正系数为α1,令Al=1–
| $\begin{aligned}[b]{S_{{\rm{l}}}} & = \frac{{{B_{\rm{l}}}}}{{(1 - {n'_{\rm{l}}})(2 - {n'_{\rm{l}}})}} \times \\& \quad \left[ {{{({H_{\rm{L}}} + H - {\textit{z}})}^{2 - n'}} - {H^{^{2 - n'}}} - {{(H - {\textit{z}})}^{^{2 - n'}}}} \right]\end{aligned}$ | (14) |
式中,HL为覆盖层深度,
综上可获得坝体任意点在施工填筑期的瞬时沉降变形Ss为:
| ${S_{\! {\rm{s}}}} = {S_{{\rm{d}}}} + {S_{{\rm{l}}}}$ | (15) |
施工期土石坝沉降变形由瞬时压缩变形和蠕变变形组成,见式(15)。任一时刻蠕变量
| ${\varepsilon _{{{t}}}} = {\varepsilon _{\rm{f}}}(1 - {{\rm{e}}^{ - \alpha {t}}})$ | (16) |
式中,
三轴蠕变试验中,任意时刻轴向蠕变变形
| $\varepsilon _{\rm{L}} = \frac{1}{3}{\varepsilon _{\rm{v}}} + 2{\varepsilon _{\rm{s}}}$ | (17) |
若以沈珠江7参数蠕变模型进行分析,最终剪切蠕变变形
| ${\varepsilon _{{\rm{sf}}}} = d\frac{{S\! L}}{{1 - S\! L}}$ | (18) |
| ${\varepsilon _{{\rm{vf}}}} = b{\left(\frac{{{\sigma _3}}}{{P_{\rm{a}}}}\right)^n}$ | (19) |
式中,b、d为蠕变材料常数,SL为应力水平。
最终轴向蠕变可按式(20)计算:
| ${\varepsilon _{{\rm{Lf}}}} = \frac{1}{3}\left[b{\left(\frac{{{\sigma _3}}}{{P_{\rm{a}}}}\right)^{{m_1}}} + c{\left(\frac{q}{{P_{\rm{a}}}}\right)^{{m_2}}}\right] + 2d{\left(\frac{{S\! L}}{{1 - S\! L}}\right)^{{m_3}}}$ | (20) |
式中,q为偏应力,m1、m2、m3为材料蠕变参数。
假设中主应力可近似表示为:
| ${\sigma _2} = \lambda \gamma {\textit{z}}$ | (21) |
令
| ${\varepsilon _{{\rm{Lf}}}} = {C_1}{{\textit{z}}^{{m_1}}} + {C_2}{{\textit{z}}^{\frac{{{m_2}}}{2}}} + D$ | (22) |
式中,z为空间点上覆土层厚度,m1、m2为材料的蠕变参数,C1、C2、D为系数。
设图2为大坝填筑历时曲线。施工期任意高程点zj的蠕变变形即等于该点以下土层在时间tc–tj范围内所产生的蠕变变形之和(tc为填筑工期):
| ${S_{{\text{z}}}} = \int_0^{{{\textit{z}}_j}} {\Delta \varepsilon ({t_{\rm{c}}} - {t_k},{t_j} - {t_k})}{\text{d}}{\textit{z}}$ | (23) |
式中,tk为填筑到高程zk对应的时间。
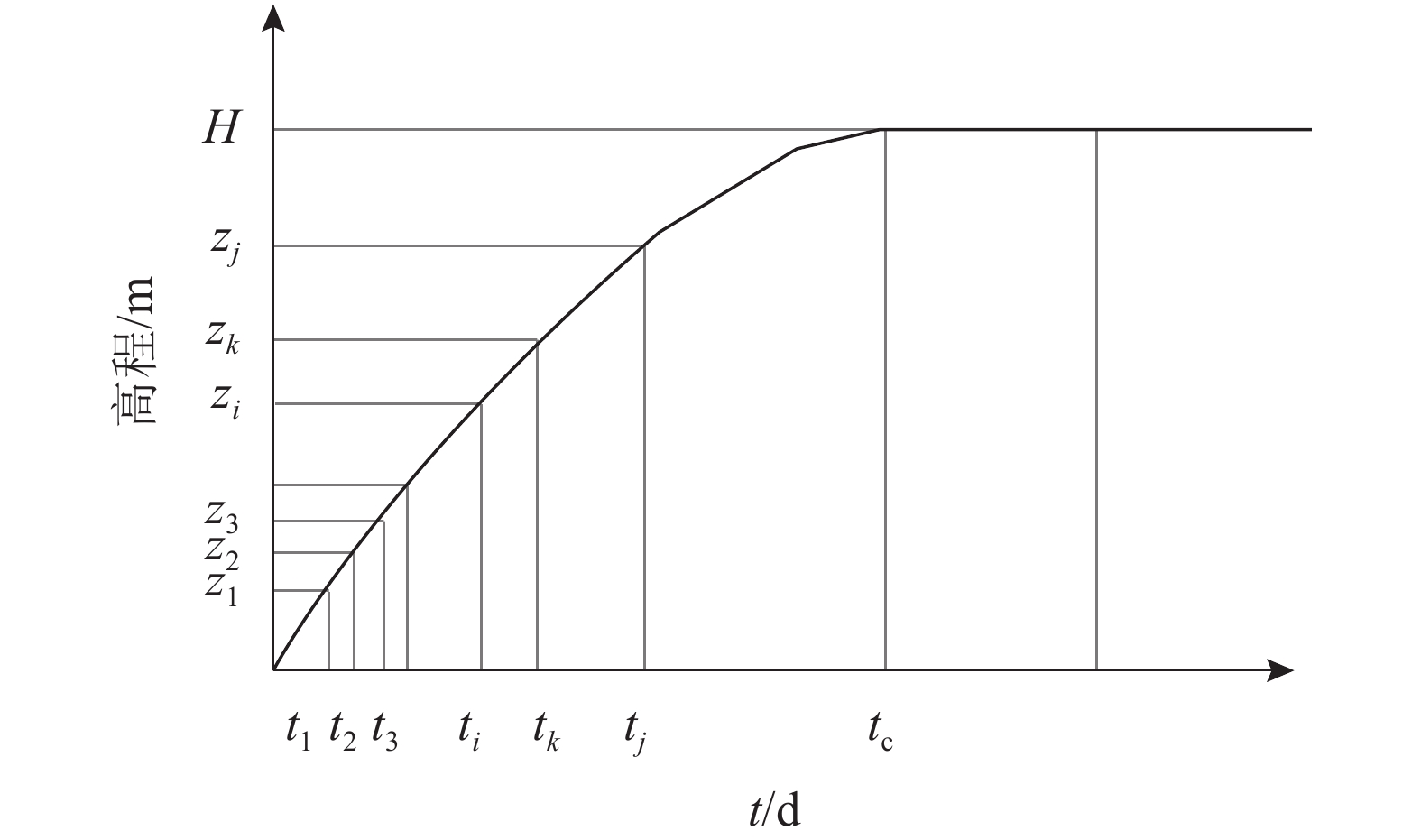 |
| 图2 坝填筑高度与时间的对应关系 Fig. 2 Corresponding relationship between filling height and time |
若用
| $\Delta S_{\! \text{z}}=\Delta {\varepsilon _i}({t_{\rm{c}}} - {t_k},{t_j} - {t_k}) =\int {f({{\textit{z}}_i},{\rm{d}}{\textit{z}})({{\rm{e}}^{ - \alpha ({t_j} - {t_k})}} - {{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_k})}})} {\rm{d}}x$ | (24) |
将坝体划分为N层,每层对应的坝体高度分别为
| $\begin{aligned}[b]{f_k}({{\textit{z}}_i}) & = {C_1}[{({{\textit{z}}_k} - {{\textit{z}}_i})^{{m_1}}} - {({{\textit{z}}_{k - 1}} - {{\textit{z}}_i})^{{m_1}}}] + \\& \quad {C_2}[{({{\textit{z}}_k} - {{\textit{z}}_i})^{\frac{{{m_2}}}{2}}} - {({{\textit{z}}_{k - 1}} - {{\textit{z}}_i})^{\frac{{{m_2}}}{2}}}] + D\end{aligned}$ | (25) |
则式(24)可化为:
| ${\Delta S_{\! \text{z}}} = \small\sum\limits_{i = 1}^j {\small\sum\limits_{k = i + 1}^N {{f_k}({{\textit{z}}_i})} } ({{\rm{e}}^{ - \alpha ({t_j} - {t_k})}} - {{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_k})}})$ | (26) |
根据式(26),合并同类项,则
| $\Delta {S_{\! \text{z}}} = \Delta {{\textit{z}}_i}(\small\sum\limits_{i = 1}^j {{a_i}{{\rm{e}}^{ - \alpha ({t_j} - {t_k})}} - } \small\sum\limits_{i = 1}^j {{a_i}{{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_k})}}} )$ | (27) |
式中,ai为中间变量。
因此:
| ${S_{\! {\text{z}}}} = \small\sum\limits_{i = 1}^j {{K_i}{\textit{z}}({{\rm{e}}^{ - \alpha ({t_j} - {t_i})}} - {{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_i})}})}$ | (28) |
式中,Ki为常系数,z为测点所在的高程,α为材料的蠕变参数,ti、tj分别为不同的时间节点,Sz0表示坝基的蠕变量。
综上,施工填筑期坝体任一点的总沉降S为:
| $S= {S_{\! {\rm{d}}}} + {S_{\! {\rm{l}}}} + {S_{\! {\text{z}}}} + {S_{\! {\text{z}}0}}$ | (29) |
式中,Sz0为坝基的蠕变量。
由式(29)可知,坝体填筑材料一定时,不同点的变形不仅与坝体的填筑高度有关,还与点的空间位置密切相关,其沉降变形量为填筑高度和位置空间信息的非线性函数。
1.2.2 水平变形高心墙堆石坝上、下坝坡坡度较为接近,为简化计算,将坝体及河谷地形均以对称考虑。
对顺河向x方向的水平变形进行推导:
| ${S_{\! xi}} = \int_0^x {{\varepsilon _x}{\rm{d}}\! x = \int_0^x {{\nu _{{\textit{z}}x}}} } {\varepsilon _{\textit{z}}}{\rm{d}}x$ | (30) |
式中,Sxi为i点水平方向变形,
材料的泊松比ν与压缩模量Es和体积模量Bt之间的关系为:
| ${B_{\rm{t}}} = \frac{{{E_{\rm{s}}}}}{{3(1 - 2\nu )}}$ | (31) |
即
| $\nu = 0.5 - \frac{{{E_{\rm{s}}}}}{{6{B_{\rm{t}}}}}$ | (32) |
在邓肯-张模型中,体积模量Bt可为:
| ${B_{\rm{t}}} = {k_{\rm{b}}}{\left(\frac{{{\sigma _3}}}{{P_{\rm{a}}}}\right)^{m}}$ | (33) |
式中,kb为试验参数。
令
| $\nu = 0.5 - E$ | (34) |
将式(34)代入式(30):
| ${S_{xi}} = \left( {0.5 - E} \right)\int_0^x {\left( {\int_0^{H - {\textit{z}}} {\frac{{\alpha \gamma {\rm{d}}{\textit{z}}}}{{{E_{\rm{s}}}}}} } \right)} {\rm{d}}x$ | (35) |
令
| ${S_{xi}} = G\frac{{{{(H - {\textit{z}})}^{1 - {n}}}}}{{1 - n}}x$ | (36) |
式中,
将筑坝材料视为各项同性材料,横河向(y轴方向)坝体变形受岸坡约束不存在临空面,因此可假设岸坡和x轴线上的横河向变形为0,取1/4坝体为研究对象,其简化示意图见图3。
 |
| 图3 坝轴向变形示意图 Fig. 3 Schematic diagram of axial deformation of dam |
此时,横河向水平变形为:
| ${S_{yi}} = \int_0^y {{\varepsilon _y}} {\rm{d}}y$ | (37) |
因为
| ${\varepsilon _y} = \frac{{{\sigma _y}}}{{{E_{\rm{s}}}}} = \frac{{{k_y}\gamma ({H_y} - y)}}{{{E_{\rm{s}}}}}$ | (38) |
将式(38)代入式(37)得:
| ${S_{\! yi}} = {k_{y}}\gamma (H_y^2 - {({H_y} - y)^2})/{E_{\rm{s}}}$ | (39) |
式中,ky为Y向侧压力系数,Hy为测点到z轴的距离,其他符号意义同前。
从蠕变变形的组成来看,某点的蠕变由体积蠕变和剪切蠕变组成。其中,剪切蠕变与空间点的应力状态相关。考虑到体积蠕变对主应力空间各方向上的贡献一致,那么,某点水平向的蠕变与竖直向蠕变量值的差异主要由剪切蠕变造成。因此,当应力状态稳定时,具体点的竖直向蠕变与水平向蠕变仅与时间有关,二者的比值可近似常量,设水平向蠕变与竖直向蠕变的比值系数分别为ωxz,ωyz,则一点的水平向蠕变为:
| ${\varepsilon _{xt}} = {\omega _{{\textit{zx}}}}{\varepsilon _{\textit{zt}}},{\varepsilon _{yt}} = {\omega _{{\textit{zy}}}}{\varepsilon _{{\textit{zt}}}}$ | (40) |
结合式(24),由蠕变产生的坝体水平变形为:
| ${S_{\! x}} = \int {{\varepsilon _{xt}}} {\rm{d}}x = \left(\small\sum\limits_{i = 1}^j {{\omega _{{\textit{z}}xi}}} {{\rm{e}}^{ - \alpha ({t_j} - {t_i})}} - \small\sum\limits_{i = 1}^j {{\omega _{{\textit{z}}xi}}} {{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_i})}}\right)x$ | (41) |
| ${S_{\! y}} = \int {{\varepsilon _{yt}}} {\rm{d}}y = \left(\small\sum\limits_{i = 1}^j {{\omega _{{\textit{z}}yi}}} {{\rm{e}}^{ - \alpha ({t_j} - {t_i})}} - \small\sum\limits_{i = 1}^j {{\omega _{{\textit{z}}yi}}} {{\rm{e}}^{ - \alpha ({t_{\rm{c}}} - {t_i})}}\right)y$ | (42) |
因此,施工期间坝体顺河向与横河向的水平变形可分别由式(43)和(44)计算:
| ${H_{xi}} = {S_{\! xi}} + {S_{\! x}} + {S_{\! x0}}$ | (43) |
| ${H_{yi}} = {S_{\! yi}} + {S_{\! y}} + {S_{\! y0}}$ | (44) |
式中,S0为常数,用于考虑漏测或模型构建误差的影响。
1.3 多点变形预测空间插值模型从上述推导结果可知,坝体任意一点的变形与空间位置、填筑高程、蓄水高度呈多元幂函数关系,与时间增量呈指数关系。幂函数中幂的取值和指数函数中指数系数的取值与填筑材料的物理力学性质相关。当大坝的边界条件、结构分区和填筑材料物理力学性质不变时,单点变形很容易按如上推导的变形与环境量关系进行拟合分析和预测。考虑到同一期监测点的变形能在一定程度上反应监测点变形的空间联系,可根据已知监测点的变形通过空间插值进行坝体3维变形预测。
常用的空间插值方法有样条函数插值、克里金插值和反距离加权平均法[17]。其中样条插值有2个基本条件:表面必须完全通过样本点,表面的2阶曲率最小,这在实际运用中实现起来是比较困难的。反距离加权平均法的计算结果容易受到点集群的影响。克里金插值是根据空间样本点的相关程度对空间数据赋以权重,实现位置空间数据的最优、线性无偏估计,适用于区域化变量存在空间相关性的情况[18]。
1.3.1 一般克里金插值根据监测数据可计算空间变异函数γ(h)的估计值γ*(h):
| ${\gamma ^*}(h) = \frac{1}{{2n}}\small\sum\limits_{i = 1}^n {{{\left[\delta ({h_i}) - \delta ({h_i} + {h_{\rm{s}}})\right]}^2}}$ | (45) |
式中,hs为样本空间的空间分隔距离,
在克里金插值中,常用的变异函数有指数模型、球形模型和高斯模型等。其中,球形模型是较通用的一种变异函数[19]:
| $\gamma (h) = \left\{ \begin{aligned} & 0, \ h = 0\text{;}\\& {C_0} + C\left(1.5\frac{h}{a} - 0.5\frac{{{h^3}}}{{{a^3}}}\right),\ 0 < h \le a\text{;}\\& {C_0} + C, \ h > a\end{aligned} \right.$ | (46) |
式中,C0为块金值,C0+C为基台值,C为偏基台值,a为变程,相关量的基本关系如图4所示。变异函数反映了采样点与空间相邻点之间的空间关系,变程范围内任意两点的数据都相关,其相关程度一般随两点距离的增大而减弱。块金系数为块金值与基台值的比值,用于反映空间自相关的程度,其值越小表明自相关程度越高,变形函数中的各参数可根据式(45)的估计值拟合得到。
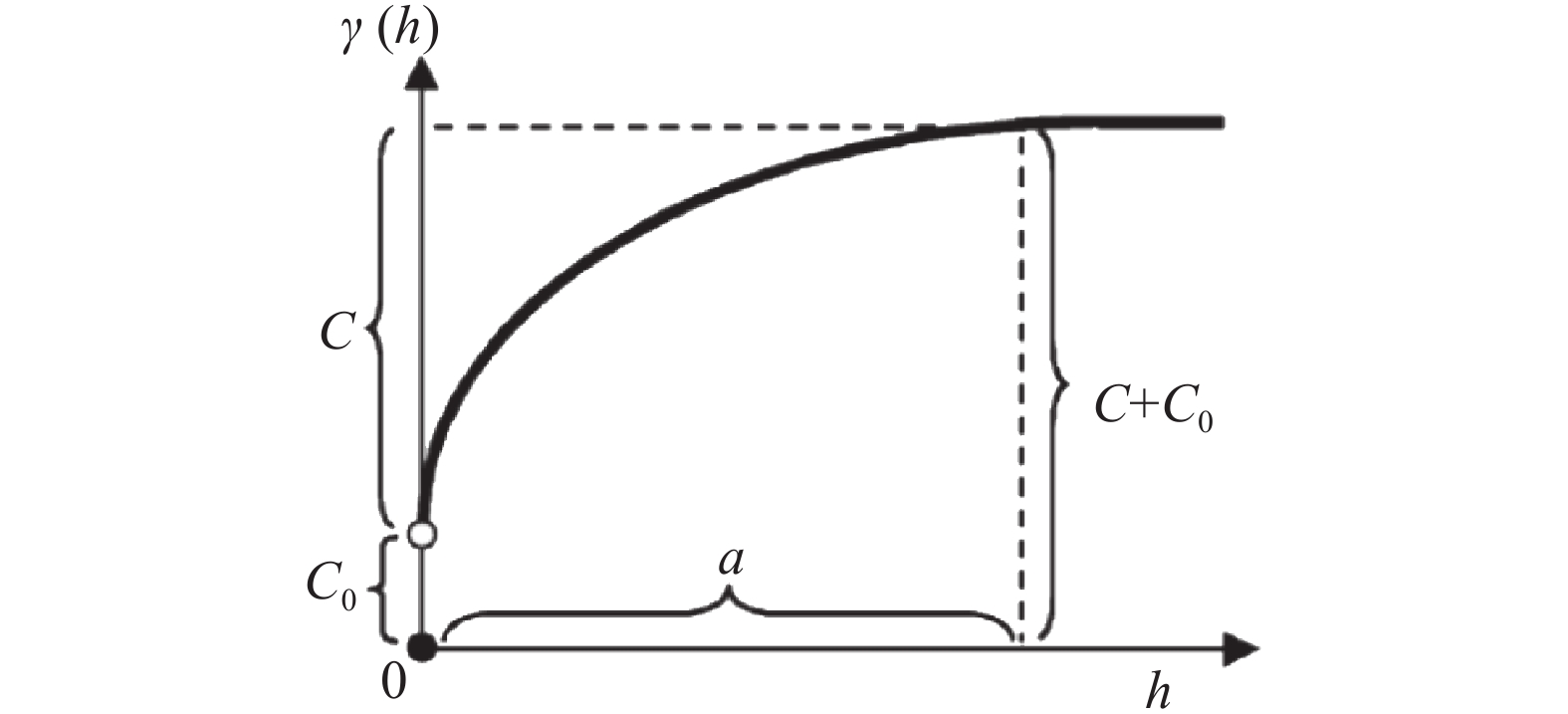 |
| 图4 变异函数各参数相关关系 Fig. 4 Correlation of parameters of variation function |
用空间变异函数计算各观测点变形的权重系数λi,参考文献[20–21],权重系数可通过引入拉格朗日乘除数获取:
| ${\mathit{\boldsymbol{A\lambda}}} = {\mathit{\boldsymbol{R}}}$ | (47) |
其中:
一般克里金法基于的理论是线性无偏估计,插值中要求样本数据服从2阶平稳过渡且均值为常数。根据文献[22],高心墙堆石坝的变形在时间尺度上兼顾趋势性和随机性,若变形在空间上的分布特性与时间尺度相似,区域化变量值是非平稳的,观测值由趋势值和残差两部分组成:
| $Z(S) = m(S) + R(S)$ | (48) |
式中,m(S)为趋势量,R(S)为残差量。
对于以上区域变量存在趋势性的问题,运用泛克里金插值法。在泛克里金插值法中常用确定性的函数模拟或拟合方法计算趋势量,趋势函数可表示为:
| $m(S) = \small\sum\limits_{i = 1}^k {{w_i}} {f_i}(S)$ | (49) |
式中:
用均值为0的平稳随机函数模拟残差R(S),可采用一般克里金插值方法进行预测。
泛克里金空间插值法在实际应用中,常采用趋势性拟合或逐步回归方法确定趋势多项式的次数[23–24],常用的趋势性函数有常量漂移、一次漂移和二次漂移。因此在高心墙堆石坝变形的空间插值中,可先对原始数据进行空间尺度的分离处理,再用克里金插值方法进行空间预测。
1.4 预测模型计算步骤根据模型构建原理,高心墙堆石坝施工期变形时空预测模型的计算步骤可归纳为:
1)基于堆石坝的施工期的原观变形数据,对其进行可靠性分析;
2)参考可分离型模型的构建,分割数据时间和空间的相关信息;
3)根据基于物理成因分析的施工期单点变形预测模型,计算单点变形时间序列
4)根据多点变形预测空间插值模型,计算空间变异函数的权重系数λi,继而用克里金插值方法进行空间预测。
2 工程应用 2.1 工程概况瀑布沟工程位于大渡河下游河段四川省汉源县和甘洛县交界处,电站总装机容量3 300 MW,是目前四川最大的水电工程之一。坝基河床覆盖层厚度一般40~60 m,最深达77.9 m,覆盖层层次结构复杂,厚度变化大,局部架空明显,存在坝基不均匀变形、渗透稳定及地震时砂土液化等工程地质问题。瀑布沟大坝坝体变形监测以桩号分别为0+240、0+310和0+431 m的3个监测断面为代表,测点布置分别如图5、6和7所示。
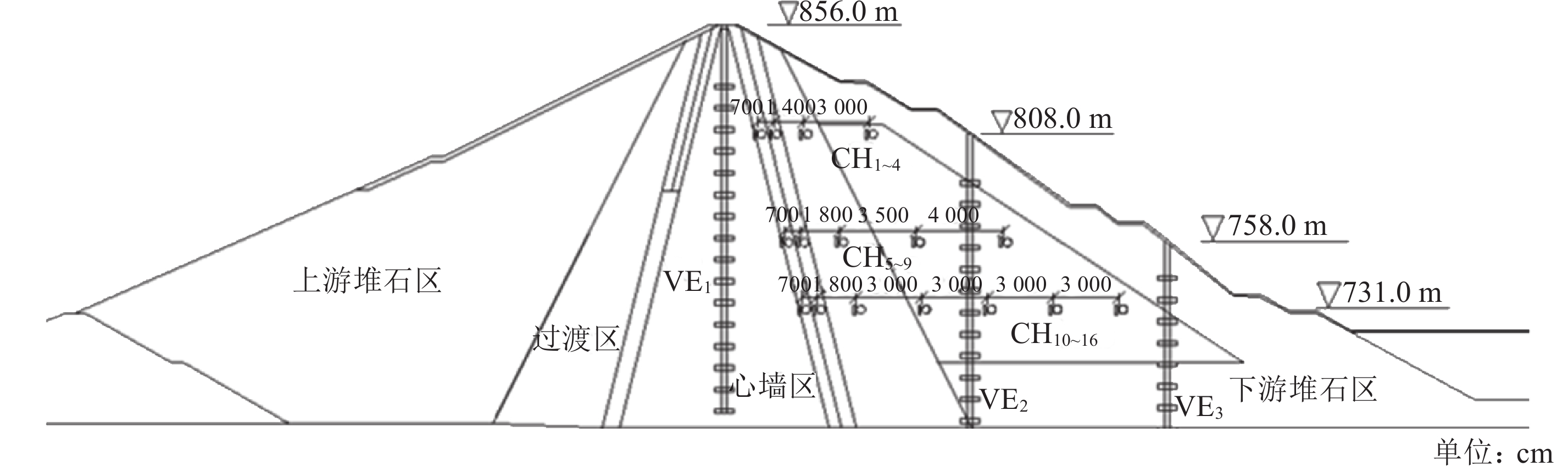 |
| 图5 0+240 m断面变形监测点布置 Fig. 5 Deformation monitoring layout in 0+240 m section |
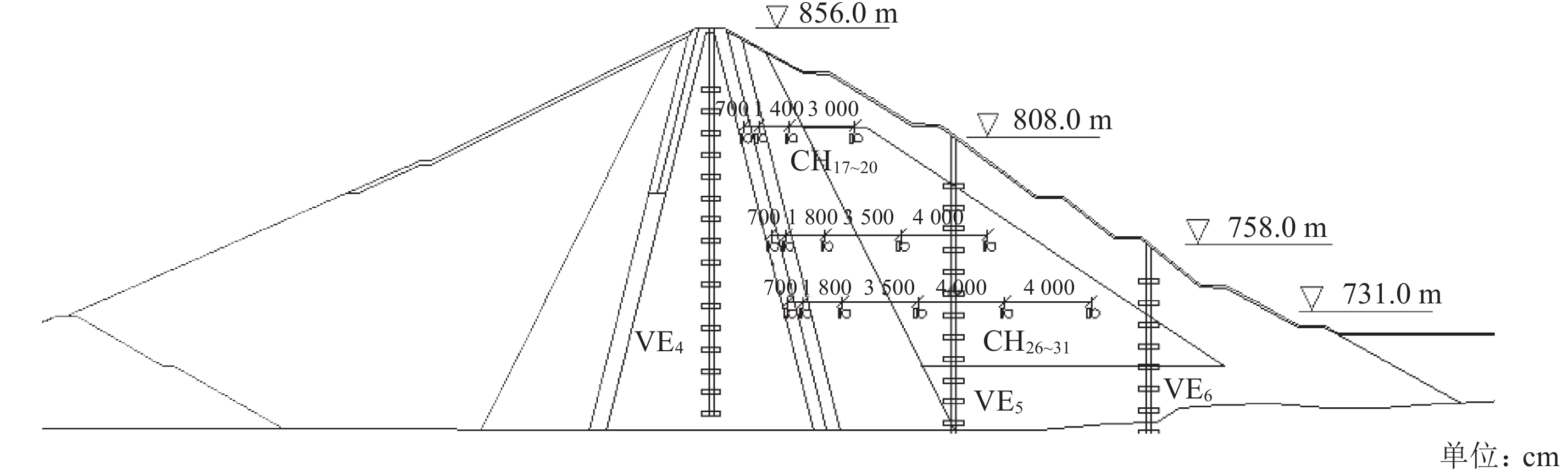 |
| 图6 0+310 m断面监测点布置 Fig. 6 Deformation monitoring layout in 0+310 m section |
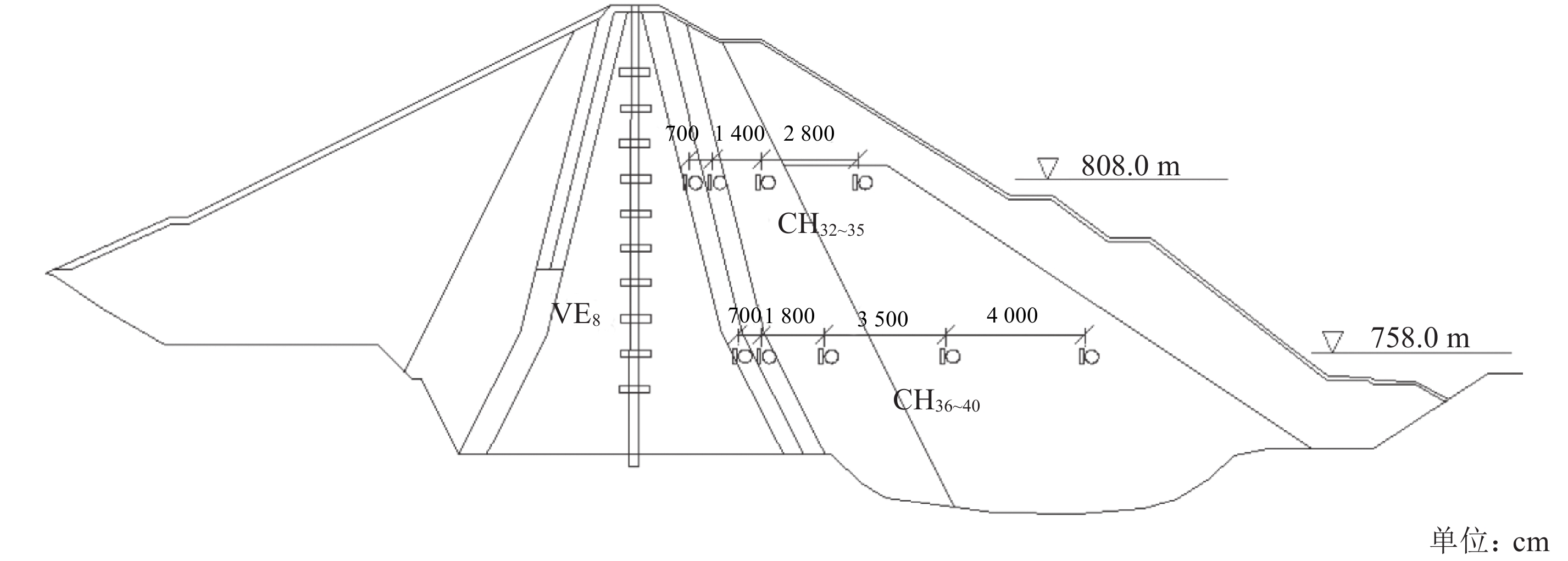 |
| 图7 0+431 m断面监测点布置 Fig. 7 Deformation monitoring layout in 0+431 m section |
2.2 沉降变形模型验证
经过监测数据可靠性分析后,选用测点VE1和VE2施工期沉降变形监测序列予以模拟分析,图8和9为2个典型测点(VE1-18和VE2-37)沉降变形计算值与实测值历时过程对比示例。从监测点变形序列的发展过程来看,本文所建坝体施工期单点沉降变形预测模型能较好地描述测点变形的历时过程,预测效果较好。
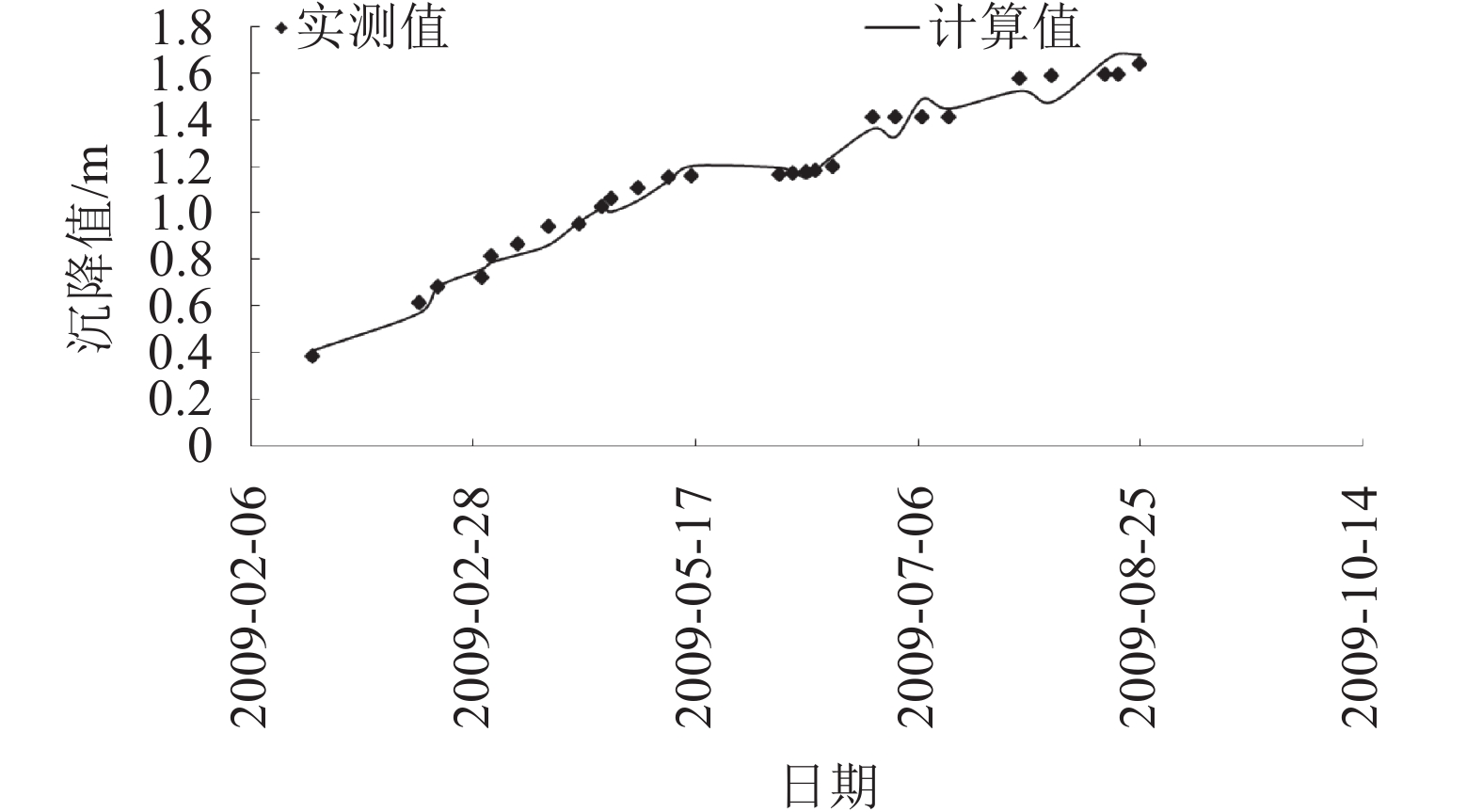 |
| 图8 VE1-18测点施工期沉降实测值和计算值 Fig. 8 Measured and calculated values of settlement in VE1-18 |
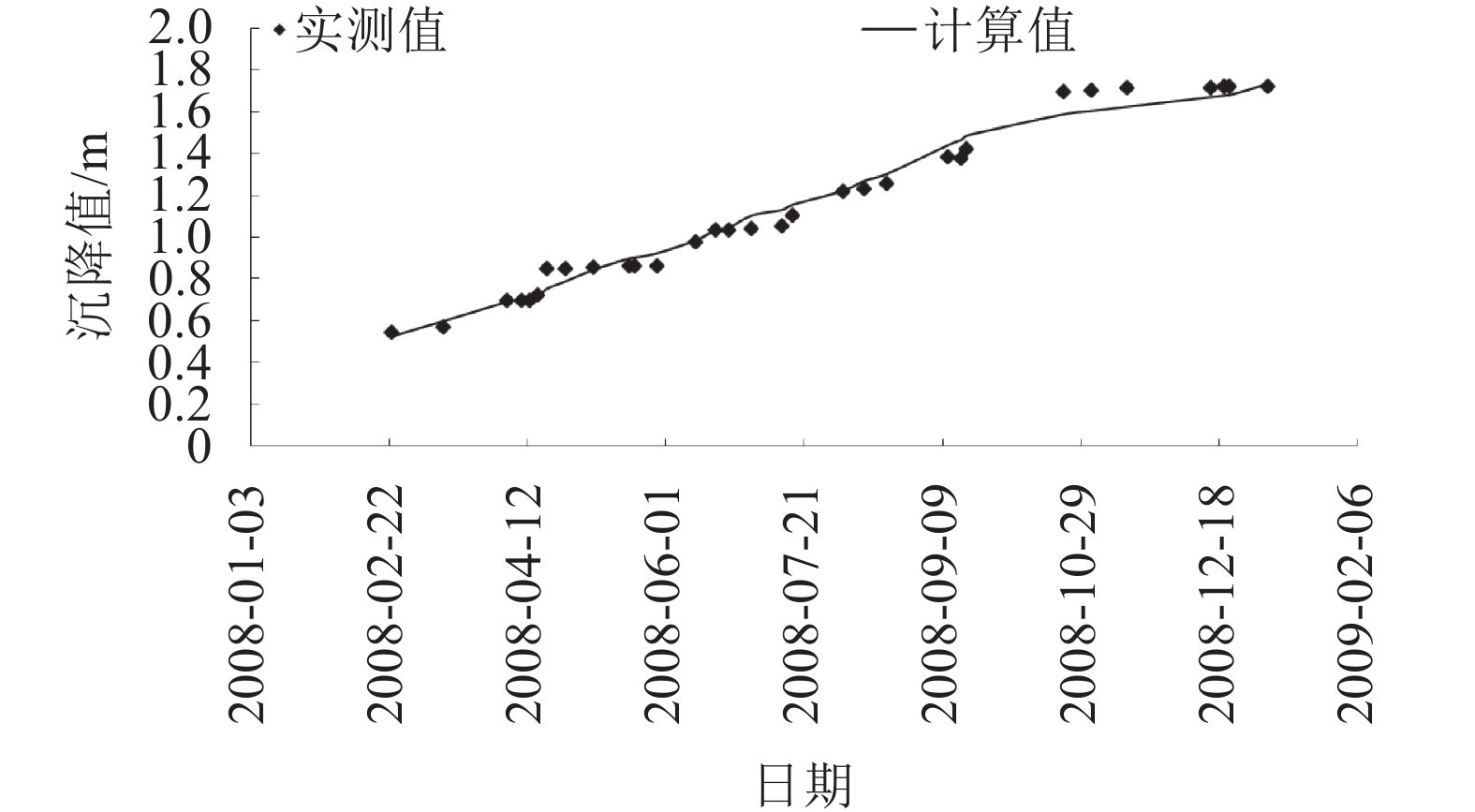 |
| 图9 VE2-37测点施工期沉降实测值和计算值 Fig. 9 Measured and calculated values of settlement in VE2-37 |
2.3 水平变形模型验证
用CH监测系列的顺河向水平变形数据验证施工期水平变形物理成因预测模型,图10和11为典型水平监测序列模型拟合值与实测值历时过程对比,模型拟合效果与实测趋势吻合程度较好。
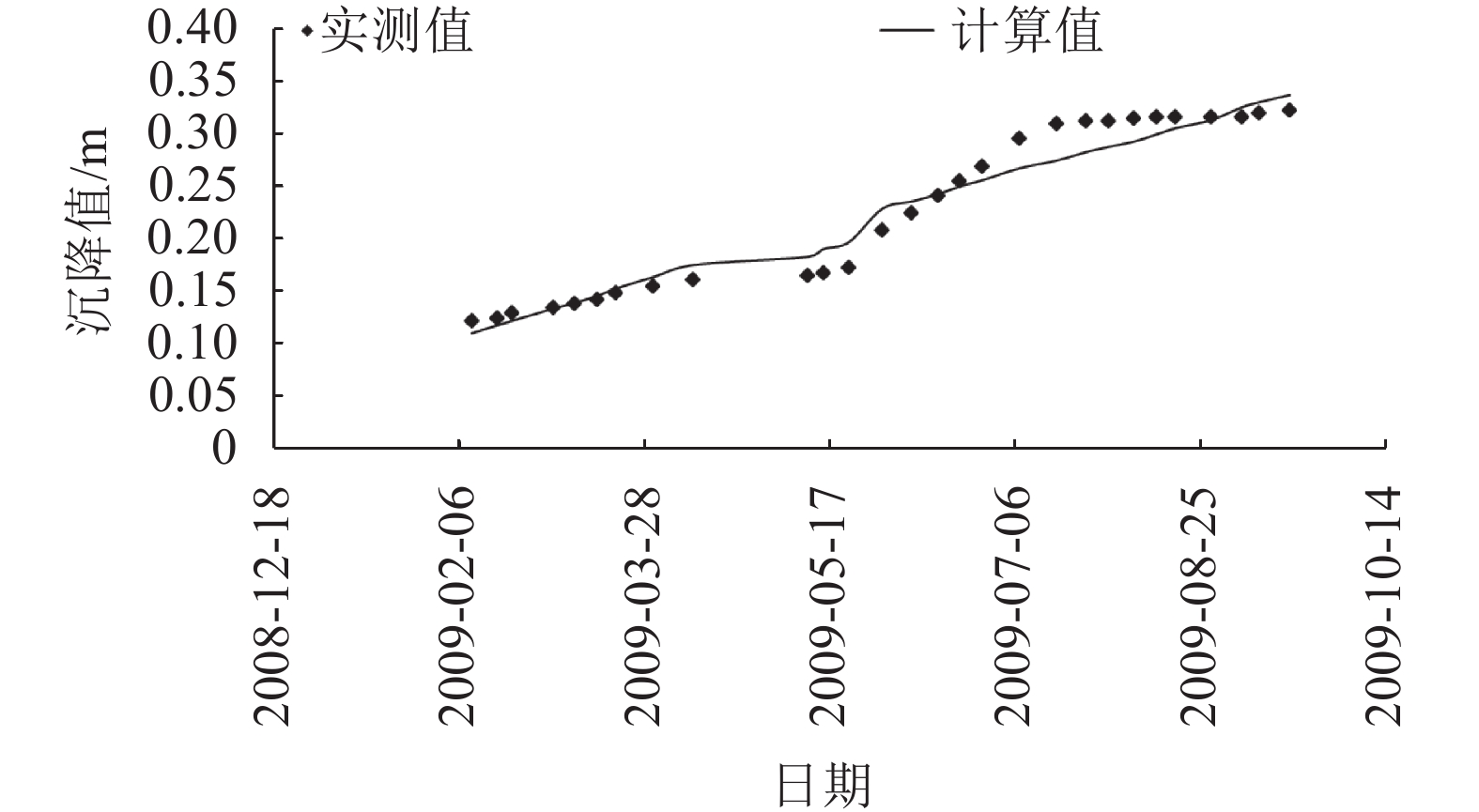 |
| 图10 CH12测点施工期水平变形实测值和计算值 Fig. 10 Measured and calculated values of horizontal deformation in CH12 |
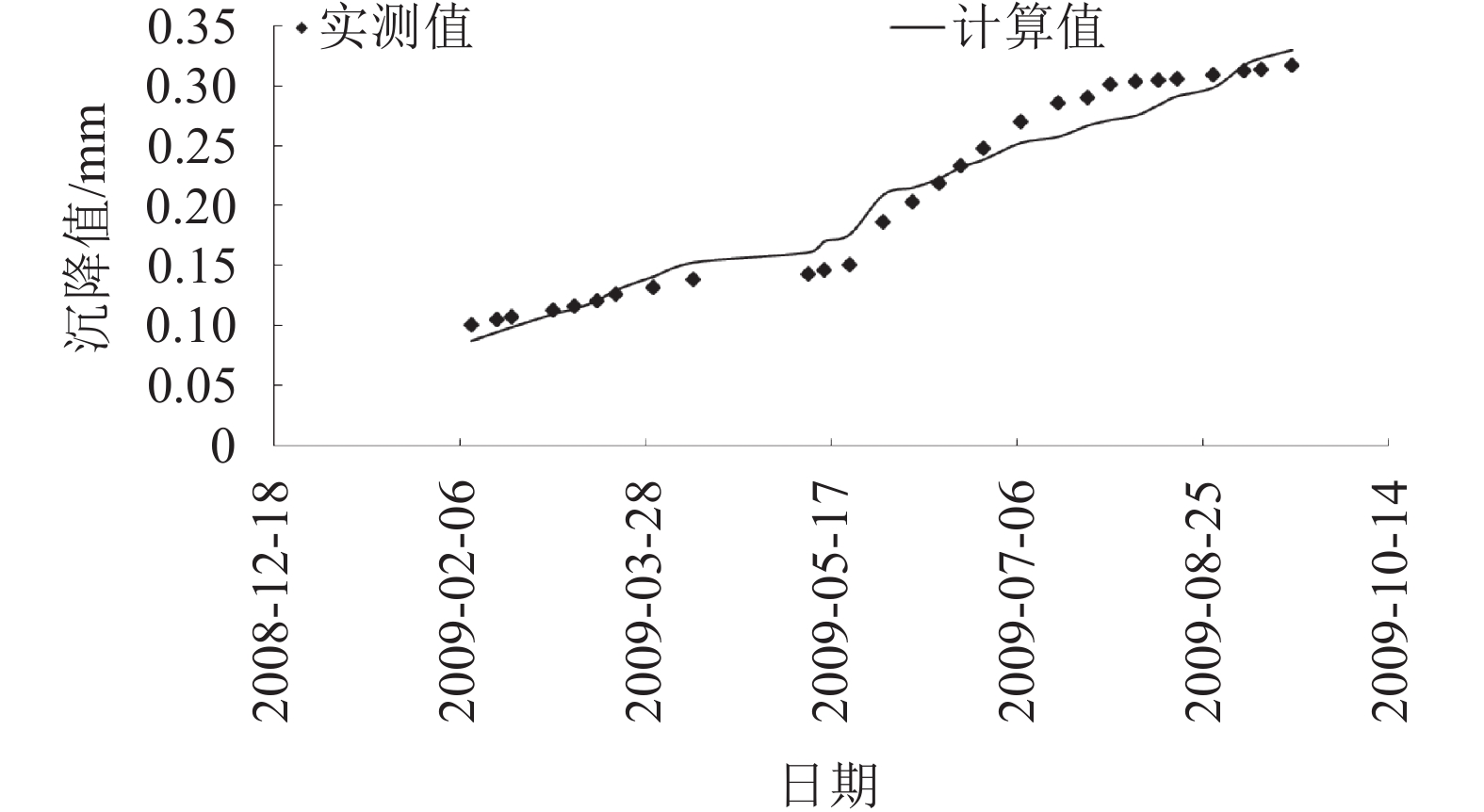 |
| 图11 CH13测点水平变形施工期实测值和计算值 Fig. 11 Measured and calculated values of horizontal deformation in CH13 |
2.4 空间插值模型验证
验证以2009年9月10日和2010年10月25日两期的瀑布沟高心墙堆石坝下游区沉降变形监测点(序列编号为CH1~CH40)监测数据为例,基于克里金插值流程,对比分析各点空间插值预测结果与实测值,如图12和13所示。可知,利用泛克里金插值时,测点的插值变形值与实测值相对误差较小,除波动较大的个别点外,其他测点吻合程度较好。
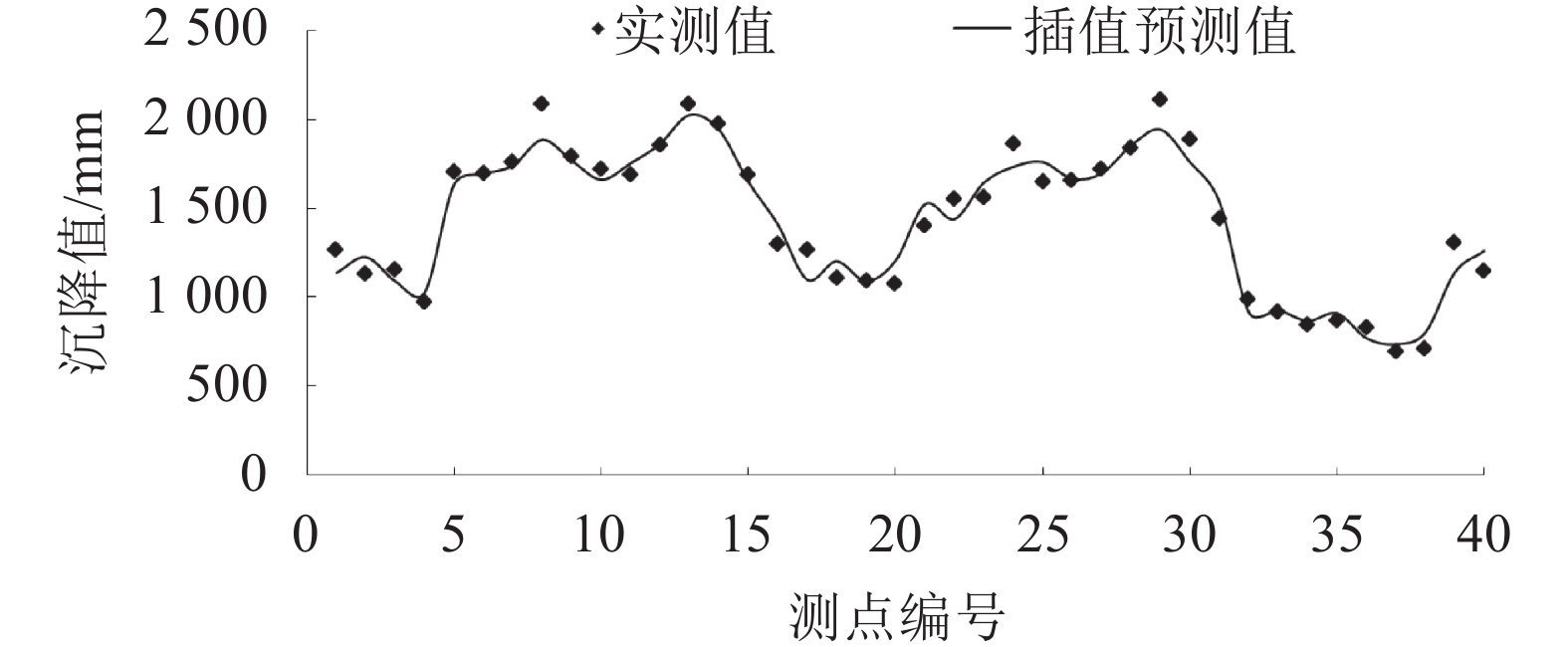 |
| 图12 2009-09-10变形的泛克里金插值结果与实测对比 Fig. 12 Comparison of universal kriging interpolation results with the measured values of deformation on September 10th, 2009 |
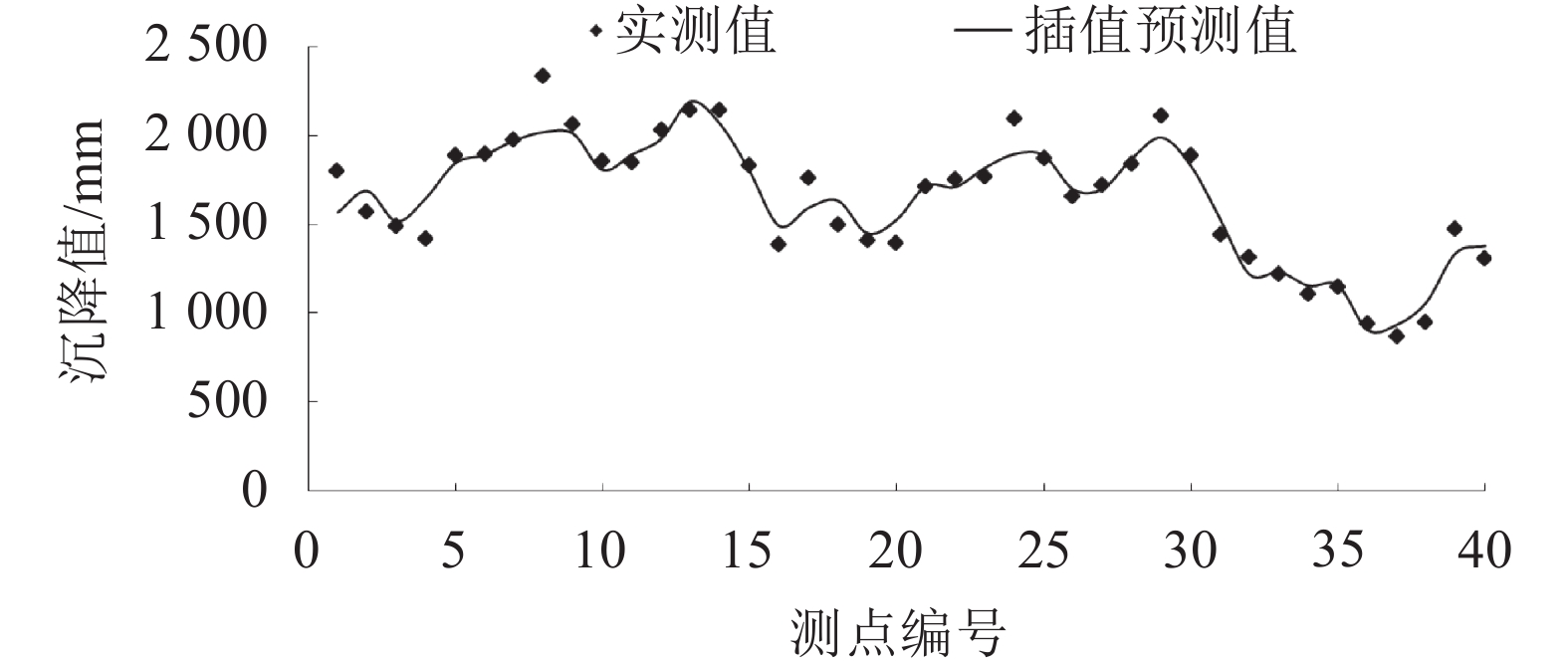 |
| 图13 2010-10-25期变形的泛克里金插值结果与实测对比 Fig. 13 Comparison of universal kriging interpolation results with the measured values of deformation on October 25th, 2010 |
2.5 瀑布沟高心墙堆石坝坝顶变形预测分析
针对瀑布沟高心墙堆石坝2010年8月26日发生在坝顶的纵向裂缝,通过构建的高心墙堆石坝变形预测时空模型模拟了坝顶2010年8月26日沉降变形分别见图14、15。
由图14可知,坝顶沉降变形从两岸至河谷呈增大趋势,整体上河床坝段上游测沉降变形大于下游,最大沉降值出现在距右岸240 m处坝轴线附近,这与坝顶测点整体变形趋势一致。
由图15可知,坝顶沉降变形倾度下游侧大于上游侧,且由河床坝段向岸坡坝段递减。河床坝段坝顶下游侧沉降变形倾度较大,且部分区域大于1%,表明该区域坝顶可能产生开裂,这与坝顶实际开裂情况基本吻合。
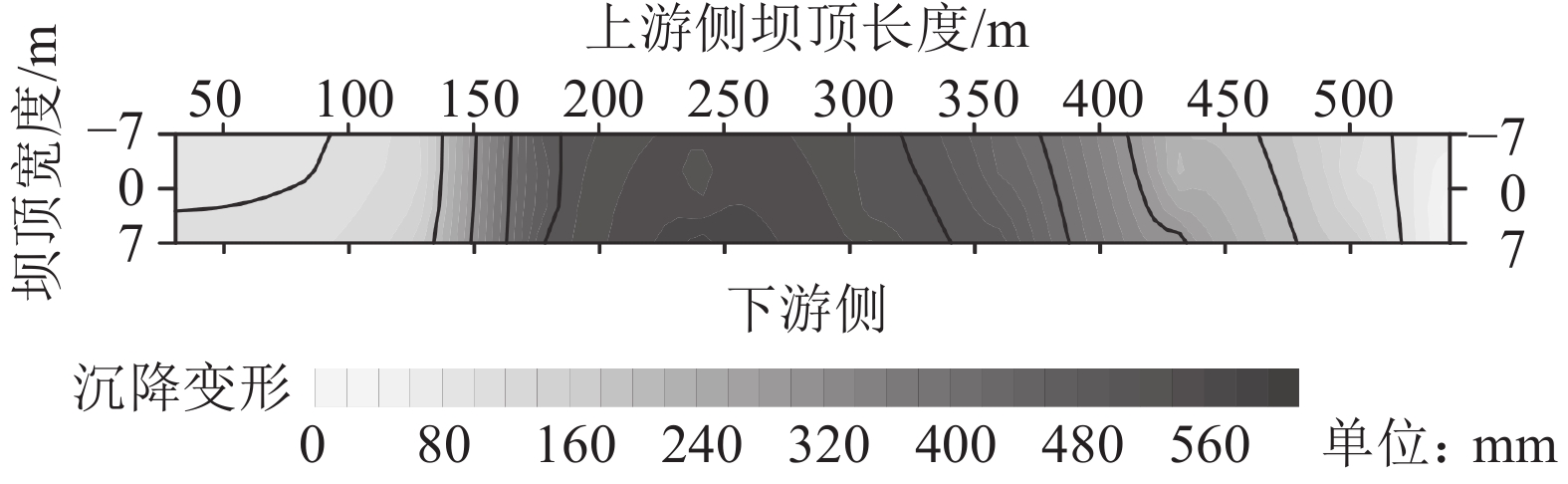 |
| 图14 基于时空模型拟合的坝顶2010年8月26日沉降变形等值线 Fig. 14 Contour line of deformation settlement on the dam crest based on spatial temporal model on August 26th, 2010 |
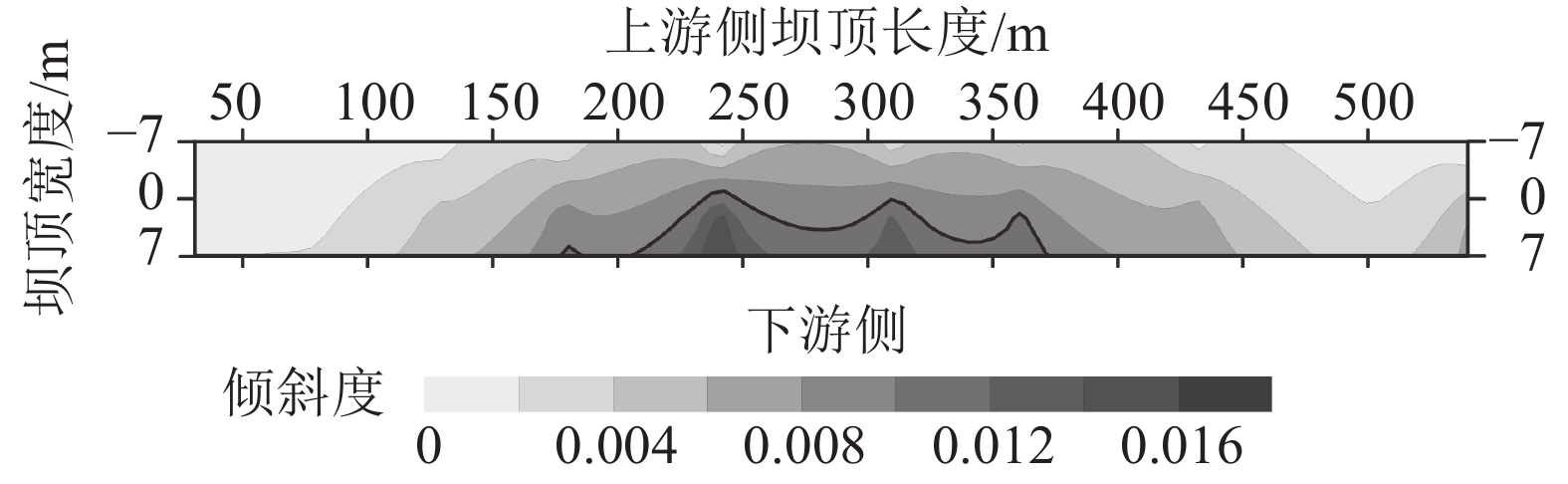 |
| 图15 基于时空模型拟合的坝顶2010年8月26日沉降变形倾度等值线 Fig. 15 Pitch contour line of deformation settlement on the dam crest based on spatial temporal model on August 26th, 2010 |
3 结 论
1)采用分离型时空模型的构建方式及单点拟合和空间插值的思路,提出高心墙堆石坝变形时空预测模型。通过对瀑布沟高心墙堆石坝原观变形分析表明,该模型在时间拟合和空间插值上均具有较高的精度,实现了基于监测序列的高心墙堆石坝整体变形的3维预测,具有较高的工程应用和推广价值。
2)基于高心墙堆石坝变形的物理成因分析,构建施工期和运行期的单点变形预测模型,通过瀑布沟高心墙堆石坝典型断面测点数据拟合分析与对比表明,所构建模型在兼顾高心墙堆石坝变形物理成因条件下,能较好地模拟和反映测点变形趋势,变形预测精度较高。
3)基于泛克里金插值法构建高心墙堆石坝变形空间插值模型,通过瀑布沟高心墙堆石坝下游堆石区测点沉降变形对比分析表明,该模型能较好地描述大坝3维变形趋势,且精度较高。
| [1] |
顾淦臣,束一鸣,沈长松.土石坝工程经验与创新[M].北京:中国电力出版社,2004.
|
| [2] |
Wu Gaojian. Research on key technologies of high earth rockfill dam construction[J]. Water Conservancy and Hydropower Construction, 2013(4): 1-7. [吴高见. 高土石坝施工关键技术研究[J]. 水利水电施工, 2013(4): 1-7.] |
| [3] |
Xu Zeping. Technologies and geotechnical problems for construction of modern rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(增刊1): 27-33. [徐泽平. 当代高堆石坝建设的关键技术及岩土工程问题[J]. 岩土工程学报, 2011, 33(增刊1): 27-33.] |
| [4] |
Wang Dangzai,Jin Wei.Crack control of high earth core rockfill dam[C].Earth-rockfill Dam Technology Conference in 2012.Beijing:China Electric Power Press,2012:234–238. [王党在,金伟.高土心墙堆石坝裂缝控制[C].2012土石坝技术会议.北京:中国电力出版社,2012.234–238.]
|
| [5] |
顾淦臣. 土石坝的若干新技术(一)[J]. 水利水电科技进展, 1995(1): 11-17. |
| [6] |
Tang Tongzhi, Li Guoying, Xu Zhuqing. Statistic prediction models of settlement for earth-rock dam[J]. Hydro-Science and Engineering, 2001(3): 29-34. [唐彤芝, 李国英, 徐竹青. 土石坝沉降统计预报模型[J]. 水利水运工程学报, 2001(3): 29-34.] |
| [7] |
Wang Pengxu, Song Wenjing. Analysis on the measured settlement and prediction modeling of statistic settlement of Shuibuya CFRD[J]. Journal of Hydroelectric Engineering, 2009, 28(4): 81-85. [王彭煦, 宋文晶. 水布垭面板坝实测沉降分析与堆石坝沉降统计预报模型[J]. 水力发电学报, 2009, 28(4): 81-85.] |
| [8] |
Jiang Jingshan, Li Zongkun. Application of improved genetic algorithm in settlement prediction of rockfill dam[J]. Journal of Zhengzhou University(Engineering Science), 2004, 25(4): 74-77. [姜景山, 李宗坤. 改进的遗传算法在堆石坝沉降预测中的应用[J]. 郑州大学学报(工学版), 2004, 25(4): 74-77.] |
| [9] |
Shen Yi, Guo Jinyun, Zhou Jun. Subsidence predictiom of earth and rockfill dam based on gray model and its improved models[J]. Journal of Shandong University of Technology(Natural Science Edition), 2014, 28(1): 4-9. [沈毅, 郭金运, 周俊. 基于灰色模型及其改进模型的堆石坝沉降预测[J]. 山东理工大学学报(自然科学版), 2014, 28(1): 4-9.] |
| [10] |
Liu Shaofeng. Monitoring model of space displacement field of concrete dam and its application[J]. Journal of Shanghai University(Natural Science Edition), 2003, 9(5): 451-455. [刘绍峰. 混凝土坝空间位移场监测模型的探讨及应用[J]. 上海大学学报(自然科学版), 2003, 9(5): 451-455.] |
| [11] |
Luan Yuanzhong. Time spatial model of dam deformation and the theory of parameter inversion[J]. Dam Observation and Geotechnical Tests, 1998, 22(2): 34-37. [栾元重. 大坝变形的时空模型及参数反演理论[J]. 大坝观测与土工测试, 1998, 22(2): 34-37.] |
| [12] |
Li Yan, Wang Lina. Research of spatio-temporal interpolation algorithm based on time series[J]. Computer Science, 2014, 41(6A): 414-416. [李彦, 王丽娜. 基于时间序列的时空插值算法改进研究[J]. 计算机科学, 2014, 41(6A): 414-416.] |
| [13] |
Zhang Jinping, Zhuang Wankang. Mathematical model of displacement distribution for dam safety monitoring[J]. Journal of Hydraulic Engineering, 1991(5): 28-35. [张进平, 庄万康. 大坝安全监测的位移分布数学模型[J]. 水利学报, 1991(5): 28-35.] |
| [14] |
Huang Ming, Ge Xiurun, Liu Jun. Deformation vector distribution model in dam safety monitoring[J]. Journal of Shanghai Jiaotong University, 2001, 35(4): 514-517. [黄铭, 葛修润, 刘俊. 大坝安全监测的多测点位移向量模型[J]. 上海交通大学学报, 2001, 35(4): 514-517.] |
| [15] |
He Jinping, Li Zhenzhao. Research on mathematical model of multi measurement points of dam structure[J]. Engineering Journal of Wuhan University, 1994, 27(2): 134-142. [何金平, 李珍照. 大坝性态结构多测点数学模型研究[J]. 武汉水利电力大学学报, 1994, 27(2): 134-142.] |
| [16] |
Cesare L D, Myer D E, Posa D. Estimating and modeling space time correlation structures[J]. Statistics & Probability Letters, 2001, 51(1): 9-14. |
| [17] |
Liu Guangmeng, Wang Yunjia, Zhang Hairong. Comparative study of several interpolation methods on spatial analysis[J]. Geomatics World, 2011(3): 41-45. [刘光孟, 汪云甲, 张海荣. 空间分析中几种插值方法的比较研究[J]. 地理信息世界, 2011(3): 41-45.] |
| [18] |
Li Xin, Cheng Guodong, Lu Ling. Comparison of spatial interpolation methods[J]. Advances in Earth Science, 2000, 15(3): 260-265. [李新, 程国栋, 卢玲. 空间插值方法比较[J]. 地球科学进展, 2000, 15(3): 260-265.] |
| [19] |
Hamid A S. Application and evaluation of Kriging and cokriging methods on groundwater depth mapping[J]. Environ Monit Assess, 2008, 138(1/2/3): 357-368. |
| [20] |
Gething P W. A local space-time Kriging approach applied to national outpatient malaria data set[J]. Computer & Geosciences, 2007, 33(10): 1337-1350. |
| [21] |
Wang Jianmin. Moving surface fitting models based on Kriging method[J]. Science of Surveying and Mapping, 2012, 37(4): 160-162. [王建民. 基于Kriging下的移动曲面拟合法研究[J]. 测绘科学, 2012, 37(4): 160-162.] |
| [22] |
Huang Ming, Huang Wei, Liu Jun. Hybrid model for monitoring settlements of embankment dams based on genetic creep theory[J]. Rock and Soil Mechanics, 2004, 25(增刊2): 164-173. [黄铭, 黄伟, 刘俊. 基于遗传蠕变理论的土石坝沉降监测混合模型[J]. 岩土力学, 2004, 25(增刊2): 164-173.] |
| [23] |
Niu Wenjie, Zhu Dapei, Chen Qiming. Research of universal Kriging[J]. Computer Engineering and Applications, 2001, 37(13): 73-75. [牛文杰, 朱大培, 陈其明. 泛克里金插值法的研究[J]. 计算机工程与应用, 2001, 37(13): 73-75. DOI:10.3321/j.issn:1002-8331.2001.13.025] |
| [24] |
Fei Lan, Du Shichang. Flatness error estimation based on universal Kriging interpolation method[J]. Journal of Mechanical Engineering, 2014, 50(15): 127-134. [费兰, 杜世昌. 面向零件平面度误差估计的空间泛克里金插值建模[J]. 机械工程学报, 2014, 50(15): 127-134.] |
 2017, Vol. 49
2017, Vol. 49


