2. 天津财经大学 理工学院,天津 300222
2. School of Sci. and Eng., Tianjin Univ. of Finance and Economics, Tianjin 300222, China
启发式优化算法具有智能性、并行性、渐进性、随机性等基本特点,近年来引起了众多学者的广泛研究,目前已成功应用于科学、工程和金融等领域。然而,传统启发式优化算法(如粒子群算法[1]、遗传算法[2]、调和搜索算法[3]等)在参数依赖性、计算复杂性、收敛速度、优化精度等方面面临许多问题。2011年,潘文超通过模拟果蝇觅食行为提出果蝇优化算法(fruit fly optimization algorithm, FOA)[4–5]。与其他算法相比,FOA具有参数少、计算简单、容易理解等优点,因此已广泛应用于参数优化[6]、PID控制器设计[7]、电力负荷预测[8]等诸多领域。
FOA算法在每次迭代过程中单纯以全局最优点为目标导向,极易陷入局部极值,导致收敛精度较低。文献[9]对FOA算法进行改进,通过动态调整搜索半径提高算法的全局寻优能力,但不足之处在于寻优结果对于搜索半径的依赖性较强,因此算法全局搜索能力较差。针对传统算法极易陷入局部最优的问题,文献[10]提出一种基于近郊区和远郊区的果蝇优化算法,该算法将果蝇在每个维度上的搜索范围分为近郊区和远郊区,通过引入局部最优导向因子动态调整果蝇在不同区域的搜索强度;该算法避免了寻优结果对搜索半径的依赖,但全局搜索结果的稳定性较差。文献[11]通过计算果蝇的适应值大小决定是否进行全局搜索,算法全局优化效果较好,但不足之处是果蝇产生的新位置随机性大,难以有效协调算法的收敛速度及稳定性。文献[12]在果蝇位置更新时引入随机因子,指出使用混沌映射能有效改善算法的优化效果,但果蝇新位置的产生受当前位置影响,因此易导致不稳定的收敛结果。文献[13]引入双子群及维度分区思想,较好地平衡了算法的全局搜索能力和局部搜索能力,但不足之处在于不同类型果蝇种群的规模固定使得算法的灵活性较差。
综上,现有的针对FOA的改进算法普遍面临以下问题:1)在全局搜索时未考虑求解区间内特定区域的特殊性,导致果蝇新位置产生过程具有一定的盲目性,使得算法优化结果不稳定;2)未充分考虑实施全局搜索及局部搜索的临界状态,难以动态协调算法的局部搜索及全局搜索强度。为此,本文对传统算法做出改进,引入群密度的概念,实现了一种基于群密度的果蝇优化算法。具体而言,本文主要贡献如下:1)为提高算法稳定性,提出一种基于最优区间回避的分区采样策略;2)为协调算法的全局搜索能力和局部搜索能力,提出一种基于群密度的种群规模动态调整策略;3)通过典型测试函数及异常检测仿真实验验证了本文在收敛精度、收敛速度、稳定性等方面的有效性。
1 传统果蝇优化算法与粒子群算法、遗传算法等类似,果蝇算法以随机值作为初始位置,在迭代寻优过程中所有个体都飞向到上一代最优个体,并通过在最优个体附近搜索寻找全局最优解。算法主要执行步骤如下:
输入:果蝇种群X={xi}(1<i≤N, N为种群中果蝇数量)、搜索范围[xmin, xmax]、最大迭代次数T。
输出:果蝇最优位置(xb1, xb2)、果蝇最优气味浓度Smellgb。
步骤1:初始化参数。具体包括:果蝇数量N、最大迭代次数T、果蝇最优位置(xb1, xb2)、果蝇最优气味浓度Smellgb(Smellgb=–∞)等。
步骤2:更新每只果蝇xi的位置(xi1, xi2):
| ${x_{i1}} = {x_{{\rm{b}}1}} + {\mathop{\rm Rand}\nolimits} (),{x_{i2}} = {x_{{\rm{b2}}}} + {\mathop{\rm Rand}\nolimits} ()$ | (1) |
其中,Rand()产生一个(0, 1)区间内的随机数。
步骤3:求得xi对应的气味浓度判定值si,如式(2)所示:
| ${d_i} = \sqrt {{x_{i1}}^2 + {x_{i{\rm{2}}}}^2} ,{s_i} = \frac{1}{{{d_i}}}$ | (2) |
步骤4:根据适应度函数Fit求得果蝇xi的气味浓度Smelli:
| $S\!mel{l_i} = Fit\left( {{s_i}} \right)$ | (3) |
步骤5:将气味浓度最大的果蝇对应的位置及气味浓度值分别记为(xm1, xm2)、Smellm。
步骤6:若Smellm>Smellgb,则执行:
| ${x_{{\rm{b1}}}} = {x_{{\rm{m1}}}},\;\;\;{x_{{\rm{b2}}}} = {x_{{\rm{m2}}}}$ | (4) |
步骤7:循环执行步骤2~6直至达到最大迭代次数。
2 本文算法 2.1 算法描述为提高全局搜索能力,文献[10]引入近郊区和远郊区的概念,避免了优化结果对搜索半径的依赖,但在远郊区产生的果蝇新位置仍有较大的随机性。文献[13]综合考虑传统果蝇算法及人工蜂群(artificial bee colony, ABC)算法的优点和不足,提出搜索果蝇和跟随果蝇的概念;基于此,该文提出一种基于维度分区的搜索果蝇位置更新算法。但该算法在分区过程中未考虑果蝇最优位置的特殊性,易导致局部最优位置被重复搜索,继而影响算法的收敛速度及稳定性。为此,本文提出一种基于最优区间回避采样的搜索果蝇位置更新策略。该策略首先在每次迭代过程中获得表现最优的前m只果蝇构造最优果蝇组,然后根据最优果蝇组中果蝇在每个维度上的取值范围确定最优区间,最后结合文献[13]对最优区间外的其他区间进行分区采样以确定搜索果蝇的新位置。
如图1所示,给定最优果蝇组GB={xi′ }(1<i≤m)、搜索区间[xmin, xmax]、步长l及维度j,按照式(5)计算xi′ 在第j维上的取值xij′ 的最小值wj、最大值zj分别为:
| ${w_j} = \mathop {\min }\limits_{{x_i}^\prime \in GB} \left( {{x_{ij}}^\prime } \right),{{\textit z}_j} = \mathop {\max }\limits_{{x_i}^\prime \in GB} \left( {{x_{ij}}^\prime } \right)$ | (5) |
 |
| 图1 基于最优区间回避的分区采样过程示意 Fig. 1 Process of optimal interval avoidance based partition sampling |
为此,将区间[wj, zj]定义为果蝇在第j维上的最优区间。由文献[13]可知,跟随果蝇的精细化搜索过程已涵盖针对最优区间的搜索,因此,本文中搜索果蝇将回避针对区间[wj, zj]的搜索,而只对区间[xmin, wj)、(zj, xmax]进行分区采样,以提升算法的全局搜索稳定性。给定采样次数g(本文取g=10)、果蝇适应值计算函数Fit,以最大化问题为例给出基于最优区间回避分区采样的搜索果蝇位置更新过程:
输入:搜索果蝇xi在维度j上的分量xij、适应值函数Fit、采样次数g、最优区间[wj, zj]。
输出:位置更新后的搜索果蝇
1. 初始化xi对应的最大适应值Fb、xi在第j维上的最优取值tb及采样步长l:
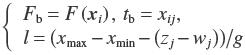
|
(6) |
2. for k=1∶1∶g
| $\quad\quad 3.\; {x_{ijk}}{\rm{ = }}{x_{{\rm{min}}}}{\rm{ + }}\left( {k{\rm{ - 1}}} \right) \times l{\rm{ + }}l \times {\mathop{\rm Rand}\nolimits} () \quad\quad\quad\quad $ | (7) |
4. if xijk>wj
| $ \quad\quad 5. \; {x_{ijk}} = {x_{ijk}} + \left( {{{\textit z}_j} - {w_j}} \right)\quad\quad\quad\quad\quad\quad\quad\quad $ | (8) |
6. end if
| $\quad\quad 7. \; {x_{ij}} = {x_{ijk}},\;\;{F_{ijk}} = Fit\left( {{x_i}} \right)\quad\quad\quad\quad\quad\quad\quad $ | (9) |
8. if
9.
10. end if
11. end for
12.
文献[13]使用搜索果蝇和跟随果蝇协调种群的全局搜索能力和局部搜索能力,但两类种群规模固定,难以根据算法收敛情况实现种群规模的动态调整。为此,定义群密度概念,通过计算跟随果蝇种群的收敛情况动态调整两类种群的规模。给定搜索果蝇种群U={x1, x2, ···, xP}(P为搜索果蝇数目)、跟随果蝇种群V={xP+1, xP+2, ···, xN},群密度σ可通过式(10)获得:
| $\sigma = \sqrt {\frac{1}{{\left( {{x_{\max }} - {x_{\min }}} \right) \times \left( {N - P} \right) \times D}}\sum\limits_{j = 1}^D {{{\sum\limits_{i = P + 1}^N {\left| {{x_{ij}} - {\mu _j}} \right|^{\rm{2}}} }}} }\!\!\!\!\!\!\!\!\!\!\! $ | (10) |
式中,
输入:果蝇种群X={xi}(1<i≤N, N为种群中果蝇数量);搜索范围[xmin, xmax];最大迭代次数T;群密度阈值thu、thl;位置向量维度D;搜索半径r最大值rmax、最小值rmin。
输出:果蝇全局最优位置向量xbp。
1. 初始化果蝇种群X、搜索果蝇种群U={x1, x2, ···,
2. for xi∈X,按照式(11)随机生成xi的位置:
| ${x_{ij}} = {x_{{\rm{min}}}} + \left( {{x_{\max }} - {x_{{\rm{min}}}}} \right) \times {\rm{Rand}}(),\;0 \le j < D$ | (11) |
式中,xij为果蝇xi的第j维数值。
3. end for
4. 设置迭代次数t=0。
5. while(t<T)
6. 获得最优果蝇组GB。
7. for each xi∈U
8. 按照式(12)产生搜索果蝇位置向量维度j:
| $j = \left\lfloor {10\;000 \times {\mathop{\rm Rand}\nolimits} \left( {} \right)} \right\rfloor \bmod D$ | (12) |
9. 利用基于最优区间回避分区采样的搜索果蝇 位置更新策略确定xij值。
10. end for
11. for each xi∈V
12. 按照式(12)产生跟随果蝇位置向量维度j。
13. 按照式(13)计算跟随果蝇维度分量xij值:
| ${x_{ij}} = {x_{{\rm{b}}j}} + r \times {\left( { - 1} \right)^{\left\lfloor {{\mathop{\rm Rand}\nolimits} \left( {} \right) \times 10\;000} \right\rfloor }} \times {\mathop{\rm Rand}\nolimits} ()$ | (13) |
式中,xbj为xbp的第j维分量。
14. end for
15. 更新全局最优果蝇xbp及搜索半径r。
16. 按照式(10)计算搜索果蝇群密度σ。
17. if σ>thu,
18. P=Pm。
19. end if
20. if σ<thl
21. P=N–Pm, r=rmax。
22. end if
23. t++。
24. end while
其中,Pm为搜索果蝇数目最小值,r为动态搜索半径,更新过程如式(14)所示[9]:
| $r{\rm{ = }}{r_{{\rm{max}}}} \times {\rm{exp}}\left( {\log \left( {\frac{{{r_{\min }}}}{{{r_{\max }}}}} \right) \times \frac{t}{{{t_{\max }}}}} \right)$ | (14) |
式中,rmin=0.001,rmax=(xmax–xmin)/2。
可见,与IFOA[11]、cFOA[12]、DPFOA[13]等算法相比,本文基于群密度改进果蝇优化算法具有两大特点:1)第9行中,通过实施基于最优区间回避分区采样的搜索果蝇位置更新策略,避免传统Rand函数、混沌映射函数等方法因随机性较大而带来的收敛结果不稳定的问题;2)第16~22行中,根据果蝇群密度大小实现不同类型果蝇种群规模的动态调整,在保证精细化搜索的同时提高算法全局搜索能力。
2.2 时间复杂度分析本文基于群密度改进果蝇优化算法中,第1~4行为种群初始化过程,对应的时间复杂度为:
| $T{C_{\rm{1}}} = {\rm{O}}\left( {D \times N} \right)$ | (15) |
第6~24行为果蝇种群位置更新及群密度计算过程,对应时间复杂度为:
| $T{C_{\rm{2}}} = {\mathop{\rm O}\nolimits} \left( {\left( {m \times N + P \times g + \left( {N - P} \right) + D \times N} \right) \times T} \right)\!\!\!\!\! $ | (16) |
其中,P、N分别为搜索果蝇数目及果蝇总数目,m为最优果蝇组中果蝇数目,g为分区采样次数。在此基础上,得到本文算法时间复杂度为:
| $\begin{aligned}[b]TC = & T{C_1} + T{C_{\rm{2}}} = {\mathop{\rm O}\nolimits} \left( {D \times N} + \right.\\& \left. { \left( {m \times N + P \times g + \left( {N - P} \right) + D \times N} \right) \times T} \right)\end{aligned}$ | (17) |
由于m、g均为常数,式(17)可化简为:
| $TC = {\mathop{\rm O}\nolimits} \left( {N \times D \times T} \right)$ | (18) |
用类似的方法分析得FOA、IFFO、IFOA、cFOA及DPFOA对应的时间复杂度分别为TCFOA=O(D×N×T)、TCIFFO=O((D+T)×N)、TCIFOA= O(D×N×T)、TCcFOA=O(D×N×T)、TCDPFOA= O((D+T)×N)。可见,本文算法时间复杂度虽高于IFFO、DPFOA算法,但与FOA、IFOA、cFOA等算法相近,这说明本文算法并未因分区采样及群密度计算过程带来显著的计算开销。
3 实验结果与分析 3.1 实验环境实验硬件环境为Intel core i7-6700 处理器、8.00 G内存,软件环境为Win7的64位操作系统、Matlab 2013。如表1所示,分别选取3个单峰基准函数(F1~F3)、3个多峰基准函数(F4~F6)进行测试[9,13]。选用的对比算法包括FOA[4–5]、IFFO[9]、IFOA[11]、cFOA[12]及DPFOA[13]。设置不同算法对应的果蝇数量N=40、最大迭代次数T=5 000。
| 表1 不同函数公式表示、目标值及目标位置向量 Tab. 1 Formulas, target values and target position vectors of different functions |
 |
3.2 群密度阈值thu、thl的选择
群密度阈值thu、thl的取值大小将影响算法的全局搜索能力和局部搜索能力:若当前密度大于thu,应增加跟随果蝇的数量以提高算法局部搜索能力;若当前密度小于thl,应增加搜索果蝇的数量以提高算法的全局搜索能力。本文以果蝇群体初始化密度均值为基础计算thu,即
| $t{h_{\rm{u}}}{\rm{ = }}\frac{\theta }{{{t_{\rm{e}}}}}\sum\limits_{i = 1}^{{t_{\rm{e}}}} {{\sigma _i}} $ | (19) |
式中:te为实验次数,取te=100;θ为群密度权重控制因子,取θ=0.9;σi为在第i次实验中果蝇群体初始化状态对应的群密度。为获得较为通用的thl值,除3.1节所给出的6个测试函数外,结合文献[9]中的2个单峰函数(Sphere函数与Step函数)及2个多峰函数(Griewank函数与Whitley函数)确定最佳thl。令维度D分别取2、4、6、8、10,当thl∈(0, thu)以特定步长(0.01)递增时统计不同函数对应的最佳适应值均值(Fa)及达到收敛状态对应的迭代次数均值(Nca),结果如图2所示。
 |
| 图2 群密度阈值的选择 Fig. 2 Selection of population density thresholds |
由图2可知:当thl逐渐增加时,Nca值呈增大趋势,原因在于算法过度强调全局搜索性能而弱化了精细化搜索过程;进一步可知,Fa值随thl增加呈现出一定的波动性,但当thl∈[0.02, 0.08]时,Fa值相对较小,说明算法此时能较好地协调全局搜索及局部搜索强度。因此,为保证收敛精度的同时尽可能地减少算法达到收敛所需的迭代次数,本文取thl=0.02并将其应用于后续实验中。
3.3 全局优化能力比较Rand函数[11]、Logistic函数[11]与Circle函数[12]为现有的3种主要全局优化函数。为验证不同方法的全局优化能力,分别使用Rand函数、Logistic函数、Circle函数及本文基于最优区间回避采样的搜索果蝇位置更新策略对复杂的多极值函数F4~F6进行测试,计算100次全局搜索情况下搜索果蝇对应的适应值均值随迭代次数的变化情况,结果如图3所示。由图3可知,随着迭代次数的增加,基于最优区间回避采样的搜索果蝇位置更新策略对应结果下降明显,且在50次迭代后获得适应值均值极小值(0.40);其他方法对应的极小值均大于2,且达到极小值所需的迭代次数明显高于本文。可见,Rand、Logistic、Circle等函数搜索过程随机性较大,致使算法的收敛速度和精度受到显著影响;本文基于最优区间回避采样的搜索策略能较好地保证算法的全局寻优效果,有效提高算法的收敛速度和精度。
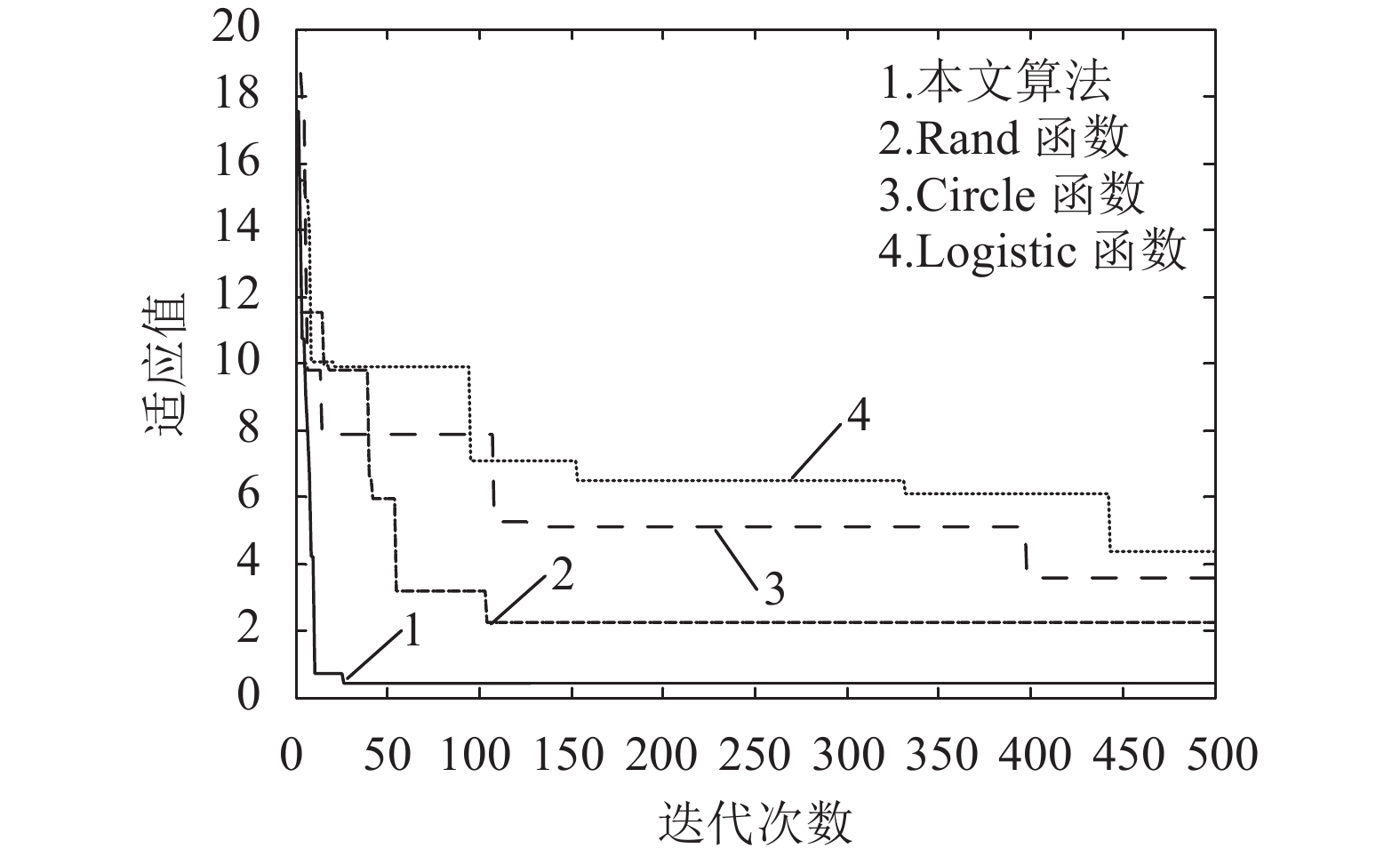 |
| 图3 Rand、Logistic、Circle函数与本文算法比较 Fig. 3 Comparison of the functions of Rand, Logistic and circle and the proposed algorithm |
3.4 不同算法的收敛精度及稳定性比较
针对每种优化算法,设置函数F1~F6的维度D分别取2、4、6、8、10,并分别针对每个D值进行100次实验,最后计算100次实验所得函数的最优值均值μ和最优值标准差ε,结果如表2所示。由表2可知,当处理目标位置分量为负数的函数F1与F6时,FOA及IFOA算法对应的μ值较低;当处理其他函数(F2、F3、F4与F5)时,FOA算法表现最差,IFFO、IFOA、cFOA对应精度与DPFOA近似,但稳定性稍差,说明基于维度分区的果蝇位置更新策略能有效改善寻优结果的稳定性。综合来看,本文算法在处理多峰函数F4~F6时具有一定优势,说明本文基于最优区间回避的分区采样策略及不同种群规模动态调整策略在提高算法收敛精度及稳定性、协调算法局部搜索及全局搜索强度方面起到一定作用。
| 表2 不同算法的优化精度及稳定性比较 Tab. 2 Comparison of optimization accuracy and stability of different algorithms |
 |
3.5 不同算法的收敛速度比较
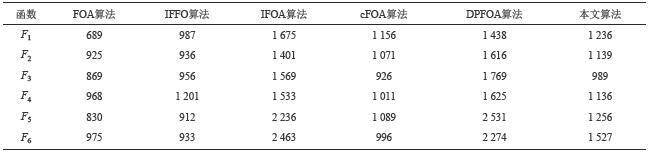
函数F1~F6的维度D分别取2、4、6、8、10前提下,针对每种参数优化算法在每个测试函数上实验100次,统计每种算法达到收敛状态时的平均迭代次数NC并将其作为反映算法收敛速度大小的指标,所得结果如表3所示。由表3可知,FOA收敛最快,IFFO与cFOA算法收敛次数近似且普遍小于其他算法,原因在于这两种算法并未在种群收敛后实施全局搜索,因此虽收敛较快但面临过早陷入局部极值的风险。与FOA、IFFO、cFOA等算法相比,本文因全局搜索操作导致算法对应NC值偏高;与IFOA与DPFOA算法相比,本文算法对应的NC值明显偏低,说明算法对应的收敛速度得到显著改善。结合表2、3可知,本文能在提升算法优化精度的同时有效加快算法全局搜索的效率,这主要是因为:1)基于最优区间回避分区采样的搜索果蝇搜索策略能较好地降低全局搜索的盲目性,提高算法的收敛速度;2)不同类型种群规模动态调整策略能灵活调整跟随果蝇种群规模,使得算法在保证全局寻优效果的前提下较好地实现种群的快速收敛。
| 表3 不同算法对应的平均迭代次数比较 Tab. 3 Comparison of average iterations of different algorithms |
 |
3.6 不同算法的综合性能比较
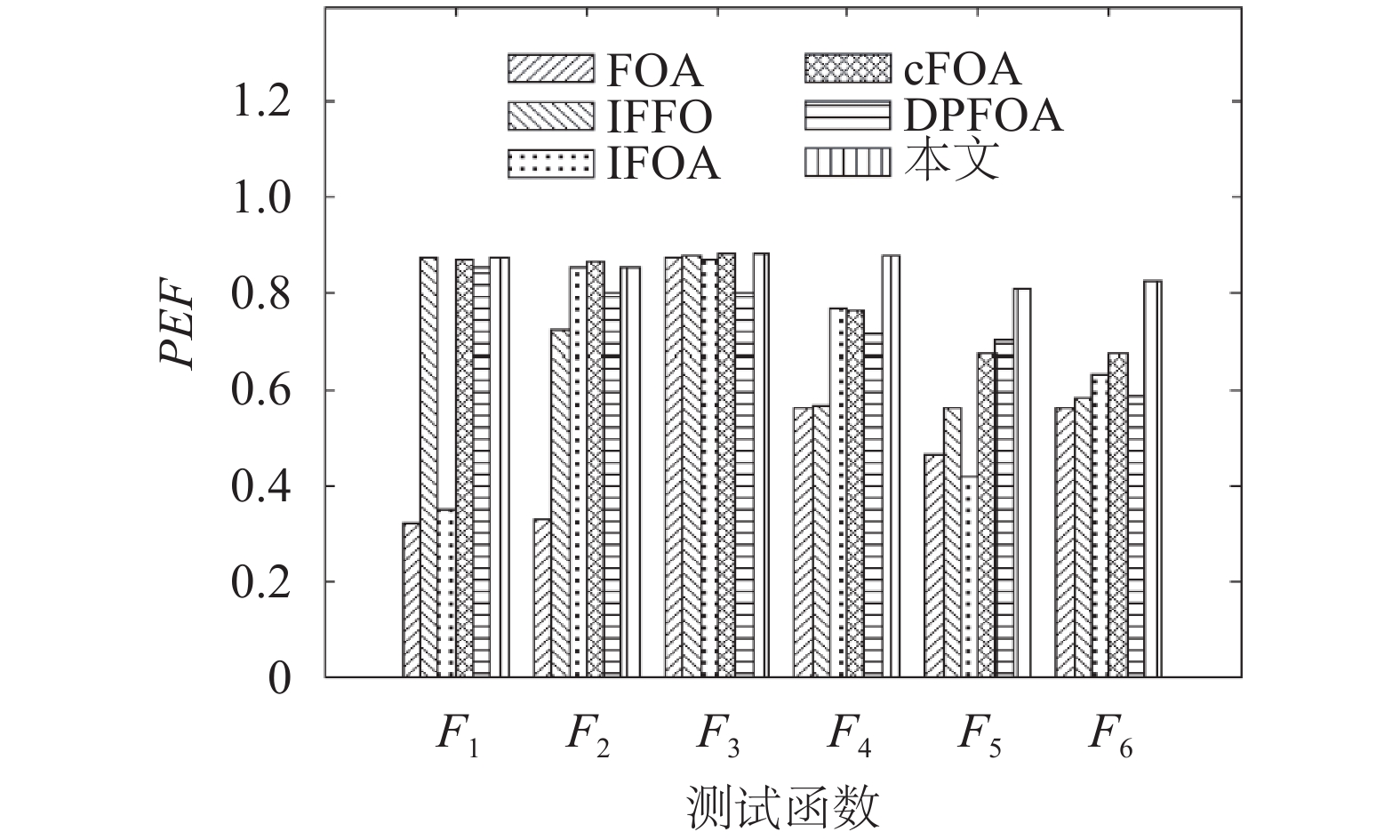
分别针对每个测试函数使用不同优化算法进行100次实验,并按照式(20)~(22)计算不同算法对应的综合性能大小PEF,所得结果如图4所示。
| $PEF = \left( {\sum\limits_{i = 1}^6 {PE{F_i}} } \right)/{\rm{6}}$ | (20) |
| $ \quad\quad\quad\quad\quad\quad PE{F_i} = \left( {{E_{iN}} + {D_{iN}} + {T_{iN}}} \right)/{\rm{3}}$ | (21) |
| ${E_{iN}} = \frac{{{E_{iM}} - {E_i}}}{{{E_{iM}} - {E_{im}}}},{D_{iN}} = \frac{{{D_{iM}} - {D_i}}}{{{D_{iM}} - {D_{im}}}},{T_{iN}} = \frac{{{T_{iM}} - {T_i}}}{{{T_{iM}} - {T_{im}}}}$ | (22) |
 |
| 图4 不同算法的综合性能比较 Fig. 4 Comparison of comprehensive performances of different algorithms |
其中,PEFi为优化算法在在测试函数Fi上的综合性能大小,EiN、DiN、TiN分别为将优化函数对应的最优值均值、标准差均值及收敛次数均值规一化至[0, 1]区间后的结果,Ei、EiM、Eim分别代表在函数Fi上不同优化函数对应的最优值均值、最优值均值最大值及最小值,Di、DiM、Dim分别代表算法在Fi上不同优化函数对应的最优值标准差、最优值标准差最大值及最小值,Ti、TiM、Tim分别代表算法在Fi上不同优化函数对应的收敛次数均值、收敛次数均值最大值及最小值。可见,在处理较为简单的单峰函数时,本文算法优势表现并不明显;但在处理较为复杂的多峰函数时,本文方法所得PEF值普遍多于其他算法,说明本文在保证算法收敛精度的同时有效提高了算法的收敛稳定性和收敛速度,获得更好的综合性能。
3.7 异常检测仿真实验异常检测将偏离正常用户行为视为入侵嫌疑,该技术可以检测到针对系统的未知攻击,于是成为入侵检测技术研究的重点[14]。目前,针对异常检测主要采用机器学习方法,包括神经网络(neural networks, NN)、朴素贝叶斯模型(naive bayesian model, NBM)、支持向量机(support vector machine, SVM)等。在基于SVM的异常检测中,惩罚系数c及RBF核函数中的g系数是影响分类性能的重要参数[15]。c值过大或过小,分类器的泛化能力将变差;g值过大或过小,分类准确率将降低。为验证本文算法的参数优化效果,采用LibSVM作为训练和测试工具,并按照下面步骤对标准数据集KDDcup99[16]进行异常检测实验:首先,参考文献[16]对数据集进行数字化、归一化等预处理;接着,为降低计算耗时,采用信息增益方法从数据集41个特征中选择10个特征并用于后续的SVM训练和分类;最后,以分类准确率为目标函数[17],使用不同算法优化c、g系数。公平起见,设置相关参数如下:c、g最小值xmin=0.000 1,c、g最大值xmax=5,果蝇数量N=10,最大迭代次数T=200。在此基础上,统计各算法中目标函数值随迭代次数的变化情况及收敛状态下对应的c、g值,结果如图5所示。
 |
| 图5 不同算法对应的目标函数值随迭代次数变化情况 Fig. 5 Comparison of objective function values of different algorithms when the iteration number changes |
由图5可知,本文达到收敛状态所需的迭代次数约为100次,明显小于DPFOA算法对应的结果(130次),这说明在迭代前期使用以跟随果蝇为主的优化策略能较明显地提高算法收敛速度。进一步发现,本文在收敛状态下对应的分类精度约为0.971,而其他算法对应的分类精度均小于0.970,这说明本文基于分区采样及群密度的果蝇优化算法能较好地避免局部最优,在获取异常检测分类器重要参数的最佳取值方面起到一定作用。
4 结 论提出了一种基于群密度的改进果蝇优化算法,主要内容包括:1)提出一种基于最优区间回避的分区采样策略更新搜索果蝇的位置,避免全局搜索过程中因盲目产生果蝇新位置而给算法的精度及稳定性带来影响;2)提出一种基于群密度的种群规模动态调整策略,有效协调算法的全局搜索及局部搜索能力。针对6个典型测试函数及异常检测仿真的实验表明,本文算法在收敛精度、收敛速度、稳定性等方面相比传统优化算法具有明显的优势。下一步将研究如何有效提高算法计算效率,并将其扩展到风险评估、工业控制等更多领域。
| [1] |
Liu E, Dong Y, Song J. A modified particle swarm optimization algorithm[J]. Natural Science, 2015, 1(2): 151-155. |
| [2] |
Li Z T, Liu J. A multi-agent genetic algorithm for community detection in complex networks[J]. Physica A:Statistical Mechanics and Its Applications, 2016, 449: 336-347. DOI:10.1016/j.physa.2015.12.126 |
| [3] |
Padberg M.Harmony search algorithms for binary optimization problems[M]//Operations Research Proceedings Zurich:Springer,2012:343–348.
|
| [4] |
Pan Wenchao. Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology (Social Sciences Edition), 2011, 29(4): 1-5. [潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报(社会科学版), 2011, 29(4): 1-5.] |
| [5] |
Pan W T. A new fruit fly optimization algorithm:Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26(2): 69-74. |
| [6] |
Wang X G, Zou Z J. FOA-based SVM parameter optimization and its application in ship manoeuvring prediction[J]. Journal of Shanghai Jiaotong University, 2013, 47(6): 884-888. |
| [7] |
Han J,Wang P,Yang X.Tuning of PID controller based on fruit fly optimization algorithm[C] //International Conference on Mechatronics and Automation.Chengdu:IEEE,2012:409–413.
|
| [8] |
Li H Z, Guo S, Li C J. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2013, 37(2): 378-387. |
| [9] |
Pan Q K, Sang H Y, Duan J H. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62(5): 69-83. |
| [10] |
Wang Youwei, Zhu Jianming, Feng Lizhou. Novel fly optimization algorithm based on near suburb and far suburb[J]. Computer Engineering, 2017, 43(2): 210-214. [王友卫, 朱建明, 凤丽洲. 基于近郊区和远郊区的果蝇优化新算法[J]. 计算机工程, 2017, 43(2): 210-214.] |
| [11] |
Wang L, Shi Y L, Liu S. An improved fruit fly optimization algorithm and its application to joint replenishment problems[J]. Expert Systems with Applications, 2015, 42(9): 4310-4323. DOI:10.1016/j.eswa.2015.01.048 |
| [12] |
Mitic M, Vukovic N, Petrovic M. Chaotic fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2015, 89(C): 446-458. |
| [13] |
Wang Youwei, Feng Lizhou, Zhu Jianming. Novel fruit fly optimization algorithm based on dimension partition[J]. Computer Science, 2016, 43(12): 264-268. [王友卫, 凤丽洲, 朱建明. 基于维度分区的果蝇优化新算法[J]. 计算机科学, 2016, 43(12): 264-268. DOI:10.11896/j.issn.1002-137X.2016.12.048] |
| [14] |
Savage D, Zhang X, Yu X. Anomaly detection in online social networks[J]. Social Networks, 2016, 39(1): 62-70. |
| [15] |
Chang C C, Lin C J. LIBSVM:A library for support vector machines[J]. Acm Transactions on Intelligent Systems & Technology, 2007, 2(3): 27. |
| [16] |
Wu Xiaonian, Peng Xiaojin, Yang Yuyang. Two-level feature selection method based on SVM for intrusion detection[J]. Journal on Communications, 2015, 36(4): 19-26. [武小年, 彭小金, 杨宇洋. 入侵检测中基于SVM的两级特征选择方法[J]. 通信学报, 2015, 36(4): 19-26. DOI:10.11959/j.issn.1000-436x.2015088] |
| [17] |
Yang J, Liu Y, Zhu X. A new feature selection based on comprehensive measurement both in inter-category and intra-category for text classification[J]. Information Processing Manage, 2012, 48(4): 741-754. DOI:10.1016/j.ipm.2011.12.005 |
 2017, Vol. 49
2017, Vol. 49

