平面点集的凸包是指包含平面点集内所有点且顶点属于平面点集的最小简单凸多边形。点集凸包的快速求取是计算几何的基本问题之一。凸包算法在图像处理[1]、地理测绘[2–3]、无线追踪[4]、机器人路径规划[5]、人群追踪[6]等方面都有广泛应用。
Graham[7]最早在1972年提出通过点与点之间的夹角或斜率大小判断一个点是否为凸包上的一点。由此计算凸包的算法不断被改进发展形成预处理算法和典型的凸包算法两大类算法。
Bouattane等[1]使用点集上的点离顶点之间连线的欧氏距离作为判定是否为凸包上的一点;即使通过顶点间的连线划分能够删除一部分点集,但还是有多余的点集需要进一步进行划分判定。王杰臣[2]提出点集分组计算和动态删除判定点的方法以提高算法的执行效率,但动态删除判定点需要一个不断的递归调用,直到没有点可以满足动态删除的条件。
叶绿等[3]针对m划分算法做出改进,提出一种没有使用限制的大n点集凸包的快速算法,然而此算法需要在计算中对点集进行排序处理,在面对数量级过大的点集时,效率会变得比较低,不能满足实际应用需求。
Tang等[4]使用机器学习中的路径规划算法计算凸包,多个不同标准的权重设置将直接影响路径规划算法的结果,且对于平面点集的分布需要多次重规划才能得到最优路径。Liu等[8]使用机器学习方法,通过视线模拟的方法改进了Graham扫描算法,同时提出增量学习的改进算法。然而,运用到了机器学习的思想,难免不会增加算法时间的复杂度,从而导致算法实现困难。
Brönnimann等[9]针对Graham扫描算法做出4种空间有效的改进方法,但这几种算法或运用排序,或划分方法的判定原则复杂,都难以使算法简单高效化。刘人午等[10]提出将数据点进行一次扫描,得到横向和纵向排序点表,再运用增点法逐步从外向内判别数据的改进算法,也需要对部分点集进行排序处理。刘光惠等[11]通过凸多边形的特性,沿着固定的方向对点集进行遍历,提出求解简单多边形凸包的新算法,但此算法首先需要对所有点至少进行一次遍历,算法复杂度较高。
刘斌[12]使用主成分分析法对点集进行预处理,再运用适当的排序规则和凸包边缘点判定原则获取凸包,但此算法较为复杂,对点集进行多次坐标系变换,若实际应用中需要的凸包要求相对初始点集的位置没有发生任何变化,还需将找到的凸包点进行一次反变换,才能满足实际应用的需求。
金文华等[13]的算法需要点集首先是有序的,在排序上会耗费较多时间。Cadenas等[14]通过对横坐标或纵坐标相同的点排序查找其中具有坐标的极值点进行凸包寻找,此预处理算法确实具有很高的效率,但通过比较极值的方法,也需对点集内的部分点集进行遍历比较,此操作需要占用一定的额外时间。Akl等[15]通过连接多个顶点将计算整体凸包的问题划分为多个小问题,然后在各个子块中寻找凸包的边缘。整体来说,通过将点集拆分,能够有效减少排序的时间,但在各个子块中排序的计算量不小。
Wang等[16]使用多目标遗传算法构建凸包,其特点是进化过程中的每代种群均生成大量的可行解可有效减少内部点集,但遗传算法中的非劣等解集的控制比较麻烦,需多次交互才能求取非劣等集。
Belotti等[17]研究了一个凸集和析取集相交的凸包。对于圆锥曲线优化的可行性和唯一性进行了证明。Li等[18]提出一种用最小区域法评定平面度误差的新方法,通过减少约束区域快速确定凸包的有效边界,凸包的边界是通过不断迭代以获取最优的解。如前所述,迭代、排序等算法需占用一定的时间。
Ng等[19]提出一个采样面积最小的含单位正方形上均匀分布的n个采样点的凸包算法,该算法需使用新的坐标系,通过新坐标系中的坐标位置数寻找凸包;但该凸包对原始点集进行了坐标处理,得出的凸包结果还需进行一次反变换才能得到最终结果。
注意到,平面上点集边缘上的点一定具有最小或者最大的坐标值(相对其所在的横坐标或纵坐标),才能使点集边缘将内部点集全部包含起来,如果通过一种简单的判定法将内部无效点集去掉,再把经过预处理剩下的点使用凸包算法计算出其凸包,则可更快地寻找到凸包。
基于这一思想,本文提出一种高效的凸包算法,分为两部分:采用多极限点的平面点集预处理算法和改进的Graham凸包扫描算法。预处理算法对点集进行预处理,寻找点集中的多极限坐标点,把凸包内部的无效点进行去除,只留下符合条件的多极限点,若点集的数量级在105及以上时,这些筛选出的多极限点只占原点集的十万分之一以下,通过将点集进行初步筛选能极大地减轻构建凸包时的计算量,使后续寻找凸包的操作能够在极短时间内完成。
使用本文的预处理算法,针对无倾角的矩形点集,最终能够筛选出4个特殊的双极限点构建矩形凸包,使构建该矩形点集的凸包时间可忽略不计。
此外,提出一种改进的Graham扫描算法,该方法实现简单,算法的时间复杂度低,且构建的凸包准确率始终为100%。
1 相关定义及定理依据 1.1 相关术语定义为更好地说明算法,先对本文涉及的名称进行解释说明。
平面点集:位于一个有界平面上的有限点集。
点集矩阵:把平面点集上的点一一对应到一个m
N(N≤4)极限坐标点:在点集矩阵上的每个有效点所在行(列)均存在最大(或最小)行(列)坐标,具有N个最大(或最小)行(列)坐标的点称为N极限坐标点。
在寻找极限点时,N极限点一定具有M(M<N)极限点的极限特征,故N极限点点集也包含于M极限点点集。存在几个极限值就成为几极限坐标点,见图1。图1中的3极限坐标点在其所在的列中既具有最大列坐标值,也具有最小列坐标值;且在其所在的行中,具有最小的行坐标值。其余的多极限点也在图1中有示例,S、D、T、F分别代表单、双、3、4极限坐标点。
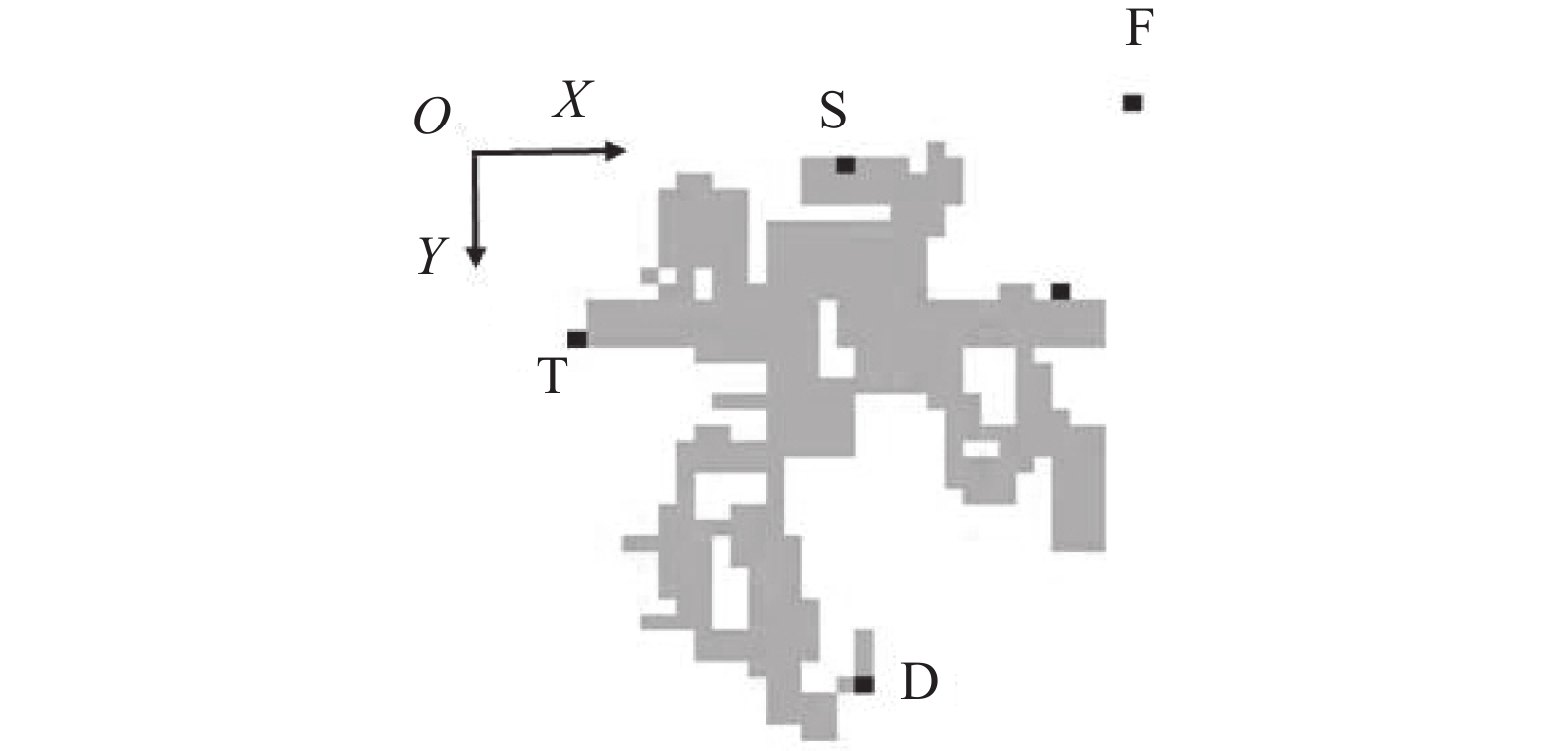 |
| 图1 多极限点说明 Fig. 1 An example of points with extreme coordinates |
1.2 采用双极限点的理论依据
定 理 对于一个平面点集C,设其所有包含的点都保存在一个B=H
下面分2步证明:
Step1:证明所有普通点都位于连接单极限点所成的多边形内部。
假定点集矩阵上任意一个点h(i,j)位于i行、j列。其中:h(i,j)点所在的行、列均具有极大极小的值点,如m(i,a)、n(i,b)、p(c,j)、q(d,j),满足c≤i≤d、a≤j≤b;a和b分别为所有位于第j列的有效点的最小及最大行坐标值,c和d分别为所有位于第i行的有效点的最小及最大列坐标值。通过m、n、p、q这4个单极限坐标点就可以画一个多边形把点h(i,j)包含在多边形内部。若把所有极限点(包括单极限点和多极限点)用一个闭合曲线连接起来,则所有非极限点都在此闭合曲线内。
Step2:证明所有单极限点都位于连接所有多极限点所形成的多边形内部或位于多边形的边上。
以图2所示的位置关系证明:
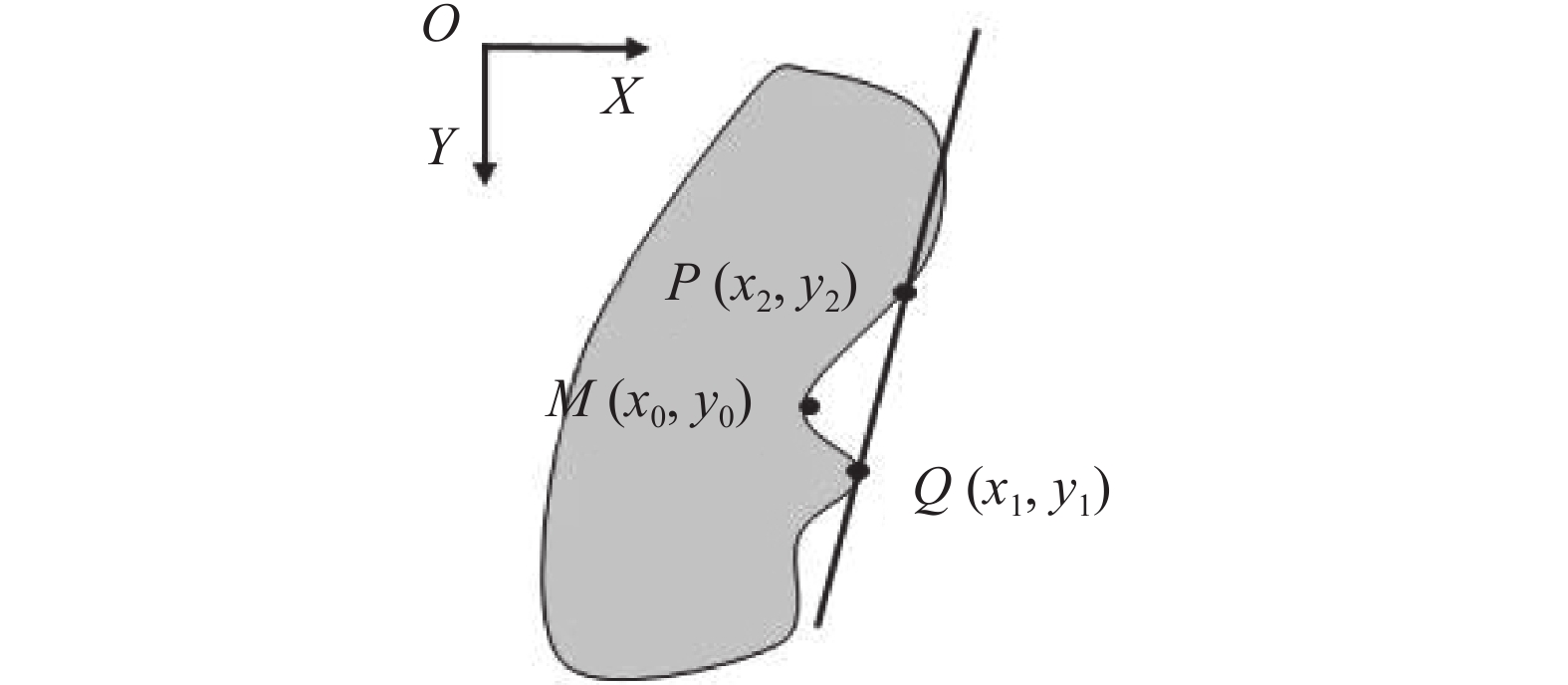 |
| 图2 单极限点与多极限点关系 Fig. 2 Relationship between points with one extreme coordinate and points with extreme coordinates |
在灰色区域的有效点集上取任一单极限点M(x0,y0),P(x2,y2)、Q(x1,y1)为离M点最近的不同侧的两个多极限点,且x0<x1<x2、y1>y0>y2,直线PQ方程为:
| $Y{\rm{ = }}ax + by + c = 0$ | (1) |
其中:
| $a = \left( {{y_2} - {y_1}} \right),$ | (2) |
| $b = \left( {{x_1} - {x_2}} \right),$ | (3) |
| $c = {x_2}{y_1} - {x_1}{y_2}$ | (4) |
将M(x0,y0)点横坐标代入直线PQ方程中,计算可得(y2–y1)x0+(x1–x2)y0+x2y1–x1y2<0,即点M(x0,y0)在直线PQ的下方。在
3极限点和4极限点为满足双极限特征的点,视其为普通双极限点,在Step2中已证明,故不再讨论。
因此,对于一个平面点集C,设其所有包含的点都保存在一个B=H
平面点集内部的点在参与计算凸包时,若不使用一些预处理技术,平面点集内部的绝大部分非凸包点就会在计算凸包时占用过多的计算资源,耗费很大一部分时间。因而在计算凸包时,先对平面点集进行预处理去掉大部分内部点,这在近年来出现的许多凸包算法上有具体体现。根据定理,可直接使用平面点集的双极限点寻找平面点集的凸包。
本文算法流程:首先通过对平面点集进行初步的预处理,再结合改进的Graham算法寻找平面点集的凸包。其算法核心是通过寻找平面点集的双极限坐标点对平面点集进行预处理,如图3所示。
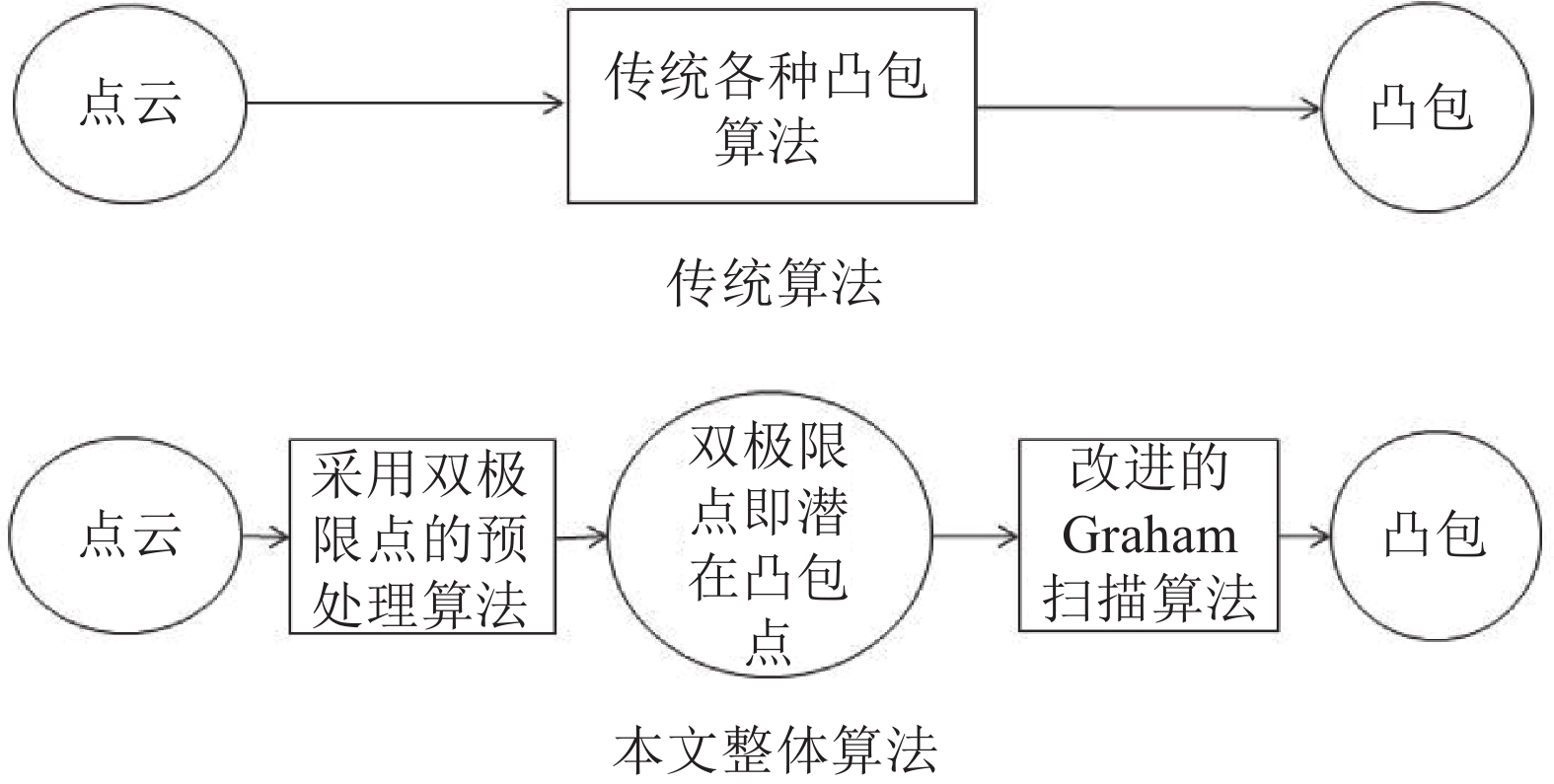 |
| 图3 2种算法总体流程 Fig. 3 Workflow of the two convex hull algorithms |
2.1 采用双极限点的预处理算法
定理说明可通过连接平面点集的所有多极限点画一个多边形把平面点集内部的点包裹起来,凸包一定可以通过这个多边形寻找到。
因此在对平面点集进行预处理时,对所有有效点先经简单判定是否为单极限点,再在这些满足单极限点条件的点集中寻找双极限点。
本文的预处理算法步骤为:
1)对平面点集矩阵中的每一行的每个有效点进行预先扫描,判断其是否为单极限点,若是,标记并存储在一个点集LR中。
2)对平面点集矩阵中每一列的每个有效点进行预先扫描,判断其是否为单极限点,若是,标记并存储在一个点集LC中。
3)从点集LR和LC中选择出双极限点,并存储在点集L中:
| ${{L}} = {{{L}}_{\rm{R}}} \cap {{{L}}_{\rm{C}}}$ | (5) |
图4具体说明了上述过程。
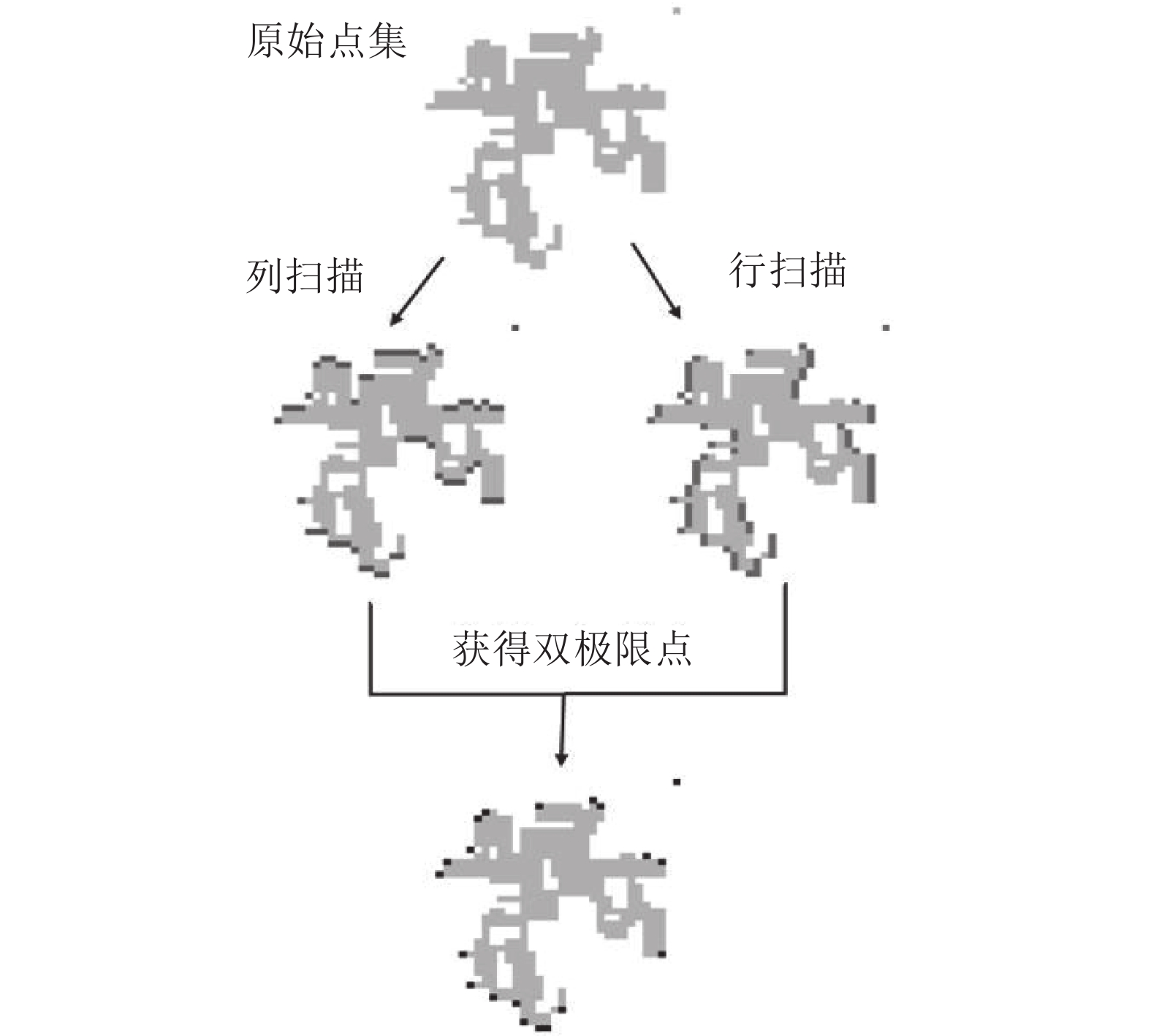 |
| 图4 本文预处理算法步骤 Fig. 4 Steps of proposed preconditioning algorithm |
2.2 改进的Graham扫描算法
经典的Graham[7]扫描算法为先寻找到一个纵坐标最小的点,然后使用这个点作为基点与其他点进行斜率或夹角的比较,通过角度的关系寻找下一个基点,直到所有基点被寻找完,最后连接所有找到的基点,即得到凸包。在判断夹角或者斜率关系时候的判断法较为复杂。
通过对平面点集进行分块处理,就能简化夹角或斜率关系的判断法则,且减轻每次循环的计算量。
首先可以使用平面点集的4个顶点,因为这4个顶点一定是凸包点,将平面点集分成4个基本块(可能会出现不具有顶点的内部块),再在4个基本块上按照一定方向(如逆时针方向)分别寻找顶点之间的凸包线。由于凸包线处于两个相邻顶点之间,相邻凸包关键点连接成的直线斜率应保持同号,那么比较斜率时不必考虑斜率符号的变换。所以,从某个顶点到下一个顶点寻找凸包点时,可只考虑行坐标及列坐标均单调性变化的点。在计算斜率时就不用考虑排序等算法,可使算法复杂度降低到O(n)。改进的Graham扫描算法原理及结果如图5所示。
 |
| 图5 改进的Graham扫描算法原理及结果 Fig. 5 Workflow of the improved Graham scan and convex hull result |
3 实验结果
实验所用平台处理器为Intel i3-2120四核处理器,内存为4 G,算法使用Matlab脚本语言实现。
实验数据来自Singh[20]的一系列动物骨骼原始样本、随机生成的均匀分布的圆形点集和无倾角的矩形点集。实验主要说明本文采用的多极限点预处理算法的优势,并简要比较了文献[12]和本文改进的Graham扫描算法的优劣。
文献[12]已经证明了其算法优于传统算法,故本文仅与文献[14]及文献[12]做比较。文献[12]对点集进行主成分分析法划分处理后,进行一系列坐标转换,使原点及相应的坐标发生变化,凸包结果会旋转一定角度。
3.1 动物骨骼的凸包动物骨骼原始数据样本的3维坐标只精确到小数点后2位,本文算法将其投影到一个矩阵平面,采用精度均为0.000 5的网格,能够避免精度损失,图6为动物骨骼的二值投影矩阵,表1为对动物骨骼进行预处理的筛选结果;图6中对应的名称为表1中第1列的值。
 |
| 图6 动物骨骼投影 Fig. 6 Animals’ skeleton projection images |
| 表1 2种预处理算法候选凸包点点数比较 Tab. 1 Remained points results of the two preconditioning algorithms |
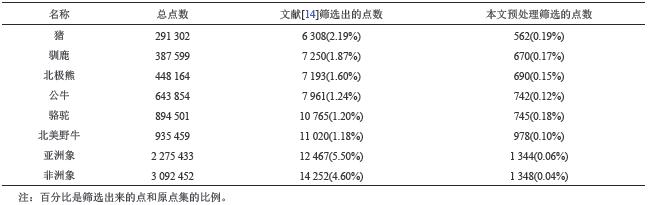 |
由表1可知,经预处理之后,能够略去大量点集,文献[14]剩下的候选凸包点集约占原点集的万分之一,本文算法筛选的候选凸包点集约占原点集的十万分之一。参与构建凸包的有效点数目相对文献[14]而言减少了90%以上。
筛选出候选凸包点后,使用下列4种不同的组合方式计算动物骨骼的凸包。
方式1:使用文献[12]的凸包计算方法。
方式2:使用文献[14]的预处理及文献[12]的凸包计算方法。
方式3:使用本文预处理及本文凸包方法。
方式4:使用本文预处理及文献[12]凸包计算方法
图7为驯鹿骨骼凸包结果。图7中包围在骨骼外部的线条为凸包,尽管图7(a)及(b)在显示上有差异,但两类算法的处理结果精确度一致,在下文会对此做详细说明。
2种预处理算法针对这些骨骼进行预处理的时间均为50~400 ms,本文预处理算法与文献[14]预处理算法相比时间差距范围为100~300 ms。预处理时间对后续构建凸包时间影响不大,故不比较2种预处理算法的处理时间,只对2种算法筛选出的候选凸包点数目进行比较。所用时间和对应的时间对数图分别如表2及图8所示。
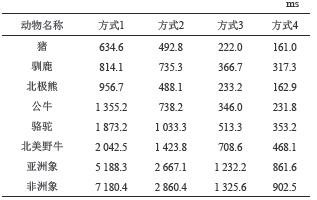
| 表2 4种凸包构建方式对动物骨骼的构建凸包处理的总体时间比较 Tab. 2 Runtime results of four building convex hull algorithms on animals’ skeletons |
 |
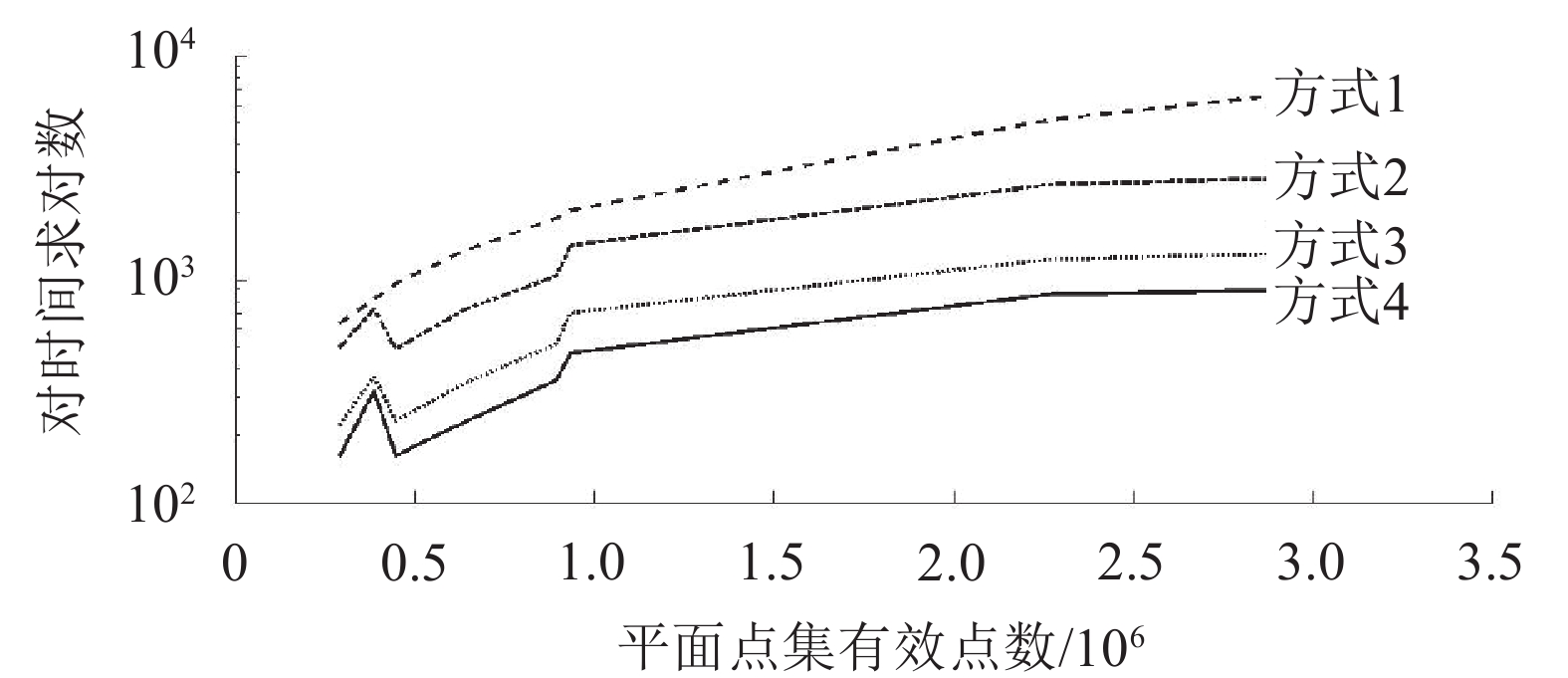 |
| 图8 在对数时间域下对4种方式动物骨骼的运行时间比较 Fig. 8 Runtime results of four methods on animals’ skeletons in the logarithm time field |
表2详细说明了4种不同的运算方式从输入原始点集到获取点集凸包的详细运行时间结果。
由图8可知,在点数的数量级较大时,经过对点集预处理之后,可有效提高计算凸包时的效率。随着点数的数量级不断增长,经2种预处理算法处理后凸包计算时间仍然很小,若直接使用文献[12]的凸包算法,那么受点集数目影响较大。表2中Reindeer数据出现异常及对应的图8中出现的尖锐凸起是由于在平面点集有效点数数目较小,投影所生成的平面矩阵过大,有效点数较少,如图7所示,空白的部分在投影面中占据了超过60%的面积。本文的预处理算法会对2维矩阵平面图的每行、每列进行遍历,对投影面的点集二值矩阵上大量无效的点判别是否为极限点,此步骤会占用较多时间。
从整体计算时间来看,4种计算方式所用时间方式1最多,方式4最少。在均使用了文献[12]的凸包算法构建凸包的方式1、2、3中,方式3使用了本文的预处理方式,相对文献[12]而言,时间平均减少了约6倍;相对使用文献[14]预处理方法的方式2而言,时间平均减少了约3倍。
方式3、4均使用了本文的预处理方法,但方式3结合了文献[12]的方法,方式4结合了本文改进的Graham扫描算法。时间上,方式4平均比本文改进的Graham算法减少了约300 ms。文献[12]的凸包计算方法对原平面点集进行了多次坐标变换,算法实现复杂。如果需要构建的凸包坐标相对于原平面点集而言不能发生变化,需再对生成的凸包点集进行坐标反变换,这限制了文献[12]的应用范围。
虽然本文所实现的改进的Graham扫描算法在运行时间上比文献[12]的方法表现要差一点,但并未对原始点集进行任何坐标变换,能保证算法的时间复杂度为O(n),实现简单,这也是文献[12]所不具有的优点。
3.2 2种算法的精确度比较对于本文提到的2种凸包构建算法,虽然文献[12]中提到的方法对坐标进行了一系列变换,但可把本文算法中计算得到的凸包点坐标经过相同的坐标变换之后,与文献[12]及[14]中的凸包坐标比较(均在同一坐标系下),如图9所示。
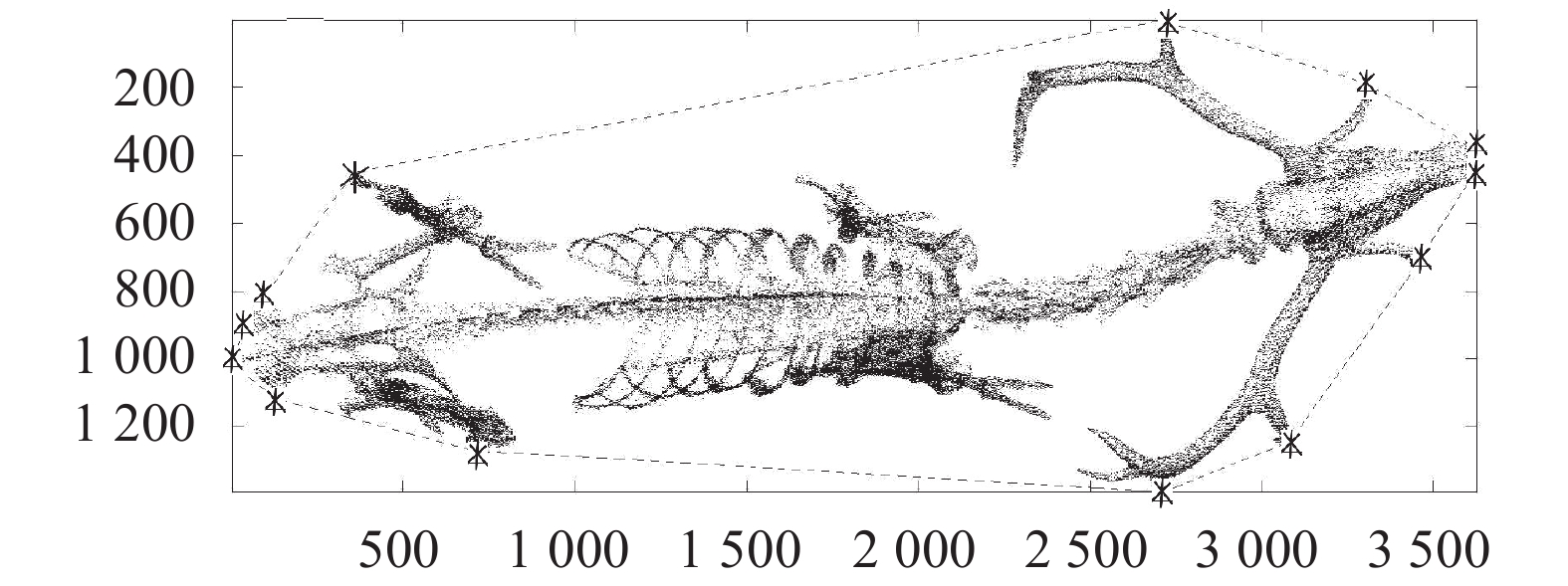 |
| 图9 本文算法的凸包关键点坐标转换到文献[12]后在驯鹿骨骼上的验证结果 Fig. 9 Certificate the convex hull key points of proposed algorithm in the coordination of reference [12] on reindeer skeleton points set |
图9中的“*”即为本文算法寻找到的凸包关键点,虚线点即为根据文献[12]的凸包点所连接成的凸包。将本文找到的凸包关键点通过文献[12]提到的相关坐标转换,并与文献[12]找到的凸包点进行比较,本文算法中的凸包点即为文献[12]中凸包点的子集;且将文献[14]的凸包进行相同的坐标转换后,本文算法得到的凸包点也即为文献[14]的凸包点的子集。即本文预处理之后得到的凸包点与另两种方式比较,能得到更为高效的候选凸包点集,且准确度为100%。
3.3 圆形点集和特殊矩形点集的凸包圆形点集试验是为说明扫描到的所有双极限点均为凸包点。通过随机产生一组圆形点集,每个圆形点集的点数目为1 638 400,位于3 000
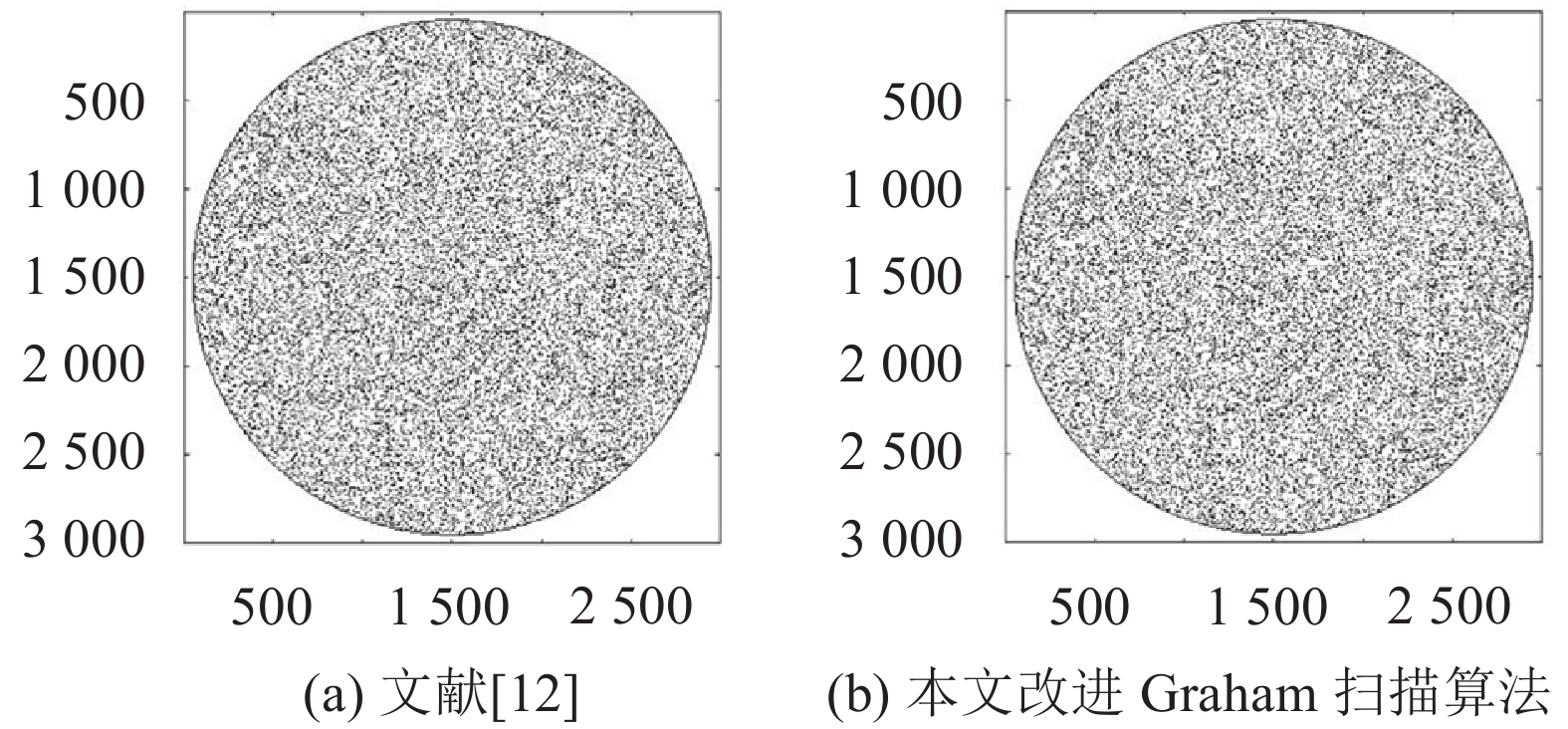 |
| 图10 文献[12]和本文改进Graham扫描算法的凸包结果 Fig. 10 Convex hull of reference [12] and proposed improved Graham scan on circle points set |
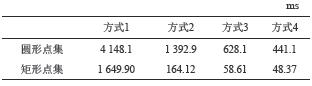
| 表3 4种方式对特殊点集的处理时间 Tab. 3 Time of four algorithms on the two special points sets |
 |
矩形点集试验说明可以通过最少4个双极限点构建凸包。通过随机产生一组矩形点集,每个矩形点集的点数目为819 481,位于1 030
 |
| 图11 文献[12]和本文的改进Graham扫描算法对矩形点集的凸包结果 Fig. 11 Convex hull of reference [12] and proposed improved Graham scan on rectangle points set |
由表3可知,本文的预处理方法即使在最差的情况下(圆形点集),依然具有较高的时间效率,相对直接使用文献[12]方法的方式1而言,方式3时间平均减少了7倍;相对方式2即采用了文献[14]的预处理方法而言,方式3时间平均减少了3倍左右。且方式3与4的整体运行时间依然相差在0.2 s以内,说明本文改进的Graham扫描算法确实表现良好。
特殊矩形点集经各处理方法处理后剩余点数之间的关系如表4所示。
| 表4 4种方式对矩阵点集的处理点数结果 Tab. 4 Points results of four algorithms on rectangle points set |
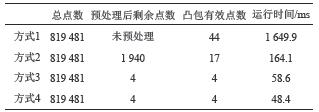 |
由表4可知,对于无倾角的正矩形,在后续步骤中使用凸包构建算法时,参与计算凸包的点数越少,越能够有效地提升计算速度。与方式1的处理时间相比,通过本文预处理方法处理后的方式3求取凸包的整体运行时间整体减少了30倍以上。此特殊的矩形点集也说明针对这类特殊的无倾角正矩形点集,本文的多极限点处理方法可始终保证参与构建矩形凸包的点数目为4。
4 结 论本文提出一种平面点集预处理算法及改进的Graham扫描算法。结合两种方法能够高效简便地计算平面点集的凸包。
其中,采用多极限点对平面点集进行预处理是本文的核心。该预处理算法只对平面点集的多极限点进行筛选,在点集数量级为105时,能筛选掉99.9%以上的点。且可以注意到,有效点的数量级越大,本文的预处理算法能使运算时间减少3倍以上。
本文改进的Graham扫描算法实现简单,效率较高。在求取平面点集的凸包时,如果平面点集的数目比较少,则可以采用本文改进的Graham扫描法,能够准确地找出凸包。在平面点集数目较大时,可以首先使用本文的多极限点预处理算法对点集进行预处理,获取到候选凸包点之后,再使用改进的Graham算法或其他优秀算法如文献[12]的算法求取凸包。
本文预处理算法所采用的思想是基于多极限点的思想,虽然只是针对平面点集,但可推广至3维空间中的凸包面。
3维凸包面可形象化为蒙在某个物体上的一只气球。对于3维空间中一个立方体,可以从6个角度去观察它,构成3维凸包面的点也至少具有一个极限坐标,如果只需要考虑具有3个极限坐标以上的点来构建凸包面,相信也可如2维平面点集一样,筛选掉大量内部的点,这正是下一步要做的工作。
| [1] |
Bouattane O, Elmesbahi J, Rami A. A fast parallel algorithm for convex hull problem of multi-leveled images[J]. Journal of Intelligent & Robotic Systems, 2002, 33(3): 285-299. |
| [2] |
Wang Jiechen. Study of optimizing method for algorithm of minimum convex closure building for 2D spatial data[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(1): 82-86. [王杰臣. 2维空间数据最小凸包生成算法优化[J]. 测绘学报, 2002, 31(1): 82-86.] |
| [3] |
Ye Lu, Zhao Jiasen. A quick algorithm to determine convex hull for a point set in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 319-322. [叶绿, 赵家森. GIS 中点集凸包的快速算法[J]. 测绘学报, 2004, 33(4): 319-322.] |
| [4] |
Tang S H, Motlagh O, Ramli A R. A novel GA-FCM strategy for motion learning and prediction:Application in wireless tracking of intelligent subjects[J]. Arabian Journal for Science and Engineering, 2012, 37(7): 1929-1958. DOI:10.1007/s13369-012-0274-6 |
| [5] |
Escande A, Miossec S, Benallegue M. A strictly convex hull for computing proximity distances with continuous gradients[J]. IEEE Transactions on Robotics, 2014, 30(3): 666-678. DOI:10.1109/TRO.2013.2296332 |
| [6] |
Asghar H J, Li S, Pieprzyk J. Cryptanalysis of the convex hull click human identification protocol[J]. International Journal of Information Security, 2013, 12(2): 83-96. DOI:10.1007/s10207-012-0161-x |
| [7] |
Graham R L. An efficient algorithm for determining the convex hull of a finite planar set[J]. Information Processing Letters, 1972, 1(4): 132-133. DOI:10.1016/0020-0190(72)90045-2 |
| [8] |
Liu R Z, Tang Y Y, Fang B. An enhanced version and an incremental learning version of visual-attention-imitation convex hull algorithm[J]. Neurocomputing, 2014, 133: 231-236. DOI:10.1016/j.neucom.2013.11.013 |
| [9] |
Brönnimann H, Iacono J, Katajainen J. Space-efficient planar convex hull algorithms[J]. Theoretical Computer Science, 2004, 321(1): 25-40. DOI:10.1016/j.tcs.2003.05.004 |
| [10] |
Liu Renwu, Yang Dehong, Li Yan. An improved algorithm for producting minimum convex hull[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 130-133. [刘人午, 杨德宏, 李燕. 一种改进的最小凸包生成算法[J]. 大地测量与地球动力学, 2011, 31(3): 130-133.] |
| [11] |
Liu Guanghui, Chen Chuanbo. New algorithms for computing the convex hulls of a simple polygon and a planar point set[J]. Computer Science, 2007, 34(12): 222-226. [刘光惠, 陈传波. 求解简单多边形和平面点集凸包的新算法[J]. 计算机科学, 2007, 34(12): 222-226. DOI:10.3969/j.issn.1002-137X.2007.12.060] |
| [12] |
Liu Bin. An efficient convex hull algorithm for planar point set based on recursive method[J]. ACTA Automatica Sinica, 2012, 38(8): 1375-1379. [刘斌. 一种高效的平面点集凸包递归算法[J]. 自动化学报, 2012, 38(8): 1375-1379.] |
| [13] |
Jin Wenhua, He Tao. A fast convex hull algorithm of planar point set based on sorted simple polygon[J]. Chinese Journal of Computers, 1998, 21(6): 533-539. [金文华, 何涛. 基于有序简单多边形的平面点集凸包快速求取算法[J]. 计算机学报, 1998, 21(6): 533-539.] |
| [14] |
Cadenas J O, Megson G M, Hendriks C L L. Preconditioning 2D integer data for fast convex hull computations[J]. PloS One, 2016, 11(3): e0149860. DOI:10.1371/journal.pone.0149860 |
| [15] |
Akl S G, Toussaint G T. A fast convex hull algorithm[J]. Information Processing Letters, 1978, 7(5): 219-222. DOI:10.1016/0020-0190(78)90003-0 |
| [16] |
Wang P, Emmerich M, Li R. Convex hull-based multiobjective genetic programming for maximizing receiver operating characteristic performance[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(2): 188-200. DOI:10.1109/TEVC.2014.2305671 |
| [17] |
Belotti P,Góez J C,Pólik I,et al.A conic representation of the convex hull of disjunctive sets and conic cuts for integer second order cone optimization[M]//Numerical Analysis and Optimization.Abingdon:Springer International Publishing,2015:1–35.
|
| [18] |
Li P, Ding X M, Tan J B. A hybrid method based on reduced constraint region and convex-hull edge for flatness error evaluation[J]. Precision Engineering, 2016, 45: 168-175. DOI:10.1016/j.precisioneng.2016.02.008 |
| [19] |
Ng C T, Lim J, Lee K E. A fast algorithm to sample the number of vertexes and the area of the random convex hull on the unit square[J]. Computational Statistics, 2014, 29(5): 1187-1205. DOI:10.1007/s00180-014-0486-1 |
| [20] |
Singh J. FigShare[J]. Journal of Pharmacology and Pharmacotherapeutics, 2011, 2(2): 138. DOI:10.4103/0976-500X.81919 |
 2017, Vol. 49
2017, Vol. 49



