高水头、大流量、高泄洪功率是中国大型水利枢纽工程的普遍特点。因此，泄洪消能建筑物的安全性面临较为严峻的考验^[1]，并得到设计、施工和科研单位的普遍重视。工程实践中，许多泄洪消能建筑物，如闸门^[2–3]、闸墩^[4–6]、表中孔^[7]、导墙^[8–9]、边墙^[10]和水垫塘底板^[11–13]等均发生过不同程度的破坏。随着对各类结构破坏机理的深入研究，通过优化设计、改进施工等措施基本能避免上述工程问题^[14–15]。然而，正如高坝泄流安全领域相关专家指出，随着水利枢纽建设技术成熟，问题多发地由于引起广泛关注而一般不出现问题，不为人注意或普遍认为安全度较高的地方反而易发生工程问题。近年来，有某水利枢纽水垫塘护坡坡脚及相邻马道发生大规模破碎现象，其破坏原因至今未有令人信服的结论。

乌东德水垫塘护坡结构模型试验研究表明，与水垫塘底板破坏机理不同，导致护坡板块破坏的上举力不仅来自于背/迎水面瞬时脉压差，还来自于渗流压力，水垫塘波面高度是影响护坡板块所受渗流压力的主要因素。相对于水垫塘波面研究的缺乏，海浪波面高度的研究较为充分。由于水垫塘波面与海浪波面具有相同的表现形式（均为水面波动），因此可以考虑采用海浪波面概率模型描述水垫塘波面。传统观点基于线性理论，根据中心极限定理，推导出海浪波面高度服从正态分布^[16]。然而，海浪波面变化理论上是非线性的^[17–18]，试验观测也反复证明用正态分布描述海浪波面具有明显的偏差^[19–20]。水垫塘波面又受到水舌入水角度、速度、位置、空中碰撞、入水形状、破碎液滴跌落、边界条件及水面波动的反射、干涉和衍射等因素影响，相对主要由空气运动引起的海浪波面而言，非线性性质更加明显。本文采用基于非线性理论形成并逐渐发展的Gram-Charlier概率模型^{[17,19,21–22]}描述水垫塘波面高度，取得了良好效果，并考虑护坡板块受力条件和破坏机理，对传统的水垫塘底板安全监控指标的适用性和可能产生的偏差进行分析。研究结果将对护坡板块的设计和水垫塘实时安全监控系统的构建提供理论支撑。

乌东德水电站坝高达270 m，装机容量为1.02 $ \times $ 10⁷ kW。坝身为混凝土双曲拱坝，泄水孔采用5表6中的布置方式。坝身设计泄流量20 185 m³/s，其中表孔泄量10 793 m³/s，中孔泄量9 392 m³/s。下游利用水垫塘消能，水垫塘尾部设置碾压混凝土重力式二道坝；水垫塘深度接近100 m，基岩条件良好，抗冲流速8～10 m/s，采用护坡不护底形式，下游边坡开挖量较少，护坡板块与天然边坡相互贴合，多数护坡板块为空间曲面结构。

乌东德水弹性模型比尺为1∶100，满足水力学及结构动力学条件相似^[23]，模拟范围包含拱坝坝身、水垫塘、二道坝和地基；地基范围为坝肩左右90 m，坝踵向上游110 m，坝趾向下游350 m，地基深度190 m，模型从坝肩两侧边界向坝身方向削角25°，呈倒梯形。图1为乌东德水弹性模型照片。

图1(Fig. 1)

图1 乌东德水弹性模型 Fig. 1 Hydroelastic model of Wudongde project

试验中最不利工况下板块的设计和波高仪的布置如图2所示。板块底部、左侧和右侧止水完好，顶部止水失效，排水设施失效，波高仪竖直布置在靠近脉压测点处。这种情况下，水垫塘内涌浪或溅水可以通过板块顶部失效止水渗入板块与基岩间隙，一部分脉动压力也可由此传入，而排水通道全部失效，在水垫塘内水位上下波动的瞬间，渗水无法排出。试验中，护坡板块与基岩贴合处经严格整平，在板块四周粘贴0.2 mm厚的紫铜片，使间隙宽度尽量保持在0.2 mm，避免由于间隙太小致使水流不容易渗入或毛细力大于重力起主导作用和间隙太大致使渗水排出时间延长且缝隙不易封堵等问题。为捕捉不同高程处的压强时程，在板块迎、背水面由上至下分别布置6个测点，由于高程最低处的测点能够更完整地反映护坡板块迎、背水面水位差造成的渗流压力，因此后续分析中主要用到了测点K和L的压强数据。

图2(Fig. 2)

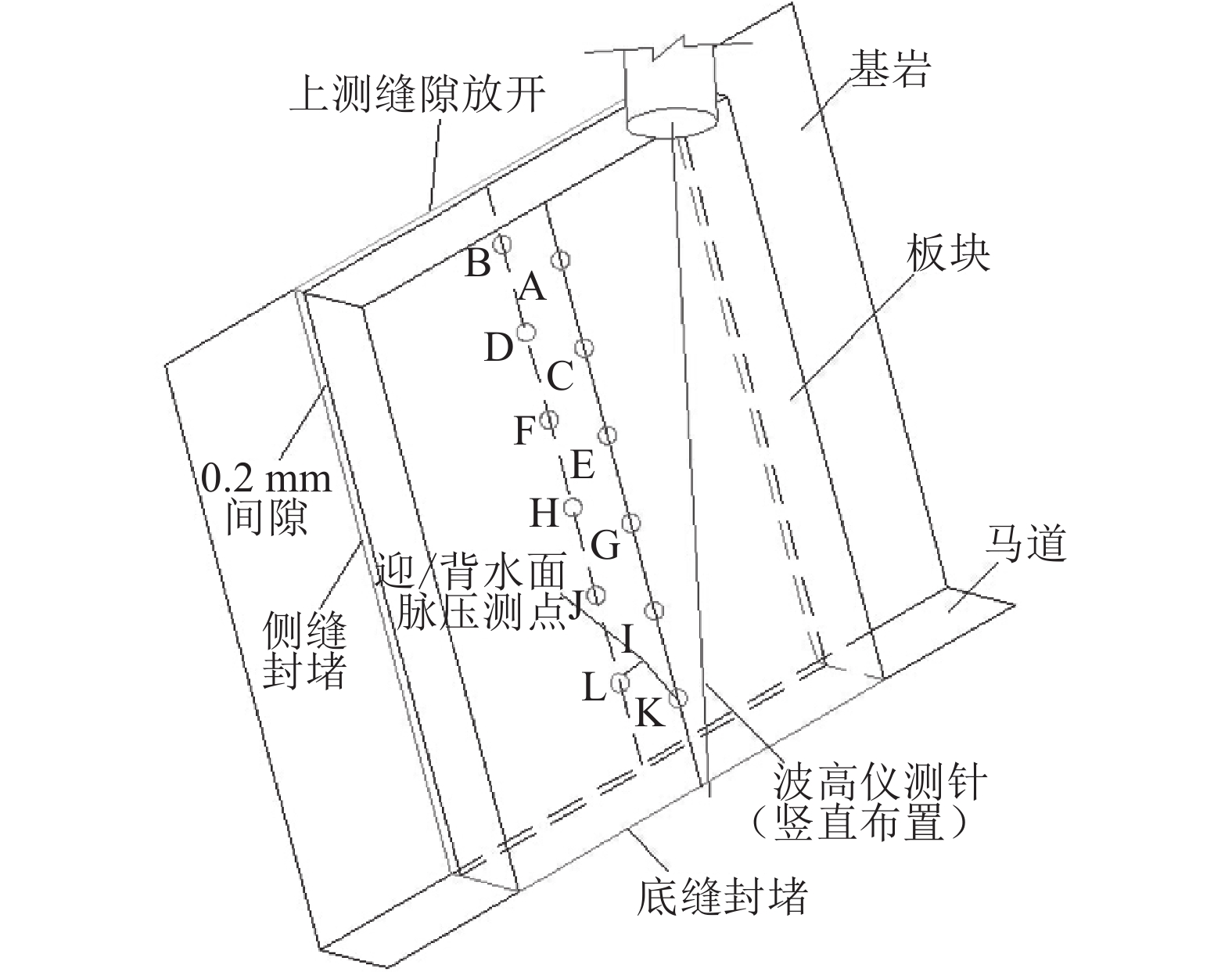图2 板块设计和波高仪布置 Fig. 2 Slope lining plate design and the arrangement of wave height measuring instrument

表1给出了部分压强与水垫塘内水面波高同步测试试验工况，现选取工况1数据进行分析，如图3所示。

表1(Tab. 1)

表1 试验工况 Tab. 1 Experimental conditions

表1 试验工况 Tab. 1 Experimental conditions 工况 上游水位/m 坝身泄量/(m3·s–1) 下游水位/m 开孔方式 表孔 中孔 1 975.00 7 270.00 827.19 全开 全关 2 975.00 16 421.50 847.89 全开 全开 3 979.38 20 185.00 849.73 全开 全开

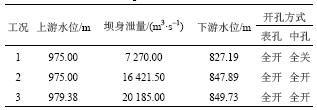板块与基岩间隙内由于排水失效导致渗水无法及时排出，当水充满间隙空间后水量不再增加，即测点上方水深不再变化，而脉动压力仍不时沿顶部缝隙传入，如图3（a）所示，测点L压强时程基本呈平稳状态，同时伴随间歇性的正向脉压波动。迎水面测点压强时程不仅体现水流脉动情况，同时也反映了测点上方水位的变化。对波面高度的同步测量发现，其变化趋势与迎水面K点压强的变化趋势相同，但局部变化不完全一致，这种差别是由水流脉动导致的。因此，分析认为护坡板块迎水面所受压强与测点上方水位变化趋势一致，水流脉动对局部波动情况产生影响，但这种影响不足以改变整体趋势。

图3(Fig. 3)

图3 板块所受压强与波面高度的关系（工况1） Fig. 3 Relationship between the pressure on the plate and the wave surface elevation (case 1)

由于背水面所受压强整体波动不大，因此，板块所受背/迎水面压强差的变化趋势与迎水面压强相反，也即与脉压测点附近水垫塘内波面高度变化趋势相反，这一点在图3中有所反映。图4中给出了不同工况下波面高度、迎水面压强和背/迎水面压强差时程的平滑曲线，以更清楚地说明波面高度对板块所受压强的影响。

图4(Fig. 4)

图4 波面高度对板块所受压强的影响 Fig. 4 Effect of the wave surface elevation on the pressure acting on the plate

如图4所示，各工况下波面高度、迎水面压强和背/迎水面压强差时程曲线变化趋势与前述分析较为符合，说明水垫塘内水位变化对板块所受压强差产生了重要贡献，这部分贡献即为渗流压力。由此可知，护坡板块破坏机理与传统的水垫塘底板破坏机理既有相似也有区别。相似之处在于，二者均是由迎、背水面压强不平衡引起的；区别之处在于底板的不平衡压强来源于水流脉动沿缝隙的传播，而护坡的不平衡压强来源于迎、背水面水位差导致的渗流压力和水流脉压不相关性导致的瞬时压强差^[24]。

图5描述了护坡板块的破坏机理，其中锚固力和重力对板块稳定起到积极作用；迎、背水面脉动压力由于间隙和塘内水体连通性较差，可以看作2个相互独立的随机过程^[24]，一般认为其服从正态分布^[11–13,23]；渗流压力主要是由板块迎、背水面水位差所产生，由于间隙内水位不变，即主要取决于塘内波面高度。由塘内水位波动产生的渗流压力在水工结构安全分析中考虑较少，为合理地评估护坡的安全性，需要对渗流压力的取值空间及概率分布情况有准确的认识。

图5(Fig. 5)

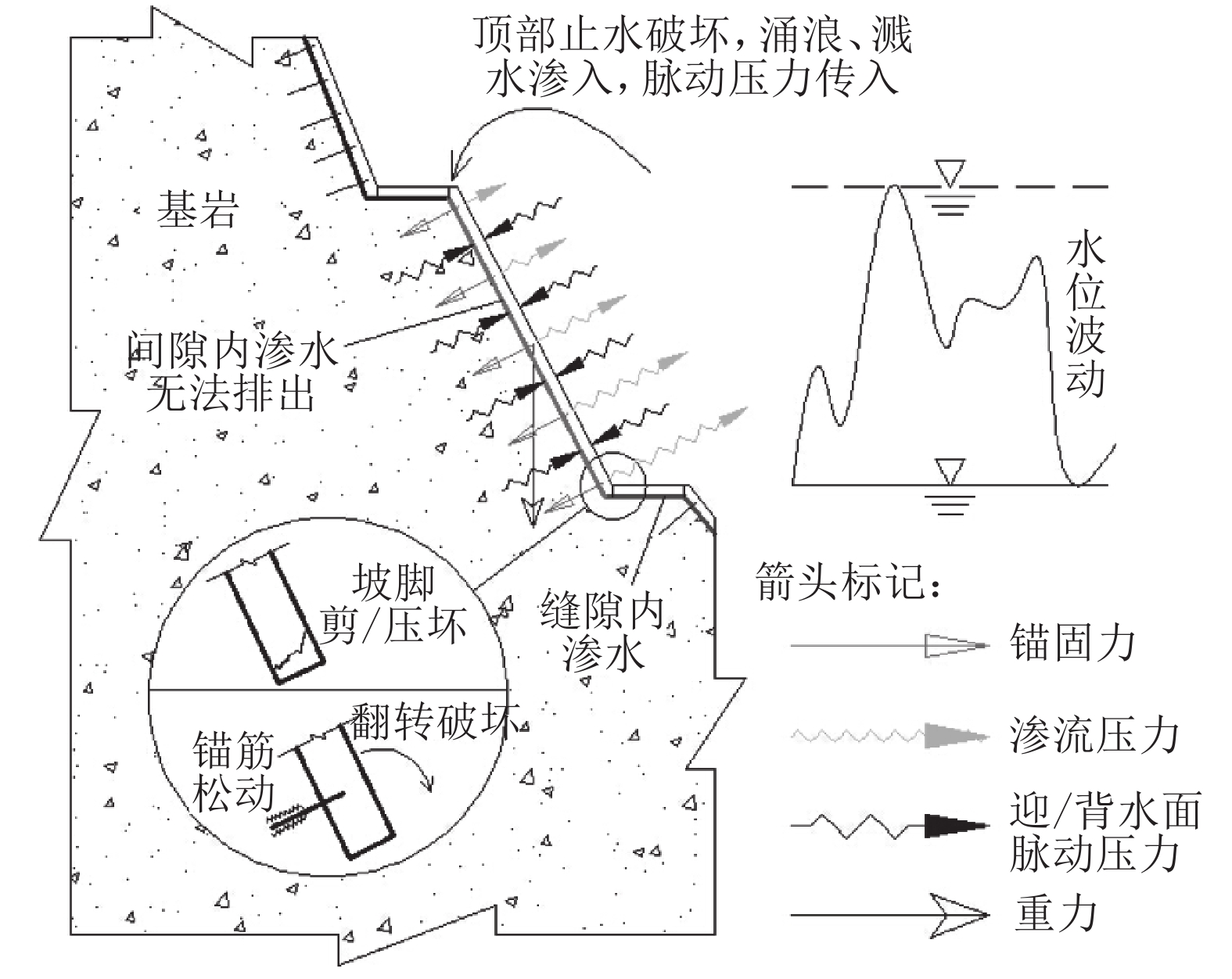图5 护坡板块破坏机理 Fig. 5 Failure mechanism of the slope lining plate

为整体把握水垫塘内波面高度分布，在近坝平静水面区域和表中孔水舌入水区之外布置9个水位测点。图6给出了工况2条件下各测点波面高度的最大值和均方根，分别体现了水位能够达到的最大值及其波动情况。在不同工况下，波面高度分布具有一般规律：近坝区水面平静，水位最大值和均方根均较小；水舌落水点两侧最大波面较高且波动剧烈；临近水垫塘处水位产生一定雍高，但波面波动较为平缓。但是由于护坡结构破坏机理的复杂性，并不能简单地由水位波动最大值或均方根判断某处的护坡板块承受更大的破坏风险，因为不能从上述2个指标中直接得出板块背、迎水面的最大水位差。导致护坡破坏的瞬时脉压差和渗流压力均来源于板块与基岩间隙内的渗水，因此保护板块不受破坏的核心在于尽量避免水流渗入护坡背面，同时做好排水措施，一旦止水发生破坏能够及时将渗水排出。

图6(Fig. 6)

图6 工况2水垫塘波面高度空间分布 Fig. 6 Space distribution for the wave surface elevation in the cushion pool in case 2

目前水垫塘内波面高度的研究较为缺乏，而在海浪统计学研究中，关于波面高度变化规律的成果则较多。传统的研究观点依据线性理论，把实际发生的随机波面简化为无穷多个独立简谐波动的叠加，再根据中心极限定理，在数学上可以严格推导出波面高度服从正态分布。然而，大量外海观测和室内试验表明用正态分布描述海浪波面高度具有一定偏差，因为海浪波面本质上是非线性的。Huang等依据非线性理论推导出了更加准确的Gram-Charlier级数波面分布^[17,19]，如式（1）～（5）所示：

其中， ${P}\left( \eta \right)$ 表示波高η的概率密度，σ表示波面高度的标准差，m_r表示波面高度的r阶中心矩。

海浪波面的形成主要受空气运动的影响，而水垫塘波面与水舌淹没射流的入水角度、速度、位置、空中碰撞、入水形状、破碎液滴跌落、边界条件及水面波动的反射、干涉和衍射等多种因素相关，其非线性性质更加明显。因此采用基于非线性原理的Gram-Charlier级数分布描述水垫塘波面高度。Huang等^[17,19,21]试验研究表明式（1）中参数角标取至4时，概率分布函数与实际吻合最好。

根据不同工况下各测点的波面高度数据，可知其概率密度曲线相对正态分布具有向x轴负方向偏移的特点，体现在波浪外观特征上则为波峰较陡，波谷平缓的非对称特征。因此正态分布常造成对波面高度较大值考虑不足，而对较小值发生概率估计偏大的情况，这一点与海浪波面研究情况相似^[18,20]。如图7所示，采用Gram-Charlier级数分布，可对实际概率分布曲线最大值较高和向左偏移的情况有更好的拟合效果。由于篇幅所限，图7中只给出了工况2条件下3个测点数据的拟合情况，通过对比分析其他工况下各测点的拟合情况，发现Gram-Charlier级数的拟合效果均好于正态分布。

图7(Fig. 7)

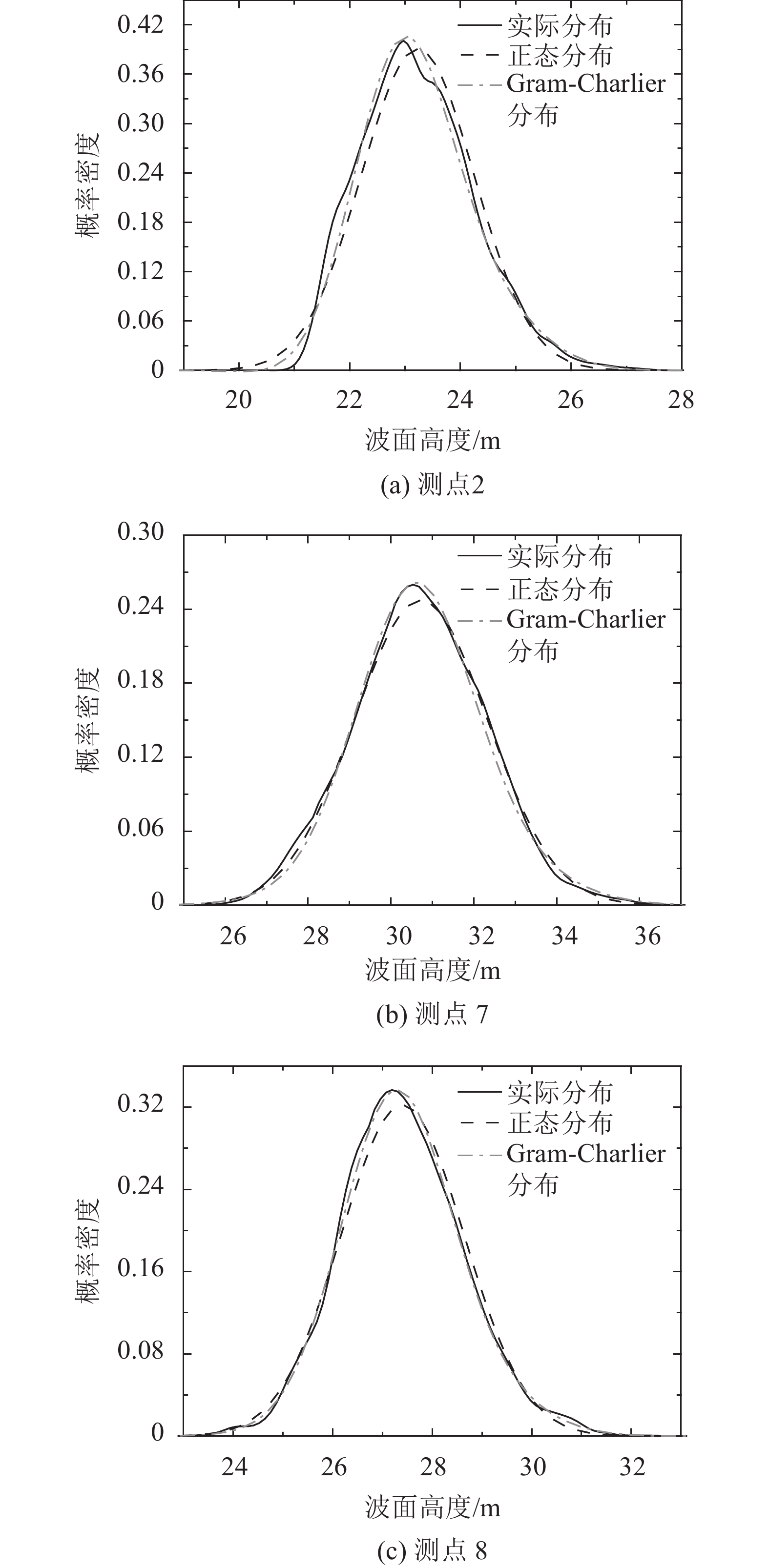图7 不同测点波面高度数据拟合 Fig. 7 Data fitting for the wave surface elevation of different measuring points

基于以上分析，可知水垫塘护坡的破坏是由一列服从Gram-Charlier级数分布和两列互不相关的服从正态分布的随机过程共同作用的结果，这3列随机过程分别对应板块受到的渗流压力和迎、背水面水流脉动压强。传统的水垫塘安全监控指标主要是针对水垫塘底板提出的，从不同角度描述了底板的工作状态，其中常用的有振动时程的主频、极值、均方根和K值（即双幅值与均方根之比）^[12]。由于水垫塘底板所受脉压服从正态分布，其概率密度函数对称，因此均方根在均值两侧对应相同的频率界限。但是对于护坡结构，每一时刻压强差的概率都体现为渗流压力和迎、背水面脉动压强这3个随机变量的联合分布，因此采用均方根作为标准估计压强差的分布情况，会对高渗流压力（对应水垫塘内的低水位）过分考虑，而对底渗流压力（对应水垫塘内的高水位）考虑不足，最终结果可能偏于保守。由于渗流压力与脉动压力的时频域特征都较为相似，因此难以通过模态识别或者滤波的方式将各个随机变量对总体压强差的贡献严格区分出来。根据3σ准则，正态分布压强差的最大值以99.85%的概率小于均值加3倍标准差。表2给出了不同概率分布情况下，压强差大于均值与3倍均方差之和的概率，所选数据来自不同工况和不同测点，每个样本持续时长为2 min，数据总量为24 000个。结果表明，对于正态分布，压强差大于给定值的概率远大于实际情况，Gram-Charlier级数分布的超出概率与实际分布则较为接近，证明了上述分析中采用正态分布进行最大压强差估计将使结果偏于保守的结论。

表2(Tab. 2)

表2 不同概率分布条件下的最大压强差估计偏差 Tab. 2 Estimation error for the pressure difference under different probability distribution

表2 不同概率分布条件下的最大压强差估计偏差 Tab. 2 Estimation error for the pressure difference under different probability distribution 工况 测点 最大值估计 超出概率/% 实际情况 正态分布 Gram-Charlier级数分布 2 2 μ+3σ 0.058 0.150 0.026 2 7 μ+3σ 0.050 0.150 0.034 3 2 μ+3σ 0.042 0.150 0.030 3 7 μ+3σ 0.050 0.150 0.022

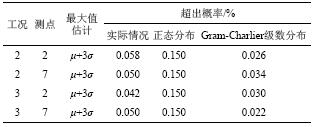从表2中可以看出，虽然Gram-Charlier级数分布更符合实际情况，但其可能对最大波面高度（渗压）的估计略有不足。实际应用中，对于基岩较差、锚固不充分、安全裕度较小的情况，可以依经验对监测指标适当修改以使监测结果准确反映结构运行状态变化。

本文首先分析了水垫塘护坡板块背、迎水面压强差的形成原因，结果表明主要受水垫塘波面高度影响的渗流压力和背、迎水面脉动压力共同构成了导致护坡板块破坏的压力差。

为进一步了解渗流压力的变化规律，通过模型试验研究给出水垫塘波面高度的空间分布情况，并结合水垫塘波面非线性性质较为明显的特点，采用Gram-Charlier级数函数描述波面高度的概率分布。由实测数据拟合可知，该函数相比正态分布能更好地符合实际波面高度的概率分布。

因此，认为水垫塘护坡的破坏机理是由一列服从Gram-Charlier级数分布和两列互不相关的服从正态分布的随机过程共同作用的结果。传统的安全监控指标是针对水垫塘底板提出的，而底板所受脉压差符合正态分布。理论及实测结果均表明，将传统的安全指标用于水垫塘护坡分析，会导致计算结果偏于保守。