2. 国网四川省电力公司,四川 成都 610041;
3. 国网四川省电力公司技能培训中心,四川 成都 611133
2. State Grid Sichuan Electric Power Co.,Chengdu 610041,China;
3. State Grid Sichuan Technical Training Center,Chengdu 611133,China
电网脆弱性[1]研究是一种对电网动态风险的研究。某些电网故障可能产生“雪崩效应”,导致事故反复感染扩大。“雪崩效应”不但存在于电网元件中,也存在于区域电网间。目前电网普遍采用“区域电网+关键联络线路”的结构模式,最初开始于一个区域电网的崩溃可能导致与其互联的多个区域电网相继崩溃[2–3],同时区域电网脆弱性研究通常存在电网运行分析人员无法得知区域外部电网的精确运行信息及其对自身电网影响程度的情况,因此如何解决互联区域模式下的电网脆弱性综合评估问题具有十分重要的意义。
目前,电网脆弱性研究针对元件脆弱性与电网整体性的研究,并取得了一定成就。文献[4–9]从结构、状态或二者结合的角度对节点支路为代表的元件脆弱性进行了深入剖析。文献[10–14]从电网的整体脆弱性进行了研究:文献[10]基于复杂网络理论研究大电网脆弱性,从小世界模型结构脆弱性角度分析电网脆弱性,解决了电网的拓扑分析和连锁故障模拟问题;文献[11]从电网结构和状态两个角度评估电网脆弱性,在考虑元件结构脆弱性的同时考虑了状态脆弱性,细化区别了各单元的脆弱强度,提高了模型的辨识精度;文献[12]建立了一种基于网损理论与最大流理论的脆弱性评估方法,指出了电网潮流沿所有可能路径传播,潮流具有方向性的特点,较好的刻画了电网潮流从电源节点向负荷节点传输问题;文献[13]将2维平面数学方法引入电网脆弱性分析,提供了一种新的脆弱性评估数学方法,该方法能从电网运行角度给出电网脆弱性的定性描述,并快速找到脆弱线路,具有在线应用的潜力。文献[14]从电网支路故障退出后的电网脆弱性变化情况分析电网脆弱性,基于不同故障组合对脆弱性影响不同,建立了基于支路N-k连锁故障的评估模型,并根据路径风险脆弱性和结构脆弱性函数,建立了一种基于故障演化角度的脆弱性分析方法,可很好反映电网的隐性故障。
上述研究从故障传播机理等方面对电网脆弱性进行了详细分析,但在大电网互联的情况下,电网规模过于庞大,上述文献采用的电网全局评估方法并不适合实际区域电网的脆弱性评估。当前电网普遍采用“区域电网+关键联络线路”结构模式。电网管理人员关心外部电网的输入特性,但对外部电网运行细节并不十分关心,同时由于诸多因素的限制,电网管理人员也不具备掌握外部电网细节的条件。因此,需要根据电网的实际特征,针对当前区域互联电网评估方法的不足,对现有脆弱性评估方法进行改进,使评估方法更能适应互联区域电网。
联络线簇[15]将若干电力系统、供电区域联接起来,充分发挥并提高各区域电网的潜在供电能力,降低负荷损失概率,提高各区域电网抵御电网运行风险的能力,将电网整体分割为几个相对独立的控制区域[16–17],提高电网运行控制的灵活性。联络线簇两侧电网通常具有较大灵活运行空间,在该运行空间内可以“随意”运行,并不会导致自身和相邻电网脆弱性的明显增减。因此,可以通过对联络线簇能量传输模式的研究,评估各区域电网及其电网内部关键区域的运行特性,完成区域电网的脆弱性综合评估。
针对区域电网的固有层次结构与控制模式,首先,使用熵模型修正了传统的节点结构和支路负载率两个元件脆弱性评估指标,使原有的元件脆弱性评估指标能更好反映电网宏观特征;其次,对互联电网的扰动抵御水平和极限负载水平进行研究;然后,使用变异系数法确定上述指标客观权重并进行多指标综合处置,完成了规避主观因素干扰的,基于联络线簇能量传输模式的区域电网脆弱性评估,解决了现有脆弱性评估模型对区域互联电网网间作用关系考虑不足的问题,最后用IEEE57仿真模型验证了本文方法的合理性。
1 节点结构性与支路状态性指标基于联络线簇的区域电网脆弱性评估仍考虑电网节点支路的元件脆弱性。通常电网节点较支路对电网结构脆弱性影响更大,而支路状态较节点状态更能反映电网状态,因此采用统筹考虑节点结构脆弱性和支路状态脆弱性的评估方法。
定义节点i的结构脆弱性指标Si如下:
| ${S_i} = {W_i} \cdot \sqrt {\sum\limits_{i = 1,i \ne j}^{{W_i}} {{G_{ij}}{W_j}} } $ | (1) |
式中,Wi、Wj分别为目标节点及与目标节点相连节点的度数,Gij为节点间支路导纳。本文新建立的指标Si考虑了节点自身结构和相邻节点的耦合支撑作用,并用运算系数区分了二者的重要程度,因此较传统节点度数指标合理。同时,指标Si采用的支路导纳等参数均是电网的基本电气参数,指标值比较符合电网的电气特征。
本文用负载率Li定义支路i状态脆弱性指标:
| ${L_i} = \left| {\frac{{L_i^0}}{{L_i^{\max }}}} \right|,\;\;\;\;i = 1,2, \cdots ,{N_i}$ | (2) |
式中,
节点结构与支路负载率两个指标能较好反映单个节点的结构特征与单个支路的状态特征,上述指标应用于电网整体评估时,须对指标的电网宏观特性再次优化。
1.1 电网平衡因子熵理论[18]可基于个体的运行特性提炼出整体运行特征,并用于电网的脆弱性评估中。电网管理人员在求取熵值时需间接求取待评估样本在各分布区间的分布概率。分布区间的划分数量具有主观特性,不同规模电网分布区间划分数量不统一。由于人们主观设置的概率分布区间窗口宽度与窗口密度的大小影响熵结果值和熵辨识度,为消除不同电网规模和人为主观性对评估结果的影响,此处引入电网规模平衡因子
| $\lambda \propto R = \lg ({A_{\max }} + {A_{\min }})$ | (3) |
式中:
| 表1 电网平衡因子 Tab. 1 Balance factor of power grid scale |
 |
1.2 修正后的节点结构性与支路状态性指标
此处使用熵系数
| $ \begin{aligned} H = - \mu \displaystyle\sum\limits_{i = 1}^\lambda {P(i)\ln }\; {\rm{ }}P(i)\end{aligned} $ | (4) |
其中,
| $ \begin{aligned} P(i) = \frac{{{n_i}}}{{\displaystyle\sum\limits_{i = 1}^\lambda {{n_i}} }}\text{。}\end{aligned} $ | (4) |
式中,ni表示
| $\mu = \left\{ \begin{aligned}& {S_{\min }},\;\;\;\;\;\;\;\mu {\text{修正}}S{\text{熵值}}H{\text{时}};\\& 1/{L_{\max }},\;\;\;\mu {\text{修正}}L{\text{熵值}}H{\text{时}}\end{aligned} \right.$ | (5) |
定义一序列区间
| ${\phi _i} = {X_{\min }} + i \times \left( {{X_{\max }} - {X_{\min }}} \right)/\lambda $ | (6) |
式中,X可取指标S或L。当X取指标S时,熵H表示修正后的节点结构脆弱性指标值;当X取指标L时,熵H表示修正后的支路负载率脆弱性指标值。
传统的基于熵模型的脆弱性评估指标,在求解熵模型时并没有考虑概率区间窗口大小与密度对熵值的影响,忽视该问题将导致因主观原因导致的熵值差异。修正后的节点结构性与支路负载率指标较好解决上述弊端,可以更好体现指标的区域电网宏观特征。
2 扰动抵御水平与极限负载率指标电网能量平衡条件是电网运行需要满足的基本运行条件,若出现能量平衡困难,即使目标区域电网不存在单个元件状态脆弱性问题,目标区域电网也不能整体继续运行[19],此时电网管理人员通常采取依据负荷重要性按轮次切除负载措施,该措施将直接导致负荷损失。因此,负荷损失指标是衡量电网运行的核心指标。同时,考虑到主干电网满足常规扰动下负荷不损失的事实[20],可采用目标电网极限负载率的方式逆向评估电网负荷损失。联络线簇传输能量对目标电网能量平衡有重要作用,而任何电网支路均存在扰动和负载不均衡等问题,联络线簇能量传输模式对目标电网有重要影响,因此需要进行基于联络线簇能量传输模式的电网脆弱性评估。
为更好描述区域电网间的作用关系,本文基于联络线簇能量传输模式提出了扰动抵御水平和极限负载率两个新指标。扰动抵御水平指标考虑了联络线簇功率扰动,以电网区域偏差控制指标[21]为基础,消除了时变波动频率因子的干扰,反映电网对能量冲击的抵御水平;极限负载率指标考虑了目标电网联络线簇功率依赖,以电网负荷损失为核心,表示区域电网可承担当前负荷的最大水平,反映了电网负荷损失的逆向距离,评估电网负荷承担深度调整水平。
2.1 扰动抵御水平指标扰动抵御水平指标反映电网运行时对外部电网短时间尺度能量交互关系,考虑到目标电网正负备用能量不足的正反依赖,扰动抵御水平指标J定义公式如下:
| $\begin{aligned}{J^2} = & B \times f/|\Delta F| = \\& \frac{f}{{\left| {\displaystyle\sum\limits_{i = 1}^{{N_{\rm tiel}}} {{F_i}} } \right|}} \times (\displaystyle\sum\limits_{m = 1}^{{N_{\rm G}}} {{k_{{\rm G},m}}{E_{{\rm G},m}}} + \displaystyle\sum\limits_{m = 1}^{{N_{\rm Ld}}} {{k_{{\rm Ld},m}}{E_{{\rm Ld},m}}} )\end{aligned}$ | (7) |
式中,B为控制区域的频率响应能力,|ΔF|为联络线簇能量水平绝对值,f为国标频率偏差允许值;
负荷损失率是电网运行的核心指标。联络线簇传输能量将有助于支撑目标电网负荷,降低负荷损失水平,对联络线簇能量传输性质的研究可更全面了解电网的负荷承担水平。此处,用极限负载率指标表示区域电厂可承担的最大负荷倍数,以此逆向评估电网负荷损失率。
统计表明电力系统发生事故的概率服从泊松分布[22],令电网联络线线路故障概率为ξ,联络线簇支路总数量为n,则n条联络线簇中m条线路故障的总概率如下:
| ${P_{n,m}} = \frac{{{{\left( {\xi \cdot n} \right)}^m}{{\rm{e}}^{ - \xi \cdot n}}}}{{m!}}$ | (8) |
式中,e为自然常数,则特定m条支路组合的故障概率为:
| ${\widetilde P_{n,m}} = \frac{1}{{C_n^m}}{P_{n,m}} = \frac{{(n - m)!{{\left( {\xi \cdot n} \right)}^m}{{\rm{e}}^{ - \xi \cdot n}}}}{{n!}}$ | (9) |
式中,C为概率中的排列运算符。目标控制区域电网功率来源于控制区域自身机组出力和外部电网支撑功率。目标电网可以通过增加备用机组出力以及增加联络线簇功率的方式平衡负荷的增加。联络线簇扰动将降低联络线簇自身可传输能量值。如果目标电网联络线簇传输能量的降低幅度大于目标区域电网机组出力的增加幅度,则目标控制区域电网则会出现负荷受限。作为承担区域电网能量交换载体的联络线簇通常由最高电压等级线路承担,除电网丰枯方式倒换、主干网络的重大检修外,通常的电网细节运行变化并不会对联络线能量传输产生影响,联络线簇极限传输能量可由上级校核后下发或由电网详细参数确定。
根据电网运行参数,可对联络线簇的能量传输能力进行计算。联络线
| $\left\{ \begin{aligned}{P^{\rm L}_{ki}} = & U_k^2{G_{ki}} - {U_k}{U_i}({G_{ki}}\cos {\;\theta _{ki}} + {B_{ki}}\sin {\;\theta _{ki}}),\\{Q^{\rm L}_{ki}} = & - U_k^2({B_{ki}} + {y_{ki0}}) - \\& U{}_k{U_i}({G_{ki}}\sin {\;\theta _{ki}} - {B_{ki}}\cos {\;\theta _{ki}})\end{aligned} \right.$ | (10) |
采用简化快速算法[23]对关键联络线的极限传输水平进行计算。满足机组实际出力
| $\left\{\!\!\!\! \begin{array}{l}K = \displaystyle\frac{{{E_{\max }}}}{{{E_{{\rm{base}}}}}};\\{E_{\max }} = \displaystyle\sum\limits_{i = 1}^{{N_{\rm{G}}}} {E_{{\rm{G}},i}^{\max }} + \displaystyle\sum\limits_{i = 1}^{{N_{{\rm{tiel}}}}} {E_{{\rm{tiel}},i}^{\max }} - \displaystyle\sum\limits_{i = 1}^{{N_{{\rm{tiel}}}}} {{E_{{\rm{Ls}},i}}{{\widetilde P}_{{N_{{\rm{tiel}}}},i}};} \\{\rm{s}}{\rm{.t }}\;\;\;\;{\;E_{{\rm{G}},i}} \le E_{{\rm{G}},i}^{\max },{F_{{\rm{tiel}},i}} \le 1\end{array} \right.$ | (11) |
式中:
变异系数法[24]是一种客观的权重赋值方法,可有效避免主观因素对评估结果的干扰。统计学上通常用来衡量单一样本群体内个体的差异或多样本的总体贡献度。其基本思想是:评价指标体系中差异性越大的指标,越能反映被评价单位的特性,该指标权重就更大。对于有m个评估指标的系统,该系统的综合评估值
| $\left\{ {\begin{aligned}& \psi = \displaystyle\sum\limits_{i = 1}^m {{{( - 1)}^\theta } \times {\psi _i} \times {w_i}},\\& {w_i} = {\widetilde w_i}/\displaystyle\sum\limits_{i = 1}^m {{{\widetilde w}_i}}\end{aligned}} \right.$ | (12) |
其中,
| $ \begin{aligned}{\widetilde w_i} = \displaystyle\frac{{{\sigma _i}}}{{{x_i}}} \times \frac{1}{{\displaystyle\sum\limits_{i = 1}^m {(\frac{{{\sigma _i}}}{{{x_i}}})} }} \text{。}\end{aligned} $ |
式中:wi、
变异系数法的计算过程为:首先,根据样本空间某分指标值
应用变异系数法的区域电网综合脆弱性评估流程如图1所示,其具体步骤如下:
1)根据式(1)和(2)对节点结构和支路负载率指标进行初始计算;
2)根据式(3)确定电网规模平衡因子;
3)根据式(4)和(5)求修正后的节点结构与支路负载率脆弱性评估指标;
4)根据式(7)求区域电网扰动抵御水平指标;
5)根据式(9)和(11)求极限负载率指标;
6)根据式(12)确定评估指标权重,归一化数据并得出综合脆弱性评估结果。
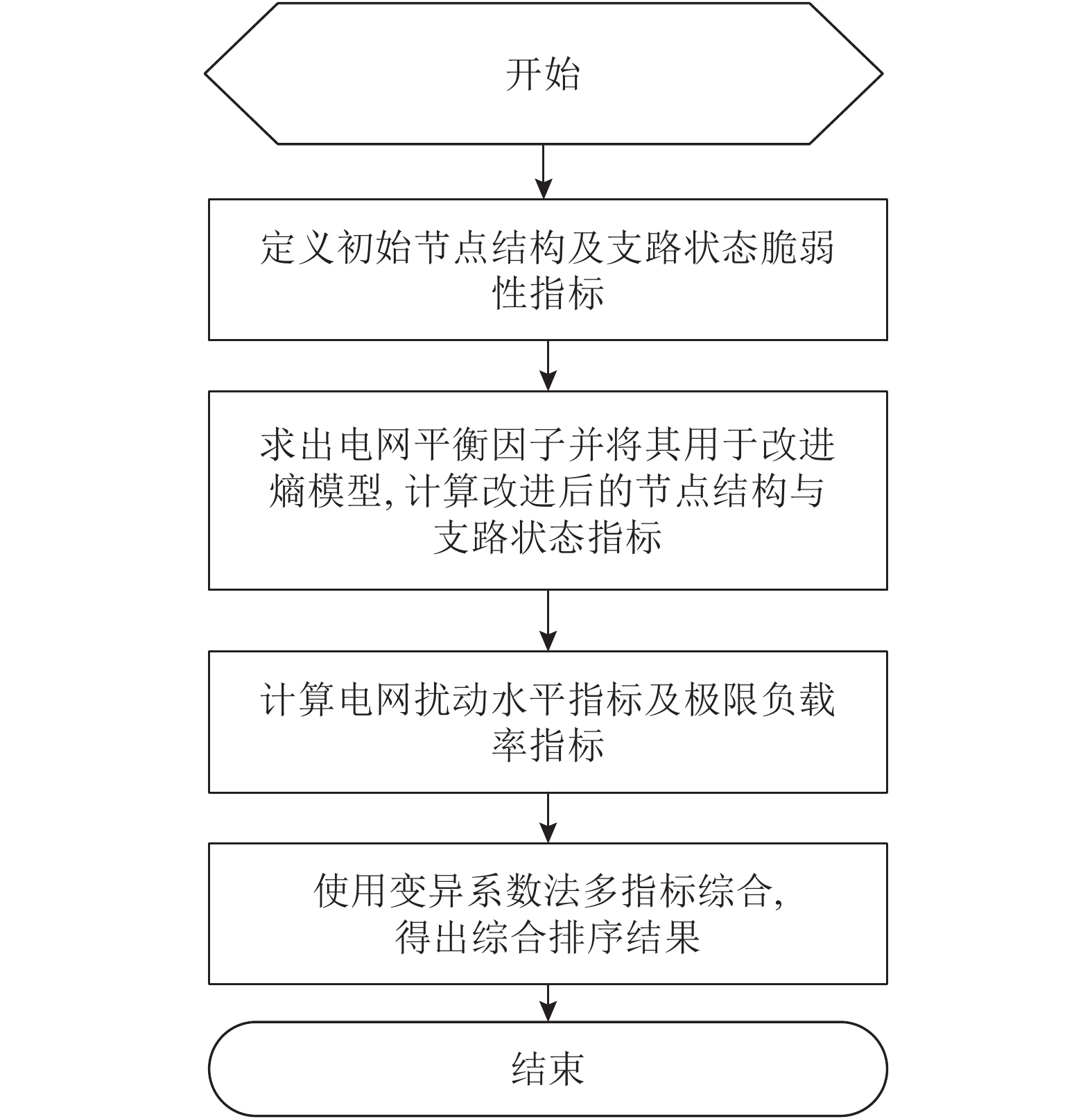 |
| 图1 评估算法流程图 Fig. 1 Flow chart of vulnerability assessment |
4 仿真计算 4.1 仿真结果分析
仿真模型采用图2所示的IEEE57标准系统。
关键联络线可根据电网的电气特征确定[25],图2中,实线为仿真模型中实际存在的输电线路,虚线为划分的电网区域。将与图2中虚线交汇的支路定义为关键联络线路,并从该标准模型中提取4个电网区域。定义包含8、26、54等节点的区域为电网区域Ⅰ,包含11、25、31等节点的为区域Ⅱ,包含5、7等节点的为区域Ⅲ,包含1、9、10等节点的为区域Ⅳ。
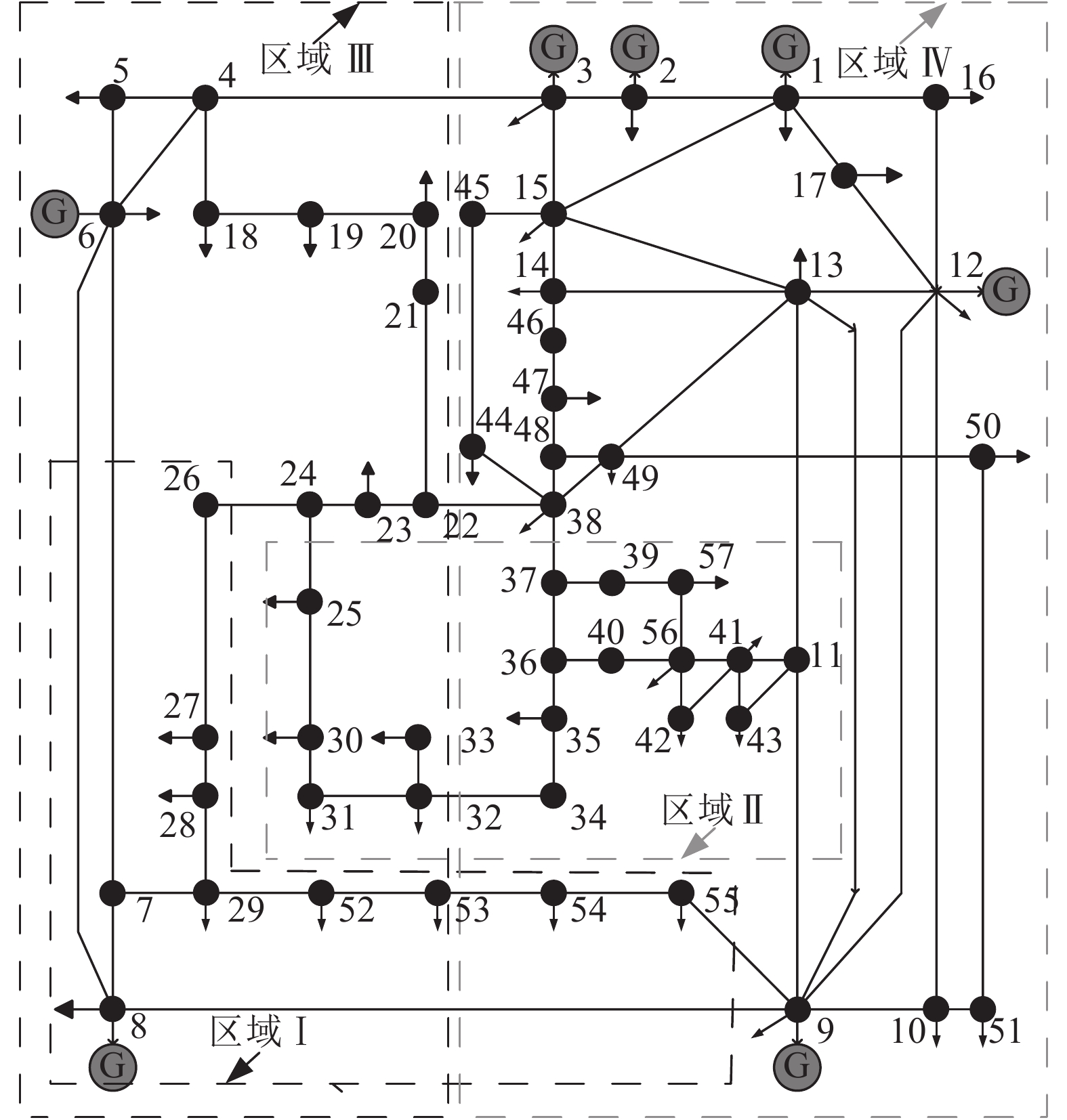 |
| 图2 IEEE57节点系统接线 Fig. 2 Connection diagram of IEEE57-bus system |
表2为脆弱性分指标及其权重。由表2可知,当前的电网运行方式下,电网扰动抵御水平指标(J)对区域电网脆弱性的影响强,电网节点结构性指标(S)与支路状态性指标(H)对区域电网脆弱性影响弱。造成这种结果的原因是各区域电网的发电机规模和备用能量差异性较大,导致该指标因子突出,而各区域电网节点结构与支路状态差异小,影响弱。
| 表2 脆弱性分指标计算结果 Tab. 2 Results of vulnerability indices |
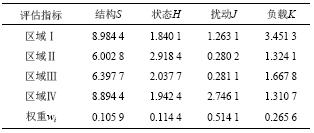 |
采用忽略高阶扰动影响的2阶校核模型,区域电网脆弱性综合评估方法(De)与网络连通度方法[10](Dt)的计算结果如表3所示。由表3可知:区域Ⅱ最脆弱,区域Ⅱ脆弱的主要原因是因为没有内部电源支撑,其应对负荷增长和扰动的能力较弱;区域Ⅳ最不脆弱,其原因是该区域节点度数值较大使其节点结构坚强,且电网支路导纳值大使其电气结构紧密;区域Ⅳ具有与自身负荷相适应的机组配置,电网结构性和抵御扰动能力指标较优越。表3中,区域Ⅰ与区域Ⅲ的排序有所差异,这是因为Dt方法仅考虑了电网结构特征但没有考虑状态和电气参数。虽然区域Ⅰ呈现电网联系相对薄弱的链式分布,但各节点间支路导纳值较大,电气联系十分紧密,同时由于区域Ⅰ内部有大容量机组支撑,所以区域Ⅰ的脆弱性综合排名得到提升。
| 表3 脆弱性综合计算值和方法对比 Tab. 3 Comparison between two methods |
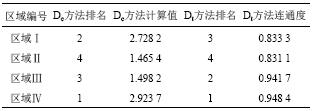 |
4.2 区域电网对联络线簇传输能量依赖性
定义区域电网外部依赖性水平为联络线簇传输功率与区域自身出力及联络线功率之和的比值。当前和极限模式下各区域电网负载联络线簇功率依赖比率如图3所示。虽然目标区域电网可以通过增加内部出力的方式,提高自身负载供给水平,降低对联络线簇能量依赖,但是,计算结果表明当前与极限负载情况下,各区域电网均对联络线簇严重依赖,其中,电网区域Ⅱ的负荷供给完全依赖联络线簇。图3的结果证明了联络线簇传输能量对目标区域电网运行的重要性,也证明了本文方法的全面性和有效性。
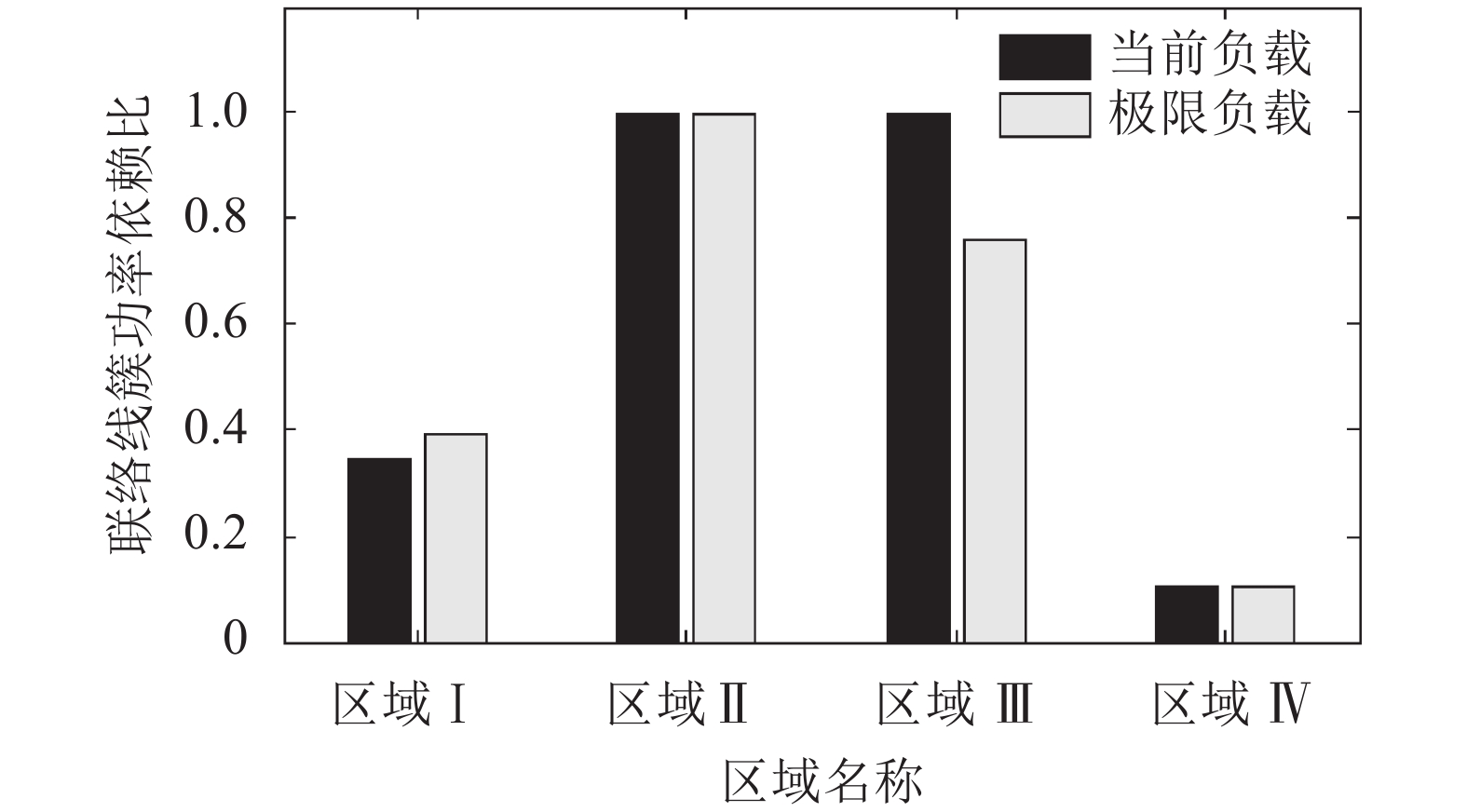 |
| 图3 电网功率外部依赖水平 Fig. 3 Power level rely on external grids |
4.3 联络线簇传输中无功电压问题
联络线簇功率传输受无功电压约束。电网节点无功电压通常采取就地平衡策略,无功就地备用通常满足电网正常和常见扰动时的电网运行要求。N–1阶扰动下关键联络线路两端节点电压波动如图4所示。由图4可知,部分联系薄弱地区故障扰动电压波动大。按扰动后电压不低于0.95 p.u.校核,就地无功未参与电网运行调整情况下,节点30、37的节点电压不满足校核要求;但若上述节点有大于2 MVar无功就地备用,上述节点电压最低值可升至0.957 1 p.u.以上。仿真模型电网节点有功负荷均值为22.43 MW,无功备用率不到节点功率的10%。图4表明了联络线簇传送能量受制于无功电压约束以及联络线簇近区无功就地充分补偿的重要性。
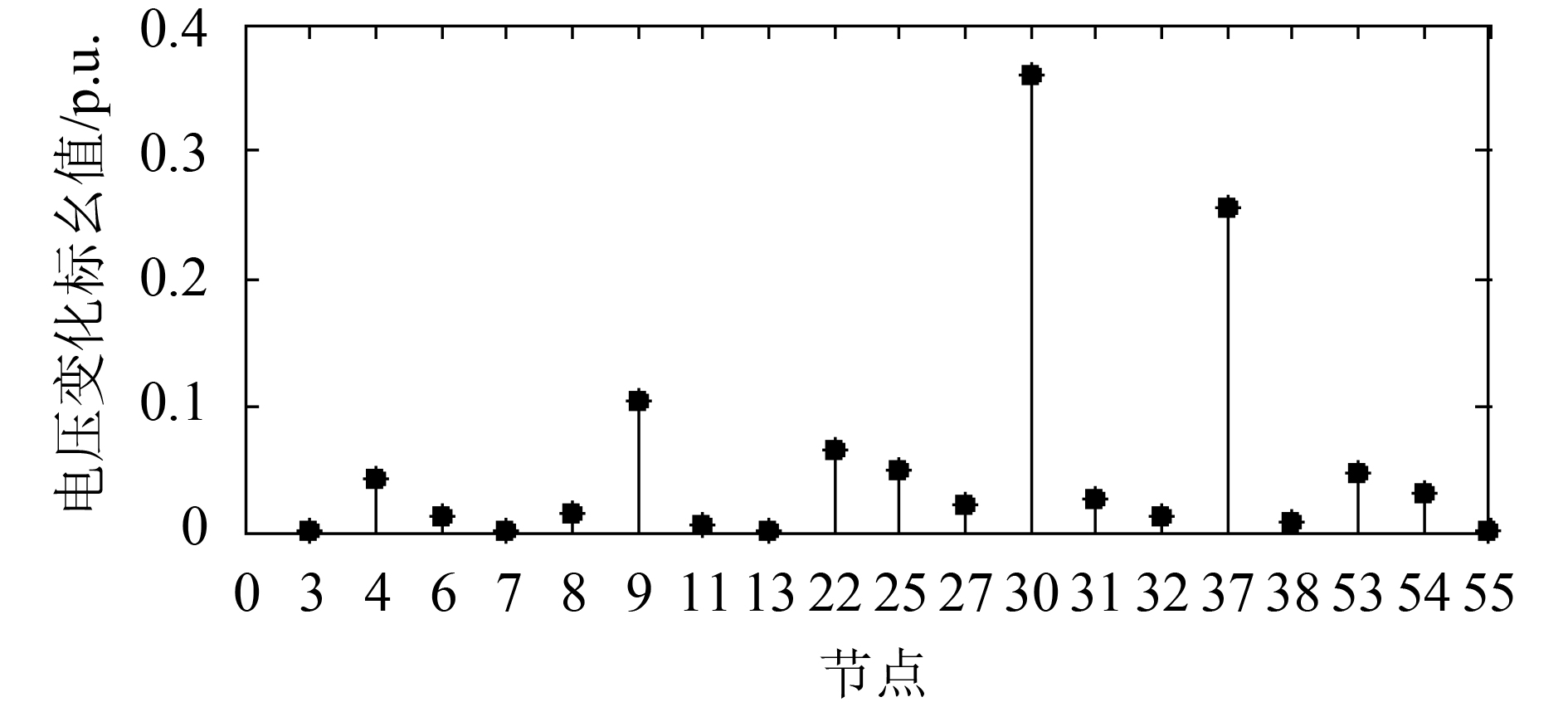 |
| 图4 节点电压波动性校核 Fig. 4 Calculates and checks of nodes voltage |
5 结 论
考虑了电网固有的层次结构和运行控制特性,指出了当前脆弱性评估方法不适合大区域互联电网评估的原因,采用了基于联络线簇能量传输模式的脆弱性评估,修正了原有区域电网脆弱性评估指标的不足,提出了符合电网实际运行特性的新评估指标,将变异系数法引入了脆弱性评估。仿真模型验证了基于联络线簇能量传输模式区域电网脆弱性评估的有效性,解决了目前评估方法对电网实际运行特征和网间作用关系考虑不足的问题,有较强工程实际应用意义和价值。
本文考虑了电网静态评估问题,下一步将研究电网暂态条件下的评估问题。
| [1] |
Fouad A A, Zhou Qin, Vittal V. System vulnerability as a concept to assess power system dynamic security[J]. IEEE Transactions on Power Systems, 1994, 9(2): 1009-1015. DOI:10.1109/59.317643 |
| [2] |
Meyer D H,Rusnov T,Silverstein A,et al.Final report on the August 14,2003 Blackout in the United States and Canada:Causes and recommendations[EB/OL].(2004-03-31)[2017-03-01].https://energy.gov/oe/downloads/blackout-2003-final-report-august-14-2003-blackout-united-states-and-canada-causes-and.
|
| [3] |
Li Chunyan, Sun Yuanzhang, Chen Xiangyi. Preliminary analysis of large scale blackout in Western Europe power grid on November 4 and measures to prevent large scale blackout in China[J]. Power System Technology, 2006, 30(24): 17-21. [李春艳, 孙元章, 陈向宜. 西欧 " 11.4”大停电事 故的初步分析及防止我国大面积停电事故的措施[J]. 电网技术, 2006, 30(24): 17-21.] |
| [4] |
Bai Hao, Miao Shihong. Hybrid flow betweenness approach for identification of vulnerable line in power system[J]. IET Generation Transmission & Distribution, 2015, 9(12): 1324-1331. |
| [5] |
Xu Qingshan, Wang Wei, Liu Jiankun. Application of weighted electric betweenness considering sensitivity factor in identification of vulnerable grid lines[J]. Electric Power Automation Equipment, 2013, 33(10): 53-58. [徐青山, 王伟, 刘建坤. 计及灵敏度因子的加权电气介数在电网脆弱性线路识别中的应用[J]. 电力自动化设备, 2013, 33(10): 53-58. DOI:10.3969/j.issn.1006-6047.2013.10.009] |
| [6] |
Zhang Cheng, Yu Yongjun, Li Huaqiang. Analysis of nodal comprehensive vulnerability considering energy margin and weight factor for power system[J]. Electric Power Automation Equipment, 2016, 36(3): 136-141. [张程, 于永军, 李华强. 考虑能量裕度及权重因子的电力系统节点综合脆弱性分析[J]. 电力自动化设备, 2016, 36(3): 136-141.] |
| [7] |
Bompard E, Napoli R, Xue F. Extended topological approach for the assessment of structural vulnerability in transmission networks[J]. IEEE System Journal, 2012, 6(3): 481-487. DOI:10.1109/JSYST.2012.2190688 |
| [8] |
Li Yang, Su Huiling. Critical line affecting power system vulnerability under N-k contingency condition
[J]. Electric Power Automation Equipment, 2015, 35(3): 60-67. [李扬, 苏慧玲. N-k故障下影响电力系统脆弱性的关键线路研究
[J]. 电力自动化设备, 2015, 35(3): 60-67.] |
| [9] |
Liu Limin, Liu Junyong, Wei Zhenbo. Transmission line vulnerability assessment based on synergetic effect analy-sis[J]. Electric Power Automation Equipment, 2016, 36(5): 30-36. [刘利民, 刘俊勇, 魏震波. 基于协同效应分析的输电线路脆弱评估方法[J]. 电力自动化设备, 2016, 36(5): 30-36.] |
| [10] |
Ding Ming, Han Pingping. Small-word topological model based vulnerability assessment algorithm for large-scale power grid[J]. Automation of Electric Power Systems, 2006, 30(8): 7-10. [丁明, 韩平平. 基于小世界拓扑模型的大型电网脆弱性评估算法[J]. 电力系统自动化, 2006, 30(8): 7-10.] |
| [11] |
Wei Zhenbo, Liu Junyong, Zhu Guojun. A new integrative vulnerability evaluation model to power grid based on running state and structure[J]. Automation of Electric Power Systems, 2009, 33(8): 11-14. [魏震波, 刘俊勇, 朱国俊. 基于电网状态与结构的综合脆弱评估模型[J]. 电力系统自动化, 2009, 33(8): 11-14. DOI:10.7500/AEPS200811198] |
| [12] |
Wang Zhouyang, Chen Guo, Hill D. A power flow based model for the analysis of vulnerability in power networks[J]. Physica A, 2016, 460: 105-115. DOI:10.1016/j.physa.2016.05.001 |
| [13] |
Ding Jian, Bai Xiaomin, Zhao Wei. Grid vulnerability analysis based on two-dimensional accumulation means[J]. Automation of Electric Power Systems, 2008, 32(8): 1-4. [丁剑, 白晓民, 赵伟. 基于二维平面拟合的电网脆弱性分析[J]. 电力系统自幼化, 2008, 32(8): 1-4.] |
| [14] |
Wu Xu, Zhang Jianhua, Qiu Wei. Vulnerability evaluation of district power grid based on N-k contingen-cy
[J]. Proceedings of the CSEE, 2012, 32(4): 93-99. [吴旭, 张建华, 邱威. 基于N-k故障的区域电网脆弱性评估
[J]. 中国电机工程学报, 2012, 32(4): 93-99.] |
| [15] |
Oni B, Graham H, Walker L. Investigation of nonlinear tie line bias control of interconnected power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(5): 2350-2356. |
| [16] |
Wang C, Shahidehpour S. A deconposition approach to non-linear multi-area generation scheduling with tie-line constraints using expert systems[J]. IEEE Transactions on Power Systems, 1992, 7(4): 1409-1418. DOI:10.1109/59.207362 |
| [17] |
Pan Zhijun, Zhang Yan, Zhao Teng. A Multi-objective transmission expansion planning considering power flow distribution unevenness of tie-line groups[J]. Automation of Electric Power Systems, 2013, 37(23): 56-62. [潘智俊, 张焰, 赵腾. 计及联络线簇潮流分布非均匀性的多目标输电网规划[J]. 电力系统自动化, 2013, 37(23): 56-62. DOI:10.7500/AEPS20130507009] |
| [18] |
Cao Yijia, Wang Guangzeng, Cao Lihua. An Identi-fication Model for Self-organized Criticality of Power Grids Based on Power Flow Entropy[J]. Automation of Electric Power Systems, 2011, 35(7): 1-5. [曹一家, 王光增, 曹丽华. 基于潮流熵的复杂电网自组织临街态判断模型[J]. 电力系统自动化, 2011, 35(7): 1-5.] |
| [19] |
Kennedy T,Hoyt S M,Abell C F.Variable,nonlinear tie-line frequency bias for interconnected systems control[J].IEEE Transactions on Power Systems,1988,3(3):1244–1253.
|
| [20] |
中国国家标准化管理委员会.电力系统安全稳定控制技术导则:GB/T 26399—2011[S].北京:中国标准出版社,2001.
|
| [21] |
Jaleeli N, Vanslyck L S. NERC’s new control performance standards[J]. IEEE Trans on Power Systems, 1999, 14(3): 1092-1099. DOI:10.1109/59.780932 |
| [22] |
Carreras B A, Newman D E, Dobso I. Evidence for self-organized criticality in a time series of electric power system blackouts[J]. IEEE Transactions on Circuits and System, 2004, 51(9): 1733-1740. DOI:10.1109/TCSI.2004.834513 |
| [23] |
Wang Chengmin, Li Xiang, Zhang Guoqing. A simple arithmetic of total transfer capability of interconnected electric power systems[J]. Journal of Shanghai Jiaotong University, 2005, 39(增刊1): 45-48. [王承民, 李响, 张国庆. 大型互联电网区域间交换能力的简化计算方法[J]. 上海交通大学学报, 2005, 39(增刊1): 45-48.] |
| [24] |
Freedman D,Pisani R,Purves R,等.统计学[M].北京:中国统计出版社,1997.
|
| [25] |
Yang Wenhui, Bi Tianshu, Huang Shaofeng. An approach for critical lines identification based on the sur-vivability of power grid[J]. Proceedings of the CSEE, 2011, 31(7): 29-35. [杨文辉, 毕天姝, 黄少锋. 基于电网生存性评估的关键线路识别方法[J]. 中国电机工程学报, 2011, 31(7): 29-35.] |
 2017, Vol. 49
2017, Vol. 49

