弯道水流中螺旋流动及分离现象的出现，使得水流中紊流结构变得复杂。诸多学者对水流的紊动特性进行了大量研究^[1–5]，由于流动问题的复杂性尚无法得出其解析解，通常采用试验方法研究紊流结构的变化规律^[6]。

研究表明，弯道几何形态中宽深比对水流紊动结构有重要影响^[7]。大宽深比是目前研究的主要内容，其范围集中在5～30。刘月琴等^[8]在宽深比分别为10及7.5的连续弯道中分析了水流的紊动特性。白玉川等^[9]对宽深比为2.67弯道水流的脉动进行了统计分析，研究了典型断面的紊动强度、紊动切应力、紊动能的分布。王虹等^[10]在宽深比为4.08的连续弯道中分析了紊动能谱、紊动强度、紊动切应力、紊动能等的断面分布。邓安军等^[11]对宽深比为8.0～29.4的天然河流流速进行测量，建立了纵向紊动强度与流速、流速梯度之间的定量关系。van Balen等^[12]采用试验与模拟的方法对3种宽深比（12、8.2、6.3）工况下急弯弯道中水流紊动结构进行了研究，并讨论了二次流的变化。Constantinescu等^[13]采用直接数值模拟的方法对宽深比为9.2的193°急弯弯道中的水流进行了模拟，并对流速分布、紊动特性及曲率对主流及二次流的影响进行了研究。Liu等^[14]对宽深比为20的弯道水流进行了测量，得出直段环流强度小于弯道段，且弯顶断面环流强度小于过渡段。

综上所述，目前对小宽深比（<5）条件下弯道水流特性的研究较少，然而该弯道在山区河流的上游及实验室弯道水槽中比较常见。鉴于此，本文采用声学多普勒流速仪（ADV）对3种小宽深比情况下U型弯道的3维流速进行了精细测量，得到了完整的水力要素。基于测量结果研究了弯道水流结构的紊动特性，并对相应的现象与规律进行了讨论与分析。

研究在U型弯道模型中进行，水槽试验段侧壁及底部均由水泥垒成。整套循环系统由水泵、矩形盛水槽、量水堰、U型水槽、地下水库、地下引水管道组成。弯道总流程s=17.02 m，水槽宽B=0.4 m，内径r₁=0.6 m，外径r₂=1.0 m，中心曲率半径r₀=0.8 m，入口直道L₁=6.0 m，出口直道L₂=6.0 m。弯道模型及其断面设置如图1所示，其中，n、s分别代表水流的纵向与横向。

图1(Fig. 1)

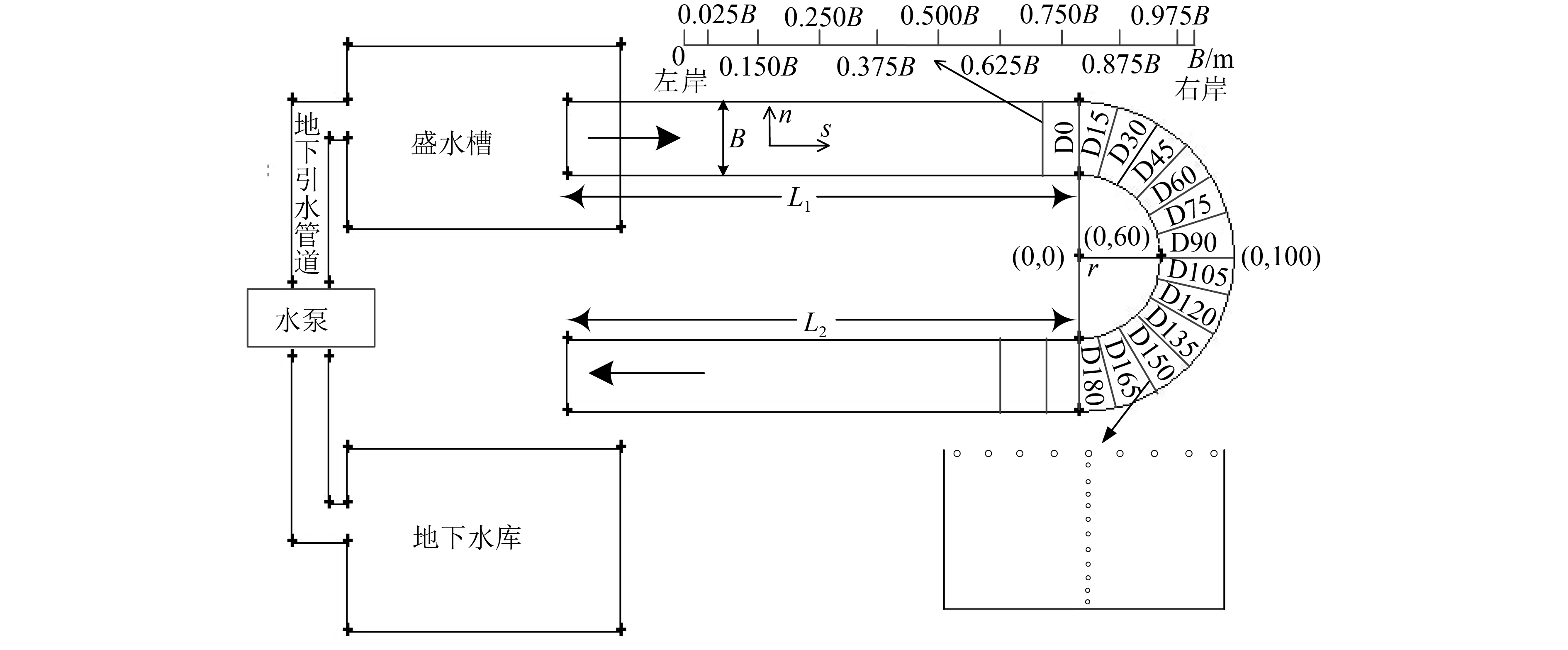图1 U型弯道断面布置 Fig. 1 Cross section setting of the U-shaped bend

水深、流速和流量为反应水流特性的重要参数，试验中采用同一流量，3种不同水深，具体参数见表1。

表1(Tab. 1)

表1 试验工况参数设定 Tab. 1 Test working parameters

表1 试验工况参数设定 Tab. 1 Test working parameters 工况 流量/L 入口水位/cm 出口水位/cm 入口 流速/(cm·s–1) 傅汝德数Fr R·B–1 B·H–1 1 37.5 26.69 25.34 34.72 0.21 2.0 1.5 2 37.5 20.28 19.03 46.23 0.28 2.0 2.0 3 37.5 13.41 12.25 69.91 0.43 2.0 3.0

试验所需流量通过阀门调节，并采用流量公式^[15]进行定量计算：

式中，m₀为流量系数，b为堰宽，h为堰上水头。流量系数采用雷伯克经验公式计算

式中，a为堰高。

采用测针对沿程各断面（图1）水位进行测量。各从左岸到右岸表层横向布置9个测点，分别为δ=0.025B、0.150B、0.250B、0.375B、0.500B、0.625B、0.750B、0.875B、0.975B。

采用多普勒超声测速仪（ADV）对沿程各断面各条垂线上（图2）的流速分布进行测量，其测量误差为1%。为消除测量探头对水流的干扰，采样体位于探头前方5 cm处。从左岸到右岸横向布置与水位测点相同，从水底到表层测量底层距渠底 $\textit{z}$ =0.5 cm，以2 cm为间距依次递增。

图2(Fig. 2)

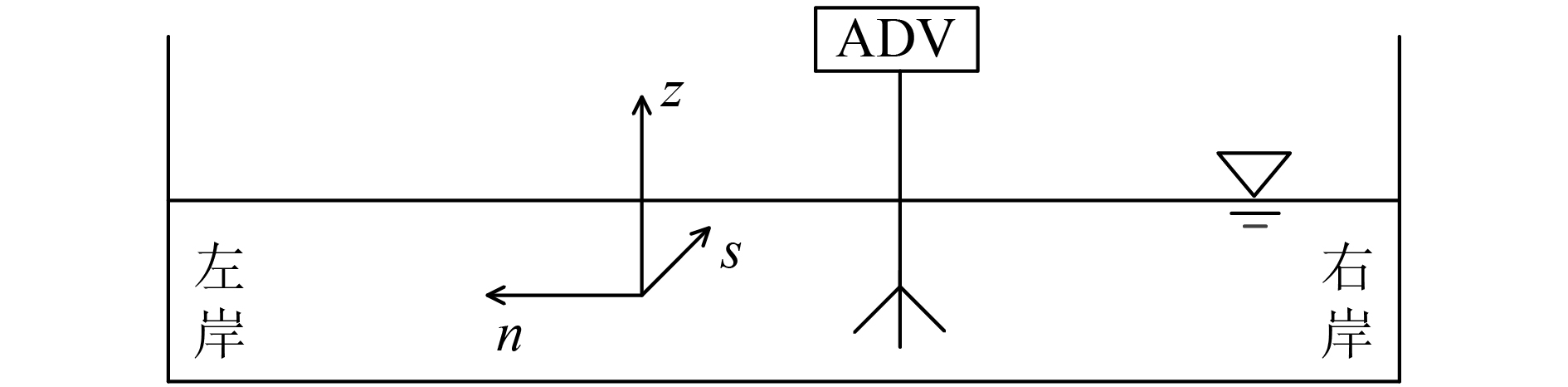图2 ADV测量水流速度示意图 Fig. 2 Measurement of water flow velocity by ADV

水流动力轴线为各断面最大纵向水深平均流速点所在位置的连线，又称为主流线。根据测量结果可得上述不同工况的水流动力轴线，如图3所示。

图3(Fig. 3)

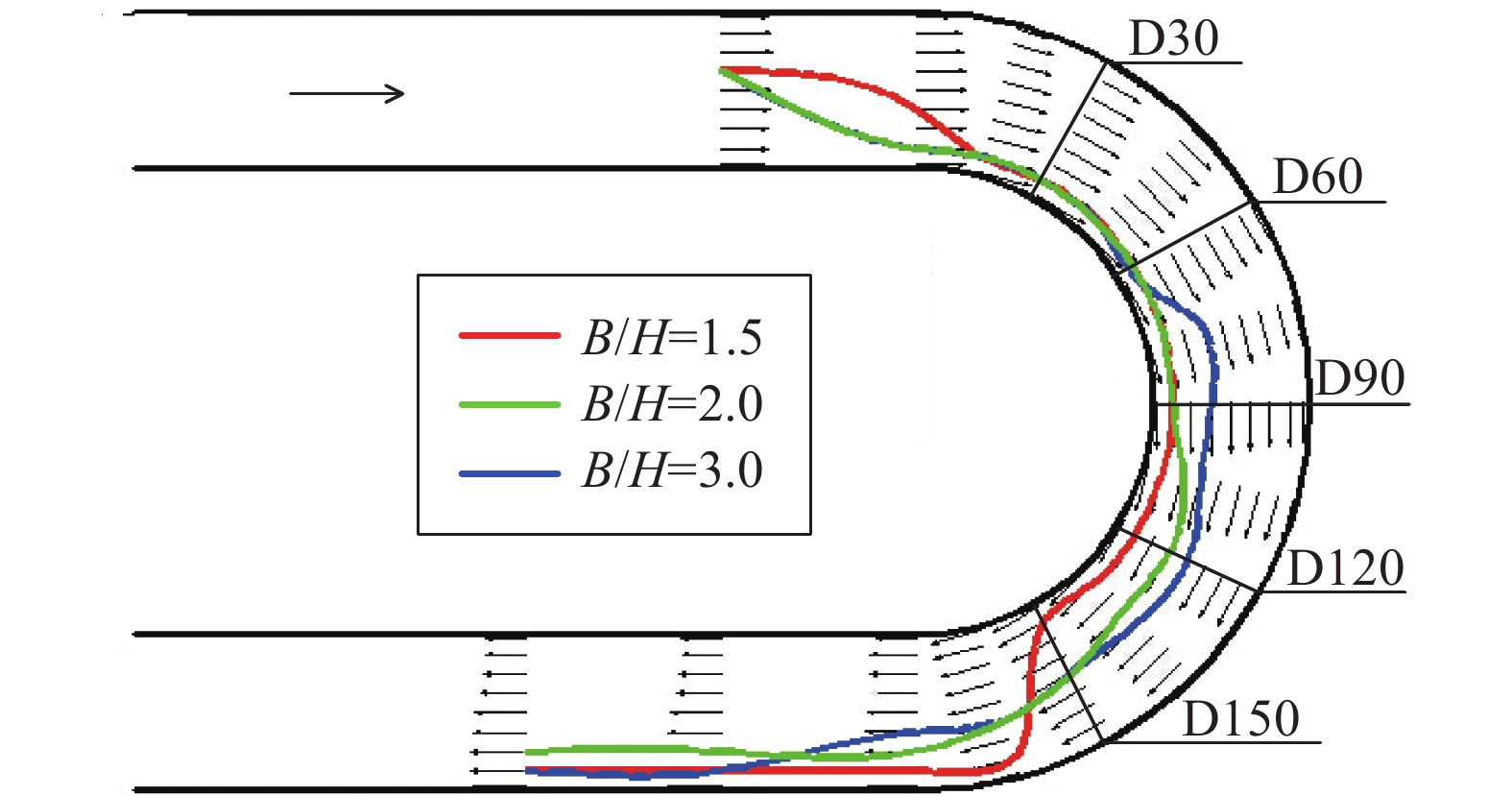图3 水流动力轴线及水深平均流速矢量图 Fig. 3 Diagram of the main stream lines and the vector of depth averaging velocities

弯道水流受到离心力的作用，不同工况的水流动力轴线在弯道入口断面均向凸岸偏移，随后向凹岸偏移并沿凹岸流出。然而，不同工况对应的水流动力轴线向凹岸偏移的位置不同。在断面D60之前，3种工况的水流动力轴线基本一致；在断面D60后，宽深比越大的工况对应的水流动力轴线向凹岸偏移的位置越靠近上游，B/H=1.5、2.0、3.0所对应的水流动力轴线向凹岸偏移的位置分别为断面D150、D105与D90。由于3种工况中入口流量相同，入口流速大小与弯道宽深比成正比。因而，弯道中小流速沿着凸岸流动，而大流速则更早地向凹岸偏移。

断面纵向流速u沿垂线分布如图4所示。

图4(Fig. 4)

图4 断面纵向时均流速沿垂线分布 Fig. 4 Distribution of longitudinal time averaging velocities along the vertical line

弯顶断面以前，各工况在各断面垂线上的纵向流速分布在 $\textit{z}$ /H>0.5水深范围内呈对数型分布，而在 $\textit{z}$ /H<0.5水深范围内纵向流速分布均出现不同程度的减小。对于凹岸区（0.025B～0.375B）与中心区（0.375B～0.750B），纵向流速沿垂线分布较均匀。对于凸岸区域（0.750B～0.950B），流速沿垂线分布在断面D60之前相对均匀，断面D60后流速沿垂线分布开始发生变化，随着弯道的深入，沿程纵向流速梯度变化增大；越接近水面，流速分布越不均匀，并且沿程向越不均匀的趋势发展，越临近水面，流速越小，特别是纵向流速分布在 0.975B垂线表层变化最为明显。进一步观察图4可知，3种工况，随着宽深比的增大，各断面上纵向时均流速依次增大，凸岸区（0.750B～0.950B）表层附近纵向流速波动依次增大，且波动位置依次提前，其位置分别为断面D120、断面D90及断面D60。

断面横向时均流速沿垂线分布如图5所示。

图5(Fig. 5)

图5 断面横向时均流速沿垂线分布 Fig. 5 Distribution of transverse time averaging velocities along the vertical line

水流进入弯道后，横向流速v分布表现为垂线上部流向凹岸，近底流向凸岸，形成环流。在凹岸区（0.025B～0.375B）与中心区（0.375B～0.750B），横向流速沿垂线分布整体上较均匀，基本呈指数型分布；在凸岸区（0.750B～0.950B），断面D60以前横向流速分布较均匀；断面D60以后，在 $\textit{z}$ /H<0.5水深范围内横向流速分布较均匀，在 $\textit{z}$ /H>0.5水深范围内横向流速分布出现波动，在0.950B垂线表层，横向流速分布出现由正变负的分布形式。进一步观察图5可知，断面D60之前以及之后在凹岸0.025B到中心线0.500B之间，3种工况的横向流速相差不大，分布形式相似。在断面D60之后的中心线0.500B到凸岸0.975B之间，不同工况中横向流速的波动强度随着宽深比的增大增强，并且波动位置相应提前，其位置分别为断面D150、断面D120及断面D90，由于主流区位置的偏移位会导致横向流速在凸岸发生波动，不同工况中横向流速开始波动的位置与主流向凹岸偏移的位置（图3）相吻合。

断面横向环流分布如图6所示，左、中、右3列分别对应工况B/H=1.5、B/H=2.0与B/H=3.0。

图6(Fig. 6)

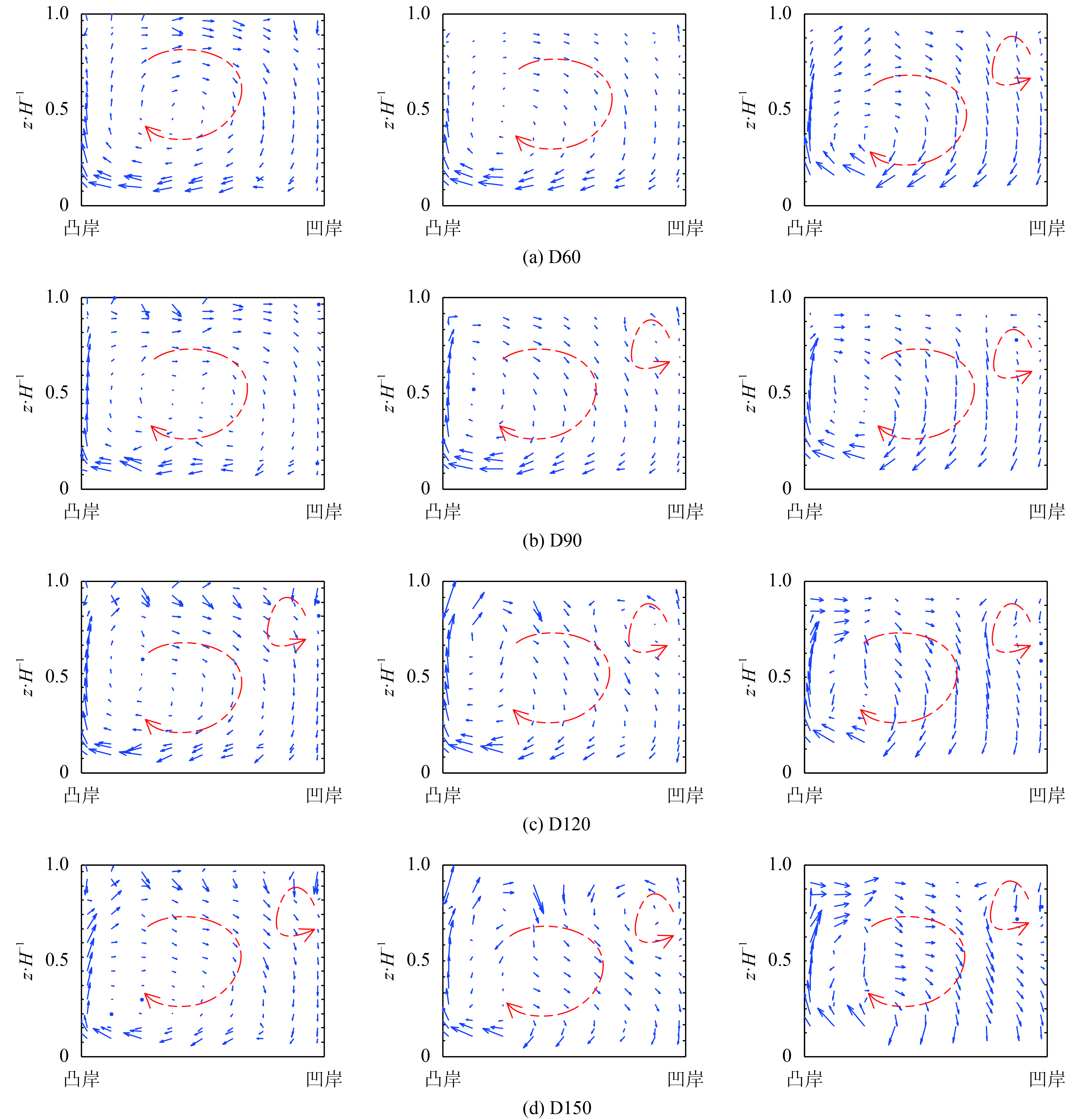图6 断面横向环流分布 Fig. 6 Distribution of transverse circulation

不同工况中，各断面环流结构表现为上部流向凹岸，下部流向凸岸，形成一主环流，其中心位置位于凸岸偏下处。这对动床中泥沙的横向运动有重要影响，主环流使得凹岸近底处河床不断被冲刷，泥沙被带到凸岸附近，逐渐沉积。过断面D60之后凸岸环流强度大于凹岸环流强度。进一步观察图6可知，不同工况中由弯道入口到出口，凹岸表层形成与主环流方向相反的次生环流，此次生环流沿程不断发展；随着宽深比的增大，环流强度不断增强导致次生环流的强度及范围不断增加；且次生环流出现的位置依次提前，分别对应不同工况中的断面D120、断面D90及断面D60。同一断面，不同工况的宽深比越大，环流中心位置越靠近凸岸。

紊动强度是明渠紊流中反映水流紊动特性的重要参数。与横向及垂向水流紊动强度相比，纵向紊动强度远大于其他2个方向，其分布较复杂，对弯道水流的影响较大，文中仅讨论纵向紊动强度特性。其数值大小通常以脉动流速的均方根来表示^[16]：

式中： ${u_i^{'}} $ 为纵向脉动流速；i为样本数据序列；N为样本数，其值为5 000。断面纵向紊动强度沿垂线分布见图7。

图7(Fig. 7)

图7 断面纵向紊动强度沿垂线分布 Fig. 7 Distribution of transverse turbulent intensities along the vertical line

不同工况中，纵向紊动强度在凹岸到中心线区域分布较均匀，在中心线到凸岸区域沿垂线分布出现不同程度的波动。观察图7可知，随着宽深比的增大，纵向紊动强度均依次增强。由于弯道水流中紊动强度与断面二次流的形态相关^[14]，因而当凹岸表层出现次生环流时，紊动强度在的表层波动开始增大。结合图6可以发现，不同工况次生环流出现的位置不同，紊动强度增大的位置也有所不同，3种工况中紊动强度波动增大的位置分别为断面D120、断面D90与断面D60。

当床面附近扰动波或拟序结构及水流自身所产生的床面底部剪切应力大于Shields剪切应力后，床面即产生响应。因而，剪切力是预测动床冲刷程度的重要参数，其分布直接决定床面冲刷形态。本文采用紊动能方法来分析床面剪应力，计算公式为^[17]：

式中，ρ为水体密度，C₁=0.19。

3种工况中弯道处床面剪切力分布如图8所示。进入弯道之后，剪切力开始增大，且凹岸侧大于凸岸侧。剪切力最大值位置出现在弯顶断面之前，其沿弯道纵向从凹岸向凸岸移动，弯道后半段剪切力较前半段小。

图8(Fig. 8)

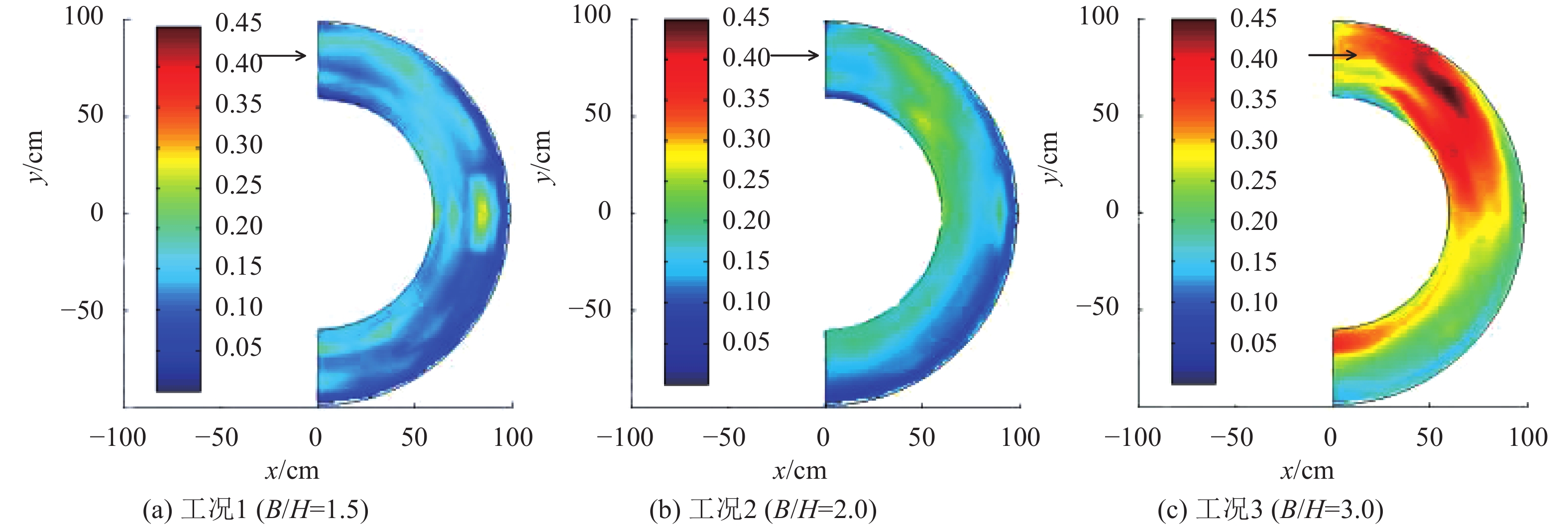图8 弯道处床面剪切力分布 Fig. 8 Distribution of bed shear stress of the bend

过弯顶断面后，床面剪切力与弯顶断面之前呈现相反的分布特性，其在凸岸处的数值大于凹岸。结合弯道环流在整个弯道的变化，可知紊动切应力与弯道环流之间相互影响。弯道环流中心位置解释了床面剪应力最大值的分布（图6）。不同工况中，床面剪切力随着宽深比的增加依次增大。这说明在动床中，相同流量条件下，宽深比越大，河底泥沙的冲刷程度越大，特别是在弯顶断面之前的凹岸侧。

本文采用ADV流速仪对小宽深比条件下的U型弯道的3维流速进行了测量，并基于测量结果分析了水流特性，得到如下结论：

1）宽深比越大，水流动力轴线向凹岸偏移的位置越提前；断面纵向及横向时均流速沿垂线分布均依次增大，二者在凸岸附近发生波动的位置依次提前。

2）在同一断面上，随着宽深比的增大，弯道环流强度不断增强，与主环流方向相反的次生环流出现的位置依次提前。

3）随着宽深比的增大，纵向紊动强度沿水深分布依次增强，与之相应的波动发生位置依次提前，分别为断面D120、D60以及D30，且波动强度依次增强。

4）不同工况中最大床面剪切力位置均出现在弯道前半段。过弯顶断面后，凸岸位置处的床面剪切力大于凹岸；随着宽深比的增大，整个弯道中床面剪切力依次增大。