水电建设的推进中由大坝修建带来的生态环境问题受到广泛关注。高坝泄水时,大量气体被水舌卷入水垫塘内,并在水垫塘深处的高压环境下溶解入水体中,使水体中的溶解气体相对大气来说达到总溶解气体(total dissolved gas,TDG)过饱和状态。过饱和的溶解气体在向下游河道输移过程并不会很快释放逸出[1–2],由此对河道内鱼类等水生生物产生不利影响,导致鱼类患气泡病(gas bubble disease)甚至死亡[3–4]。国内外已经报道过多起泄洪引起的溶解气体过饱和导致大规模鱼类死亡的事件[5–7]。随着梯级电站的建设,当泄水下游水体为水库时,释放速度更加缓慢,观测表明漫湾电站泄水经过大朝山水库约90 km的释放后,其TDG饱和度仅降低4%[8],由此梯级水库运行条件下的过饱和TDG释放问题应更受关注。鱼道是恢复由于大坝阻隔造成的鱼类洄游连通性破坏的重要手段[9–10],统计部分电站的过鱼设施主要过鱼期见表1,表明主要过鱼期覆盖3—9月,其中6—9月一般为汛期,电站弃水的可能性较大。当上游库区水体为TDG过饱和状态时,TDG过饱和水流作为鱼道的补给水流,对鱼道内通行的鱼类带来的不利影响值得关注。另外,由于鱼道结构复杂,过饱和TDG在其中的输移释放规律与顺直河道不同,因此有必要开展鱼道内过饱和TDG输移释放规律的研究。
| 表1 部分电站过鱼设施的主要过鱼期统计 Tab. 1 Major fish passing season of fishway of different power stations |
 |
关于过饱和TDG释放规律的研究,美国陆军工程兵团在Columbia河及其支流Snake河上布设监测网络,开展大量原型观测工作[11]。华盛顿大学基于对原型观测数据的分析,提出过饱和TDG的释放服从1阶动力学过程,由此提出适用于河道的过饱和TDG纵向1维输移释放模型。Johnson[12]采用Perkins[13]提出的平面2维模型MASS2对Wells坝下的过饱和TDG释放过程及与发电尾水的掺混过程进行了模拟。Politano等[14]建立了3维水气两相流模型,对近坝区数公里范围内过饱和TDG释放过程开展预测。在国内,陈永柏等[15]对三峡泄水下游的长江干流DO变化开展预测研究。Feng[16]对四川大学在雅砻江、金沙江、大渡河、澜沧江、长江、岷江等多条河流的过饱和TDG释放过程分析研究基础上,提出过饱和TDG释放系数的估算公式。在对天然河道过饱和TDG释放规律研究基础上,近年学者们逐渐开展了加快TDG释放的研究。冯镜洁等[17]通过室内试验提出泥沙有利于过饱和溶解气体的释放;Niu等[18]在室内开展了利用多孔介质促进过饱和溶解气体释放的试验研究。关于在类似鱼道的复杂结构流动水体中的过饱和TDG释放规律的研究较少,仅见雍晓东等[19]初步研究认为复杂水域内的绕流、回流等水力学现象有助于过饱和TDG的释放的报道,但试验工况较少,并未对复杂结构带来的水动力学参数的变化对过饱和TDG释放系数的影响开展系统研究。
鱼道作为一种特殊形式的河道建筑,受隔板结构的影响,存在回流、绕流及流速突变区,由此带来的水动力学条件的变化对过饱和TDG释放规律的影响值得研究。本文利用T型鱼道结构开展不同流量条件下的过饱和TDG释放过程试验,利用数值模拟方式反算得到过饱和TDG释放系数,并分析释放系数与水深、流速、紊动动能、紊动动能耗散率间的相关关系。
1 试验设计及结果 1.1 试验装置目前鱼道型式以竖缝式鱼道为主,内部型式设计多样,有T型、L型、“一”字型等,试验以四川大学对某电站设计的T型方案鱼道模型作为试验水槽。试验系统见图1。鱼道总长度为6.72 m,宽度为0.2 m,高度为0.2 m,坡降为4.2%。前设休息池,尺寸为0.3 m
 |
| 图1 鱼道内过饱和TDG释放试验系统装置图 Fig. 1 Skech of experimental system of TDG dissipation in a fishway |
1.2 试验仪器与方法
试验过程中观测记录三角堰堰顶水头、水槽内水深和水温变化及入流断面和出流断面TDG饱和度。
水体内TGP的测定采用加拿大Point Four公司生产的TGP测定仪。仪器关于TDG饱和度的测量范围为0~200%,仪器精度为1%。三角堰堰顶水头和水槽内水深采用钢尺测量,水槽内流量通过三角堰堰顶水头计算得到。
1.3 试验工况及结果试验共设计了11种流量条件,流量范围为0.29~1.26 L/s,对部分流量工况开展了平行试验,试验工况共15个,详见表2。
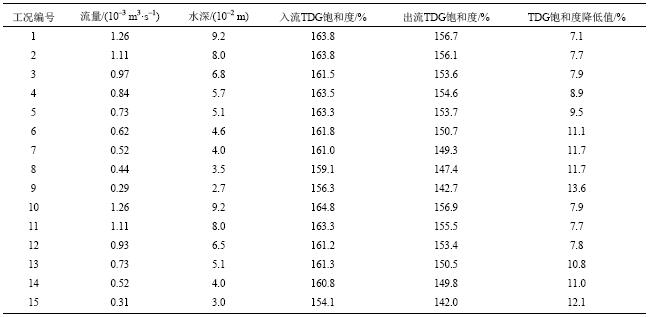
| 表2 试验水槽内过饱和TDG释放试验结果统计表 Tab. 2 Experimental results of TDG dissipation in a fishway |
 |
试验过程中鱼道内水流和TDG释放的照片见图2。各流量条件下水流形态接近,单级入口窄缝处出现壅水现象,流速较高。上池形成环形主流区,通过T型挡板尾部后下池内流态紊乱,出现回流现象,最低流速区出现在横挡板与边壁交角处(图2(a))。试验过程中还观测到探头表面和边壁附着大量小气泡(图2(b)),分析认为,溶解气体首先从气核形成小气泡,再碰撞聚并形成大气泡后上浮至水面,实现溶解态到游离态的释放。探头、边壁及挡板等固壁壁面的存在为溶解气体的析出提供了可依附的载体,有助于气泡更快速聚并和析出,从而加快了水体中过饱和TDG的释放。
 |
| 图2 鱼道内过饱和TDG释放实验照片 Fig. 2 TDG dissipation in experimental fishway |
各流量工况下上下游测量断面过饱和TDG变化列于表1中。由于挡板的存在改变了水槽内水流形态,增加了水体的紊动强度,同时绕流和回流的出现增加了水流滞留时间,有利于水体中过饱和TDG的释放。结果显示,过饱和水流经过直线长度仅为6.72 m的鱼道模型时TDG饱和度降低明显,最大降低值为13.6%,最小降低值为7.1%。总体趋势表明,随着流量和水深的减小,上下游TDG饱和度降低至增大。
2 过饱和TDG释放系数变化规律分析 2.1 过饱和TDG释放系数确定为采用紊流数值模拟方法,通过过饱和TDG模拟结果与试验结果的比较,分析确定各试验工况下的过饱和TDG释放系数kT值。
2.1.1 紊流数学模型方程采用平面2维紊流数学模型。模型方程如下:
1)连续方程
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0$ | (1) |
2)动量方程
| $u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial x}}({\nu _{\rm e}}\frac{{\partial u}}{{\partial x}}) + \frac{\partial }{{\partial y}}({\nu _{\rm e}}\frac{{\partial u}}{{\partial y}})$ | (2) |
| $u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \frac{\partial }{{\partial x}}({\nu _{\rm e}}\frac{{\partial v}}{{\partial x}}) + \frac{\partial }{{\partial y}}({\nu _{\rm e}}\frac{{\partial v}}{{\partial y}})$ | (3) |
式中:u、v为纵向和横向流速,m/s;p为压力,Pa;ρ为水体密度,kg/m3;ve为综合扩散系数,ve=v+vt,m2/s;v为分子黏性系数,m2/s;vt为紊动涡黏系数,m2/s。方程如下:
| $\nu_{\rm t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }$ | (4) |
采用k-ε紊流模型模拟紊动涡黏系数,紊流模型方程组为:
3)k方程
| $u\frac{{\partial k}}{{\partial x}} \!+\! v\frac{{\partial k}}{{\partial y}} \!=\! - \frac{\partial }{{\partial x}}\left[ {\frac{{\nu_{\rm t}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial x}}} \right] \!-\! \frac{\partial }{{\partial y}}\left[ {\frac{{\nu_{\rm t}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial y}}} \right] \!+\! 2\nu_{\rm t}(\frac{{\partial u}}{{\partial y}} \!+\! \frac{{\partial v}}{{\partial x}})\frac{{\partial u}}{{\partial y}} \!-\! \varepsilon $ | (5) |
4)ε方程
| $\begin{aligned}u\frac{{\partial \varepsilon }}{{\partial x}} + v\frac{{\partial \varepsilon }}{{\partial y}} =& \frac{\partial }{{\partial x}}\left[ {\frac{{\nu_{\rm t}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial x}}} \right] + \frac{\partial }{{\partial y}}\left[ {\frac{{\nu_{\rm t}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial y}}} \right] + \\ & 2\nu_{\rm t}{C_{\varepsilon 1}}\frac{\varepsilon }{k}(\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}})\frac{{\partial u}}{{\partial y}} - {C_{\varepsilon 2}}\frac{{{\varepsilon ^2}}}{k}\end{aligned}$ | (6) |
式中:k为紊动动能,m2/s2;ε为紊动动能的耗散率,m2/s3;σk、σε为紊动动能和紊动动能的耗散率的Prandtl数,分别为1.0和1.3。
其他常数模型分别为Cμ=0.09,Cε1=1.44,Cε2=1.92。
5)TDG的输移扩散方程
| $u\frac{{\partial \varPhi }}{{\partial x}} + v\frac{{\partial \varPhi }}{{\partial y}} = \frac{\partial }{{\partial x}}(\frac{{{\nu _x}}}{{{\sigma _{\rm C}}}}\frac{{\partial \varPhi }}{{\partial x}}) + \frac{\partial }{{\partial y}}(\frac{{{\nu _y}}}{{{\sigma _{\rm C}}}}\frac{{\partial \varPhi }}{{\partial y}}) + {S_{\phi {\rm G}}}$ | (7) |
式中:Φ为TDG过饱和度;σC为普朗特数,通常取为1.0;SϕG为TDG的源项。通常假定TDG释放过程遵循1阶动力学反应,则TDG源项方程表达式为:
| ${S_{\phi {\rm G}}} = - {k_{\rm T}}\varPhi $ | (8) |
式中,kT为TDG释放系数,其量纲为T–1。
2.1.2 网格划分与边界条件设置模拟区域为鱼道物理模型中休息池至第28级单池出口间的水流区域。为提高计算收敛性,网格划分采用结构化矩形网格。
鱼道模型入口定义为速度入口,入流流速边界条件采用模型试验中测得的流量、水深和槽宽计算得到,入流TDG饱和度采用实测值。鱼道模型出口定义为自由出流边界。
2.1.3 释放系数的率定对各试验工况,利用假定的过饱和TDG释放系数初值,采用平面2维紊流数学模型模拟过饱和TDG释放过程。根据下游观测断面TDG过饱和度的模拟结果与模型试验观测结果的对比,调整过饱和TDG释放系数值,直至模拟结果与试验结果之差达到误差允许范围(误差限为1%)内,即得到过饱和TDG的释放系数。释放系数率定结果及水动力学计算结果见表3。
| 表3 各工况过饱和TDG释放系数率定结果表 Tab. 3 Results of calibrated TDG dissipation coefficients of the experimental cases |
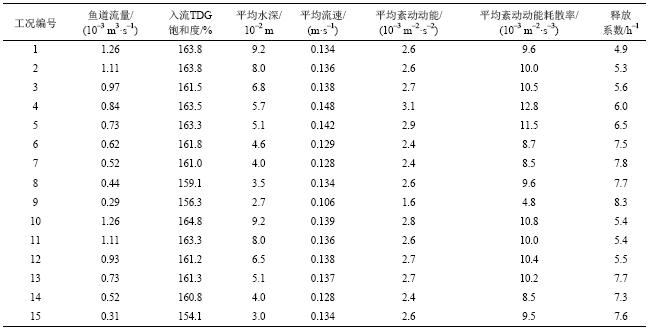 |
2.2 释放系数与水动力学条件变化分析
计算区域的流速、紊动动能、紊动动能耗散率分布见图3~6所示。鱼道28级单池的设计参数均相同,为清晰起见,图3只展示第2#~4#单池流场分布。
 |
| 图3 计算水槽内流场分布(工况3) Fig. 3 Flow field of the fishway (Case 3) |
 |
| 图4 计算水槽内纵向流速分布(工况3) Fig. 4 Longitudinal velocity distribution of the fishway (Case 3) |
 |
| 图5 计算水槽内紊动动能分布(工况3) Fig. 5 Turbulent kinetic energy distribution of the fishway (Case 3) |
 |
| 图6 计算水槽内紊动动能耗散率分布(工况3) Fig. 6 Turbulent kinetic energy dissipation rate distribution of the fishway (Case 3) |
从图3中可以看出进入单池时在束窄区域流速较大,主流在接近T型挡板时分两股绕两侧流动,在水槽中心线区域水流保持高流速直至流入下一级单池,主流区外的单池入口及出口两侧形成明显回流区,近T型挡板外壁处均形成低流速区。单池内紊动动能的分布与流速有一定差异,在T型挡板周围形成T形高紊动动能区,紊动动能最大值出现在横挡板上游侧边缘处,其值高达0.013 m2/s2,在下池近边壁处紊动动能最低。紊动耗散率高值区与主流区大致重合,最大值也出现在横挡板上游侧边缘处,以横挡板为界,上池内紊动耗散率明显高于下池。
模拟区域内过饱和TDG的沿程变化(工况3)见图7。随着水流的输移释放,TDG饱和度沿程降低。从各级单池的TDG分布来看,入口处TDG饱和度较大,随着单池内水体紊动等对释放的促进,到单池出口处TDG饱和度略有降低,而饱和度值降低最显著的区域在下池仅边壁两侧,图中看出水流绕过T型挡板抵达横挡板时TDG饱和度降低,水流进入横挡板下游的回流区后饱和度进一步降低,在回流中心区域其值达到谷值,谷值饱和度远小于单池出口处TDG饱和度。经过分析,横挡板下游区域饱和度值低的原因有二,其一,接近横挡板时紊动动能和紊动耗散率便开始迅速增长,到达横挡板上游侧边缘处紊动动能和紊动动能耗散率都达到最高值,强烈的水体紊动极大地促使了过饱和TDG的快速释放,从而进入横挡板下游非主流区后饱和度值降低明显;其二,水流进入横挡板下游区域后流速降低,形成明显的低速回流区,如此便延长了水体的滞留时间,使得释放过程更为充分,因而TDG饱和度较低。
 |
| 图7 鱼道内过饱和TDG浓度分布(工况3) Fig. 7 Supersaturated TDG distribution of the fishway (Case 3) |
2.3 释放系数与水动力学条件的关系分析
根据实测得到的过饱和TDG饱和度变化及平均水深,以及数值模拟得到的平均流速、平均紊动动能和平均紊动动能耗散率,建立过饱和TDG释放系数与水动力学因子的关系,如图8所示。
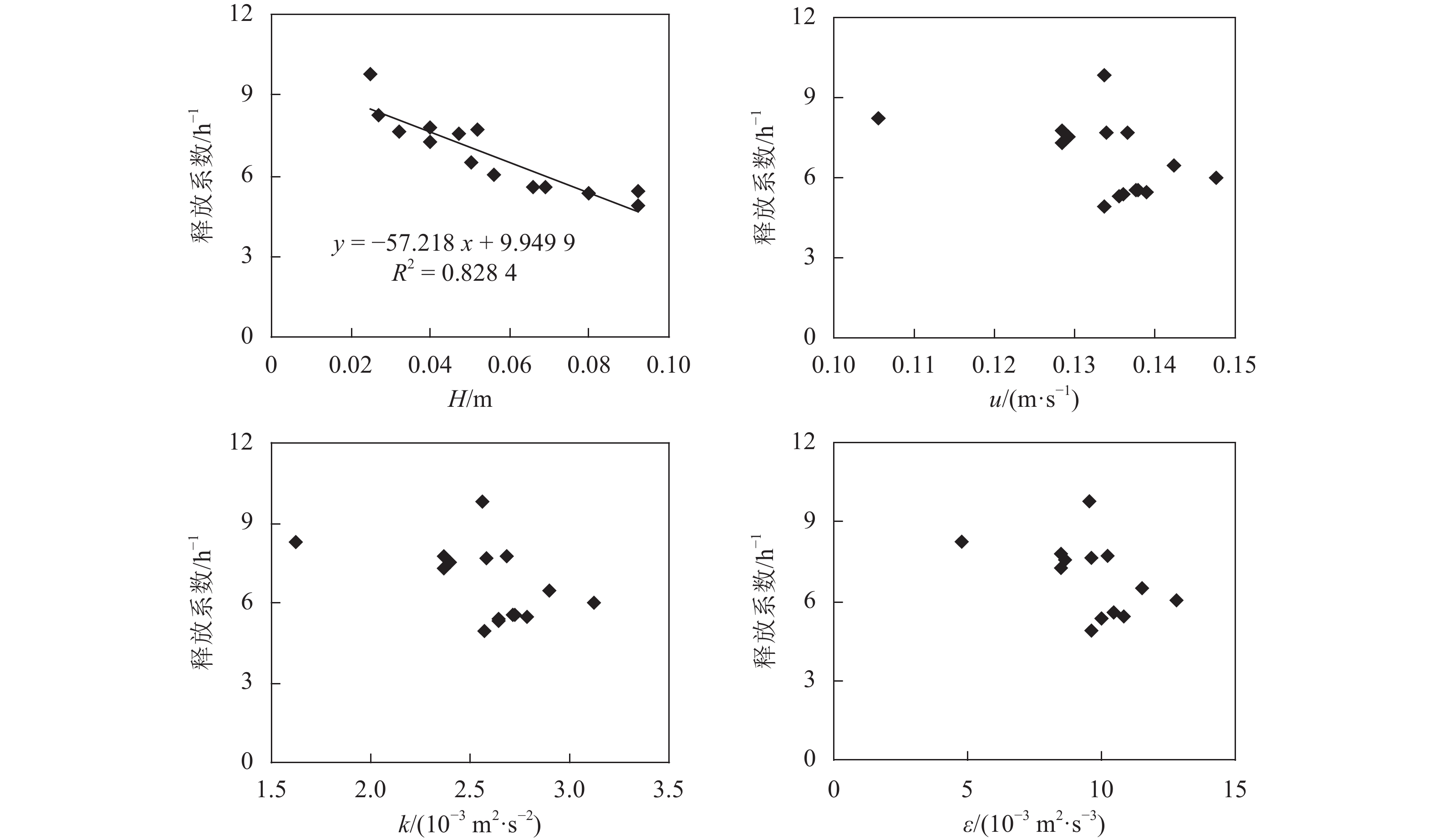 |
| 图8 释放系数与水动力学单因子关系 Fig. 8 Relations between TDG dissipation coefficients and hydrodynamic factors |
由图8可知,释放系数与水深呈现较好的单一线性关系,随着水深的增加,释放系数降低,因此在过饱和TDG释放过程中,水深是决定释放速度快慢的重要参数。
一般研究认为释放系数随流速、紊动强度和紊动耗散率的增加而增大,但由图8看出释放系数与这些水动力学因子间的相关系数较低,分析认为本文数据分析采用的释放系数并未剔除其他因子的影响,所以得到的单因子关系不好。已有研究[16]采用u/H作为表征释放系数的重要因子,对试验中的相关关系分析见图9,结果显示释放系数随着u/H的增大而减小,表明水深H对释放系数的影响更大。对水深、流速、紊动动能、紊动动能耗散率等因子进行无量纲化处理,得到释放系数与无量纲因子的关系见图10,表明释放系数与无量纲因子εH/(uk)间具有较好的负指数关系,为kT=7.47εH/(uk)–0.381。
 |
| 图9 释放系数与u/H关系 Fig. 9 Relations between kT and u/H |
 |
| 图10 释放系数与εH/(uk)关系图 Fig. 10 Relations between kT and εH/(uk) |
水槽内复杂的回流和绕流对过饱和TDG的释放也会产生重要影响。将本节得到的释放系数与文献[21]中明渠水槽试验结果进行对比。本文流量为0.62 L/s的清水工况(工况6)过饱和TDG释放系数为8.8 h–1,唐春燕[21]顺直水槽清水试验中流量为0.64 L/s的工况过饱和TDG释放系数为0.8 h–1,两者流量相当,但鱼道模型内释放系数为顺直水槽内释放系数的11倍。可见,鱼道内挡板结构使水流形态发生改变,紊动动能、紊动耗散率和水体滞留时间增加,促进了过饱和TDG的释放。尽管鱼道内过饱和TDG释放速度显著大于无挡板结构的河道内,但总的来说其释放速度缓慢,因此鱼道内过饱和TDG对鱼类的不利影响仍值得关注和研究。
3 结 论本文通过在自主设计的鱼道内开展不同流量条件下的过饱和TDG输移释放试验,并根据试验条件开展平面2维数值模拟计算,得到不同工况条件下的过饱和TDG释放系数。通对比鱼道这类具有复杂内部结构的水槽与无挡板结构的空白水槽中过饱和TDG释放过程,显示挡板结构延长了水流流程,增加了水体在水槽内的滞留时间,释放更加充分,鱼道内过饱和TDG释放系数显著大于空白水槽。数据分析并探讨了过饱和TDG释放系数与水深、流速、紊动动能、紊动动能耗散率之间的关系,研究结果表明水深是影响过饱和TDG释放快慢的重要参数,过饱和TDG释放系数随着水深的增加而减小;而过饱和TDG释放系数与流速、紊动动能、紊动动能耗散率间的单因子关系不显著;释放系数与u/H和εH/(uk)间有较好的相关关系。
该研究为探讨梯级联合运行条件下,由于上游梯级泄水生成的TDG过饱和水流对下一梯级过鱼通道内鱼类的不利影响的研究提供参考。试验得到复杂挡板结构有利于过饱和TDG的释放这一结论和释放系数与εH/(uk)的定量关系,为过饱和TDG不利影响的减缓措施研究提供了新思路和参考,初步得到对于水利工程中水生生态保护具有实际应用价值。
| [1] |
Jiang Liang, Li Ran, Li Jia. The supersaturation of dissolved gas in downstream of high dam[J]. Jounal of Sichuan University (Engineering Science Edition), 2008, 40(5): 69-73. [蒋亮, 李然, 李嘉. 高坝下游水体中溶解气体过饱和问题研究[J]. 四川大学学报(工程科学版), 2008, 40(5): 69-73.] |
| [2] |
Feng Jingjie, Li Ran, Li Kefeng. Study on the release process of supersaturated total dissolved gas downstream of high dam[J]. Journal of Hydroelectric Engineering, 2010, 29(1): 7-12. [冯镜洁, 李然, 李克锋. 高坝下游过饱和TDG释放过程研究[J]. 水力发电学报, 2010, 29(1): 7-12.] |
| [3] |
Liang R F, Li B, Li K F. Effect of total dissolved gas supersaturated water on early life of David’s schizothoracin (Schizothorax davidi)[J]. Journal of Zhejiang University Science B, 2013, 14(7): 632-639. DOI:10.1631/jzus.B1200364 |
| [4] |
Tan Decai.Research on the lethal effect of the dissolved gas super-saturation resulted from Three Gorges Project to fish[D].Chongqing:Southwest University,2006. [谭德彩.三峡工程致气体过饱和对鱼类致死效应的研究 [D].重庆:西南大学,2006.]
|
| [5] |
Weitkamp D E.Total dissolved gas supersaturation biological effects,Review of literature 1980–2007 [R].Bellevue:Parametrix Inc,2008:1–65.
|
| [6] |
长江流域水资源保护局.葛洲坝工程泄水与鱼苗气泡病调查[R] 武汉:长江流域水资源保护局,1983.
|
| [7] |
中国水产科学研究院长江水产研究所.金沙江下游气体过饱和监测报告[R] 武汉:中国水产科学研究院长江水产研究所,2014.
|
| [8] |
Feng J. A laterally averaged two-dimensional simulation of unsteady supersaturation total dissolved gas in deep reservoir[J]. Journal of Hydrodynamics, 2013, 25(3): 396-403. DOI:10.1016/S1001-6058(11)60378-9 |
| [9] |
Chen Kaiqi, Chang Zhongnong, Cao Xiaohong, et al. Status and prospection of fish pass construction in China[J]. Journal of Hydraulic Engineering, 2012, 43(2): 182-197. [陈凯麒, 常仲农, 曹晓红. 我国鱼道的建设现状和展望[J]. 水利学报, 2012, 43(2): 182-197.] |
| [10] |
Mao Xi.Study of fish-friendly fishway hydraulics in mountainous rivers of southwest China[D].Chengdu:Sichuan University,2015. [毛熹.中国西南山区河流鱼类友好型鱼道水力学研究[D].成都:四川大学,2015.]
|
| [11] |
US Army Corps of Engineers.Technical analysis of TDG processes[R].Washington D C:US Army Corps of Engineers,Northwest Division,Environmental Resources and Fish Planning Offices,2005.
|
| [12] |
Johnson E. Estimating adult Chinook Salmon exposure to dissolved gas supersaturation downstream of hydroelectric dams using telemetry and hydrodynamic models[J]. River Research and Applications, 2007, 23(9): 963-978. DOI:10.1002/(ISSN)1535-1467 |
| [13] |
Perkins W A,Richmond M C.MASS2,Modular aquatic simulation system in two dimensions:Theory and numerical methods[R].PNNL-14820–1.Pacific Northwest National Laboratory,Richland,Washington.2004.
|
| [14] |
Politano M, Amado A A. Evaluation of operational strategies to minimize gas supersaturation downstream of a dam[J]. Computers & Fluids, 2012, 68(5744): 168-185. |
| [15] |
Chen Yongbo, Peng Qidong, Liao Wengen. The evolvement study on supersaturation of dissolved gas in the middle reaches of Yangtze River after the Three Gorges Project running[J]. Journal of Hydroecology, 2009, 2(5): 1-5. [陈永柏, 彭期冬, 廖文根. 三峡工程运行后长江中游溶解气体过饱和演变研究[J]. 水生态学杂志, 2009, 2(5): 1-5.] |
| [16] |
Feng J. Experimental and field study on the dissipation coefficient of supersaturated total dissolved gas[J]. Journal of Central South University, 2014, 21(5): 1995-2003. DOI:10.1007/s11771-014-2148-4 |
| [17] |
Feng Jingjie, Li Ran, Tang Chunyan, et al. Experimental study on the sediment effect on releasing process of supersaturated total dissolved gas[J]. Advances in Water Science, 2012, 23(5): 720-708. [冯镜洁, 李然, 唐春燕. 含沙量对过饱和总溶解气体释放过程影响分析[J]. 水科学进展, 2012, 23(5): 720-708.] |
| [18] |
Niu J L, Li R, Shen X. Experimental research on the promotion of supersaturated total dissolved gas dissipation by the use of activated carbon[J]. Nature Environment and Pollution Technology, 2015, 14(2): 367-372. |
| [19] |
Yong Xiaodong, Yi Wenmin, Li Ran, et al. Total dissolved gas dissipation coefficient in complicated flow conditions[J]. Advances in Science and Technology of Water Resources, 2012, 32(1): 62-66. [雍晓东, 易文敏, 李然. 复杂流动条件下过饱和TDG释放系数的确定[J]. 水利水电科技进展, 2012, 32(1): 62-66. DOI:10.3880/j.issn.1006-7647.2012.01.014] |
| [20] |
李然,黄翔,李克锋,等.水体总溶解气体生成及其对鱼类影响研究的装置:中国,ZL 2009 1 0164299.3[P].2011-07-20.
|
| [21] |
Tang Chunyan.Study of sediment impact on total dissolved gas supersaturation [D].Chengdu:Sichuan University,2011. [唐春燕.泥沙对水体总溶解气体过饱和的影响研究[D].成都:四川大学,2011.]
|
 2017, Vol. 49
2017, Vol. 49


