活齿传动是由少齿差行星齿轮传动演变出的一种大功率、宽速比、高承载的传动形式,由于中间体(活齿)的形状及运动方式的不同而形成了推杆活齿传动、摆动活齿传动、滚动活齿传动以及钢球活齿传动等多种典型的活齿传动类型[1]。近年来,众学者以典型活齿传动为基础,在齿形及结构方面进行创新,改善了活齿传动的性能并扩展了其应用范围。赵纯可, 梁尚明等[2–3]提出了一种摆杆活齿传动,解决了活齿偏心引起的啮合副间的强制性滑动问题以及偏心激波器导致的附加动载荷问题,同时分析了温度对中心轮结构模态的影响。Xu等[4]将谐波传动与活齿传动结合,提出了一种具有响应快、精度高、重量轻等特点的电磁谐波活齿传动系统,给出了电磁力计算公式,研究了输出转矩随系统参数的变化关系,相比传统谐波传动,该系统的柔轮无轮齿且输出转矩较大。Xu等[5–6]融合谐波传动、压电传动及活齿传动,提出了一种机电集成谐波压电传动系统,较现有压电电机,该系统提高了输出转矩、使用寿命和传动效率。宜亚丽等[7]在滚动活齿传动齿形设计过程中引入了五次多项式类曲线,给出了齿廓方程和压力角公式,并对机构的传力特性进行了讨论。李剑锋等[8]用标准椭圆激波器代替偏心圆激波器,提出了一种双相凸轮激波滚动活齿传动,其从原理上消除了偏心引起的振动激励,讨论了机构的几何设计;李剑锋等[9]又将双相凸轮激波滚动活齿传动与行星齿轮传动串联,设计了一种具有更大速比范围的传动机构并对其啮合副受力进行了分析。沈煜等[10]将活齿传动原理引入到分度凸轮机构设计中,提出了一种输入、输出同转速的新型分度凸轮机构,推导了凸轮齿廓方程,并对机构进行动态静力分析。刘大伟等[11]以非圆齿轮传动原理为基础,设计了一种变速推杆活齿传动机构,给出了齿廓方程以及连续传动条件,并对机构传动特性进行了研究。
传统摆动从动件凸轮机构实现大摆角范围输出时需要较大结构尺寸,且凸轮与从动件间多为单个高副接触,承载能力相对较弱,使其应用受到了一定程度的限制。因此,作者在融合活齿传动和凸轮机构优点的基础上,提出了一种摆动输出活齿凸轮机构。该机构作为一种新颖的、可摆动输出的传动形式,与现有摆动机构相比,摆动输出活齿凸轮机构能实现全齿同时啮合,从而提高了承载能力,并且能够在较小结构尺寸条件下实现大摆角范围的精确摆动输出。
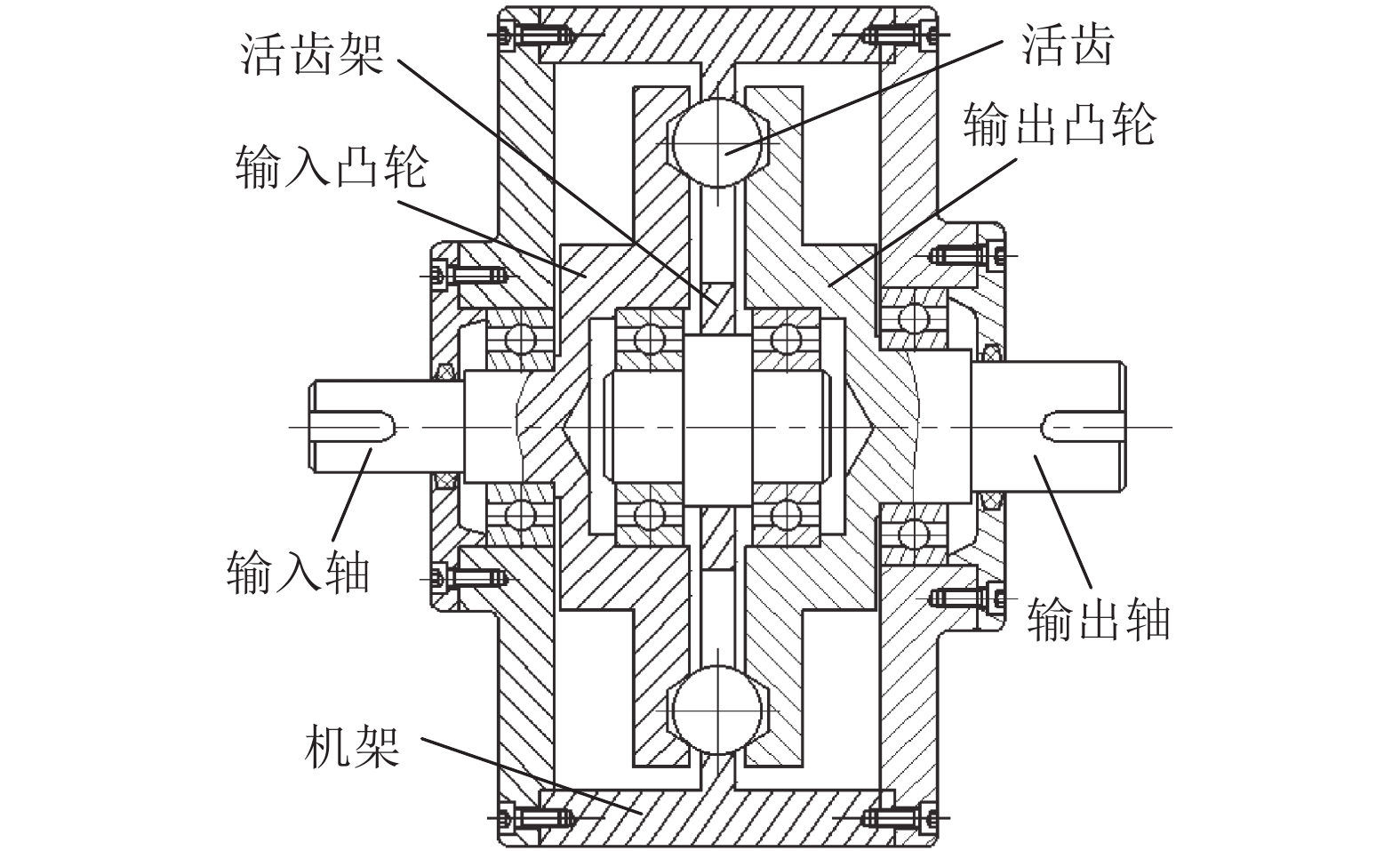 |
| 图1 摆动输出活齿凸轮机构结构简图 Fig. 1 Structure sketch of swing output movable teeth cam mechanism |
1 机构组成与传动原理
摆动输出活齿凸轮机构的结构简图如图1所示,机构主要包括输入轴、输入凸轮、活齿架、钢球活齿、输出凸轮、输出轴及机架等构件。其中:输入轴与输入凸轮连为一体构成输入组件作为激波器;活齿架与机架连为一体构成固定组件;输出凸轮与输出轴连为一体构成输出组件;活齿作为传动中介体,时刻处于输入凸轮与输出凸轮实际廓面的交错区域中,其在输入凸轮实际廓面的驱动下以及活齿架廓面的限制作用下推动输出组件作摆动输出。
2 凸轮理论廓线方程与实际廓面方程凸轮曲线是从动件按照某种运动规律输出的曲线,影响着机构的运动和动力特性。在摆动输出活齿凸轮机构中,输入凸轮理论廓线为余弦曲线;活齿架理论廓线为直线;输出凸轮理论廓线为多条相同的连续非封闭曲线。活齿、活齿架及输入、输出凸轮的实际廓面类型分别为球面、直廓面和V型槽面[12]。
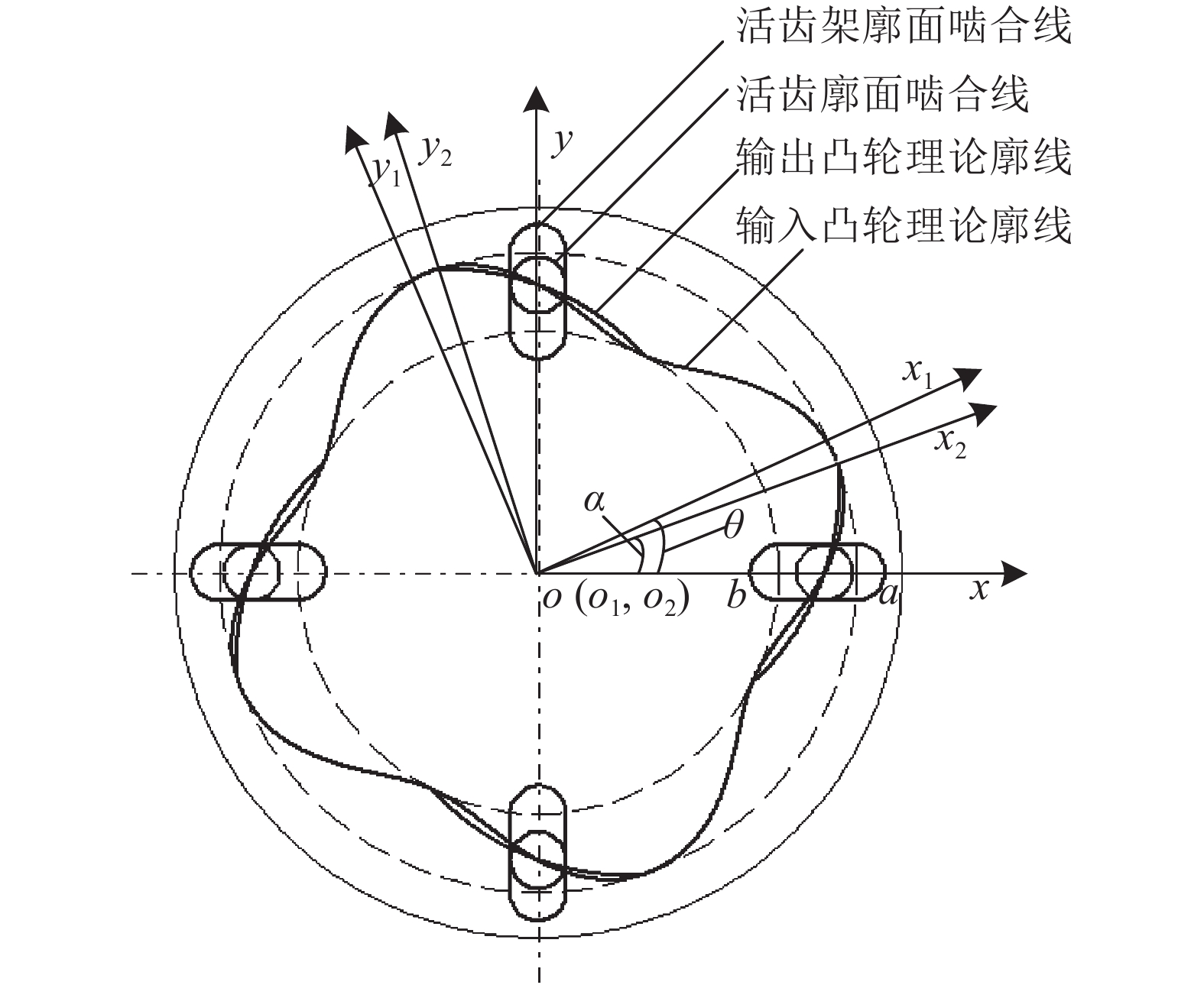 |
| 图2 输出凸轮理论廓线形成原理 Fig. 2 Formation principle of output cam theoretical profile line |
2.1 输入、输出凸轮理论廓线方程
如图2、3所示,分别建立活齿架、输入凸轮、输出凸轮连体坐标系
输入凸轮理论廓线为余弦曲线,其方程为:
| $\left\{ \begin{aligned}&x = P\cos \ \theta ,\\&y = P\sin \ \theta \end{aligned} \right.$ | (1) |
式中,
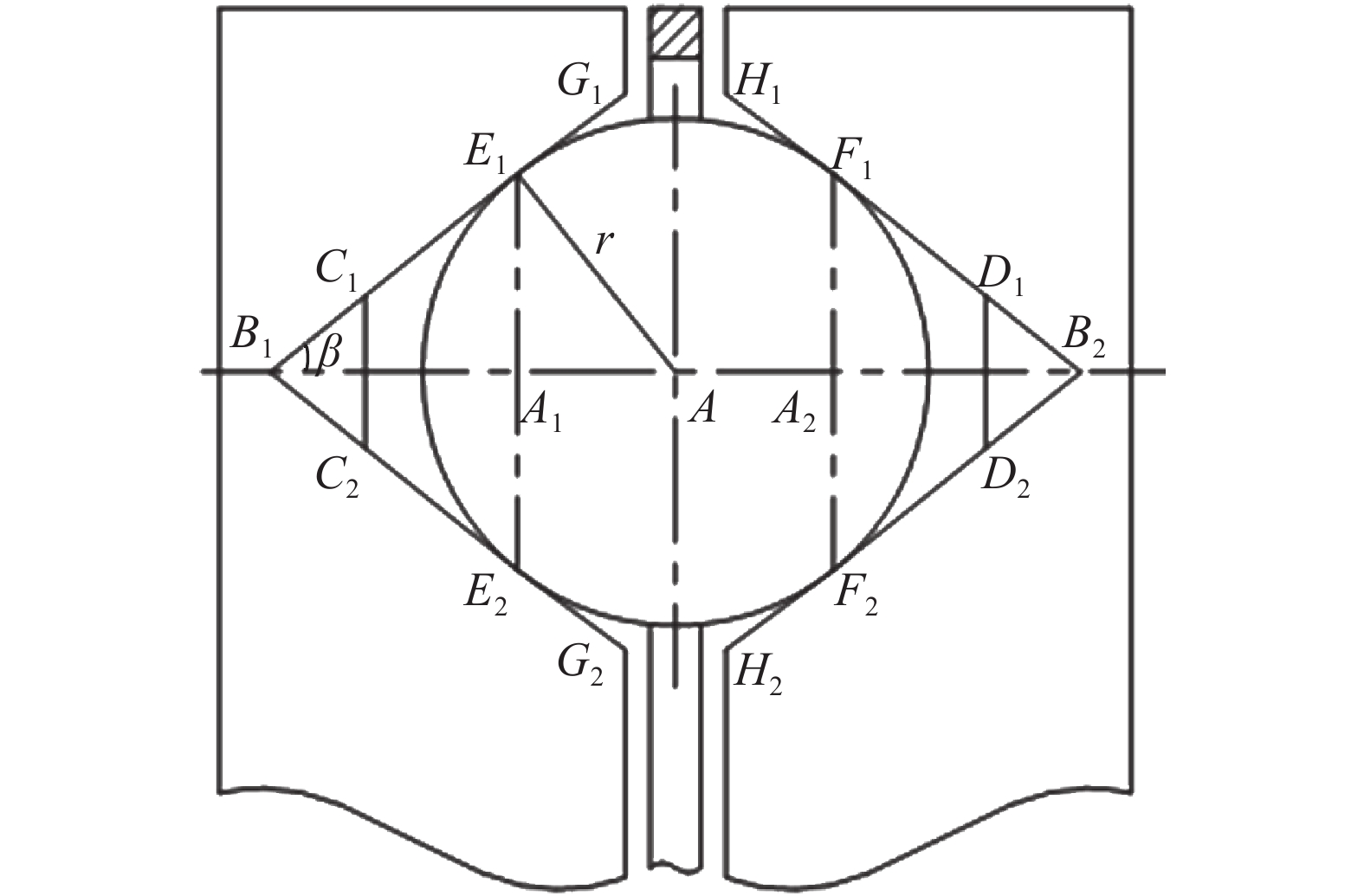 |
| 图3 啮合副径向剖视图 Fig. 3 Radial sectional view of the meshing pair |
令输入凸轮连体坐标系
| $\left\{ \begin{aligned}&X = P\cos \left( { - \alpha } \right),\\&Y = P\sin \left( { - \alpha } \right)\end{aligned} \right.$ | (2) |
式中,
参考文献[12]所述推导V型廓面方程的方法,建立输入凸轮内侧、外侧廓面方程为:
| $\left\{ \begin{aligned}& {x_1} = P\cos \ \theta - \frac{{{{y_T}'}}}{{\sqrt {{{({{x_T}'})}^2} + {{({{y_T}'})}^2}} }}r\cos \ \beta {t_{\rm i1}},\\& {y_1} = P\sin \ \theta + \frac{{{{x_T}'}}}{{\sqrt {{{({{x_T}'})}^2} + {{({{y_T}'})}^2}} }}r\cos \ \beta {t_{\rm i1}},\\& {{\textit{z}}_1} = r\cos \ \beta \cot \ \beta \left( {{t_{\rm i1}} - 1} \right)\end{aligned} \right.$ | (3) |
| $\left\{ \begin{aligned}& {x_2} = P\cos \ \theta + \frac{{{{y_T}'}}}{{\sqrt {{{({{x_T}'})}^2} + {{({{y_T}'})}^2}} }}r\cos \ \beta {t_{\rm i2}},\\& {y_2} = P\sin \ \theta - \frac{{{{x_T}'}}}{{\sqrt {{{({{x_T}'})}^2} + {{({{y_T}'})}^2}} }}r\cos \ \beta {t_{\rm i2}},\\& {{\textit{z}}_2} = r\cos \ \beta \cot \ \beta \left( {{t_{\rm i2}} - 1} \right)\end{aligned} \right.$ | (4) |
式中:
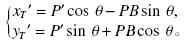
|
式中,
同理,可得输出凸轮内、外侧实际廓面方程分别为
| $\left\{ \begin{aligned}& {X_1} = P\cos \left( { - \alpha } \right) + \frac{{{{Y_T}'}}}{{\sqrt {{{({{X_T}'})}^2} + {{({{Y_T}'})}^2}} }}r\cos \ \beta {t_{\rm o1}},\\& {Y_1} = P\sin \left( { - \alpha } \right) - \frac{{{{X_T}'}}}{{\sqrt {{{({{X_T}'})}^2} + {{({{Y_T}'})}^2}} }}r\cos \ \beta {t_{\rm o1}},\\& {Z_1} = r\cos \ \beta \cot \ \beta \left( {{t_{\rm o1}} - 1} \right)\end{aligned} \right.$ | (5) |
| $\left\{ \begin{aligned}& {X_2} = P\cos \left( { - \alpha } \right) - \frac{{{{Y_T}'}}}{{\sqrt {{{({{X_T}'})}^2} + {{({{Y_T}'})}^2}} }}r\cos \ \beta {t_{\rm o2}},\\& {Y_2} = P\sin \left( { - \alpha } \right) + \frac{{{{X_T}'}}}{{\sqrt {{{({{X_T}'})}^2} + {{({{Y_T}'})}^2}} }}r\cos \ \beta {t_{\rm o2}},\\& {Z_2} = r\cos \ \beta \cot \ \beta \left( {{t_{\rm o2}} - 1} \right)\end{aligned} \right.$ | (6) |
式中,参数
| $\left\{ \begin{aligned}&{{X_t}'} = P'\cos \left( { - \alpha } \right) + AP\sin \left( { - \alpha } \right),\\&{{Y_t}'} = P'\sin \left( { - \alpha } \right) - AP\cos \left( { - \alpha } \right)\end{aligned}\right.$ |
式中,
凸轮理论廓线的曲率是描述凸轮实际廓面几何特性的重要参数,影响了实际廓面的弯曲程度以及活齿半径的选取,同时也是传动机构承载能力评估以及润滑情况的重要参考依据之一。
3.1 输入、输出凸轮理论廓线曲率分析根据微分几何可知,凸轮理论廓线在平面直角坐标系中的曲率及曲率半径公式分别为:
| $k = \frac{{x'y'' - y'x''}}{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}}}$ | (7) |
| $\rho = 1/k$ | (8) |
式中,
| $\left\{ \begin{align}& x'' = P''\cos \ \gamma - 2CP' \sin \ \gamma - {C^2}P\cos \ \gamma, \\& y'' = P{''}\sin \ \gamma + 2CP' \cos \ \gamma - {C^2}P\sin \ \gamma \text{。}\end{align}\right.$ |
式中,
在如表1所示的参数条件下,输入、输出凸轮理论廓线的曲率分别如图4、5所示。
| 表1 理论廓线参数 Tab. 1 Parameters of theoretical profile line |
 |
综合分析式(8)和图4、5可知,对于输入凸轮:当
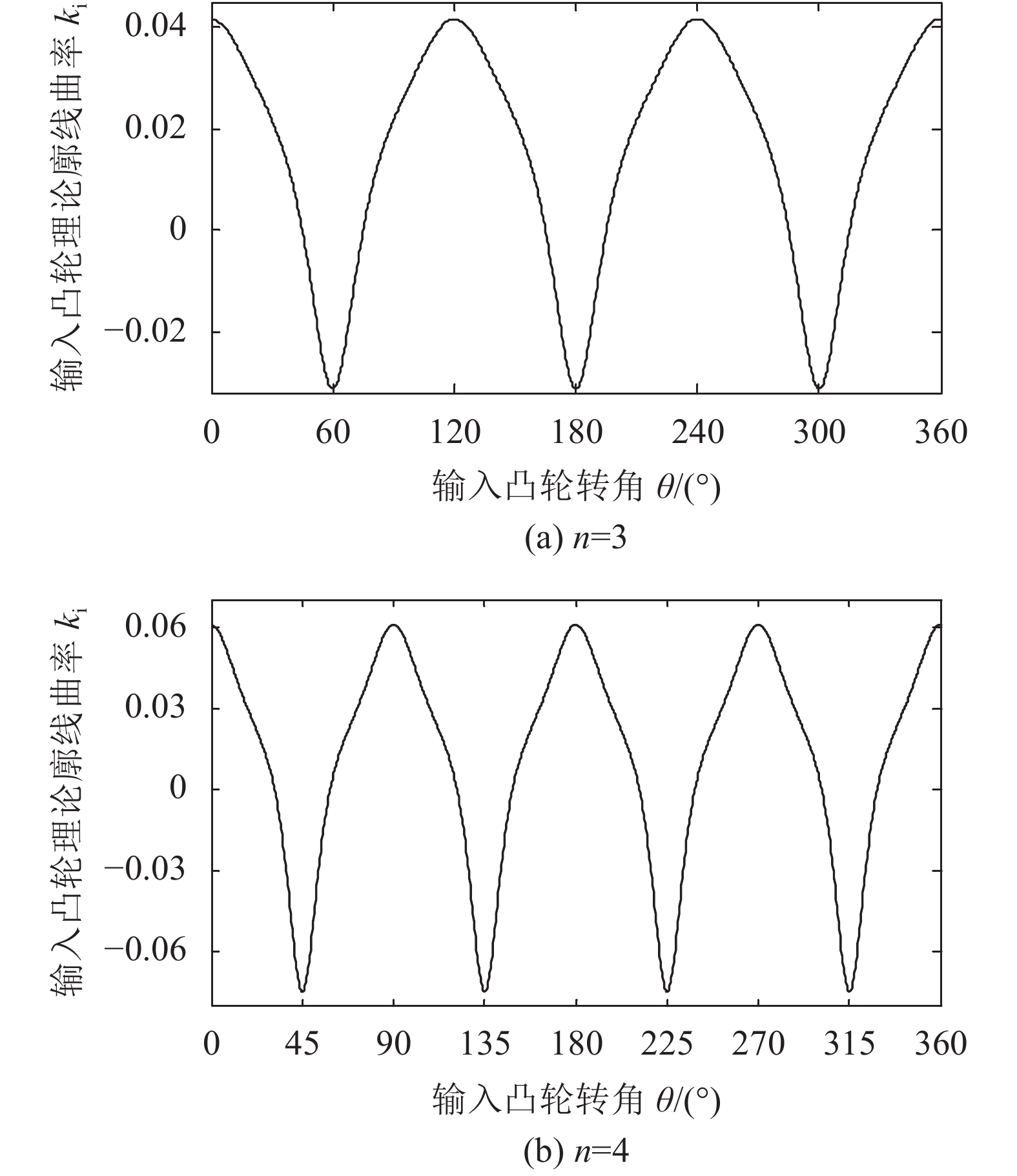 |
| 图4 输入凸轮理论廓线曲率 Fig. 4 Curvature of input cam theoretical profile line |
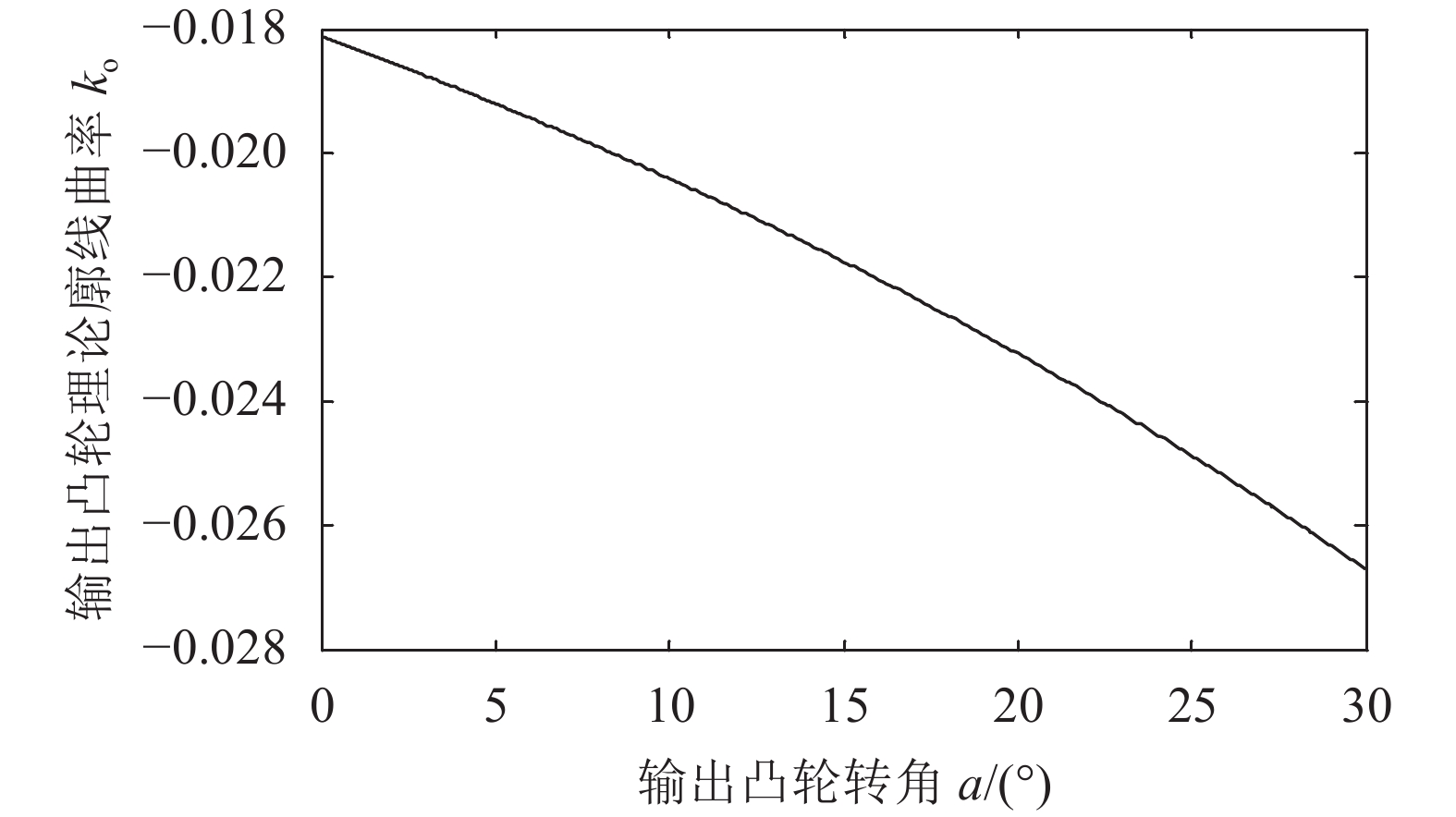 |
| 图5 输出凸轮理论廓线曲率 Fig. 5 Curvature of output cam theoretical profile line |
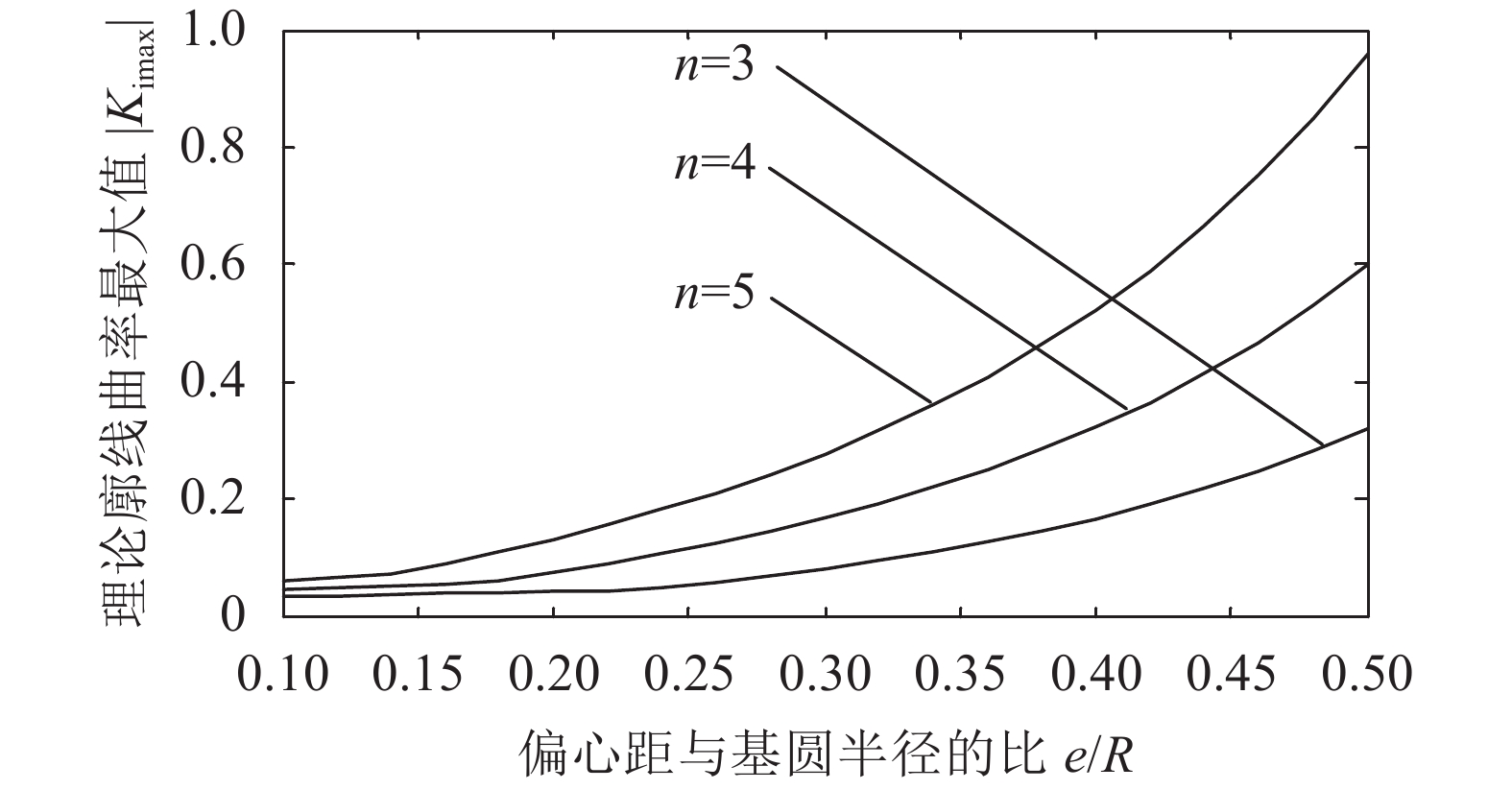 |
| 图6 R=50时,输入凸轮理论廓线曲率最大值 Fig. 6 When R=50, maximum value of curvature of input cam theoretical profile line |
3.2 参数对凸轮理论廓线曲率最大值的影响
输入凸轮理论廓线曲率最大值随偏心距与基圆半径的比
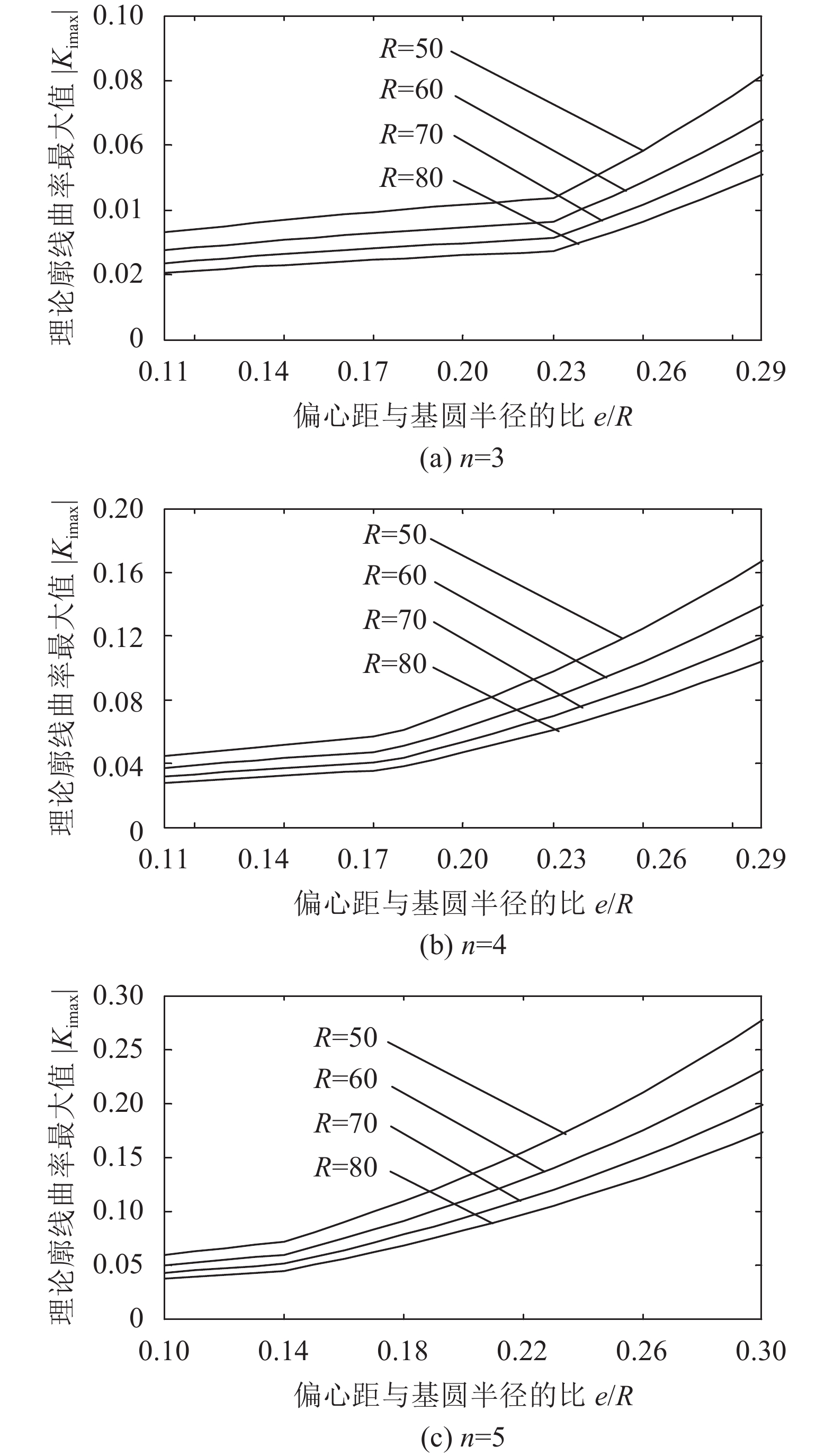 |
| 图7 不同齿数条件下输入凸轮理论廓线曲率最大值 Fig. 7 Under the condition of different number of teeth, maximum value of curvature of input cam theoretical profile line |
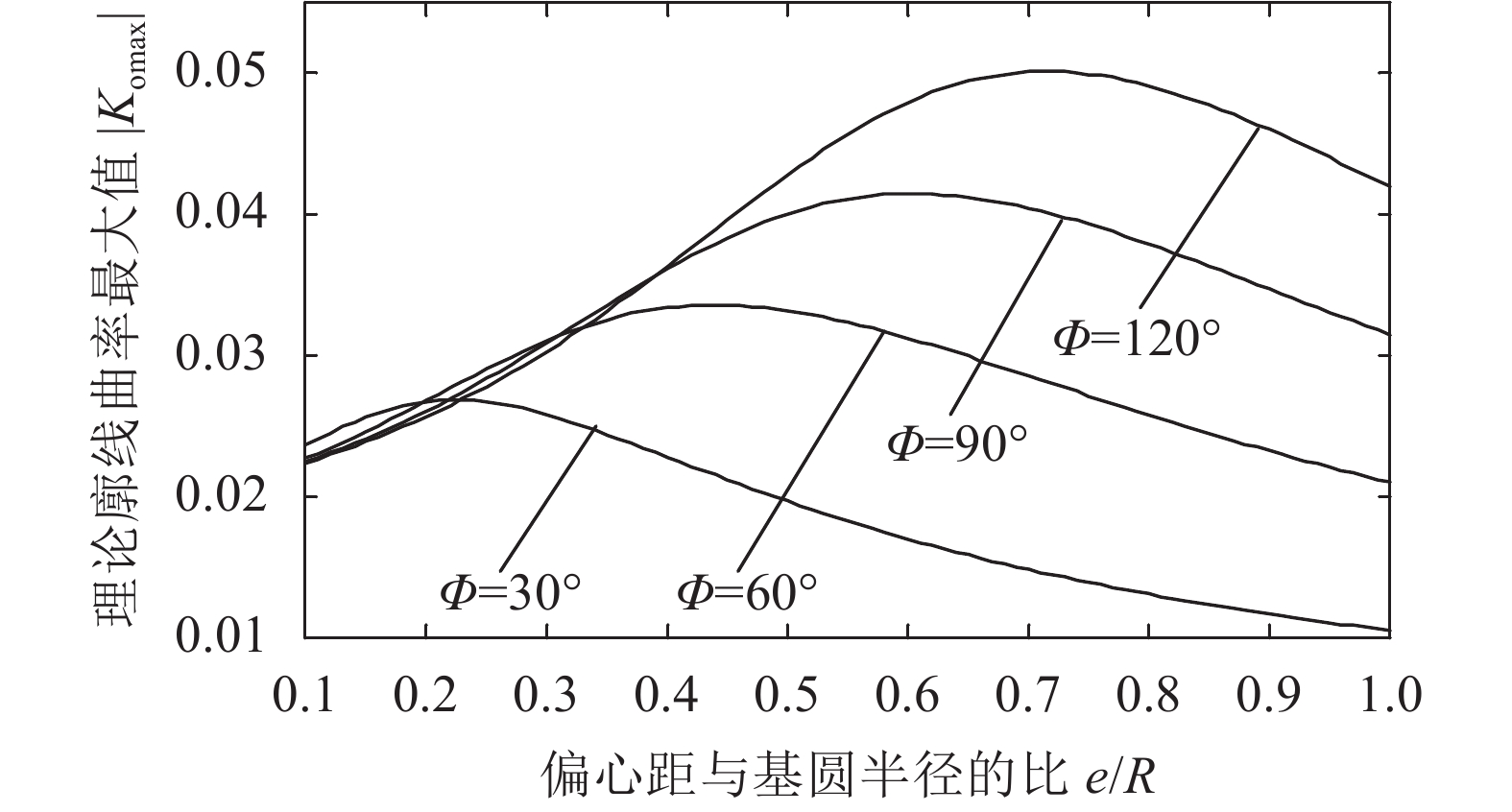 |
| 图8 R=50时,简谐曲线规律下输出凸轮理论廓线曲率最大值 Fig. 8 Under the condition of R=50 and harmonic curve, maximum value of curvature of output cam theoretical profile line |
简谐曲线规律下输出凸轮理论廓线曲率最大值随偏心距与基圆半径的比
 |
| 图9 简谐曲线规律下输出凸轮理论廓线曲率最大值 Fig. 9 Under the condition of harmonic curve, maximum value of curvature of output cam theoretical profile line |
4 凸轮实际廓面干涉分析 4.1 凸轮实际廓面截线曲率半径
由凸轮实际廓面方程可知,当廓面参数
| ${\rho _1} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}}}{{x'y'' - y'x''}}} \right| \pm {t_1}r\cos \ \beta $ | (9) |
| ${\rho _2} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}}}{{x'y'' - y'x''}}} \right| \pm {t_2}r\cos \ \beta $ | (10) |
式(9)、(10)中,“±”号与凸轮理论廓线的凹凸性有关。内侧实际廓面截线凸、凹分别取“﹢”“﹣”号,外侧实际廓面截线则与之相反[12]。
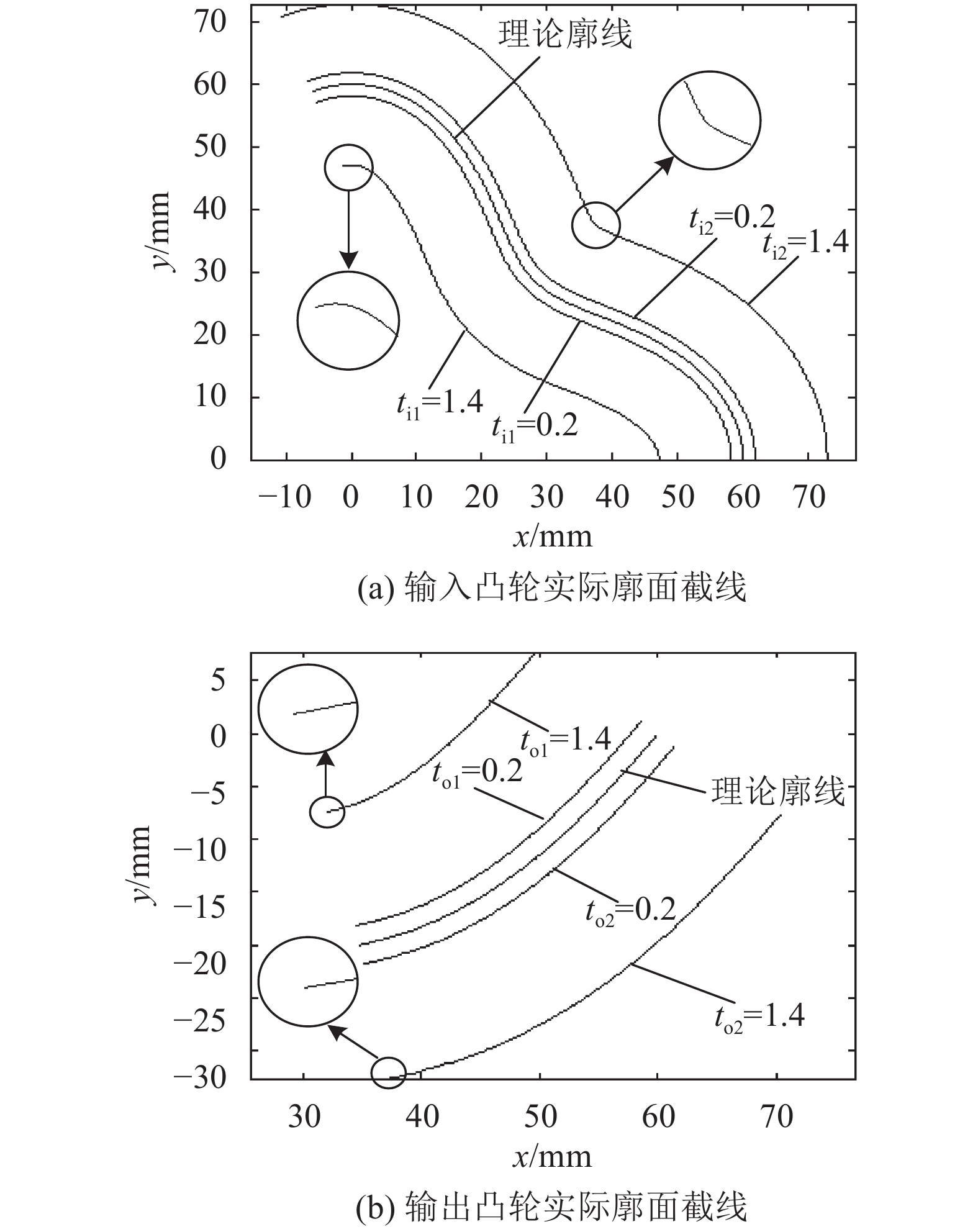 |
|
图10 |
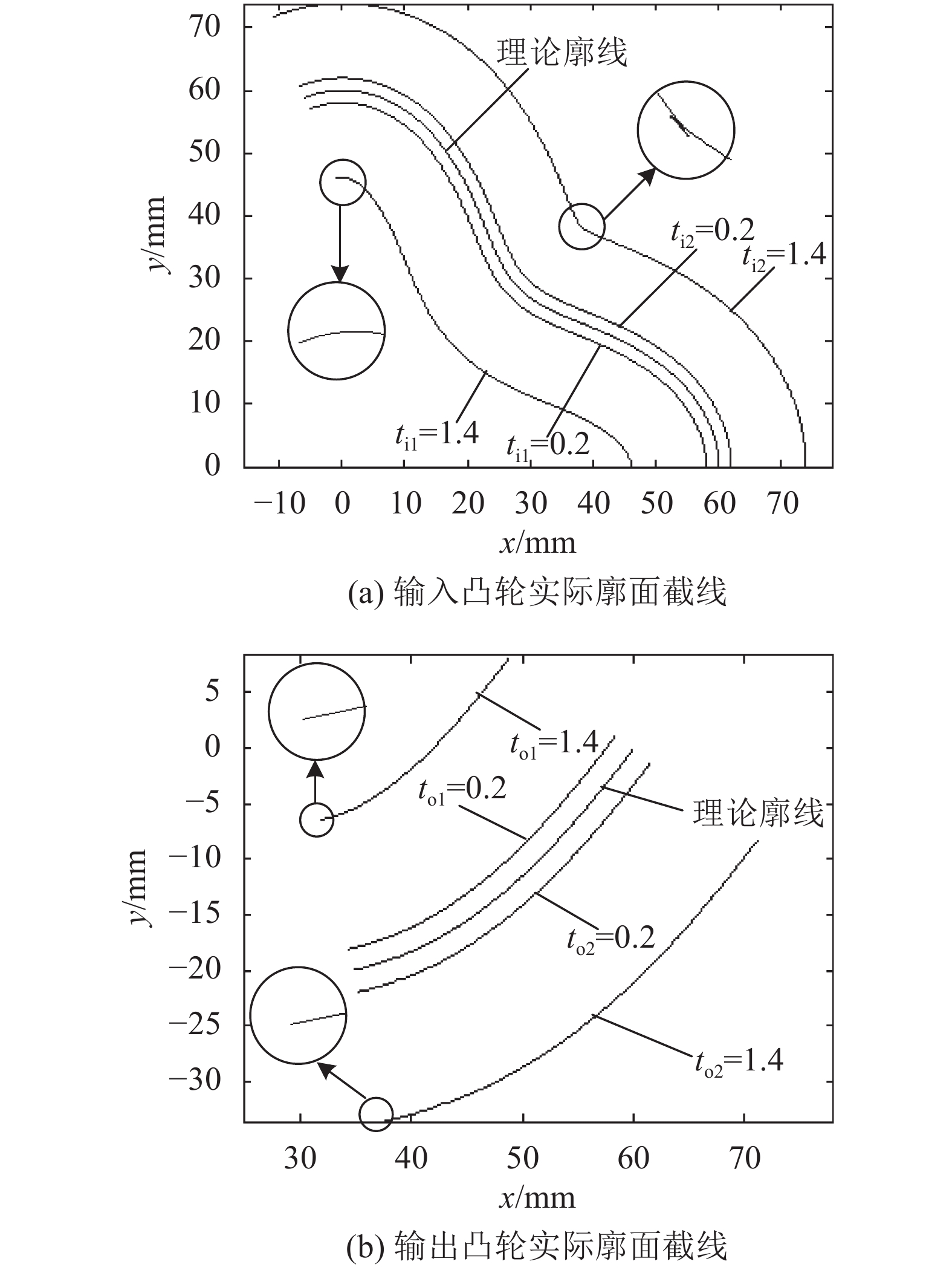 |
|
图11 |
4.2 凸轮实际廓面不干涉条件
凸轮实际廓面上任意一点处最小法曲率
| ${k_{\rm max}} = k/ \cos\ \beta $ | (11) |
进而,由式(9)、(10)可得凸轮内、外侧实际廓面主曲率半径分别为:
| ${\rho _{1\min }} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}\cos \ \beta }}{{x'y'' - y'x''}}} \right| \pm {t_1}r{\cos ^2}\ \beta $ | (12) |
| ${\rho _{2\min }} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}\cos \ \beta }}{{x'y'' - y'x''}}} \right| \pm {t_2}r{\cos ^2}\ \beta $ | (13) |
当给定参数取值范围
| ${\rho _{1\min }} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}\cos \ \beta }}{{x'y'' - y'x''}}} \right| - {t_1}r{\cos ^2}\ \beta \ge 0$ | (14) |
| ${\rho _{2\min }} = \left| {\frac{{{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right)}^{\frac{3}{2}}}\cos \ \beta }}{{x'y'' - y'x''}}} \right| - {t_2}r{\cos ^2}\ \beta \ge 0$ | (15) |
由3.1节可知,表1所示的参数条件下输入、输出凸轮理论廓线曲率最大值分别为|
1)提出了一种新颖的摆动输出活齿凸轮机构,具有结构紧凑、摆角范围宽、运动规律多样等优点,扩展了活齿传动的应用范围。
2)分析了摆动输出活齿凸轮机构的结构组成及传动原理,推导了凸轮理论廓线方程和实际廓面方程的一般表达式。
3)输入、输出凸轮理论廓线曲率最大值随比值
4)在理论分析的基础上,结合凸轮理论廓线曲率的变化规律,给出了凸轮实际廓面不发生干涉的条件。
| [1] |
曲继方.活齿传动理论[M].北京:机械工业出版社,1993.
|
| [2] |
Zhao Chunke,Liang Shangming,Zhang Jie.Tooth profile analysis and simulation of the tow-tooth difference swing-rod movable teeth transmission[J].Journal of Sichuan University(Engineering Science Edition),2015,47(Supp1):151–157. [赵纯可,梁尚明,张杰.二齿差摆杆活齿传动的齿形分析与仿真[J].四川大学学报(工程科学版),2015,47(增刊1):151–157.] http://kns.cnki.net/KCMS/detail/detail.aspx?filename=sclh2015s1026&dbname=CJFD&dbcode=CJFQ
|
| [3] |
Liang Shangming, Zhou Jian, Li Hua. Study on modal of two-tooth difference swing-rod movable teeth transmission based on thermal analysis[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(6): 99-104. [梁尚明, 周剑, 李华. 基于热分析的二齿差摆杆活齿传动中心轮模态研究[J]. 四川大学学报(工程科学版), 2016, 48(6): 99-104.] |
| [4] |
Xu Lizhong, Liang Yongli. Torque for an electromagnetic harmonic movable tooth drive system[J]. Mechanism and Machine Theory, 2016, 98(2): 190-198. |
| [5] |
Xu Lizhong, Li Chong. Coupled dynamics for an electromechanical integrated harmonic piezodrive system[J]. Journal of the Brazilian Society of Mechanical Science & Engineering, 2014, 39(12): 9137-9159. |
| [6] |
Xu Lizhong,Li Huaiyong.An electro-mechanical integrated harmonic piezodrive system[C]//Proceedings of the 2014 IEEE International Symposium on Intelligent Control.Piscateway:IEEE,2014:274–276.
|
| [7] |
Yi Yali, Liu Pengpeng, An Zijun. Tooth profile design and meshing characteristics analysis for any tooth-differenc pure rolling movable tooth transmission[J]. Chinese Journal of Mechanical Engineering, 2016, 52(11): 50-56. [宜亚丽, 刘朋朋, 安子军. 任意齿差纯滚动活齿传动齿形设计方法及啮合特性研究[J]. 机械工程学报, 2016, 52(11): 50-56.] |
| [8] |
Li Jianfeng, He Aiying, Dong Xinrui. Geometrical design of the movable rolling tooth transmission with cam actuating[J]. Chinese Journal of Mechanical Engineering, 2011, 47(1): 24-30. [李剑锋, 何爱颖, 董新蕊. 凸轮激波滚动活齿传动的几何设计[J]. 机械工程学报, 2011, 47(1): 24-30.] |
| [9] |
Li Jianfeng, Dong Xinrui. Method of meshing force analysis for the movable rolling tooth transmission with cam actuating[J]. Chinese Journal of Mechanical Engineering, 2008, 44(5): 39-44. [李剑锋, 董新蕊. 凸轮激波滚动活齿传动的啮合力分析方法[J]. 机械工程学报, 2008, 44(5): 39-44.] |
| [10] |
Shen Yu, Yang Yuhu, Zhang Dawei. Kinetostatic analysis of a new type of oscillating tooth indexing cam mechanism[J]. Journal of Tianjin University(Science and Technology), 2008, 41(8): 972-977. [沈煜, 杨玉虎, 张大卫. 新型活齿分度凸轮机构的原理及动态静力分析[J]. 天津大学学报(自然科学与工程技术版), 2008, 41(8): 972-977.] |
| [11] |
Liu Dawei, Ren Tingzhi, Zhang Yulin. Transmission theory and typical structure of nonuniform mechanism with movable teeth[J]. Chinese Journal of Mechanical Engineering, 2014, 50(1): 47-54. [刘大伟, 任廷志, 章裕琳. 非匀速活齿机构的传动原理及典型结构[J]. 机械工程学报, 2014, 50(1): 47-54.] |
| [12] |
Li Jianfeng, Su Jian, Chen Xing. Tooth profile equation and interference analysis of two-tooth difference steel ball movable tooth transmission[J]. Journal of Beijing University of Technology, 2014, 40(5): 641-647. [李剑锋, 苏健, 陈兴. 二齿差钢球活齿传动的齿廓方程及齿廓干涉分析[J]. 北京工业大学学报, 2014, 40(5): 641-647.] |
| [13] |
刘昌祺,刘庆立,蔡昌蔚.自动机械凸轮机构实用设计手册[M].北京:科学出版社,2013.
|
| [14] |
傅则绍.微分几何与齿轮啮合原理[M].东营:石油大学出版社,1999.
|
 2018, Vol. 50
2018, Vol. 50

