2. 河海大学 港口海岸与近海工程学院,江苏 南京 210098
2. College of Harbour Coastal and Offshore Eng.,Hohai Univ.,Nanjing 210098,China
潮波进入河口以后,变形进一步加剧,在一定条件下,形成水位遽然升高的涨潮潮波前峰线,即为涌潮。涌潮是向河口上游推进的波列,强度比较小时,表面无破碎,为波状涌潮;强度变大时,表面破碎,发展成漩滚涌潮,即为强涌潮。强涌潮潮波与落潮流相遇后,潮波破碎,卷入大量空气,潮头形成乳白色的水气混合体,溯源挺进,气势汹涌,甚为壮观。
针对涌潮这一独特的水力学现象,国内外学者进行了系统的观测调查及研究。Abbott[1]、Dracos等[2]、Whitham等[3]用波前展开法研究了浅水流中涌潮形成条件和形成地点;Tricker[4]和Lynch[5]认为涌潮的形态依赖于涌潮下游水深与上游水深的比值,若比值接近于1,涌潮形态不破碎,若比值接近1.4,涌潮就破碎;Koch等[6]应用水槽试验研究了自由表面能否破碎的Froude数临界值;Madsen等[7]和Svendsen等[8]研究了涌波的紊动;Yeh等[9]应用模型试验研究了涌波的紊动以及与水跃的差异;Chanson[10]应用模型试验研究了波状涌潮的流场;Wolanskia等[11]根据实测涌潮水位、流速、泥沙等资料分析戴利河口波状涌潮的水动力特性;Chanson等[12]观测了法国加仑河的涌潮过程及其含沙量变化;Chanson[13]还对圣米歇尔山海湾水域涌潮到达前后的轰鸣声进行了观测记录,分析了其变化规律;Simpson等[14]应用英国迪河河口的观测资料,分析了涌潮水位、流速、雷诺剪切应力和紊动动能等因素。国外学者大多针对自由表面尚未破碎的波状涌潮的水力学结构进行过研究,这可能与国外涌潮大多较小有关。而国内学者主要针对钱塘江涌潮这一独特的强涌潮进行了深入的研究。林炳尧等[15]分析了涌潮的反射和碰撞,分析了不同形式反射现象的形成条件;曾剑等[16]应用BP神经网络建立了盐官站潮头高度的预测模型,定量地分析了潮量和径流量对涌潮形态的影响程度;潘存鸿等[17]根据一维连续性方程和动量方程推导了涌潮传播速度与上、下游水深的关系,建立了涌潮传播速度的解析计算公式和涌潮流速与潮前水深和涌潮高度的关系;杨火其等[18]分析了涌潮垂线平均流速与潮前水深、涌潮高度及涌潮传播速度的关系;黄静等[19–21]在玻璃水槽中模拟了波状涌潮和漩滚涌潮,研究了涌潮传播速度、涌潮高度、流速垂向分布等水动力学特征;谢东风等[22–23]利用实测资料初步研究了钱塘江涌潮的水动力学特性和紊动特性。考虑到涌潮潮头的掺气与水跃掺气的相似性,Hager[24]主要研究了经典水跃的水跃翻滚的长度;Chanson[25]在实验室内研究了强水跃和稳定水跃的气泡两相流特性;Chanson等[26]研究了强涌潮潮头破碎时的紊动特性,发现其呈现出与传统的稳定水跃结果类似的自相似分布规律;Leng等[27]对强涌潮潮头的翻卷传播特性进行了新的试验。综上所述,国内外众多学者针对涌潮的形态、传播速度、流场结构及紊流特性等方面做出了丰富的研究成果。前人的研究着重于涌潮的形成、传播及其蔚为壮观的景观形态,以及其与水跃掺气的相似特性等方面。
总之,强烈掺气的涌潮潮头具有强烈的紊动特性,其必然会对水域的环流结构、泥沙的输移、污染物的扩散,甚至于整个河口区域的生态平衡等都产生巨大的影响。因此,针对涌潮潮头的掺气特性,作者运用模型试验的方法在水槽中模拟涌潮的潮头,利用高速摄像系统记录涌潮潮头的立面2维形态,分析涌潮潮头的掺气过程及其变化规律,创新地引入涌潮潮头的掺气长度的概念,研究强涌潮潮头的相对掺气长度随涌潮强度和涌潮Froude数之间的关系,最终获得计算涌潮掺气长度的经验公式,并以此作为探究涌潮潮头掺气的量化特征。
1 涌潮潮头的模拟与验证试验在长50 m、宽1.2 m、高0.6 m的涌潮玻璃水槽中进行。涌潮产生设备由计算机控制系统和上下游变频器控制的多组水泵组成,利用变频调速器直接控制潜水泵转速以突然增加水槽前段的流量从而生成涌潮的潮头,可参见文献[19]。涌潮玻璃水槽模型示意图及其实现的涌潮潮头如图1所示。试验中,利用高速摄像系统(仪器实物如图2所示)记录潮头形态的变化情况。
 |
| 图1 涌潮玻璃水槽模型示意图及其实现的涌潮潮头 Fig. 1 Model of the glass rectangular flume and its generated tidal bores |
 |
| 图2 高速摄像记录系统 Fig. 2 System of high-speed camera |
影响涌潮大小的主要因素是径流和外海潮汐强弱。潮前水深和潮前落潮流速是径流因素,外海潮汐强弱可以由涌潮潮头传播速度和涌潮高度衡量。故选取潮前水深
图3给出了当
 |
|
图3 |
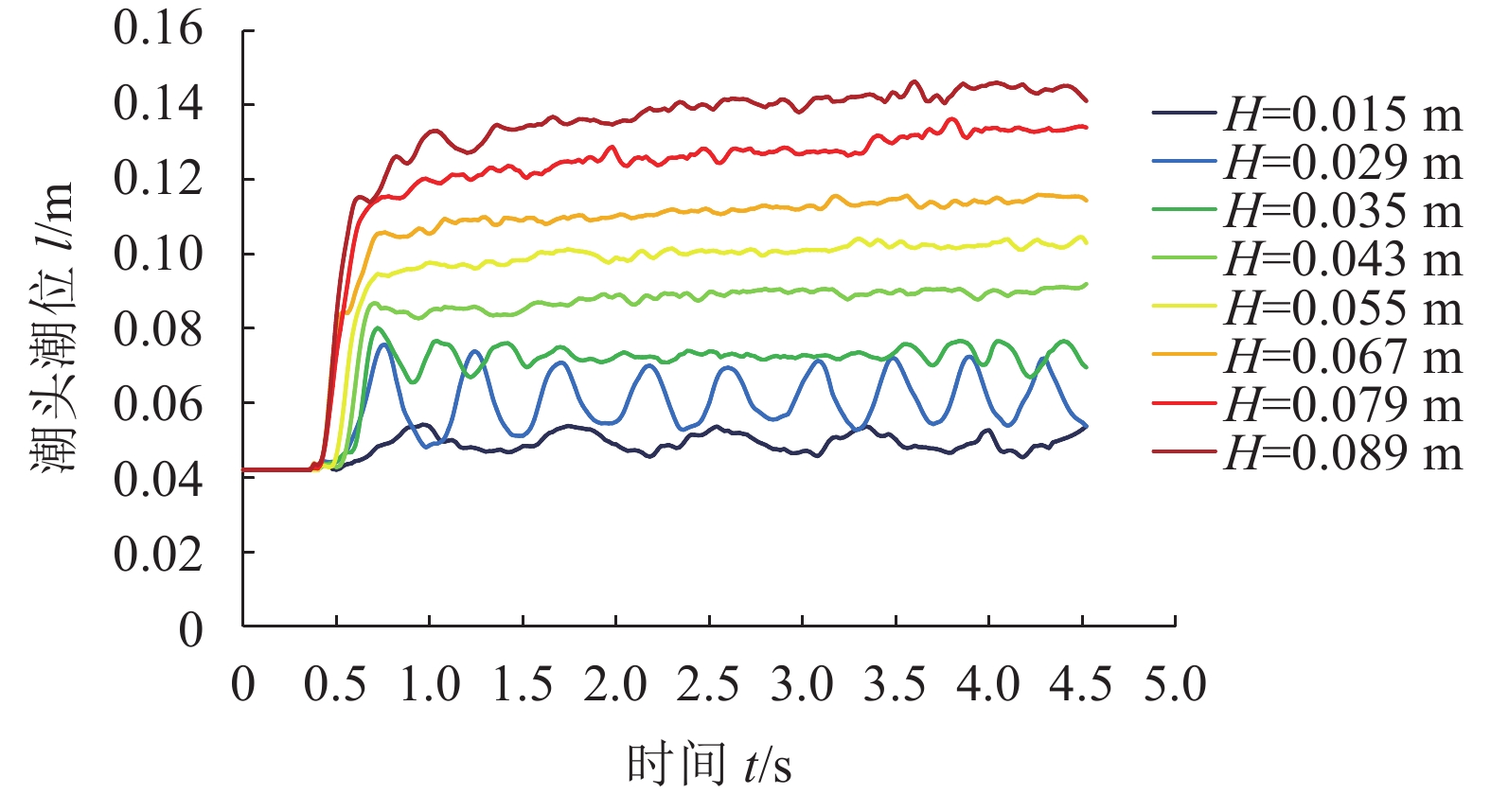 |
|
图4 |
 |
| 图5 钱塘江盐官河段观测到的涌潮形态 Fig. 5 Field observation of tidal bores in the Qiantang River |
利用水槽试验,Koch等[6]认为涌潮潮头自由表面能否破碎取决于涌潮的Froude数
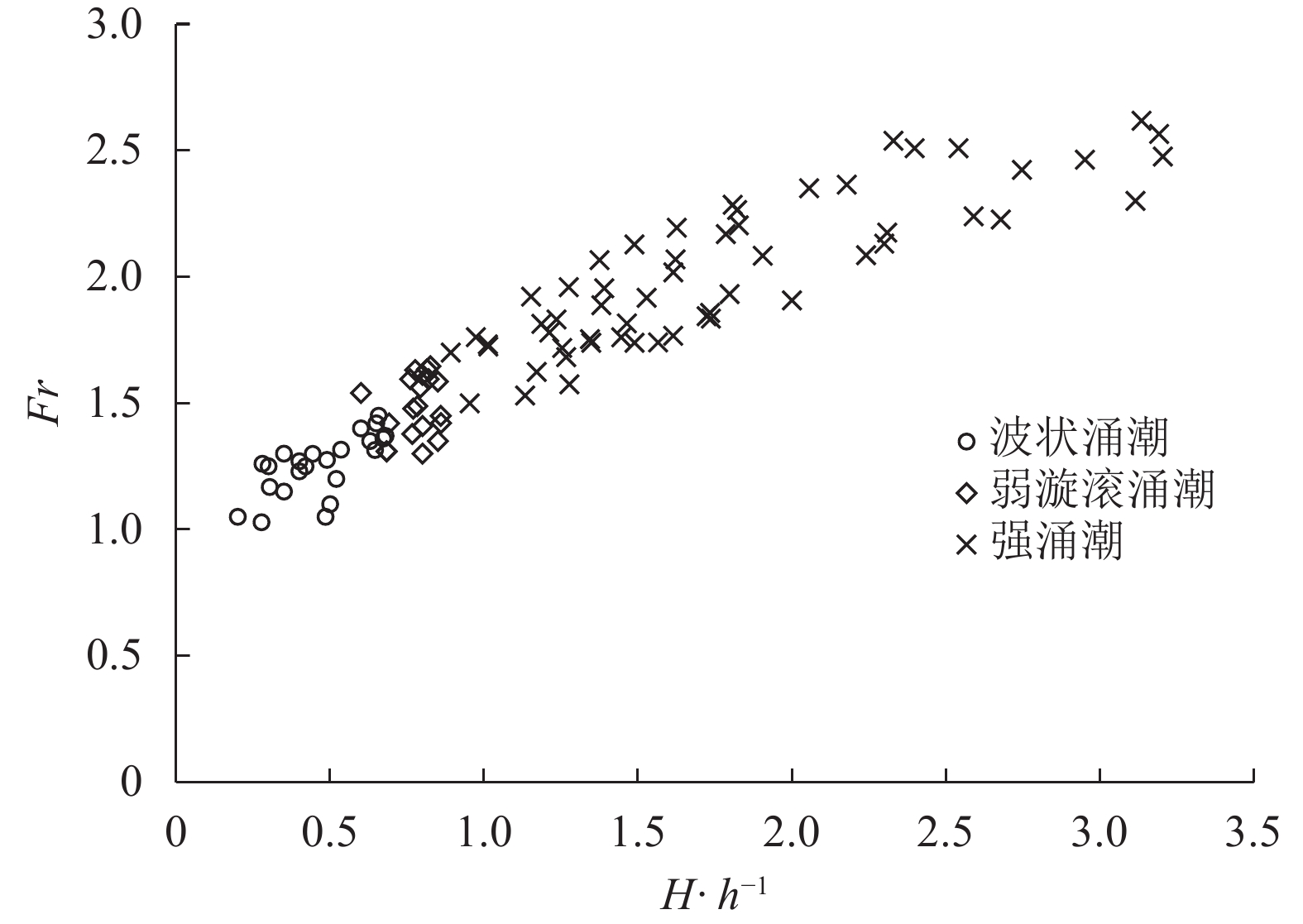 |
|
图6 涌潮形态与
|
2 涌潮潮头掺气的过程及其变化规律
涌潮潮头掺气的过程是涌潮潮波破碎卷入气体的过程。通过试验观测如图7所示,潮头掺气的过程主要有4个阶段。第1阶段,在涨潮潮波前峰峰面上,落潮水流相向运动,在交界面发生相互作用,气体以气体包的形式被卷入到水体中(图7(a));第2阶段,气体包被分裂成大量不同尺寸的气泡,气泡在随涌潮传播运动的过程中受到的湍流剪切应力远大于其表面张力,发生变形和破裂形成气泡云(图7(b));第3阶段,气泡云将在涌潮潮头运动的过程中开始向涌潮潮头表面逃逸,逃逸的气体使得潮头更加破碎,重新将气体以气体包的形式卷入到水体中(图7(c));第4阶段,重新卷入的气体包将受到第2阶段所形成的气泡云作用,发生变形、破裂,破裂后继续形成气泡云(图7(d))。试验中,随着涌潮潮头的继续向前运动,4个阶段的掺气过程将持续发生,在潮头后方不断地形成一系列的气泡云,气泡云在水体中运动最终向水体表面运动,并在潮头表面聚集,形成直径较大的气泡后破裂并逃逸。
 |
| 图7 试验中涌潮潮头掺气的过程示意 Fig. 7 Aeration process of the tide bore front |
涌潮潮头的形态随着潮头掺气的程度而变化。因此,试验中运用高速摄像系统采集不同涌潮高度情况下潮头的掺气形态,如图8、9、10所示。
 |
|
图8 |
如图8所示,在潮前水深为0.073 m、落潮流速为0 m/s时,涌潮潮头的高度小于0.06 m时,涌潮潮头呈波状,并随着潮头高度的增加波形也随之变化,从正弦波变为立波,波长变小;当涌潮潮头的高度大于0.06 m后,涌潮潮头开始部分破碎并开始掺气,随着涌潮的高度增加,潮头破碎的程度越大,使得卷入的气体越多,掺气的剧烈程度越大,也即潮头掺气的长度越大,掺入水体的气体在随涌潮潮头运动的距离也越长,掺入水体的气体也在随涌潮潮头向前运动的过程中呈现气泡云的形态向水面以下运动,气泡到达一定的水深后就开始向上运动。从图8中可知:涌潮潮头表面掺入的大片气体进入潮头后,将进一步发生变形和破裂,并沿水平和垂直方向扩散形成气泡云,气泡的直径大约为2~3 mm,部分气泡向深处运动,当涌潮高度大于0.14 m之后,气泡已可到达底板。随着潮头的前进,气泡到达最深处以后开始从深处向表面逸出,在逸出的过程中气泡直径变大,并且与向深处运动的气泡发生碰撞,气泡运动呈螺旋状,并在潮头向前运动的过程中逸出水面,在水面形成直径大约在6~9 mm的气泡,这些直径较大的气泡随后在潮水表面破裂后逃逸。
如图9和10所示,在潮前水深为0.073 m、落潮流速分别为0.2和0.3 m/s时,涌潮潮头的高度小于0.05 m时,涌潮潮头呈波状;当涌潮潮头的高度大于0.05 m后,涌潮潮头开始部分破碎并掺气,随着涌潮的高度增加,潮头破碎的程度越大,使得卷入的气体越多,掺气的剧烈程度越大,掺入水体的气体在随涌潮潮头运动的距离也越长,掺入水体的气体也在随涌潮潮头向前运动的过程中呈现气泡云的形态向水面以下运动,气泡到达一定的水深后开始向上运动。
 |
|
图9 |
 |
|
图10 |
从图9和10可知:涌潮潮头表面掺入的大片气体进入潮头后开始破碎为直径约为2~3 mm的气泡云向深处运动,当涌潮高度大于0.12 m之后,部分气泡已可到达底板。随着潮头的前进,气泡到达最深处以后开始向表面逸出,在逸出的过程中气泡直径变大,并且与向深处运动的部分气泡相遇后形成直径约4~8 mm的气泡,这些气泡呈螺旋状运动,并在潮头向前运动的过程中向潮水面运动,这些气泡在水面处相遇,形成直径约9~12 mm的气泡,这些直径较大的气泡随后在潮水表面破裂后逃逸。
通过对比图8、9和10可知:随着落潮流速的变大,涌潮潮头破碎时潮头的高度变小;而当涌潮潮头高度相同时,落潮流速越大,涌潮潮头陡度越大,潮头水体变形越剧烈,潮头破碎越剧烈,掺入的气体量也越大,到达水体底部的气泡也越多,气体在水体中运动的距离和运动的深度也越大。
3 涌潮潮头掺气的长度破碎涌潮的潮头有一个做剧烈翻腾滚动运动的表面漩滚,掺入了大量气体。涌潮潮头在运动过程中,从潮头表面漩滚起点的断面到潮后水体表面气泡云完全逸出点的断面之间的水平距离称为涌潮潮头的掺气长度
 |
|
图11 涌潮潮头掺气长度
|
在涌潮潮头运动过程中,涌潮潮头的掺气长度越大,则潮头对整个水域的环流结构、泥沙的输移、污染物的扩散及生态平衡等的影响就越大,故确定涌潮潮头掺气长度具有重要的实际意义。但是,具有强烈掺气的涌潮潮头的运动非常复杂,针对涌潮潮头掺气长度提出一个较完善的、可供实际应用的理论公式是非常困难的,因此本文利用试验资料求得涌潮潮头掺气长度的计算公式。
试验中,涌潮潮头的掺气长度
| $\frac{L}{h} = f\left( {\frac{H}{h},Fr} \right)$ | (1) |
当水深一定时,涌潮高度越大,涌潮潮头破碎越剧烈,紊动强度也越大,潮头掺气越剧烈,气体随潮头运动的距离越长;涌潮潮头的流速
| $L/h = f(H/h)$ | (2) |
| $L/h = f(Fr)$ | (3) |
通过对试验中不同水深
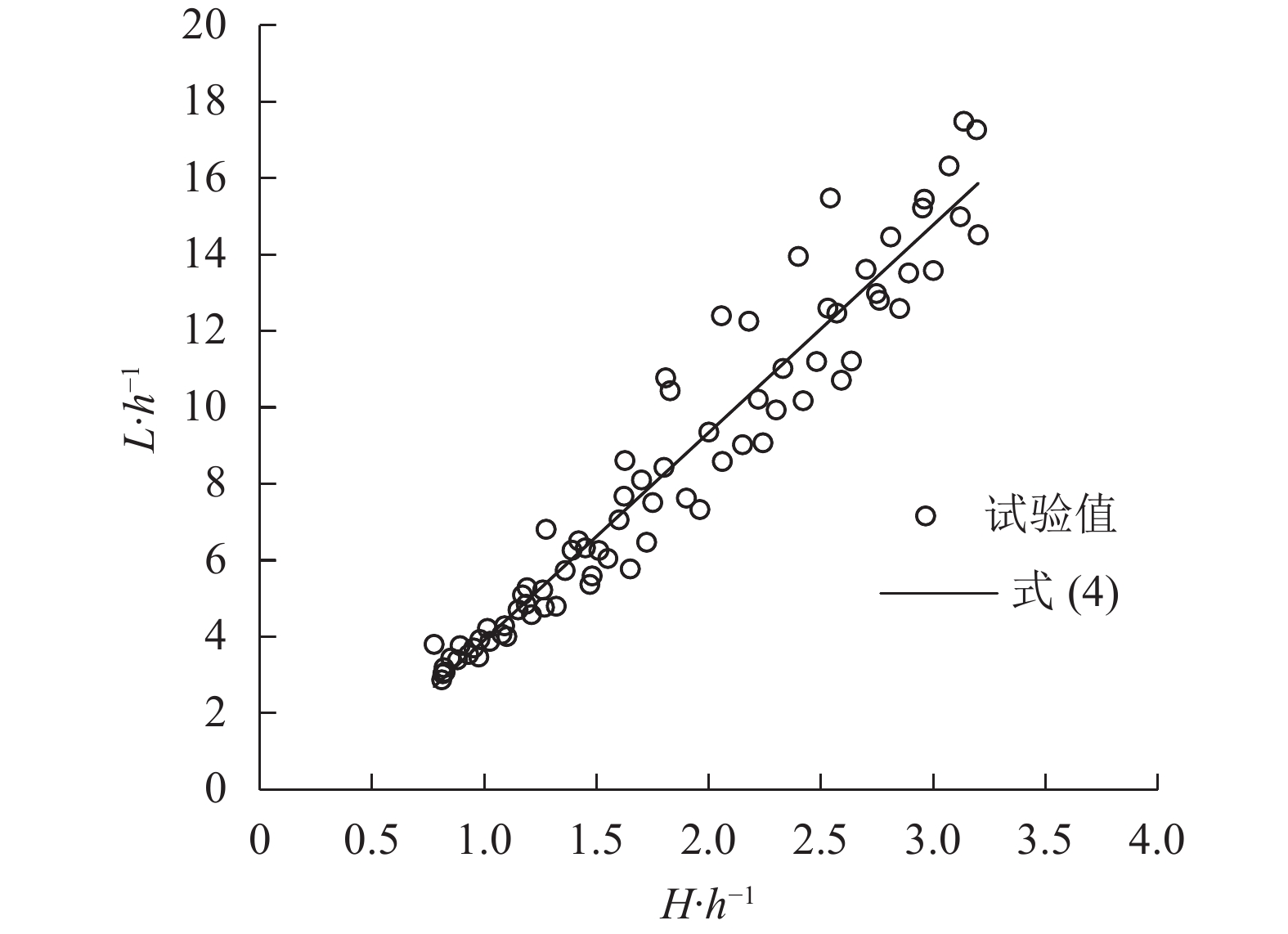 |
|
图12 |
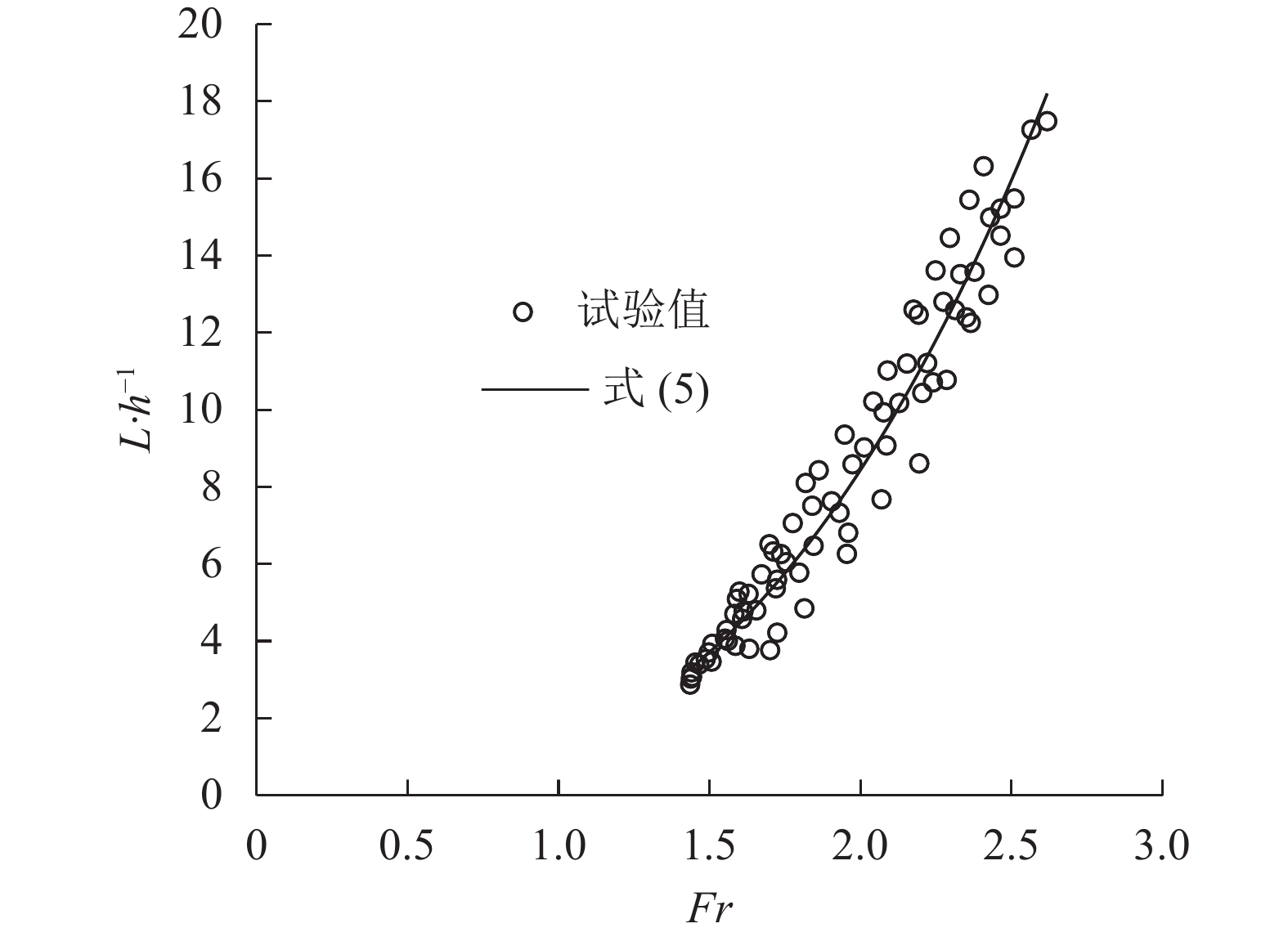 |
|
图13 |
图12中,通过数据拟合可知
| $L/h = 3.976\;5{(H/h)^{1.202\;6}},\;\;\;{R^2} = 0.91$ | (4) |
图13中,通过数据拟合可知
| $L/h = 1.169\;8F{r^{2.852\;6}},\;\;\;{R^2} = 0.95$ | (5) |
由式(4)、(5)知
式(4)、(5)分别单独地考虑涌潮强度
| $\frac{L}{h} = f\left( {\frac{H}{h},Fr} \right) = a{\left( {\frac{H}{h}} \right)^b}F{r^c}$ | (6) |
则通过对试验数据的二元非线性回归分析可得:
因此,强涌潮潮头相对掺气长度经验公式为:
| $L/h = 1.993{(H/h)^{0.555}}F{r^{1.592}}$ | (7) |
式中:
为验证式(7)的准确性,图14给出了涌潮潮头的相对掺气长度的试验值和式(7)计算值之间的对比关系,由图14可以看出式(7)对试验值的拟合关系非常好。
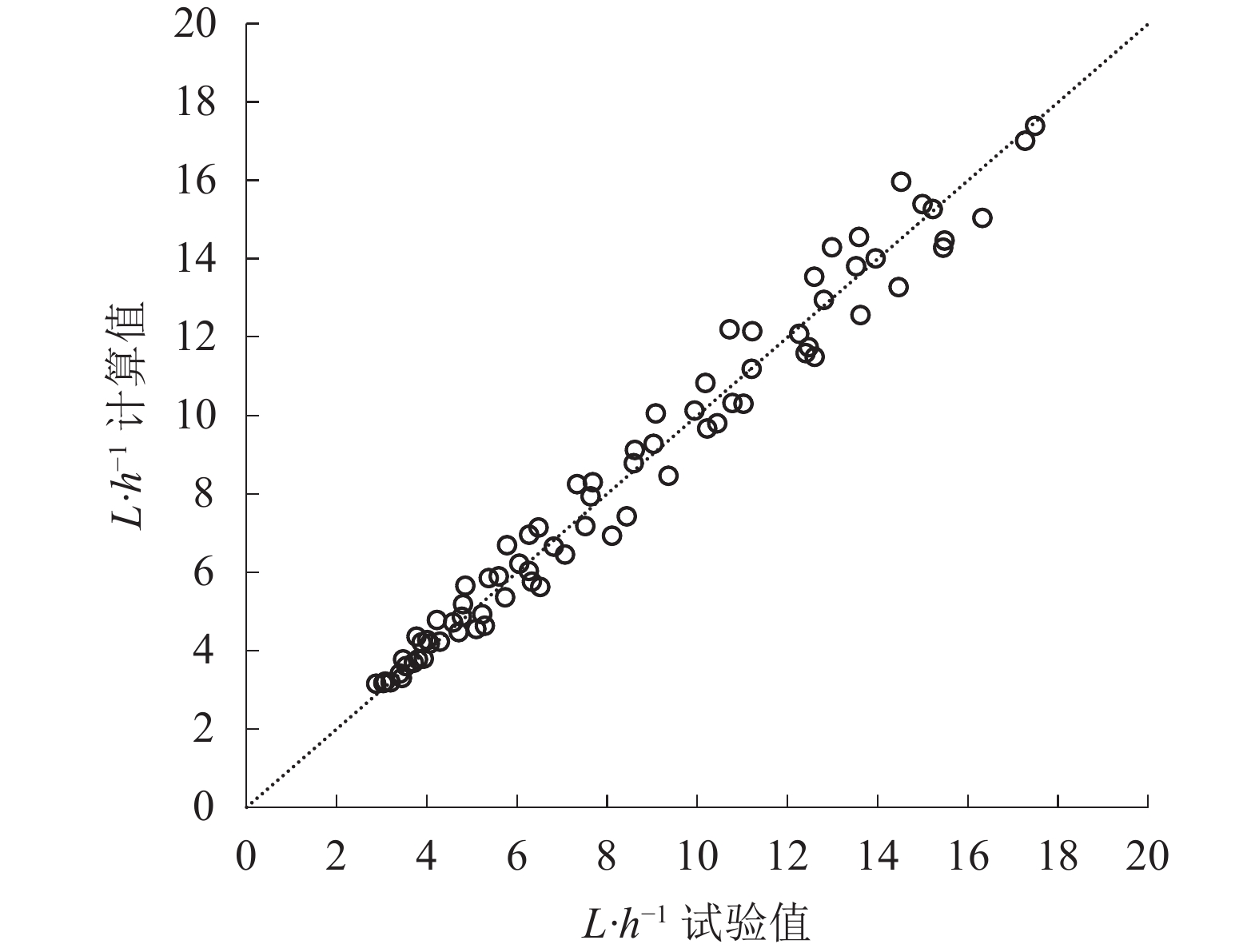 |
|
图14 |
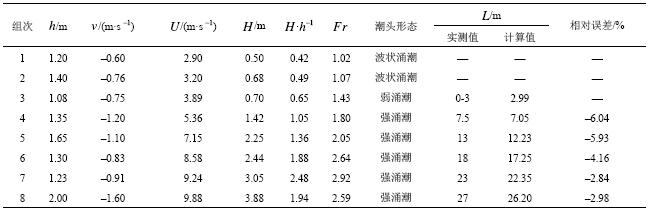
同时为了验证式(7)的实用性,对钱塘江盐官段涌潮潮头掺气长度的几组观测值与式(7)的计算值进行对比,结果如表1所示。
由表1中实测值与式(7)计算值的对比分析知,式(7)的计算结果小于实测值,主要原因可能是在试验中涌潮掺气的尺度与实际中涌潮掺气的尺度相比是较小的。但是,式(7)的计算结果与实测值的结果非常接近,相对误差比较小,这说明可以应用式(7)计算涌潮潮头的掺气长度。
| 表1 涌潮潮头掺气长度的实测值与式(7)计算值的对比 Tab. 1 Comparisons between the field observation and the experimental formula calculation |
 |
4 结 论
通过在玻璃水槽中实现涌潮潮头的准确模拟,并观测涌潮潮头掺气的状态提出了强涌潮潮头破碎后掺气的过程和状态,通过采集强涌潮潮头的掺气长度,研究了强涌潮潮头的相对掺气长度
1)涌潮形态的判别。当
2)潮头掺气的过程。潮头掺气的过程主要受4个阶段控制:涌潮水体与落潮水流相向运动,在交界面发生相互作用,气体首先以气体包的形式被卷入到水体中;在潮头水体与落潮水体产生强湍流对流过程中,气体包被分裂成大量不同尺寸的气泡,气泡变形和破裂后形成气泡云;气泡云向涌潮潮头表面逃逸,使得潮头更加破碎,重新将气体以气体包的形式卷入到潮头水体中;重新卷入的气体包发生变形、破裂,继续形成气泡云。随着涌潮潮头的继续向前运动,四个阶段的掺气过程不断重复,将在潮头后方不断的形成一系列的气泡云,并向水体表面运动,并在潮头表面聚集为大的气泡后破裂并逃逸。
3)潮头掺气形态的变化规律。随着落潮流速的变大,涌潮潮头破碎时潮头的高度变小;而当涌潮潮头高度相同时,落潮流速越大,涌潮潮头陡度就越大,潮头水体变形就越剧烈,潮头破碎就越剧烈,掺入的气体量也越大,到达水体底部的气泡也就越多,气体在水体中运动的距离也越大。
4)潮头掺气长度的计算。涌潮潮头的相对掺气长度
| [1] |
Abbott M R. A theory of the propagation of bores in channels and rivers:proceedings[J]. Cambridge Philosophical Society, 1956, 52(2): 344-362. DOI:10.1017/S0305004100031327 |
| [2] |
Dracos T A, Glenne B. Stability criteria for open-channel flow[J]. Journal of the Hydraulics Division, 1967, 93(6): 79-101. |
| [3] |
Whitham G B.Linear and nonlinear waves[M].New York:John Wiley & Sons,1974.
|
| [4] |
Tricker R A R.Bores,breakers,waves,and wakes-an introduction to the study of waves on Water [M].New York:Elsevier,1965.
|
| [5] |
Lynch D K. Tidal bores[J]. Scientific American, 1982, 247(4): 146-156. DOI:10.1038/scientificamerican1082-146 |
| [6] |
Koch C,Chanson H.An experimental study of tidal bores and positive surges:Hydrodynamics and turbulence of the bore front[R].Australia:The University of Queensland,2005.
|
| [7] |
Madsen P A, Svendsen I A. Turbulent bores and hydraulic jumps[J]. Journal of Fluid Mechanics, 1983, 129(4): 1-25. |
| [8] |
Svendsen I A, Madsen P A. A Turbulent bore on a beach[J]. Journal of Fluid Mechanics, 1984, 148(11): 73-96. |
| [9] |
Yeh H H, Mok K M. On turbulence in bores[J]. Physics Fluid A, 1990, 2(5): 821-828. DOI:10.1063/1.857630 |
| [10] |
Chanson H. Physical modeling of the flow field in an undular tidal bore[J]. Journal of Hydraulic Research, 2005, 43(3): 234-244. DOI:10.1080/00221680509500118 |
| [11] |
Wolanskia E, Williamsb D, Spagnola S. Undular tidal bore dynamics in the Daly Estuary,Northern Australia[J]. Estuarine,Coastal and Shelf Science, 2004, 60(4): 629-636. DOI:10.1016/j.ecss.2004.03.001 |
| [12] |
Chanson H, Reungoat D, Simon B. High-frequency turbulence and suspended sediment concentration measurements in the Garonne River tidal bore[J]. Estuarine,Coastal and Shelf Science, 2011, 95(2): 298. |
| [13] |
Chanson H. The rumble sound generated by a tidal bore event in the Baie du Mont Saint Michel[J]. Journal of the Acoustical Society of America, 2009, 125(6): 3561-3568. DOI:10.1121/1.3124781 |
| [14] |
Simpson J H, Fisher N R, Wiles P. Reynolds stress and TKE production in an estuary with a tidal bore[J]. Estuarine,Coastal and Shelf Science, 2004, 60(4): 619-627. DOI:10.1016/j.ecss.2004.03.006 |
| [15] |
Lin Bingyao, Huang Shichang, Zhou Chaosheng. The reflection and collision of the tidal bore,the back bore and the cross bore[J]. Journal of Zhejiang Water Conservancy and Hydropower College, 2000, 12(1): 6-10. [林炳尧, 黄世昌, 周潮生. 涌潮的反射和碰撞:回头潮和交叉潮[J]. 浙江水利水电专科学校学报, 2000, 12(1): 6-10.] |
| [16] |
Zeng Jian, Sun Zhilin, Xiong Shaolong. Radial basis function network based tidal bore model and its application to Qiantang Estuary[J]. Journal of Zhejiang University (Engineering Science), 2006, 42(9): 1457-1461. [曾剑, 孙志林, 熊绍隆. 基于径向基函数网络的钱塘江涌潮模型及其应用[J]. 浙江大学学报(工学版), 2006, 42(9): 1457-1461.] |
| [17] |
Pan Cunhong, Lu Haiyan, Zeng Jian. Characteristic and numerical simulation of tidal bore in Qiantang River[J]. Hydro-Science and Engineering, 2008, 39(2): 1-9. [潘存鸿, 鲁海燕, 曾剑. 钱塘江涌潮特性及其数值模拟[J]. 水利水运工程学报, 2008, 39(2): 1-9.] |
| [18] |
Yang Huoqi, Pan Cunhong, Zhou Jianjiong. Experiment study on hydraulic properties of tidal bore[J]. Water Resources and Power, 2008, 26(4): 136-138. [杨火其, 潘存鸿, 周建炯. 涌潮水力学特性试验研究[J]. 水电能源科学, 2008, 26(4): 136-138.] |
| [19] |
Huang Jing, Pan Cunhong, Chen Gang. Experimental simulation and validation of the tidal bore in the flume[J]. Hydro-Science and Engineering, 2013, 44(2): 1-8. [黄静, 潘存鸿, 陈刚. 涌潮的水槽模拟及验证[J]. 水利水运工程学报, 2013, 44(2): 1-8.] |
| [20] |
Huang Jing, Pan Cunhong, Kuang Cuiping. Experimental hydrodynamic study of the Qiantang River tidal bore[J]. Journal of Hydrodynamics, 2013, 25(3): 481-490. DOI:10.1016/S1001-6058(11)60387-X |
| [21] |
Huang Jing.Study on the hydrodynamics and turbulent characteristics of the tidal bore[D].Shanghai:Tongji University,2013. [黄静.涌潮的水动力及紊动特性研究[D].上海:同济大学,2013.]
|
| [22] |
Xie Dongfeng, Pan Cunhong, Lu Bo. Study on the hydrodynamic characteristics of the tidal bore on the Qiantang Estuary[J]. Chinese Journal of Hydrodynamics, 2012, 27(5): 501-508. [谢东风, 潘存鸿, 陆波. 基于实测资料的钱塘江涌潮水动力学特性研究[J]. 水动力学研究与进展(A辑), 2012, 27(5): 501-508.] |
| [23] |
Xie Dongfeng, Pan Cunhong. A preliminary study of the turbulence features of the tidal bore in the Qiantang River,China[J]. Journal of Hydrodynamics, 2013, 25(6): 903-911. DOI:10.1016/S1001-6058(13)60439-4 |
| [24] |
Hager W H.Energy dissipators and hydraulic jump[M].Dordrecht:Kluwer Academic,1992.
|
| [25] |
Chanson H. Bubbly two-phase flow in hydraulic jumps at large froude numbers[J]. Journal of Hydraulic Engineering, 2011, 137(4): 451-460. DOI:10.1061/(ASCE)HY.1943-7900.0000323 |
| [26] |
Chanson H, Toi Y H. Physical modeling of breaking tidal bores:Comparison with prototype data[J]. Journal of Hydraulic Research, 2015, 53(2): 264-273. DOI:10.1080/00221686.2014.989458 |
| [27] |
Leng X, Chanson H. Turbulent advances of a breaking bore:Preliminary physical experiments[J]. Experimental Thermal and Fluid Science, 2015, 62(4): 70-77. |
 2018, Vol. 50
2018, Vol. 50

