与单用户多输入多输出(single user multi-input multi-output,SU-MIMO)系统不同,在多用户多输入多输出(multiuser multi-input multi-output,MU-MIMO)系统中,不同用户所接收到的信号不仅会经历噪声及天线间的干扰[1–2],还会受到多用户间干扰(multiuser interference,MUI)的影响。在下行链路中,由于各独立用户设备间协作困难,所以用户间干扰应当通过预编码技术在发射端消除[3–4]。
脏纸编码(dirty paper coding,DPC)[3]可以达到多用户MIMO广播信道的容量上限,但它是一种非线性预编码,因此在现实中很难实现。在可实现的线性预编码算法中,最具代表性的无疑是块对角化(block diagonalization,BD)算法[4]。通过使用BD算法,可以将MU-MIMO信道转化成等价的多个SU-MIMO信道,完全消除用户间干扰,并能够实现接近脏纸编码的信道容量。然而,传统BD算法由于需要进行多次奇异值分解(singular value decomposition,SVD),其运算复杂度仍然较高,因此不断地有改进BD算法被提出。Ling[5]、Hashem[6]等研究了基于格基规约算法的低复杂度预编码算法。Zu等[7]通过将BD算法与LR相结合,得到的改进算法不但能够减少算法的计算复杂度,同时还能在一定程度上提升系统误码性能。Chou等[8]利用改进的平方根分解法对等效单用户MIMO信道进行块对角化处理,可以进一步降低BD算法的复杂度。An等[9]则用LQ分解取代了QR分解,相较于传统BD算法也降低了复杂度。巫健[10]提出一种在BD算法前半部分采用伪逆与QR分解代替高复杂度奇异值分解的方法,并提出进一步改进方案,仅对联合信道矩阵求一次伪逆,再次降低复杂度。此外,巫健[10–11]等还分别提出了通过增加一次QR分解或格拉姆施密特正交化来避免进行复杂度较高的伪逆运算的改进方案,由于QR分解可以通过施密特正交化来实现,所以这两种方案本质上是相同的。
综上所述,传统的BD算法由于复杂度很高,限制了其应用。巫健[10–11]等虽然通过避免复杂的伪逆运算降低了BD算法的复杂度,但是该算法的误码率性能并没有获得提升。为了进一步提高BD算法的性能,作者提出了一种基于Givens变换的QR分解改进BD算法,相较于传统BD算法,该算法不仅降低了复杂度,也改善了误码性能。而与巫健[10–11]等提出的改进算法对比,在略微增加复杂度的前提下可以提高算法的误码率性能。
1 系统模型考虑一个如图1所示处于平坦衰落信道下的单小区多用户MIMO系统,基站拥有
| ${{{y}}_k} = {{{H}}_k}{{{W}}_k}{{{x}}_k} + \sum\limits_{i = 1,i \ne k}^K {{{{H}}_i}{{{W}}_i}{{{x}}_i}} + {{{n}}_k}$ | (1) |
式中,
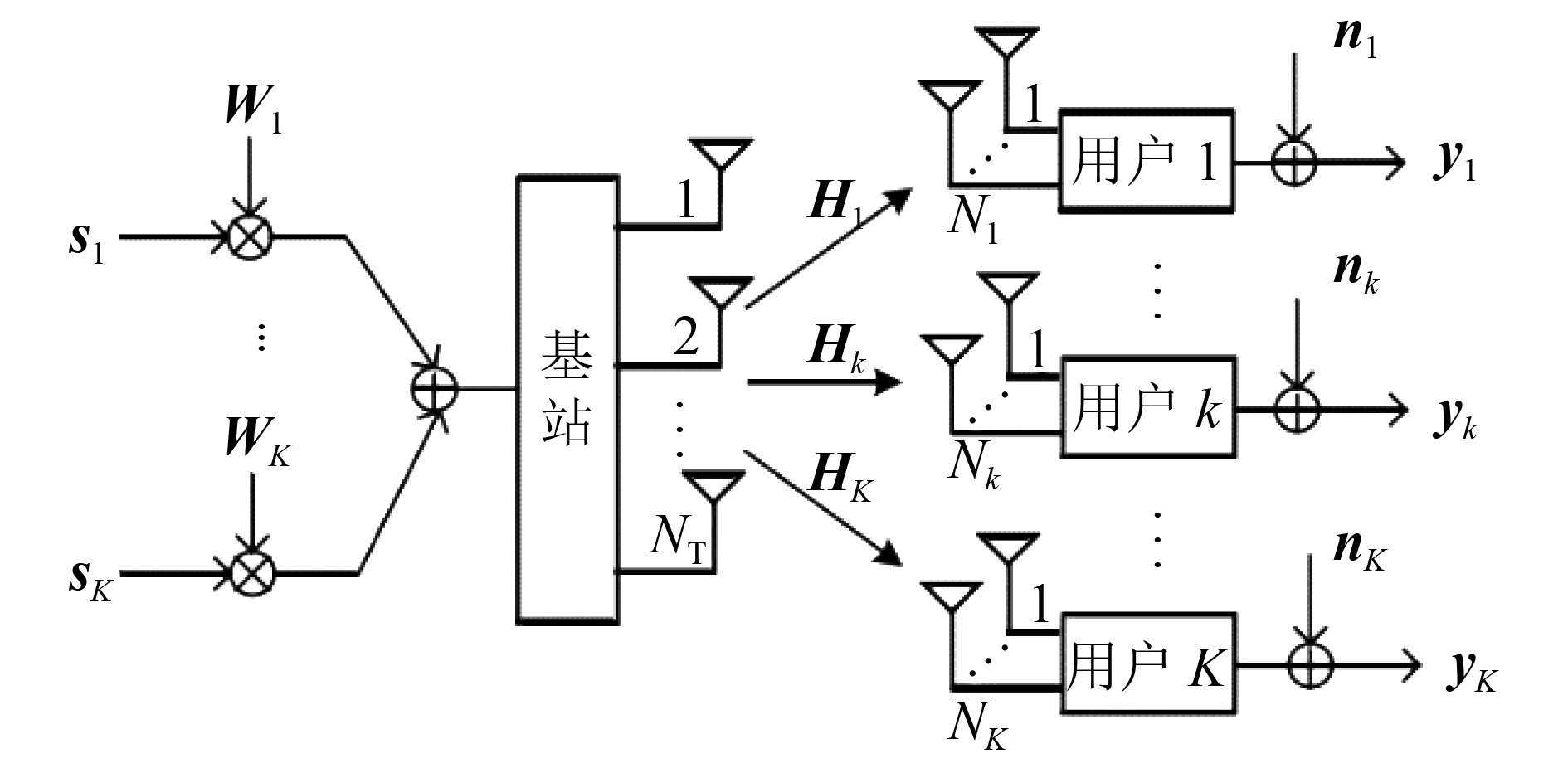 |
| 图1 多用户MIMO预编码系统模型 Fig. 1 Multiuser MIMO precoding system model |
2 传统块对角化算法
一般地,对于拥有
为了达到用户间干扰最小化,传统BD算法要求用户
| ${{\widetilde{ H}}_k} = {[{{H}}_{{1}}^{{T}},{{H}}_{{2}}^{{T}}, \cdots \!,\;{{H}}_{k - 1}^{{T}},{{H}}_{k + 1}^{{T}}, \cdots\! ,\;{{H}}_K^{{T}}]^{{T}}}$ | (2) |
假设所有用户均满足维数条件,令
| ${{\widetilde{ H}}_k} = {{\widetilde{ U}}_k}\left[ {\begin{array}{*{20}{c}} {{{{\widetilde{ \varSigma }}}_k}} & 0 \\ 0 & 0 \end{array}} \right]{\left[ {{\widetilde{ V}}_k^{(1)},{\widetilde{ V}}_k^{(0)}} \right]^{{H}}}$ | (3) |
式中,
| ${{W}}_k^{{o}} = {\widetilde{ V}}_k^{(0)}$ | (4) |
遍历所有
| ${{W}}_k^{{o}} = [{{W}}_1^{{o}},{{W}}_2^{{o}}, \cdots ,{{W}}_K^{{o}}]$ | (5) |
定义用户
| ${{H}}_k^{{{eff}}} = {{{H}}_k}{{W}}_k^{{o}} = {{{U}}_k}{{{\varSigma }}_k}{[{{V}}_k^{(1)},{{V}}_k^{(0)}]^{{H}}}$ | (6) |
式中,
| ${{W}}_k^{{g}} = {{V}}_k^{(1)}$ | (7) |
遍历所有用户,可以得到联合预编码矩阵的第2部分为:
| ${{{W}}^{{g}}} = {{diag}}\{ {{W}}_1^{{g}},{{W}}_2^{{g}}, \cdots ,{{W}}_K^{{g}}\} $ | (8) |
综上,BD预编码算法的最终联合预编码矩阵
| ${{W}} = {{{W}}^{{o}}}{{{W}}^{{g}}}$ | (9) |
同时,接收矩阵为:
| ${{{B}}_k} = {{U}}_k^{{H}}$ | (10) |
由矩阵论知识可知,QR分解可以通过Gram-Schmidt正交化、Givens变换与Householder变换这3种方式实现,实现方式的不同会得到不同计算复杂度、不同正交性矩阵的QR分解[12]。因此,提出一种改进的BD算法——QR-Givens-BD算法,与文献[10–11]不同的是,在做第2次QR分解时,使用基于Givens变换的QR分解算法。
如前所述,QR-Givens-BD算法同样可以分为两步进行,即第1步求取预编码矩阵
首先,对联合信道矩阵的共轭转置
| ${{{H}}^{{H}}} = {{QR}}$ | (11) |
式中,
| $\begin{aligned}[b] {{{H}}^{\text{†}} } = & {{{H}}^{{H}}}{({{H}}{{{H}}^{{H}}})^{ - 1}} = {{QR}}{({{{R}}^{{H}}}{{{Q}}^{{H}}}{{QR}})^{ - 1}} = \\& {{QR}}{{{R}}^{ - 1}}{({{{R}}^{{H}}})^{ - 1}} = {{Q}}{({{{R}}^{{H}}})^{ - 1}}\end{aligned}$ | (12) |
令
对子矩阵
| ${{Q}}{{{L}}_k} = {{\overline{ Q}}_k}{{\overline{ R}}_k}$ | (13) |
式中,
| ${{\widetilde{ H}}_k}{{Q}}{{{L}}_k} = {{\widetilde{ H}}_k}{{\overline{ Q}}_k}{{\overline{ R}}_k} = 0$ | (14) |
由于
| ${{{W}}^{{o}}} = {{\overline{ Q}}_k}$ | (15) |
遍历所有
| ${{W}}_k^{{o}} = [{{W}}_1^{{o}},{{W}}_{{2}}^{{o}}, \cdots ,{{W}}_{{K}}^{{o}}]$ | (16) |
经过
| ${{H}}{{{W}}^{{o}}} = {{diag}}\{ {{{H}}_1}{{W}}_{{1}}^{{o}},{{{H}}_1}{{W}}_2^{{o}}, \cdots ,{{{H}}_K}{{W}}_K^{{o}}\} $ | (17) |
定义用户
| ${{H}}_k^{{eff}} = {{{H}}_k}{{W}}_k^{{o}} = {{{U}}_k}{{{\varSigma }}_k}{[{{V}}_k^{(1)},{{V}}_k^{(0)}]^{{H}}}$ | (18) |
式中,
| ${{W}}_k^{{g}} = {{V}}_k^{(1)}$ | (19) |
遍历所有用户,可以得到联合预编码矩阵的第2部分为:
| ${{{W}}^{{g}}} = { diag}\{ {{W}}_1^{{g}},{{W}}_2^{{g}}, \cdots ,{{W}}_K^{{g}}\} $ | (20) |
综上,QR-Givens-BD预编码算法的最终联合预编码矩阵
| ${{W}} = {{{W}}^{{o}}}{{{W}}^{{g}}}$ | (21) |
同时,接收矩阵为:
| ${{{B}}_k} = {{U}}_k^{{H}}$ | (22) |
对所提的QR-Givens-BD算法的复杂度进行分析,并与传统BD算法及基于Gram-Schmidt正交化的QR-GSO-BD算法[10–11]的复杂度进行对比。为方便计算,假设每个用户的天线数
1)与
2)矩阵奇异值分解所需浮点运算数为
3)基于修正Gram-Schmidt正交化的QR分解所需浮点运算数为
4)基于Givens变换的QR分解所需浮点运算数为
5)
对于传统BD算法而言:1)对每个用户进行一次奇异值分解,共
| $\begin{aligned}[b]{\varPsi _{{{BD}}}} = & 24{K^2}{N_k}N_{{T}}^2 + (56{K^2} - 40K + 48)N_k^2{N_{{T}}} - \\& 2K{N_k}{N_{{T}}} + 54({K^3} - 3{K^2} + 4K - 1)N_k^3 - 2KN_k^2{{ = }}\\& O({K^2}{N_k}N_{{T}}^2)\end{aligned}$ | (23) |
对于QR-GSO-BD算法而言:1)对联合信道矩阵进行QR分解,所需浮点运算数为
| $\begin{aligned} {\varPsi _{{{QR}} - {{GSO}} - {{BD}}}} = & 24K{N_k}N_{{T}}^2 + (24{K^2} + 56K)N_k^2{N_{{T}}} - 4K{N_k}{N_{{T}}} + \\& (4{K^3}/3 \!+\! 8{K^2} \!+\! 54K)N_k^3 - 2KN_k^2 \!=\! O(K{N_k}N_{{T}}^2)\end{aligned}$ | (24) |
对于QR-Givens-BD算法而言,与QR-GSO-BD算法相比较,除矩阵相乘步骤的顺序外,仅第3)步所需浮点运算数不同,共需
| $\begin{aligned}[b]{\varPsi _{{{QR}} \!-\! {{Givens}} \!-\! {{BD}}}} \!= & 24K{N_k}N_{{T}}^2 \!+\! (24{K^2} + 56K)N_k^2{N_{{T}}} - 4K{N_k}{N_{{T}}} + \\& (4{K^3}/3 \!+\! 24{K^2} \!+\! 48K)N_k^3 \!-\! 2KN_k^2 \!=\! O(K{N_k}N_{{T}}^2)\end{aligned}$ | (25) |
由式(23)~(25)可以看出,QR-Givens-BD算法复杂度数量级与QR-GSO-BD算法相当,且二者均为传统BD算法的
固定每用户天线数为2,发射天线数为24,图2与3分别比较了QR-Givens-BD算法与传统BD算法及QR-GSO-BD算法随着用户数变化的计算复杂度。
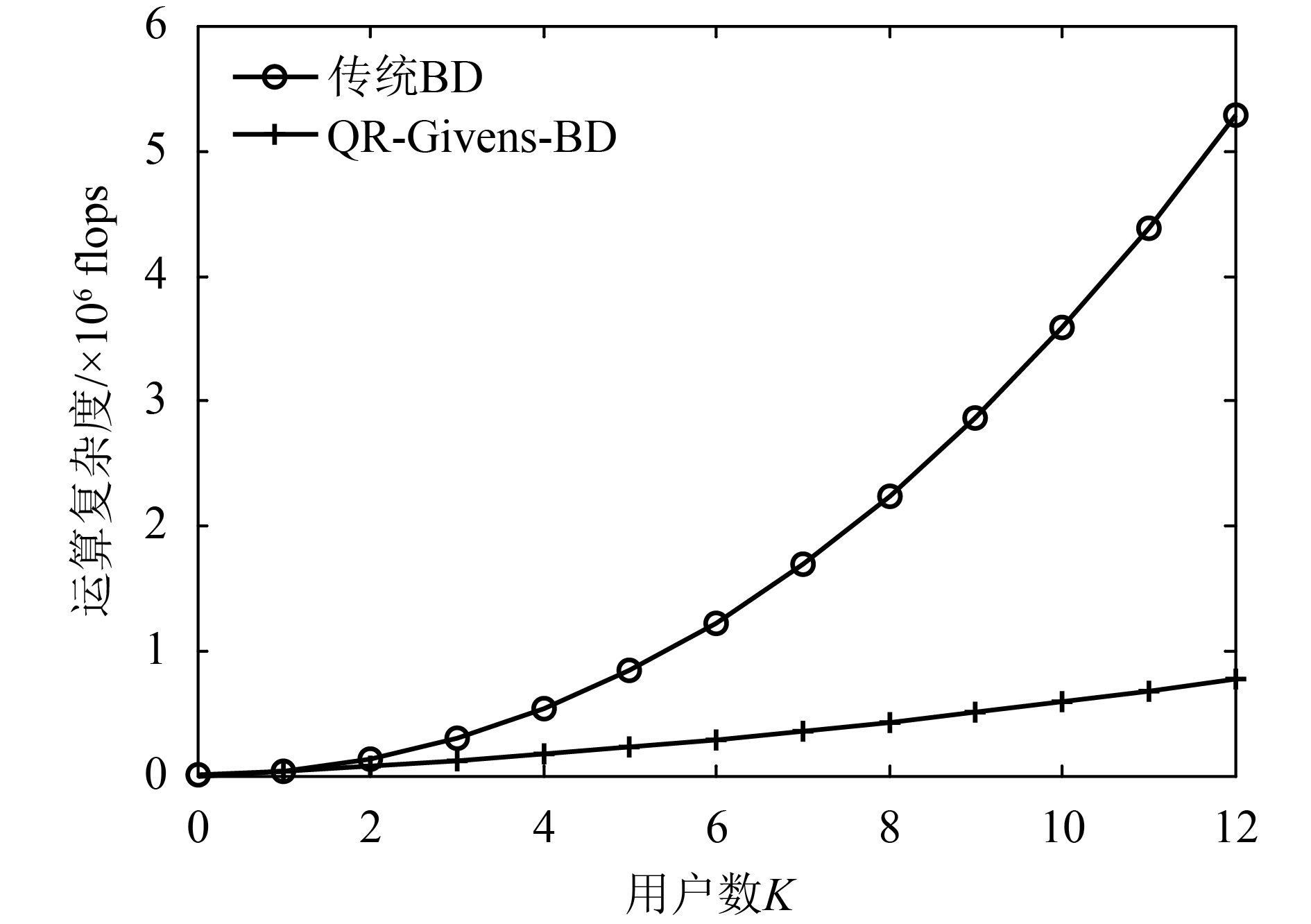 |
| 图2 BD与QR-Givens-BD复杂度比较 Fig. 2 Comparison of complexity between BD and QR-Givens-BD |
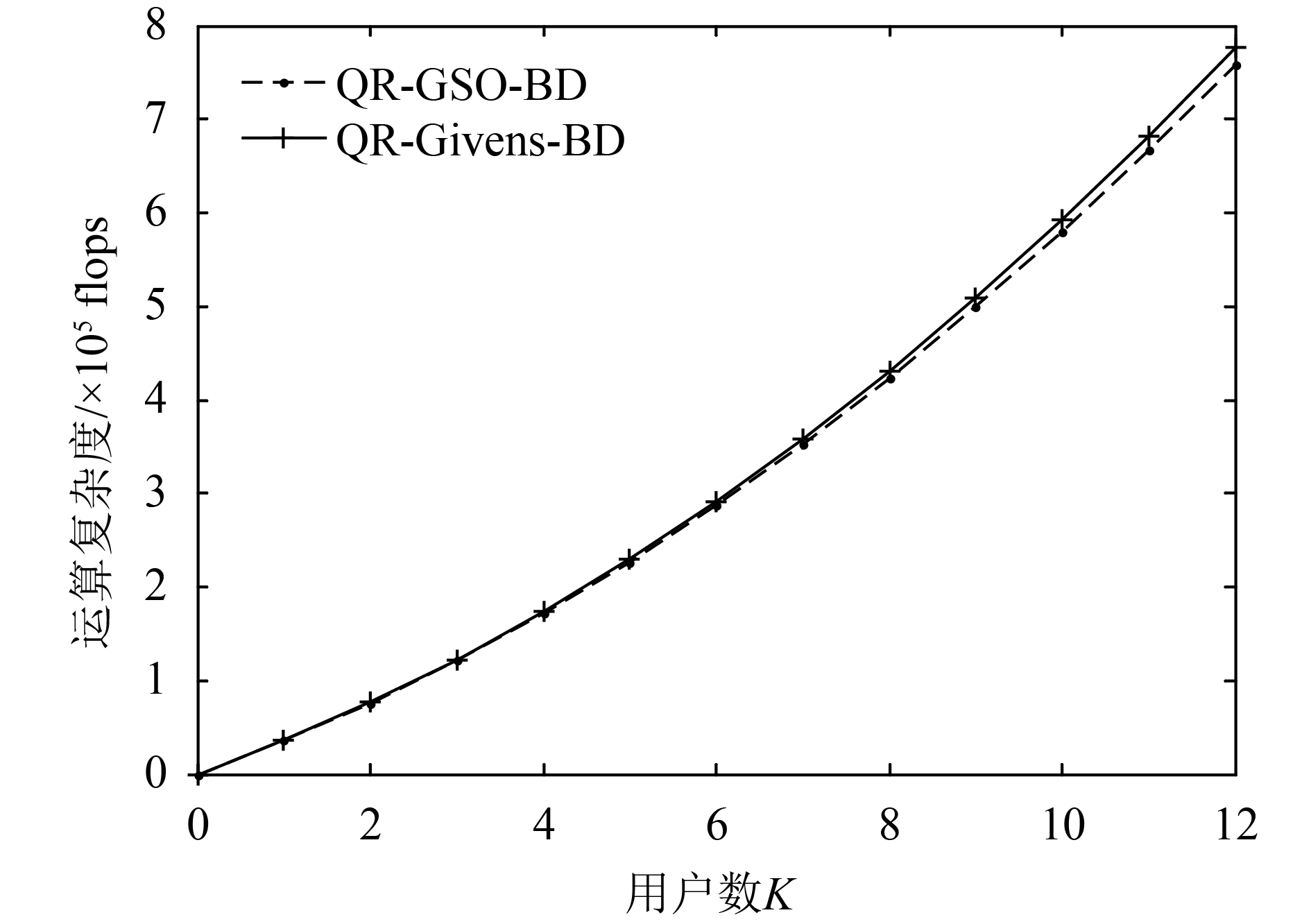 |
| 图3 QR-GSO-BD与QR-Givens-BD复杂度比较 Fig. 3 Comparison of complexity between QR-GSO-BD and QR-Givens-BD |
从图2中可以看出,由于算法复杂度数量级的下降,随着用户数的增加,QR-Givens-BD算法的复杂度远远低于传统BD算法。当用户数为12时,前者的计算复杂度仅约为后者的14.7%。从图3中可以看出,尽管基于Givens变换QR分解的复杂度约为基于修正Gram-Schmidt正交化QR分解复杂度的2倍[12],但其在整个算法中只占很小一部分,因此QR-Givens-BD和QR-GSO-BD算法在计算复杂度上相差不大。当用户数较低时,两种算法的复杂度基本相同,当用户数较多时,算法复杂度略有增加,例如,当用户数为12时,前者相对于后者只增加了约2.4%的计算复杂度。
4.2 误码性能仿真通过MATLAB仿真平台,对传统BD、QR-GSO-BD与QR-Givens-BD算法的误码性能进行了仿真。假设信道为准静态平坦瑞利衰落信道,调制方式为QPSK,信道矩阵元素为独立同分布零均值单位方差的复高斯随机变量。
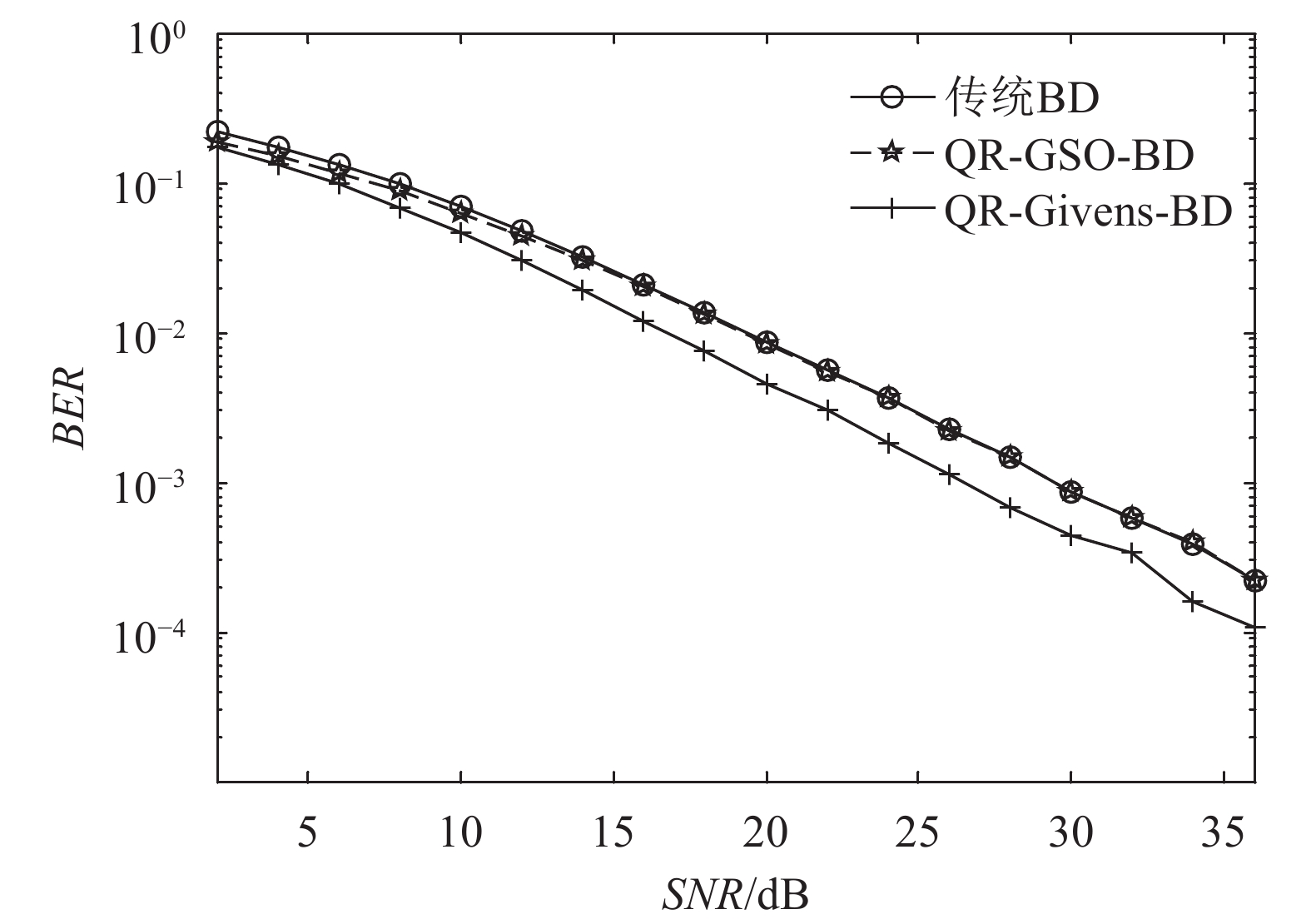
图4为发射天线数为6、用户数为3、每用户天线数为2的情景下3种BD算法的误码率仿真曲线。从图4可以看出,QR-GSO-BD算法虽然计算复杂度相较于传统BD算法有所降低,但其误码率性能仍与传统BD算法持平,因此在图4中两条曲线重合。而在QR-Givens-BD算法中,即使基于Givens变换的QR分解会引入额外复杂度,但其分解所得的正交矩阵正交性却比基于Gram-Schmidt正交化的QR分解更好[12],因此由图4可以看出QR-Givens-BD算法的误码性能比QR-GSO-BD算法及传统BD算法好2~4 dB,并且其计算复杂度仅约为传统BD算法的14.7%,相较于QR-GSO-BD算法也仅增加了约2.4%的计算复杂度。
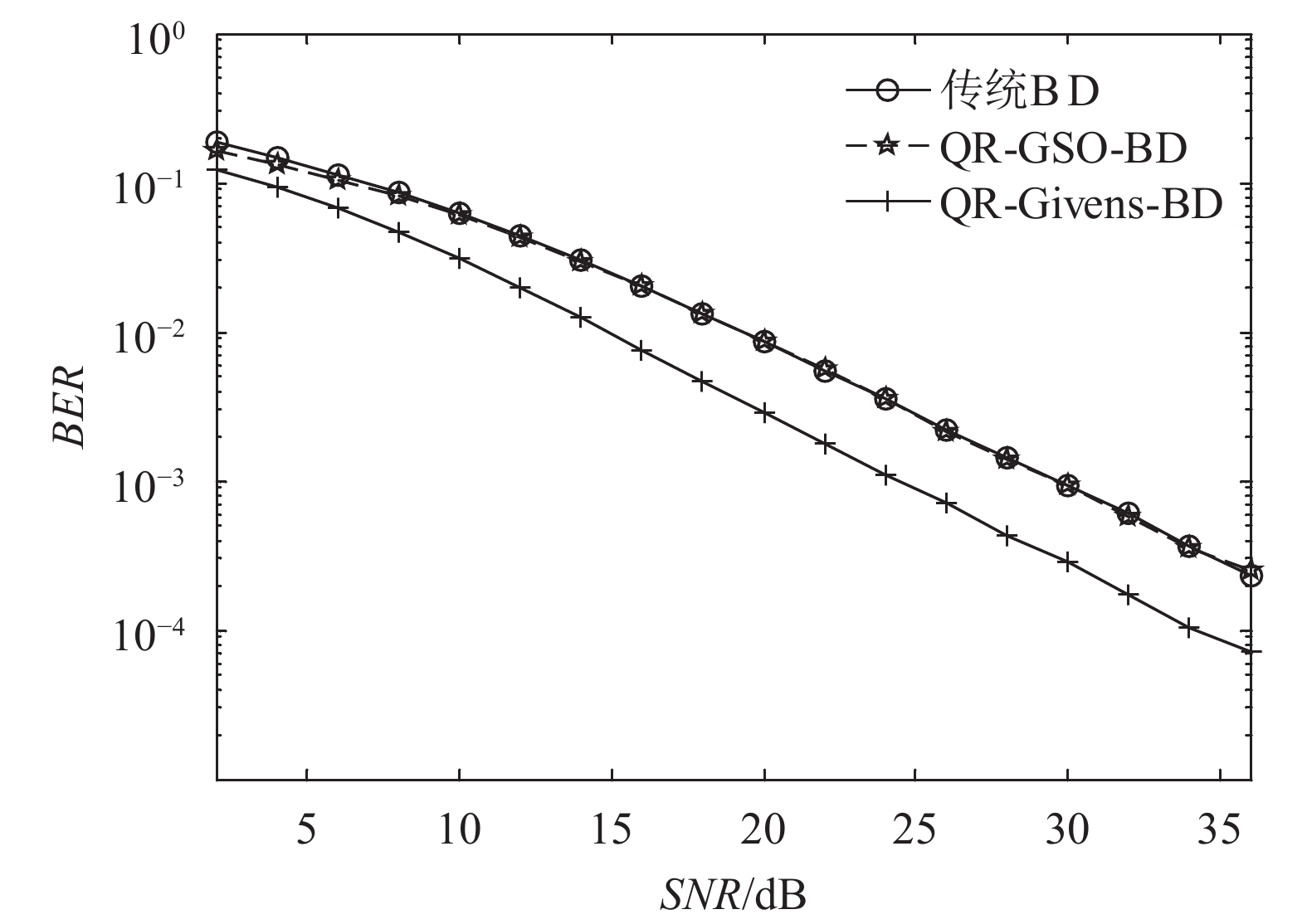
图5为发射天线数为18、用户数为6、每用户天线数为3的情景下3种算法的误码率仿真曲线。由图5误码仿真结果可以看出,QR-GSO-BD算法与传统BD算法的误码率曲线重合,具有相同的误码率性能,而QR-Givens-BD算法的误码性能优于QR-GSO-BD算法及传统BD算法3~5 dB。结合图4与5可以看出,随着天线数目和用户数目的增加,所提出的算法的误码率性能提升越大。
 |
|
图4 误码率仿真结果(
|
 |
|
图5 误码率仿真结果(
|
5 结 论
提出了一种改进块对角化算法,算法通过采用基于Givens变换的QR分解代替传统BD算法中的SVD分解,使得系统最终求得的预编码矩阵具有更好的正交性。所提出的算法实现复杂度低,具有良好的误码率性,因此,所提出的算法是一种可行的下行多用户MIMO预编码方案。下一步的工作中,将继续研究快速Givens变换中的溢出问题,在解决溢出问题的基础上研究基于快速Givens变换的BD算法,进一步降低算法复杂度。
| [1] |
Nguyen D, Nguyenle H, Lengoc T. Block-diagonalization precoding in a multiuser multicell MIMO system competition and coordination[J]. IEEE Transactions on Wireless Communications, 2014, 13(2): 968-981. DOI:10.1109/TWC.2013.010214.130724 |
| [2] |
Zarei S, Gerstacker W, Schober R. Low-complexity widely-linear precoding for downlink large-scale MU-MISO systems[J]. IEEE Communications Letters, 2015, 19(4): 665-668. DOI:10.1109/LCOMM.2015.2392751 |
| [3] |
Weingarten H, Steinberg Y, Shamai S. The capacity region of the Gussian MIMO broadcast channel[J]. IEEE Transactions on Information Theory, 2006, 52(9): 3936-3964. DOI:10.1109/TIT.2006.880064 |
| [4] |
Spencer Q H, Swinlehurst A L, Haardt M. Zero-forcing methods for downlink spatial multiplexing in multi-user MIMO Channels[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 461-471. DOI:10.1109/TSP.2003.821107 |
| [5] |
Ling Cong. On the proximity factors of lattice reduction aided decoding[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2795-2808. DOI:10.1109/TSP.2011.2123889 |
| [6] |
Hashem M, Khan A, Chung J. Lattice reduction aided with block diagonalization for multiuser MIMO systems[J]. EURASIP Journal on Wireless Communications, 2015, 2015(1): 1-9. |
| [7] |
Zu K, Lamare R C, Haardt M. Generalized design of low-complexity block diagonalization type precoding algorithms for multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(2): 4232-4242. |
| [8] |
Chou C C, Wu J M. Low-complexity MIMO precoder design with LDLH channel decomposition
[J]. IEEE Transactions on Vehicular Technology, 2011, 60(5): 2368-2372. DOI:10.1109/TVT.2011.2151889 |
| [9] |
An Jie, Liu Yuanan, Liu Fang. A low complexity block diagonalization precoding method for multiuser MIMO downlink[J]. Journal of Computational Information Systems, 2012, 8(12): 5187-5194. |
| [10] |
Wu Jian.Research on lattice reduction based low-complexity precoding technique for multi-user MIMO systems[D].Chengdu:University of Electronic Science and Technology of China,2015. 巫健.多用户MIMO系统中基于格基规约的低复杂度预编码技术研究[D].成都:电子科技大学,2015. |
| [11] |
Wu Jian,Fang Shu,Li Lei,et al.QR decomposition and Gram Schmidt orthogonalization based low complexity multi-user MIMO precoding[C]//Proceedings of 10th International Conference on Wireless Communications,Networking and Mobile Computing.Beijing:IET,2014:61–66.
|
| [12] |
Golub G H,van Loan C F.矩阵计算:英文版[M].4版.北京:人民邮电出版社,2014:199–210.
|
| [13] |
Ren Yuwei, Song Yang, Su Xin. Low-complexity channel reconstruction methods based on SVD-ZF precoding in massive 3D-MIMO systems[J]. China Communications, 2015, 12(Supplement1): 49-57. |
| [14] |
Fang Shu, Wu Jian, Lu Chengyi. Simplified QR-decomposition based and lattice reduction-assisted multi user multiple input multiple output precoding scheme[J]. IET Communications, 2016, 10(5): 586-593. DOI:10.1049/iet-com.2015.0643 |
| [15] |
Ali-Khan M H, Chung J G, Lee M H. Lattice reduction aided with block diagonalization for multiuser MIMO systems[J]. EURASIP Journal on Wireless Communications, 2015, 2015(254): 1186-1195. |
 2018, Vol. 50
2018, Vol. 50

