2. 四川川投田湾河开发有限责任公司,四川 成都 610000
2. Sichuan Chuantou Tianwanhe Development Corp. Ltd.,Chengdu 610000,China
中国在应对气候变化及能源结构转型的过程中,尽可能地利用水能这一可再生能源,对于减轻环境压力和能源可持续发展意义重大。梯级水电站年总发电量主要取决于年径流量与其分布,以及水库调度管理。为提高水能利用率和供电水平,应充分发挥有调节性能水库的容量效益,实行梯级水电站经济调度[1–3]。由于梯级水库间复杂而密切的水力、电力联系,梯级水电站经济调度呈多维数、动态性、非线性等特点,涉及水库入流、库容、水头、出力等多个变量,求解复杂。
当前,为解决水电站经济调度问题,学者们引进了较多的求解算法。传统的经典算法有非线性规划(NLP)[4]、拉格朗日松弛法(LR)[5]、动态规划(DP)[6]、逐步优化算法(POA)[7]等,现代启发式随机搜索方法有遗传算法(GA)[8]、差分进化算法(DE)[9]、人工蜂群算法(ABC)[10]、粒子群算法(PSO)[11]、蝙蝠算法(BA)[12]等。其中,蝙蝠算法是2010年提出的新兴启发式随机搜索群智能算法,具有并行性、分布式、收敛速度快等特点,目前在科学领域已得到广泛应用[13],但该算法也存在一些不足。
针对BA中缺乏变异机制而导致的种群多样性较低,全局搜索能力较差,易陷入局部最优、收敛精度不高等缺点,将差分算法变异、选择操作引入蝙蝠算法中,改进种群更新策略,提出一种改进的蝙蝠算法(IBA)。将其运用于梯级水电站经济调度问题中。
1 数学模型通常梯级水电站群中长期优化调度是根据给定的入流过程和综合利用要求,以发电流量为决策变量,制定并实施水电站中长期最优化运行调度方式,以获得调度周期内总发电量最大或总发电效益最大。随着中国社会经济发展及能源结构转型,电网安全稳定运行需要大容量机组参与调峰运行。尤其是对以水电为主的四川电网而言,在枯水期需提供给电网尽可能大而稳定的出力值,以保证电力系统供电的稳定性。因此,为充分发挥有调节性能水库容量效益,保障电网安全稳定运行,同时替代火力发电,减少碳排放,本文建立了兼顾梯级最小出力最大化的梯级总发电量最大模型。
1.1 目标函数1)梯级总发电量最大
| $E = { max}\sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {{K_{i,t}}} } \cdot {Q_{i,t}} \cdot {H_{i,t}} \cdot {M_t}$ | (1) |
2)梯级电站年内最小出力最大化
| $NP = { max}\;\mathop { min}\limits_{1 \le t \le T} \sum\limits_{i = 1}^n {{K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}}} $ | (2) |
式中:
上述梯级水库调度模型是一个多目标复杂优化决策类问题,模型求解较为复杂,通常采用线性加权法、约束法将其转化为单目标优化问题[1]。本文采用约束法将整个梯级调度周期内最小出力最大化的目标转化为一个约束条件,转化后有:
| $\mathop { min}\limits_{1\le t \le T} \sum\limits_{i = 1}^n {{K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}} \ge \varepsilon } $ | (3) |
式中,
在目标函数1)中加入梯级电站最小出力约束作为惩罚项,最终的目标函数为:
| $E \!=\! { max} \!\!\sum\limits_{t ={{1}}}^T {\left[\!\! {\sum\limits_{i = 1}^n {\!\!{K_{i,t}} \cdot {Q_{i,t}}} \cdot {H_{i,t}} \!-\! {\sigma _t} \cdot \lambda \cdot \!\left| {\varepsilon \!-\!\! \sum\limits_{i = 1}^n {{K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}}} } \right|} \!\right]} \cdot \!{M_t}$ | (4) |
式中,
| ${\sigma _t} = \left\{ {\begin{aligned} & {0,\;\sum\limits_{i = 1}^n {{K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}} \ge \varepsilon } }; \\ & {1,\;\sum\limits_{i = 1}^n {{K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}} < \varepsilon } \;} \end{aligned}} \right.$ | (5) |
1)水库水量平衡
| ${V_{i,t + 1}} = {V_{i,t}} + ({I_{i,t}} - {Q_{i,t}} - {S_{i,t}}) \cdot {M_t}$ | (6) |
2)梯级水库水力联系
| ${I_{i + 1,t}} = {Q_{i,t}} + {S_{i,t}} + {R_{i,i + 1,t}}$ | (7) |
3)水库水位约束
| ${\textit{Z}}_{i,t}^{\min } \le {{\textit{Z}}_{i,t}} \le {\textit{Z}}_{i,t}^{\max }$ | (8) |
4)过机流量约束
| $Q_{i,t}^{u,\min } \le {Q_{i,t}} \le Q_{i,t}^{u,{ max}}$ | (9) |
5)下泄流量约束
| $Q_{i,t}^{\min } \le {Q_{i,t}} + {S_{i,t}} \le Q_{i,t}^{\max }$ | (10) |
6)单站出力约束
| $N_{i,t}^{\min } \le {K_{i,t}} \cdot {Q_{i,t}} \cdot {H_{i,t}} \le N_{i,t}^{\max }$ | (11) |
7)调度期末水位限制
| ${{\textit{Z}}_{i,{{start}}}} = {{\textit{Z}}_{i,{{end}}}}$ | (12) |
8)所有变量非负约束(
其中,
蝙蝠算法[15–17]是Yang根据微型蝙蝠回声定位能力于2010年提出的新型元启发式算法。微型蝙蝠通过超声波进行回声定位,探测猎物,且随着自身与目标距离的减小,逐渐增大脉冲发射频率,减小脉冲音量。Yang将其与优化目标功能相联系,提出一种启发式随机搜索的蝙蝠算法。
对于目标函数为
Step1:参数初始化。模型参数具体包括种群个体数
Step2:蝙蝠位置初始化。蝙蝠在
Step3:蝙蝠的搜索脉冲频率、速度、位置更新。种群在每一次迭代过程中,更新搜索脉冲频率、速度、位置,称之为全局搜索,公式如下:
| ${f_j} = {f_{\min }} + ({f_{\max }} - {f_{\min }}) \cdot \beta $ | (13) |
| ${ V}_j^{g + 1} = { V}_j^g + ({ X}_j^g - {{ X}_ * }) \cdot {f_j}$ | (14) |
| ${ X}_j^{g + 1} = { X}_j^g + { V}_j^{g + 1}$ | (15) |
式中:
Step4:生成均匀分布随机数
| ${{ X}_{{{new}}}} = {{ X}_{{{old}}}} + [\theta \cdot {{A}^g}]$ | (16) |
式中,
Step5:计算种群所有个体适应度函数值
| $r_j^{g + 1} = {R_0} \cdot \left[ {1 - \exp ( - \gamma \cdot g)} \right]$ | (17) |
| $A_j^{g + 1} = \alpha A_j^g$ | (18) |
式中,
Step6:计算所有蝙蝠的适应度值,确定当前种群最优解和最优值。
Step7:重复Step3~6,直至满足设定的终止条件。
Step8:输出全局最优解和最优值。
2.2 算法的改进从2.1节可知,在蝙蝠算法中,每只蝙蝠个体脉冲频率随迭代而更新,操作较复杂、费时。并且,蝙蝠算法无条件接受局部搜索产生的新解代替全局搜索产生的解,有条件接受本次迭代更新产生的新解。也即:当前迭代更新产生的所有个体适应度函数值要与当前种群最优值比较,只有优于当前种群最优的蝙蝠个体的位置更新才被接受。然而,对于有多个峰值的目标函数而言,这一更新策略很容易使函数值陷入局部最优而难以跳出。在蝙蝠算法中,只有蝙蝠个体的新解被接受,才更新其脉冲发射率
1)在作者提出的改进蝙蝠算法中,每只蝙蝠个体的脉冲频率不随个体 迭代而更新,减少计算时间。蝙蝠个体脉冲频率初始化公式为:
| ${f_{j,i}} = {f_{\min }} + ({f_{\max }} - {f_{\min }}) \cdot {\beta _{j,i}}$ | (19) |
式中,
2)更改新解接受条件,即无条件接受全局搜索产生的新解
3)蝙蝠个体脉冲发射率
4)更改速度更新公式,如式(20)所示,缩小新个体与当前种群最优个体的偏离值,使新个体靠近当前种群最优个体。经实验证明,这一举措可以明显减少计算时间,提高计算精度。
| ${ V}_j^g = { V}_j^{g - 1} - ({ X}_j^{g - 1} - {{ X}_ * }) \cdot {{ f}_j}$ | (20) |
5)针对蝙蝠算法中缺乏变异机制,种群多样性较低,算法易陷入局部最优的不足,引入DE算法中的变异、选择操作。
2.3 求解步骤经以上改进,本文的改进蝙蝠算法为:
Step1:参数初始化。模型参数具体包括种群个体数
Step2:蝙蝠位置初始化。蝙蝠在
Step3:确定初始化种群最优个体。计算所有个体适应度函数值
Step4:种群全局搜索、更新。种群在每一次迭代过程中,分别按照式(20)、(15)、(17)、(18)更新搜索速度、位置、脉冲发射率、脉冲音量,对蝙蝠位置进行越界处理。
Step5:种群局部搜索。生成均匀分布随机数
Step6:种群差分变异、选择。生成均匀分布随机数
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!CR = 0.6 + g/(2 \cdot {g_{\max }})$ | (21) |
| ${{ X}_{2,j}}(g) = {{ X}_ * } + F \cdot \left( {{{ X}_b}(g) - {{ X}_c}(g)} \right)$ | (22) |
式中,
Step7:计算所有蝙蝠的适应度值,确定当前种群最优解和最优值。
Step8:重复Step4~7,直至满足设定的终止条件。
Step9:输出全局最优解和最优值。
在本文的改进蝙蝠算法中,按式(21)动态更新种群变异概率,使得随着算法迭代次数增加,变异概率增加;由于迭代后期个体间差异较小,也增强了算法局部搜索能力。按式(22)产生的新个体继承了当前种群最优个体的特征,同时,吸收了种群其他个体信息,增加了种群多样性,加快收敛速度。
3 实 例将改进蝙蝠算法用于求解瀑布沟、深溪沟、枕头坝一级3个梯级水电站经济调度问题。其中,瀑布沟水电站具不完全年调节性能,深溪沟、枕头坝一级水电站均为径流式电站。3个梯级水电站基本参数如表1所示,其中,瀑布沟水电站月水位变幅不超过30 m。
| 表1 梯级水电站基本参数 Tab. 1 Parameters setting for cascade hydropower stations |
 |
3.1 算法参数测试与分析
改进蝙蝠算法(IBA)的主要控制参数有种群个体数
| 表2 典型年径流资料 Tab. 2 Reservoir inflows |
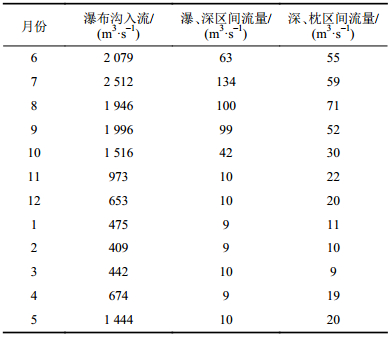 |
实验测试平台:操作系统Windows 10中文版,CPU为Intel(R)Core(TM)i5–5200U,主频为2.20 GHz,内存为4.00 GB;基于VS2010平台,采用C#语言编程。
选取种群个体数
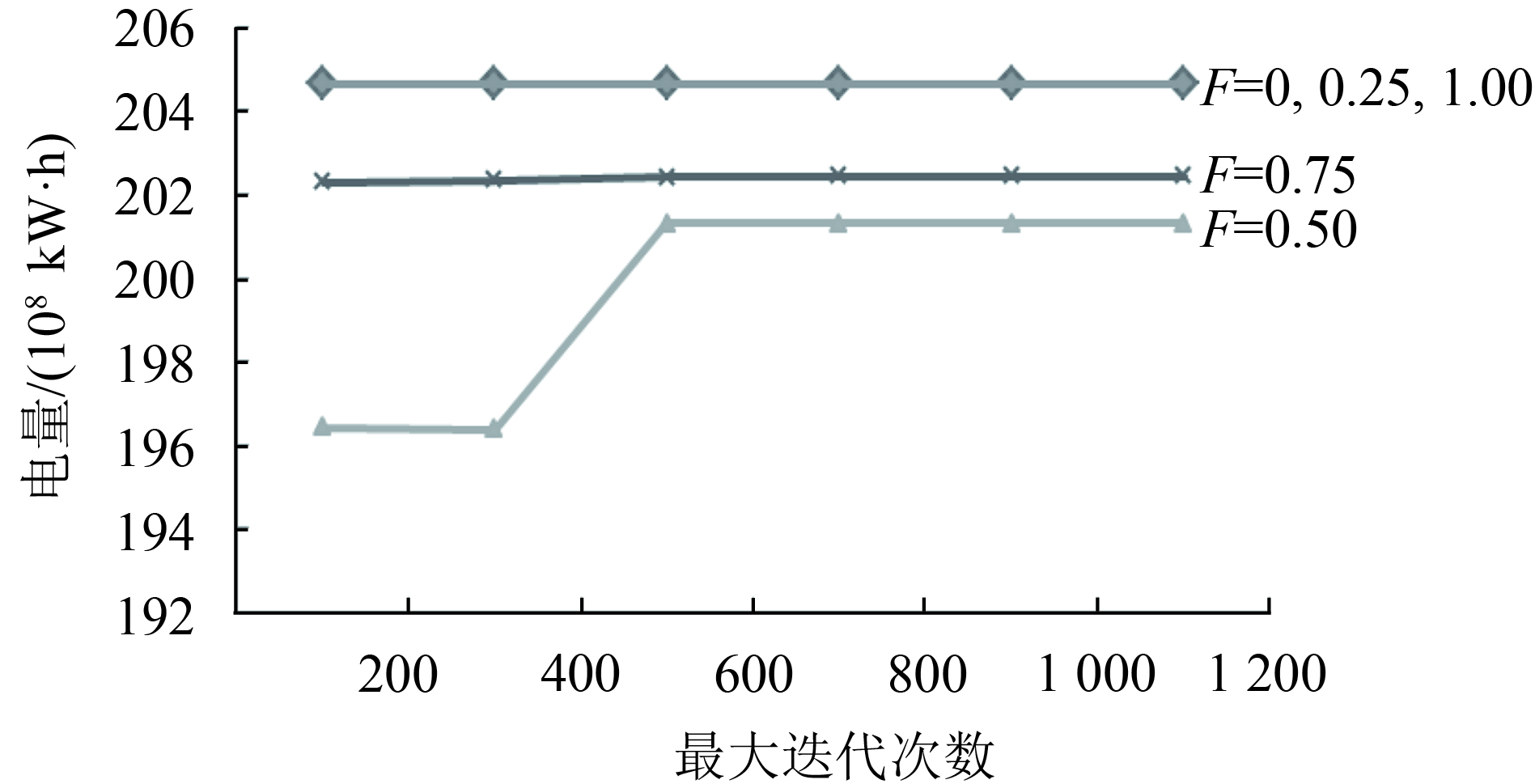 |
| 图1 算法参数测试结果 Fig. 1 Test results of the parameters for IBA |
由图1可看出:在其他参数相同的情况下,最大迭代次数
|
表3
|
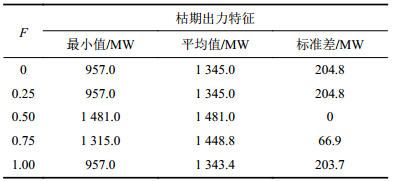 |
3.2 模拟计算结果及分析
采用IBA对典型年径流资料进行模拟计算,其中,
| 表4 改进蝙蝠算法优化结果 Tab. 4 Optimal solution of IBA |
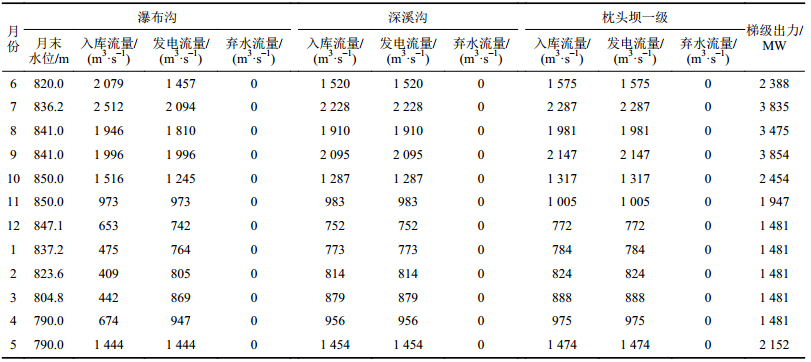 |
由表4可知,梯级水电站在丰水期(6—10月)蓄水,在枯水期(12月—次年4月)供水,没有发生弃水现象,水位变化及梯级电站出力过程符合调度要求,改进蝙蝠算法模拟优化调度结果合理。
为分析比较算法的性能,分别用标准BA算法和容易实现且可快速收敛的POA算法进行模拟计算。实验中,蝙蝠算法的种群个体数、脉冲音量最大值、脉冲发射率最大值、脉冲频率范围、搜索精度、最大迭代次数、算法终止条件、初始种群生成方式等均与改进蝙蝠算法相同,POA算法搜索步长为0.01 m,最大迭代次数
| 表5 不同算法优化结果比较 Tab. 5 Comprision of different methods on economic dispatch |
 |
从表5中实际梯级最小出力值来看,IBA、BA、POA算法分别为1 481、1 051、708 MW,设定梯级最小出力值为1 481 MW,BA、POA算法不满足梯级最小出力约束,未能实现梯级最小出力最大化目标。此外,IBA算法得到的梯级最小出力满足梯级电站设计保证出力要求,超过梯级设计保证出力96 MW。从梯级电站枯期出力平均值及标准差来看,IBA算法优化后的枯期出力大而均匀,明显优于另两种算法。这表明采用IBA算法进行梯级电站优化调度,更能保障电网安全稳定运行,这对于接入大量风电、光电等出力波动率大的新能源电力系统而言意义重大。从梯级年发电量和算法运行时间来看,IBA算法获得的发电量较BA算法高出107 kW·h,运行时间略短于后者;尽管POA算法运行时间与年发电量都优于IBA算法,但其出力值却偏小而波动率大。因此,对于梯级水电站经济调度问题,本文的IBA算法明显优于BA算法,也优于传统的POA算法。
4 结 论为给电网提供尽可能大而稳定的枯期出力,建立了兼顾梯级最小出力最大化的总发电量最大数学模型,研究了基于差分变异、选择因子的改进蝙蝠算法及其在梯级水电站中长期经济调度中的应用,并对算法主要控制参数进行了测试分析。通过工程实例检验,表明本文的改进蝙蝠算法能在给电网提供尽可能大而稳定的枯期出力,同时缩短计算时间,获得更高质量的解。但该算法仍然存在参数选择问题,下一阶段将引入动态控制机制,避免人工试算。
| [1] |
Wang Jinlong, Huang Weibin, Ma Guangwen. An improved partheno genetic algorithm for multi-objective economic dispatch in cascaded hydropower systems[J]. International Journal of Electrical Power & Energy Systems, 2015(67): 591-597. |
| [2] |
Fang Rengcun, Li Chaoshun, Pu Guilin. Optimal regulation of cascaded hydropower stations based on ACABC[J]. Yellow River, 2017, 39(2): 102-106. [方仍存, 李超顺, 蒲桂林. 基于自适应混沌蜂群算法的梯级电站优化调度[J]. 人民黄河, 2017, 39(2): 102-106.] |
| [3] |
Shi Yajun, Peng Yong, Xu Wei. Optimal operation model of cascade reservoirs based on grey discrete differential dynamic programming[J]. Journal of Hydroelectric Engineering, 2016, 35(12): 35-44. [史亚军, 彭勇, 徐炜. 基于灰色离散微分动态规划的梯级水库优化调度[J]. 水力发电学报, 2016, 35(12): 35-44. DOI:10.11660/slfdxb.20161204] |
| [4] |
Yeh W W G. Reservoir management and operations models:A state-of-the-art review[J]. Water Resources Research, 1985, 21(12): 1797-1818. DOI:10.1029/WR021i012p01797 |
| [5] |
Yan Jing, Sun Fan, Yue Chaoyuan. An optimal scheduling of hydro system based on the lagrangian relaxation method[J]. Control Theory and Applications, 2007, 26(7): 13-15. [严婧, 孙帆, 岳超源. 基于拉格朗日松弛法的梯级水电优化调度系统[J]. 自动化技术与应用, 2007, 26(7): 13-15.] |
| [6] |
Mei Yadong, Xiong Ying, Chen Lihua. A dynamic programming method for the multi-purpose operation of cascade reservoirs[J]. Journal of Hydroelectric Engineering, 2007, 26(2): 1-4. [梅亚东, 熊莹, 陈立华. 梯级水库综合利用调度的动态规划方法研究[J]. 水力发电学报, 2007, 26(2): 1-4.] |
| [7] |
Zhou Jia, Ma Guangwen, Zhang Zhigang. Study on the mid-long term optimal dispatching of cascaded hydropower stations on Yalong river based on POA modified adaptive algorithm[J]. Journal of Hydroelectric Engineering, 2010, 29(3): 18-22. [周佳, 马光文, 张志刚. 基于改进POA算法的雅砻江梯级水电站群中长期优化调度研究[J]. 水力发电学报, 2010, 29(3): 18-22.] |
| [8] |
Wu Chengguo, Wang Yimin, Huang Qiang. Study on combined optimal operation of cascade hydropower stations based on accelerating genetic algorithm[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 171-177. [吴成国, 王义民, 黄强. 基于加速遗传算法的梯级水电站联合优化调度研究[J]. 水力发电学报, 2011, 30(6): 171-177.] |
| [9] |
Wang Liang.Application of differential evolution algorithm to the short-term optimal scheduling of cascaded hydroelectric plants[D].Wuhan:Huazhong University of Science & Technology,2009. 王亮.差分进化算法在梯级水电站短期优化调度中的应用[D].武汉:华中科技大学,2009. |
| [10] |
Li Wenli, Li Yuxia, Ren Ping’an. Optimal operation of cascade reservoirs based on cloud variation-artificial bee colony algorithm[J]. Journal of Hydroelectric Engineering, 2014, 33(1): 37-42. [李文莉, 李郁侠, 任平安. 基于云变异人工蜂群算法的梯级水库群优化调度[J]. 水力发电学报, 2014, 33(1): 37-42.] |
| [11] |
Huang Weibin, Ma Guangwen, Wang Hekang. Application of chaos particle swarm optimization algorithm to mid-long term optimal operation of hydropower station[J]. Journal of Hydroelectric Engineering, 2010, 29(1): 102-105. [黄炜斌, 马光文, 王和康. 混沌粒子群算法在水库中长期优化调度中的应用[J]. 水力发电学报, 2010, 29(1): 102-105.] |
| [12] |
Tang Haidong, Rui Jun, Wu Zhengyi. Research on the optimal operation of cascade hydropower station based on the hybrid bat algorithm[J]. Hydropower and Pumped Storage, 2015, 1(4): 36-40. [唐海东, 芮钧, 吴正义. 基于混合蝙蝠算法的梯级水电站群优化调度研究[J]. 水电与抽水蓄能, 2015, 1(4): 36-40.] |
| [13] |
Xiao Huihui, Duan Yanming. Research and application of improved bat algorithm based on DE algorithm[J]. Computer Simulation, 2014, 31(1): 272-277. [肖辉辉, 段艳明. 基于DE算法改进的蝙蝠算法的研究及应用[J]. 计算机仿真, 2014, 31(1): 272-277.] |
| [14] |
Zhan Yang, Huang Weibin, Ma Guangwen. The analysis of compensation benefits based on coordinated optimal operation in Dadu river[J]. China Rural Water and Hydropower, 2015(10): 197-201. [湛洋, 黄炜斌, 马光文. 大渡河梯级联合优化运行下发电补偿效益分析[J]. 中国农村水利水电, 2015(10): 197-201. DOI:10.3969/j.issn.1007-2284.2015.10.048] |
| [15] |
Yang Xinshe.A new metaheuristic bat-inspired algorithm[M]//Studies in Computational Intelligence.Berlin:Springer,2010.
|
| [16] |
Yang Xinshe. Bat algorithm for multi-objective optimization[J]. International Journal of Bio-Inspired Computation, 2011, 3(5): 267-274. DOI:10.1504/IJBIC.2011.042259 |
| [17] |
Yang Xinshe, Gandomi A H. Bat algorithm:A novel approach for global engineering optimization[J]. Engineering Computations, 2012, 29(5): 464-483. DOI:10.1108/02644401211235834 |
 2018, Vol. 50
2018, Vol. 50


