2. 中国科学院 水利部 成都山地灾害与环境研究所,四川 成都 610041
2. Inst. of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China
滚石常发生于地形陡峭的山区,具有多发性、随机性和突发性等特点,运动轨迹预测比较困难,严重威胁山区人民经济财产与生命安全[1–3]。棚洞工程作为一种有效的滚石防护措施被广泛应用于山区公路滚石防护。传统的棚洞结构(图1(a))上部覆盖一定厚度的砂砾石垫层以吸收滚石冲击能量[4],但其存在一定的缺陷,例如自重大、施工成本高、耗能效果不佳等。近年来,Delhomme、何思明等[5–7]通过在棚洞支座处增设金属耗能器替代砂石垫层(图1(b)),在一定程度上达到了耗能减震、降低滚石冲击力、减轻棚洞结构自重的目的。
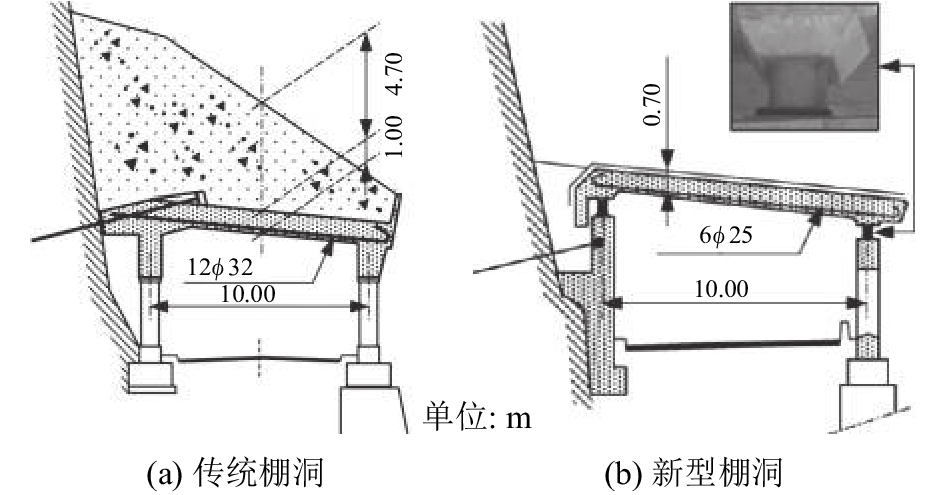 |
| 图1 传统棚洞和新型棚洞 Fig. 1 Traditional shed tunnel and structurally dissipating shed tunnel |
圆管状金属耗能器是工程实践中常见的缓冲吸能结构,在轴向压缩荷载作用下,金属耗能器在压力到达初始屈服荷载之前基本保持线弹性状态;耗能器一旦屈服,压力急剧下降,进入一个稳态渐进屈曲阶段,即耗能器的轴向荷载围绕平均压垮荷载上下波动,直至结构被压至密实化[8]。然而,从Alexander[9]、Andrews[10]和Guillow[11]等的研究成果中可以发现,常用的圆管金属耗能器初始屈服强度较大,一般约为平均压垮载荷的2倍。在滚石冲击棚洞结构设计过程中,为确保滚石冲击荷载下棚洞工程的安全,要求金属耗能器先于棚洞结构屈服,棚洞结构自身的抗滚石冲击强度要大于金属耗能器的初始屈服荷载。因此,圆管状金属耗能器要求棚洞结构具有更高的抗冲击能力,且结构更易发生瞬间破坏。此外,准静态压缩载荷下,圆管状金属耗能器一般发生轴对称叠缩破坏模式,而滚石冲击属于动态过程,且滚石冲击位置一般不位于金属耗能器的中心,因此耗能器的屈曲一般为非轴对称叠缩模式[12]。相对而言,轴对称破坏模式耗散能量效率高,便于控制,载荷–位移曲线相对稳定,为更理想的结构形式。
为此,提出一种新型波纹圆管状金属耗能器。通过将普通的圆管状金属耗能器的薄壁加工为波纹状的形式,即以人为设置塑性铰的方式降低金属耗能器初始屈服荷载、稳定金属耗能器的屈曲过程。研究首先采用压缩试验对其开展力学分析,然后引入动力有限元对物理模型试验进行验证,最后开展滚石冲击波纹圆管状金属耗能器棚洞的动力响应过程研究,揭示耗能器缓冲作用机理。
1 压缩试验及数值模拟物理模型试验选取高度300 mm、直径260 mm、壁厚3 mm、波纹弧度25 mm的波纹圆管状金属耗能器(图2(a))作为研究对象,利用MTS试验机进行压缩试验(图2(c)),记录试验过程中轴向载荷大小与压缩量的关系。为对压缩试验结果进行验证,采用ABAQUS有限元软件对压缩试验进行数值模拟。首先构建与压缩试验相同参数的波纹圆管状金属耗能器数值模型(图2(b)),并令其顶部与底部分别与两块刚体板接触(图2(d)),采用通用接触处理,摩擦系数设为0.3,采用罚函数接触算法。限制底板的运动,通过顶板沿着耗能器的轴线向下运动模拟压缩试验过程,得到相关数据与物理试验所得进行对比。
 |
| 图2 波纹圆管状金属耗能器 Fig. 2 Corrugated cylinder metal energy dissipator |
以往研究[12–16]表明,圆管金属耗能器在压缩过程中管壁以塑性铰叠缩形式逐次向下进行,在形成每一个叠缩的过程中管壁以最终形成的叠缩凸点(内或外)为铰点转动并向下移行,未发生屈曲部分的管壁强度基本不变,因此每一个叠缩开始形成时都相当于一种次弹性屈曲。本次波纹圆管状金属耗能器的压缩试验过程与数值模拟结果如图3所示。当载荷施加至耗能器的初始屈服载荷时,金属耗能器以表面的波纹状结构为铰点开始产生叠缩,而未发生叠缩的部分亦产生明显变形。随后,当第1层发生叠缩的部分压缩至一定程度之后,剩余结构继续以褶皱的形式渐进屈曲,最终在波纹状结构的引导下以轴对称破坏的形式被压至密实,形成3组明显的叠缩结构。
 |
| 图3 压缩试验数值模拟过程 Fig. 3 Numerical simulation of compression test process |
物理试验和数值模拟所得出的荷载–位移曲线如图4所示,二者曲线吻合较好,均分为3个阶段。在
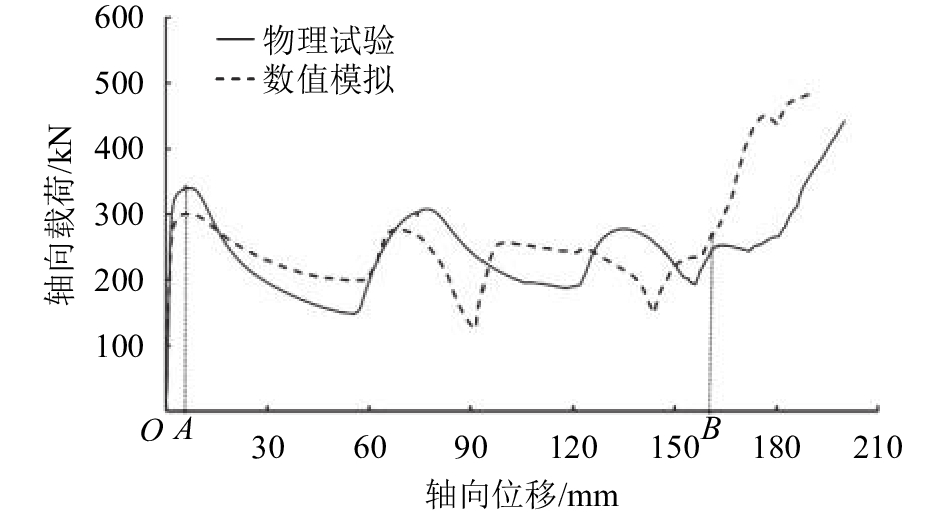 |
| 图4 波纹圆管状金属耗能器荷载与位移曲线 Fig. 4 Curves of load and displacement of corrugated cylinder metal energy dissipator |
为对比两种不同金属耗能器受力变形特性的差异,再次构建不带波纹状结构的圆管金属耗能器数值模型,并进行压缩试验模拟,最终得出两者荷载位移曲线对比如图5所示。由图5可知,圆管状金属耗能器的初始屈服荷载远超带有波纹状结构的金属耗能器,约为后者的3倍。在轴向压缩量不断增大的过程中,圆管金属耗能器的荷载不断减小,没有产生一个明显的耗能平台,说明其耗能潜力没有得到充分发挥。因此,当采用圆管状金属耗能器作为棚洞工程耗能缓冲的手段时,不论是对于棚洞工程自身抗冲击的要求,还是对冲击能量阈值的要求,都远高于采用波纹圆管状金属耗能器的棚洞。
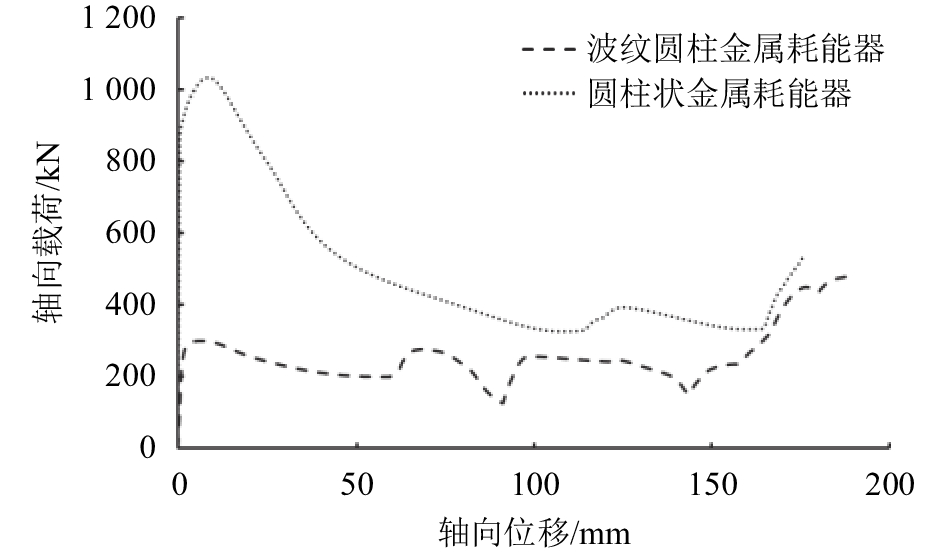 |
| 图5 两种不同金属耗能器荷载与位移曲线的对比 Fig. 5 Contrast of load-displacement curves of two different metal energy dissipator |
通过物理压缩试验及数值模拟可以得出以下结论:1)较之圆管金属耗能器,波纹圆管状金属耗能器的初始屈服强度远低于圆管金属耗能器,当棚洞顶板遭受滚石冲击时,能够更快地进入屈曲耗能阶段耗散能量;2)波纹圆管状金属耗能器在承受轴向压缩荷载时,由于波纹状结构的引导作用,更易发生轴对称破坏,形成一个稳定的屈曲阶段,充分发挥自身变形耗能的特性。
2 滚石冲击波纹圆管状金属耗能器棚洞动力有限元模型构建图4和5中,波纹圆管状金属耗能器压缩试验数值模拟所得的结果与物理试验结果进行对比,表明无论是压缩过程还是位移荷载曲线,两者都基本吻合,使得耗能器数值模型得到验证。进一步地,利用ABAQUS动态有限元程序开展滚石冲击作用下波纹圆管状金属耗能器动力响应机理研究。
2.1 计算模型构建棚洞计算模型如图6所示。
假定一半径为0.5 m、密度为2 500 kg/m3的球状滚石以一定速度冲击棚洞顶板。其中,棚洞梁截面为0.6 m
 |
| 图6 滚石冲击棚洞的计算模型 Fig. 6 Calculation model of impact of rolling stone on rock tunnel |
研究工况如下:
工况1 设置波纹圆管状金属耗能器棚洞在滚石冲击下的动力响应。
工况2 设置圆管状金属耗能器棚洞在滚石冲击下的动力响应。
工况3 未设置金属耗能器棚洞在滚石冲击下的动力响应。
2.2 材料参数及本构模型棚洞板及梁混凝土强度等级为C30,本构参照过镇海等[17]提出的单轴受压应力–应变全曲线,表达式为:
| $y(x) = \left\{ \begin{aligned}& {\alpha _{\rm a}}x + (3 - 2{\alpha _{\rm a}}){x^2} + ({\alpha _{\rm a}} - 2){x^3},x \le 1;\\& \frac{x}{{{\alpha _{\rm d}}{(x - 1)^2} + x}},x > 1\end{aligned} \right.$ |
式中,
混凝抗压强度
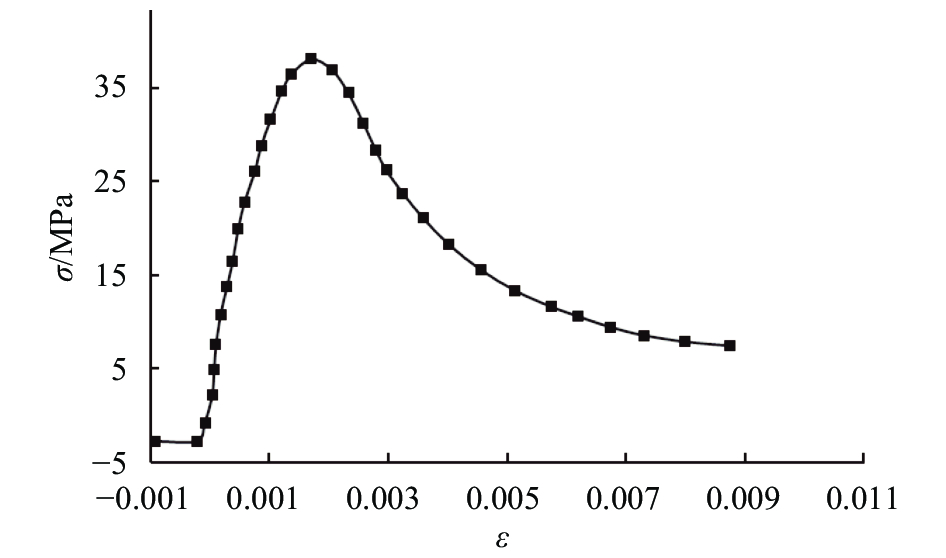 |
| 图7 混凝土本构模型 Fig. 7 Concrete constitutive model |
金属耗能器及钢筋采用线性弹塑性模型,假设塑性硬化模量为弹性模量的1/10[4],屈服强度遵循von Mises应力准则,本构模型见图8,计算所需参数见表1。
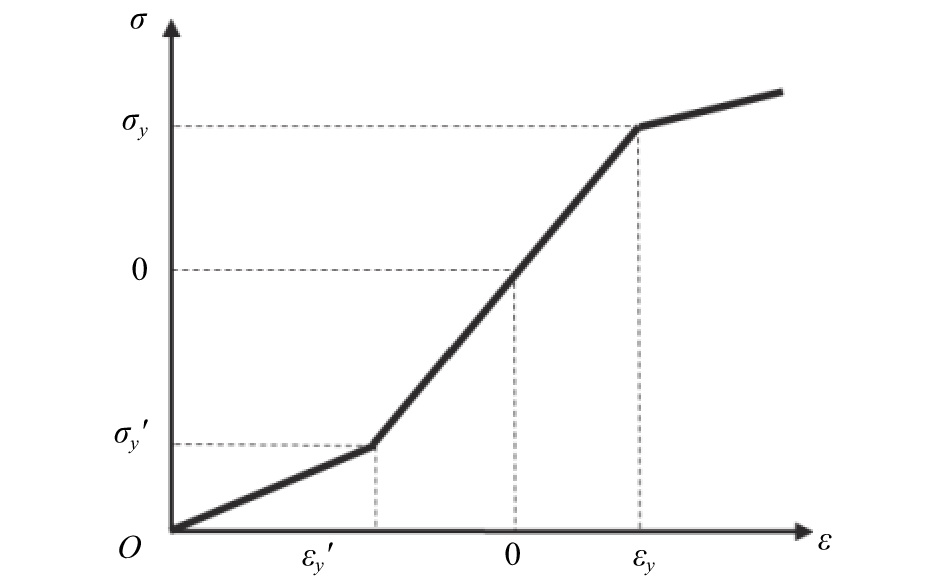 |
| 图8 钢筋及金属耗能器材料本构参数 Fig. 8 Constitutive relation of rebar and metal energy dissipator |
| 表1 钢筋及金属耗能器材料参数 Tab. 1 Calculation parameters of rebar and metal energy dissipator |
 |
2.3 数值计算模型
根据上述几何模型的描述,建立数值计算模型如图9所示。数值模型分为5个部分,即软钢阻尼器、棚洞梁、棚洞顶板、钢筋和滚石。
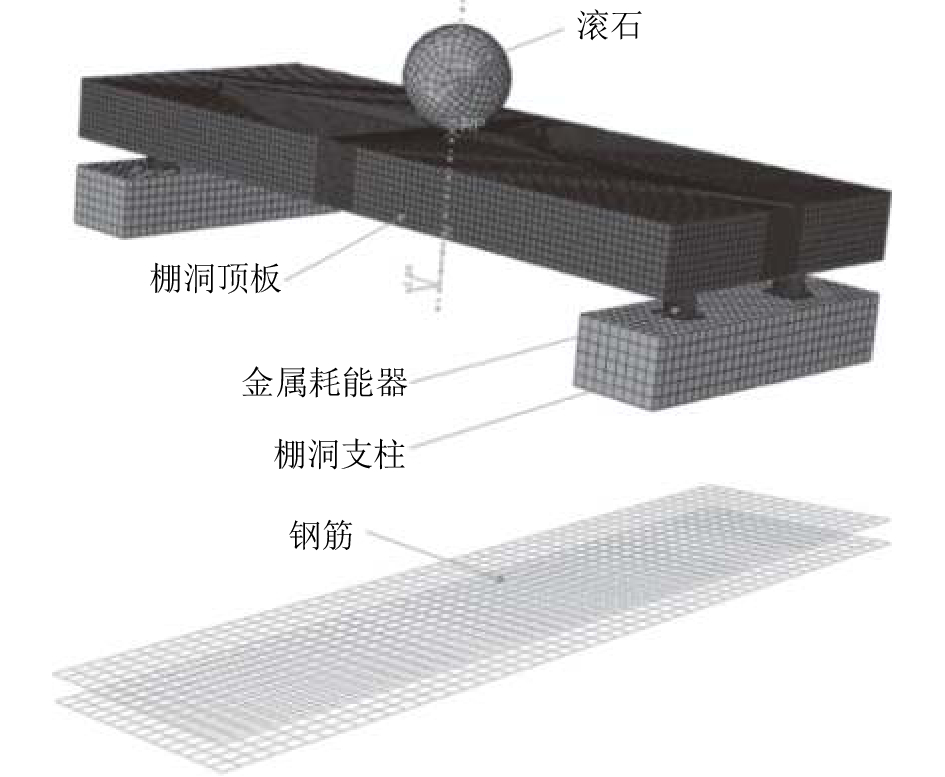 |
| 图9 数值模拟模型 Fig. 9 Model of numerical simulation |
计算采用ABAQUS/Explicit有限元软件进行,根据滚石冲击棚洞过程问题描述,数值分析过程进行如下设置:
耗能器模型:两种金属耗能器的高度
网格划分:棚洞梁、棚洞板采用8节点六面体实体单元C3D8R。为体现钢筋的抗弯性能,钢筋选用双节点线性梁单元T3D2。金属耗能器的网格划分长度为5 mm,采用四边形壳体单元S4。滚石及金属耗能器底板设置为离散刚体,采用4节点刚体单元R3D4。
荷载及边界条件:根据滚石冲击的实际情况考虑边界条件,棚洞梁底部施加全约束边界条件。在初始分析步中对整个模型施加重力荷载,重力加速度为9.8 m/s2;对球体施加初始竖向速度20 m/s。
分析步:除初始分析步initial外,创建一个接触分析步contact、冲击分析步impact和冲击结束后的结构振动情况分析步vibration。在initial中施加位移边界条件、contact中施加约束条件进行模拟,设置冲击过程持续时间为0.4 s。
接触定义:滚石和棚洞顶板之间的相互作用采用通用接触处理,耗能器内外表面分别设置为自接触,以上两种接触均采用罚函数接触算法,摩擦系数设为0.3。耗能器底板与棚洞板及棚洞支柱之间设置为共节点,钢筋与棚洞板混凝土为嵌入约束。
3 计算结果与分析采用第2节构建的有限元模型,分别对3种研究工况进行数值模拟。通过对不同金属耗能器的破坏模式、应力云图,以及对棚洞顶板的挠度、棚洞底部承载力变化、金属耗能器变形吸能总量进行比较,分析两种金属耗能器运用在棚洞工程中的优劣。
3.1 金属耗能器破坏模式及应力云图分别选取2种不同金属耗能器,对比其在棚洞静置和受到3种不同速度的滚石冲击下的破坏模式及应力云图(图10~11)。
 |
| 图10 不同滚石冲击速度下圆管金属耗能器的破坏模式与应力云图 Fig. 10 Failure conditions and stress nephogram of cylindrical metal damper under different rolling impact velocities |
 |
| 图11 不同滚石冲击速度下波纹圆管金属耗能器的破坏模式与应力云图 Fig. 11 Failure mode and stress nephogram of cylindrical metal damper under different rolling impact velocities |
如图10所示,在棚洞遭受滚石冲击时圆管金属耗能器发生的叠缩十分有限,正是由于其较高的初始屈服强度不利于冲击能量的耗散,导致棚洞抗冲击能力不足。由图11可知,随着滚石冲击速度的提升,波纹圆管状金属耗能器的叠缩程度明显增大。通过应力云图对比,发现圆管金属耗能器在发生一次叠缩之后应力在发生叠缩破坏处的集中现象十分明显,相反波纹圆管状金属耗能器应力分布依然均匀,便于多次叠缩,更多地吸收滚石冲击的能量。
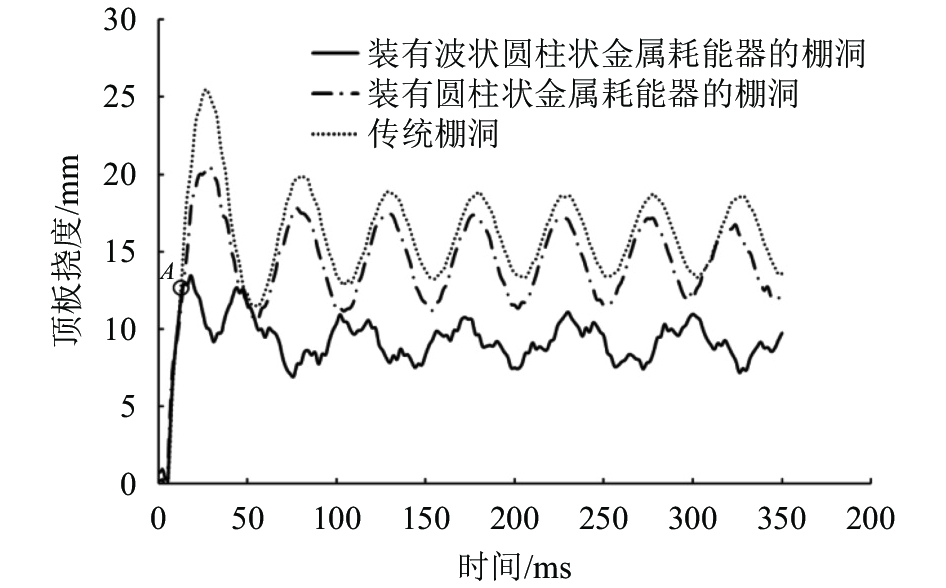
3.2 顶板挠度与时间的关系棚洞顶板挠度与时间的关系曲线如图12所示,3种不同棚洞的最大挠度有明显区别,传统棚洞的挠度最大值为25.50 mm,装有圆管状金属耗能器棚洞的挠度最大值为20.47 mm,装有波纹圆管状金属耗能器棚洞的挠度最大值为13.45 mm。前两者挠度的最大值都产生于滚石冲击后27 ms左右,装有波纹圆管状金属耗能器的棚洞挠度达到最大值的时间明显提前,为冲击后约18 ms。
 |
| 图12 棚洞顶板挠度与时间的关系曲线 Fig. 12 Curves of deflection of shed roof and time in three kinds of structure |
由图12可知,在冲击后的短时间内,三者的挠度曲线几乎没有区别;随着耗能器产生作用,3条曲线于
图12中,约50 ms之后的曲线表明棚洞顶板在冲击结束后持续振动,未装缓冲措施的棚洞顶板的振动曲线与安装圆管金属耗能器的棚洞顶板基本一致,表明此时圆管金属耗能器与棚洞支柱所起的作用基本一致,无法起到缓冲作用。装有波纹圆管状金属耗能器棚洞顶板的振动曲线与前两者有着明显差异,表明此刻金属耗能器依然在发挥其缓冲作用。
经过对顶板挠度与时间关系的分析可以看出,圆管状金属耗能器较高的初始屈服荷载使得滚石对于棚洞顶板的冲击无法让其及时叠缩变形并大量耗能,只能通过弹性变形和少数塑性变形消耗少部分冲击能量。波纹圆管状金属耗能器及时发挥其耗能作用,消耗大量冲击能量,有效保护棚洞顶板的安全。冲击结束后,波纹圆管状金属耗能器能有效减小冲击给棚洞顶板带来的振动,保障棚洞工程的整体安全。
3.3 棚洞建筑对地面的压力与时间的关系在地质条件较为复杂的山区修筑棚洞工程时,由于空间受限,地基承载力往往是需要考虑的一个极为重要的指标。因此,在实现滚石冲击力防护的前提下尽量减少棚洞结构对地基承载力的要求也是棚洞工程建设过程中一个重要的考虑因素。
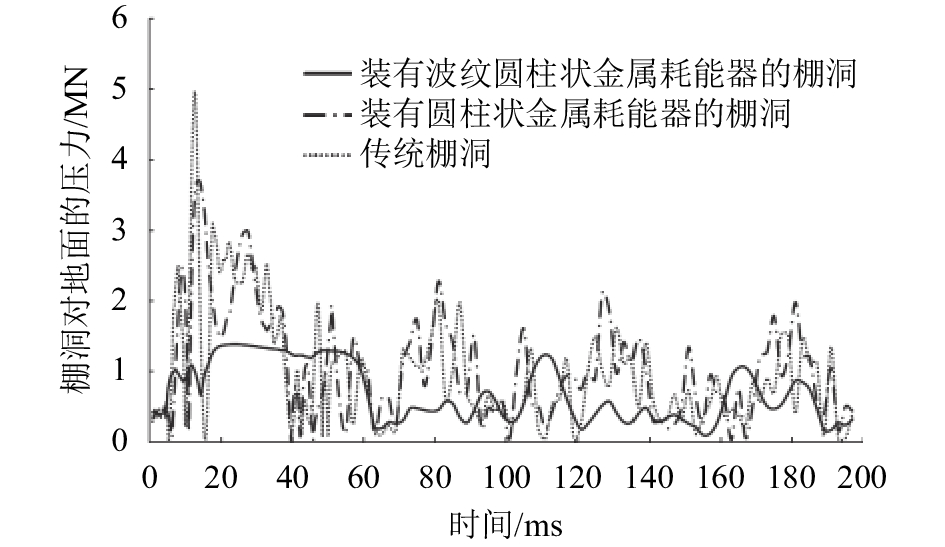
图13为滚石以20 m/s的速度冲击棚洞顶板时,棚洞结构对地面的压力与时间的关系。
 |
| 图13 棚洞对地面的压力与时间的关系曲线 Fig. 13 Curves of pressure on the ground and time in three kinds of structures |
由图13可知,没有安装金属耗能器的棚洞对地面的压力最大达到了4.97 MN。由于没有缓冲措施,棚洞在耗散瞬时的冲击能量时,曲线的振幅非常剧烈,表明棚洞整体结构经历了剧烈的振动,显然这种情况不利于建筑结构的整体稳定。安装有圆管状金属耗能器的棚洞对地面的压力曲线在趋势上大体与传统棚洞保持一致,但由于耗能器对于冲击能量的耗散及缓冲作用,使得棚洞对于地面的最大压力降低到了3.71 MN。装有波纹圆管状的金属耗能器的棚洞对地面的压力曲线则显得与前两者大相径庭,曲线上升到1 MN左右便不再上升,进入了一个几乎没有振动的相对平稳的阶段,对地面最大的压力仅为1.39 MN,正好约等于物理压缩试验中该型号金属耗能器屈服强度的4倍左右。因为棚洞顶板是由4个此型号的耗能器制成,因此进一步说明当波纹圆管状金属耗能器受到的轴向载荷超过其屈服载荷后,继续施加力并不会使得耗能器的载荷继续增加,而是围绕平均压垮载荷进行叠缩变形,并在此阶段大量消耗能量。因此,在数值模拟计算中,4个波纹圆管状金属耗能器共同承受着约1.3 MN的载荷,平稳地消耗滚石冲击及其所引起的棚洞顶板振动的能量,使得棚洞工程的地基不必承受变化的振动载荷,大大降低了对于建设区域地质条件的要求。
为进一步探究滚石冲击时两种耗能器的缓冲效果,再以30和40 m/s的滚石冲击棚洞顶板中心,得到如图14的结果。
 |
| 图14 棚洞对地面的压与时间的关系曲线 Fig. 14 Curves of pressure on the ground and time in three kinds of structures |
由图14可知,随着滚石冲击速度进一步提升,传统棚洞对于地面的压力不断增大,分别达到了11.10和12.20 MN。装有圆管状金属耗能器的棚洞对地面的最大压力稳定在3.72 MN不再上升,表明实际上圆管状金属耗能器都已进入屈服阶段,开始变形耗能;仅当滚石的冲击速度为40 m/s时,产生了如波纹圆管状金属耗能器的耗能平台,即对地基的压力曲线基本稳定于一个固定的值,说明此刻该金属耗能器的耗能特性开始得到较好发挥,缓解了棚洞工程遭受冲击后对地基不断变化的振动荷载。
通过对比图14(a)、(b)可以发现,当滚石以30或40 m/s的速度冲击装有波纹圆管状金属耗能器的棚洞时,棚洞结构对地面的压力随时间变化曲线与滚石以20 m/s的速度冲击时基本没有差异,说明耗能器的耗能特性始终得到了充分的发挥。由此可见,在缓冲耗能、提升棚洞对地基条件的适应性上而言,圆管状金属耗能器确实能够发挥缓冲的作用,但在滚石速度不是很大时效果不明显,且不能有效阻止结构受到冲击后的振动。波纹状结构能够显著提升棚洞整体结构的稳定性,降低棚洞对安装地的地基承载力的要求。
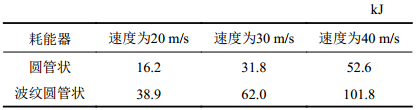
3.4 两种金属耗能器的总吸能为进一步比较不同初始损伤设置方式下金属耗能器的耗能特性,从总吸能情况进行对比分析。表2给出了两种金属耗能器棚洞遭受不同速度的滚石冲击时的耗能总量。不难看出,由于圆管状金属耗能器较难达到屈服强度的特性,使得其在棚洞遭受较低速的滚石冲击时无法进入屈曲阶段快速耗能;当滚石冲击速度较大时,圆管状金属耗能器又因其平均压垮载荷远小于屈服载荷,依旧不能稳定持续地耗散滚石冲击能量。这也导致其总吸能量始终只有波纹圆管状金属耗能器的一半左右。
| 表2 耗能器总吸能 Tab. 2 Total energy absorption of metal energy dissipator |
 |
4 结 论
冲击荷载下圆管金属耗能器具有较高的初始屈服荷载,远远超过其平均压垮荷载,导致滚石防护棚洞成本偏高,且在动力冲击下吸能效果不好,因此不利于大规模推广应用。针对该问题,提出在金属耗能器的薄壁上设置波纹状构造以降低初始屈服荷载、稳定屈曲阶段,进而提升棚洞结构的抗冲击能力,提高棚洞工程的区域适应性。为揭示不同构造金属耗能器在棚洞结构遭受滚石冲击时的动力响应,采用动力有限元方法构建了不同的棚洞有限元模型,建立完整的3维模型,研究了不同滚石冲击速度下装有不同金属耗能器的棚洞遭受滚石冲击时的不同表现,分析了不同金属耗能器在此过程中的耗能效果,结果表明:
1)波纹圆管状金属耗能器的初始屈服荷载远小于圆管状金属耗能器,又由于其压垮载荷和屈服载荷的差距不大,因此对冲击的反应较圆管状金属耗能器更为敏感,能够更快地进入耗散能量的状态而保证棚洞结构的安全。
2)安装有波纹圆管状金属耗能器的棚洞对地基承载力的要求大大降低,且滚石冲击能量越大,降低程度越大。同时波纹状结构良好的减震功能可最大限度地避免结构相互之间的振动而导致受损。
3)波纹圆管状金属耗能器不管在棚洞承受能量较低的冲击时还是能量较高的冲击时均能更好地吸收冲击能量,总吸能量大约为圆管状金属耗能器的两倍左右。
波纹圆管状金属耗能器具有良好的耗能效果和较低的初始屈服荷载,可大幅降低棚洞工程对于地基的要求,有利于新型滚石防护棚洞的推广应用。下一步将尝试根据不同型号的波纹圆管状金属耗能器研究其自身的结构对于冲击能量的敏感性,做出优化和改良。
| [1] |
Zhang Luqing,Yang Zhifa,Xu Bing. Rock falls and rock fall hazards[J]. Journal of Engineering Geology, 2004, 12(3): 225-231. [张路青,杨志法,许兵. 滚石与滚石灾害[J]. 工程地质学报, 2004, 12(3): 225-231.] |
| [2] |
Pei Xiangjun,Huang Runqiu,Pei Zuan,et al. Analysis on the movement charateristics of rolling rock on slope caused by intensitive earthquake[J]. Journal of Engineering Geology, 2011, 19(4): 498-504. [裴向军,黄润秋,裴钻,等. 强震触发崩塌滚石运动特征研究[J]. 工程地质学报, 2011, 19(4): 498-504.] |
| [3] |
Zhang Luqing,Yang Zhifa. Risk analysis of encountering rockfalls on a highway case study[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 5543-5548. [张路青,杨志法. 公路沿线遭遇滚石的风险分析——案例研究[J]. 岩石力学与工程学报, 2004, 23(21): 5543-5548.] |
| [4] |
Pei Xiangjun,Liu Yang,Wang Dongpo. Study on the energy dissipation of sandy soil cushions on the rock-shed under rockfall impact load[J]. Journal of Sichuan University(Engineering Science Edition), 2016, 48(1): 15-22. [裴向军,刘洋,王东坡. 滚石冲击棚洞砂土垫层耗能缓冲机理研究[J]. 四川大学学报(工程科学版), 2016, 48(1): 15-22.] |
| [5] |
Delhomme F,Mommessin M,Mougin J P,et al. Behavior of a structurally dissipating rock-shed:Experimental analysis and study of punching effects[J]. International Journal of Solids and Structures, 2005, 42(14): 4204-4219. DOI:10.1016/j.ijsolstr.2004.12.008 |
| [6] |
Delhomme F,Mommessin M,Mougin J P,et al. Simulation of a block impacting a reinforced concrete slab with a finite element model and a mass-spring system[J]. Engineering Structures, 2007, 29(11): 2844-2852. DOI:10.1016/j.engstruct.2007.01.017 |
| [7] |
He Siming,Wu Yong. Research on cushioning mechanism of new-typed energy dissipative rock shed[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 926-932. [何思明,吴永. 新型耗能减震滚石棚洞作用机制研究[J]. 岩石力学与工程学报, 2010, 29(5): 926-932.] |
| [8] |
Zhang Xiong.Crashworthiness analysis and design optimization of light thin-walled structures[D].Dalian:Dalian University of Technology,2008. 张雄.轻质薄壁结构耐撞性分析与设计优化[D].大连:大连理工大学,2008. |
| [9] |
Alexander J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. Quarterly Journal of Mechanics & Applied Mathematics, 1960, 13(1): 10-15. |
| [10] |
Andrews K R F,England G L,Ghani E. Classification of the axial collapse of cylindrical tubes under quasi-static loading[J]. International Journal of Mechanical Sciences, 1983, 25(9/10): 687-696. |
| [11] |
Guillow S R,Lu G,Grzebieta R H. Quasi-static axial compression of thin-walled circular aluminium tubes[J]. International Journal of Mechanical Sciences, 2001, 43(9): 2103-2123. DOI:10.1016/S0020-7403(01)00031-5 |
| [12] |
杜星文,宋宏伟.圆柱壳冲击动力学及耐撞性设计[M]. 北京:科学出版社,2004.
|
| [13] |
Karagiozova D.Jones N. On dynamic buckling phenomena in axially loaded elastic–plastic cylindrical shells[J]. International Journal of Non-Linear Mechanics, 2002, 37(7): 1223-1238. DOI:10.1016/S0020-7462(01)00146-9 |
| [14] |
Karagiozova D,Alves M,Jones N. Inertia effects in axisymmetrically deformed cylindrical shells under axial impact[J]. International Journal of Impact Engineering, 2000, 24(10): 1083-1115. DOI:10.1016/S0734-743X(00)00028-2 |
| [15] |
Karagiozova D,Jones N. Dynamic elastic-plastic buckling of circular cylindrical shells under axial impact[J]. International Journal of Solids & Structures, 2000, 37(14): 2005-2034. |
| [16] |
Karagiozova D,Jones N. Dynamic effects on buckling and energy absorption of cylindrical shells under axial impact[J]. Thin-Walled Structures, 2001, 39(7): 583-610. DOI:10.1016/S0263-8231(01)00015-5 |
| [17] |
Guo Zhenhai,Zhang Xiuqin,Zhang Dacheng,et al. Experimental study on the complete stress-strain curves of concrete[J]. Journal of Building Structures, 1982, 3(1): 1-12. [过镇海,张秀琴,张达成,等. 混凝土应力-应变全曲线的试验研究[J]. 建筑结构学报, 1982, 3(1): 1-12.] |
| [18] |
Abramowicz W,Jones N. Dynamic progressive buckling of circular and square tubes[J]. International Journal of Impact Engineering, 1986, 4(4): 243-270. DOI:10.1016/0734-743X(86)90017-5 |
 2018, Vol. 50
2018, Vol. 50

