2. 燕山大学 信息科学与工程学院,河北 秦皇岛 066004
2. College of Info. Sci. and Eng., Yanshan Univ., Qinghuangdao 066004,China
符号网络是边带有正负符号属性的社会网络[1],节点间的链接类型有正负两种。其中,正链接表示朋友、支持、喜欢等积极关系;负链接表示敌人、反对、讨厌等消极关系。有关符号网络的研究主要致力于其结构及演化分析,对社会网络演化过程研究的一个计算性问题就是链接预测,即通过对网络已知信息如节点属性、拓扑结构等进行分析,预测网络中尚不相连的节点间产生链接的可能性[2]。链接预测是社会网络分析领域的热点话题,在信息领域的推荐系统、态度预测以及生物领域等有着广泛的理论研究价值及实践指导意义。例如,在人人网、合著网等社交网络中,通过链接预测可以分析两个用户在将来是否会形成某种关系,或者识别研究者在将来进行合作的可能性,从而进行朋友推荐。在淘宝、京东等电子商务平台中,通过链接预测可以分析用户的喜好和需求,预测其购买趋势,进而为其推荐感兴趣的产品,帮助网站提升销售量。在安全领域中,通过链接预测可以发现潜在的犯罪团伙之间的秘密关系,从而为控制犯罪行为的蔓延提供有力的决策支持。
在将负关系纳入信任传播模型之前,研究者主要关注仅包含单一正关系的边值模型,对同时包含正负链接的符号网络边值预测问题的研究相对较少。然而,Epinions等网站的实际经验表明用户间的负关系同样不容忽视[3]。符号网络边值预测问题的研究有助于分析正负关系在符号网络中发挥的作用,推进社会网络中个性化推荐、异常用户识别、用户决策行为预测等多方面的研究发展及应用。于是,研究人员从不同角度设计了不同算法对符号网络正负关系预测问题进行了研究,主要分为两大类:基于矩阵的符号预测方法和基于分类的符号预测方法[4]。
1)基于矩阵的符号预测方法。将符号网络视为矩阵,利用信任传播模型、矩阵分解或矩阵填充等进行符号预测。Agrawal等[5]指出对矩阵进行奇异值分解、特征值分解或利用一些核函数的矩阵分解都可以有效预测未知的边的符号。Hsieh等[6]将符号预测问题转化为低秩矩阵填充问题,用MC-SVP算法有效预测边的符号。此外,一些基于矩阵的符号预测方法将预测结果矩阵中的连续元素通过阈值转化为离散值±1,以获得最终的正负关系预测结果。上述基于矩阵的符号预测算法中矩阵分解和矩阵填充算法能够达到较高的预测准确率,但相关算法未能有效融合结构平衡理论,预测所得符号网络模型不能很好地体现结构平衡性。然而,大量实证分析表明结构平衡理论能够很好地捕获无向符号网络中节点间的相互作用模式,有助于符号网络的链接预测研究以及网络结构平衡性分析。且Leskovec等[7]的研究发现,真实符号网络中符合结构平衡理论的三元环数目远大于不平衡的三元环数目。自此之后,研究人员开始结合结构平衡理论对符号网络中的符号预测问题进行研究。目前,结构平衡理论中的一些规律已被普遍应用于符号网络正负链接预测算法中。
2)基于分类的符号预测方法。将符号网络中正负链接预测视为二值分类问题,构建特征集,利用分类算法进行符号预测。根据构建特征集所用信息的不同,可分为基于网络结构信息的算法和基于网络上下文信息的算法。前者结合结构平衡理论,利用符号网络结构信息设计符号预测算法;后者利用上下文信息构建特征集,通过分类算法对边的符号进行预测。Leskovec等[7]分析了真实符号网络中正负链接模型与预测的链接之间的区别,对无向符号网络中的边值演化问题进行了分析。随后,Leskovec等[8]结合结构平衡理论,使用Epinions、Slashdot和Wikipedia这3个数据集通过有监督的机器学习,利用逻辑回归模型对潜在社会网络中的链接符号进行了预测,该方法准确度较高,但仅考虑了网络局部信息。Chiang等[9]基于Katz指标提取网络中长度为
从总体研究现状而言,基于分类的符号预测方法虽涌现出不少优秀成果,但仍然存在一些问题,主要体现在以下两方面:
1)基于相似性的链接预测算法大多仅单一地考虑了网络图的局部或全局特性,在预测准确率和计算复杂度上难以均衡,且无法直接应用于包含正负二元边值关系的符号网络。研究发现,基于网络结构信息的特征比基于网络上下文信息的特征更重要[17],且大多数真实社会网络的上下文信息难以获取。因此,当前主流的链接预测算法是通过节点固有属性定义节点相似性,主要分为两类:一类是基于节点局部信息的相似性算法,主要利用了节点及邻居节点的度信息,如CN指标、Jaccard算法等。此类算法思路简单,容易实现,计算复杂度较低,但忽略了邻居节点间的联系,不能有效挖掘路径信息对节点间相似性的影响,针对不同的网络,预测精度不稳定。另一类是基于路径结构的相似性算法,主要利用了路径个数、路径长度以及路径上节点间的信息来定义相似性,如最短路径算法、Katz指标等。该类算法考虑了连接两节点的全部或部分路径对于节点的相似性贡献,预测准确率较高。但其忽略了路径上传输节点的局部相似度对于两节点的相似性影响,且没有区分相同长度的不同路径对于相似性的影响力。此外,计算两节点间所有路径信息的复杂度较高。因此,基于符号网络的结构特征,如何结合结构平衡理论,有效融合节点局部信息和路径结构信息来定义相似性,在提高预测准确率的同时有效降低计算复杂度是符号网络链接预测算法研究的重点之一。
2)已有符号预测算法仅能对已经存在但缺失链接类型的边的符号进行预测,无法同时实现未来边的链接预测和符号预测。主流的符号预测算法主要基于结构平衡理论和机器学习,该类算法往往假定边集固定不变,基于现有的节点集与边集,通过机器学习完成已有边的符号预测。该类算法没有考虑网络结构演变中未来链接的建立及其对网络结构平衡性的影响,而真正意义上的边值预测包括网络结构上的链接预测和符号预测,即要对符号网络中的已有链接、未来链接及其符号类型同时做出准确预测。因此,如何结合结构平衡理论构建特征集,或利用符号网络的拓扑结构信息完成未来边的链接预测和符号预测是值得深入探讨的问题。
鉴于以上问题,作者以符号网络在某一时刻的瞬时快照图为研究对象,以节点相似性度量为出发点,从符号网络结构特征入手,改进传统单一相似性指标的不足之处,定义融合节点局部属性相似性和全局路径结构相似性的度量指标,以提高预测准确率,降低计算复杂度。同时,在深入研究反映和影响符号形成因素的机制之上,基于结构平衡理论,设计融合多特征的符号预测算法。最后,构建融合相似性和结构平衡理论的符号网络边值预测算法(prediction for signed networks based on the balance and similarity,PSNBS)。
1 预备知识Heider于1946年提出的结构平衡理论为符号网络结构分析提供了理论基础,它用一种平衡模型描述了用户间就正负向链接形成的关系的结构和冲突等的来源。随后,Cartwright和Harary将该理论推广至图论中,用数学语言将其形式化描述为符号网络。2010年,Leskovec等首次将结构平衡理论应用于符号预测问题[7]。
1.1 结构平衡三角形结构平衡理论是围绕三角形的平衡性分析开始的,考虑了3个节点组成的三元组所有可能的组合模式。在无向符号网络中这种组合模式共有4种,分别记为
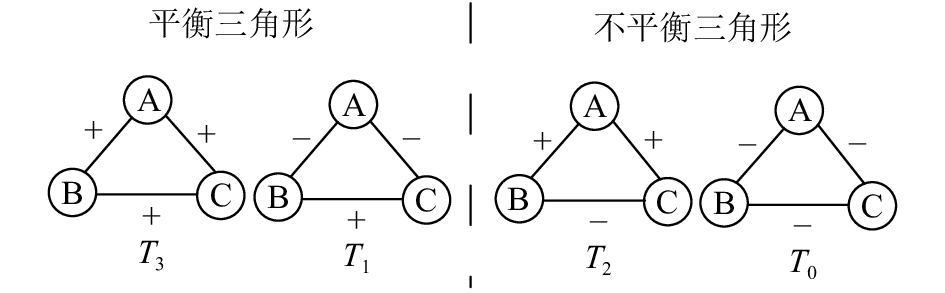 |
| 图1 结构平衡三角形和不平衡三角形示意图 Fig. 1 Diagrams of balanced and unbalanced triangles |
1.2 结构平衡环
上述三角形的结构平衡性判定方法可扩展至分析环的结构平衡性,即一个环是结构平衡的当且仅当环上所有边的符号之积为正,如图2所示。
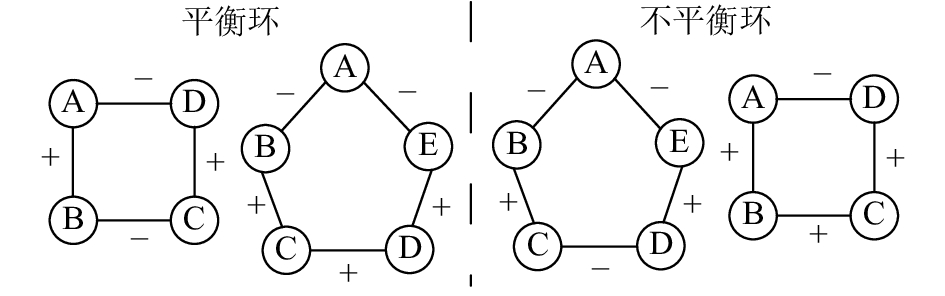 |
| 图2 结构平衡环和不平衡环示意图 Fig. 2 Diagrams of balanced and unbalanced circles |
1.3 符号网络平衡性分析
若无向符号网络中所有的环都是结构平衡环,则该网络是平衡网络。Anchuri等[18]对大规模符号网络Epinions和Slashdot的平衡性进行了研究,结果如表1所示。
| 表1 符号网络整体平衡性分析 Tab. 1 Analysis of global balance of signed networks |
 |
研究发现,这两个真实网络中符合结构平衡理论的三元环数远大于不平衡的三元环数。Hassan等[19]的研究表明,在自动构建的符号网络中,
PSNBS算法的目标是对未来链接及其符号同时做出准确预测,也可对网络中已经存在但缺失符号类型的边的符号做出预测。算法的一个重要假设前提是两节点相似度越高,两者建立链接的可能性越大。
首先,鉴于局部特征和路径结构对相似性的影响,综合考虑了两节点间的所有路径以及路径上的中间节点对于两节点的相似性贡献。先提取连接两节点的长度为
其次,考虑到未来链接对网络结构的平衡性影响,相似性指标的定义还要结合结构平衡理论,选取能从多角度反映符号形成机理的网络属性,以准确预测未来链接的符号类型。在度量未来链接对网络结构的平衡性影响时,将连接两节点的某条路径对于该未来链接的符号影响定义为该路径上所有已知边的符号乘积,以使未来链接所在的环是一个结构平衡环。
此外,张维玉等[23]的研究表明,三角形结构平衡理论可以为符号预测提供重要支持,在引入四边形结构平衡特征后,其预测准确率与仅使用三角形结构平衡特征的相比有显著提高,这也进一步验证了适当扩大结构平衡环的长度可以为连边符号预测提供更多的信息。同时,Liu等所提出的STNMP算法[24]中最优步长选择部分的实验结果也表明,提取连接两节点的步长大于3的路径计算相似度时,复杂度显著加大,预测准确率反而没有明显提高。鉴于此,结合相关研究成果,为降低复杂度,本文算法只考虑连接两节点的长度为2和3的路径对于相似性的影响,旨在达到较高预测准确率的同时保证算法效率。
最后,考虑到不同步长的路径对于两节点相似性以及未来链接符号的不同影响程度,对两种不同长度的路径赋予不同的可调步长影响因子。最终,用两节点基于步长为2和3的所有路径的相似性得分之和作为两节点基于相似性和结构平衡理论的边值预测得分。得分的绝对值度量了两节点的相似程度,即未来链接建立的概率;得分的正负即为未来链接的符号预测结果。
有一种特殊情况:若两节点的边值预测得分为0,则或许是因为连接两节点的步长为2和3的路径都不存在,又或者是两节点基于步长为2和步长为3的路径相似性得分的正负值相抵为0,导致无法获得未来链接的符号类型。此时,采用节点自身特征信息进行符号预测。引入负密度的概念,分析待测链接对应的两节点在网络中与其他节点的连边的符号倾向。当两节点的负密度都大于网络平均负密度时,表明这两个节点趋向于和其他节点建立负链接关系,此时,待测链接符号预测结果为负;否则,符号预测结果为正。
3 PSNBS算法 3.1 符号说明为准确描述所提算法,给出如下符号变量定义及说明:
1)
2)
3)
4)
5)
6)
7)
8)
9)
设
| $\begin{gathered} BS\!cor{e_2}({v_i},{v_j}) = S\!core({v_i},{v_{tk}},{v_j}) = \hfill \\ \sum\limits_{k = 1}^{|{N_1}({v_i}) \cap {N_1}({V_j})|} {\frac{2}{{k({v_{tk}})}}} \cdot s({v_i},{v_{tk}})\cdot s({v_{tk}},{v_j}) \hfill \\ \end{gathered} $ | (1) |
式中,
设
| $\begin{aligned} & BS\!cor{e_3}({v_i},{v_j}) = S\!core({v_i},{v_{pk}},{v_{qk}},{v_j}) = \\ & \quad \sum\limits_{|{l_k}| = 3} {\frac{{3 \cdot s({v_i},{v_{pk}})\cdot s({v_{pk}},{v_{qk}})\cdot s({v_{qk}},{v_j})}}{{k({v_{pk}}) + k({v_{qk}}) - 1}}}\end{aligned} $ | (2) |
式中:
设
| $\begin{aligned} & BS\!core({v_i},{v_j}) = \lambda \cdot BS\!core_2({v_i},{v_j}) + \\&\;\;\;\;\quad (1 - \lambda )\cdot BS\!core_3({v_i},{v_j}) \end{aligned} $ | (3) |
式中,
设
| ${D^ - }({v_i}) = \frac{{{k^ - }({v_i})}}{{k({v_i})}}$ | (4) |
设
| ${D^ - }(G) = \frac{{\displaystyle\sum\limits_{i = 1}^n {{D^ - }({v_i})} }}{n}$ | (5) |
将基于相似性与结构平衡理论结合的符号网络边值预测结果定义如下:
1)链接预测结果。节点对〈
2)符号预测结果。若
输入:图
输出:待测边的符号预测结果及图
对于图
第1步:查找
第2步:查找
第3步:计算节点对的边值预测得分
第4步:进行链接预测。
1)对已存在的边进行符号预测
①若节点对边值预测得分不为0,则待测边符号类型与边值预测得分的符号类型相同。
②若节点对边值预测得分为0,则当两节点的负密度都大于网络平均负密度时,待测边的符号预测结果为负;否则,符号预测结果为正。
③对未来链接进行边值预测
将节点对的边值预测得分的绝对值降序排序,将前
PSNBS算法实现过程如下:
1:ReadGraphFile
2:Initialize matrix
3:For each
4:If
5:{ Find all
6:Find all
7:Compute
8:If
9:{Calculate
10:If
11:Else
12:Else if
13:Else
14:Output
15:Sort
首先,通过网络获取实验所需数据集,将实验过程分为训练验证和比较实验两个阶段。其次,针对符号网络拓扑特征,采用改进的适合于符号网络的链接预测准确率评价指标对所提算法边值预测准确率进行评估,验证算法的正确性。最后,将所提算法与经典的同类型的符号网络链接预测方法进行对比分析。
4.1 实验所用数据集从http://snap.stanford.edu/下载获取3个经典的大规模真实符号网络数据集Epinions、Slashdot和Wikipedia,抽取得到其子集。本研究中忽略链接的方向,将这3个数据集转化为无向符号网络进行边值预测研究。各数据集拓扑信息见表2,详细信息如下:
1)Epinions。消费者评论网站,用户可在网站上查看其他用户对商品的评论等,并可创建有向符号链接表达对他人的信任或不信任。
2)Slashdot。技术博客网站,用户可对公布在该网站的新闻发表意见,同时可将其他用户添加至朋友或敌人列表。
3)Wikipedia。收集了维基百科用户对选举其管理员的投票信息构建所得的一个网络,用户可对候选人的晋升投支持票或反对票。
| 表2 实验所用数据集拓扑结构信息 Tab. 2 Topology information of datasets |
 |
4.2 训练集与测试集的划分
为衡量算法预测结果的准确率,需将已知的边集
常用的评价链接预测算法精度的指标有
| $AU{C_{^{{\rm{BS}}}}} = \frac{{n' + 0.5n''}}{n}$ | (6) |
与
| $Precisio{n_{{\rm{BS}}}} = \frac{{{N_{{\rm{s\_correct}}}}}}{{{N_{{\rm{s\_total}}}}}}$ | (7) |
式中:
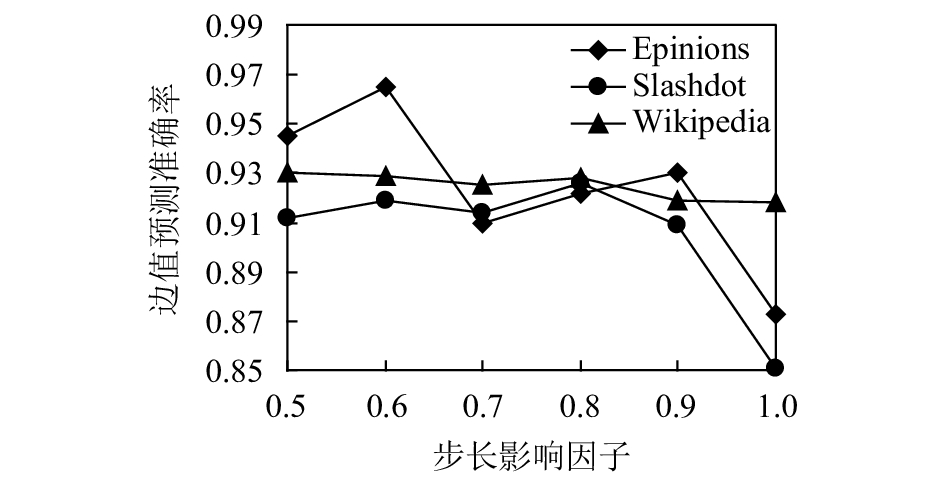
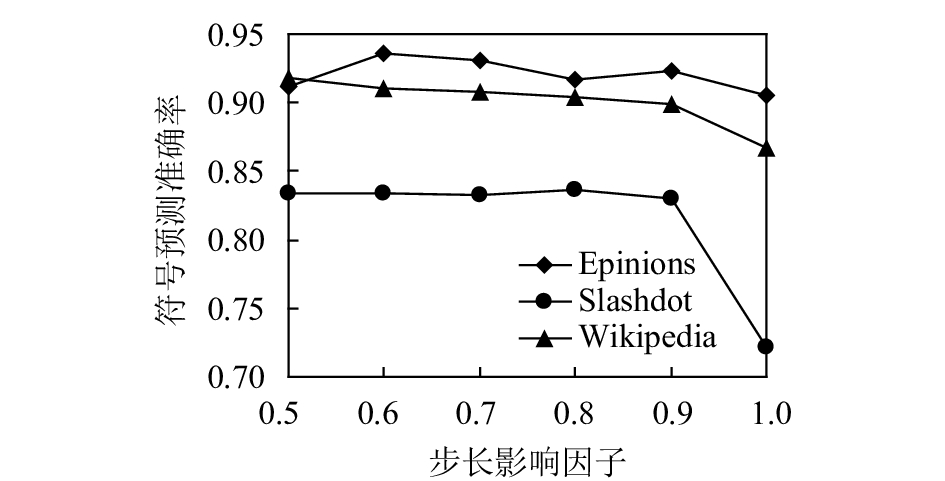
PSNBS算法引入可调步长影响因子
| 表3 基于AUCBS评价指标的PSNBS算法预测准确率 Tab. 3 Prediction accuracy of PSNBS algorithm based on AUCBS evaluation index |
 |
由表3可知,针对3个数据集,PSNBS算法预测准确率基本可达93%以上。实验结果显示了PSNBS算法对于大规模符号网络较为理想的边值预测效果。此外,针对实验所用数据集,算法在
真实符号网路中,许多边的符号类型是未知的。比如,蛋白质相互作用网络中,酵母菌蛋白质之间80%的相互作用是不为人知的[27]。针对此类缺失符号类型的符号网络,若先采用链接预测算法对未知的符号类型进行预测,在此基础上指导试验过程,便有可能大大减少试验次数,提高成功率,降低实验成本,加快人类对于网络中隐含的链接信息的认识。
为进一步验证所提算法对于未知的边的符号类型预测的有效性及正确性,后期实验中,采用
| 表4 基于PrecisionBS评价指标的PSNBS算法符号预测准确率 Tab. 4 Sign prediction accuracy of PSNBS algorithm based on PrecisionBS evaluation index |
 |
从表4可知,PSNBS算法在3个数据集上均达到了较高的符号预测准确率。此外,比较表3和4可知,针对3个符号网络,采用
 |
|
图3 |
 |
|
图4 |
4.6 与经典算法性能对比
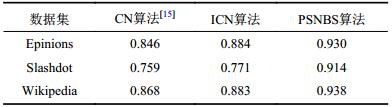
PSNBS算法在扩展结构平衡环概念的基础上,通过定义基于节点局部信息和路径结构相结合的相似性度量实现了边值预测,在一定程度上达到预测准确率和计算复杂度较好的均衡。为进一步验证算法性能,将该算法与符号网络链接预测CN[15]和改进的ICN[15]算法进行了对比实验,同时,采用
由表5可知,以
提出基于相似性与结构平衡理论的符号网络边值预测算法PSNBS,综合考虑了节点自身属性和路径特征定义节点相似性度量,改进了已有相似度指标的不足之处;结合结构平衡理论预测符号类型,在提高准确率的同时,能够实现链接及其符号双重预测。采用
| [1] |
Cheng Suqi,Shen Huawei,Zhang Guoqing,et al. Survey of signed network research[J]. Journal of Software, 2014, 25(1): 1-15. [程苏琦,沈华伟,张国清,等. 符号网络研究综述[J]. 软件学报, 2014, 25(1): 1-15. DOI:10.13328/j.cnki.jos.004503] |
| [2] |
Liu Dawei,Lv Yuanna,Yu Zhihua. An improved algorithm for link prediction in complex networks[J]. Journal of Chinese Computer Systems, 2016, 37(5): 1071-1074. [刘大伟,吕元娜,余智华. 一种改进的复杂网络链路预测算法[J]. 小型微型计算机系统, 2016, 37(5): 1071-1074.] |
| [3] |
Zolfaghar K,Aghaie A.Mining trust and distrust relationships in social web applications[C]//Proceedings of the 2010 IEEE 6th International Conference on Intelligent Computer Communication and Processing.NewYork:IEEE,2010:73–80.
|
| [4] |
Lan Mengwei,Li Cuiping,Wang Shaoqing,et al. Survey of sign prediction algorithms in signed social networks[J]. Journal of Computer Research and Development, 2015, 52(2): 410-422. [蓝梦微,李翠平,王绍卿,等. 符号社会网络中正负关系预测算法研究综述[J]. 计算机研究与发展, 2015, 52(2): 410-422. DOI:10.7544/issn.1000-1239.2015.20140210] |
| [5] |
Agrawal P,Garg V K,Narayanam R.Link label prediction in signed social networks[C]//Proceedings of the 23rd International Joint Conference on Artificial Intelligence.Beijing:AAAI,2013:2591–2597.
|
| [6] |
Hsieh C J,Chiang K Y,Dhillon I S.Low rank modeling of signed networks[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.NewYork:ACM,2012:507–515.
|
| [7] |
Leskovec J,Huttenlocher D,Kleinberg J.Signed networks in social media[C]//Proceedings of the SIGCHI International Conference on Human Factors in Computing Systems.NewYork:ACM,2010:1361–1370.
|
| [8] |
Leskovec J,Huttenlocher D,Kleinberg J.Predicting positive and negative links in online social networks[C]//Proceedings of the 19th International World Wide Web Conference Committee (IW3C2).NewYork:ACM,2010:641–650.
|
| [9] |
Chiang K Y,Natarajan N,Tewari A,et al.Exploiting longer cycles for link prediction in signed networks[C]//Proceedings of the 20th ACM International Conference on Information and Knowledge Management.NewYork:ACM,2011:1157–1162.
|
| [10] |
Ye Jihang,Cheng Hong,Zhu Zhe,et al.Predicting positive and negative links in signed social networks by transfer learning[C]//Proceedings of the 22nd International Conference on World Wide Web.NewYork:ACM,2013:1477–1488.
|
| [11] |
Yang Shuanghong,Smola A J,Long Bo,et al.Friend or frenemy?:Prediction signed ties in social networks[C]//Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval.New York:ACM,2012:555–564.
|
| [12] |
Facchetti G,Iacono G,Altafini C. Computing global structural balance in large-scale signed social networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(52): 20953-20958. DOI:10.1073/pnas.1109521108 |
| [13] |
Symeonidis P,Tiakas E. Transitive node similarity:Prediction and recommending links in signed social networks[J]. World Wide Web (Internet & Web Information Systems), 2014, 17(4): 743-776. DOI:10.1007/s11280-013-0228-2 |
| [14] |
Patidar A,Agarwal V,Bharadwaj K K.Predicting friends and foes in signed networks using inductive inference and social balance theory[C]//Proceedings of IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining.New York:ACM,2012:384–388.
|
| [15] |
She Hongjun,Hu Mengyuan. Research of link prediction based on signed networks[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2015, 37(5): 464-468. [佘宏俊,胡梦缘. 基于符号网络的边值预测方法研究[J]. 武汉理工大学学报(信息与管理工程版), 2015, 37(5): 464-468. DOI:10.3963/j.issn.2095-3852.2015.05.017] |
| [16] |
Zeng Jiangfeng,Zhou Ke,Ma Xiao,et al.Exploiting cluster-based meta paths for link prediction in signed networks[C]//Proceedings of the 2016 ACM Conference on Information and Knowledge Management.New York:ACM,2016:1905–1908.
|
| [17] |
David E,Jon K.Networks,crowds,and markets:Reasoning about a highly connected world[M].New York:Cambridge University Press,2010:119–152.
|
| [18] |
Anchuri P,Magdon-Ismail M.Communities and balance in signed networks:A spectral approach[C]//Proceedings of International Conference on Advances in Social Networks Analysis and Mining.New York:ACM,2012,235–242.
|
| [19] |
Hassan A,Abu-Jbara A,Radev D.Extracting signed social networks from text[C]//Proceedings of the TextGraphs-7 Workshop on Graph-based Methods for Natural Language Processing.Stroudsburg:Association for Computational Linguistics,2012:6–14.
|
| [20] |
Brusco M,Doreian P,Mrvar A,et al. Two algorithms for relaxed structural balance partitioning:Linking theory,models and data to understand social network phenomena[J]. Sociological Methods & Research, 2011, 40(1): 57-87. DOI:10.1177/0049124110384947 |
| [21] |
Malekzadeh M,Fazli M A,Khalidabadi P J,et al.Social balance and signed network formation games[C]//Proceedings of the 5th Workshop on Social Network Mining and Analysis.New York:ACM,2011.
|
| [22] |
Szell M,Lambiotte R,Thurner S. Multirelational organization of large-scale social networks in an online world[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(31): 13636-13641. DOI:10.1073/pnas.1004008107 |
| [23] |
Zhang Weiyu,Wu Bin,Liu Yang. Integrating multi-feature for link sign prediction in signed networks[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(5): 80-84. [张维玉,吴斌,刘旸. 融合多特征的符号网络连边符号预测[J]. 北京邮电大学学报, 2014, 37(5): 80-84. DOI:10.13190/j.jbupt.2014.05.017] |
| [24] |
Liu Miaomiao,Guo Jingfeng,Luo Xu. Link prediction based on the similarity of transmission nodes of multiple paths in weighted social networks[J]. Journal of Information Hiding and Multimedia Signal Processing, 2016, 7(4): 771-780. |
| [25] |
Lü Linyuan,Zhou Tao. Link prediction in complex networks:A survey[J]. Physica A Statistical Mechanics & Its Application, 2011, 390(6): 1150-1170. DOI:10.1016/j.physa.2010.11.027 |
| [26] |
Huang Y J,Powers R,Montelione G T. Protein NMR recall,precision,and F-measure scores (RPF scores):Structure quality assessment measures based on information retrieval statistics[J]. Journal of the American Chemical Society, 2005, 127(6): 1665-1674. DOI:10.1021/ja047109h |
| [27] |
Yu H,Braun P,Yildirim M A,et al. High-quality binary protein interaction map of the yeast interactome network[J]. Science, 2008, 322(5898): 104-110. DOI:10.1126/science.1158684 |
 2018, Vol. 50
2018, Vol. 50