2. 成都信息工程大学 控制工程学院,四川 成都 610225;
3. 国网四川省电力公司技能培训中心,四川 成都 610072
2. School of Control Eng.,Chengdu Univ. of Info. Technol.,Chengdu 610225,China;
3. State Grid Sichuan Electric Power Co. Skill Training Center,Chengdu 610072,China
随着分布式发电技术的迅速发展,可再生能源(RES)在智能配电网中的渗透率日益增加,但其较强的间歇性、随机性给配电网的运行、控制带来诸多不确定因素[1–2],而在配电网中接入储能系统(ESS)可以减小不确定性带来的风险,是解决RES大规模并网问题的有效措施之一[3–4]。因此,如何充分利用ESS实现配电网高效可靠运行成为目前关注的重点。
在ESS的优化运行方面,文献[5–12]以电池储能系统(BESS)为研究对象,对其充放电策略展开了深入的研究,并取得一定的成果。Gabash等[5]以配电网收益最大为目标,构造一个两阶段优化模型,由上层优化得到BESS的充放电时刻,下层优化模型得到充放电功率,虽然实现了BESS的灵活优化运行,但日内充放电次数较多,影响了BESS的寿命。Gabash、Levron[6–7]等以购电成本最小为目标,提出包含BESS的主动配电网或微电网潮流优化模型。采用动态递归法求解模型。Teng等[8]提出了一种基于恒电流–恒电压控制策略的BESS充放电数学模型。杨艳红等[9]通过推导得出了反应蓄电池每一次放电损耗的数学模型,以考虑BESS寿命的发电单元综合费用最低为目标函数,建立微电网优化运行的数学模型。朱泽锋等[10]通过计算电池循环寿命,以包含BESS等效运行成本的配电网购电成本最小为目标函数,建立优化模型,采用分支定界–原对偶内点法进行求解,实现了BESS和配电网的经济运行。因此,文献[5–10]主要聚焦于BESS对于配电网或微电网削峰填谷方面的作用,建立了单目标优化模型。Coelho等[11]将混合电动汽车的电池作为储能单元,以微电网的运行费用和电动汽车电池使用成本最低为目标,基于多个场景建立了微电网多目标优化模型;胡晓通等[12]构造了以发电成本最低、环境效益最好及电池损耗最低为优化目标的微电网多目标优化模型;但这两个文献都没有涉及ESS对系统的调压作用。
ESS的运行具有明显的时序特性,其运行优化涉及多个时间断面,是一个大规模非线性规划问题,对优化算法的收敛速度有较高的要求。Macedo、赵金利[13–14]等针对储能系统参与配电网运行调节的优化模型求解问题,提出了锥优化算法;该算法将解的搜索空间限制在有限的凸锥范围内,能够提高求解速度,但是,对目标函数有严格的要求,即必须是线性函数或可转换为线性函数。Teng、胡晓通[8,12]等采用适用性广、对求解条件要求宽松的智能算法进行求解,但是,依然存在收敛速度慢和收敛精度差等问题,有待改进和提高其寻优性能。
综上所述,作者以降低配电网购电成本、网络损耗以及改善电压质量为目标,建立储能系统的多目标优化运行模型。针对蓄电池寿命影响问题,通过限定蓄电池的荷电状态范围及日循环次数以延长蓄电池寿命。采用PSO算法求解多目标优化模型时,针对PSO算法存在早收敛、收敛精度差等问题,将纵横交叉算子引入粒子群算法,同时,采用交叉搜索的方法,得出一种改进的混合粒子群优化(CS-PSO)算法。最后,在含BESS和高渗透率DG的IEEE34节点系统上,对提出的多目标优化模型和CS-PSO算法的正确性和有效性进行测试验证。
1 蓄电池模型采用蓄电池的荷电状态SOC描述其储能状态。蓄电池在时刻
充电状态
| ${S\!_{{\rm{OC}}}}(t + 1) = {S\!_{{\rm{OC}}}}(t)(1 - \sigma ') - \frac{{{P_{{\rm{BS}}}}(t)\Delta t}}{{{W_{{\rm{rt}}}}}}{\eta _{\rm{C}}}$ | (1) |
放电状态
| ${S\!_{{\rm{OC}}}}(t + 1) = {S\!_{{\rm{OC}}}}(t)(1 - \sigma ') - \frac{{{P_{{\rm{BS}}}}(t)\Delta t}}{{{\eta _{\rm{D}}}{W_{{\rm{rt}}}}}}$ | (2) |
式中,
重点考虑电池储能系统对配电网提供削峰填谷、降低网络损耗和调节电压的支撑作用,建立其多目标运行优化模型,实现配电网经济运行,并提高配电网的电压质量。
2.1 目标函数 2.1.1 配电网购电成本假设不允许配电网向主网售电,电价采用峰谷分时电价,则配电网购电成本为:
| ${f_{\rm{p}}} = \sum\limits_{t = 1}^T {{c_{\rm{s}}}(t){P_{\rm{s}}}(t)} \Delta t$ | (3) |
式中,
有功损耗是配电网经济运行的重要指标之一。调度周期内配电网的有功损耗费用为:
| ${f_{{\rm{loss}}}} = \sum\limits_{t = 1}^T {{c_{\rm{s}}}(t){P_{{\rm{loss}}}}(t)} \Delta t$ | (4) |
式中,
| ${P_{{\rm{loss}}}}(t) = \sum\limits_{i = 1}^n {\sum\limits_{j \in i\atop j \ne i} {{g_{ij}}[V_i^2(t) + V_j^2(t) - 2{V_i}(t){V_j}(t)\cos\; {\theta _{ij}}(t)]} }.$ |
其中,
调度周期内配电网的电压调节成本费用为:
| ${f_{{\rm{vr}}}} = \sum\limits_{t = 1}^T {{c_{{\rm{vr}}}}(t){{(V_i(t) - {V_{{\rm{ref}}}})}^2}} \Delta t$ | (5) |
式中:
将以上3个目标转化为以综合费用为优化目标的单一目标函数,得:
| $f = {\gamma _1}{f_{\rm{p}}} + {\gamma _2}{f_{{\rm{loss}}}} + {\gamma _3}{f_{{\rm{vr}}}}$ | (6) |
式中,
1)节点潮流平衡方程
| $\begin{align} &{P_{{\rm{DG,}}i}}(t) + {P_{{\rm{S,}}i}}(t) + {P_{{\rm{BS,}}i}}(t) - {P_{{\rm{L,}}i}}(t) - \\ &\quad{V_i}(t)\sum\limits_{j \in i} {{V_j}(t)({G_{ij}}\cos\; {\theta _{ij}}(t) + {B_{ij}}\sin\;{\theta _{ij}}(t))} = 0 \end{align} $ | (7) |
| $\begin{align} &{Q_{{\rm{DG,}}i}}(t) + {Q_{{\rm{S,}}i}}(t) - {Q_{{\rm{L,}}i}}(t) - \\& \quad{V_i}(t)\sum\limits_{j \in i} {{V_j}(t)({G_{ij}}\sin\;{\theta _{ij}}(t) - {B_{ij}}\cos\;{\theta _{ij}}(t} )) = 0 \end{align} $ | (8) |
式中,
2)电池储能系统运行约束
| $ \left\{ {\begin{aligned}& {0 \le {P_{{\rm{SB,}}i}}(t) \le P_{{{\rm{dis,}}i}}^{\max }, {\text{放电}};}\\& { - P_{{{\rm{ch,}}i}}^{\max } \le {P_{{\rm{SB,}}i}}(t) \le 0, {\text{充电}}}\end{aligned}} \right. $ | (9) |
| $S\!_{{\rm{OC}}}^{{\rm{min}}} \le {S\!_{{\rm{OC}}}}(t) \le S\!_{{\rm{OC}}}^{{\rm{max}}}$ | (10) |
式中,
为了保证BESS在新的调度周期内具有相同的调节性能,BESS在调度周期最后时刻的剩余电量应该与初始时刻相同,即
| $ {S\!_ {\rm{OC}}}\left( T \right) = {S\!_ {\rm{OC}}}\left( 0 \right) $ | (11) |
此外,为了延长蓄电池的使用寿命,规定一天内蓄电池充放电循环次数不超过一次(一次完整的循环通常定义为从充电到放电再到充电)。
3)分布式发电单元运行约束
| $ \left\{ {\begin{aligned}& {0 \le {P_{{\rm{DG,}}i}}(t) \le P_{_{{\rm{DG,}}i}}^{\max },}\\& {Q_{_{{\rm{DG,}}i}}^{\min } \le {Q_{{\rm{DG,}}i}}(t) \le Q_{_{{\rm{DG,}}i}}^{\max }}\end{aligned}} \right. $ | (12) |
式中,
4)配电网与主网交换功率约束
为了抑制配电网功率波动对主网造成的影响,需将主网输入配电网的功率限制在一定范围内,即:
| $ \left\{ {\begin{aligned}& {0 \le {P_{\rm{S}}}(t) \le P_{\rm{S}}^{\max },}\\& {Q_{\rm{S}}^{\min } \le {Q_{\rm{S}}}(t) \le Q_{\rm{S}}^{\max }}\end{aligned}} \right. $ | (13) |
式中,
5)网络运行约束
| $ \left\{ {\begin{aligned}& {{V_{\min }} \le {V_i}(t) \le {V_{\max }},}\\& {{S\!_l}(t) \le S\!_l^{{\rm{max}}}}\end{aligned}} \right. $ | (14) |
式中,
粒子群优化算法(particle swarm optimization,PSO)是一种基于种群的随机搜索算法,具有操作简单、搜索效率高和收敛快速等优点[16],适用于求解混合整数非线性约束优化模型。
基本的PSO算法在前期的局部搜索能力强,收敛比较快,但后期全局搜索能力不足,容易出现早熟问题。纵横交叉算法(crisscross optimization algorithm,CSO)的前期收敛速度不如PSO,但由于采用贪婪选择思想,并引入横向交叉和纵向交叉机制,全局收敛能力强且具有更快的总体收敛速率。因此,作者将这两种算法融合,提出一种改进的混合粒子群优化算法——纵横交叉粒子群优化(CS-PSO)混合算法,增强PSO的全局搜索能力并提高收敛速度。
3.1 CSO算法纵横交叉算法(crisscross optimization algorithm,CSO)是一种全新的群智能优化算法,包括横向交叉和纵向交叉两种搜索机制[17]。
1)横向交叉
横向交叉是在两个不同粒子的相同维之间进行的一种算术交叉,交叉前须对种群中所有粒子进行两两不重复配对。假设父代粒子
| $\left\{\begin{aligned} & {{M}}{{{H}}_{i,d}} = {r_1} \cdot {{{X}}_{i,d}} + (1 - {r_1}) \cdot {{{X}}_{j,d}} + {c_1}({{{X}}_{i,d}} - {{{X}}_{j,d}}),\\& {{M}}{{{H}}_{j,d}} = {r_2} \cdot {{{X}}_{j,d}} + (1 - {r_2}) \cdot {{{X}}_{i,d}} + {c_2}({{{X}}_{j,d}} - {{{X}}_{i,d}}) \end{aligned} \right.$ | (15) |
式中,
横向交叉后进入竞争机制,更新种群。
2)纵向交叉
纵向交叉是指种群中一个粒子的两个不同维之间进行的一种算数交叉。纵向交叉前须将所有维进行配对,并进行归一化处理。假设粒子
| ${{M}}{{{V}}_{i,{d_1}}} = r \cdot {{{X}}_{i,{d_1}}} + (1 - r) \cdot {{{X}}_{i,{d_2}}}$ | (16) |
式中,
纵向交叉采用一个交叉概率
3)竞争算子
竞争算子为父代种群与子代种群提供相互竞争机制,加快收敛速度。其流程为:计算子代粒子适应度,若大于父代粒子适应度,则取代父代进入迭代;否则,保留父代粒子。
3.2 CS-PSO算法CS-PSO算法的基本思想为:采用PSO的搜索过程,同时,利用CSO的全局搜索优势进行寻优。流程图如图1所示。
 |
| 图1 CS-PSO算法流程图 Fig. 1 Flow chart of CS-PSO algorithm |
具体步骤为:
1)PSO迭代算子
设群体由
| $ \left\{\begin{aligned} &{{{X}}_{i,d}^{k + 1}} = {{X}}_{i,d}^k + {{V}}_{i,d}^{k + 1}, \\ & {{V}}_{i,d}^{k + 1} \!=\! \omega \cdot {{V}}_{i,d}^k \!+\! {c_3}{r_3}({{{X}}_{{\rm{pb}}i,d}} \!-\! {{X}}_{i,d}^k) \!+\! {c_4}{r_4}({{X}}_{{\rm{gb}}} \!-\! {{X}}_{i,d}^k) \end{aligned}\right. $ | (17) |
式中,
2)群体的集聚程度
为了减轻计算负担,仅当粒子的集聚状态达到一定程度时,采用纵向交叉操作使粒子分散开。为此,计算适应度的方差:
| ${\sigma ^2} = \sum\limits_{i = 1}^N {{{(\frac{{{F_i} - {F_{{\rm{av}}}}}}{F})}^2}} $ | (18) |
其中,
| $F=\left\{ {\begin{aligned}& {\mathop {\max }\limits_{1 \le i \le N} (\left| {{F_i} - {F_{{\rm{av}}}}} \right|),\left| {{F_i} - {F_{{\rm{av}}}}} \right| > 1};\\& {1, {\text{其他}}}\end{aligned}} \right.$ | (19) |
式中,
当
作者以修改后的IEEE34节点配电网为电池储能系统多目标优化算例,并用CS-PSO算法进行求解,验证作者提出的多目标优化运行策略的有效性。其网络结构如图2所示,节点1是配电网连接主电网的根节点,两台风力发电机(WT)分别安装在节点18和22,每个负荷母线处都安装有光伏发电(PV)单元,节点22、34各连接一个锂离子电池储能系统BESS (BESS22、BESS34),自放电率
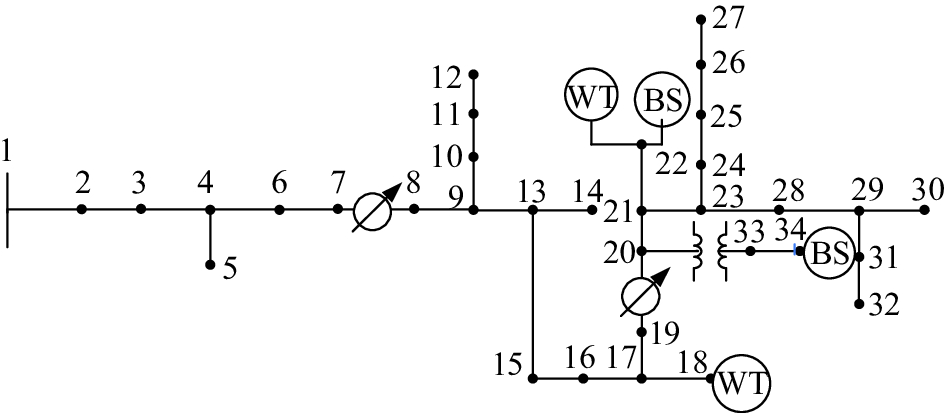 |
| 图2 IEEE34节点测试系统 Fig. 2 IEEE34-node test system |
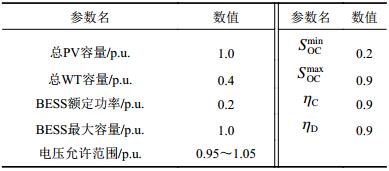
假设PV和WT均运行于单位功率因素。取基准功率
| 表1 输入参数 Tab. 1 Input parameters |
 |
4.2 CS-PSO算法参数设置
设定种群规模为50,最大迭代次数为200,惯性权重采用线性递减权重,即最大、最小值分别为0.9和0.4,学习因子均为2,变异阈值为10,纵向交叉概率为0.6。
4.3 粒子位置矢量表达采用CS-PSO算法求解BESS充放电优化模型时,粒子位置可以表达为一个
根据式(10)得到充放电功率,如式(20)所示:
| $ {P_{{\rm{BS}}}}_j(t) = \left\{ {\begin{aligned}& {{W_{{\rm{rt}}}}\frac{{S\!_{{\rm{OC}}j}(t) - S\!_{{\rm{OC}}j}(t + 1)}}{{\eta \Delta t}},t < T;}\\& {{W_{{\rm{rt}}}}\frac{{S\!_{{\rm{OC}}j}(T) - S\!_{{\rm{OC}}j}(1)}}{{\eta \Delta t}},t = T}\end{aligned}} \right. $ | (20) |
式中,充电状态时
当前时段为
以夏天中的某一天为例,次日24 h的负荷及各分布式电源有功出力预测曲线如图3所示。
 |
| 图3 日负荷和DG功率预测曲线 Fig. 3 Profiles of daily load and DG predictive power |
4.4.1 优化结果分析
采用MATLAB2011b版本进行算法程序编写,运行环境为Windows7系统。CPU为i5-2 450 M,2.5 GHz,内存为6 GB。将配电网的节点数据、支路数据、分布式发电和负荷预测功率等数据输入到Matpower包中,建立配电网潮流模型。
1)多目标优化结果
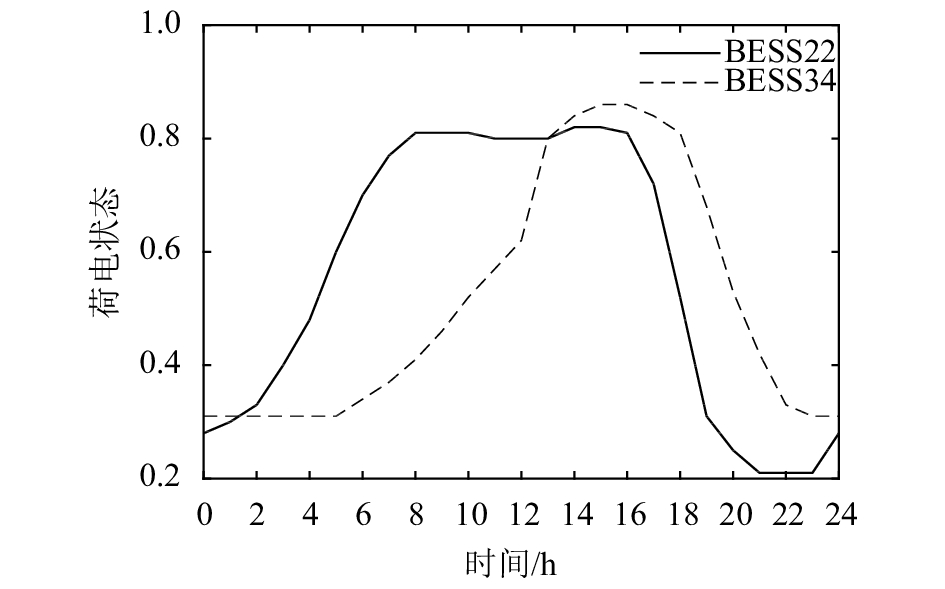
采用提出的优化模型和优化算法,得到电池储能系统BESS的荷电状态如图4所示。
 |
|
图4 两个BESS的荷电状态 Fig. 4 |
图4中:BESS22在低电价时段充电,在高电价时段放电;BESS34在高电价时段放电,但不仅在低电价时段充电,而且部分高电价时段(9:00:00—14:00:00)也在充电。这是由于该时段是光伏发电高峰期,本地负荷较小的PV节点由于逆流导致电压偏高,因此,BESS34通过吸收部分有功功率以降低这些节点的电压。由此表明,储能单元不仅通过在低电价时购电存储,在高电价且负荷大于DG出力时放电以降低购电成本,还会通过充放电控制调节节点电压,使节点电压接近电压参考值。所以,本文的优化运行方法使储能单元的充放电策略得到了合理的分配。
为了考察BESS优化运行对系统电压质量的影响,比较了两种情况即情况①系统没安装BESS,情况②系统安装了BESS22、BESS34下,采用提出的优化运行方案得到系统母线电压的累计概率密度,如图5所示。
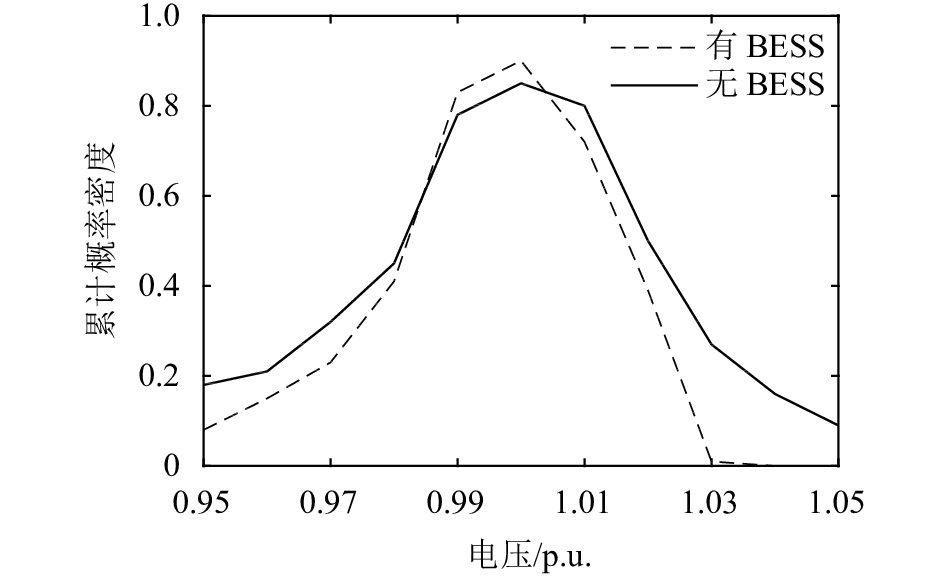 |
| 图5 两种情况下的节点电压PDFs Fig. 5 Node voltage PDFs for the two cases |
由图5可看出:在情况②下,电压在0.985~1.005 p.u.范围内的概率高于情况①,各节点电压大多数情况下接近参考值1.0 p.u.;而低于0.955 p.u.与高于1.015 p.u.的概率很小(小于0.15)。由此说明,系统中安装采用优化运行方案的BESS能够有效改善电压的分布情况,从而提高配电系统的电压质量。
2)不同目标的优化结果比较
采用提出的优化方法分别求解3个单一目标和多目标情况下的蓄电池优化运行问题,得到购电成本、能量损耗及电压偏差(最大值与最小值之差)这3个指标的优化值,如表2所示。
| 表2 仿真结果 Tab. 2 Simulation results |
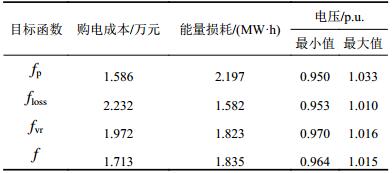 |
由表2可看出:任何一个单目标优化都不能保证3个指标同时获得满意效果。目标
分别采用本文提出的CS-PSO算法、基本的PSO算法及GA-PSO[18]算法求解电池储能优化运行问题,将其优化结果及求解效率进行对比。这3种算法中的共有参数(如种群规模、最大迭代次数等)取相同的值。
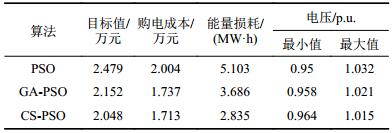
3种优化方法得到的目标函数值和3个指标值(购电成本、能量损耗及电压的最大和最小值)如表3所示,计算效率见表4所示。
| 表3 仿真结果比较 Tab. 3 Compare of simulation results |
 |
| 表4 求解效率比较 Tab. 4 Compare of solving efficiency |
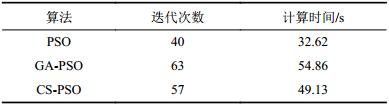 |
综合分析表3和4可看出:PSO算法优化得出的目标函数值及3个指标值都是最大的,而迭代次数最小、计算时间最短,这是由于PSO算法陷入了局部最优,无法跳出,暴露了易出现早熟的问题;与PSO算法相比,GA-PSO算法的优化效果有明显改善,目标函数值减小了13.19%,其他3项指标也分别降低了13.32%、27.78%和30.16%,但其迭代次数和计算时间最长;CS-PSO算法的优化效果最好,其目标函数值和3项指标都是3种方法中最小的,虽然购电成本与GA-PSO算法非常接近,但能量损耗和电压偏差分别比后者降低了23.09%和19.48%,而迭代次数和计算时间比GA-PSO算法稍小。这表明,CS-PSO算法得到的优化结果更合理,在相近的购电成本下,能使配电网的能量损耗更小、电压质量更高,而且收敛速度较快。由此说明,CS-PSO算法在收敛精度上得到了很好的改进效果,具有很强的全局搜索能力,同时,具有较高的计算效率。
5 结 论为了充分发挥储能系统在提高智能配电网中可再生能源(RES)的渗透率、电网的经济效益、电压质量等方面的重要作用,作者考虑峰谷电价,以降低配电网购电成本、网络损耗以及改善电压质量为目标,建立了储能系统的多目标优化运行模型。并提出一种改进的混合粒子群优化(CS-PSO)算法求解多目标优化模型。为了有效改善粒子群算法的全局收敛性能,将纵横交叉算子引入粒子群算法,并通过交叉搜索维护种群的多样性;同时,为了提高计算速度,引入群体集聚程度概念,仅当粒子的集聚程度达到一定阈值时才进行纵向交叉。
算例结果表明:电池储能系统的多目标优化运行不仅能提高配电网运行的经济效益,还能提高配电网的电压质量;多目标的优化效果比单目标有较显著的改善;CS-PSO算法的优化结果比PSO和GA-PSO算法更合理,且收敛速度较快。但是,作者没有考虑电池储能系统在运行过程中的损耗成本,因此,储能单元充放过程中自身的损耗特性有待进一步研究,以得到更加精确的目标函数。另外,所提的CS-PSO算法虽然在文中的算例中收敛性很好,计算效率较高,但是当粒子矩阵维数过大时,求解时间会迅速增加,不能满足调度间隔过小的优化模型,后续研究中可考虑使用并行计算方法实现快速求解。
| [1] |
Zhao Bo,Wang Caisheng,Zhou Jinhui,et al. Present and future development trend of active distribution network[J]. Automation of Electric Power Systems, 2014, 38(18): 125-135. [赵波,王财胜,周金辉,等. 主动配电网现状与未来发展[J]. 电力系统自动化, 2014, 38(18): 125-135. DOI:10.7500/AEPS20131218007] |
| [2] |
Eltantawy A B,Salama M M A. Management scheme for increasing the connectivity of small-scale renewable DG[J]. IEEE Transactions on Sustainable Energy, 2014, 5(4): 1108-1115. DOI:10.1109/TSTE.2014.2329647 |
| [3] |
Zheng Le,Hu Wei,Lu Qiuyu,et al. Research on planning and operation model for enegy system to optimize wind power integration[J]. Proceedings of the CSEE, 2014, 34(16): 2533-2543. [郑乐,胡伟,陆秋瑜,等. 储能系统用于提高风电接入的规划和运行综合优化模型[J]. 中国电机工程学报, 2014, 34(16): 2533-2543. DOI:10.13334/j.0258-8013.pcsee.2014.16.003] |
| [4] |
Ye Jilei,Xue Jinhua,Wang Wei,et al. Application of energy storage technology and its prospect in power system[J]. Electric Power, 2014, 47(3): 1-5. [叶季蕾,薛金花,王伟,等. 储能技术在电力系统中的应用现状与前景[J]. 中国电力, 2014, 47(3): 1-5. DOI:10.3969/j.issn.1004-9649.2014.03.001] |
| [5] |
Gabash A,Li Pu. Flexible optimal operation of battery storage systems for energy supply networks[J]. IEEE Transaction on Power Systems, 2013, 28(3): 2788-2797. DOI:10.1109/TPWRS.2012.2230277 |
| [6] |
Gabash A,Li Pu. Active-reactive optimal power plow in distribution networks with embedded generation and battery storage[J]. IEEE Transaction on Power Systems, 2012, 27(4): 2026-2035. DOI:10.1109/TPWRS.2012.2187315 |
| [7] |
Levron Y,Guerrero J. Optimal flow in microgrids with energy storage[J]. IEEE Transaction on Power Systems, 2013, 28(3): 3226-3234. DOI:10.1109/TPWRS.2013.2245925 |
| [8] |
Teng J H,Luan S W,Lee D J. Optimal charging /disccharging scheduling of battery storage systems for distribution systems interconnected with sizeable PV generation systems[J]. IEEE Transaction on Power Systems, 2013, 28(2): 1425-1433. DOI:10.1109/TPWRS.2012.2230276 |
| [9] |
Yang Yanhon,Pei Wei,Deng Wei. Day-ahead scheduling optimization for microgrid withbattery life model[J]. Transactions of China Electro Technical Society, 2015, 30(22): 172-180. [杨艳红,裴玮,邓卫,等. 计及蓄电池储能寿命影响的微电网日前调度优化[J]. 电工技术学报, 2015, 30(22): 172-180. DOI:10.3969/j.issn.1000-6753.2015.22.021] |
| [10] |
Zhu Zefeng,Zhao Jinquan,Wei Wenhui,et al. Optimal charging and discharging scheme of battery energy storage system in active distribution network[J]. Automation of Electric Power Systems, 2016, 40(20): 47-53. [朱泽锋,赵晋泉,魏文辉,等. 主动配电网中电池储能系统最优充放电策略[J]. 电力系统自动化, 2016, 40(20): 47-53. DOI:10.7500/AEPS20160417004] |
| [11] |
Coelho VN,Coelho I M,Coelho B N,et al. Multi-objective energy storage power dispatching using plug-in vehicles in a smart-microgrid[J]. Renewable Energy, 2016, 89: 730-742. DOI:10.1016/j.renene.2015.11.084 |
| [12] |
Hu Xiaotong,Liu Tianqi,He Chuan,et al. Multi-objctive optimal operation of microgrid considering the battery loss characteristics[J]. Proceedings of CSEE, 2016, 36(10): 2674-2681. [胡晓通,刘天琪,何川,等. 计及蓄电池损耗特性的微网多目标优化运行[J]. 中国电机工程学报, 2016, 36(10): 2674-2681. DOI:10.13334/j.0258-8013.pcsee.2016.10.011] |
| [13] |
Macedo L H,Franco J F,Rider M J,et al. Optimal operation of distribution networks considering energy storage devices[J]. IEEE Transaction on Smart Grid, 20, 6(6): 2825-2036. DOI:10.1109/TSG.2015.2419134 |
| [14] |
Zhao Jinli,Yu Yingying,Li Peng,et al. A fast calculation method of energy storage system for distribution network regulation based on conic programming[J]. Automation of Electric Power Systems, 2016, 40(2): 30-35. [赵金利,于莹莹,李鹏,等. 基于锥优化的储能系统参与配电网运行调节快速计算方法[J]. 电力系统自动化, 2016, 40(2): 30-35. DOI:10.7500/AEPS20150417002] |
| [15] |
Liu Zhipeng,Wen Fushuan,XueYusheng,et al. Optimal siting and sizing of distributed generators considering plug-in electric vehicles[J]. Automation of Electric Power Systems, 2011, 35(18): 11-16. [刘志鹏,文福拴,薛禹胜,等. 计及可入网电动汽车的分布式电源最优选址和定容[J]. 电力系统自动化, 2011, 35(18): 11-16.] |
| [16] |
纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.
|
| [17] |
Meng Anbo,Mei Peng,Lu Haiming. Crisscross optimization algorithm for combined heat and power economic dispatch[J]. Power System Protection and Control, 2016, 44(6): 90-97. [孟安波,梅鹏,卢海明. 基于纵横交叉算法的热电联产经济调度[J]. 电力系统保护与控制, 2016, 44(6): 90-97. DOI:10.7667/PSPC150890] |
| [18] |
Ma Chao,Deng Chao,Xiong Yao,et al. An intelligent optimization algorithm based on hybrid of GA an PSOA[J]. Journal of Computer Research and Development, 2013, 50(11): 2278-2286. [马超,邓超,熊尧,等. 一种基于混合遗传和粒子群的智能优化算法[J]. 计算机研究与发展, 2013, 50(11): 2278-2286. DOI:10.7544/issn1000-1239.2013.20111484] |
 2018, Vol. 50
2018, Vol. 50


