2. 四川大学 国家空管自动化系统技术重点实验室,四川 成都 610065
2. National Key Lab. of Air Traffic Control Automatization System Technol., Sichuan Univ., Chengdu 610065, China
航班轨迹预测是空中交通管理与仿真系统的基础技术,例如,空中交通流量预测与管理、飞行冲突探测、空域灵活使用和空中交通流仿真等都需要以精确的预测轨迹为基础。国内外学者在轨迹预测研究方面已取得了相关成果。陈志杰[1]将航班飞行过程分为多个飞行阶段,通过在各阶段建立运动学和动力学方程并求解来完成航班轨迹预测。张军峰等[2]提出了一种基于飞机基础性能参数(base of aircraft data,BADA)和航空器意图的航班4维轨迹预测方法。吴鹍等[3]提出了一种基于回归分析的历史数据挖掘方法来预测航班飞行过程中经过航路关键点的时间和高度。国外相关研究中,Hansen等[4]提出了一种基于混合系统理论对航班爬升阶段轨迹预测方法,并采用协方差自适应调整的进化策略(covariance matrix adaptation evolution strategy,CMA-ES)对模型进行优化。Zhou等[5]采用一种改进的多项式滑窗方法拟合历史轨迹以完成航班轨迹估算。Khalil等[6]提出了一种基于时间的离散转移矩阵的算法以估计目标轨迹。运用车联网思想,Barrios等[7]利用手机GPS定位采集数据挖掘目标轨迹的运动规律并实现轨迹预测。虽然上述方法取得了一定的研究成果,但是存在如飞行过程阶段划分不准确、飞机性能参数选择偏差较大、回归模型难以确定等局限,从而导致预测结果不太理想。
作者提出了一种基于历史雷达数据和机器学习的航班轨迹预测算法。航班历史飞行轨迹是航班在考虑了飞行过程中的真实环境因素产生的,已被证明是可行且更加高效、安全和完善保障的飞行路径。提出算法的主要思想是以相邻时刻的相对位置偏移量为基础进行航班位置预测,航班在不同的飞行阶段(如加速爬升、匀速巡航等)具有不同的运动规律。提出的轨迹预测算法基于概率统计模型,其预测结果描述了样本在总体分布中的各种可能性,因此,提出的算法在预测航班轨迹的基础上还能获得其整体概率分布情况。首先,基于高斯混合模型(Gaussian mixture model,GMM)对航班飞行过程的相邻时刻相对位置偏移量进行建模;随后,以该航班的历史飞行轨迹为训练数据,采用期望最大化(expectation maximization,EM)算法对GMM参数进行估计,并基于已学习模型和起飞机场位置信息采用序贯蒙特卡洛(sequential Monte Carlo,SMC)思想预测航班各时刻相对位置偏移向量和航班位置,最终完成航班轨迹预测。算法还采用预测结果误差进行评估,当预测误差超过一定阈值时对模型参数进行更新,也可定时和手动更新模型参数。实验结果表明,与传统的方法相比,提出的方法具有较高的预测精度。同时,针对传统方法在航班爬升和下降阶段的误差稳定性差的问题,基于真实历史数据进行学习亦能获得较为精确的预测结果。
1 轨迹数据库结构假设通过监视设备采集到的航班历史飞行轨迹保存在轨迹数据库中,在预测前已经按航班号和飞行日期建立轨迹搜索树,并对单次飞行轨迹进行去噪、平滑、插值等处理[8–9]。数据库的组织结构如图1所示。
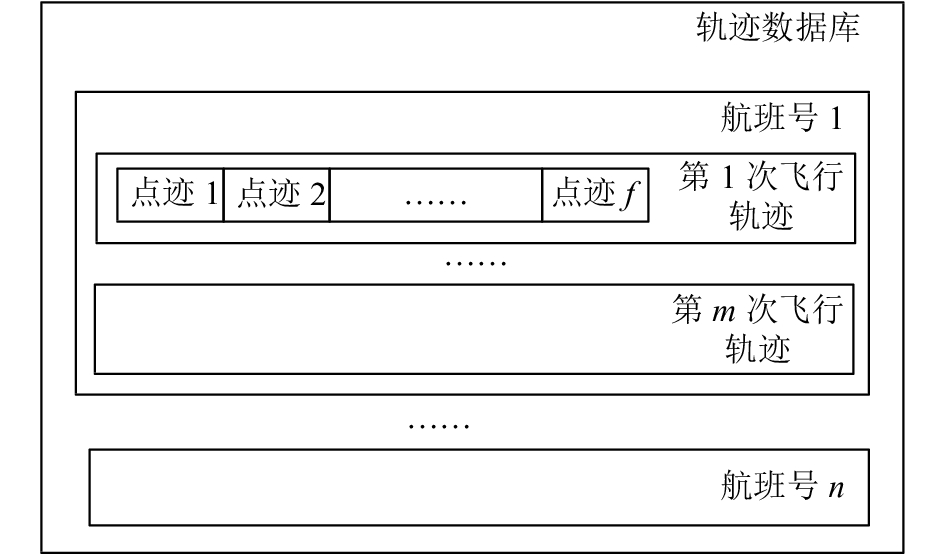 |
| 图1 轨迹数据库结构 Fig. 1 Structure of trajectory database |
其中,轨迹数据库包含了
| ${{s}} = {[x,y,{\textit{z}},t]^{\rm{T}}}$ | (1) |
式中,
高斯混合模型是一类参数性概率密度函数,由一系列带权重高斯过程线性相加组成。任何连续概率密度函数都可以使用足够数量的高斯过程线性和表示[10]。GMM表示如下:
| $p(\Delta {{s}}|\varphi ) = \sum\limits_{i = 1}^k {{\alpha _i}G(\Delta {{s}}|{{ \mu}_i},{{{\varSigma}} _i})} $ | (2) |
式中:该混合高斯随机过程包含
| $\varphi = \{ {\varphi _1},{\varphi _2}, \cdots ,{\varphi _k}\} ,{\varphi _i} = \{ {\alpha _i},{{ \mu} _i},{{{\varSigma}} _i}\} $ | (3) |
考虑航班的飞行剖面图[1],选择高斯过程数量为
1)建立包含未知参数的相对位置偏移向量概率分布模型
2)根据该航班历史飞行轨迹进行模型最优化参数估计
3)基于已学习模型预测航班各时刻的相对位置偏移量矩阵为
根据轨迹数据库中该航班历史飞机轨迹,计算每次飞行时相邻时刻的相对位置偏移序列
1)E-Step:计算当前模型参数条件下的对数似然函数期望。
2)M-Step:估计模型参数值,使得E-Step中的似然函数期望最大化。
GMM需要设置模型初始参数,以BADA中各阶段参数平均值对模型进行初始化。算法迭代执行EM算法的两步计算直到满足迭代终止条件,此时的参数即为该概率模型框架下最优参数[14]。EM算法的迭代目标函数为:
| ${\varphi ^{(g + 1)}} = \arg \mathop {\max }\limits_\varphi \{ \underbrace {\int_{\textit{z}} {\log (p(\Delta {{S}},{\textit{Z}}|\varphi ))p({\textit{Z}}|\Delta {{S}},{\varphi ^{(g)}}){\rm{d}}{\textit{z}}} }_{K(\varphi ,{\varphi ^{(g)}})}\} $ | (4) |
式中:
| $\begin{gathered} p(\Delta {{S}},{\textit{Z}}|\varphi ) = \mathop \prod \limits_{i = 1}^N p(\Delta {{{s}}_i},{{\textit{z}}_i}|\varphi ) = \\ {\rm{ }}\mathop \prod \limits_{i = 1}^N \underbrace {p(\Delta {{{s}}_i}|{{\textit{z}}_i},\varphi )}_{G({{ \mu}_{{{\textit{z}}_i}}},{{{\varSigma}} _{{{\textit{z}}_i}}})}\underbrace {p({{\textit{z}}_i}|\varphi )}_{{\alpha _{{{\textit{z}}_i}}}} \\ \end{gathered} $ | (5) |
| $\begin{aligned}[b] & p({\textit{Z}}|\Delta {{S}},\varphi ) = \mathop \prod \limits_{i = 1}^N p({{\textit{z}}_i}|\Delta {{{s}}_i},\varphi ) = \\ & \quad \quad\mathop \prod \limits_{i = 1}^N \frac{{{\alpha _{{{\textit{z}}_i}}}G({{ \mu}_{{{\textit{z}}_i}}},{{{\varSigma}} _{{{\textit{z}}_i}}})}}{{\displaystyle\sum\limits_{l = 1}^k {{\alpha _l}G({{\mu}_l},{{{\varSigma}} _l})} }} \end{aligned} $ | (6) |
那么,通过迭代目标函数可得到参数解为:
| $\alpha _l^{(g + 1)} = \frac{1}{N}\sum\limits_{i = 1}^N {p(l|\Delta {{{s}}_i},{\varphi ^{(g)}})} $ | (7) |
| ${ \mu} _l^{(g + 1)} = \frac{{\displaystyle\sum\limits_{i = 1}^N {\Delta {{{s}}_i}p(l|\Delta {{{s}}_i},{\varphi ^{(g)}})} }}{{\displaystyle\sum\limits_{i = 1}^N {p(l|\Delta {{{s}}_i},{\varphi ^{(g)}})} }}$ | (8) |
| $\begin{aligned}[b] {{\varSigma}} _l^{(g + 1)} = & \sum\limits_{i = 1}^N {{\rm{\{ }}[\Delta {{{s}}_i} - { \mu} _l^{(i + 1)}]{{[\Delta {{{s}}_i} - { \mu} _l^{(i + 1)}]}^{\rm{T}}}\times} \\& {\rm{ }}p(l|\Delta {{{s}}_i},{\varphi ^{(g)}}){\rm{\} /}}\sum\limits_{i = 1}^N {p(l|\Delta {{{s}}_i},{\varphi ^{(g)}})}\end{aligned} $ | (9) |
| $p(l|\Delta {{{s}}_i},{\varphi ^{(g)}}) = \frac{{G(\Delta {{{s}}_i}|{{ \mu} _l},{{{\varSigma}} _l})}}{{\displaystyle\sum\limits_{t = 1}^k {G(\Delta {{{s}}_i}|{{ \mu} _t},{{{\varSigma}} _t})} }}$ | (10) |
在完成模型参数学习之后,该GMM模型描述了航班飞行位置偏移的总体分布。在每个时刻的航班位置偏移量服从学习的总体分布,其具体偏移值采样自模型分布。提出的算法中的隐变量
根据预测航班的起飞机场信息,如跑道位置和机场标高,初始化轨迹预测初始点。参照SMC思想[9]进行航班轨迹预测,其具体步骤如下:
1)初始化轨迹初始位置为:
2)计算上一预测周期的偏移向量属于各高斯分布的权重值:
3)分别运用SMC思想对各高斯分布进行采样,即
4)在
上述过程的预测步骤2)和3)也可以从贝叶斯全概率理论角度进行解释,即:
| $\Delta {{{s}}_{t + 1}} = \sum\limits_{i = 1}^k G ({ {\mu}_i},{{{\varSigma}} _i}|{\textit{z}} = i)p({\textit{z}} = i|\Delta {{{s}}_t})$ | (11) |
为了检验作者所提出的航班轨迹预测算法的性能,在以下数据条件进行仿真实验:
1)轨迹数据库来源于某大型空中交通流量管理系统2012-07-31—2015-08-15各航班的历史飞行轨迹;
2)以其中某航班为例,利用2012-07-31—2015-08-14的历史飞行轨迹预测该航班在2015-08-15的飞行轨迹,并与轨迹数据库中已采集的轨迹进行比较。该航班的采集轨迹更新周期为4 s,共有2 301个离散轨迹点。
同时,将本文的预测结果与现有的运动学模型和回归模型预测方法进行对比验证算法的预测精度和稳定性。两种对比算法简要描述如下:
1)运动学模型。在每个飞行阶段建立运动学方程[1],该方程包含飞行过程中的速度、加速度变化规律等。根据BADA中的典型飞行参数和航班的起始位置初始化模型,通过迭代计算已完成航班轨迹预测。
2)回归模型。根据同次航班执行过程中的航班位置通过多项式回归模型预测下一时刻位置[3]。使用预测时刻前5 min的航班位置预测当前位置。
下面先引入轨迹预测精度的衡量因子[10],以衡量不同算法的预测性能,已知预测轨迹点与采集轨迹点之间的欧式距离误差:
| $d(p,c) = \sqrt {{{({x_p} - {x_c})}^2} + {{({y_p} - {y_c})}^2} + {{({{\textit{z}}_p} - {{\textit{z}}_c})}^2}} $ | (12) |
那么,整个预测轨迹的均方根误差为:
| $RMS\!E = \frac{{\displaystyle\sum\limits_{t = 1}^T {d({{{s}}_t},{{{c}}_t})} }}{T}$ | (13) |
式中:
实验运行硬件为Intel Core i5-3470,3.2 GHz,内存为4 GB,操作系统为Windows7,所有算法在MATLAB环境下实现并仿真。
3.1 GMM参数学习在确定采用GMM模型对航班相邻时刻相对位置偏移量序列建模之后,首先需要进行GMM参数学习,按照第2.1节讨论选择
 |
| 图2 GMM参数学习示例 Fig. 2 Example of GMM parameters learning |
3.2 训练数据对模型精度的影响
本文算法中,GMM模型参数受训练数据集的样本数影响,下面分别在不同训练数据集样本数情况下比较采用本文算法和回归模型预测的轨迹预测结果的均方根误差(RMSE),如图3所示,作者采用的空间数据库中共有预测航班的1 110次历史飞行轨迹。
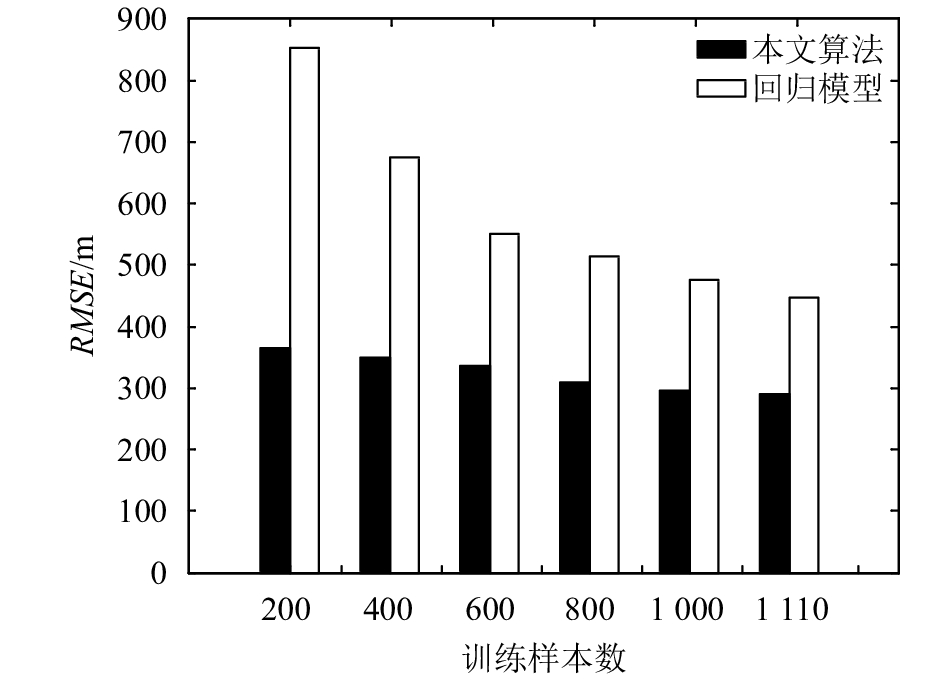 |
| 图3 不同样本数下的预测误差比较 Fig. 3 Prediction error comparison of different sample numbers |
由图3可知:本文提出的基于历史雷达数据的GMM预测算法和回归模型算法的预测精度都随着训练数据样本数增加而提高,但是,基于GMM的算法在训练数据样本数较少时比回归模型有更准确的预测结果,且能保持较稳定的预测精度[15]。训练样本数对回归模型的影响更大。
3.3 预测结果比较为进一步验证本文所提出算法的精度,将预测的估计结果与采集轨迹(真实轨迹)相比较,同时,采用运动学和线性回归模型对该航班的轨迹进行预测,并将不同算法的预测轨迹进行对比,如图4所示。
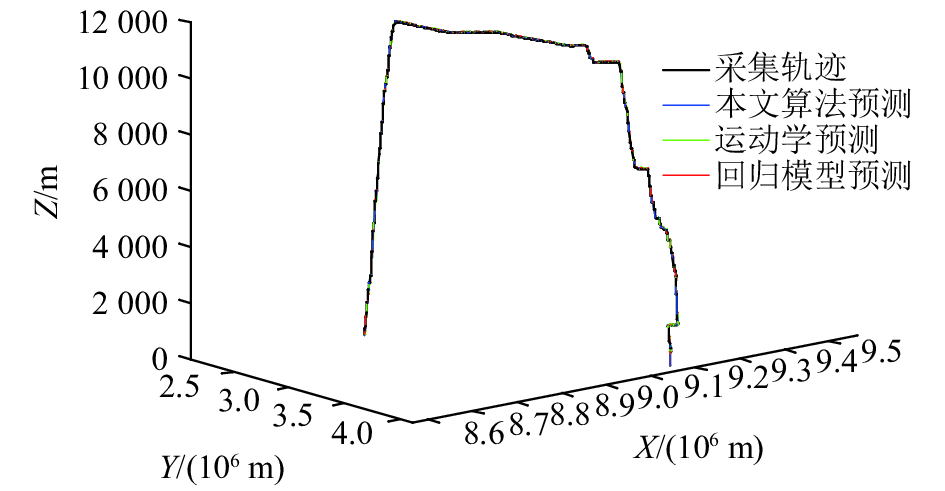 |
| 图4 不同算法预测结果比较 Fig. 4 Prediction results comparison of different algorithm |
同时,为了准确对比各预测方法的性能,分别计算真实采集的航班轨迹与本文算法、运动型模型和回归模型预测轨迹在各预测时刻的位置点误差,如图5所示。
 |
| 图5 不同算法预测位置点误差比较 Fig. 5 Prediction position error comparison with different algorithm |
通过图4~5可知,本文提出的基于历史雷达数据的GMM预测方法在预测精度上优于运动学和回归模型预测方法,基于运动学模型、回归模型和本文提出方法的RMSE分别为466、449和292 m。同时,从图5的预测误差可以看出,本文预测算法受航班飞行过程的起飞和下降阶段的机动性影响较小,预测结果更加平稳。
4 结 论航班轨迹预测是空中交通管理系统的基础技术,针对现有航班计划轨迹预测方法的不足,在已有历史雷达数据的基础上,提出了一种基于历史雷达数据和机器学习方法的轨迹预测算法。该算法中,作者运用GMM对航班相邻时刻相对位置偏移量进行建模,利用机器学习算法估计模型参数,在预测得到航班各时刻的相对位置偏移的基础上,根据起飞机场的跑道和标高信息估算航班轨迹。通过实验结果比较证明了本文算法的正确性和精度。
同时,下一步研究的重点是:建立更加合理高效的历史雷达数据搜索和预处理模型,采用更加合理高效的算法确定GMM高斯分布数以提高模型精度。
| [1] |
陈志杰.空域管理理论与方法.北京:科学出版社,2012,237–248.
|
| [2] |
Zhang Junfeng,Jiang Haixing,Wu Xiaoguang,et al. 4D trajectory prediction based on BADA and aircraft intent[J]. Journal of Southwest Jiaotong University, 2014, 49(3): 553-558. [张军峰,蒋海行,武晓光,等. 基于BADA及航空器意图的四维航迹预测[J]. 西南交通大学学报, 2014, 49(3): 553-558. DOI:10.3969/j.issn.0258-2724.2014.03.028] |
| [3] |
Wu Kun,Pan Wei. 4D trajectory prediction model based on data mining[J]. Computer Applications, 2007, 27(11): 2637-2639. [吴鹍,潘薇. 基于数据挖掘的四维飞行轨迹预测模型[J]. 计算机应用, 2007, 27(11): 2637-2639.] |
| [4] |
Hansen N,Muller S,Koumoutsakos P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES)[J]. Evolutionary Computation, 2003, 11(1): 1-18. DOI:10.1162/106365603321828970 |
| [5] |
Zhou Zhijing,Chen Jinliang,Shen Hua,et al.Trajectory prediction based on improved sliding window polynomial fitting prediction method[C]//Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design.Hangzhou:IEEE,2016,202–205.
|
| [6] |
Khalil M,Rui Xiaoting,Hendy H. Discrete time transfer matrix method for projectile trajectory prediction[J]. Journal of Aerospace Engineering, 2015, 28(2): 04014057. DOI:10.1061/(ASCE)AS.1943-5525.0000381 |
| [7] |
Barrios C,Motai Y,Huston D. Trajectory estimations using smartphones[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7901-7910. DOI:10.1109/TIE.2015.2478415 |
| [8] |
Zheng Yu,Zhou Xiaofang.Computing with spatial trajectories[M].New York:Springer,2011:167–171.
|
| [9] |
Alligier R,Gianazza D,Durand N. Machine learning and mass estimation methods for ground-based aircraft climb prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3138-3149. DOI:10.1109/TITS.2015.2437452 |
| [10] |
Wiest J,Höffken M,Kreßel U,et al.Probabilistic trajectory prediction with Gaussian mixture models[C]//Proceedings of the 2012 Intelligent Vehicles Symposium.Alcalá de Henares:IEEE,2012:141-146.
|
| [11] |
Qiao Shaojie,Jin Kun,Han Nan,et al. Trajectory prediction algorithm based on Gaussian mixture model[J]. Journal of Software, 2015, 26(5): 1048-1063. [乔少杰,金琨,韩楠,等. 一种基于高斯混合模型的轨迹预测算法[J]. 软件学报, 2015, 26(5): 1048-1063. DOI:10.13328/j.cnki.jos.004796] |
| [12] |
Mahler R P S.Statistical multisource- multitarget information fusion[M].Boston:Artech House,2013:27-42.
|
| [13] |
Jeung H,Shen Hengtao,Zhou Xiaofang.Mining trajectory patterns using hidden Markov models[M]//Data Warehousing & Knowledge Discovery.Heidelberg:Springer-Verlag,2007:470-480.
|
| [14] |
Qiao Shaojie,Shen Dayong,Wang Xiaoteng,et al. A self-adaptive parameter selection trajectory prediction approach via hidden Markov models[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 284-296. DOI:10.1109/TITS.2014.2331758 |
| [15] |
Schreier M,Willert V,Adamy J. An integrated approach to maneuver-based trajectory prediction and criticality assessment in arbitrary road environments[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2751-2766. DOI:10.1109/TITS.2016.2522507 |
 2018, Vol. 50
2018, Vol. 50


