近年来,随着双目立体视觉技术在虚拟现实、目标识别、3D-SLAM地图重建等领域中的广泛应用,双目立体视觉已经成为计算机视觉领域的研究热点。在双目立体视觉的研究中,立体匹配是最为关键的一部分,直接影响着目标物体深度信息的获取精确度,是双目立体视觉领域的研究难点。
按照图像表示的基元不同,双目立体匹配可分为区域立体匹配算法、基于特征点的立体匹配算法、基于相位的立体匹配算法3种。基于特征点的立体匹配[1]存在匹配精度受特征点匹配正确率和均匀性影响大、视差计算量大等缺点;基于相位的立体匹配[2]需将图像从时域转换到频域,存在相位奇点的问题,且随视差范围增大匹配精度也有所降低。因此众多区域立体匹配算法[3–10]被提出。Scharstein等[11]对区域立体匹配算法进行概括和总结,将算法分为匹配代价计算、代价聚合、视差选择和视差优化4个部分,其中匹配代价计算是基础,影响立体匹配性能。Wang等[3]以图像像素点的颜色信息为匹配代价,易受光照等条件变化所产生的噪声影响。Ma等[4]对ICT、INV、TADc、TADg这4个匹配代价进行合成,运算复杂度高,并且代价之间会彼此消弱差异,导致匹配精度不高。Jellal等[5]只以像素点横纵的梯度变化为匹配代价,缺少图像的原始信息,易出现变化相同而造成的误匹配。Hirschmuller[6]利用MI作为匹配代价,涉及到熵,包含对数与积分运算,运算复杂度高,且没有利用到图像的纹理变化信息,匹配性能不高。Zhang等[7]利用BRIEF描述算子计算匹配代价,对于存在重复纹理的图像匹配效果差。Shahbazi等[8]利用本征曲线计算匹配代价,隐含了视差梯度小的假设,当视差梯度大时,匹配精度差。Keselman[9]、Peña[10]、Woodfill[12] 等均采用了Census变换算法进行匹配代价计算。Census变换能够抑制噪点的影响,在灰度变换小的平滑区域匹配效果好,但在具有类似结构的重复区域内匹配效果不理想。Birchfield等[13]采用灰度绝对差AD作为匹配代价。AD变换可以较好地反映像素点的灰度变化,在纹理丰富的图像边缘区域具有良好的匹配效果,但AD变换对由光照变化产生的噪点十分敏感,鲁棒性较差。Mei等[14]针对AD变换和Census变换的不足,提出AD-Census变换算法;该匹配代价的计算算法将AD变换和Census变换得到的代价合成一个综合代价,弥补了单个变换的不足。但在合成时,两个代价的权重固定,没能根据像素点位于图像的区域特点设定权重。作者针对AD-Census变换的匹配代价合成不能反映像素点在图像中区域特征的问题,引入变权重的思想,进行匹配代价合成;并基于能够反映像素点所在图像区域特征的十字支撑窗口的最短臂长,提出AD变换与Census变换的权重自适应设置算法,使自适应权重AD-Census变换算法进行匹配代价计算,图像中不同区域像素点的AD变换代价和Census变换代价对匹配代价计算的影响不同,得到了更好的匹配效果。此外,为能够进一步提升匹配效果,还通过增加窗口内连续像素点的灰度阈值条件,改善十字支撑窗口。
1 双目立体匹配双目立体视觉是模仿人的双眼成像过程,通过平行放置的两台摄像机共同拍摄场景,获得两张视图的双目图像。两张视觉图像的共同像素点(即匹配点)在纵向上没有偏差,其在横向上的偏差被称为视差。通过视差可获得像素点的3维坐标,用于各种应用。双目立体匹配即通过寻找双目视觉图像的匹配点获得视差的过程,如图1所示,可分为匹配代价计算、代价聚合、视差选择和视差优化4个阶段[11]。
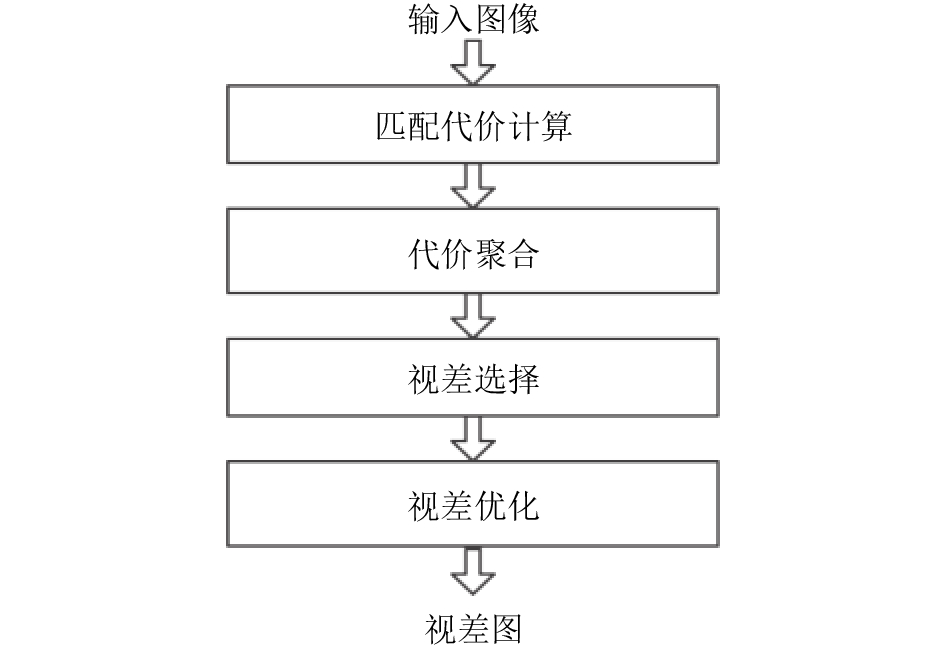 |
| 图1 立体匹配基本流程 Fig. 1 Flow of stereo matching |
根据亮度/色彩一致性假设,空间点映射到双目视觉两张图像上的像素点(匹配点)的灰度、颜色等参数理论上应该相同。进而由灰度、颜色衍生的参数,例如灰度梯度也应该相同。也即匹配像素点是相似的,匹配代价即为相似度的衡量参数。以灰度绝对差AD[12]变换算法为例,假设双目视觉图像的左图中待匹配点为
| ${C_{{\rm{AD}}}}\left( {p,q} \right) = {I_{\rm{L}}}(x,y) - {I_{\rm{R}}}((x - d),y)$ | (1) |
由于物体距离像机的远近有一定范围,因而在进行匹配时,需要考虑的视差是在一定取值范围内的,匹配代价计算也即将右图中与点
基于单个像素点计算的匹配代价往往会受到图像噪声、光照不均等的影响,相似度可靠性不高。代价聚合是指采用窗口滤波的方式对匹配代价进行滤波,以提高匹配代价的可靠性。视差选择即通过聚合后匹配代价选择匹配点,计算视差。局部匹配算法通常采用WTA(winner take all)[14]策略进行视差计算,通过选取聚合代价最小值对应的视差作为该像素点的初始视差。视差优化是一个相对独立的过程,是针对上述初始视差包含太多误匹配点的情况,提出的优化策略。视差优化策略方法较多[14],如左右一致性原理检测、迭代直方图分布法等。为得到更加精确的视差,可采用多种优化方法联合的方式。
2 基于自适应权重AD-Census变换的立体匹配 2.1 AD-Census变换性能分析AD变换反映像素点的灰度变化,在纹理丰富区域具有良好的匹配效果。但Hirschmuller[15]指出,AD变换易受光照变化影响,在光照不均时图像匹配精度相对较低;Census变换对光照变化的适应性好,对由光照不均引起灰度变化有很好的修正作用。
由于图像的连续性,如果一对像素点是匹配的,则其邻域一般情况也是匹配的。Census变换[13]通过对以待匹配点为中心点的邻域做变换计算代价。变换的规则是比较邻域内像素点和中心点的灰度大小关系,将灰度小于中心点灰度的记为1,大于的记为0,得到一个1/0字节串;然后通过比较字节串的Hamming距离计算匹配点的相似程度,计算过程如图2所示。
图2(a)中的数字表示窗口内各像素点的灰度,图2(b)表示Census变换的结果。变换的匹配代价利用邻域窗口的信息描述该中心点,由于不依赖灰度值,而是依赖邻域窗口内像素点灰度的相对大小,因此能够很好地克服图像中由于噪声和光照不均等引起的误差。
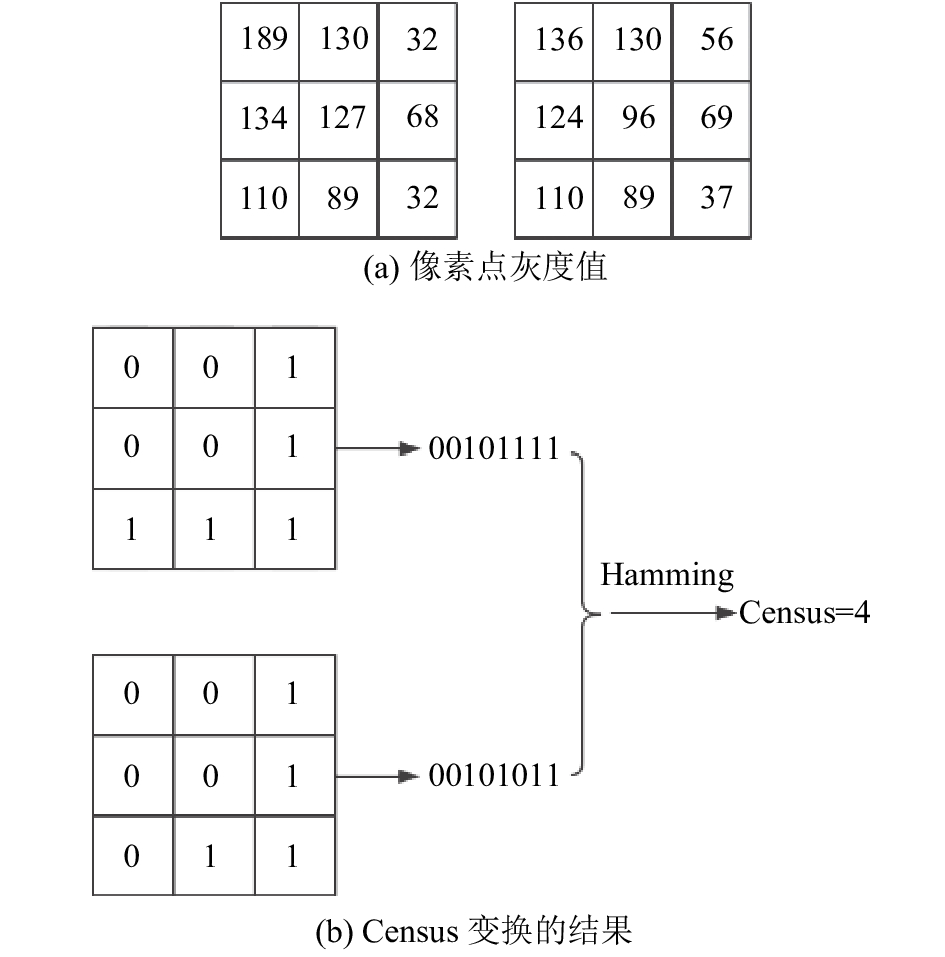 |
| 图2 Census变换示例图 Fig. 2 Example of Census transform |
Census变换虽对由光照不均引起灰度变化误差有很好的修正作用,但Census变换只是简单地用0/1位字节串表示两个像素点灰度的差距,导致特征描述符太过单一,当邻域窗口内灰度变化波动较大或出现纹理类似的重复区域时,Census变换得到的匹配代价就不能很好地表征相似度。如图3所示,图3(a)代表灰度完全不同的两个邻域窗口,图3(c)为此两个邻域窗口Census变换得到的代价,其结果相同;AD变换直接采用灰度做差的方式直接计算匹配代价(图3(b)),反而能够表现出两个窗口的相似度。故AD变换较适用于图像中灰度变换较明显的区域,即纹理丰富的区域,而Census变化则在该区域效果有限。
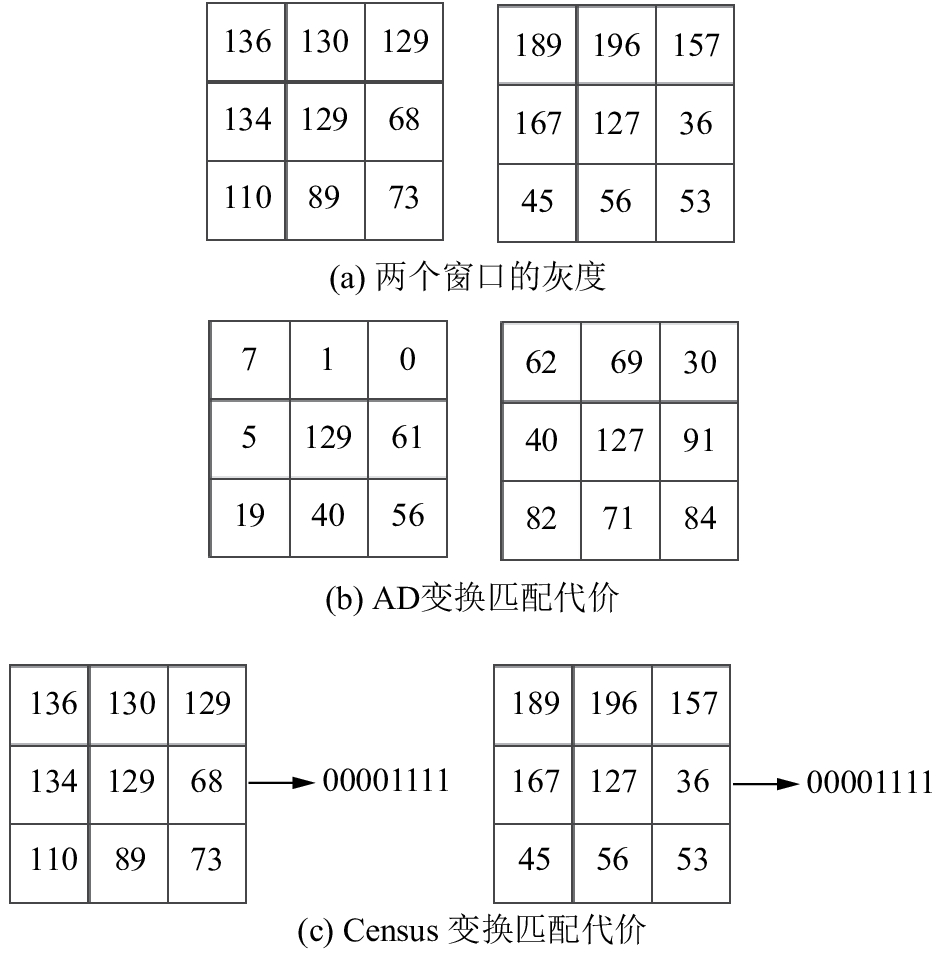 |
| 图3 AD、Census变换比较示例 Fig. 3 Example of comparison of AD and Census |
为能够利用AD、Census变换各自的优点,一种AD-Census变换[14]被提出,该变换将AD、Census变换产生的代价合成一个代价用于双目视觉立体匹配,其变换公式见式(2)、(3):
| $C(p,d) = \rho ({C_{{\rm{census}}}}(p,d),{\lambda _{{\rm{census}}}}) + \rho ({C_{{\rm{AD}}}}(p,d),{\lambda _{{\rm{AD}}}})$ | (2) |
| $\rho (C,\lambda ) = 1 - \exp (\frac{{ - C}}{\lambda })$ | (3) |
式中,函数
分别利用AD、Census变换、AD-Census变换作为代价计算的方法,在Middlebury第3代评估图像Piano的平滑区域与边缘区域得到视差见图4。上行取灯罩边缘与灯座边缘为比较窗口,属图像边缘区域;下行取桌下地毯为比较窗口,属平滑区域。比较窗口见图4中的方形框。
 |
| 图4 AD、Census、AD-Census不同算法变换视差 Fig. 4 Disparity images by AD, Census, and AD-Census |
图4(a)为从Piano图像中截取的部分区域的原始图像,图4(b)为Middlebury评估平台提供的真实视差图,图4(c)~(e)分别为通过AD、Census、AD-Census变换得到的视差图。对比可知,图像平滑区域,采用Census变换得到的视差图效果比AD要好;在图像边缘,采用AD变换得到的视差图效果更好。AD-Census变换结合了AD和Census变换的优点,在平滑区域和边缘区域均能得到较好的匹配效果。但由式(2)可知,AD-Census变换合成代价时,在平滑区域与边缘区域的权重固定,没能最大化两种方法的优点。
2.2 AD-Census的自适应权重设定AD-Census采用固定权重对AD、Census变换得到的代价进行合成,在图像平滑区域和在图像纹理丰富的边缘区域的像素点的匹配代价计算方式相同,没能利用像素点在图像中的区域特性。由于在图像平滑区域,Census变换比AD变换计算出的视差图精度高;而在图像纹理区域,采用AD变换得到的视差图效果更好。因此,为进一步提高匹配效果,可采用自适应的方式设置合成权重。自适应权重的AD-Census变换计算公式如式(4)所示,式中
| $ C(p,d) = \alpha \rho ({C_{{\rm{AD}}}}(p,d),{\lambda _{{\rm{AD}}}}) + (1 - \alpha )\rho ({C_{{\rm{census}}}}(p,d),{\lambda _{{\rm{census}}}})$ | (4) |
式(4)中自适应权重设定的关键在于如何使得
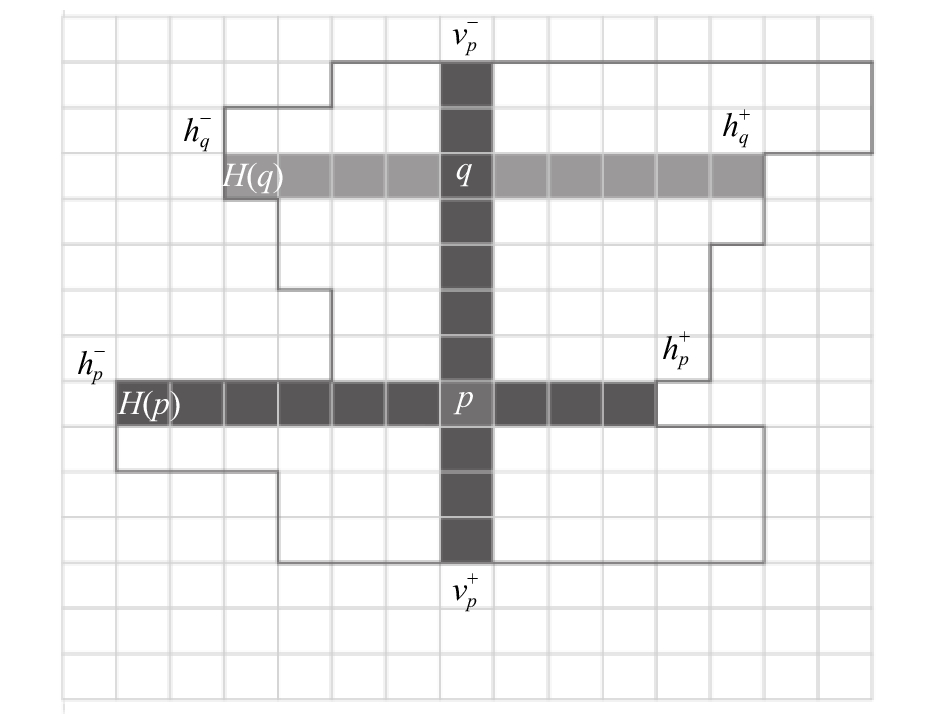 |
| 图5 十字支撑自适应窗口 Fig. 5 Upright cross support region construction |
| $\left\{ \begin{aligned}& \left| {I(x,y) - I({x_i},{y_i})} \right| < \tau ,\\& D(p,{p_i}) < l\end{aligned} \right.$ | (5) |
Mei等[14]基于式(5)对计算臂长的条件进行进一步限制,减少因臂长必须小于
| $\left\{ \begin{aligned}& \left| {I(x,y) - I({x_i},{y_i})} \right| < {\tau _1}, \left| {I({x_i},{y_i}) - I({x_i} + 1,{y_i})} \right| < {\tau _1};\\& D(p,{p_i}) < {l_1};\\& \left| {I(x,y) - I({x_i},{y_i})} \right| < {\tau _2}, {l_2} < D(p,{p_i}) < {l_1};\end{aligned} \right.$ | (6) |
式(6)中第一个条件表示向左遍历时,不仅要求
为进一步增加灰度变化影响臂长计算,可基于式(6)进一步严格限制同一区域内的灰度变化,如式(7)所示:
| $\left\{ \begin{aligned}& \left| {I(x,y) - I({x_i},{y_i})} \right| < {\tau _1},\left| {I({x_i},{y_i}) - I({x_i} + 1,{y_i})} \right| < {\tau _1};\\& D(p,{p_i}) < {l_1};\\& \left| {I(x,y) - I({x_i},{y_i})} \right| < {\tau _2},\left| {I({x_i},{y_i}) - I({x_i} + 1,{y_i})} \right| < {\tau _2};\\& {l_2} < D(p,{p_i}) < {l_1}\end{aligned} \right.$ | (7) |
计算臂长的过程中,如臂长已经大于
利用式(7)在图像Tsukuba上得到一些像素点的4个方向的臂长如图6所示。臂长能充分反映该像素点在图6中的位置,在平滑的区域像素点的4个臂长值都很大;在靠近边缘的地方,越靠近边缘,该方向的臂长值越小。
 |
| 图6 图像Tsukuba上臂长示意图 Fig. 6 Some examples of the arm’s length on Tsukuba image |
为了根据像素位于图像区域的特征自适应设置AD-Census变换的权重,突出AD变换在边缘区域及Census变换在平滑区域的优点,利用最小臂长采用式(8)所示的指数函数进行
| $\alpha = 1 - {\rm{exp}}( - \frac{{{\gamma _{\rm{h}}}}}{{{h_{\min }}}})$ | (8) |
式中:
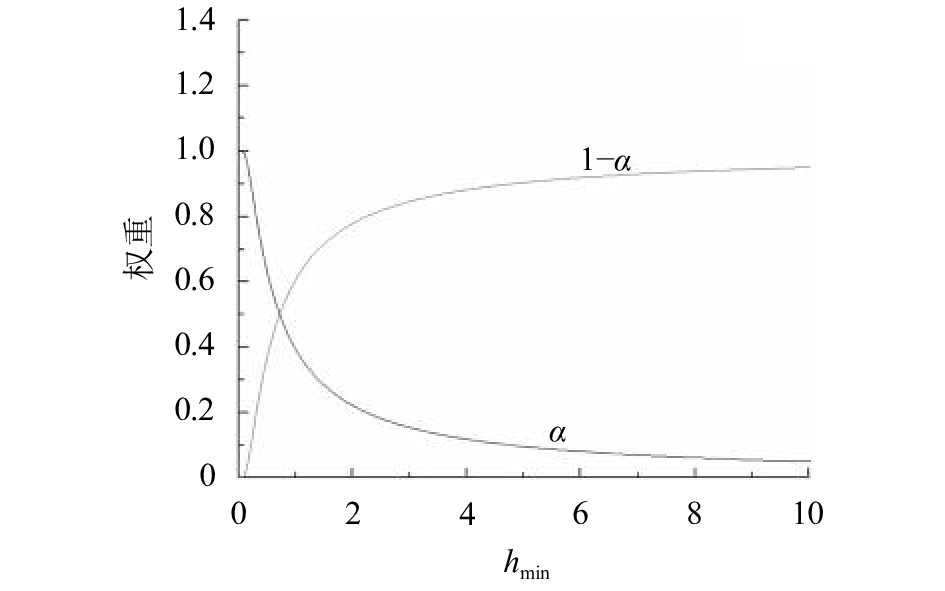 |
| 图7 不同权重特征曲线 Fig. 7 Characteristic curves of weight |
由于最短臂长可反映像素点位于图像区域的位置,像素点距离图像边缘近,最短臂长小,根据式(8)设置的AD权重大,Census权重小;像素点距离图像边缘远,则最短臂长大,AD权重小,Census权重大。并且即使是位于重复区域的像素点,由于最短臂长的不同,自适应设置的权重也不同,进而合成的匹配代价也不同,避免此类误匹配。因此自适应设置权重的算法更适合纹理丰富、具有重复区域的图像。
2.3 立体匹配基于自适应权重AD-Census变换的立体匹配流程如图8所示。
在最初的代价计算阶段,利用自适应权重AD-Census变换方法进行代价计算;在代价聚合阶段,使用根据改进限制条件得到的十字支撑自适应窗口作为滤波窗口,采用与AD-Census立体匹配[14]相同的算法进行代价聚合;视差选择与视差优化采用与AD-Census立体匹配[14]相同的方法,视差选择采用WTA策略进行视差选择;视差优化采用左右一致性检测、迭代直方图分布法、十六方向插值法、深度不连续区域边缘修正法、亚像素求精、中值滤波进行多过程视差优化。
 |
| 图8 基于自适应权重AD-Census变换的立体匹配流程 Fig. 8 Flow of stereo matching system with the adaptive weight AD-Census |
3 实验与分析
Middlebury[17]双目立体匹配评估平台是立体匹配研究领域公认的测试平台,本文在其最新的第3代双目立体匹配评估平台上进行相关实验,实验对象包括平台上所有图像集合。
分别将式(6)与本文提出的式(7)得到的自适应窗口运用到AD-Census匹配系统中[14]进行代价聚合得到的视差图比较情况如图9所示。
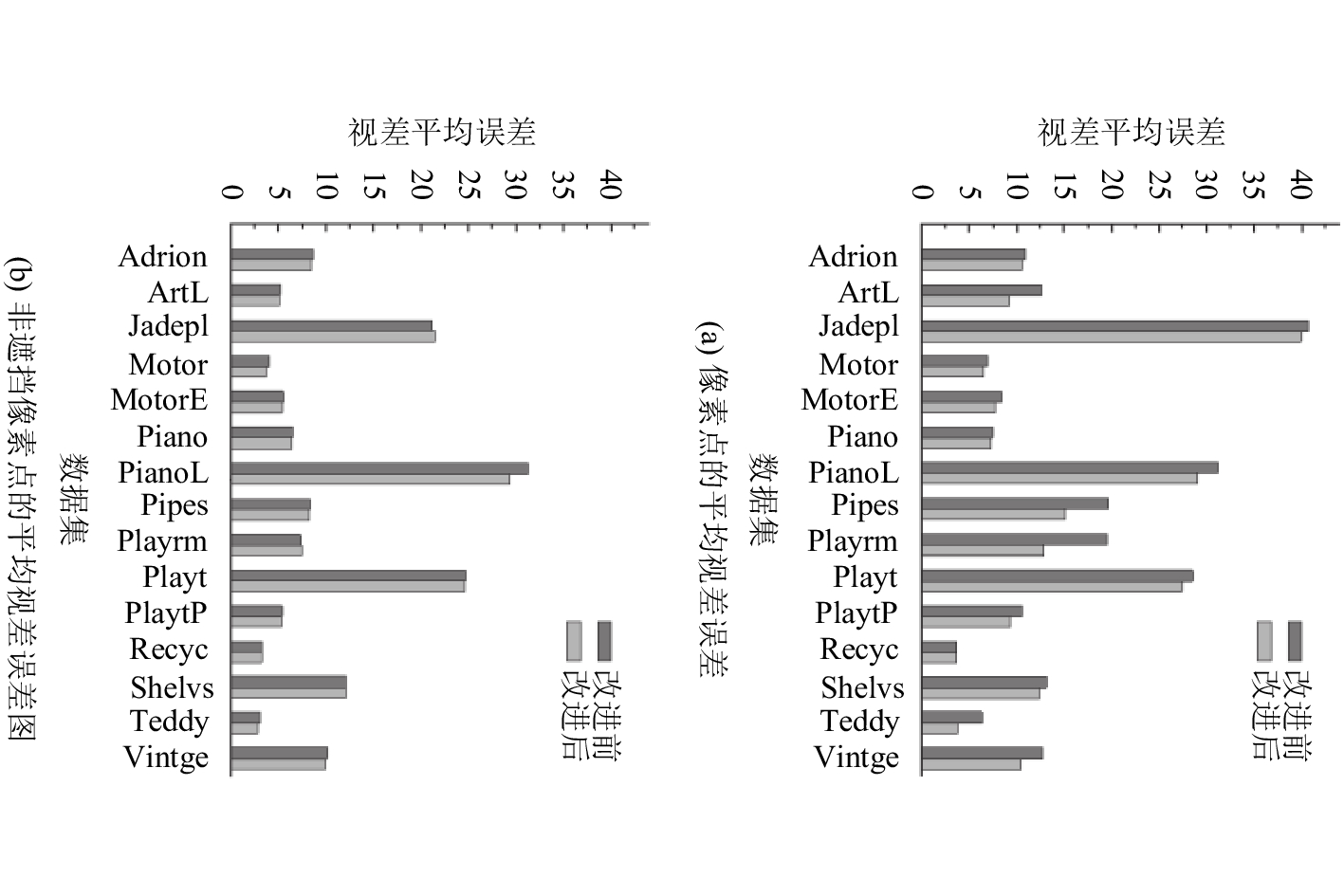 |
| 图9 两种十字支撑自适应窗口视差平均误差比较 Fig. 9 Average disparity errors of two kinds of upright cross support region construction |
图9(a)为Middlebury第3代评估平台所有图像全部像素点的平均视差误差,横坐标为各个图像名。图9(b)为评估平台所有图像的非遮挡像素点的平均视差误差。由图9可知,采用改进的十字支撑自适应窗口的视差图平均误差更小,能够取得比较好的代价聚合效果,可应用于其他立体匹配系统。
基于自适应权重的双目立体系统在Middlebury立体匹配评估平台上匹配过程的参数设置如表1所示,除新引进
| 表1 参数设定 Tab. 1 Parameters settings for the Middlebury experiments |
 |
得到的Recyc图像视差图如图10(c)所示,接近真实视差图10(b)。全部图像评估结果如表2、3所示。与2代平台不同,3代平台只给出了更能代表匹配效果的非遮挡像素点视差误差、全部像素点视差误差。表2~3中的平均误差是评估平台根据各个图像的视差误差自动计算而来。基于自适应权重AD-Census变换的立体匹配与基于AD-Census变换的立体匹配[14]在视差选择阶段与视差优化阶段完全相同,但由于采用了式(8)所示的根据最小臂长自适应方法进行AD与Census权重设置,可最大程度体现像素点所处的图像特征,因此性能得到了提升,全部像素点的视差平均误差减小了25%,非遮挡像素点的视差平均误差减小了20%。
 |
| 图10 Recyc图像视差图 Fig. 10 Disparity maps of Recyc |
基于自适应权重AD-Census变换的立体匹配系统在所有图像集上的平均匹配效果也优于最近相关文献[4–10];特别是在纹理丰富、含有多重复纹理的图像集合Adir、Jad、Mote、Pial、Playrm、Rec上匹配效果最佳,因此更适用于此类图像。
| 表2 不同算法非遮挡像素点的视差平均误差比较 Tab. 2 Aaverage disparity errors of non-occlusion pixels |
 |
| 表3 不同算法全部像素点的视差平均误差比较 Tab. 3 Average disparity errors of all pixels |
 |
4 结束语
立体匹配是双目计算机视觉的基础。AD-Census变换由于是将AD代价与Census变换代价合成了一个匹配代价,综合利用了二者的优点,具有较好的匹配效果,但两个代价的合成权重固定,没能体现像素点的区域特性。因此基于像素十字支撑自适应窗口的最短臂长,提出一种自适应权重AD-Census变换的立体匹配算法。由于十字支撑窗口的最短臂长可反映像素的区域特性,故合成所得的匹配代价可反映像素所处图像区域的区域特征,提升了立体匹配的匹配精度;为了使十字支撑窗口的最短臂能够更好地反映像素的区域特性,通过增加相邻像素的灰度阈值条件,改善了十字支撑窗口。实验结果表明自适应权重AD-Census变换与改进的十字支撑窗口可以用于立体匹配,特别是更加适合纹理丰富、含有重复区域的图像。此外,可对Census变换进行进一步研究,使得Census变换本身就能够反映像素点区域特性,进一步提升匹配效果。
| [1] |
Poddar S,Sahu H,Bangale M R,et al.Feature based dense disparity estimation[C]//International Conference on Industrial Instrumentation and Control.Pune:IEEE,2015:950–955.
|
| [2] |
Fleet D J,Jepson A D,Jenkin M R M. Phase-based disparity measurement[J]. CVGIP:Image Understanding, 1991, 53(2): 198-210. DOI:10.1016/1049-9660(91)90027-M |
| [3] |
Wang Z F,Zheng Z G. A region based stereo matching algorithm using cooperative optimization[J]. Acta Automatica Sinica, 2009, 35(5): 1-8. DOI:10.1109/CVPR.2008.4587456 |
| [4] |
Ma N,Men Y B,Men C G,et al. Accurate dense stereo matching based on image segmentation using an adaptive multi-cost approach[J]. Symmetry, 2016, 8(12): 159-180. DOI:10.3390/sym8120159 |
| [5] |
Jellal R A,Lange M,Wassermann B,et al.LS-ELAS:Line segment based efficient large scale stereo matching[C]//IEEE International Conference on Robotics and Automation.Singapore:IEEE,2017:146–152.
|
| [6] |
Hirschmuller H. Stereo processing by semiglobal matching and mutual information[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 30(2): 328-341. DOI:10.1109/TPAMI.2007.1166 |
| [7] |
Zhang K,Li J Y,Li Y J,et al.Binary stereo matching[C]//International Conference on Pattern Recognition.Tsukuba:IEEE,2012:356-359.
|
| [8] |
Shahbazi M,Sohn G,Théau J,et al. Revisiting intrinsic curves for efficient dense stereo matching[J]. Isprs Annals of Photogrammetry Remote Sensing & Spatial Informa, 2016, III-3: 123-130. DOI:10.5194/isprsannals-III-3-123-2016 |
| [9] |
Keselman L,Woodfill J I,Grunnetjepsen A,et al.Intel RealSense stereoscopic depth cameras[C]//Computer Vision and Pattern Recognition Workshops (CVPRW).Honolulu:IEEE,2017:1267–1276.
|
| [10] |
Peña D,Sutherland A.Disparity estimation by simultaneous edge drawing[C]//Asian Conference on Computer Vision.Taipei:Springer Cham,2016:124–135.
|
| [11] |
Scharstein D,Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International Journal on Computer Vision, 2002, 47(1/2/3): 7-42. DOI:10.1109/SMBV.2001.988771 |
| [12] |
Zabih R,Woodfill J.Non-parametric local transforms for computing visual correspondence[C]//European Conference on Computer Vision.Heidelberg:Springer Berlin,1994:151–158.
|
| [13] |
Birchfield S,Tomasi C. A pixel dissimilarity measure that is insensitive to image sampling[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(4): 401-406. DOI:10.1109/34.677269 |
| [14] |
Mei X,Sun X,Zhou M,et al.On building an accurate stereo matching system on graphics hardware[C]//IEEE International Conference on Computer Vision Workshops.Barcelona:IEEE,2012:467–474.
|
| [15] |
Hirschmuller H.Accurate and efficient stereo processing by semi-global matching and mutual information[C]//Computer Vision and Pattern Recognition 2005.Diego:IEEE,2005:807–814.
|
| [16] |
Zhang K,Lu J,Lafruit G. Cross-based local stereo matching using orthogonal integral images[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2009, 19(7): 1073-1079. DOI:10.1109/TCSVT.2009.2020478 |
| [17] |
Scharstein D,Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International Journal of Computer Vision, 2002, 47(1/2/3): 7-42. DOI:10.1109/SMBV.2001.988771 |
 2018, Vol. 50
2018, Vol. 50

