2. 郑州大学 互联网医疗与健康服务河南省协同创新中心,河南 郑州 450000
2. Cooperative Innovation Center of Internet Healthcare, Zhengzhou Univ., Zhengzhou 450000, China
小额支付是指在一定时间内对多笔支付业务进行轧差处理,净额清算资金[1]。小额支付系统的广泛使用为社会提供了低成本的支付清算服务,但由于小额支付系统具有交易金额小、时效性强、交易频次高等特点[2],其对于交易安全性和支付效率都提出了比较高的要求。为此,张红等[3]利用混沌系统迭代过程的单向性构造出Hash支付链,实现了信息服务的逐单位释放,保证了整个交易过程的公平性;陈莉等[4]设计了一种基于自更新Hash链机制的小额支付协议,解决了用户恶意透支和协议执行时限问题;邹嘉等[5]提出了一种新的充分利用P2P系统特性的小额支付协议CPay,利用P2P系统异构性实现负载均衡。但上述方案均采用中心式交易数据处理结构,一旦数据中被攻陷,交易数据的安全性、隐私性均难以保障。
区块链技术[6]的出现为安全、稳定的去中心化小额交易提供了新的解决方案。它是一种融合了去中心化计算、共识机制、分布式数据存储和点对点传输的新型密码学系统,在数字资产交易、股权清算、跨境支付、保密文档存储、公证等众多领域不断获得开创性的应用。但在目前的区块数据生成方式下[7],小额交易场景很容易遭遇瓶颈。具体原因是,一个数据区块的形成要汇集众多节点的多笔交易数据,并由一个遴选的记账节点进行记录,每个区块间存在一个定长的时间间隔
在文献[11]的基础上,作者构造了一种时延控制Petri网(delay control Petri nets,DCPN)模型,并以此为基础,提出一种区块链小额实时交易策略(real-time micro trading strategy with blockchain, RMTSB),从整体上提高了区块链应用中小额交易的时效性。
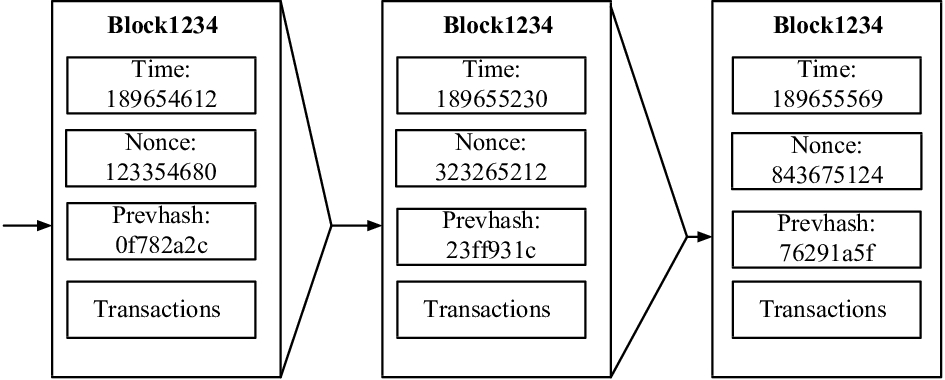
1 区块链技术相关知识 1.1 区块链的技术原理区块链技术起源于化名为“中本聪”(Satoshi Nakamoto)的学者在2008年发表的奠基性论文《比特币: 一种点对点电子现金系统》[12]。简单来说,区块链是一种由任意多的节点通过密码学方法,以去中心化、去信任化的方式集体维护一个可靠数据库的技术方案。区块链的数据结构主要分为两个部分[13]:1)区块头。主要包含上一个区块的哈希散列值,用于连接前一区块,保证区块链的完整性。2)区块主体。包含本区块的主要信息(如交易信息),这些信息和上一个区块的哈希散列值以及随机数共同构成本区块的哈希散列值。
区块链的数据结构(图1)使得链上每个区块的信息都可以由前驱节点追溯,并影响后继节点的信息构成。其密码学方法保证了恶意攻击无法篡改信息,从而确保数据的安全性和完整性。区块链的构建遵循一整套共识和协议机制[14],全网每个节点都可验证或写入记录,但只有当全网大部分节点(甚至全部节点)一致确认某个记录的正确性,相应数据才允许被写入区块中。
 |
| 图1 区块链数据结构 Fig. 1 Blockchain data structure |
1.2 全节点验证和轻节点验证
区块链验证交易数据的方法主要有两种[13]:全节点验证和轻节点验证。其中,全节点验证(full node verification,FNV)[6]是应用最为广泛的一种模式。以比特币为例,全节点中记录了从创世区块[13]至今的所有交易信息,包括交易方、交易金额以及所有用于交易的比特币的来源等。通过全节点可以准确无误地验证任何一笔交易,但全节点也存在一个明显的弊端:数据量过于庞大。现阶段比特币的数据量已经超过100 GB,且随着区块链技术的普及,数据增量将越来越大。
轻节点验证(simplified payment verification, SPV)[12]是一种代替全节点验证的方式。轻节点只在初始同步过程中下载区块头,并根据需要从全节点中下载历史数据。不论总区块的数据量有多大,轻节点模式仅需存储每个区块头的约80字节数据,大大减少了数据存储量。区块头中的Merkle root连同Merkle branch可以向SPV客户端证明区块中是否嵌入了有问题的交易,因此,轻节点只需下载整个区块链的一小部分就可以安全地确定任何一笔比特币交易的状态和账户的当前余额。这种利用轻节点进行验证的方式应用非常广泛,如文献[15]的VP(validation peer)就是一种专门用来验证交易的节点,由于仅需验证peer leader block中的信息,从而有效地缩短了验证处理时间。
2 时延控制Petri网交易系统本质上是一种异步并发的信息系统,小额实时交易则对时间属性提出了更高要求。作者在文献[11]的基础上构造一种时延控制Petri网(delay control Petri nets,DCPN),用于对带有时延控制信息的系统进行描述和分析评估。
定义1 (时延控制Petri网) 它是一个十元组,即
| ${DCPN} = (S,T,F,R,C,DI,DC,CF,OP,{M_0}){\text{。}}$ |
其中:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
DCPN的示例如图2所示。其中,常规库所
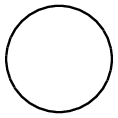 表示,模糊库所
表示,模糊库所
表示;常规变迁
表示,时延变迁
表示,控制弧
表示,抑止弧
表示。
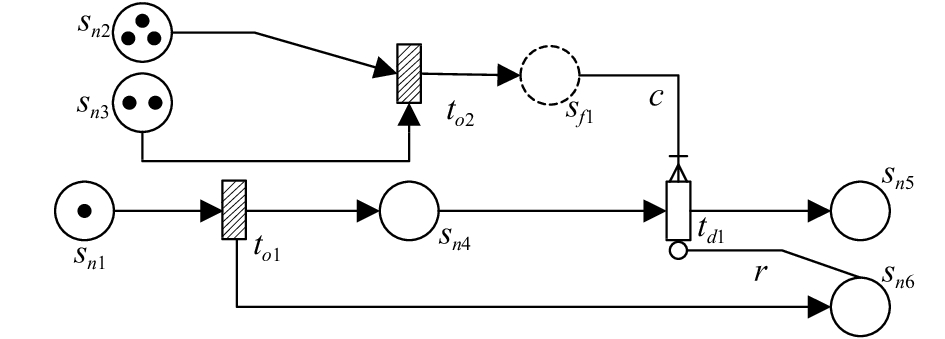 |
| 图2 DCPN示例模型 Fig. 2 DCPN example model |
定义2(DCPN的状态标志集
由于在DCPN中涉及两类库所,对于常规库所
性质1(DCPN的运行规则)
1)对
2)对
①
②
则变迁
3)若
| ${M_{{i} + 1}}(s) = \left\{ \begin{aligned}& 0,t \in T \wedge s \in {S\!_{N}} \wedge s \in {}^ \bullet t \wedge (s,t) \in F;\\& {\rm max}({M_{{i}}}(s),CF(t,s)),t \in {T_{{O}}} \wedge \\& \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s \in {S\!_{F}} \wedge s \in t{}^ \bullet ;\\& {M_i}(s) + OP(t,s),t \in T \wedge s \in {S\!_{N}} \wedge s \in t{}^ \bullet ;\\& {M_i}(s),{\text{其他}}\end{aligned} \right.$ | (1) |
定义3 (时延控制函数
| $DC(\alpha ) = \left\lfloor {\frac{{ - 1}}{{1 + {{\rm{e}}^{\omega {\rm{ \times }}\alpha - \xi }}}} + \sigma } \right\rfloor $ | (2) |
式中,
定义4(置信度函数
| $CF(t,s) = \frac{2}{{\text{π}} }(\arctan \frac{{\prod {{M_{{i}}}{(^ \bullet }t} )}}{\rho })$ | (3) |
式中,
定义5 (输出函数
| $OP(t,s) = \left\{ \begin{aligned}& \psi ,\exists t' \in T \wedge t' \ne t \wedge (s,t') \in {\mathbb{R}};\\& 1,{\text{其他}}\end{aligned} \right.$ | (4) |
式中,
在使用比特币、莱特币[16]等基于区块链的支付工具进行小额实时交易时,交易等待时间过长的问题已成为区块链技术在小额交易应用中的瓶颈。针对该问题,作者基于DCPN提出一种区块链小额实时交易策略(real-time micro trading strategy with blockchain, RMTSB)。
3.1 数据区块结构及信用度评估方法为了记录和评估交易过程,首先,给出一种含个人信用指标的交易数据区块结构(如图3所示),每笔交易都包括支付方账号(payer identity, PID)、收款方账号(receiver identity, RID)、当前交易金额(current transactions amount, CTA)、支付方的正常交易记录集(normal transactions set, NDS)及不良交易记录集(bad transactions set, BDS)。
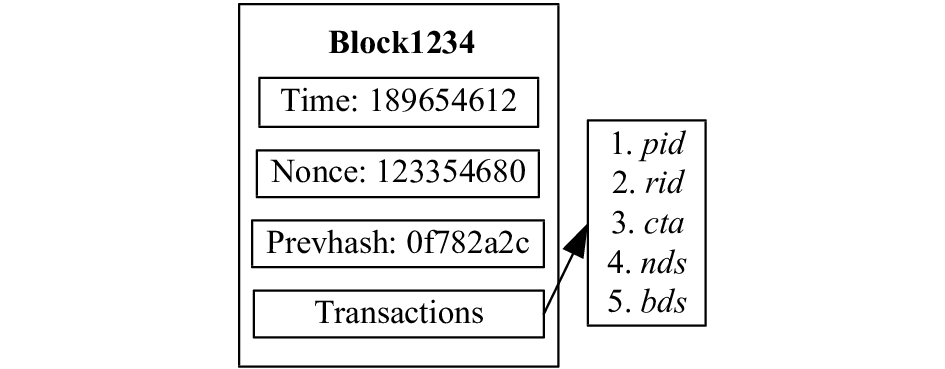 |
| 图3 含个人信用指标的交易数据区块结构 Fig. 3 Transaction block structure with personal credit indicators |
文中提到的“高频次、低额度交易”,一般需要满足以下两个条件:1)
在该种情况下可通过支付方的交易次数、交易金额和不良交易记录集共同刻画该支付方一贯的交易特点和信用情况。采用信用度
| $\varepsilon {\rm{ = }}Amount(nd\!s) - \eta \times Amount(bd\!s)$ | (5) |
| $\phi {\rm{ = }}Count(nd\!s) - \kappa \times Count(bd\!s)$ | (6) |
| $\alpha = \frac{2}{{\text{π}} }(\arctan \frac{{\varepsilon \times \phi }}{\rho })$ | (7) |
式中,
在使用基于区块链的支付方式进行交易时,由于收款方需在区块形成后方可确认该笔交易,因此往往存在交易等待时间过长的问题。作者在信用度
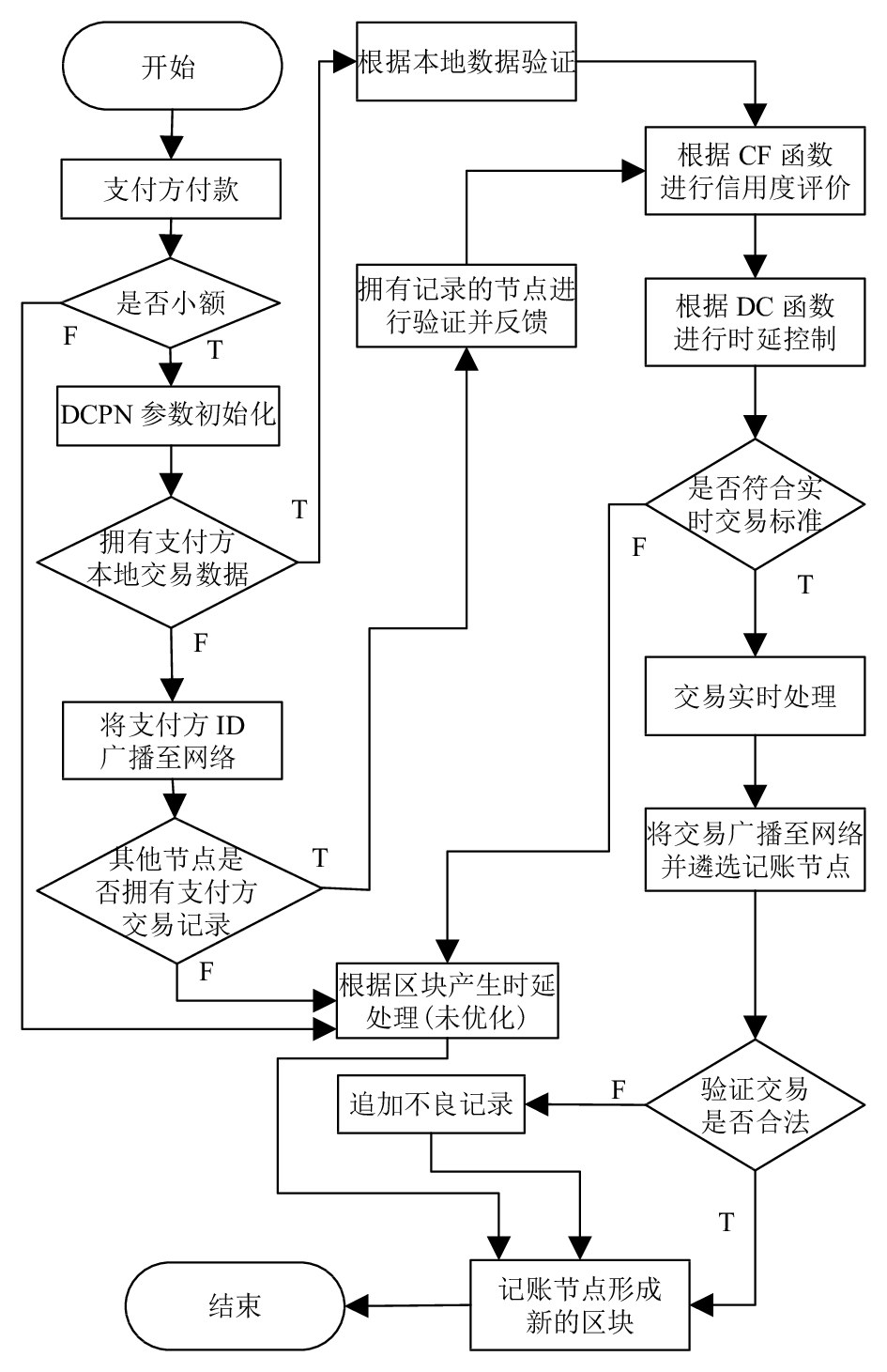 |
| 图4 RMTSB策略 Fig. 4 RMTSB strategy |
具体步骤如下:
1)支付方使用基于区块链的支付工具进行支付,若为大额,则转至步骤9);若为小额,根据实际问题为置信度函数
2)若收款方本地拥有支付方以往的交易数据区块,则使用该数据进行历史交易验证,转到步骤4);否则将广播至网络;
3)若网内其他节点保存了支付方以往的交易数据区块,则使用该数据进行历史交易验证,并反馈至当前收款方节点,转至步骤4),否则,转至步骤9);
4)根据
5)以
6)进行交易的实时处理(交易时延
7)记账节点对交易进行合法性验证,若通过验证,则转到步骤10);若未通过验证,则转到步骤8);
8)向支付方的不良交易记录集中加入本次交易信息,转到步骤10);
9)根据区块产生的时延,等待处理(交易时延
10)记账节点形成新的区块;
11)结束。
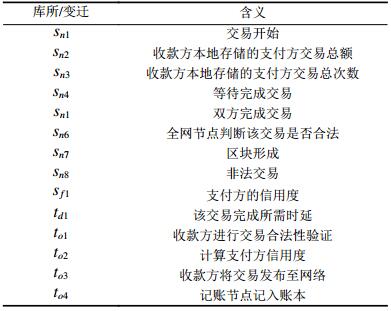
3.3 全节点的区块链小额实时交易过程在RMTSB策略中,如果收款方是一类区块链交易的全节点(FNV),则其必拥有支付方以往的全部交易数据区块,则可根据该信息进行信用度评价并实施时延控制。其交易过程相对简单(如图5所示),相应库所及变迁的含义如表1所示。
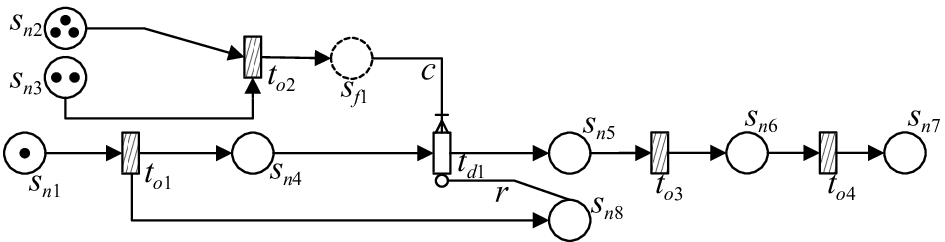 |
| 图5 基于DCPN的全节点的小额实时交易过程 Fig. 5 Real-time micro trading with FNV based on DCPN |
| 表1 全节点小额实时交易的库所/变迁含义 Tab. 1 Meaning of each place/transition inreal-time micro trading with FNV |
 |
3.4 轻节点的区块链小额实时交易过程
在RMTSB策略中,若收款方为一类区块链交易的轻节点(SPV),则收款方不一定拥有支付方以往的全部历史交易数据。该情况下必须借助其他验证节点对支付方进行信用度评估,并在交易结束后根据全网节点的验证最终核实交易。在验证过程中,只有拥有支付方全部历史数据的验证节点才可以对其进行验证。如果收款方在下一区块形成前没有收到验证反馈,则按照未优化的情形处理交易。其交易过程如图6所示,相应库所及变迁的含义如表2所示。
 |
| 图6 基于DCPN的轻节点小额实时交易过程 Fig. 6 Real-time micro tradingwith SPV based on DCPN |
| 表2 轻节点小额实时交易过程的库所/变迁含义 Tab. 2 Meaning of each place/transition in real-time micro trading with SPV |
 |
3.5 交易过程分析
对上述过程做如下分析:
1)由于收款方是交易后果的第一影响人,交易合法性的验证对其收益的保障至关重要。RMTSB策略对小额交易给出一种快速处理方法,运用支付方的历史交易记录作为信用背书,以期加快区块链应用中小额交易处理速度,并在交易完成后进行基于共识方法的验证和不良记录的追加,在一定程度上可降低非验证环节的交易风险。
2)当收款方为全节点时,该节点将利用本地数据进行历史交易验证。此类节点使用
3)当收款方为轻节点时,则该节点不一定拥有支付方的全部历史交易数据。此类节点将支付方ID广播至网络,由其他拥有支付方历史记录的节点对其进行验证,每个节点的验证方式同2)中所述。此类情形下,不具备本地验证能力的轻节点也能通过网络节点反馈达到加快支付速度的效果。由于在区块链网络中,轻节点的数量占到了绝大多数,此类策略也为小额实时交易在所有节点中的实现提供了有效方法。
4)上述过程基于支付方的历史信用进行交易确认,在提高支付效率的同时,也不可避免地会遭遇非法交易(例如,双花问题)。但通过合理设置小额交易额度上限,设计相应惩罚机制,以及与公民个人信用等级绑定等措施,将会有效抑制非法交易的出现。在本文策略中,设置了交易额的上限,约定了只有小额交易才能使用上述信用策略。此外,还引入了一定的信用惩罚机制,当出现非法交易时,记账节点将向支付方的不良交易记录集加入本次交易信息。
4 仿真实验 4.1 仿真实验为了验证RMTSB策略的有效性,作者使用MATLAB构建了仿真程序,并以一个小额交易过程为例进行仿真实验和对比分析。
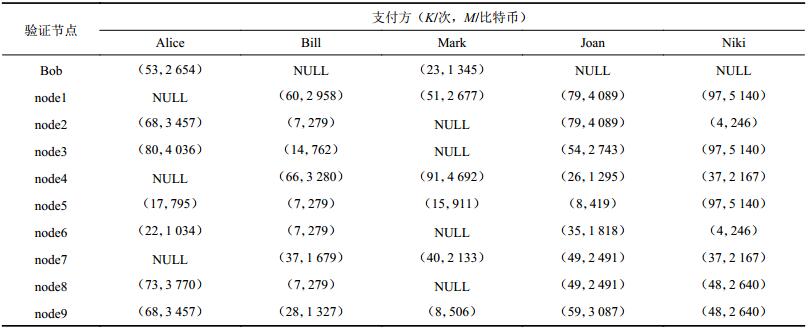
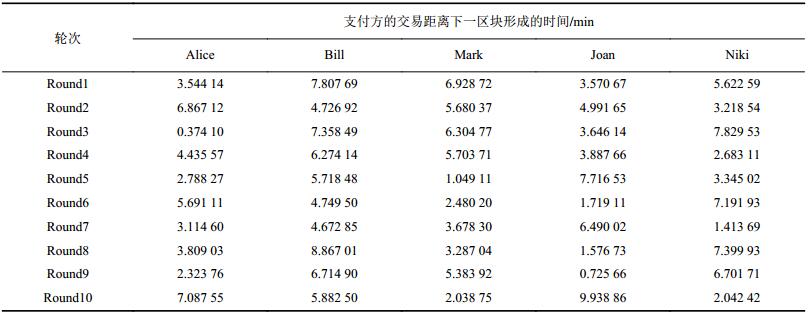
设零售商Bob与支付方Alice、Bill等5人正在进行小额交易,交易金额均小于200人民币(约为0.020 833 3比特币),交易的验证由Bob及其他9个零售商(共10个节点)作为验证节点完成。其中,这10个验证节点所拥有的支付方历史交易数据如表3所示,K为交易总次数,M为交易总金额,NULL表示节点未存储该信息。对5笔交易进行10轮仿真,各交易启动时距下一区块形成的时间如表4所示。
| 表3 Bob和验证节点存储的支付方信息 Tab. 3 Payer information stored in the Bob and authentication nodes |
 |
| 表4 各交易距离下一区块形成的时间 Tab. 4 Time to wait for each transaction when the next block is formed |
 |
令DCPN模型中、
| 表5 各支付方的信用度 Tab. 5 Credit of each payment party |
 |
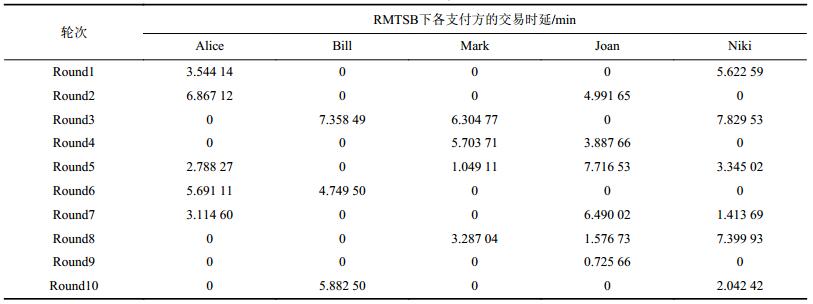
运用RMTSB策略进行小额交易,每轮仿真的交易时延值如表6所示。
| 表6 RMTSB的交易时延 Tab. 6 Transaction delay of RMTSB |
 |
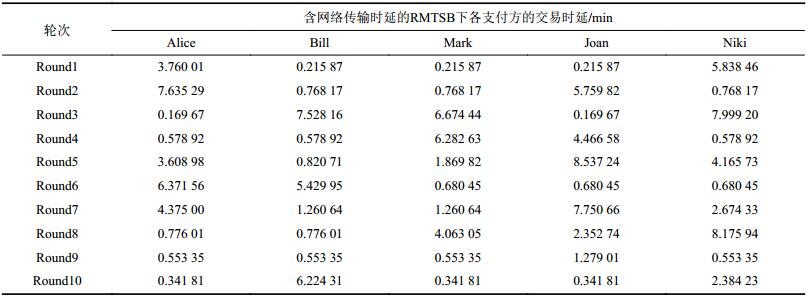
为了进一步模拟真实交易中存在网络延迟的情况,可在对交易处理过程进行仿真时,引入网络传输时延变量。各轮仿真的网络时延分别取随机数为0.215 87、0.768 17、0.169 67、0.578 92、0.820 71、0.680 45、1.260 64、0.776 01、0.553 35、0.341 81。运用RMTSB策略进行含网络传输时延变量的小额交易,每轮仿真的交易时延值如表7所示。
| 表7 含网络传输时延的RMTSB的交易时延 Tab. 7 Transaction delay of RMTSB with network transmission delay |
 |
4.2 对比分析
根据文献[17]所述的区块链常规交易方式,每轮交易后应等待新的区块形成后方可确认。因此,各笔交易的确认等待时间为表4中各交易距离下一区块形成时间。而第4.1节中,运用RMTSB策略进行小额交易(简称 RMTSB(A)),会将大量拥有较高信用度的交易提前完成确认,避免了大多数无谓的等待(如表6所示);进一步,将网络传输时延变量融入RMTSB策略(简称为RMTSB(B)),则刻画出真实交易环境中,RMTSB策略对实际交易数据的进一步拟合(如表7所示)。
| $\forall t \in T \to \max (D{I_{\rm{A}}}(t),D{I_{\rm{B}}}(t)) \le D{I_{\rm{ref}17}}(t){\text{。}}$ |
式中,
对每轮交易的时延累计情况进行对比分析可知:
| $\sum\limits_{t \in T} {D{I_{\rm{A}}}(t)} \le \sum\limits_{t \in T} {D{I_{\rm{B}}}(t)} \le \sum\limits_{t \in T} {D{I_{\rm{ref}17}}(t)}{\text{。}}$ |
多轮交易的总时延对比如图7所示。与区块链常规交易过程相比,RMTSB策略以支付方信用度为背书,有效提高了交易验证的效率。其交易时延与常规交易过程相比可降低50%~75%。
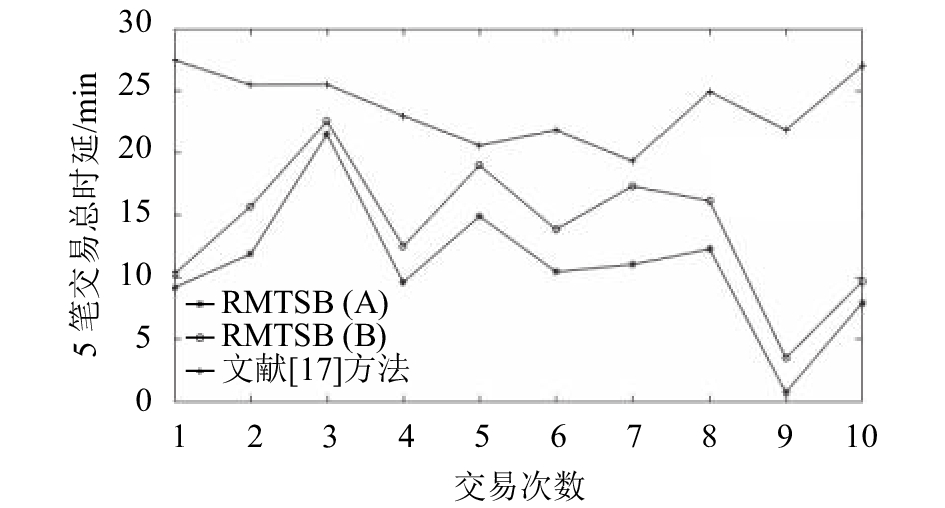 |
| 图7 交易总时延对比 Fig. 7 Comparison of total delay |
5 结 论
构造了一种DCPN模型,并以此为基础,提出了RMTSB策略,通过对支付方信用进行量化评估,有选择地为区块链框架下的交易进行信用背书,在“高频率、低额度”的交易中可有效控制交易时延,从整体上提高小额交易认证效率。仿真实验验证了方法的有效性。
目前,RMTSB策略还处于理论研究阶段,尚有需进一步研究和完善之处:1)DCPN模型中的置信度函数CF和时延控制函数DC的确定还需要大量数据进行拟合,以满足实际商业交易的需求;2)区块链技术目前大多应用于金融方面,在零售业、城市服务业等小额交易的典型领域,可考虑使用“区块链+物联网”或“区块链+位置服务”的结构对RMTSB策略进行改进,以期进一步减少计算量、增强安全性。
| [1] |
Song W,Framkom,Kou W,Tan C J.An investigation on multiple e-payments and micro-payment:A technical and market view[C]//Proceedings of the 16th International Parallel and Distributed Processing Symposium.Ft. Lauderdale:IEEE,2002:8
|
| [2] |
Patil V,Shyamasundar R K.An efficient,secure and delegable micro-payment system[C]//Proceedings of the 2004 IEEE International Conference on e-Technology,e-Commerce and e-Service.Taipei:IEEE,2004:394–404.
|
| [3] |
Zhang Hong,Li Bo,Xiao Di. A chaos-based scheme for Web fair micro-payment[J]. Computer Engineering, 2005, 31(17): 124-125. [张红,李波,肖迪. 一个基于混沌理论的Web公平小额支付方案[J]. 计算机工程, 2005, 31(17): 124-125. DOI:10.3969/j.issn.1000-3428.2005.17.045] |
| [4] |
Chen Li,Zhang Haojun,Zhu Yuefei. New micro-payment protocol for mobile commerce[J]. Journal of Computer Applications, 2007, 27(8): 2059-2061. [陈莉,张浩军,祝跃飞. 一种新的移动商务小额支付协议[J]. 计算机应用, 2007, 27(8): 2059-2061.] |
| [5] |
Zou Jia,Si Tiange,Huang Liansheng,et al. Micropayment model based on P2P systems[J]. Journal of Tsinghua University(Science & Technology), 2006, 46(4): 563-567. [邹嘉,司天歌,黄连生,等. 一种新的基于P2P系统的小额支付协议[J]. 清华大学学报(自然科学版), 2006, 46(4): 563-567. DOI:10.3321/j.issn:1000-0054.2006.04.030] |
| [6] |
Swan M.Blockchain:Blueprint for a new economy[M].Sebastopol:O’Reilly Media,Inc.,2015.
|
| [7] |
Kishigami J,Fujimura S,Watanabe H,et al.The blockchain-based digital content distribution system[C]//Proceedings of the 2015 IEEE Fifth International Conference on Big Data and Cloud Computing (BD Cloud).Dalian:IEEE,2015:187–190.
|
| [8] |
Yasaweerasinghelage R,Staples M,Weber I.Predicting latency of blockchain-based systems using architectural modelling and simulation[C]//Proceedings of the 2017 IEEE International Conference on Software Architecture (ICSA).Gothenburg:IEEE,2017:253–256.
|
| [9] |
Alqassem I,Svetinovic D.Towards reference architecture for cryptocurrencies:Bitcoin architectural analysis[C]//Proceedings of the 2014 IEEE International Conference on Internet of Things (iThings),and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber,Physical and Social Computing (CPSCom).Taipei:IEEE,2014:436–443.
|
| [10] |
Lundqvist T,Blanche A D,Andersson H R H.Thing-to-thing electricity micro payments using blockchain technology[C]//Proceedings of the 2017 Global Internet of Things Summit(GIoTS).Geneva:IEEE,2017:1–6.
|
| [11] |
Zheng Shu Wen.Credit model based on P2P electronic cash system bitcoin[D].Shanghai:Shanghai Jiao Tong University,2012. 郑书雯.P2P网络基于Bitcoin虚拟货币的信用策略[D].上海:上海交通大学,2012. |
| [12] |
Nakamoto S.Bitcoin:A peer-to-peer electronic cash system[EB/OL].(2008-10-31)[2017-04-20]. https://nakamotoinstitute.org/bitcoin.
|
| [13] |
Yuan Yong,Wang Feiyue. Blockchain:The state of the Art and future trends[J]. Acta Automatica Sinica, 2016, 42(4): 481-494. [袁勇,王飞跃. 区块链技术发展现状与展望[J]. 自动化学报, 2016, 42(4): 481-494. DOI:10.16383/j.aas.2016.c160158] |
| [14] |
Antonopoulos A M.Mastering bitcoin:Unlocking digital cryptocurrencies[M].Sebastopol:O’Reilly Media Inc,2014.
|
| [15] |
Min Xinping,Li Qingzhong,Liu Lei,et al.A permissioned blockchain framework for supporting instant transaction and dynamic block size[C]//Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA.Tianjin:IEEE,2016:90–96.
|
| [16] |
谭磊,陈刚.区块链2.0[M].北京:电子工业出版社,2015.
|
| [17] |
He Pu,Yu Ge,Zhang Yanfeng,et al. Survey on blockchain and its application prospect[J]. Computer Science, 2017, 44(4): 1-7. [何蒲,于戈,张岩峰,等. 区块链技术与应用前瞻综述[J]. 计算机科学, 2017, 44(4): 1-7. DOI:10.11896/j.issn.1002-137X.2017.04.001] |
 2018, Vol. 50
2018, Vol. 50


