腐蚀是引发油气管道泄漏的最主要的原因，目前石化行业普遍面临金属管道因腐蚀造成的内壁减薄问题，对于地面以上的管道可以采用涡流检测^[1]、超声波定点测厚^[2]等技术进行检测。然而上述技术无法实现对埋地管道或者海底管道的检测。此外，随着完整性管理概念的深入，传统的离线检测技术必然会被长期在线监测技术所替代。

基于直流电位降法的（direct current potential drop，DCPD）的场指纹技术（field signature method，FSM）属于一种高效的长期在线的金属管道壁厚监测技术，可以用于监测埋地管道、海底管道和普通地面上的工业管线以及桥梁结构安全等^[3–6]。FSM在国外已经使用了近30年，而国内从21世纪初也陆续引进了FSM技术^[7–8]。相对于传统的检测技术，FSM具有很多优点：属于非侵入式的无损检测技术^[9]，被测原件不存在损耗问题，使用寿命长^[10]，灵敏度高于一般的检测手段^[11]，适用温度范围广，可以在–20～500 ℃的范围内工作。

图1(Fig. 1)

图1 埋地FSM系统 Fig. 1 Underground FSM system

图1为一个实际埋地管道的FSM系统，其工作原理如下^[12]：

在被测管道的外壁按照一定规则安装测量电极矩阵，接上信号测量电缆;然后在被测管道的两端施加直流激励电流，管道内壁的厚度情况会影响测量电极间的电位降信号，因此可以通过分析被测管道壁厚减薄前后的电压差来分析壁厚损失情况。在实际应用中，为了降低背景噪声等对电压信号检测的影响，还在FSM系统中引入了参考板，参考板置于管道外壁，通过电流激励电缆与被测管道串联。最后再在管道探针区域浇灌环氧树脂，包裹防护层。2个相邻探针间的管道金属块可以等效成1个电阻，因此整个FSM系统可以等效成1个电阻模型，如图2所示。

被测区域的壁厚损失程度可以用指纹系数（fingerprint coefficient， $FC$ ）来评判：

式中： $V_i \left( {{t_{0}}} \right)$ 、 $V_i\left( {{t_x}} \right)$ 为电极对 $i$ 在 ${{t_0}}$ 和 ${{t_x}}$ 时刻的电压； $V_{\rm ref}\left( {{t_0}} \right)$ 、 $V_{\rm ref}\left( {{t_{x}}} \right)$ 为标准电极对在 ${{t_{0}}}$ 和 ${{t_{x}}}$ 时刻的电压。

由 $FC$ 值可以得到管道的壁厚（wall thickness）计算公式：

式中， $WT\left( {{t_x}} \right)$ 为当前被测管道的壁厚， $WT\left( {{t_0}} \right)$ 原始管道壁厚。

图2(Fig. 2)

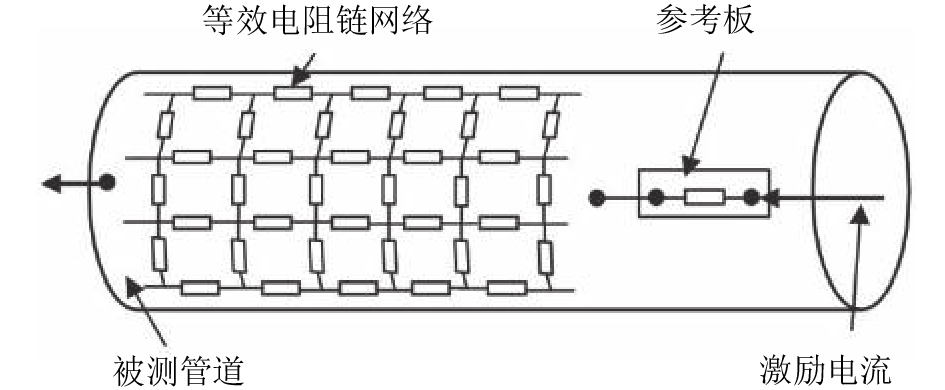图2 FSM等效电阻模型 Fig. 2 Equivalent resistor network of FSM

1）测数据极易受系统漂移的干扰。

由式（1）可知，在FSM系统长期服役期间，每次测量得到的电压值都必须与系统安装之初测量得到的原始电压值进行比值运算，而作为长期在线监测系统，随着元器件老化、被测环境改变等，仪器系统必然会发生各种漂移问题，而这势必会干扰FSM最终的测量结果。

2）励电流大，电源激励模块易损坏。

由于被测金属管道为良好导体，其等效电阻的电阻值极低，在被测管道两端施加数十安培的直流激励电流，探针间的电压值也只有几十微伏，为了提高被测电压的信噪比，直流激励电流的幅值应越大越好，目前FSM系统最大的激励电流已经达到了350 A^[13]，但是长期高幅值的工作电流极易造成激励电流模块损坏，一般一至两年就需要更换1次激励电流模块，增加了使用成本，也降低了系统的可靠性。

3）能测量相对壁厚减薄。

由式（2）可知，FSM技术只能够测量相对壁厚减薄量，因此系统安装之初必须对被测管道的原始壁厚进行精确测量。由于FSM技术的测量探针区域得到了良好的保护，且测量探头不存在损耗问题，因此FSM的管道部分一般都不会损坏失效。相反，其硬件电气系统发生故障的概率相对较高，在仪器发生故障之后，尤其是对电路系统进行整体更换之后，需要采集被测管道的实际厚度作为新的初始壁厚值。但是对于埋地管道或者海底管道而言，这项工作是极难完成的。

4）考板与管道的温度差会极大地影响壁厚监测的准确性。

参考板与被测管道之间填充有绝缘层，因此两者之间往往会出现较大的温度差异，导致最终的壁厚损失检测结果为负值，因此一定要通过温度修正降低温差引起的不利影响。对于埋地管道和海底管道而言，一旦温度传感器损坏，将是极难修复的，图3所示为中海油番禺油田海底管道某FSM的壁厚损失监测结果，由于其温度传感器失效，导致壁厚损失出现了大量的负值。

图3(Fig. 3)

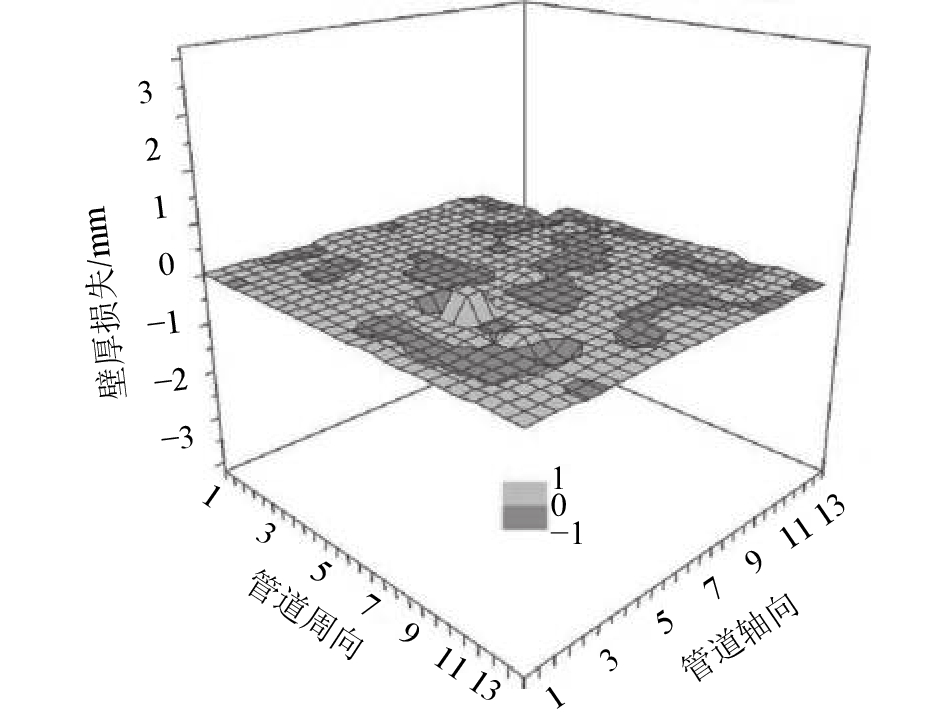图3 番禺油田FSM壁厚损失监测数据 Fig. 3 Metal loss of FSM in panyu oil field

图4(Fig. 4)

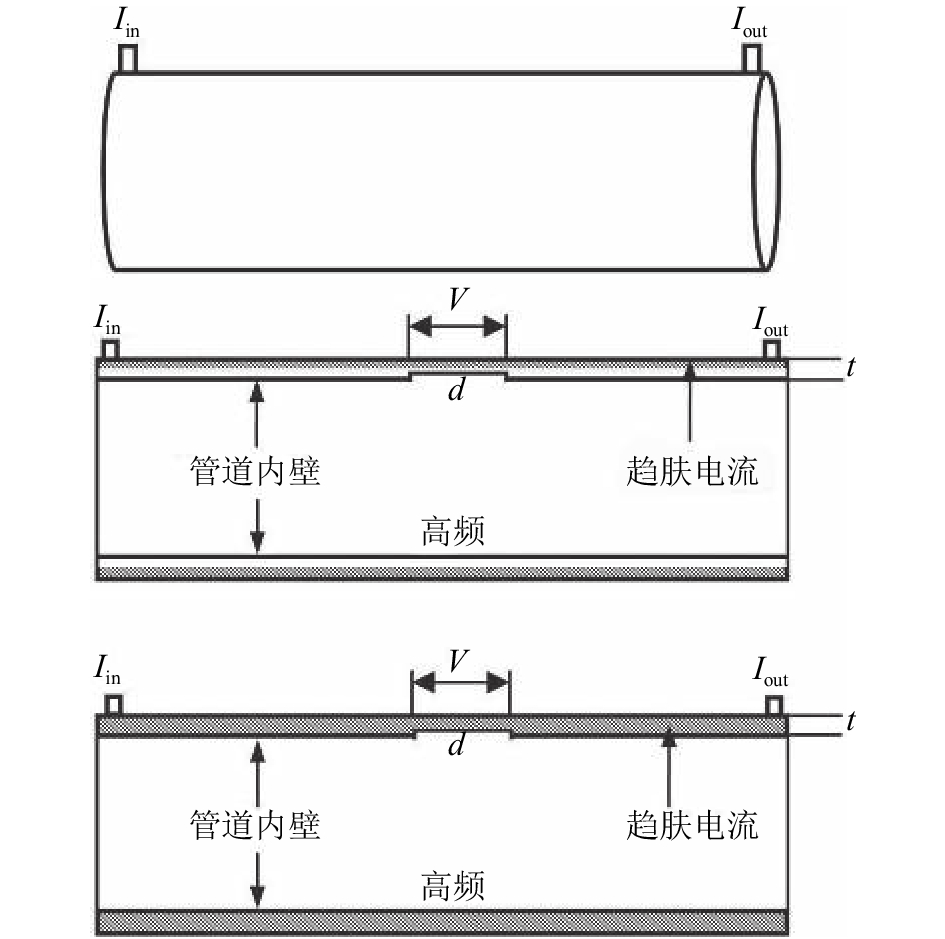图4 金属管道趋肤电流分布，Iin和Iout为电流注入点 Fig. 4 Skin current distribution of metal pipeline，and Iin and Ioutare current injection points

顾名思义，交流FSM的激励电流为交流激励电流，其本质为交流电位降法。该技术最初被用于检测金属件的外表面缺陷。如图4所示，在金属管道的两端布置电流激励电极，由于交流电位降法存在趋肤效应（skin effect），即被测金属件施加高频交流激励电流的时候，被测金属件中的电流将大量存在于金属表面浅层中，如图5所示。趋肤深度的计算公式为^[14]：

式中， ${\mu _0}$ 为真空磁导率， ${\mu _{\rm r}}$ 为被测件金属材料的相对磁导率， $\sigma $ 为被测件金属材料的电导率， $f$ 为激励电流的频率。由于趋肤效应的存在，交流电位降法只需要施加幅值很小的激励电流即可获得较高强度的测量电压，这也是交流电位降法相对于直流电位降法最大的优点之一。

图5(Fig. 5)

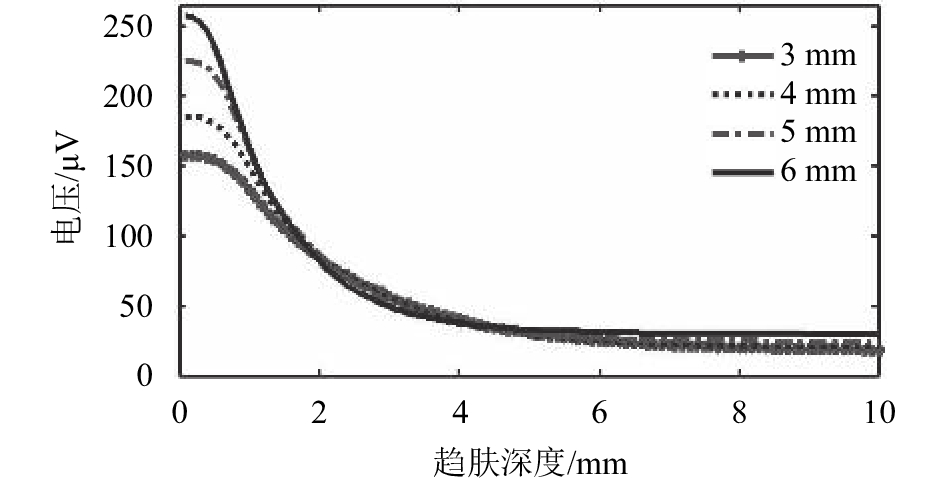图5 不同深度缺陷对应的电压曲线 Fig. 5 Voltage Curves of different defect

由式（3）可知，对金属管道施加高频交流激励电流，趋肤电流只存在于被测管道的外壁；对金属管道施加低频交流激励电流时，随着趋肤深度的增加，电流可以渗透整个管壁。因此，当激励电流的频率较高时，趋肤深度较低，测量电极之间的等效电阻的阻抗较大，测量得到的电压值较高；随着频率的降低，趋肤深度逐渐增加，测量电极间等效电阻的阻抗减小，测量得到的电压值逐渐降低。当趋肤深度等于被测管道的壁厚时，随着激励电流频率的降低，受限于壁厚尺寸，趋肤深度将不再降低，测量电极之间的电压值将保持不变。这种通过控制趋肤电流的深度，逐层检测管道内壁缺陷的技术可以形象地比作是“分层扫描”技术。

在COMSOL软件^[15]中建立一个如图5所示的模型，管壁厚度为10 mm，外径为150 mm，金属材料的相对电导率为5.5×10⁶ s/m，相对磁导率为110，在管道外壁布置两个测量电极，电极的间距为50 mm。在该电极对对应的管道内壁上依次模拟宽度为50 mm，深度为3 、4 、5和6 mm的缺陷。根据公式（3）计算出从0.1 mm到11 mm、间隔为0.1 mm的趋肤深度对应的激励电流频率，依次向管道输入相应的频率从高到低的110种激励电流，记录测量电极间的电压，电压曲线如图5所示。

图6(Fig. 6)

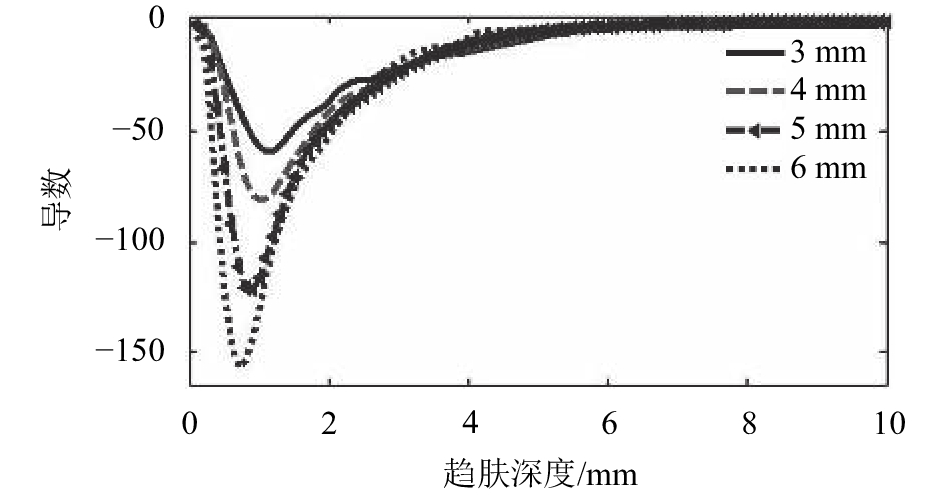图6 不同缺陷电压的导数曲线 Fig. 6 Derivative curve of voltage of defects

如图5所示，随着激励电流频率的降低，电压值逐渐降低，但是不同深度的缺陷有不同的电压曲线。前文中提到，由于趋肤效应的存在，在高频的时候电流将主要集中在靠近金属外壁的浅层里，但并非所有的电流都会存在于靠近金属外壁的浅层里。由图5可知，在高频的时候，缺陷仍旧会影响测量电极间的电压，而且缺陷深度越深，高频时的电压越高。但是在低频的时候，不同缺陷的电压都会逐渐趋于稳定，而且彼此间的电压差要远远小于高频时的电压差。

由于随着激励电流频率的降低，电压值将逐渐减小并趋于稳定，因此如果对电压曲线进行求导，得到的一系列导数将会从负数逐渐增加到零，因此必然会出现一个极值点（最小值）。图6所示为不同深度的缺陷的电压导数曲线，由该图可知各个电压的导数曲线的确是从负数逐渐增大到零并趋于稳定，并且不同深度的缺陷有不同的极值点，缺陷深度越深其导数的极值点越小，如表1所示。因此，导数的极值点可以用于求解缺陷的深度。但是由于目前还没有准确的数学公式求解不同频率下电流的分布情况，因此也无法计算不同频率对应的电压值。但是随着有限元仿真技术的发展，可以通过仿真来建立缺陷深度与电压导数极值点的关系式。文献[4]既是利用有限元仿真建立了针对小腐蚀坑的腐蚀数据库，利用直流FSM技术测量得到了主辅电压，通过匹配算法计算得到了小腐蚀坑的深度，取得了较好的效果。

图7(Fig. 7)

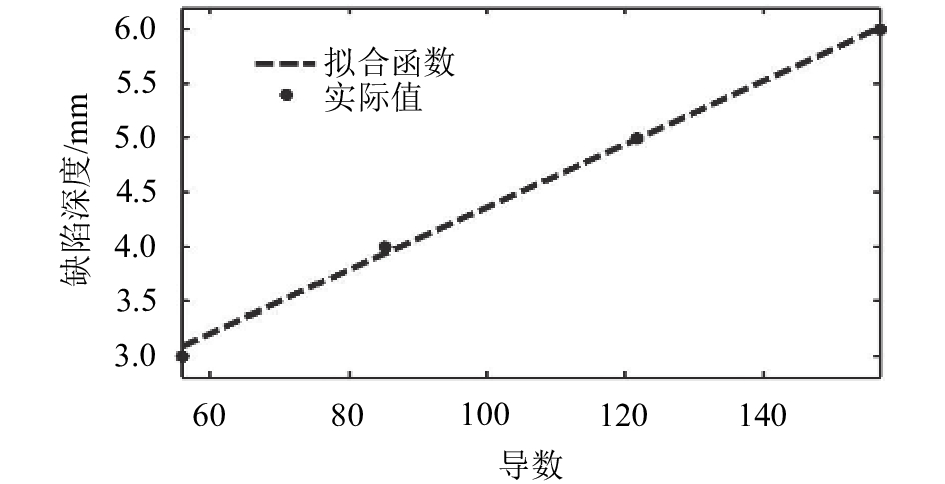图7 缺陷深度与导数拟合曲线 Fig. 7 Fitted line of defect depth and absolute value of extreme of derivative of voltage curve

表1(Tab. 1)

表1 不同缺陷电压导数的极值 Tab. 1 Extreme value of voltage derivative of defects

表1 不同缺陷电压导数的极值 Tab. 1 Extreme value of voltage derivative of defects 缺陷深度/mm 3 4 5 6 极值 –56.12 –85.31 –121.70 –156.96

由于利用MATLAB做线性拟合时要求拟合数据为非负数，因此本文用极值的绝对值来拟合求解缺陷深度与极值的关系式，结果如图7所示。

拟合得到的缺陷深度与导数极值的关系式为：

其中d为缺陷深度，x为电压曲线导数极值的绝对值。

由式（4）可知，这种基于多频率电位降法的缺陷深度检测技术，不再需要将测得的电压与原始电压进行比较，而仅仅只是将电压值进行求导。仪器发生漂移是一个缓慢的过程，在一次测量过程中仪器的各项性能可认为是稳定的，因此MACFSM消除了系统漂移对测量造成的不利影响。同时由式（4）可知，MACFSM也不需将被测对象的原始壁厚纳入计算。

选取了一段外径为522 mm，壁厚为10 mm、材质为20^#碳钢的金属管道作为研究对象。在管道外壁焊接测量电极矩阵，轴向上每行布置8个电极，探针间距为40 mm；圆周方向上每圈布置30电极，探针间距为54 mm。在管道某对测量电极所对应的管道内壁加工一个槽状缺陷，缺陷宽度和长度均为50 mm，缺陷深度为3.5 mm。测试系统采用美国斯坦福生产的SR850锁相微弱信号测试仪，利用SR850激发出频率可控的交流信号，通过美国斯坦福生产的SR560放大滤波之后产生0.1 A的交流激励信号，施加于测量区域两端的电极。以0.1 mm的趋肤深度为起点，按照0.1 mm的趋肤深度间距，依次向被测管道注入频率从高到低的100个激励信号，测量得到的信号电压如图8所示。

图8(Fig. 8)

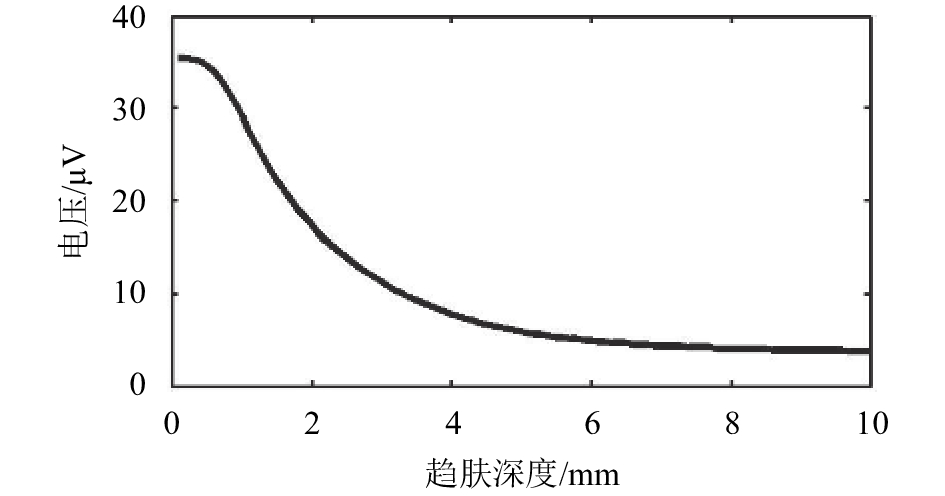图8 缺陷测量电压曲线 Fig. 8 Voltage curve of defects

图9(Fig. 9)

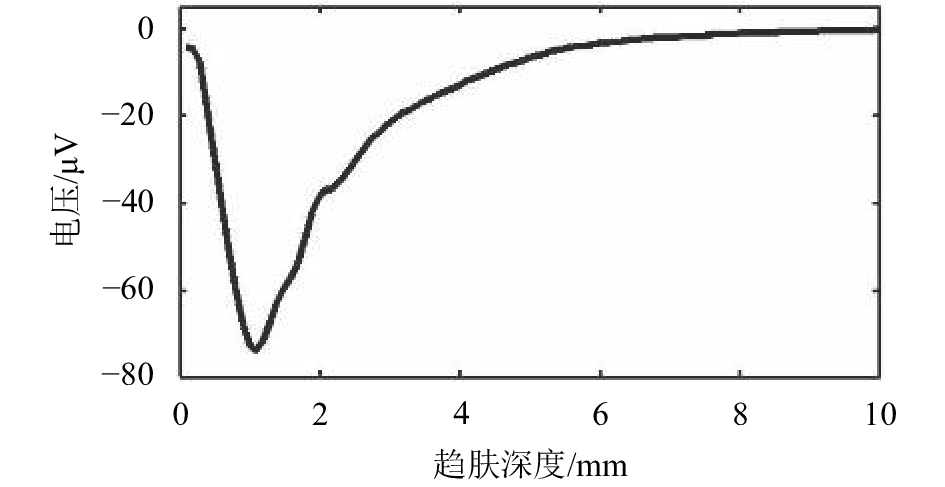图9 缺陷电压的导数曲线 Fig. 9 Derivative curve of defect voltage

图9所示为缺陷电压的导数曲线，其导数的极值为–73.28。根据公式（4），利用导数极值的绝对值，求得缺陷的深度d=3.58 mm，也即是求解误差为0.08 mm，相对误差为2.29%。

在传统直流FSM技术的基础上，提出了一种多频交流FSM技术（MACFSM）。MACFSM不再设置参考板，无需采集原始电压数据，利用电压导数极值对缺陷深度进行求解，可直接求解被测管道的绝对壁厚损失，在保留传统直流FSM优点的基础上，很好地克服了传统FSM的不足，提高了作为长期在线监测技术的准确性和可靠性。