2. 华北水利水电大学 水利学院,河南 郑州 450046
2. School of Water Conservancy, North China Univ. of Water Resources and Electric Power, Zhengzhou 450046, China
河道堤防工程在防治洪水灾害方面具有重要作用,一旦堤防发生溃决,将会造成巨大的经济损失[1]。黄河下游共有120多个自然滩,面积约4 050 km2,占下游河道总面积的80%[2]。下游滩区不仅是近190万群众赖以生存的场所,同时也兼具行洪、蓄洪、沉沙的功能,因此洪水风险仍是滩区社会经济发展的潜在威胁[3]。据不完全统计,自新中国成立至2013年,黄河下游滩区遭受不同程度的洪水漫滩20余次,累计受灾887.2万人次,受淹耕地174.6万hm2,给滩区群众的生命和财产造成了灾难性损失[4]。尽管小浪底水库运用后黄河下游的防洪压力已大大减轻,但小花间产生的区间洪水仍无法控制,下游发生超过10 000 m3/s大洪水的风险依然存在[5];经过近10多年的蓄水拦沙运用,下游河道主槽过流能力已显著提高,但局部河段的平滩流量仍不到4 000 m3/s,“二级悬河”河段的洪水威胁依然严重[6–7]。当遭遇大洪水时,极易引发主槽两侧修建的生产堤发生溃决,产生漫滩洪水。因此开展黄河下游典型滩区的溃堤洪水演进模拟的研究仍是当前滩区治理中迫切需要解决的关键问题。
溃堤洪水是极为复杂的水流运动,溃堤洪水模拟的主要方法有模型试验与数值模拟两种[8]。近年国内外许多学者采用模型试验开展溃坝(堤)洪水的研究,取得了大量研究成果[9–12]。但这些研究一般将库区内初始水体视为静水,且不考虑滩槽实际形态。Roger等[13]采用物理模型试验研究了河道水流影响下的溃堤洪水演进过程。陆灵威等[1]通过物理模型试验模拟了溃堤后洪泛区内的洪水演进与河道内落水波的传播过程。但上述试验未考虑实际河道的平面形态、滩槽纵横比降等因素的影响。而数值模拟多侧重于数值解法与计算精度问题,被用来模拟堤坝溃决后的洪水演进过程及下游河床冲淤变化[13–16],而同时考虑主槽和滩区的溃堤洪水模型鲜有涉及。另外,也有一些学者同时采用模型试验与数值模拟研究溃坝(堤)洪水运动,并取得了丰富的研究成果[13,17]。
本文针对黄河下游夹河滩至高村河段的滩槽形态和地形特点,设计能够反映弯曲河槽形态、河道纵比降及滩区横比降影响的概化水槽模型,进而开展生产堤溃决后主槽与滩区内的洪水演进特性研究;同时建立相应的2维数学模型,并对数学模型中溃口内部边界的变化进行改进,实现内部开边界局部变化的精细模拟;利用验证后的模型精细模拟溃堤后漫滩洪水在滩区的演进过程及滩槽内水位、流速的变化特性,重点分析滩区不同糙率取值对洪水演进的影响。
1 概化模型试验近年来,受气候变化及人类活动的影响,黄河上游来水偏少,黄河下游洪水漫滩几率明显降低,但下游河道“槽高、滩低、堤根洼”的“二级悬河”形势依然严峻。2003年9~10月,黄河下游发生了严重秋汛,兰考东明滩区因蔡集工程生产堤决口出现大漫滩洪水,造成了严重的灾害,洪水淹没范围如图1(a)所示。
本次漫滩范围上起兰考黄河大堤桩号146+700,下至东明谢寨闸,黄河大堤偎水35 km,152个自然村被水围困,淹没面积27.75万亩[18]。作者依据黄河下游夹河滩至高村河段的河槽形态及兰考东明滩区的地形特点进行了概化水槽模型试验设计。黄河下游夹河滩至高村河段为典型的游荡型宽滩河段,该河段纵比降约为0.019%。兰考东明滩区位于该河段右侧,纵向长约32.5 km,横向最大宽度约12.0 km,纵横比为2.7∶1。滩面横比降约为1/2 000~1/3 000,河道横比降远大于纵比降。
1.1 模型设计综合考虑该研究河段的滩槽地形特点,依据相似原理进行了概化水槽模型设计,其平面布置如图1(b)所示。概化水槽模型全长18 m,宽度为8 m,包含了主槽、嫩滩、右侧滩区及生产堤。模型前池尺寸为8 m
 |
| 图1 2003年10月兰考东明滩区淹没范围及概化水槽模型平面布置与特征测点位置分布 Fig. 1 Inundated area on the Lankao-Dongming floodplain during the October 2003 flood and sketch of a physical model with the layout of measurement points |
概化水槽试验采用循环式供水系统,包括试验室地下水库、输水管路、模型前池、尾水池等,均可满足模型试验流量及退水要求。进口流量采用流量控制系统控制。利用变频水泵、E-MAG 电磁流量计、阀门及输水管道系统,实现地下水库水流循环输送。
概化水槽模型主要部分包括河槽与滩区,其中河槽由主槽和嫩滩组成。河槽与滩区之间设有一连续生产堤,堤宽约6 cm,在生产堤的第一个弯道顶端设有一个溃口口门,口门宽度为0.5 m。滩区初始条件为干河床,通过控制口门的突然开启塑造出溃堤洪水在滩区干河床上的演进过程,并引起主槽水位的变化。模型进口通过电磁流量计精确控制流量,模型出口通过尾门控制给定一个水位边界。由于实际生产堤溃决受土质、水位、流速等多种因素影响,溃堤位置及溃口宽度具有随意性,对溃堤水流的演进过程有直接影响。因此根据弯道水流运动特性,将溃口口门固定选取在弯道顶冲部位,且每组试验溃口口门宽度保持不变。
1.2 试验方案1)试验过程
漫滩水流试验在概化水槽模型中进行,通过控制生产堤高度保证河槽内水位不发生漫顶,水流只能通过预留的溃口口门流入滩区。试验进行初始阶段,生产堤溃口口门关闭,水流仅在河槽内流动,通过调节电磁流量计控制进口流量稳定,同时保证下游尾门开度始终不变,河槽内水流逐渐趋于恒定;待水流最终稳定后,瞬间打开预留口门,形成溃堤洪水,同时引起滩槽内的水位变化。经验证,该试验流程可保证水槽试验的重复性,极大提高试验成果的可信度。
2)试验方案
滩地阻力是由洪水漫滩引起的,由于人类活动的影响,黄河下游滩区地貌种类较多,涉及耕地、村庄及避水台、道路、生产堤及渠堤、控导护滩工程等,直接影响滩区洪水的演进过程。因此试验中考虑到滩区阻力的影响,对滩区进行了加糙处理。由于黄河下游滩区植被种类多,且阻水建筑物分布复杂,滩地阻力不易确定。故本次试验滩区糙率采用统一数值。试验采用草垫加糙的方法,所用草垫为塑料草,草垫上花(槽)间距为1 cm,花开度(槽宽)为0.8 cm,花高(槽深)1 cm。如图2所示。研究表明该型草垫加糙后,糙率能达到0.028 2~0.062 1[19]。
为了分析生产堤瞬间溃决后,水流量级及滩区阻力对主槽内水位变化特性及溃堤水流在滩区演进过程的影响,水槽试验设计了6组试验工况。各工况具体的进口流量、主槽出口水位及滩区植被情况见表1。
| 表1 概化水槽模型试验工况 Tab. 1 Flow conditions used in different experimental scenarios |
 |
 |
| 图2 滩区加糙草垫照片 Fig. 2 Photos showing grass cushion on the floodplain region |
3)水力要素测量
流量采用电磁流量计配合变频器和电子阀门实现自动控制;概化模型试验测量采用水位自动跟踪仪记录由于生产堤溃决引起主槽和滩区非恒定流的水位变化过程,同时配合水位测针记录稳定时的水位;漫滩洪水演进速度采用秒表人工计时。另外还通过高分辨率摄像机全程跟踪溃堤后漫滩洪水在滩区的演进过程。
2 数学模型滩区洪水演进模拟的计算精度一般取决于阻力、挟沙力的计算、合适的控制方程及数值求解方法等[15]。作者采用三角形非结构网格,建立溃堤洪水流动的2维有限体积算法模型。该模型[15]采用Roe-MUSCL格式及时间方向上的预测校正格式,使模型具有时空2阶计算精度,同时采用非常有效的干湿界面处理方法。然后利用模型试验成果对该模型进行验证,最后模拟滩区不同糙率条件下溃堤洪水的传播过程,研究滩区不同糙率取值对计算结果的影响。
2.1 控制方程溃堤洪水在河流、渠道及洪泛区内的演进,一般可用2维浅水控制方程来描述,但通常必须满足以下假定,如静水压力分布、自由水面、垂向加速度较小及河床坡降较小等。水深平均的2维浅水流动控制方程由连续方程及
| $\frac{\partial }{{\partial t}}\left( h \right) + \frac{\partial }{{\partial x}}\left( {hu} \right) + \frac{\partial }{{\partial y}}\left( {hv} \right) = {q_{\rm s}}$ | (1) |
| $\begin{aligned} & \frac{\partial }{{\partial t}}(hu) + \frac{\partial }{{\partial x}}(h{u^2} + \frac{1}{2}g{h^2}) + \frac{\partial }{{\partial y}}(huv) = \\&\;\;\quad\quad\quad h{v_{\rm t}}\left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) + gh\left( {{S_{{\rm b}x}} - {S_{{\rm f}x}}} \right)\end{aligned} $ | (2) |
| $\begin{aligned} & \frac{\partial }{{\partial t}}(hv) + \frac{\partial }{{\partial x}}(huv) + \frac{\partial }{{\partial y}}(h{v^2} + \frac{1}{2}g{h^2}) = \\& \;\;\quad\quad\quad h{v_{\rm t}}\left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) + gh\left( {{S_{{\rm b}y}} - {S_{{\rm f}y}}} \right)\end{aligned} $ | (3) |
式中:
1)数值方法
模型采用三角形非结构网格及单元中心格式的有限体积法,具有良好的守恒性且能够较好处理陆地及给定流量过程的边界条件。该格式将所有变量的值存储于单元中心,相邻两个单元的公共面作为控制体的一个计算界面。在有限体积法中,沿水深平均的2维浅水方程在每一个控制单元内离散,能较好地保证质量与动量守恒。采用效率较高的近似Riemann 解来计算通过界面的法向水流通量,该格式不仅能准确捕获激波界面,还可通过引入合适的通量限制器,消除水跃等间断流附近的数值振荡。
模型采用计算精度较高的Roe-MUSCL格式计算界面水流通量;采用分片线性逼近的MUSCL 格式,进行状态变量的空间重构。同时,为了保证计算格式稳定,模型采用Roe与Baines提出的minmod 函数作为限制函数,使得Roe-MUSCL 格式具有空间2阶精度[15]。源项主要包括床面底坡项与摩阻项等,在非结构三角形网格中,可根据已知3个顶点的坐标及高程求出该网格上的平面函数及相应底坡项;采用较稳定的半隐式计算格式处理摩阻项。此外模型还采用常见的预测–校正格式Runge-Kutta 方法获得2阶精度的时间离散格式。
2)干湿边界处理
在模拟溃堤洪水流动时,滩面初始为干河床,溃堤后产生的漫滩洪水在干河床上演进。由于滩区水位变化,使得实际计算区域不断变化。为准确模拟这种动边界过程,模型引入最小水深来判断单元干湿,同时借鉴并改进了前人提出的规则计算网格中的干湿处理方法,使其能适用于非结构三角形网格。该方法的具体步骤可参见文献[15]。改进后的方法不仅考虑了界面干湿处理时的水流流向,而且可将无效干单元暂时从计算区域中剔除,有利于提高计算效率。
3)局部变化的内部开边界处理
数学模型需要模拟生产堤溃决前,水流仅在河槽内流动;当河槽内水流稳定后,生产堤在指定位置发生瞬间溃堤。因此口门开启的时间、位置及宽度等局部内部边界变化的处理尤为重要,直接影响计算成果的可信度。溃堤水流实际是一种边界与水流都在不断变化的非恒定流动,溃口口门的高程、宽度及其两侧水头差都在随时间改变。这是一个内部开边界水流动态变化的过程,考虑到水流运动与阻力密切相关,阻力大小通常用糙率表示,本文试图将口门处的水流变化用糙率的变化来间接反映。在冲积河流中,河床糙率随时间和空间位置不断变化。其变化原因,一方面是由于断面形态和泥沙粒径发生了调整,导致横断面上的肤面阻力发生变化;另一方面由于水深(或单宽流量)发生变化,引起床面沙波形态发生调整,从而导致河床形态阻力发生变化。因此,糙率是水流与河床相互作用过程中,反映河道边界粗糙程度、河床形态、含沙量浓度等所有影响水流阻力因素的综合系数。
解决生产堤溃口口门瞬间开启的基本思路为基于边界阻力的时间、空间控制,实现对溃口口门处流速随时空变化的模拟。分析水力学谢齐公式可知:流速与糙率成反比,即当糙率趋于无穷大时,流速趋向为零。基于此,在2维数学模型计算程序中加入局部阻力变化模块,通过模块中的糙率变化来实现溃口口门处流速的变化。具体过程为:在生产堤溃决前,将生产堤溃口口门处局部区域的糙率设置为极大值,形成的局部大阻力确保该区域边界不过水,即水流不会通过口门流入滩区;待河槽内水流稳定时,将口门区糙率减小至正常值,在该区域内形成生产堤溃决,起到闸门瞬间开启的作用。采用局部阻力变化模块可以准确改变局部过流状态,迅速形成新的过流内部开边界,可应用于堤坝溃决及河道滩区分洪的数值模拟中。
2.3 模型验证采用所建2维数学模型计算了无草皮条件下不同量级洪水在溃堤发生后主槽的水位变化及滩区水流的演进过程,并与概化模型试验结果进行了对比。图3给出了EXP-3工况下,数值模拟与模型试验所得主槽与滩区内各测点水位的变化过程。从图3中可知,在生产堤溃口发生至水流最终达到稳定的整个过程中,主槽与滩区内各测点的计算水位变化过程总体与模型试验结果吻合较好。验证结果表明该模型能够较好的模拟生产堤溃决产生的溃堤洪水的演进过程。
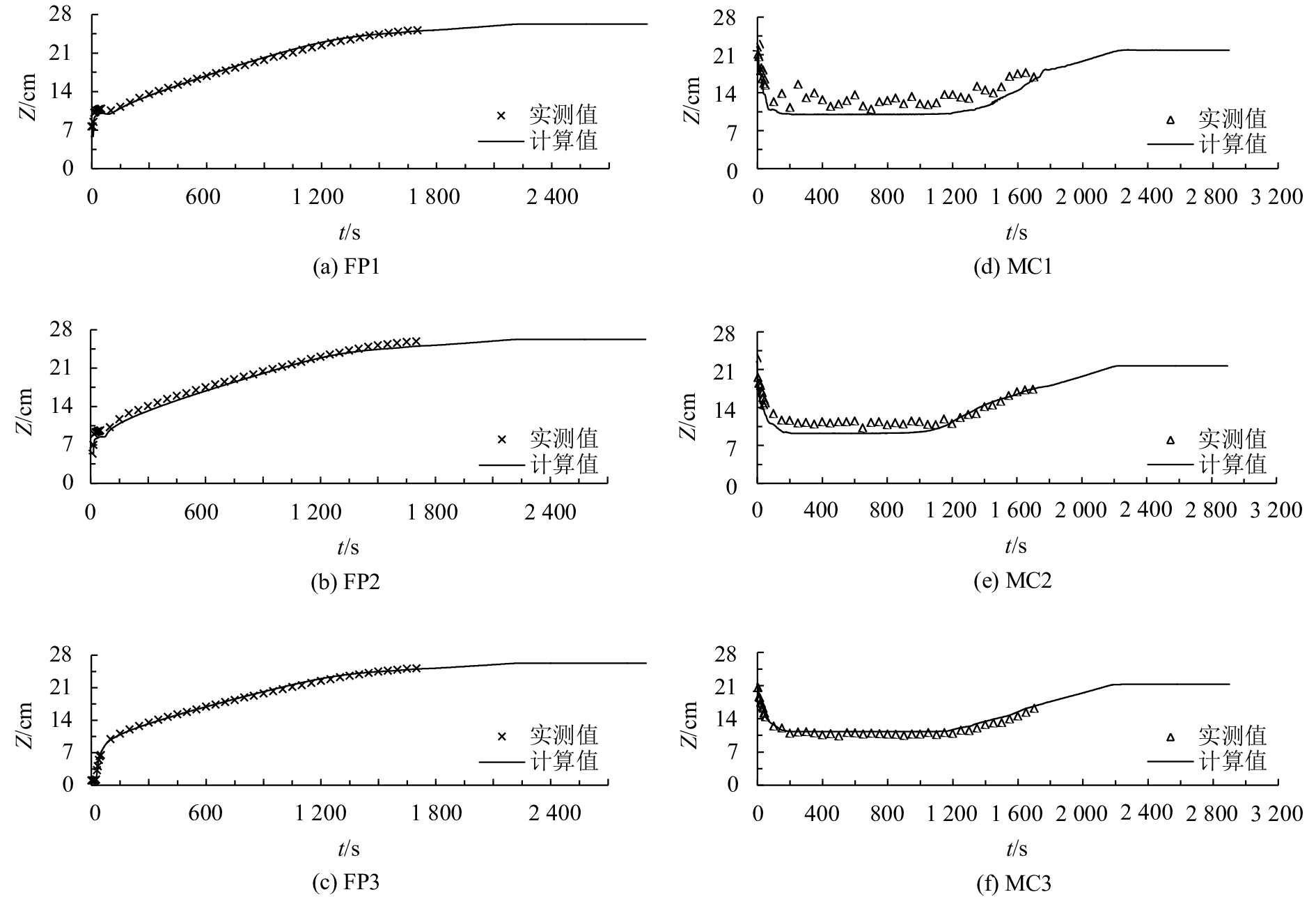 |
| 图3 EXP-3工况下各测点计算与实测水位过程比较 Fig. 3 Comparisons between the calculated and measured water levels at different sites in EXP-3 |
图4给出了EXP-3工况下,生产堤溃决后2 s和10 s时溃堤水流的水深流速分布。从图4中可以看到生产堤溃决后溃堤洪水波前的形状及其演进变化过程,以及溃堤水流进滩引起的主槽内水位与流速的变化。从图中还可以看到,该溃堤水流不同于静水条件下溃堤水流在底坡为零的滩区的演进过程。由于受滩区横比降远大于纵比降的影响,溃堤后漫滩水流沿横向演进速率大于纵向演进速率。
 |
| 图4 EXP-3工况溃堤洪水流速场变化过程 Fig. 4 Distributions of water depths and flow velocities in EXP-3 at different times |
3 成果及分析 3.1 试验成果及分析
选择一组具有代表性的试验成果(EXP-2)进行重点分析,其进口流量为34 L/s,下边界水位为24.39 cm。为了分析试验中滩槽内的水位变化过程,在主槽内布设5个水位测针(C1~C5)用于测量主槽水流稳定后的水位,另外在主槽进口、溃口口门附近及主槽出口设有3台水位自动跟踪仪(1#、2#、6#)用于全程记录主槽内特征点(MC1~MC3)的水位变化过程;同时在滩区内布设3台水位自动跟踪仪(3#~5#)用于记录生产堤溃决后滩区内特征点(FP1~FP3)的水位变化过程,见图1(b)。利用秒表人工记录溃堤后漫滩水流波前到达滩区11个特征点(FP1~FP3、A~H)的时间。
1)滩槽水位变化分析
图5(a)给出了EXP-2工况下主槽内测点MC1~MC3的水位变化过程。分析可知:主槽内水位的变化过程主要包括4个阶段,生产堤溃决前,主槽内水流基本达到稳定,水位较为平缓,水面纵比降为0.093%。生产堤溃决后,水流进滩导致主槽内水位迅速降低,溃口口门附近MC2点处水位下降2.20 cm,MC1与MC3点处水位分别下降了2.20 cm和1.94 cm;待进滩流量基本稳定后,主槽内水位在一定时段(1 500 s)内保持稳定,该阶段持续时间与进口流量成反比。随着滩区水位升高,溃口两侧滩槽水位差减小,使得进滩流量也随之减少,导致主槽内水位逐渐增加,直至主槽内水位升至与溃口前相同,主槽内水流再次趋于稳定。
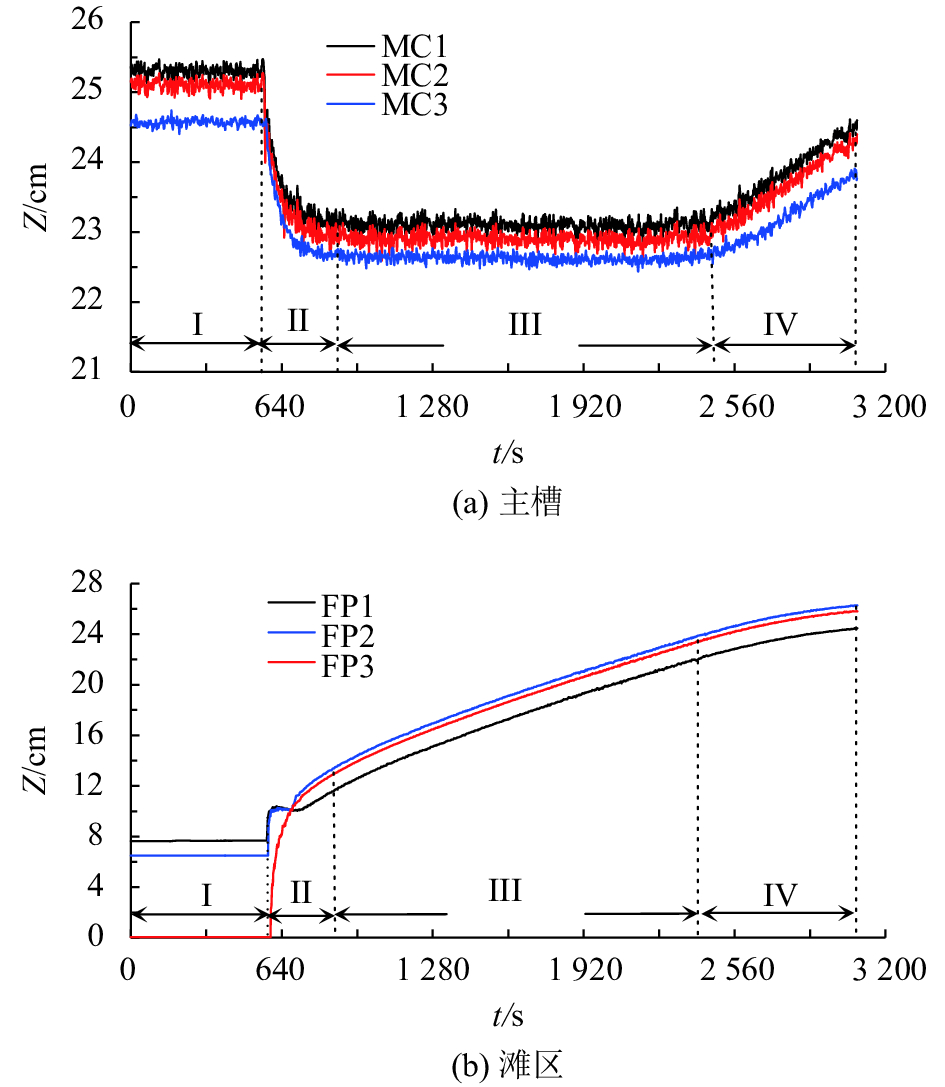 |
| 图5 EXP-2工况下各测点水位变化过程 Fig. 5 Measured water level hydrographs at different observation sites in EXP-2 |
溃堤发生前,滩区为干河床;溃堤发生后,主槽内水流迅速向滩区扩散,使得滩区内水位迅速抬升。滩区内水位变化经历4个阶段,见图5(b)。由图5可知:各测点起始读数为相应滩面高程,溃堤发生后,主槽内水流以扩散波的形式通过溃口口门,依次演进至测点FP1~FP3,使得各点水位迅速抬升。相应主槽区的水位降落,发生落水波,滩区内水位则呈上升趋势,发生涨水波。生产堤溃决前,溃口两侧水位落差最大;溃堤发生后,主槽水流迅速向滩区演进,滩区内水位随之升高,溃口附近主槽内水位迅速降低,溃口两侧水位落差相应减小,待主槽内水位达到稳定后,进滩流量基本保持不变,此后一段时间内,各测点水位升高的速率维持不变,水位继续升高;当滩区内水位的抬升影响到紧邻溃口滩面处的水流时,溃口两侧水位落差将进一步减小,使得各测点水位升高的速率也随之减缓,直至溃口两侧水位基本相同时,滩区不再进流,滩区内各测点水位趋于稳定。EXP-2工况下,溃堤后8.31 s,漫滩水流传播至FP1点,该处水位迅速升高,水位增加速率约为0.23 cm/s,在后续120 s内该处水位基本维持不变,直到受下边界反射后的水流向上游壅高影响到FP1点时,该处水位将继续升高,此后水位增加速率明显减缓,约为0.006 cm/s,进入第4阶段后,水位增加速率进一步减小,直至水位基本稳定。FP2点的水位变化过程与FP1点类似。由于FP3点位置的特殊性,在第二阶段其水位始终在升高,平均增加速率约为0.012 cm/s。
2)滩区洪水演进分析
溃堤发生后,溃口两侧水位差使得漫滩水流以溃堤波的形式在滩区传播。分析EXP-2工况下溃堤洪水的演进过程可知,溃堤波前到达时间与滩区地形及距溃口的距离关系密切。在溃堤后8.31 s内,溃堤波前到达的时间以溃口为中心近似呈对称式分布,波前到达各点的时间与距溃口的距离有关,距溃口的距离相同时,溃堤波沿溃口轴线(与溃口口门近似垂直的中轴线)方向到达时间较短,这与滩区较大的横比降有关,该时段内溃堤涨水波的传播速率约为0.6 m/s。在8.31 s以后,已到达FP1测点的溃堤波前顺模型右侧边墙继续传播,受滩面纵、横比降的影响,溃堤波前顺边墙向下游传播的速率明显较大,约为0.54 m/s,向上游传播的速率约为0.08 m/s。此时波前到达各点的时间不仅与距溃口的距离有关,还与滩区地形有较大关系,此时距溃口的距离相同时,溃堤波前到达的时间相差很大。在溃堤后24.53 s时,溃堤波前到达滩区最低处FP3测点,然后水流分别向左侧及上游扩散。
试验过程中记录了溃堤后滩区内形成的涨水波波前到达滩区各特征点的时间,受滩区纵比降及横比降差异的影响,溃堤洪水依次演进至各特征点的次序为FP1→FP2→FP3→C→D→B→E→F→A→G→H。波前到达各特征点的时间均随主槽进流流量的增大而缩短。FP1测点基本正对溃口位置,受滩区横比降的影响,溃堤漫滩洪水最快演进至该点,EXP-2工况下到达时间为8.31 s。
3.2 数值模拟成果及分析受人类活动的影响,滩地上存在各类植被与阻水建筑物,直接影响滩区洪水的演进过程。黄河下游滩区植被种类多,阻水建筑物分布复杂,故不易确定滩地阻力[20–21]。本次计算过程中直接采用平均综合糙率来反映滩区地物地貌对洪水演进的影响。计算采用的滩区当量糙率
伴随生产堤发生溃决,主槽内的水流通过溃口口门进入滩区,导致主槽内形成洪水波。图6(a)给出了
图6(b)给出了
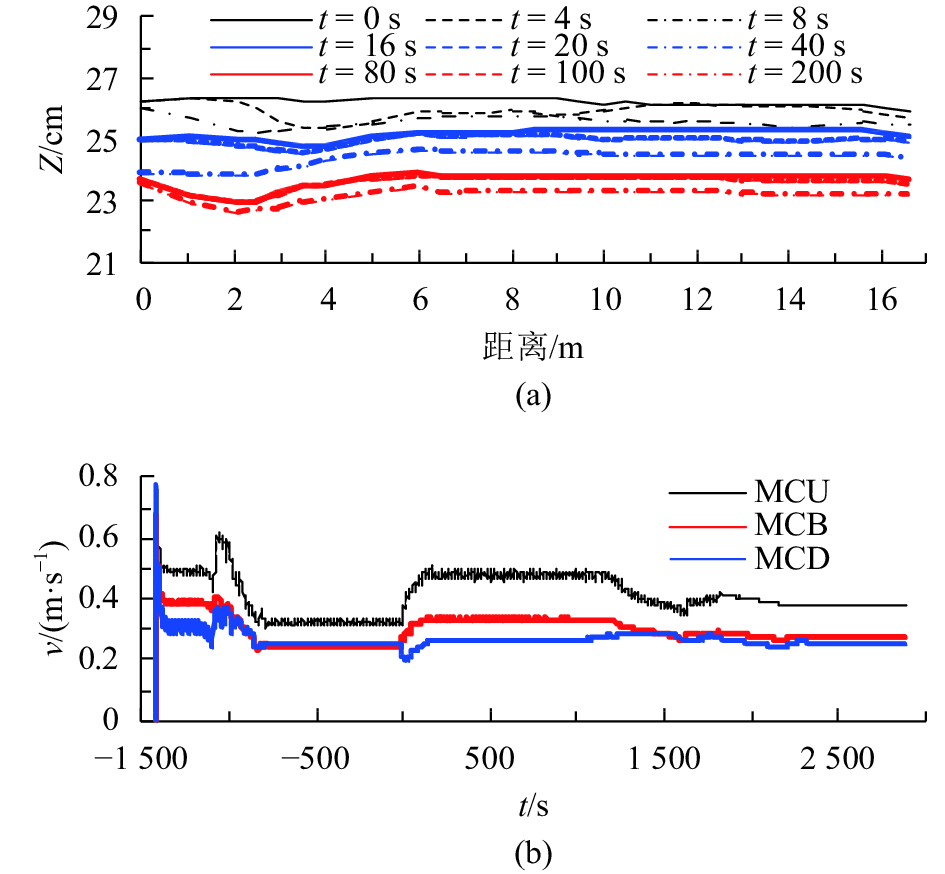 |
| 图6 主槽内沿程水位变化过程及溃口附近流速变化过程 Fig. 6 Temporal variations in the main-channel water level profile and flow velocity near the dike-breach site |
 |
| 图7 溃口两侧滩槽水位差及进滩流量的变化过程 Fig. 7 Temporal variations in the water level difference at two sides of dike breach and the discharge through breach |
3.2.2 进滩流量变化
溃口流量是溃堤洪水过程中十分关注的问题。通过分析数值模拟成果,统计了不同进流条件下,通过溃口口门进入滩区的流量变化过程。
图8给出了滩区不同糙率取值条件下,生产堤溃决后各流量级洪水的进滩流量变化过程。分析可知,生产堤溃决前,进滩流量为零。生产堤溃决后,进滩流量呈先减小,后稳定,再减小,最后趋向为零的变化趋势。以
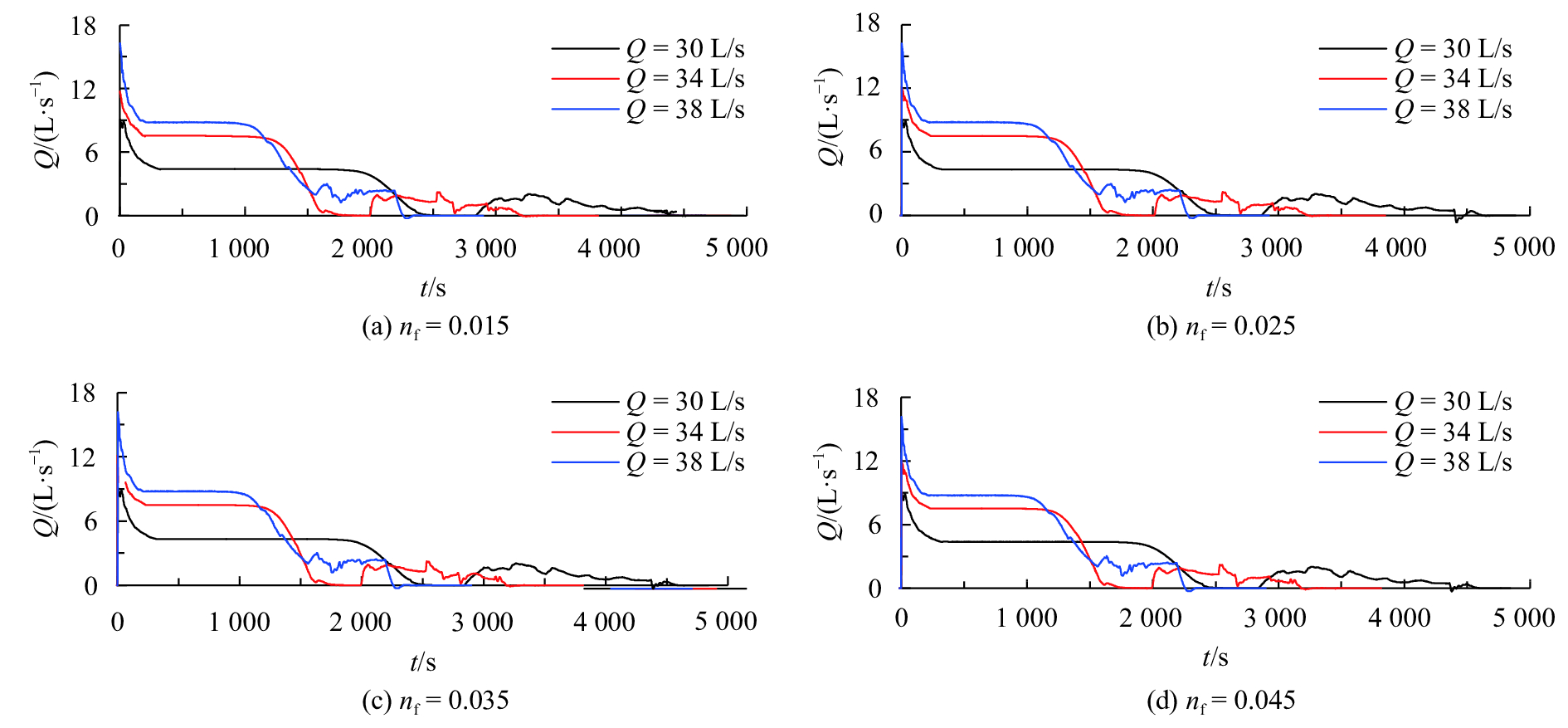 |
| 图8 滩区不同糙率条件下溃堤后进滩流量的变化过程 Fig. 8 Hydrographs of the discharge through breach under different floodplain roughness degrees |
3.2.3 滩区糙率对水位及流速的影响
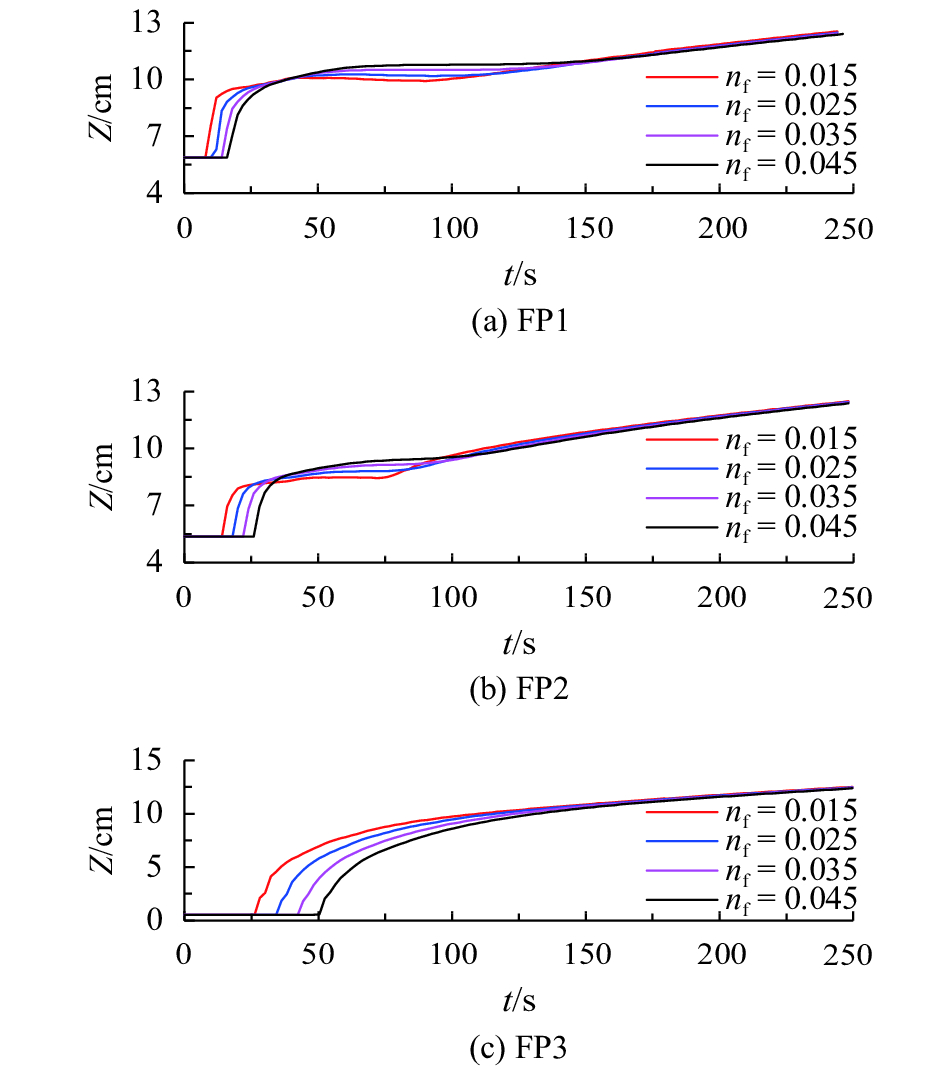
图9给出了生产堤溃决后,滩区不同糙率取值时滩区各特征测点的水位变化过程。由图9可知,滩区不同糙率取值时,滩区测点水位的变化特性相同。具体表现为:生产堤溃决后,受滩区不同糙率取值的影响,滩区洪水演进速度明显不同,这就使得相同时刻时,滩区内各特征测点的水位不同,特别是在溃堤后150 s内表现尤为突出。水位最终趋于相同数值。
 |
|
图9 溃堤后滩区不同糙率条件下水位变化过程(
|
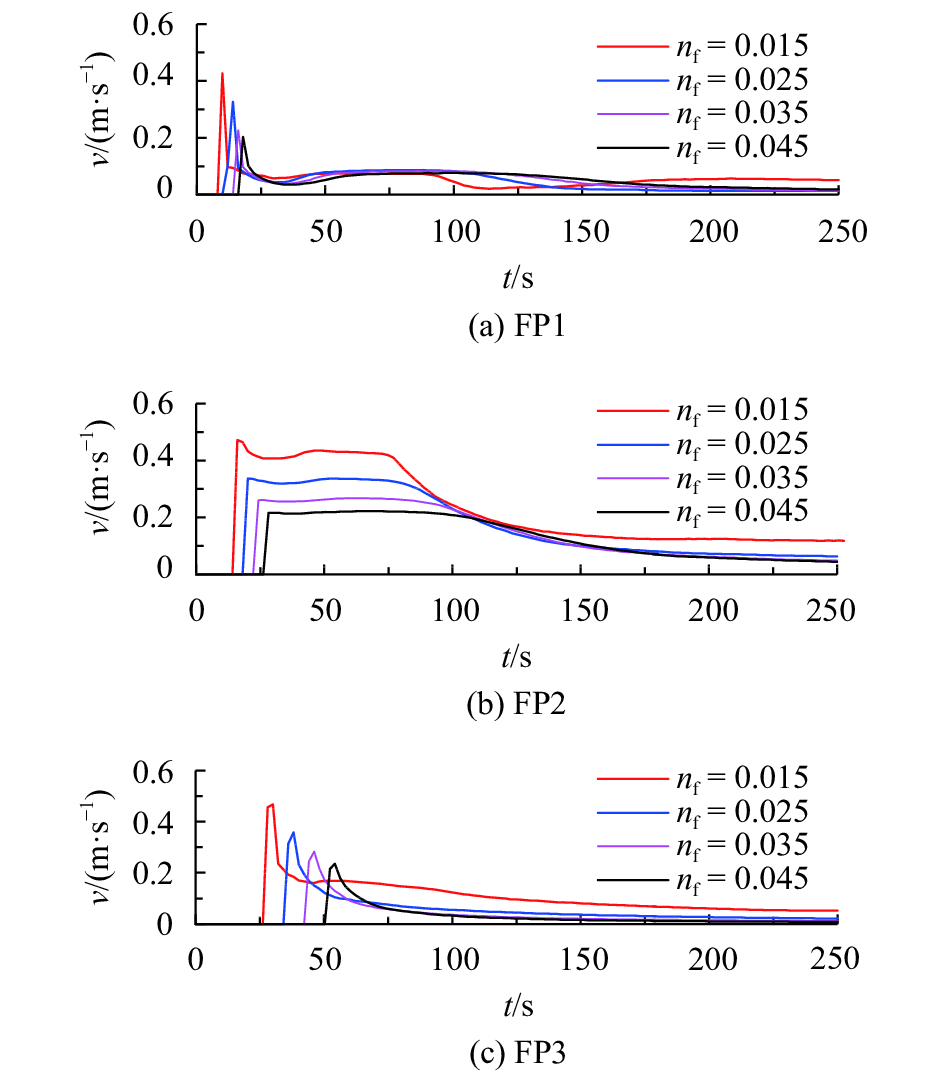
图10给出了
 |
|
图10 溃堤后滩区不同糙率条件下流速变化过程(
|
3.2.4 滩区糙率对溃堤洪水演进的影响
溃堤发生后,滩区内形成涨水波,波前到达滩区各位置的时间对于洪水预警十分重要。表2给出了生产堤溃决后,滩区不同糙率取值时溃堤洪水波前到达滩区各测点所需的时间。
| 表2 滩区不同糙率条件下溃堤洪水波前到达滩区各测点所需时间的比较 Tab. 2 Comparisons between the simulated propagation time of the dike-break flood wave fronts under different floodplain roughness degrees |
 |
总体来看,溃堤进滩流量及滩区糙率取值对溃堤洪水波前到达滩区各测点所需时间的影响均十分明显。受滩区不同糙率取值的影响,随着糙率的增大,相同进流流量条件下,溃堤洪水波前到达滩区各测点所需的时间逐渐增大。当
本文设计并开展了溃堤洪水的模型试验,建立了相应的2维数学模型,并利用试验结果对数学模型进行了验证,最后基于验证后的模型模拟了生产堤溃决后漫滩洪水在滩槽内的演进过程,深入分析了进口流量及滩区不同糙率取值对计算结果的影响。主要得到以下结论:
1)生产堤溃决导致主槽内水位呈现先下降,后稳定,再升高,再稳定的变化趋势;滩区内水位则呈现持续升高,最终趋向稳定的趋势。进滩流量呈现先减小,后稳定再减小,最后趋向为零的变化趋势;滩区各测点流速呈现先增大后减小的趋势,且流速增加速率明显大于降低速率。滩区不同糙率取值对进滩流量影响很小,滩区各特征测点最大流速随着糙率的增加而减小。
2)溃堤进滩流量及滩区糙率取值对溃堤洪水波前到达滩区各测点所需时间的影响均十分显著,溃堤洪水波前到达时间随着滩区糙率取值的增大而逐渐增大,随着洪水量级的增大而逐渐减小。当
3)实际溃堤洪水为含沙水流,滩区地物地貌种类繁多,滩区阻力分布复杂。本次模拟仅考虑主槽及滩区地形对水流演进的影响,尚不能准确反映实际漫滩洪水的演进过程。在后续研究中还需进一步考虑泥沙因素及滩区植被、村庄及道路等阻水建筑物分布的影响。
| [1] |
Lu Lingwei,Lin Binliang,Sun Jian,et al. An experimental study of propagation of dike-break waves[J]. Journal of Hydroelectric Engineering, 2016, 35(11): 25-34. [陆灵威,林斌良,孙健,等. 河道溃堤水波的物理模型实验研究[J]. 水力发电学报, 2016, 35(11): 25-34. DOI:10.11660/slfdxb.20161104] |
| [2] |
Niu Yuguo,Duanmu Liming,Geng Mingquan,et al. Discussion on zoned harnessing of the Lower Yellow River floodplain[J]. Yellow River, 2013, 35(1): 7-9. [牛玉国,端木礼明,耿明全,等. 黄河下游滩区分区治理模式探讨[J]. 人民黄河, 2013, 35(1): 7-9. DOI:10.3969/j.issn.1000-1379.2013.01.003] |
| [3] |
刘树坤,宋玉山,程晓陶,等.黄河滩区及分滞洪区风险分析和减灾对策[M].郑州:黄河水利出版社,1999.
|
| [4] |
Huang Shuge,Yang Zhengqing,Wang Ying. Probability studies of flood plain areas in the lower reaches of the Yellow River[J]. China Water Resources, 2006(18): 6-7. [黄淑阁,杨正卿,王英. 黄河下游滩区漫滩概率分析[J]. 中国水利, 2006(18): 6-7. DOI:10.3969/j.issn.1000-1123.2006.18.004] |
| [5] |
Duanmu Liming,Cheng Gang. Discussion on the comprehensive treatment and development measures of Yellow River floodplain in Henan Province[J]. China Water Resources, 2003(11): 66-67. [端木礼明,成刚. 河南黄河滩区综合治理与开发措施探讨[J]. 中国水利, 2003(11): 66-67. DOI:10.3969/j.issn.1000-1123.2003.11.024] |
| [6] |
Xia Junqiang,Wu Baosheng,Wang Yanping. Processes and characteristics of recent channel adjustment in the Lower Yellow Rvier[J]. Advances in Water Science, 2008, 19(3): 301-308. [夏军强,吴保生,王艳平. 近期黄河下游河床调整过程及特点研究[J]. 水科学进展, 2008, 19(3): 301-308. DOI:10.14042/j.cnki.32.1309.2008.03.011] |
| [7] |
Hu Chunhong,Chen Jianguo,Guo Qingchao. Shaping and maintaining a medium-sized main channel in the Lower Yellow River[J]. International Journal of Sediment Research, 2012, 27(3): 259-270. DOI:10.1016/S1001-6279(12)60034-1 |
| [8] |
中华人民共和国水利部.SL 164—2010溃坝洪水模拟技术规程[S].北京:中国水利水电出版社,2010.
|
| [9] |
Rafael D,Juliano R,Jean-Louis B,et al. Experimental study on dam-break waves for silted-up reservoirs[J]. Journal of Hydraulic Engineering, 2011, 137(11): 1385-1393. DOI:10.1061/(ASCE)HY.1943-7900.0000444 |
| [10] |
Dewals B J,Kantoush S A,Erpicum S,et al. Experimental and numerical analysis of flow instabilities in rectangular shallow basins[J]. Environmental Fluid Mechanics, 2008, 8(1): 31-54. DOI:10.1007/s10652-008-9053-z |
| [11] |
Zhang Yingke,Xu Weilin. Retarding effects of an intermediate intact dam on the dam-break flow in cascade reservoirs[J]. Journal of Hydraulic Research, 2017, 55(3): 438-444. DOI:10.1080/00221686.2016.1276103 |
| [12] |
Liu Hui,Liu Haijiang. Experimental study on dam-break hydrodynamic characteristics under different conditions[J]. Journal of Disaster Research, 2017, 12(1): 198-207. DOI:10.20965/jdr.2017.p0198 |
| [13] |
Roger S,Dewals B J,Erpicum S,et al. Experimental and numerical investigations of dike-break induced flows[J]. Journal of Hydraulic Research, 2009, 47(3): 349-359. DOI:10.1080/00221686.2009.9522006 |
| [14] |
Kamrath P,Disse M,Hammer M,et al. Assessment of discharge through a dike breach and simulation of flood wave propagation[J]. Natural Hazards, 2006, 38(1): 63-78. DOI:10.1007/s11069-005-8600-x |
| [15] |
Xia Junqiang,Wang Guangqian,Lin Binliang,et al. Two-dimensional modelling of dam-break floods over actual terrain with complex geometries using a finite volume method[J]. Advances in Water Science, 2010, 21(3): 289-298. [夏军强,王光谦,Lin Binliang,等. 复杂边界及实际地形上溃坝洪水流动过程模拟[J]. 水科学进展, 2010, 21(3): 289-298. DOI:10.14042/j.cnki.32.1309.2010.03.014] |
| [16] |
Roger S,Dewals B J,Erpicum S,et al.Hybrid modelling of dike-break induced flows.[C]//Proceedings of the 5th International Conference on Fluvial Hydraulics.Brunswick:Bundesanstalt für Wasserbau,2010:523–531.
|
| [17] |
Fraccarollo L,Toro E. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems[J]. Journal of Hydraulic Research, 1995, 33(6): 843-863. DOI:10.1080/00221689509498555 |
| [18] |
黄河水利委员会.黄河下游蔡集抗洪抢险启示录[M].郑州:黄河水利出版社,2008.
|
| [19] |
Zhao Haijing,Tian Shimin,Wang Pengtao,et al. Study on roughening method of hydraulic model with grass cushions[J]. Journal of Hydroelectric Engineering, 2015, 34(4): 77-82. [赵海镜,田世民,王鹏涛,等. 水工模型试验中的草垫加糙方法研究[J]. 水力发电学报, 2015, 34(4): 77-82.] |
| [20] |
Cheng Xiaotao,Xue Yunpeng,Huang Jinchi. 2-D simulation model of flood routing and sediment transport in the lower reach of the Yellow River[J]. Journal of Chinese Hydraulic Engineering, 1998(5): 12-17. [程晓陶,薛云鹏,黄金池. 黄河下游河道水沙运动仿真模型的开发研究[J]. 水利学报, 1998(5): 12-17. DOI:10.13243/j.cnki.slxb.1998.05.003] |
| [21] |
Chien Ning,Hon Yuchia,Mac Chewwai,et al. Channel roughness of Lower Yellow River[J]. Journal of Sediment Research, 1959, 4(1): 1-15. [钱宁,洪柔嘉,麦乔威,等. 黄河下游的糙率问题[J]. 泥沙研究, 1959, 4(1): 1-15. DOI:10.16239/j.cnki.0468-155x.1959.01.001] |
 2018, Vol. 50
2018, Vol. 50


