2. 重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆 400030;
3. 安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南 232001
2. State Key Lab. of Coal Mine Disaster Dynamics and Control, Chongqing Univ. Chongqing 400030, China;
3. Key Lab. of Safety and High-efficiency Coal Mining, Ministry of Education, Anhui Univ. of Sci. and Technol., Huainan 232001, China
土壤渗透[1]、低渗煤岩增透[2]、盐岩储气[3]及花岗岩封存高放核废料[4]均涉及液体或气体渗透,即流体通过低渗多孔介质的流动规律与相互作用。空间杂乱分布的孔隙-裂隙相互连通构成流体流经的通道,而孔隙网络的空间定量描述与精确重构是准确判断渗透特性的几何基础。对于煤与瓦斯共采工程,低渗煤岩孔隙尺寸甚至达到纳米尺度,直接对探视精细结构的实验设备精度与准度带来了巨大挑战[5–6],而低渗理论研究仍是解决问题的窗口。根据Carman-Kozeny经验公式[7],多孔介质渗透率与毛细管迂曲度近似呈反比关系,迂曲度的重要性不言而喻,但鲜有基于低渗煤岩开展迂曲度的定量研究。迂曲度反映流体流经毛细孔道历程的复杂程度,研究结果证实孔隙度与迂曲度存在正向关系[8–9]。迂曲度与渗透率都是孔隙结构的几何相关参量,是有效连通孔隙度的直接反映,因此采用渗透率半经验公式间接测试迂曲度也是主要方法,即采用理论与实验结合的方法可有效避免直接几何测量方法的误差。Purcell[10]较早提出用汞开展毛管压力与渗透率测试。由于研究对象集中于渗透率,忽略了迂曲度的影响,导致渗透率误差较大[11–13]。Boundreau[14]对有限颗粒构成的迂曲度开展模型研究,Sen等[15]认为孔隙结构分布具有自相似特性,即迂曲度可利用分形理论研究。另外迂曲度带来的流体非线性扰动也是热点[16–17],可见迂曲度的定量表述利于开展相关方向研究。早期对迂曲度的认识仅是对渗透率的误差修正,目前仍有文献资料直接对迂曲度给出估值,缺乏测量依据,易引起困惑。随着认识深入,迂曲度被定义为反映孔隙结构流程的弯曲程度,才禀赋了其内在物理意义。国内也有文献提出直接用孔隙度计算迂曲度[18],认为迂曲度曲线具有分维特征[19],提出了分形毛细管力模型[20]。
低渗煤岩孔隙通道的弯折程度影响流体的能量损耗,大流阻导致流体通过困难,定量上反映渗透率低。迂曲度刻画弯折程度为定量解析渗透率变化提供了载体,但分形截面的粗糙度在迂曲度方向上的积分效应却未引起足够的重视。基于此,本文侧重在纵向分形迂曲度结构与横向分形截面结构开展低渗理论研究,并建立气-液驱替的分形运动方程。
1 基于Hagen-Poiseuille方程的迂曲度推导低渗煤岩作为多孔介质,孔隙一般在微米-纳米尺度,微米孔可定义为毛细管孔。孔道既包括盲孔等非有效通道,也包括连通的有效通道。孔隙空间分布十分复杂,截面形状与尺寸不同位置迥异,具有随机性。甚至,在水力等外力作用下还存在着开闭状态。理论上,完备解决基于跨尺度精细结构的定量描述仍存在挑战,分形理论在解决无序结构的自相似问题上表现了极强的适应性[15]。建立煤岩的分形毛细管模型,如图1所示。
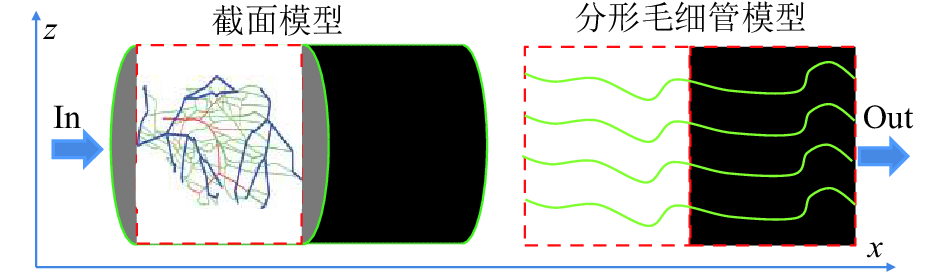 |
| 图1 分形毛细管模型 Fig. 1 Fractal modeling of capillary |
圆柱煤岩纵截面任取矩形截面,考虑一维渗流。沿
迂曲度反映了孔道在空间分布的复杂程度,存在多种定义[21]。设
| $\tau = {\left( {\frac{{{L_{\rm{e}}}}}{L}} \right)^2}$ | (1) |
还有贝尔定义
根据Hagen-Poiseuille公式[24],截面孔隙通道流量
| $q = nA \cdot \frac{{\Delta p{\text{π}} {r^4}}}{{8\mu \tau L}}$ | (2) |
式中,
根据达西定律:
| $q = \frac{{KA\Delta p}}{{\mu \tau L}}$ | (3) |
式中,
| $\phi = \frac{{An{\text{π}} {r^2}L\tau }}{{AL}} = n{\text{π}} {r^2}\tau $ | (4) |
联立式(2)、(3)与(4),得:
| $\tau = \frac{{\phi {r^2}}}{{8K}}$ | (5) |
若截面均为圆形孔道,定义水力学半径平均值
| ${R_{\rm{h}}} = \frac{S}{{\textit{Z}}} = \frac{{{\text{π}} {r^2}}}{{2{\text{π}} r}} = \frac{r}{2}$ | (6) |
式中,
根据经验,存在如下关系[26]:
| ${R_{\rm{h}}} = \frac{{\phi {D_{\rm{p}}}}}{{6\left( {1 - \phi } \right)}}$ | (7) |
式中,
结合式(5)、(6)与(7),迂曲度:
| $\tau = \frac{{{\phi ^3}D_{\rm{p}}^2}}{{72K\left( {1 - \phi } \right)}}$ | (8) |
系统由
| $\frac{{N{\text{π}} D_{\rm{p}}^2}}{4} = \left( {1 - \phi } \right)AL$ | (9) |
则迂曲度可定义为:
| $\tau = \frac{{{\phi ^3}AL}}{{18KN{\text{π}} }}$ | (10) |
另一种方法是引入毛细管压力公式,不同于Hagen-Poiseuille公式,毛细管压力公式局限于致密岩石、微尺度以下孔道渗流模型。
单根毛管压力[23]:
| $p = \frac{{2\sigma \cos \;\theta }}{r}$ | (11) |
式中,
结合式(2),得:
| $q = \frac{{V\Delta p}}{{2\mu }}{\left( {\frac{{\sigma \cos \;\theta }}{{\tau Lp}}} \right)^2}$ | (12) |
联立达西定律式(3),得:
| $K = \frac{{nV}}{{2AL}}{\left( {\frac{{\sigma \cos \;\theta }}{{\tau p}}} \right)^2}$ | (13) |
孔道一般含有一定的水分或气体,考虑饱和度
| $K = \frac{\phi }{2}{\left( {\frac{{\sigma \cos \;\theta }}{\tau }} \right)^2}\int_0^1 {\frac{{{\rm d}s}}{{{p^2}}}} $ | (14) |
则迂曲度重新定义为:
| $\tau = \sigma \;\cos \;\theta \sqrt {\frac{\phi }{{2K}}\int_0^1 {\frac{{{\rm d}s}}{{{p^2}}}} } $ | (15) |
饱和度与孔隙体积紧密相关,定义为单根毛细管充满液体的饱和度,即针对单根毛细管取1,针对整体是单根毛细管体积与孔隙度的比值。如果假设毛细管压力
| $\tau = \sigma \cos \;\theta \sqrt {\frac{\phi }{{2pK}}} $ | (16) |
式(15)与(16)即为致密煤岩孔隙迂曲度的毛细管模型算法。结合压汞实验测毛管力,即可测定迂曲度。
2 低渗煤岩分形孔道迂曲度计算基于科林斯定义,Wheatcraft和Tyler[26]建立了多孔介质迂曲流管特性的分形标度关系:
| ${L_{\rm{e}}} = \lambda _{\min }^{1 - {D_{\rm{T}}}}{L^{{D_{\rm{T}}}}}$ | (17) |
则:
| $\tau = \frac{{{L_{\rm{e}}}}}{L} = {\left( {\frac{L}{{{\lambda _{\min }}}}} \right)^{{D_{\rm{T}}} - 1}}$ | (18) |
式中,
联立式(15)与(18),得:
| ${D_{\rm{T}}} = 1 + \frac{{\ln \left( {\sigma \cos \;\theta \sqrt {\displaystyle\frac{\phi }{{2K}}\int_0^1 {\displaystyle\frac{{{\rm d}s}}{{{p^2}}}} } } \right)}}{{\ln \left( {L/r} \right)}}$ | (19) |
式(19)说明利用压汞实验可以确定迂曲孔道分维。定义分形影响系数:
| $\overline \lambda = {\left( {\frac{L}{r}} \right)^{{D_{\rm{T}}} - 1}}$ | (20) |
如图2(a)为长径比系数和分形影响系数的关系,当迂曲度分形维数
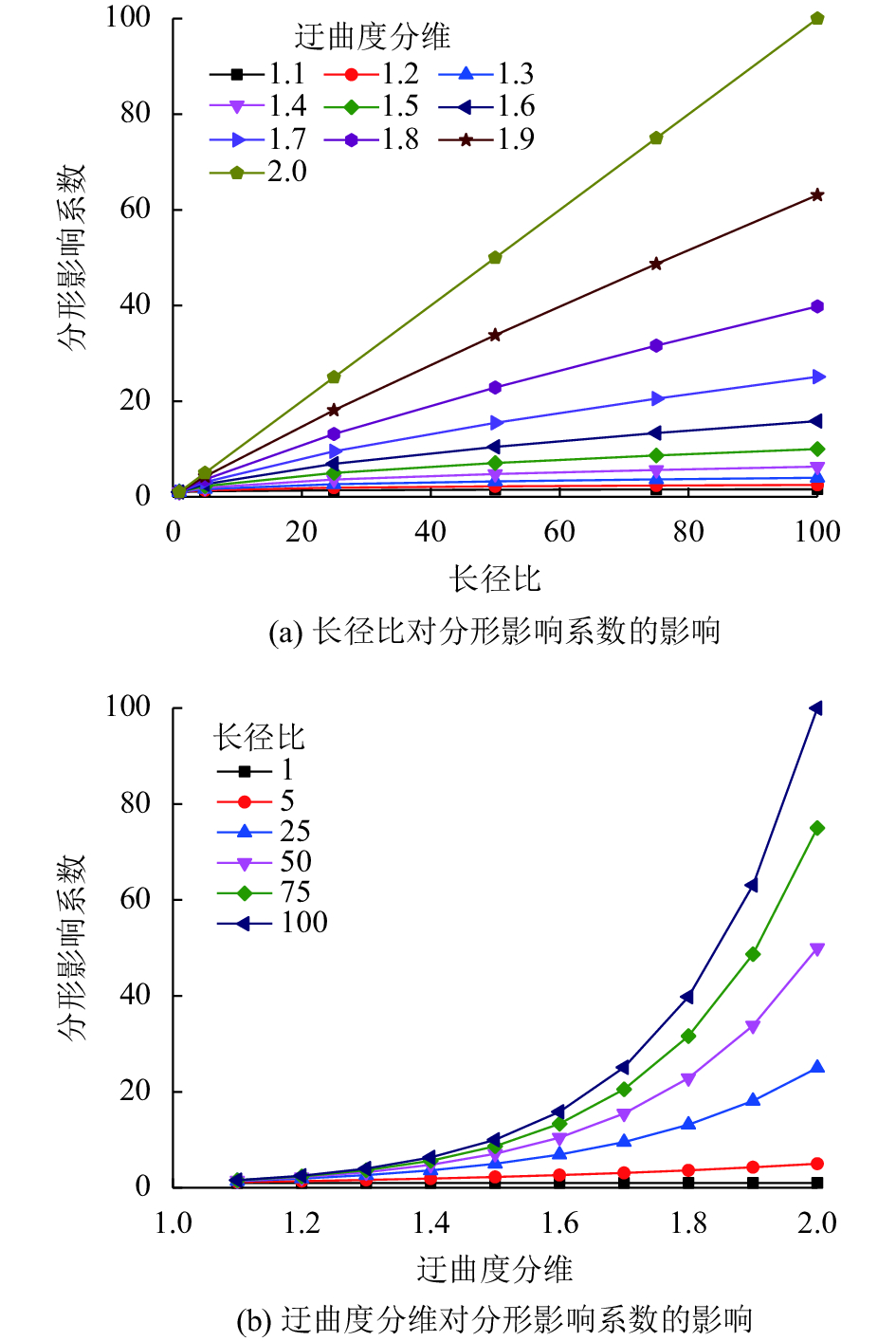 |
| 图2 长径比和迂曲度分维与分形影响系数关系 Fig. 2 Fractal coefficient with aspect ratio and fractal dimension of tortuosity |
煤岩取自平顶山矿区,埋深约1 000 m,加工成几何尺寸:
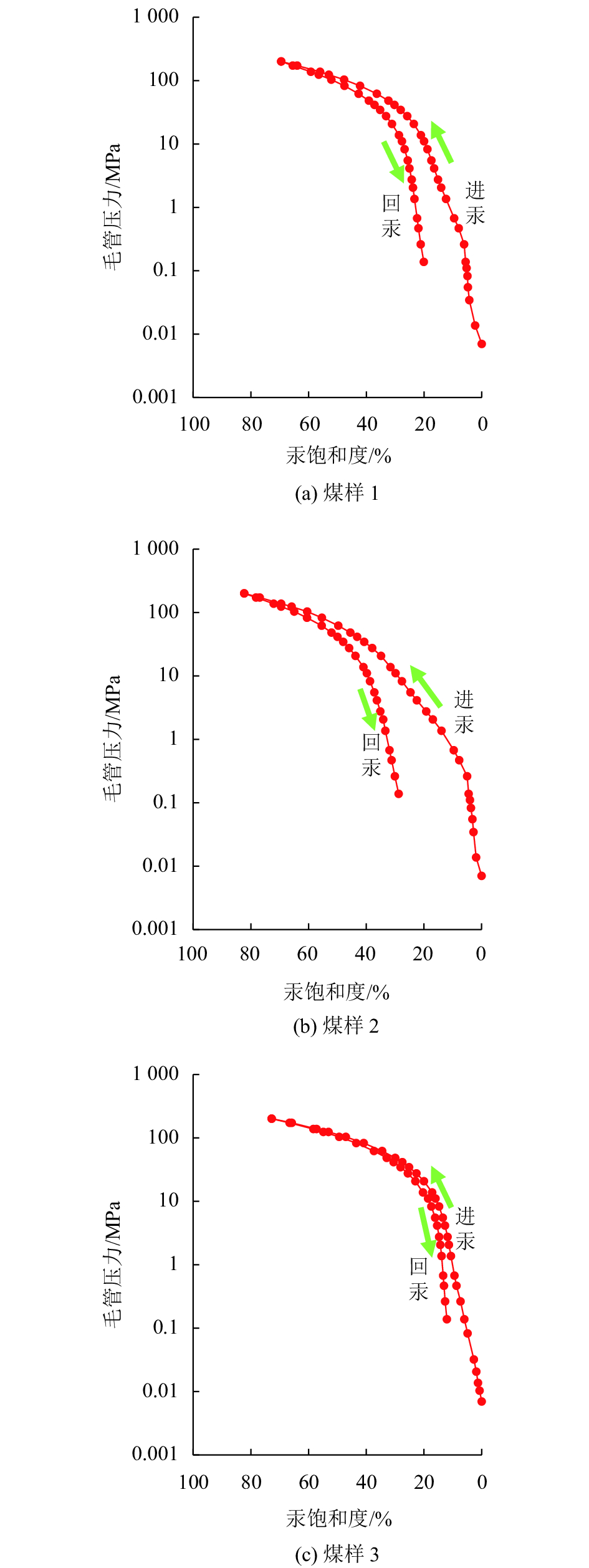 |
| 图3 毛细管压力曲线 Fig. 3 Mercury injection curve of coal samples |
图3为3个煤样的压汞曲线图,进汞及回汞曲线差异明显,初始压汞部分存在陡峭部分,即压力极速增长,说明汞未有效压入,对应的孔隙部分存在缺失,即煤岩十分致密。实验测定样品1:
图4为渗透率与迂曲系数的关系,呈直线关系。迂曲系数可以很好的反映渗透率变化,是一种几何结构参数,包括了迂曲度与迂曲分维的影响。
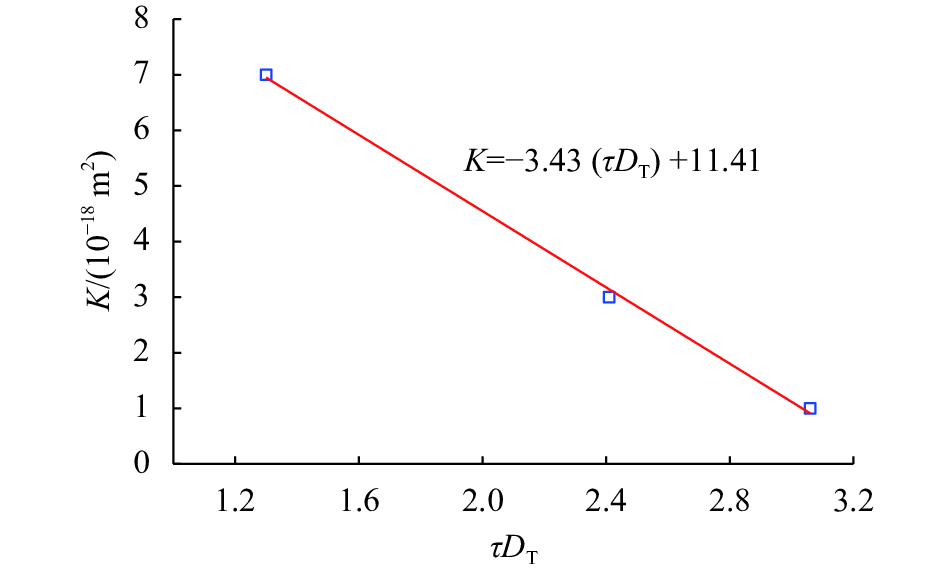 |
| 图4 渗透率与迂曲系数的关系 Fig. 4 Relationship between permeability and tortuosity coefficient |
3 低渗煤岩分形截面分维理论推导
由于毛细管微-纳米的结构“半径”,毛细管横截面润湿周长分形特性常被忽略,甚至同迂曲度分形概念混淆。假设毛细管截面为正
| $a = 2r\sin \frac{{\text{π}} }{n}$ | (21) |
| $h = r\cos \frac{{\text{π}} }{n}$ | (22) |
根据Carman-Kozeny方程[7],圆形毛细管截面渗透率
| ${K_{\rm{c}}} = \frac{{{\phi ^3}}}{{2{\tau ^2}{S^2}}}$ | (23) |
则正
| ${K_n} = \frac{{\sin \displaystyle\frac{{\text{π}} }{n}}}{{\displaystyle\frac{{\text{π}} }{n}}} \cdot {\cos ^3}\displaystyle\frac{{\text{π}} }{n} \cdot {K_{\rm c}}$ | (24) |
当
| $\mathop {\lim }\limits_{n \to + \infty } {K_n} = {K_{\rm{c}}}$ | (25) |
即正
图5为基于正六边形的5次分形截面迭代,考虑正
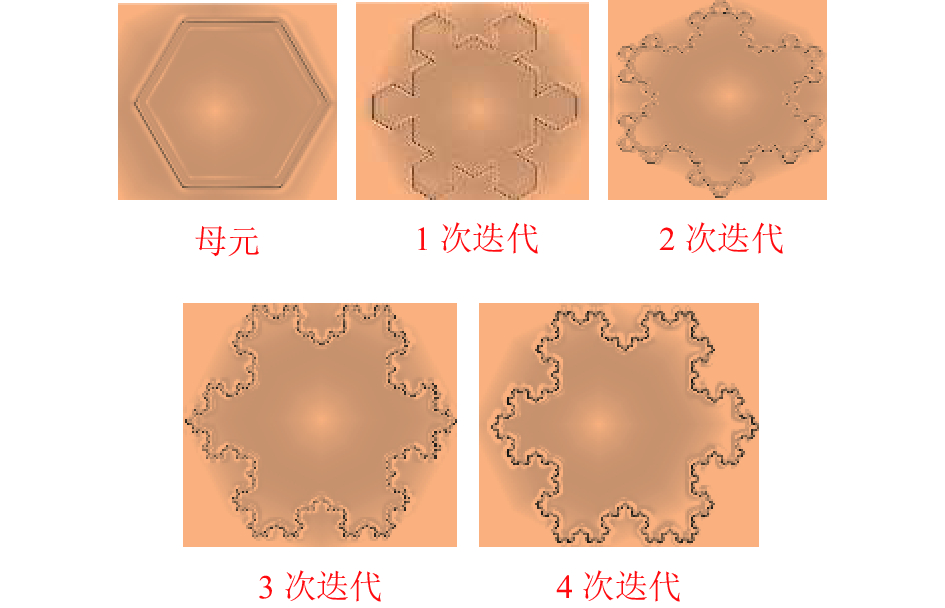 |
| 图5 分形截面迭代 Fig. 5 Fractal section iteration |
相应地4次迭代后,可以建立正
根据Washburn方程知,气-液两相流运动界面方程同时考虑截面积
对于分形结构,量测的面积存在近似关系(表2):
| ${S_i} = {S^0}{\varepsilon _i}^{1 - {D_{\rm s}}}$ | (26) |
式中:
量测的周长存在近似关系(表3):
| ${C_i} = {C^0}{\delta _i}^{1 - {D_{\rm C}}}$ | (27) |
式中:
| 表1 分形毛细管渗透率比值 Tab. 1 Permeability ratio of fractal capillary model |
 |
根据体积覆盖法[27],可以建立对应
| ${\varepsilon _i} = \frac{{3n}}{2}a_i^2\tan \frac{{2{\text{π}} }}{n},i = 0,1,2,3, \cdots $ | (28) |
定义最新生成分形子结构的最小边长
| ${\delta _i} = {a_i},i = 0,1,2,3, \cdots $ | (29) |
| 表2 面积覆盖统计 Tab. 2 Area covering statistics |
 |
| 表3 周长覆盖统计 Tab. 3 Perimeter covering statistics |
 |
则截面积的分维
| ${D_{\rm s}} = - \frac{{\lg \left( {{N_{\varepsilon ,i}}/{N_{\varepsilon ,0}}} \right)}}{{\lg \left( {{\varepsilon _i}/{\varepsilon _0}} \right)}}$ | (30) |
则周长的分维
| ${D_{\rm C}} = - \frac{{\lg \left( {{N_{\delta ,i}}/{N_{\delta ,0}}} \right)}}{{\lg \left( {{\delta _i}/{\delta _0}} \right)}}$ | (31) |
图6为气液两相驱替模型。
如图6所示,基于毛细管结构建立气液两相驱替模型,取迂曲方向上一小直段
| ${F_{\rm p}} = \Delta p \cdot {S^0}{\varepsilon _i}^{1 - {D_s}}$ | (32) |
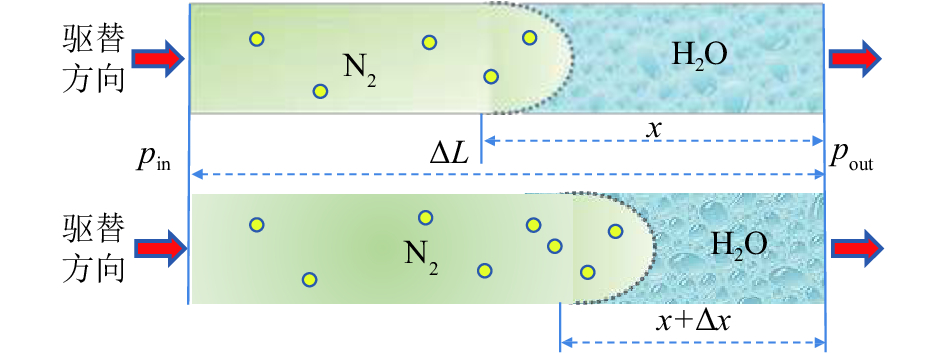 |
| 图6 气液两相驱替模型 Fig. 6 Flushing model of gas driving liquid |
式中,
| ${F_{\rm c}} = {p_{\rm c}} \cdot {S^0}{\varepsilon _i}^{1 - {D_{\rm s}}}$ | (33) |
式中,
| ${F_ {\rm f} }= \tau \left( {x + {\rm{d}}x} \right) \cdot {C^0}{\delta _i}^{1 - {D_{\rm C}}}$ | (34) |
式中,
根据牛顿第二定律:
| $ma = {F_{\rm p}} + {F_{\rm c}} + {F_{\rm f}}$ | (35) |
将式(32)、(33)与(34)代入式(35),即:
| $\begin{aligned}[b] \rho \cdot {S^0}{\varepsilon _i}^{1 - {D_{\rm s}}} \cdot x{\rm{d}}x = & \left( {\Delta p - {p_{\rm c}}} \right){S^0}{\varepsilon _i}^{1 - {D_{\rm s}}} - \\& {C^0}{\delta _i}^{1 - {D_{\rm C}}} \cdot \frac{{4\eta }}{r}\frac{{{\rm{d}}x}}{{{\rm{d}}t}}\left( {x + {\rm{d}}x} \right)\end{aligned} $ | (36) |
忽略惯性项与高阶黏性切应力,则
| ${C^0}{\delta _i}^{1 - {D_{\rm C}}} \cdot \frac{{4\eta }}{r}\frac{{{\rm{d}}x}}{{{\rm{d}}t}}x = \left( {\Delta p - {p_{\rm c}}} \right){S^0}{\varepsilon _i}^{1 - {D_{\rm s}}}$ | (37) |
此方程即为Washburn方程分形形式,简称分形Washburn方程。对方程积分,可以得到界面位置方程:
| ${x^2} = \frac{{{S^0}{\varepsilon _i}^{1 - {D_{\rm s}}}}}{{{C^0}{\delta _i}^{1 - {D_{\rm C}}}}} \cdot \left( {\Delta p - {p_{\rm c}}} \right)\frac{r}{{2\eta }}t$ | (38) |
式中,
同时可以得到界面运动
| ${v_{\rm m}} = \frac{{{S^0}{\varepsilon _i}^{1 - {D_{\rm s}}}}}{{{C^0}{\delta _i}^{1 - {D_{\rm C}}}}}\left( {\Delta p - {p_{\rm c}}} \right)\frac{r}{{4\eta x}}$ | (39) |
利用Nano CT对煤岩进行纳米-微米尺度分析,样品近似圆柱形,尺寸约65 μm。重构后截取60 μm立方体,孔隙结构十分复杂(图7)。图8为基于纳米与微米尺度的孔径与孔隙体积关系,并对内部孔隙结构进行定量分析,孔径在0.1~20 μm均有分布,主要集中2~20 μm,可见在微米尺度上孔周表面仍有可能存在更细微的结构。
 |
| 图7 纳米-微米孔隙结构重构 Fig. 7 Reconstruction of nano- and meso- scale pore structure |
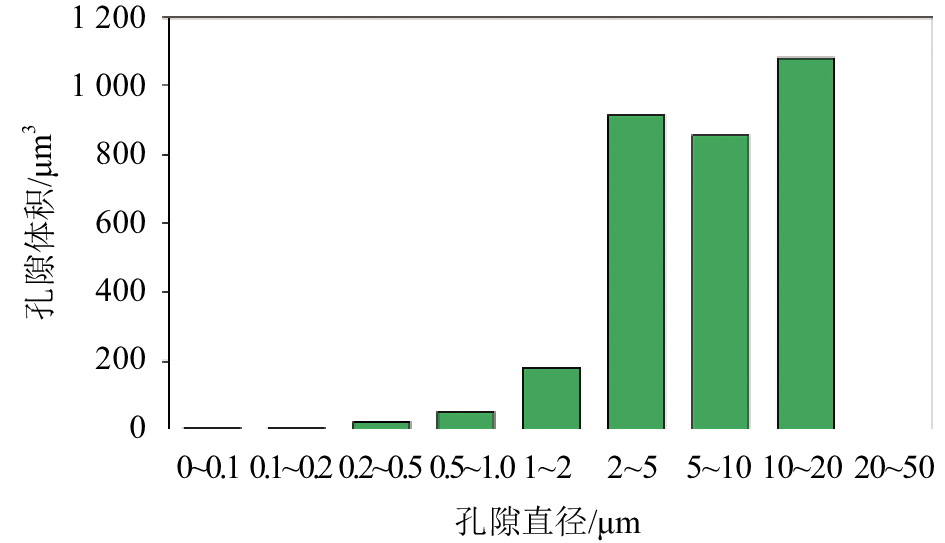 |
| 图8 孔径与孔隙体积分布 Fig. 8 Pore radius and volume distribution |
进一步基于低场NMR开展两相N2–H2O驱替实验研究,驱替压路径设计如图9所示。低渗煤岩样品尺寸为
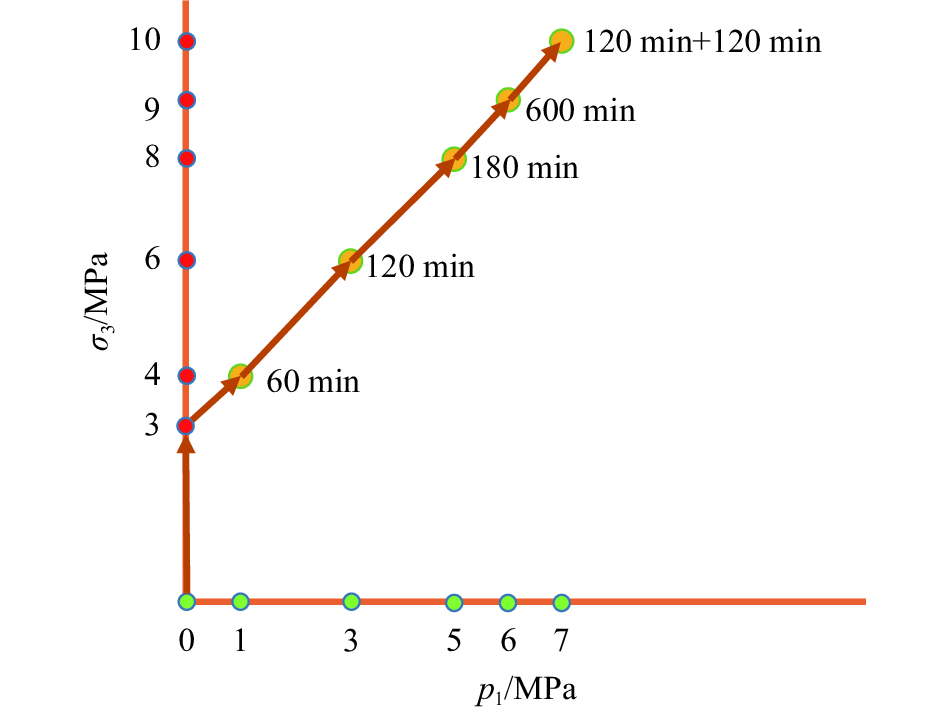 |
| 图9 驱替压路径设计 Fig. 9 Fractal dimension determined |
根据孔径分布,选取18 μm为边长的正六边形为母元进行分形结构分析,则对应的码尺分别为18、6、2、0.67与0.22 μm,基本可以覆盖主要的孔径分布,根据式(30)与(31),可计算得到面积分维
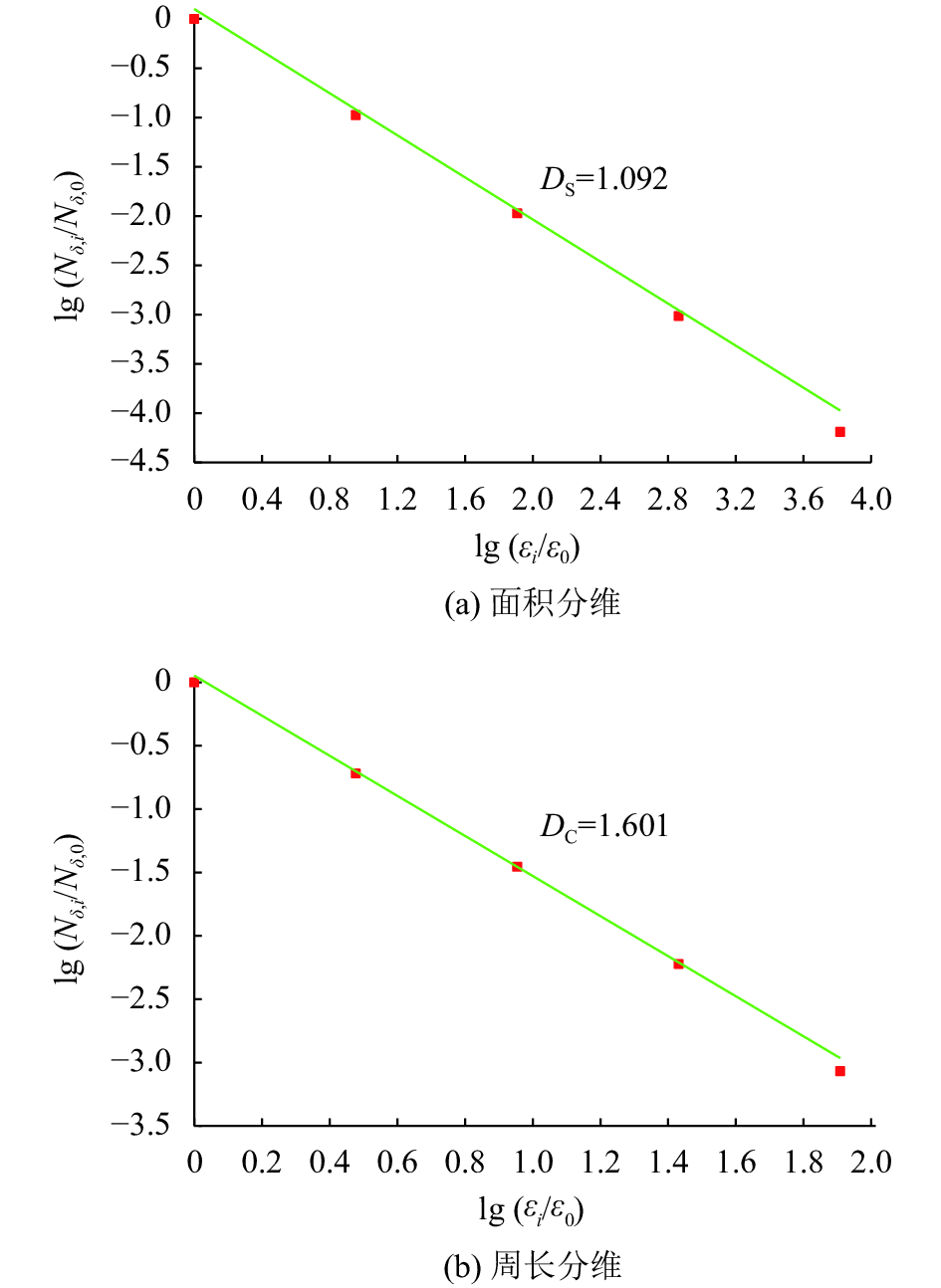 |
| 图10 分维计算 Fig. 10 Fractal dimension determined |
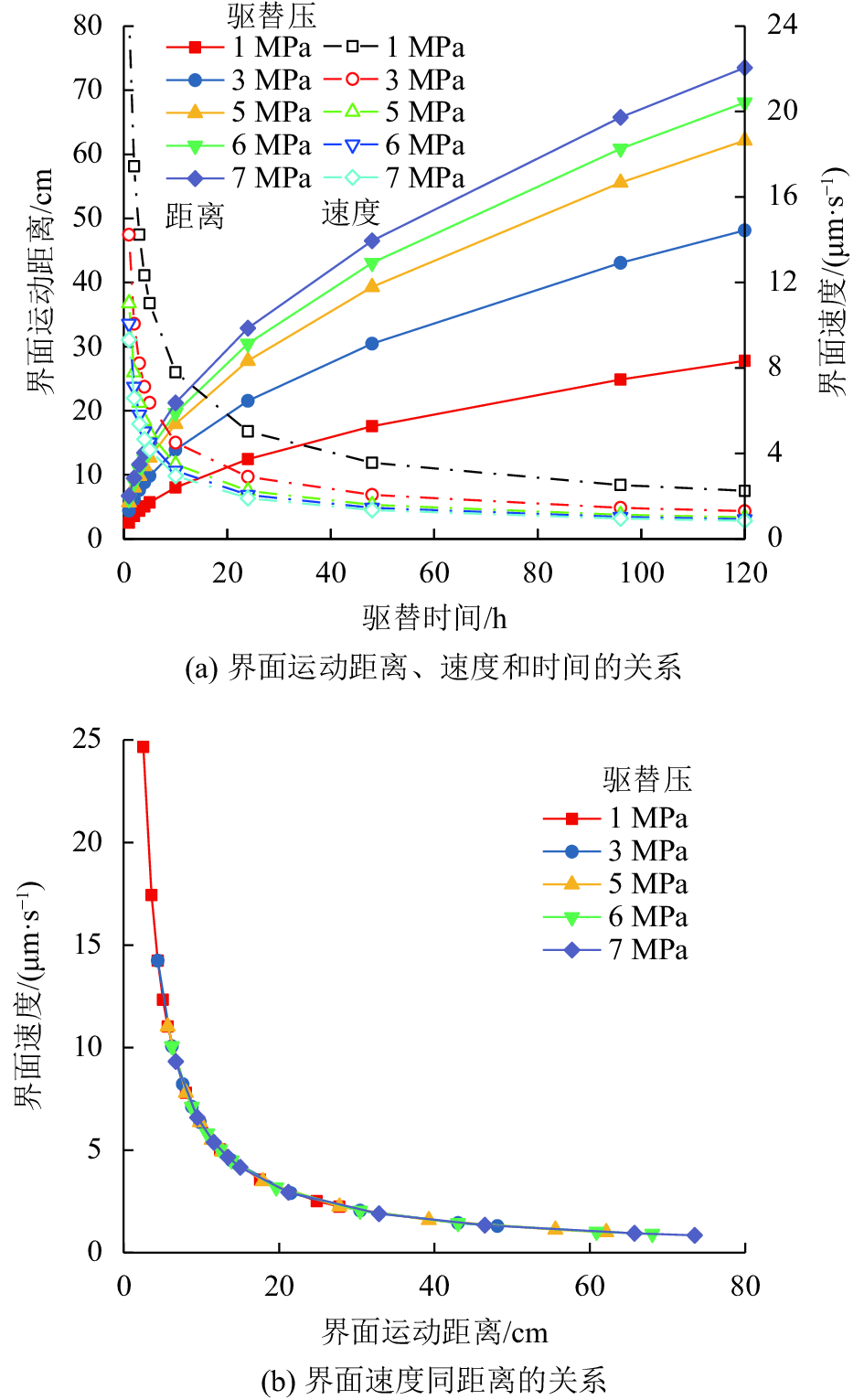 |
| 图11 母元结构气液驱替规律 Fig. 11 Gas flushing water in parent fractal structure |
针对母元,毛细管力
界面运动距离随着时间的增长,呈现非线性增长,随着驱替压的提高,增长幅度趋于缓慢;对于速度,随着时间增长快速衰减(图11(a))。
在1、3、5、6与7 MPa下,启动速度分别为111.4、192.9、249.1、272.9与294.7 μm/s,可见启动速度随着驱替压的增加也在增加。但速度随距离的衰减极快(图11(b)),不同驱替压下界面速度与界面距离单调递减,遵循相同的衰减路径。初始1 h后的衰减速度,1 MPa速度最大,7 MPa速度最小;对应运动距离,1 MPa距离最小,7 MPa距离最大。压差提供了长程驱替的能量,压差大,驱替距离远,速度衰减也最快。初始速度衰减快的原因主要为
图12为5 MPa作用下,不同迭代次数分形结构界面运动距离、速度与驱替时间的关系。界面运动距离,母元结构中移动最远:62.13 cm;1次迭代后距离衰减至26.05 cm、衰减58.1%;2次迭代后距离为10.92 cm、衰减82.4%;3次迭代后距离为4.58 cm、衰减92.6%;4次迭代为3.33 cm、衰减94.6%。可见,分形结构不同于光滑圆形结构,随着壁面粗糙程度增加,阻滞作用越趋于明显。对于液体,壁面粗糙度是不可忽略的因素。速度降落也很明显,初始速度,母元结构最大;第四次迭代分形结构速度最小。因此,壁面粗糙度同时对驱替液体界面运动距离和速度存在阻滞作用,这就需要更高的驱替压抵抗新增的阻滞。
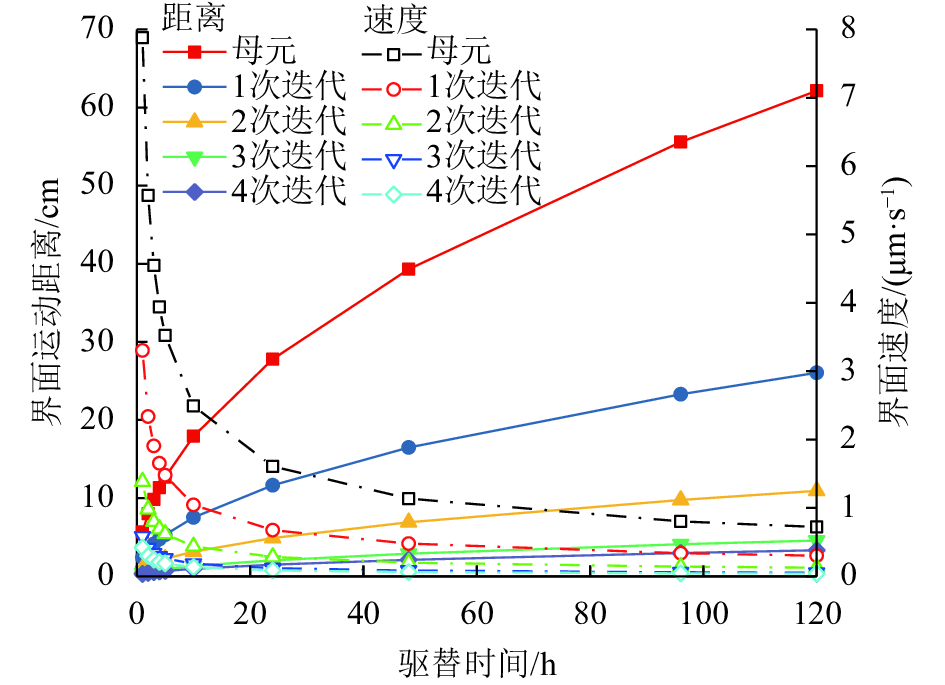 |
| 图12 不同迭代次数分形结构驱替规律 Fig. 12 Displacement in fractal structure with different iteration |
 |
| 图13 实验驱替下累计界面运动距离与速度 Fig. 13 Distance accumulated and velocity of water corresponding to the NMR test |
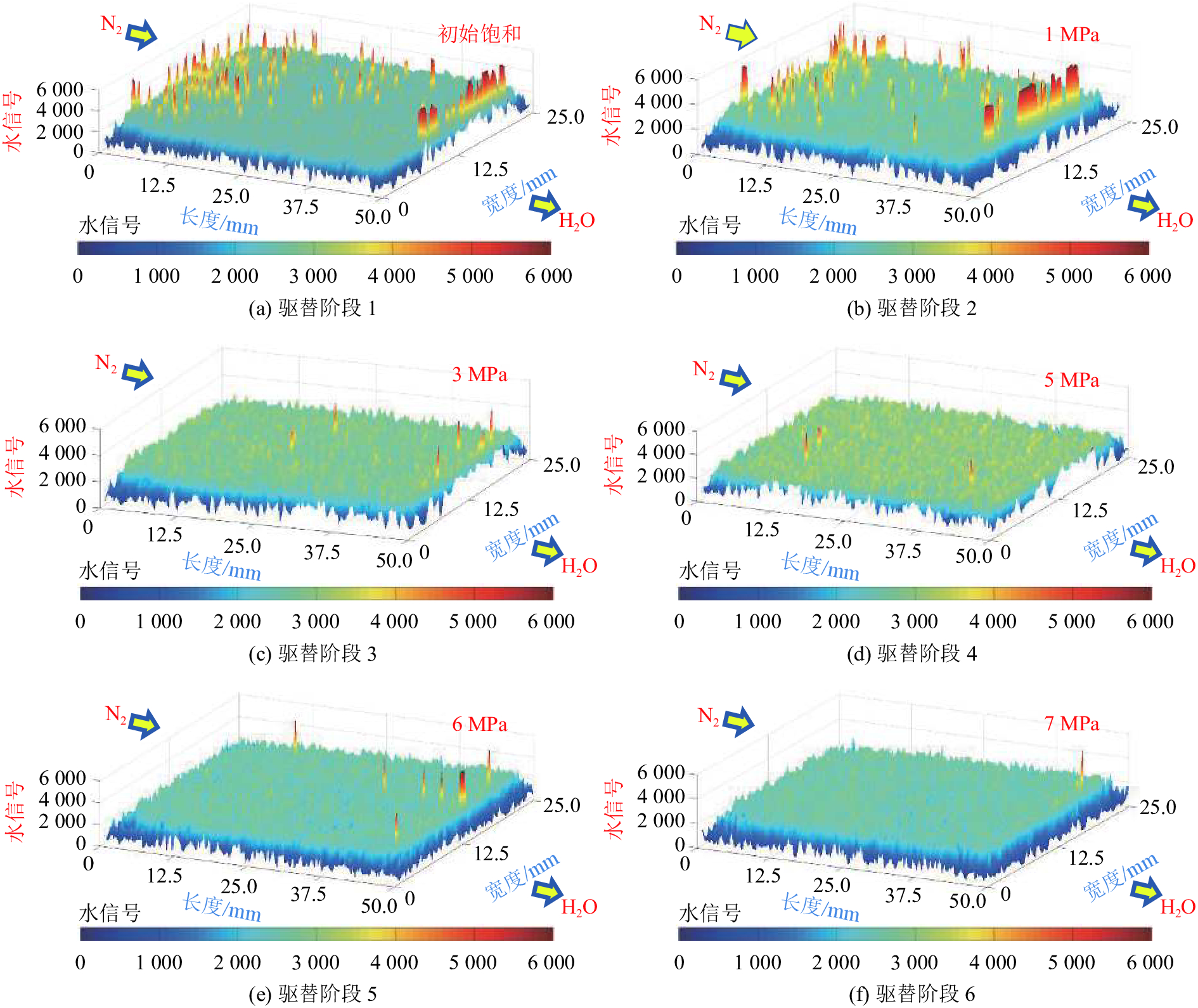 |
| 图14 NMR驱水信号分布 Fig. 14 Fractal dimension determined |
基于压汞试验并计算平均迂曲度
1)建立了分形毛细管模型,推导了基于Hagen–Poiseuille方程的低渗煤岩迂曲度两种数学表达式。第一种为理论公式,属传统定义;第二种结合压汞试验,简化了迂曲度的计算。进一步引入孔径-长度分形标度关系,获得了迂曲孔道的分维表达式。
2)开展了低渗煤岩压汞实验,获得了煤的迂曲度与迂曲分维。定义迂曲系数为迂曲度与迂曲分维的乘积,发现渗透率与迂曲系数呈线性关系。
3)建立了低渗煤岩分形截面模型,基于Carman–Kozeny方程计算渗透率验证了分形截面的可靠性。建立了截面积与周长的分维表达式,同时基于Washburn方程建立了界面运动位置方程与运动速度方程。
4)基于Nano–CT重构了低渗煤岩纳米-微米孔隙结构,获得了孔径与孔隙体积分布,结合理论模型,计算了面积分维与周长分维。并结合分形运动方程建立了运动距离、速度同时间的关系;速度同距离的关系;不同分形结构的驱替规律。结果表明:系数
5)基于NMR实验开展了两相N2-H2O驱替实验,结合理论模型获得了实验驱替下界面运动距离与速度分布。通过驱水信号分布证实了分形运动方程的有效性。
综上,在孔隙度相同条件下,煤岩低渗机制应考虑毛细孔道纵向与横向的影响。纵向主要为迂曲系数;横向主要为分形截面粗糙度系数的影响。而迂曲系数与分形截面粗糙度系数在分析压汞实验、Nano-CT重构实验与NMR实验结果时也是分开考虑的,同时考虑两个权重的影响仍有待研究。需要说明的是:
1)式(10)建立在Hagen-Poiseuille公式与达西定律的基础上,是理论求解,但模型要求存在并行分形毛细管。这点在实际验证时又带来了新的不确定性,即截面毛细管分布密度的确定问题,优点是式(10)并不要求模型严格建立在微米尺度。式(16)是式(15)的简化,是在式(10)建立原理基础上,结合压汞试验,引入饱和度巧妙避免了毛细管分布密度问题。但这种方法测定的是所有分形毛细管的综合效应,即迂曲度概念是建立在分形毛细管串联的基础上。
2)毛细管孔道,上述迂曲度定义既无法理清单条长程孔道迂曲度差异;更是忽略了迂曲度禀赋界定渗透性含义。对于分叉孔道,仍有必要基于能量原理[30]深入研究分叉孔道迂曲度的基本关系。
| [1] |
Hvorslev M J. Time lag and soil permeability in ground-water observations[J]. US Army Corps of Engineers Waterways Experiment Station Bulletin, 1951, 36(118): 1-50. |
| [2] |
Xue Dongjie,Zhou Hongwei,Kong Lin,et al. Mechanism of unloading-induced permeability increment of protected coal seam under mining[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1910-1916. [薛东杰,周宏伟,孔琳,等. 采动条件下被保护层瓦斯卸压增透机理研究[J]. 岩土工程学报, 2012, 34(10): 1910-1916.] |
| [3] |
Yang Chunhe,Liang Weiguo,Wei Donghou,et al. Investigation on possibility of energy storage in salt rock in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4409-4417. [杨春和,梁卫国,魏东吼,等. 中国盐岩能源地下储存可行性研究[J]. 岩石力学与工程学报, 2005, 24(24): 4409-4417. DOI:10.3321/j.issn:1000-6915.2005.24.002] |
| [4] |
Wang Ju,Chen Weiming,Su Rui,et al. Geological disposal of high-level radioactive waste and its key scientific issues[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(4): 801-812. [王驹,陈伟明,苏锐,等. 高放废物地质处置及其若干关键科学问题[J]. 岩石力学与工程学报, 2006, 25(4): 801-812. DOI:10.3321/j.issn:1000-6915.2006.04.015] |
| [5] |
Katz A J,Thompson A H. Fractal sandstone pores:Implications for conductivity and pore formation[J]. Physical Review Letters, 1985, 54(12): 1325-1328. DOI:10.1103/PhysRevLett.54.1325 |
| [6] |
Baker D R,Mancini L,Polacci M,et al. An introduction to the application of X-ray microtomography to the three-dimensional study of igneous rocks[J]. Lithos, 2012, 148(9): 262-276. DOI:10.1016/j.lithos.2012.06.008 |
| [7] |
Carrier III W D. Goodbye,hazen; hello,kozeny-carman[J]. Journal of geotechnical and geoenvironmental engineering, 2003, 129(11): 1054-1056. DOI:10.1061/(ASCE)1090-0241(2003)129:11(1054) |
| [8] |
Comiti J,Sabiri N E,Montillet A. Experimental characterization of flow regimes in various porous media-III:limit of Darcy's or creeping flow regime for Newtonian and purely viscous non-Newtonian fluids[J]. Chemical engineering science, 2000, 55(15): 3057-3061. DOI:10.1016/S0009-2509(99)00556-4 |
| [9] |
Szymkiewicz A.Modelling water flow in unsaturated porous media:accounting for nonlinear permeability and material heterogeneity[M].Berlin:Springer Science & Business Media,2012.
|
| [10] |
Purcell W R. Capillary pressures-their measurement using mercury and the calculation of permeability therefrom[J]. Journal of Petroleum Technology, 1949, 1(2): 39-48. DOI:10.2118/949039-G |
| [11] |
Markevich N J,Cecilio C B.Through-flow analysis for rockfill dam stability evaluations[C]//Waterpower'91:A New View of Hydro Resources.Sam Francisco:ASCE,1991:1734–1743.
|
| [12] |
Yu B,Li J,Li Z,et al. Permeabilities of unsaturated fractal porous media[J]. International Journal of Multiphase Flow, 2003, 29(10): 1625-1642. DOI:10.1016/S0301-9322(03)00140-X |
| [13] |
Romm E S.Flow Characteristics of Fractured Rocks[M].Moscow:Nedra Publishing House,1966.
|
| [14] |
Boudreau B P. The diffusive tortuosity of fine-grained unlithified sediments[J]. Geochimica et Cosmochimica Acta, 1996, 60(16): 3139-3142. DOI:10.1016/0016-7037(96)00158-5 |
| [15] |
Sen P N,Scala C,Cohen M H. A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass beads[J]. Geophysics, 1981, 46(5): 781-795. DOI:10.1190/1.1441215 |
| [16] |
Koponen A,Kataja M,Timonen J. Tortuous flow in porous media[J]. Physical Review E, 1996, 54(1): 406-410. DOI:10.1103/PhysRevE.54.406 |
| [17] |
Koponen A,Kataja M,Timonen J. Permeability and effective porosity of porous media[J]. Physical Review E, 1997, 56(3): 3319-3326. DOI:10.1103/PhysRevE.56.3319 |
| [18] |
Wu Jinsui,Hu Dezhi,Guo Junzhong,et al. Study on the relationship between tortuosity and permeability in porous media[J]. Journal of North China Institute of Science and Technology, 2016, 13(4): 56-58. [吴金随,胡德志,郭均中,等. 多孔介质中迂曲度和渗透率的关系[J]. 华北科技学院学报, 2016, 13(4): 56-58. DOI:10.3969/j.issn.1672-7169.2016.04.013] |
| [19] |
Yuan Meijuan. Effective permeability of Reiner-Philippoff fluid in a fractal capillary[J]. Journal of Wuhan University of Science and Technology, 2013, 36(2): 158-160. [员美娟. 分形毛细管中 Reiner-Philippoff 非牛顿流体的有效渗透率研究[J]. 武汉科技大学学报:自然科学版, 2013, 36(2): 158-160.] |
| [20] |
Yuan Zhe,Liu Pengcheng. A new capillary pressure model using fractal geometry for coal porous media[J]. Science Technology and Engineering, 2015, 15(9): 63-67. [袁哲,刘鹏程. 一个适用于煤岩的新的分形毛管力模型[J]. 科学技术与工程, 2015, 15(9): 63-67. DOI:10.3969/j.issn.1671-1815.2015.09.010] |
| [21] |
Bear J.Dynamics of fluids in porous media[M].New York:Elsevier,1972.
|
| [22] |
Dullien F A L.Porous media:fluid transport and pore structure[M].San Diego:Academic Press,1992.
|
| [23] |
Carman P C. Fluid flow through granular beds[J]. Chemical Engineering Research and Design, 1937, 75(1): 32-48. |
| [24] |
Sutera S P,Skalak R. The history of Poiseuille's law[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 1-20. DOI:10.1146/annurev.fl.25.010193.000245 |
| [25] |
Xu P,Yu B. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources, 2008, 31(1): 74-81. DOI:10.1016/j.advwatres.2007.06.003 |
| [26] |
Wheatcraft S W,Tyler S W. An explanation of scale‐dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry[J]. Water Resources Research, 1988, 24(4): 566-578. DOI:10.1029/WR024i004p00566 |
| [27] |
Xue Dongjie,Zhou Hongwei,Zhao Tian,et al. Algorithm of fractal dimension of rock fracture surface based on volume estimation[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1256-1261. [薛东杰,周宏伟,赵天,等. 基于体积估算岩石断面分维的算法研究[J]. 岩土工程学报, 2012, 34(7): 1256-1261.] |
| [28] |
Washburn M P,Wolters D,Yates III J R. Large-scale analysis of the yeast proteome by multidimensional protein identification technology[J]. Nature Biotechnology, 2001, 19(3): 242-247. DOI:10.1038/85686 |
| [29] |
Washburn E W. The dynamics of capillary flow[J]. Physical review, 1921, 17(3): 273-283. DOI:10.1103/PhysRev.17.273 |
| [30] |
Xue Dongjie,Zhou Hongwei,Ren Weiguang,et al. Physical Modeling on Mining-induced Energy Release of Crack Propagation in Overlying Strata Based on Steiner Minimum Tree Problem[J]. Journal of China Coal Society, 2015, 40(3): 541-547. [薛东杰,周宏伟,任伟光,等. 基于 Steiner 最小树相似模拟裂纹扩展与能量传播的机理[J]. 煤炭学报, 2015, 40(3): 541-547.] |
 2018, Vol. 50
2018, Vol. 50

