2. 河海大学 岩土工程科学研究所,江苏 南京 210098;
3. 河海大学 隧道与地下工程研究所,江苏 南京 210098
2. Geotechnical Research Inst., Hohai Univ., Nanjing 210098, China;
3. Inst. of Tunnel and Underground Eng., Hohai Univ., Nanjing 210098, China
路堤边坡的稳定性是高速公路建设中质量控制的关键环节,目前工程设计中应用较为广泛的方法是极限平衡分析法。用该方法进行稳定性分析分两步:1)对某一形状和位置已知的潜在滑动面,计算其稳定安全系数;2)对许多潜在的滑动面,确定相应最小安全系数的临界滑动面[1]。现有边坡稳定性分析的方法往往只是上述某一个步骤的解决方法[1–2],造成了两个步骤脱离开来的状况:如瑞典法等各种条分法是求解步骤1)的成熟且较精确的方法,但因其需预先确定滑动面、划分土条及公式为多项式求和的特点,使其无法真正融入到步骤2)临界滑动面的搜索过程中,目前往往仅作为安全系数的计算手段;又如遗传算法等各种搜索方法可用于确定临界滑动面,但其本身却又无法获得安全系数,且各搜索方法的搜索性都有显著的差异,都有其自身不可逾越的缺陷[2],如最突出的易陷入局部极小值的问题等。反过来,这种脱离也导致了
有学者将两步骤结合起来,以安全系数为目标函数,运用数学理论求其极小值,以期不需搜索直接解得临界滑动面和最小安全系数,但均因各自的局限性无法在实际工程上应用。如Baker[3]、Revilla[4]、Ramamurthy[5]等运用变分法求其极小值,但求解出的结果偏差较大,并不理想;之后De Josselin[6],Luceno[7]等对变分法理论应用的正确性和分析问题的局限性也都提出了质疑。为避免条分法多项式求和的特点造成变分和求偏导不易的情况,罗文强[8]和杨庚宇[9–10]等均对条分法做了改进,将安全系数表达成积分的形式,分别采用变分法和多元函数的极值条件求极小值,但其仍是条分法的一种形式,且极值条件需要对至少3个自变量求偏导解超越方程组,计算异常复杂且往往得不出结果;蒋斌松等[11]利用此法也仅仅给出了纯黏性土边坡(
为此,针对均质地基路堤,以不采用条分和搜索,将两步骤有机结合起来并给出唯一最小安全系数和临界滑动面为目的,通过对滑动面形状和位置的描述、无条分安全系数公式的推导及运用数学理论直接确定临界滑动面3方面的研究,提出一种可用于工程实际的均质地基路堤稳定性分析的新方法。
1 滑动面形状和位置的描述 1.1 自变量的选择和滑动面函数的确定路堤填土一般是均质的,当地基也为均质土时,滑动面往往为圆弧形,选取3个独立维度的自变量确定圆弧滑动面函数,方法如下:
如图1所示,路堤边坡坡率为
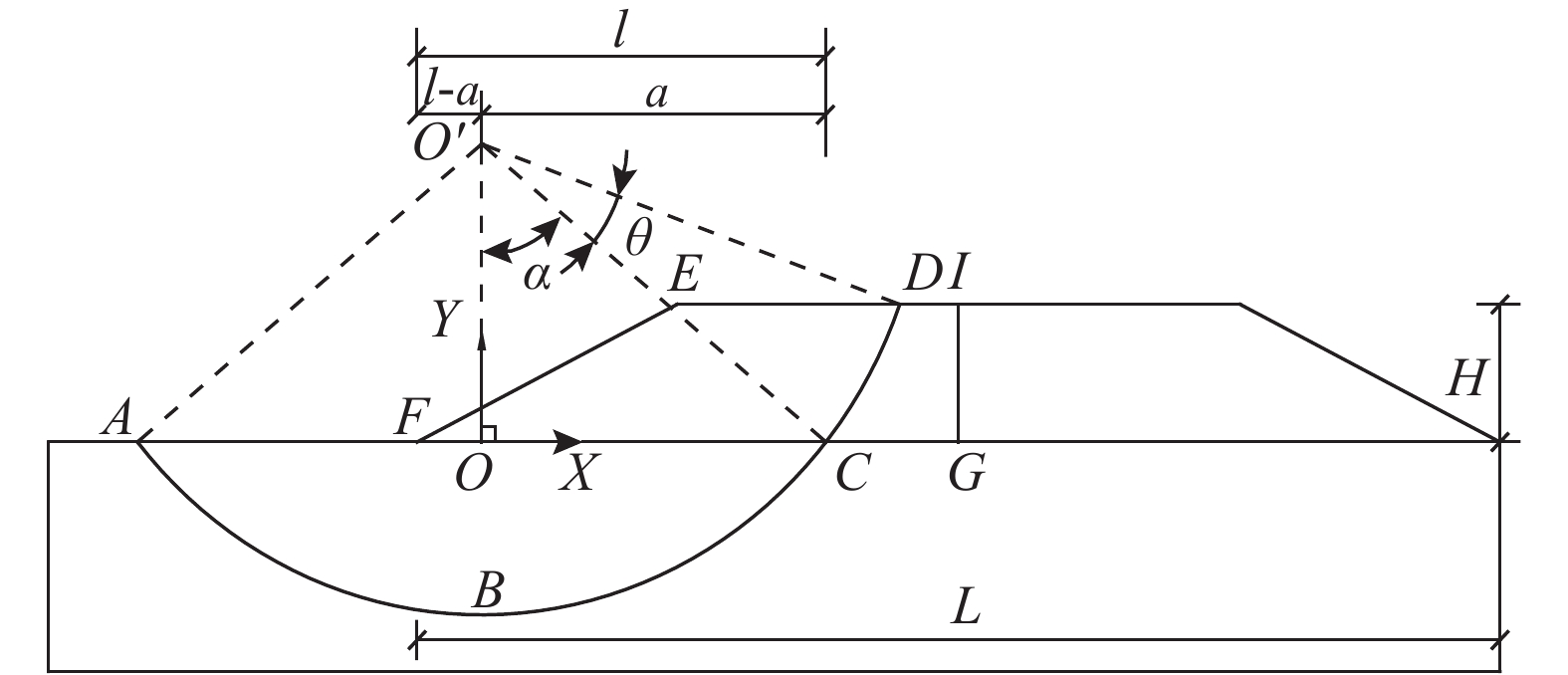 |
| 图1 自变量选取示意图 Fig. 1 Schematic of the selection of independent variables |
选取滑弧与坡脚内地平线的交点
| ${f_1}:y = kx + k\left( {l - a} \right)$ | (1) |
| ${f_2}:{x^2} + {\left( {y - a\cot \;\alpha } \right)^2} = \frac{{{a^2}}}{{{{\sin }^2}\alpha }}$ | (2) |
如图1所示,
| $0 < l < \frac{L}{2}$ | (3) |
如图1所示,
| $\frac{l}{2} < a < l$ | (4) |
如图1所示,
1)
取路堤左幅做示意图2,根据对称性,点
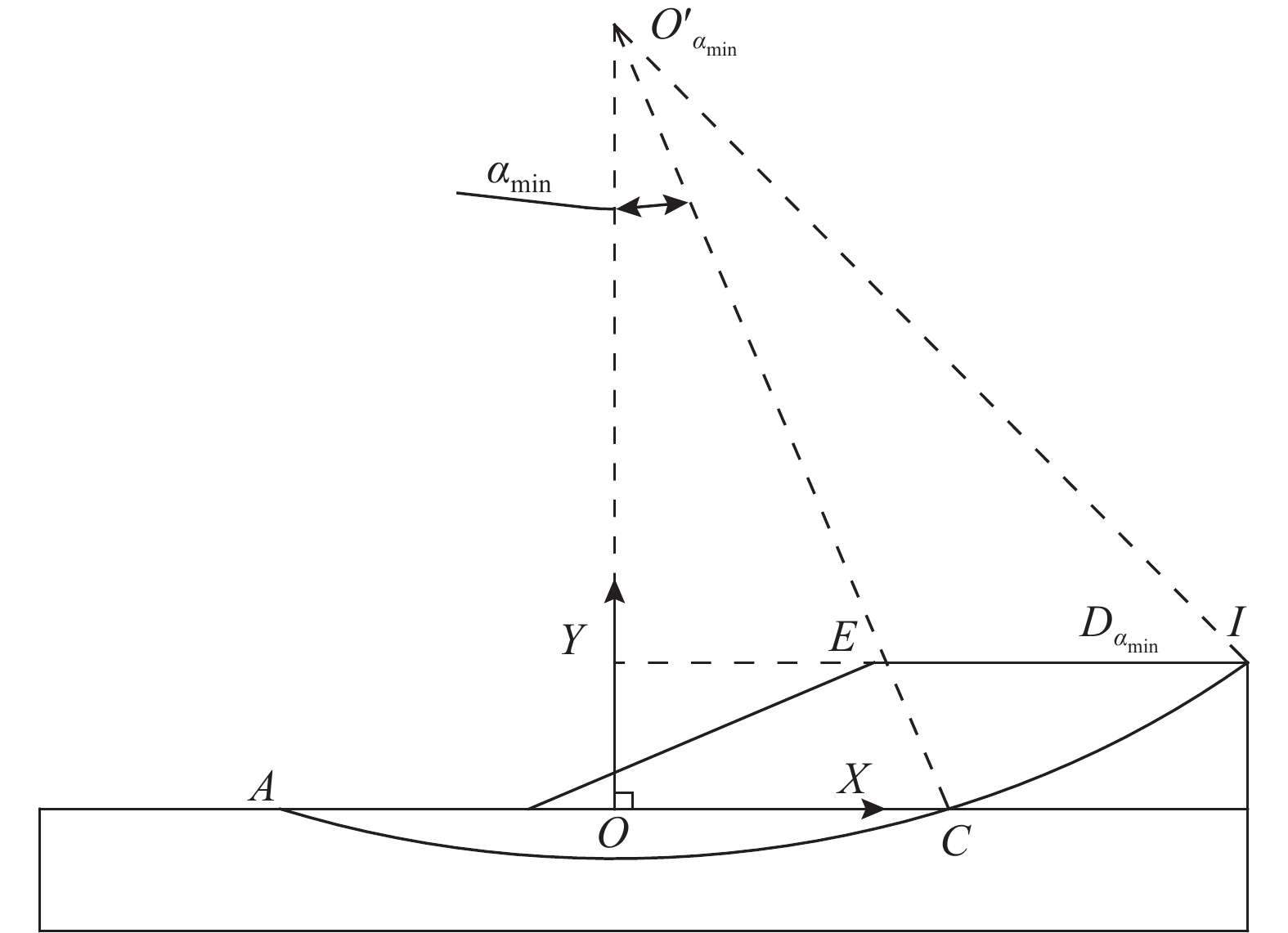 |
|
图2 |
此时
| ${a^2} +y_{O'\alpha _{\min}}^2 = x_{D\alpha _{\min }}^2 + {\left( {{y_{O'{\alpha _{\min }}}} - H} \right)^2},$ |
解得:
则
| ${\alpha _{\min }} = \arctan \frac{a}{{{y_{O'{\alpha _{\min }}}}}} = \arctan \frac{{2aH}}{{{{\left( L/2 - l + a \right)}^2} + {H^2} - {a^2}}}$ | (5) |
2)
如图3所示,当
| ${\alpha _{\max }} = \arctan \;\frac{a}{H},l > \frac{H}{k}$ | (6) |
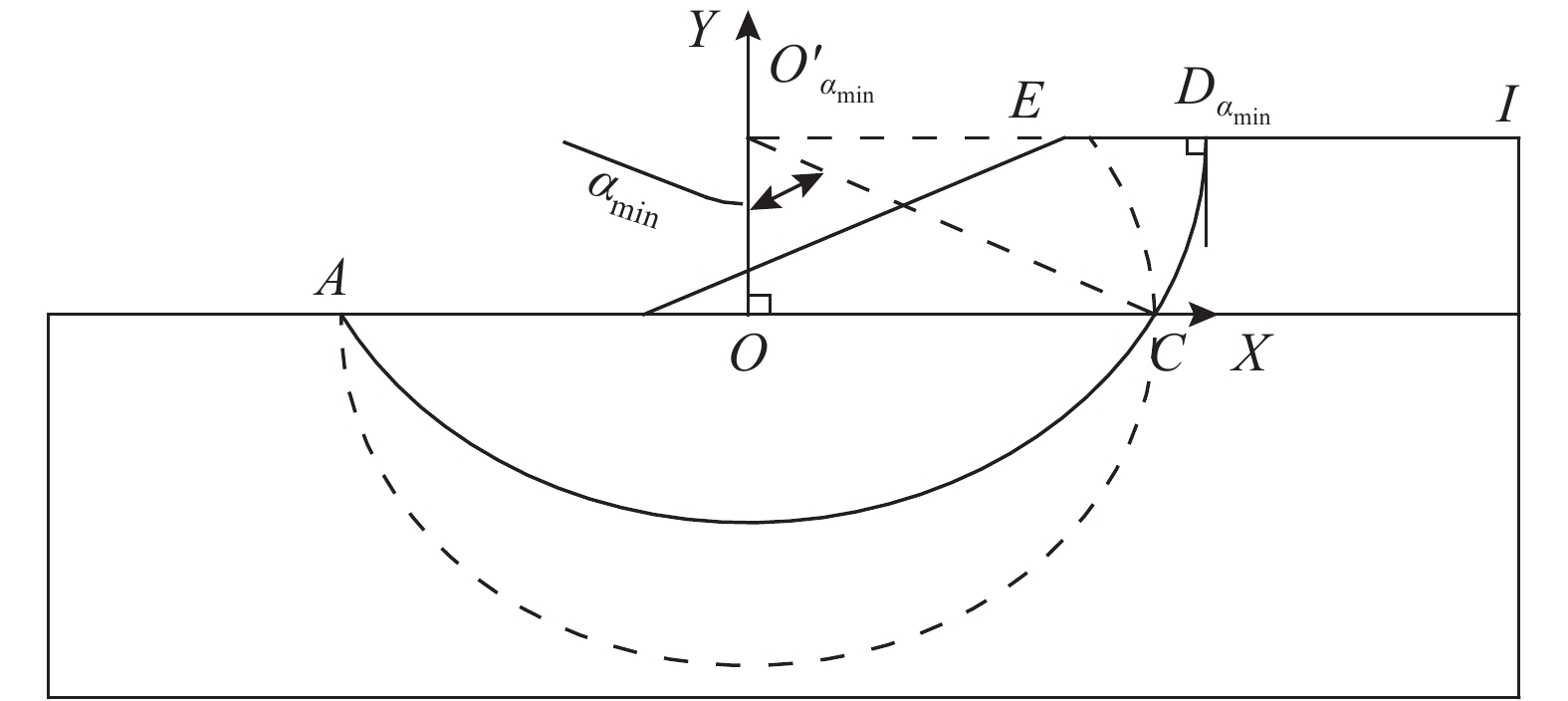 |
|
图3 |
如图4所示,当
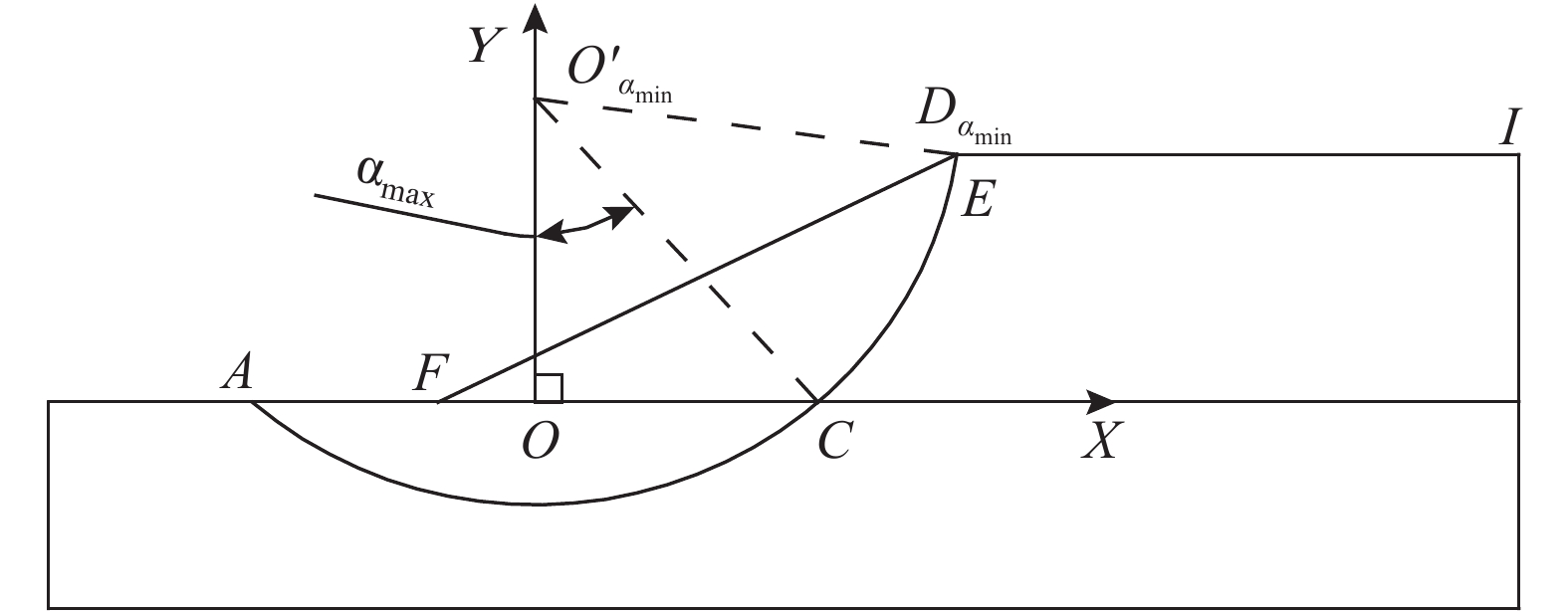 |
|
图4 |
此时
| ${a^2} + y_{O'\alpha _{\max}}^2 = x_{D\alpha _{\max }}^2 + {\left( {{y_{O'{\alpha _{\max }}}} - H} \right)^2},$ |
解得:
此时
| ${\alpha _{\max }} \!=\! \arctan \frac{a}{{{y_{O'{\alpha _{\max }}}}}} \!=\! \arctan \frac{{2aH}}{{{{\left( {{H/k} \!-\! l \!+\! a} \right)}^2} \!+\! {H^2} \!-\! {a^2}}},l < \frac{H}{k}$ | (7) |
安全系数公式的构造即已知滑动面函数
如图5所示,潜在滑动体受到自身重力、下部土体对其的抗剪力和法向力的作用。
设滑动面上的平均剪应力为
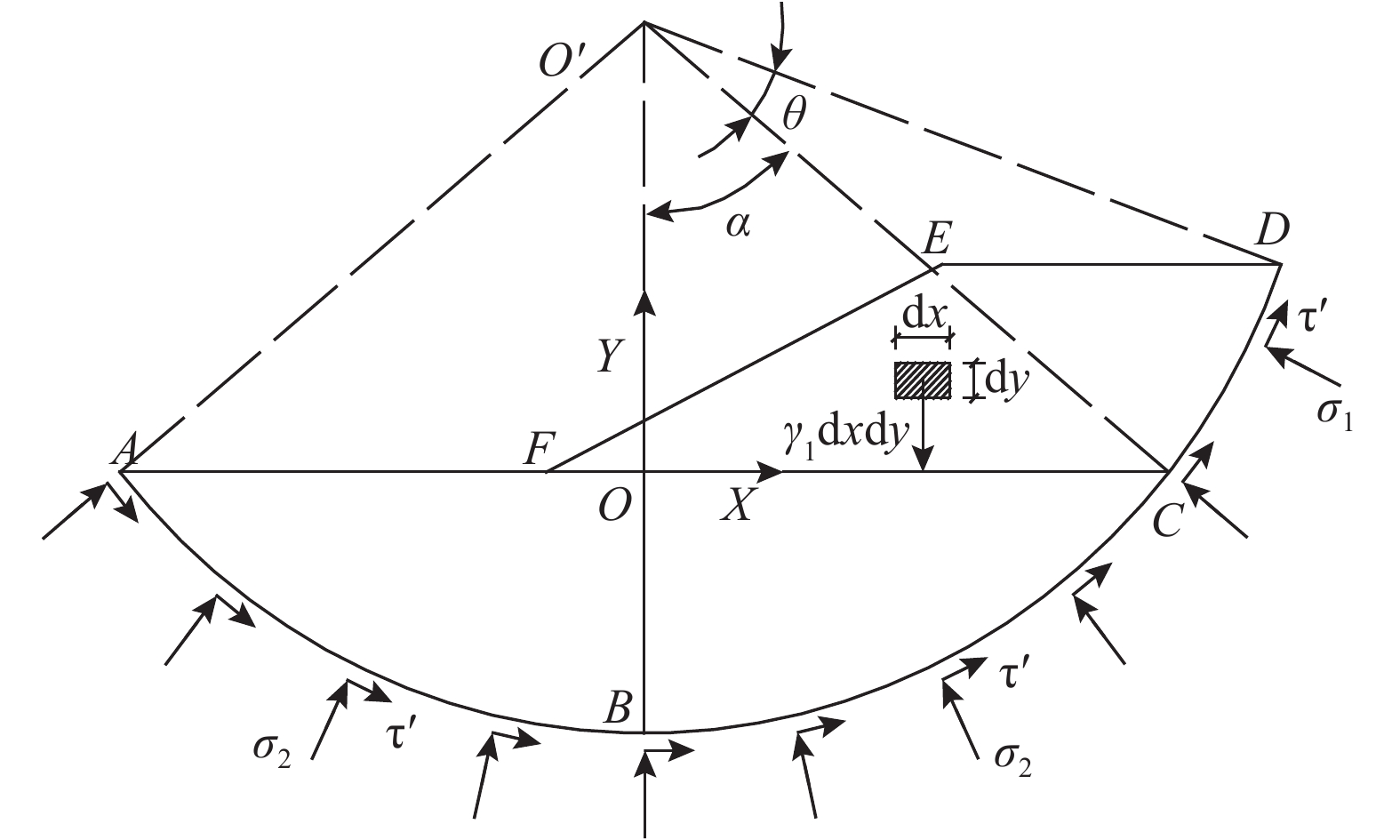 |
| 图5 潜在滑动体受力分析示意图 Fig. 5 Mechanical analysis of landslide body |
2.1 力矩平衡
根据力矩平衡条件,潜在滑动体所受的力对圆心
| $\sum {M = } {M_\sigma } + {M_G}{\rm{ + }}{M_{\tau '}} = 0$ | (8) |
式中:
在土体
| ${M_G} = - \iint\limits_{{S_{CDEF}}} {x{\gamma _1}{\rm d}x{\rm d}y} = - {\gamma _1}\int\limits_0^H {{\rm d}y\int\limits_{{f_1}\left( y \right)}^{{f_2}\left( y \right)} {x{\rm d}x} } $ | (9) |
式中,
抗剪力对圆心
| ${M_{\tau '}} = \left( {2\alpha + \theta } \right){R^2}\tau $ | (10) |
式中,
| ${X_D} = \sqrt {\frac{{{a^2}}}{{{{\sin }^2}\alpha }} - {{\left( {H - a\cot \;\alpha } \right)}^2}} {\rm{ = }}\sqrt {{a^2} - {H^2} + 2Ha\cot \;\alpha } $ | (11) |
则
| $\theta = \arcsin \frac{{\sqrt {\left( {{a^2} - {H^2}} \right){{\sin }^2}\alpha + Ha\sin\left( 2\alpha \right)} }}{a} - \alpha $ | (12) |
将式(9)~(12)代入式(8),解得滑动面上的平均剪应力
| $\tau {\rm{ = }}\tau '{\rm{ = }}\frac{{{\gamma _1}{{\sin }^2}\alpha }}{{2{a^2}}}\frac{{ - \displaystyle\frac{{1 + {k^2}}}{{3{k^2}}}{H^3} + \left( {a\cot \;\alpha - \frac{{a - l}}{k}} \right){H^2} + \left( {2a - l} \right)lH}}{{\left( {\alpha + \arcsin \displaystyle\frac{{\sqrt {\left( {{a^2} - {H^2}} \right){{\sin }^2}\alpha + Ha\sin \left(2\alpha \right)} }}{a}} \right)}}$ | (13) |
根据水平方向的静力平衡条件,潜在滑动体所受的力在
| $\int_{ - \alpha }^{\alpha + \theta } {\tau 'R\cos\; \eta {\rm d}\eta } - \int_\alpha ^{\alpha + \theta } {{\sigma _1}R\sin \;\eta {\rm d}\eta } {\rm{ = }}0$ | (14) |
解得滑动面
| ${\sigma _1}{\rm{ = }}\frac{{\sin\; \alpha + \sin \left( {\alpha + \theta } \right)}}{{\cos\; \alpha - \cos \left( {\alpha + \theta } \right)}}\tau '$ | (15) |
由几何关系对式(15)进行简化得:
| ${\sigma _1}{\rm{ = }}\frac{{\displaystyle\frac{a}{R} + \displaystyle\frac{{{X_D}}}{R}}}{{\cos \;\alpha - \displaystyle\frac{{R\cos\; \alpha - H}}{R}}}\tau ' = \frac{{a + \sqrt {{a^2} - {H^2} + 2Ha\cot \;\alpha } }}{H}\tau '$ | (16) |
根据竖直方向的静力平衡条件,潜在滑动体所受的力在
| $\sum {{F_Y}} = {F_{\tau 'Y}} + {F_{{\sigma _1}Y}} + {F_{{\sigma _2}Y}} + {F_{GY}} = 0$ | (17) |
式中,
| ${F_{\tau 'Y}} = \int_{ - \alpha }^{\alpha + \theta } {\tau 'R\sin\; \eta {\rm d}\eta } = \tau 'R\left( {\cos \;\alpha - \cos \left( {\alpha + \theta } \right)} \right)$ | (18) |
| ${F_{{\sigma _1}Y}} = \int_\alpha ^{\alpha + \theta } {{\sigma _1}R\cos\; \eta {\rm d}\eta } = {\sigma _1}R\left( {\sin \left( {\alpha + \theta } \right) - \sin \;\alpha } \right)$ | (19) |
| ${F_{{\sigma _2}Y}} = \int_{ - \alpha }^\alpha {{\sigma _2}R\cos \;\eta {\rm d}\eta } = 2{\sigma _2}R\sin \;\alpha $ | (20) |
| ${F_{GY}}{\rm{ = }}{\gamma _2}{S_2} + {\gamma _1}{S_1}$ | (21) |
其中:
| $ \begin{aligned}[b]& {S_2} = {S_{O'ABC}} - {S_{O'AC}} = \frac{1}{2} \times 2\alpha \times {R^2} - \\& \quad\quad \frac{1}{2} \times 2a \times a\cot \;\alpha = {a^2}\left( {\frac{\alpha }{{{{\sin }^2}\alpha }} - \cot \;\alpha } \right)\end{aligned} $ | (22) |
在土体
| $\begin{aligned} {S\!_1}\!\! =\!\!\!\! & \iint\limits_{{S_{CDEF}}} \!\!\!{{\rm d}x{\rm d}y}\!\! =\!\!\!\!\int\limits_0^H \!\!\!{{\rm d}y\!\!\!\int\limits_{{f_{1\left( y \right)}}}^{{f_{2\left( y \right)}}}\!\!\!{{\rm d}x} } \!\!=\!\!\!\!\int\limits_0^H \!\!{\left(\!\!\! {\sqrt {\frac{{{a^2}}}{{{{\sin }^2}\alpha }}\!\!-\!\! V{{\left( {y\!\! -\!\! a\cot \;\alpha } \right)}^2}}\!\!-\! \frac{y}{k}}\right.} \!- \\ & \Bigg.{a + l} \Bigg)\cdot {\rm d}y=- \frac{1}{{2k}}{H^2}\! +\! \left( {l \!-\! a \!+\! \frac{1}{2}\sqrt {{a^2} \!-\! {H^2}\! +\! 2aH\cot \;\alpha } } \right)H + \\ & \frac{{{a^2}}}{{2{{\sin }^2}\alpha }}\left( {\arctan \left( {\cot \;\alpha } \right) - \arctan \frac{{a\cot \;\alpha - H}}{{\sqrt {{a^2} \!-\! {H^2} \!+\! 2aH\cot \;\alpha } }}} \right)+\\ & \frac{1}{2}a\cot \;\alpha \left( {a - \sqrt {{a^2} - {H^2} + 2aH\cot \;\alpha } } \right)\end{aligned} $ | (23) |
将式(18)~(23)代入式(17),解得滑动面
| ${\sigma _2}{\rm{ = }}\frac{{{\gamma _1}{S_1} + {\gamma _2}{S_2}}}{{2a}} - \tau '\cot\; \alpha $ | (24) |
设
| $\left\{ \begin{aligned}& {\tau _{\rm f1}} = {c_1} + \frac{{a + \sqrt {{a^2} - {H^2} + 2Ha\cot \;\alpha } }}{H}\tau '\tan \;{\varphi _1},\\& {\tau _{\rm f2}}{\rm{ = }}{c_2} + \left( {\frac{{{\gamma _1}{S_1} + {\gamma _2}{S_2}}}{{2a}} - \tau '\cot \;\alpha } \right)\tan\; {\varphi _2}\end{aligned} \right.$ | (25) |
则整个滑动面上的平均抗剪强度
| ${\tau _{\rm f}} = \frac{{\theta R{\tau _{\rm f}}_1 + 2\alpha R{\tau _{\rm f}}_2}}{{\left( {2\alpha + \theta } \right)R}} = \frac{{\theta {\tau _{\rm f}}_1 + 2\alpha {\tau _{\rm f}}_2}}{{2\alpha + \theta }}$ | (26) |
则安全系数公式
| $\begin{aligned} F\!\! =\!\! & \frac{{{\tau _{\rm f}}}}{\tau }\!\! =\!\! \frac{\theta }{{\left( {2\alpha \!\!+\!\! \theta } \right)\tau }}\!\left(\!{{c_1} \!\!+\!\! \frac{{\tau '\tan\; {\varphi _1}}}{H} \!\left(\! {a \!\!+\!\! \sqrt {{a^2} - {H^2} + 2Ha\cot \;\alpha } } \right)}\!\!\right)\!+ \\ & \quad\quad \frac{{2\alpha }}{{\left( {2\alpha + \theta } \right)\tau }}\left( {{c_2} + \left( {\frac{{{\gamma _1}{S_1} + {\gamma _2}{S_2}}}{{2a}} - \tau '\cot \;\alpha } \right)\tan \;{\varphi _2}} \right)\end{aligned}$ | (27) |
式中,
对目标函数中自变量各维度求偏导,利用多元函数极值条件求得所有的极小值点,再对所有极小值点进行比较确定最小值点,可确保临界滑动面确定过程的全局性。由于对3个维度求偏导解3元超越方程组相当复杂,采取降维度求极值(只对2个维度求偏导)与迭代计算相结合的办法简化确定过程。
基本思路为(图1):先固定点
当
| $G\left( {a,\alpha } \right) = {\tau _{\rm f}} - \tau = \frac{{\theta {\tau _{\rm f}}_1 + 2\alpha {\tau _{\rm f}}_2}}{{2\alpha + \theta }} - \tau $ | (28) |
求
将式(30)~(34)中各变量的偏导代入式(29)即可求解,但式(29)为超越方程组目前尚无法得出解析解,故本文用Newton法求
在
| $\left\{ \begin{aligned} & \frac{{\partial G}}{{\partial a}} = \frac{{\left( {{\tau _{\rm f}}_1\displaystyle\frac{{\partial \theta }}{{\partial a}} + \theta \displaystyle\frac{{\partial {\tau _{\rm f}}_1}}{{\partial a}} + 2\alpha \displaystyle\frac{{\partial {\tau _{\rm f}}_2}}{{\partial a}}} \right)\left( {2\alpha + \theta } \right) - \left( {\theta {\tau _{\rm f}}_1 + 2\alpha {\tau _{\rm f}}_2} \right)\displaystyle\frac{{\partial \theta }}{{\partial a}}}}{{{{\left( {2\alpha + \theta } \right)}^2}}} - \displaystyle\frac{{\partial \tau }}{{\partial a}} = 0 , \\ & \frac{{\partial G}}{{\partial \alpha }} = \displaystyle\frac{{\left( {{\tau _{\rm f}}_1\displaystyle\frac{{\partial \theta }}{{\partial \alpha }} + \theta \frac{{\partial {\tau _{\rm f}}_1}}{{\partial \alpha }} + 2{\tau _{\rm f}}_2 + 2\alpha \displaystyle\frac{{\partial {\tau _{\rm f}}_2}}{{\partial \alpha }}} \right)\left( {2\alpha + \theta } \right) - \left( {\theta {\tau _{\rm f}}_1 + 2\alpha {\tau _{\rm f}}_2} \right)\left( {2 + \displaystyle\frac{{\partial \theta }}{{\partial \alpha }}} \right)}}{{{{\left( {2\alpha + \theta } \right)}^2}}} - \displaystyle\frac{{\partial \tau }}{{\partial \alpha }} = 0 \end{aligned} \right.$ | (29) |
| $\left\{ \begin{aligned}& \frac{{\partial \tau }}{{\partial a}} = \frac{{\gamma H\sin \;\alpha }}{{6{a^3}{k^2}{{(2\alpha + \theta )}^2}}}\left( \Bigg({\left( {3Hk(a - l) + 3{k^2}l(l - 2a) + {H^2}\left( {{k^2} + 1} \right)} \right)\sin\; \alpha - 3aH{k^2}\cos \;\alpha } \right)a\frac{{\partial \theta }}{{\partial a}}+\Bigg. \\& \quad\quad \Bigg. (2\alpha + \theta )\left( {\left( {3Hk(a - 2l) + 6{k^2}l(l - a) + 2{H^2}\left( {{k^2} + 1} \right)} \right)\sin \;\alpha - 3aH{k^2}\cos \;\alpha } \right)\Bigg) , \\& \frac{{\partial \tau }}{{\partial \alpha }} = \frac{{\gamma H}}{{6{a^2}{k^2}{{(2\alpha + \theta )}^2}}}\Bigg( \left( {\left( {3Hk(a - l) + 3{k^2}l(l - 2a) + {H^2}\left( {{k^2} + 1} \right)} \right)\sin \;\alpha - 3aH{k^2}\cos \;\alpha } \right)\sin \;\alpha \left(\frac{{\partial \theta }}{{\partial \alpha }} + 2\right)-\Bigg.\\& \quad\quad \Bigg. (2\alpha + \theta )\left( {\left( {3Hk(a - l) + 3{k^2}l(l - 2a) + {H^2}\left( {{k^2} + 1} \right)} \right)\sin \left(2\alpha\right) - 3aH{k^2}\cos \left(2\alpha \right)} \right)\Bigg) \end{aligned} \right.$ | (30) |
| $\left\{ \begin{aligned}& \frac{{\partial {\tau _{\rm f1}}}}{{\partial a}} = \frac{{\tan \;{\phi _1}}}{H}\left( {\left( {\sqrt {{a^2} - {H^2} + 2aH\cot \;\alpha } + a} \right)\frac{{\partial \tau }}{{\partial a}} + \tau \left( {\frac{{a + H\cot \;\alpha }}{{\sqrt {{a^2} - {H^2} + 2aH\cot \;\alpha } }} + 1} \right)} \right) , \\& \frac{{\partial {\tau _{\rm f1}}}}{{\partial \alpha }} = \tan\; {\phi _1}\left( {\frac{{\left( {\sqrt {{a^2} - {H^2} + 2aH\cot\; \alpha } + a} \right)}}{H}\frac{{\partial \tau }}{{\partial \alpha }} - \frac{{\tau a{{\csc }^2}\alpha }}{{\sqrt {{a^2} - {H^2} + 2aH\cot\; \alpha } }}} \right) \end{aligned} \right.$ | (31) |
| $\left\{ \begin{aligned}& \frac{{\partial {\tau _{\rm f2}}}}{{\partial a}} = \frac{{\tan\; {\phi _2}}}{{2{a^2}}}\left( {a\gamma \frac{{\partial {S_1}}}{{\partial a}} - 2{a^2}\cot \;\alpha \frac{{\partial \tau }}{{\partial a}} - \gamma \left( {{a^2}\left( {\cot\; \alpha - \alpha {{\csc }^2}\alpha } \right) + {S_1}} \right)} \right) , \\& \frac{{\partial {\tau _{\rm f2}}}}{{\partial \alpha }} = \frac{{\tan \;{\phi _2}}}{{2a}}\left( {\gamma \frac{{\partial {S_1}}}{{\partial \alpha }} - 2a\cot\; \alpha \frac{{\partial \tau }}{{\partial \alpha }} + 2a{{\csc }^2}\alpha (a\gamma - a\gamma \alpha \cot\; \alpha + \tau )} \right) \end{aligned} \right.$ | (32) |
| $\left\{ \begin{aligned} & \frac{{\partial {S_1}}}{{\partial a}} = \left( {a - \sqrt {{a^2} - {H^2} + 2aH\cot \;\alpha } } \right)\cot \;\alpha + \left( {\arctan \frac{{H - a\cot\; \alpha }}{{\sqrt {{a^2} - {H^2} + 2aH\cot\; \alpha } }} + \arctan \left( {\cot \;\alpha } \right)} \right)a{\csc ^2}\alpha - H , \\& \frac{{\partial {S_1}}}{{\partial \alpha }} = - a{\csc ^2}\alpha \left( {\left( {\arctan \frac{{H - a\cot\; \alpha }}{{\sqrt {{a^2} - {H^2} + 2aH\cot\; \alpha } }} + \arctan \left( {\cot \;\alpha } \right)} \right)a\cot \;\alpha + a - \sqrt {{a^2} - {H^2} + 2aH\cot \;\alpha } } \right) \end{aligned} \right.$ | (33) |
| $\left\{ \begin{aligned}& \frac{{\partial \theta }}{{\partial a}} = \frac{{H\sin \;\alpha \left( {H\sin \;\alpha - a\cos\; \alpha } \right)}}{{a\sqrt {{{\left( {a\cos \alpha - H\sin \alpha } \right)}^2}} \sqrt {\left( {{a^2} - {H^2}} \right){{\sin }^2}\alpha + aH\sin \left(2\alpha \right)} }} , \\& \frac{{\partial \theta }}{{\partial \alpha }}\!\! =\!\! - 1 \!\!+\!\! \frac{{aH\cos \left(2\alpha \right)\!\!+\!\! \left( {{a^2}\!\! - \!\!{H^2}} \right)\cos\; \alpha \sin\; \alpha }}{{\sqrt {{{\left( {a\cos \;\alpha \!\!-\!\! H\sin\; \alpha } \right)}^2}} \sqrt {\left( {{a^2} \!\!-\!\! {H^2}} \right){{\sin }^2}\alpha \!\!+\!\! aH\sin \left(2\alpha \right)} }} \end{aligned} \right.$ | (34) |
在式(3)的范围内变换
由程序求得每一个
算例选取《土力学》[12]中的例题7-2。已知条件为:土坡高度
| 表1 安全系数的计算过程和结果 Tab. 1 Calculation process and results of the safety factor |
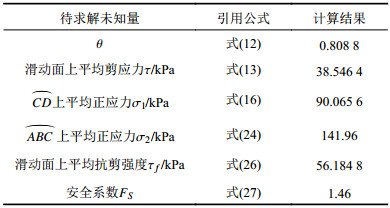 |
作为对比,用简化Bishop法、Spencer法和Morgenstern-Price法3种条分法分别求解该算例,为统一精度,土条个数均取10个(与例题瑞典法相同),具体计算过程此处略,将不同方法的结果列于表2。
|
表2 不同方法求解的算例稳定安全系数
|
 |
由表2可知,不同方法所得的安全系数很接近,进一步验证了满足平衡条件下,所得的安全系数对滑面正应力分布不甚敏感,可见设平均正应力和平均切应力的方法可取,本文方法和严格条分法的Spencer法、Morgenstern-Price法的精度很接近,偏差0.68%。
4.2 临界滑动面确定的准确性验证设该算例路堤顶宽34 m(双向6车道),则路堤底宽
| 表3 临界滑动面确定程序极小值求解和迭代计算过程及结果 Tab. 3 Process and results of the critical sliding surface determining program |
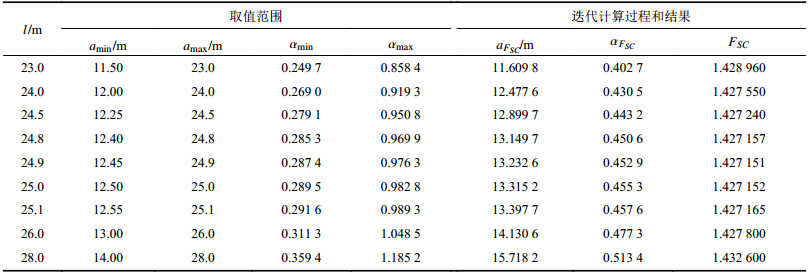 |
由表3可知,对
作为对比,利用Geo-Slope商业软件,分别基于瑞典法、简化Bishop法、Spencer法和M-P法与传统搜索方法(本文采用穷举法)的组合方式,计算各潜在滑动面(实际运算数量为2 160个)的安全系数,并取最小值为该算例路堤边坡的最小安全系数,对应滑动面为临界滑动面。建模过程中的几点关键处理有:考虑对称性取路堤的一半建立模型,滑入点范围为路堤顶面,滑出点范围为坡脚至坡脚外23 m,各条分法计算安全系数时土条个数均取30个以提高精度,计算模型见图6。
以模型左下角为坐标原点,将各方法的路堤边坡最小安全系数、临界滑动面的圆心坐标和半径列于表4,并将各法的临界滑动面位置绘于图7。
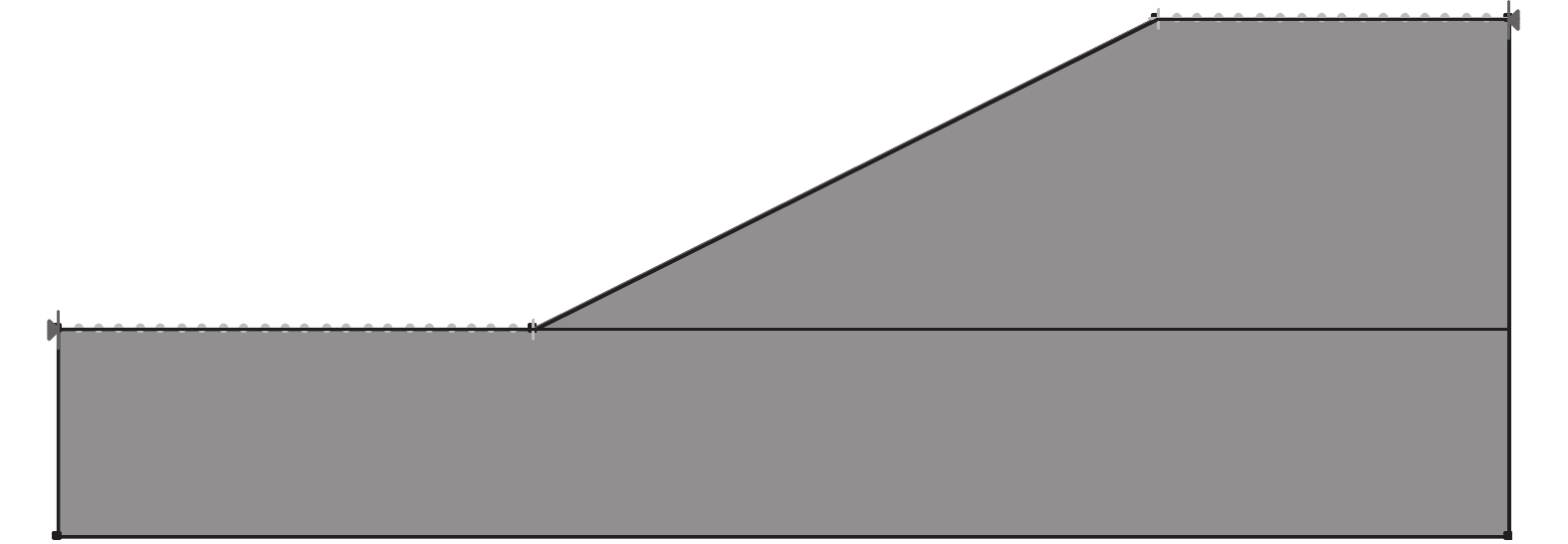 |
| 图6 Geo-Slope计算模型 Fig. 6 Calculation model of Geo-Slope |
|
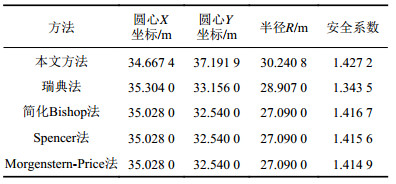
表4 各方法的路堤边坡安全系数及临界滑动面位置 Tab. 4
|
 |
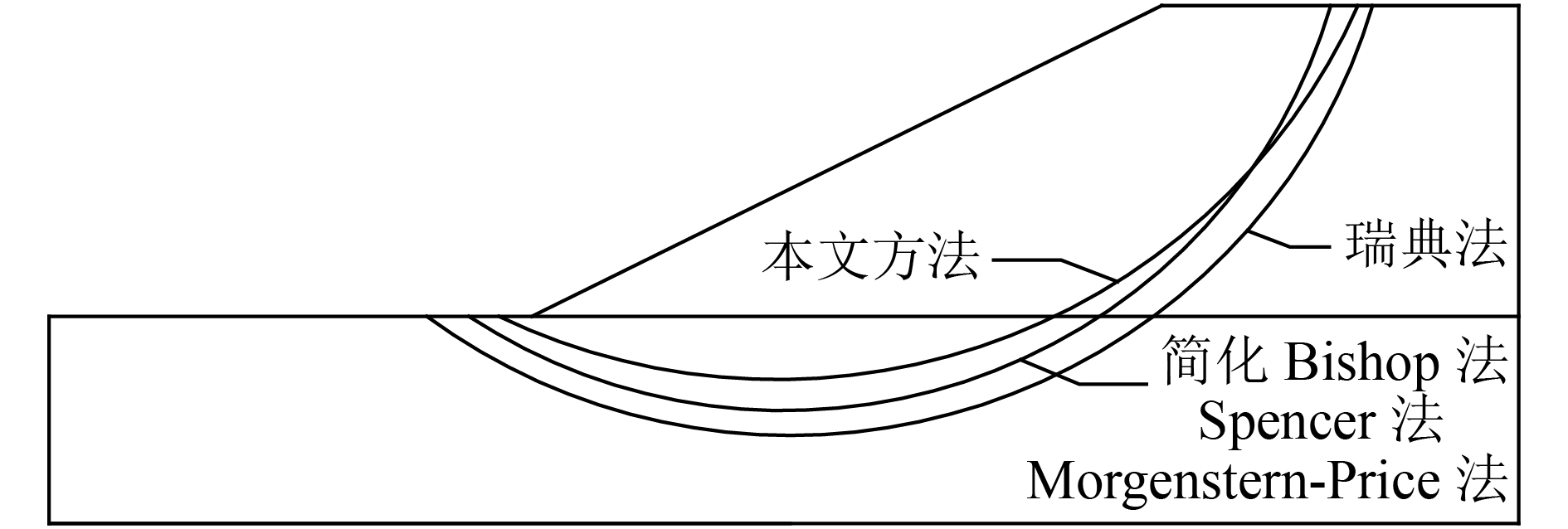 |
| 图7 各方法的临界滑动面位置示意图 Fig. 7 Critical sliding surface position of each method |
由表4和图7可知:瑞典法的潜在滑动体范围更大,滑弧入土更深,滑入点和滑出点的水平距离更大,其安全系数也最小,且较其他各法而言小的幅度较大。其根本原因是瑞典法完全忽略了条间力对滑面底部正应力的贡献,正应力最小,抗剪强度也最小,工程上更偏于保守;本文方法与简化Bishop法、Spencer法、M-P法解得的临界滑动面位置(潜在滑动体范围)相差不大,安全系数也很接近,如比M-P法大0.87%。
采用平均正应力这种形式,其实质是为了在整个潜在滑动体积分域内实现整体极限平衡分析;且在严格满足极限平衡条件的情况下,安全系数对正应力的分布并不敏感,只要精度满足工程需要,对正应力进行合理的处理或假设是可行的。由算例可见本文方法精度较高,且其最大的优点在于经自变量的选择和正应力的处理,可直接运用数学理论确定临界滑动面,即确定安全系数的最小值。
5 结 论提出一种均质地基路堤无条分稳定安全系数计算及临界滑动面确定的新方法,并编制了计算程序,该法不需搜索即可直接确定临界滑动面的位置,并可给出唯一的最小安全系数;同时该法也适用于其他类似的填挖方工程,如均质的土坡和基坑边坡、均质地基上修建的土坝、防洪/防波堤等。
1)以滑弧与坡脚内地平线的交点与坡脚的距离、该交点与圆心在地平线投影点的距离、该交点和圆心投影点所在半径的夹角,共3个维度的自变量可唯一确定圆弧形滑动面的位置,其取值范围不需经验假定,可实现临界滑动面确定范围的全局性。
2)严格满足极限平衡条件的情况下,安全系数对滑面底部正应力的分布并不敏感,对正应力进行合理的处理或假设,以潜在滑动体为研究对象进行整体极限平衡分析,可得出合理的安全系数值。
3)基于二元函数的极值条件,对积分形式的平衡方程解出的安全系数函数表达式,通过降维度求极小值与迭代计算结合,可直接确定临界滑动面位置,克服了传统搜索方法易陷入局部极小值的缺点。
4)算例结果表明:同一滑动面的安全系数,本文方法比M-P法小0.68%;本文方法确定的临界滑动面位置与严格满足极限平衡条件的条分法+传统搜索方法所确定的临界滑动面位置偏差较小;临界滑动面对应的路堤边坡最小安全系数比M-P条分法+传统搜索方法所得结果大0.87%。
| [1] |
Chen Zuyu,Shao Changming. The use of the method of optimization for minimizing safety factors in slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 1988, 10(4): 1-13. [陈祖煜,邵长明. 最优化方法在确定边坡最小安全系数方面的应用[J]. 岩土工程学报, 1988, 10(4): 1-13. DOI:10.3321/j.issn:1000-4548.1988.04.001] |
| [2] |
Wang Chenghua,Xia Xuyong. State-of-the-art:Methods for searching critical slip surface in slope stability analysis[J]. Building Science Research of Sichuan, 2002, 28(3): 34-39. [王成华,夏绪勇. 边坡稳定分析中的临界滑动面搜索方法述评[J]. 四川建筑科学研究, 2002, 28(3): 34-39. DOI:10.3969/j.issn.1008-1933.2002.03.014] |
| [3] |
Baker R,Garber M.Variational approach to slope stability[C]//Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering.Tokyo:The Japanese Society of Soil Mechanics and Foundation Engineering,1977,2:9–12.
|
| [4] |
Revilla J,Castillo E. The calculus of variations applied to stability of slopes[J]. Geotechnique, 1977, 27(1): 1-11. DOI:10.1680/geot.1977.27.1.1 |
| [5] |
Ramamurthy T,Narayan C G P,Bhatkar V P.Variational method for slope stability analysis[C]//Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering.Tokyo:The Japanese Society of Soil Mechanics and Foundation Engineering,1977:139–142.
|
| [6] |
De Josselin,De Jong G. Application of the calculus of variations to the vertical cut off cohesive frictionless soil[J]. Geotechnique, 1980, 30(1): 1-16. DOI:10.1680/geot.1980.30.1.1 |
| [7] |
Luceno A,Castillo E.Evaluation of variational methods in slope analysis[C]//International Symposium on Landslides.New-Delhi:Sarita Prakashan,1980:255–258.
|
| [8] |
Luo Wenqiang,Zhang Zhuoyuan,Huang Runqiu,et al. Model of calculus of variation used for determination of sliding surface[J]. Journal of Yangtze River Scientific Research Institute, 2000, 17(3): 35-37. [罗文强,张倬元,黄润秋,等. 滑动面确定的变分法模型[J]. 长江科学院院报, 2000, 17(3): 35-37. DOI:10.3969/j.issn.1001-5485.2000.03.009] |
| [9] |
杨庚宇. 土坡稳定分析中条分法的解析计算[J]. 力学与实践, 1995, 17(2): 59-61. |
| [10] |
杨庚宇,赵少飞.土坡稳定分析圆弧滑动法的解析解[J].工程力学,1998(增刊):440–444.
|
| [11] |
Jiang Binsong,Lyu Aizhong,Cai Meifeng. Analysis of stability for cohesive soil slopes[J]. Engineering Mechanics, 2003, 20(5): 204-208. [蒋斌松,吕爱钟,蔡美峰. 纯粘土边坡稳定性的解析计算[J]. 工程力学, 2003, 20(5): 204-208. DOI:10.3969/j.issn.1000-4750.2003.05.039] |
| [12] |
卢廷浩.土力学[M].南京:河海大学出版社,2002.
|
| [13] |
殷宗泽.土工原理[M].北京:中国水利水电出版社,2007.
|
| [14] |
Cao Ping,Zhang Ke,Wang Yixian,et al. Mixed search algorithm of critical slip surface of complex slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 814-821. [曹平,张科,汪亦显,等. 复杂边坡滑动面确定的联合搜索法[J]. 岩石力学与工程学报, 2010, 29(4): 814-821.] |
| [15] |
Zou Guangdian. A global optimization method of the slice method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 309-312. [邹广电. 边坡稳定分析条分法的一个全局优化算法[J]. 岩土工程学报, 2002, 24(3): 309-312. DOI:10.3321/j.issn:1000-4548.2002.03.009] |
 2018, Vol. 50
2018, Vol. 50


