2. 四川大学 空天科学与工程学院,四川 成都 610065;
3. 成都大学 机械工程学院,四川 成都 610106;
4. 昆明理工大学 建筑工程学院,云南 昆明 650000
2. School of Aeronautics and Astronautics, Sichuan Univ., Chengdu 610065, China;
3. School of Mechanical Eng., Chengdu Univ., Chengdu 610106, China;
4. Inst. of Civil Eng., Kunming Univ. of Sci. and Technol., Kunming 650000, China
Q345R钢具有良好的综合机械性能,广泛用于石油、化工行业,是压力容器的主要用钢。压力容器在工作中,由于间断操作和开停工作、温度变化、运行工艺压力波动以及外加载荷的反复变化等原因,这使得压力容器在服役过程中承受交变载荷,经常发生低周、超低疲劳破坏[1]。强震时,建筑物经历高应变低周、超低周疲劳过程,交变载荷应变幅极高,疲劳寿命极短,可能只有几十个周次,在极短时间内造成巨大的灾难和财产损失[2-3]。疲劳寿命在100周次以内的疲劳,是低周疲劳的极端行为,称为超低周疲劳[4–5]。中国是地震多发区域,在强地震下,压力容器所受交变载荷与高应变超低周疲劳行为极为相似,因而作为高应变超低周疲劳问题处理。但目前在压力容器设计中,仍以钢的静强度为主要依据,这对于在长期服役和强震下压力容器的可靠性是很不够的。迄今为止,尚缺乏强震下应变强化压力容器用钢Q345R钢的超低周疲劳特性研究。因此,开展压力容器材料的低周、超低周疲劳性能研究是必要且有意义的。
近年来,关于压力容器用钢(Q345R、16MnR)、建筑结构用钢超低周疲劳以及材料预应变低周疲劳已有一些报道,例如,曾涛等[2]研究了16MnR钢高应变超低周疲劳性能,获得其循环应力响应特性以及循环应力与应变的关系,并据此建立了其寿命预测公式。陈延强等[6]研究了Q345R钢的低周、超低周疲劳性能,获得材料典型迟滞回线及低周、超低周循环应力–应变曲线以及材料疲劳特性参数。段红燕等[7]对40Cr在扭转加载条件下的超低周疲劳断裂问题进行了研究,绘制了寿命与加载试样圆弧过渡半径以及径比变化的曲线图,研究结果表明,径比越大、过渡圆弧半径越小,疲劳裂纹的产生的寿命越短。罗云蓉等[8]研究了建筑结构用钢Q235的超低周疲劳性能,研究发现,材料在超低周疲劳加载情况下,其循环响应特性、寿命预测公式以及微观失效疲劳破坏机理等方面与低周疲劳失效存在一定的差异。王时越等[9]研究了不同扭转角度下45钢的低周疲劳性能,研究结果表明,扭转预应变导致材料低周疲劳寿命降低,随着扭转预应变的增大循环应力幅随之增大。吴志煌等[10]研究了扭转预应变对35CrMo钢低周疲劳性能的影响,发现预扭转不影响材料的循环响应特征,但材料的塑性应变能、循环弹性模量以及低周疲劳寿命随着预扭转角的增大逐渐降低。
综上所述,迄今为止,尚缺乏预应变对压力容器用Q345R钢超低周疲劳性能影响的研究报道。据此,作者研究了扭转预应变对压力容器用Q345R钢超低周疲劳性能的影响,以弥补这方面研究的不足。此研究对于预应变压力容器用Q345R钢安全评估和寿命预测提供了理论依据,为压力容器的动载荷强度计算校核提供了关键技术支持。
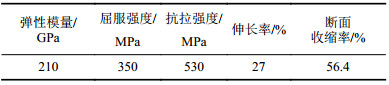
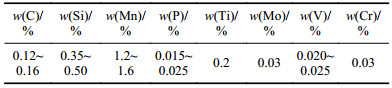
1 实验过程实验材料为压力容器用钢Q345R,热处理状态为热轧态,钢板厚度为20 mm。其力学性能和化学成分分别如表 1、2所示。
| 表1 试样钢的力学性能 Tab. 1 Mechanical propertie of test steel |
 |
| 表2 试验钢的化学成分 Tab. 2 Chemical composition of test steel |
 |
疲劳实验前,将试样加工成如图 1所示形状,并在电液伺服疲劳试验机MTS809上进行预扭转,转角分别为2°、5°等价于施加的扭转预应变为0.002和0.005。转换公式如下:
| $\gamma = \frac{{\varphi r}}{l}$ | (1) |
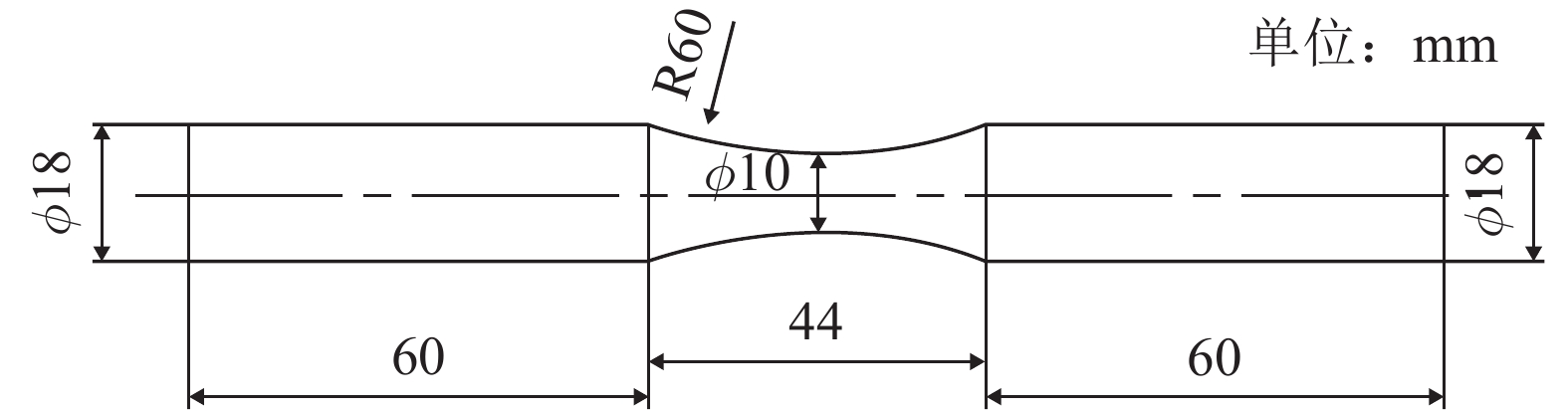 |
| 图1 预应变试件的几何尺寸 Fig. 1 Geometry of pre-strain specimen |
预扭转完成后,在MTS809液压伺服疲劳试验机上进行超低周疲劳实验,实验所用超低周疲劳试件形状为沙漏型,其几何尺寸如图 2所示,试样均由数控机床加工,并用研磨膏(W3.5)沿轴向抛光,抛光后光试样表面达到镜面光洁度。
超低周疲劳实验参照GB/T15248—2008《金属材料轴向等幅低循环疲劳实验方法》,实验在常温、大气环境下进行,采用横向引伸计控制,循环波形为三角波,频率为1 Hz,循环应变比
| $\varepsilon = (\sigma /{E})(1 - 2{\upsilon}) + 2{\varepsilon _{\rm d}}$ | (2) |
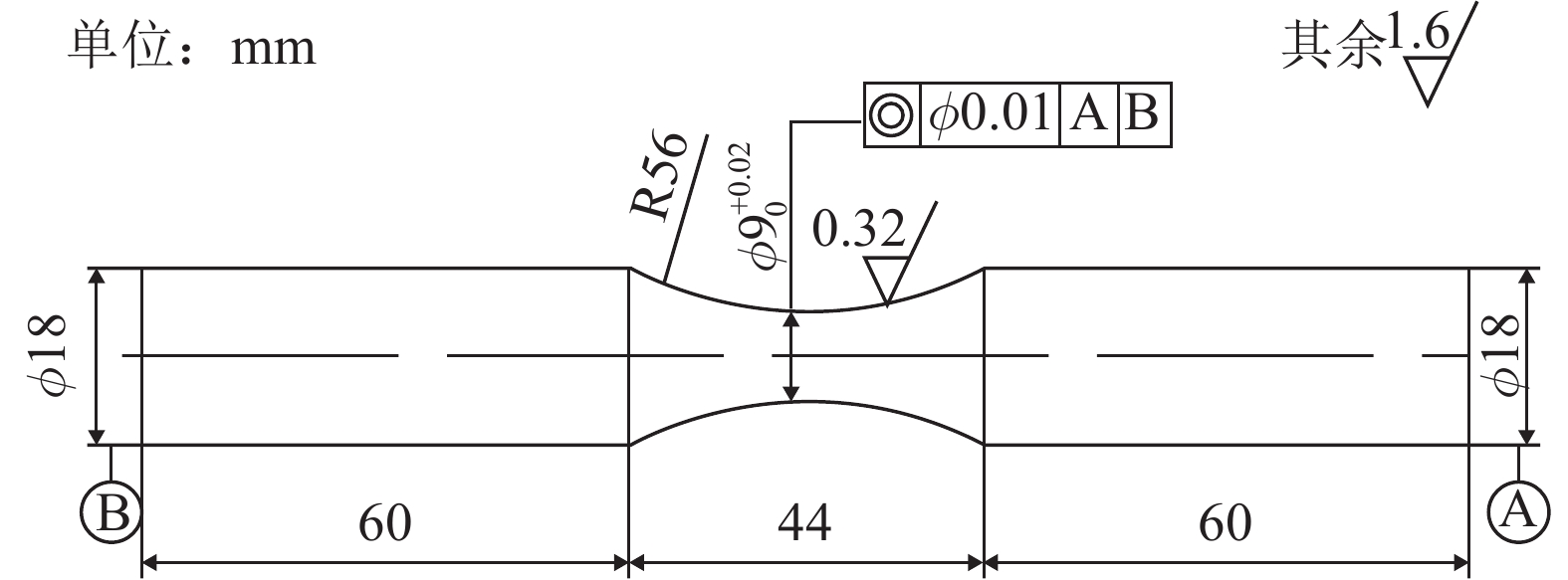 |
| 图2 超低周疲劳试件几何尺寸 Fig. 2 Geometry of ELCF specimen |
式中,
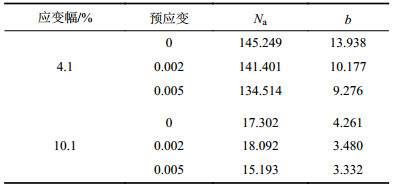
每种实验条件下测试5根试件。为讨论扭转预应变为0.002和0.005对材料的超低周疲劳性能的影响,把较低应变幅和极高应变幅的数据取出来对比分析。表 3为扭转预应变为0、0.002和0.005在纵向较低应变幅4.1%和纵向极高应变幅10.1%的疲劳寿命数据。
| 表3 实验结果 Tab. 3 Test results |
 |
从表 3中可以看出,高应变超低周疲劳寿命数据具有一定分散性。寿命数据分散性的原因很多,试样材质本身的不均匀性、加工精度和尺寸误差、疲劳试验机以及实验环境等因素的变化,都会引起疲劳寿命的分散性。因此,必须进行统计分析。
2.2 超低周疲劳寿命处理考虑到高应变超低周疲劳寿命数据的分散性,假设疲劳寿命数据服从双参数威布尔分布,威布尔分布现在已得到广泛应用[11]。因此,采用双参数威布尔分布数概率函数对疲劳寿命数据进行处理,其函数形式如下:
| $F(N) = 1 - \exp \left[ - {\left(\frac{N}{{{N_{\rm a}}}}\right)^b}\right]$ | (3) |
其对数形式为:
| $\ln \left[ {\frac{1}{{1 - F(N)}}} \right] = b(\ln N - \ln {N_{\rm a}})$ | (4) |
式中,
| $b = \frac{1}{{\displaystyle\sum\limits_{i = 1}^n {{C_{\rm I}}(n,n,i) \times \ln ({N_i})} }}$ | (5) |
| $\ln({N_{\rm a}}) = \sum\limits_{i = 1}^n {{D_{\rm I}}} (n,n,i) \times \ln ({N_i})$ | (6) |
式中:
|
表4 不同扭转预应变和应变幅下的
|
 |
将表 4的结果代入式(3)得出不同置信度下疲劳寿命如图 3所示。
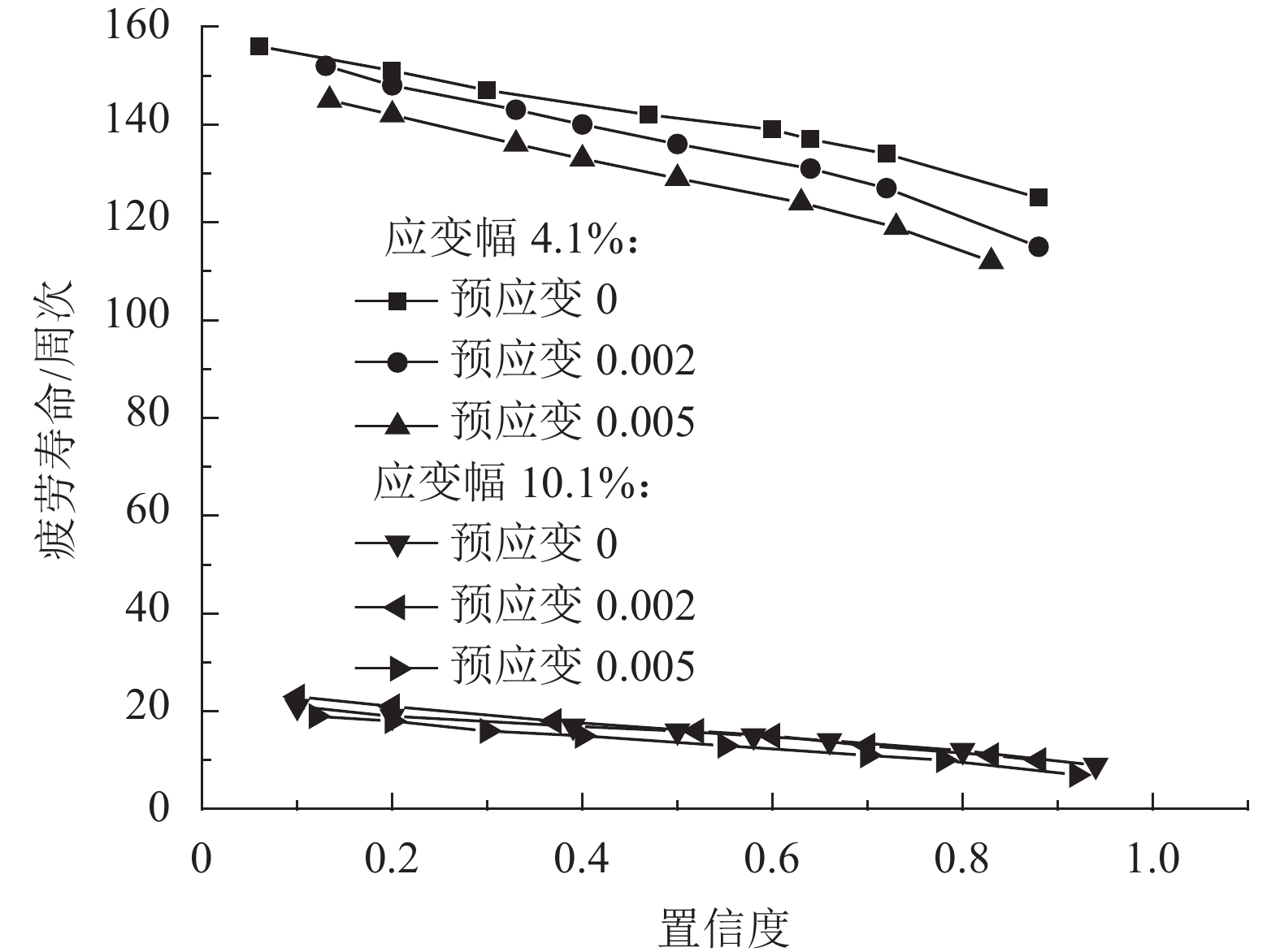 |
| 图3 不同置信度下不同预应变疲劳寿命对比 Fig. 3 Comparing the fatigue life in different pre- torsional angle and confidence coefficient |
2.3 循环响应特征
在疲劳实验中,材料从循环之初到循环稳定的变化过程中与应力、应变的形变抗力变化有关,进而使金属材料发生循环硬化、循环软化和循环稳定。图 4为扭转预应变为0、0.002和0.005在纵向较低应变幅4.1%和纵向极高应变幅10.1%下的循环特征曲线。
 |
| 图4 循环响应特征曲线 Fig. 4 Cycle stress response characteristic curves of test material |
从图 4中可得,扭转预应变为0、0.002和0.005时,在较低应变幅和极高应变幅的作用下,应力幅先是随着循环周次的增加而增加,达到一个较大的应力幅值,随后达到稳定循环状态,循环应力幅随着循环周次的增加趋于稳定,最后循环应力幅逐渐降低直到最终失效断裂。表明了预扭转对循环响应特征没有明显的影响,且在纵向较低应变幅4.1%作用下,扭转预应变为0、0.002和0.005的循环应力幅均无明显区别,表明在较低应变幅下预扭转对材料的循环应力幅和寿命影响不大。但在纵向极高应变幅10.1%作用下,预应变越大,循环应力幅值越小,由此表明预扭转一定程度上导致试样材料的内部损伤,降低了材料高应变幅下的循环抗力,加快试样的断裂,从而使得试样的疲劳寿命降低。
2.4 循环应力–应变关系根据hollomon公式:
| ${\sigma _{\rm a}} = h\varepsilon _{\rm a}^n$ | (7) |
或
| ${\sigma _{\rm a}} = k\varepsilon _{\rm pa}^{n'}$ | (8) |
式中,
| 表5 循环应力–应变关系 Tab. 5 Cyclic stress-strain relationship |
 |
2.5 循环应变–寿命关系
Manson-Coffin公式已广泛应用于应变疲劳寿命估算。根据高应变超低周疲劳统计的数据和弹塑性应变范围及总应变范围,由Manson-Coffin公式和Basquin公式:
| $\frac{{\Delta {\varepsilon _{\rm t}}}}{2} = \frac{{\Delta {\varepsilon _{\rm e}}}}{2} + \frac{{\Delta {\varepsilon _{\rm p}}}}{2} = \frac{{{{\sigma '}\!\!\!_{\rm f}}}}{{\text{E}}}{\left( {2{N_{95}}} \right)^b}+ {{\varepsilon '}\!\!\!_{\rm {\rm f}}}{\left( {2{N_{95}}} \right)^c}$ | (9) |
式中,
| 表6 Manson-Coffin拟合结果 Tab. 6 Fitting result of Manson-Coffin |
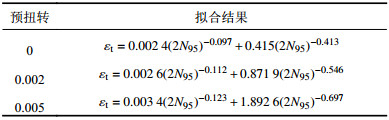 |
根据Manson-Coffin公式拟合得到曲线如图5(a)、(b)、(c)所示,图5中坐标为双对数坐标,由图5可见,实验值和拟合值的关系曲线能较好吻合,因此,Manson-Coffin公式能对高应变超低周疲劳进行疲劳寿命预测。由于扭转预应变使材料发生了加工硬化,提高了疲劳强度系数和疲劳延性系数,降低了疲劳强度指数和疲劳延性指数。
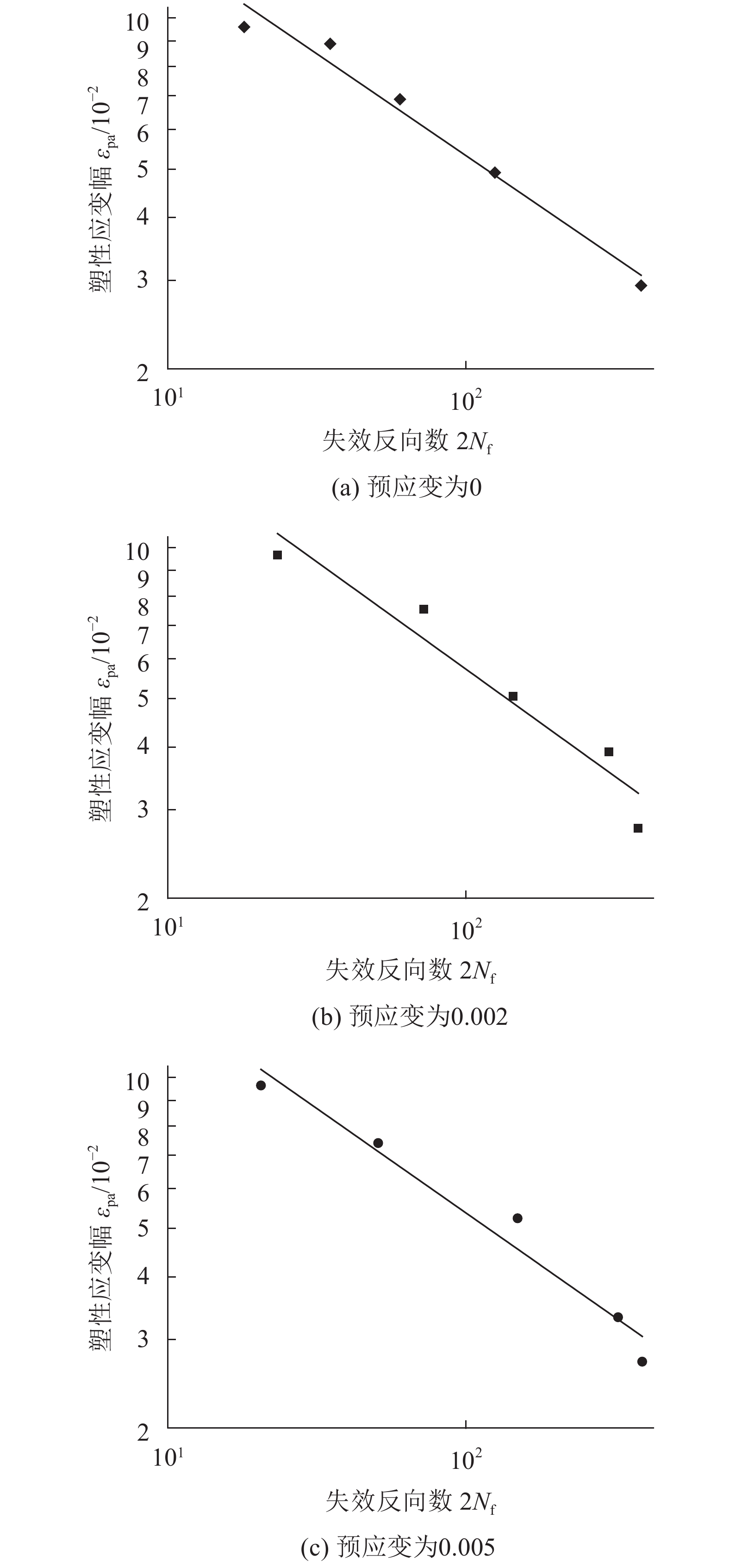 |
| 图5 Q345R超低周疲劳应变−寿命曲线 Fig. 5 ELCF Strain-life curves of Q345R |
2.6 塑性应变能和循环周次的关系
Manson-Coffin公式和Basquin公式是广泛应用的经验公式,但公式中没有反应良好的物理含义,所以Santner等[12]提出了滞回能为参数描述疲劳寿命预测公式。从能量的观点出发,材料在疲劳载荷所消耗的能力,即滞回能
| $\Delta {W_{\rm p}} = \frac{{1 - n'}}{{1 + n'}}\Delta \sigma \Delta {\varepsilon _{\rm p}}$ | (9) |
式中,
根据表 5中的公式查得循环硬化率
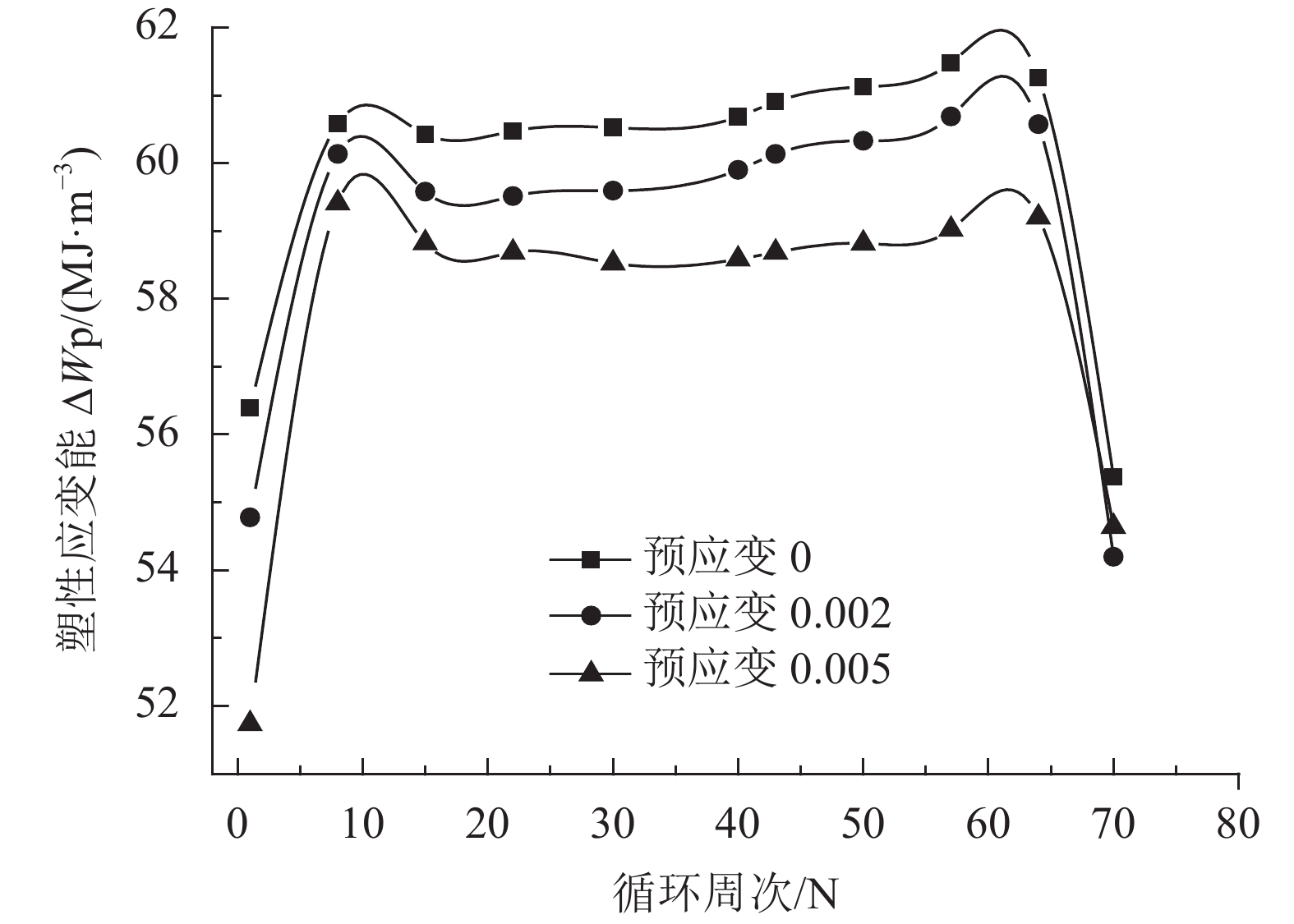 |
| 图6 塑性应变能与循环周次的关系 Fig. 6 Relationship of plastic strain energy and the cycle number |
从图6中可以看出,塑性应变能先随着循环周次的增加而增加,达到一个峰值,材料的疲劳韧性降低。疲劳韧性,即材料在损伤全过程中(单位体积)所耗散的总能量,是一个重要参量[13]。随后进入稳定状态,塑性应变能先降低,再达到相对稳定的状态,从外界吸收的塑性应变能也相应的降低,最后试件失效断裂前,循环应变能的累积,达到了材料的循环韧度,材料的塑性应变能迅速降低;预扭转应变越大的试件,其最大塑性应变能也越低,且预扭转和未预扭转的试件相比,预扭转的试件的塑性应变能低于未预扭转的试件,预扭转应变越大,其塑性应变能也越低。说明预扭转过程材料发生塑性变形而产生塑性应变,材料的一部分内能转换成塑性功,从而使材料的总能量降低[10]。
若将向应变幅为8.1%的循环应变能曲线拟合后,再进行积分,就可计算出总循环应变能,表达为:
| ${W_{\rm f}} = \int_0^{{N_{\rm f}}} {\Delta W{\rm d}N} $ | (10) |
但是,在循环载荷作用下,材料发生了循环硬化现象,导致滞回环的面积大小在不断变化,因此,不仅要考虑材料的塑性应变能的影响,同时要考虑循环硬化能(循环韧度)的影响。
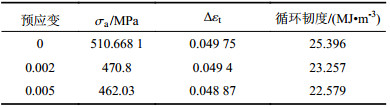
2.7 循环韧度在地震载荷中,压力容器承受的交变载荷与高应变超低周疲劳类似。因此,在地震载荷下,吸收能量越多,抗震性能就越好。研究表明[14],
| 表7 预扭转和循环韧度的关系 Tab. 7 Relationship in the pre-torsion and loop toughness |
 |
3 断口分析
图 7为试件在向应变幅为6.1%下的疲劳断口在扭转预应变为0、0.002和0.005下的扫描电镜(SEM)照片,与低周疲劳破坏不同,超低周疲劳在极低周次下发生疲劳破坏,试件疲劳断裂时间非常短,最后瞬断区也与低周有所不同,位于试件的中部。图7(a)、(b)、(c)为试件为扭转预应变为0、0.002和0.005的断口形貌,从图中可以看出超低周疲劳一般有多个疲劳源,且经过预扭转后的试件的断口中的孔洞和空穴较多。为此,将扭转预应变为0.005的断口放大显示如图7(d),疲劳断口清晰可见大量的二次裂纹。由此表明,经过预扭转后,改变了材料的内部微观组织结构,降低了材料的塑性应变能,使得材料疲劳寿命降低。
 |
| 图7 疲劳断口SEM扫描图 Fig. 7 SEM picture of fatigue fracture |
4 结 论
1) 用双参数威布尔分布对扭转预应变为0、0.002和0.005在高应变幅和低应变幅下的疲劳寿命进行统计分析,其疲劳寿命以及置信度在双对数坐标系中的线性关系良好。利用hollomon公式拟合实验数据建立了材料的循环应力–应变关系,并利用Mason-Coffin公式拟合疲劳实验数据,拟合结果表明拟合值与实验值的关系曲线能较好吻合,因此,表明了Mason-Coffin公式能对高应变超低周疲劳进行疲劳寿命预测。
2) 计算并拟合材料塑性应变能和循环周次的关系,发现预扭转后材料的塑性应变能明显比未预扭转的材料塑性应变能低。研究结果表明,预扭转导致材料发生塑性应变,材料的一部分内能转换成塑性功,从而使材料的总能量降低。
3) 研究了材料的循环韧度,计算获得未预扭转材料的循环韧度值为25.396 MJ/m3,比预扭转后的材料循环韧度高,且扭转角度越大,循环韧度越低。因此,预扭转后的材料的抗低周疲劳性能降低,材料应该避免预扭转现象。
4) 通过对材料疲劳断口的观察可知预扭转的材料比未预扭转的材料断口形貌中有较多的孔洞、空穴和二次裂纹,预扭转可能改变了材料的内部微观组织结构,孔洞和二次裂纹加剧了裂纹的扩展,降低了材料的疲劳寿命。
| [1] |
Cheng Guangxu. Study on damage mechanics theory of low cycle fatigue life of pressure vessel[J]. Journal of Xi'an Jiaotong University, 1994(8): 59-64. [程光旭. 压力容器低周疲劳寿命的损伤力学理论研究[J]. 西安交通大学学报, 1994(8): 59-64.] |
| [2] |
Zen Tao,Chen Yanqiang,Luo Yunrong,et al. High strain ultra-low cycle fatigue properties of 16MnR steel[J]. Journal of Steel Research, 2016, 28(4): 53-57. [曾涛,陈延强,罗云蓉,等. 16MnR钢的高应变超低周疲劳性能[J]. 钢铁研究学报, 2016, 28(4): 53-57.] |
| [3] |
Tao C.Extremely low cycle fatigue assessment of thick-walled steel piers[D].Nagoya:Nagoya University,2007.
|
| [4] |
Wei Yaobing,Huang Jianlong,Jin Wuyin,et al. Several problems in the design of ultra-low cycle fatigue fracture[J]. Journal of Gansu University of Technology, 1998, 24(2): 109-112. [韦尧兵,黄建龙,靳伍银,等. 超低周变幅疲劳断裂设计的几个问题[J]. 甘肃工业大学学报, 1998, 24(2): 109-112.] |
| [5] |
Zhao Xuecai.Study on fracture characteristics of Q235 under ultra-low cycle conditions[D]. Lanzhou:Lanzhou University of Technology 2007. 赵学才.超低周条件下Q235的断裂特性研究[D].兰州:兰州理工大学.2007. |
| [6] |
Chen Yanqiang,Luo Yunrong,Lin Haibo,et al. Study on the fatigue performance of Q345R steel in low-week low cycle[J]. Journal of Steel Research, 2016, 37(7): 1322-1324. [陈延强,罗云蓉,林海波,等. Q345R钢低周超低周疲劳性能研究[J]. 钢铁研究学报, 2016, 37(7): 1322-1324.] |
| [7] |
Duan Yanhong,Li Youtang,Tian Li,et al. Study on ultra-low cycle fatigue fracture of 4 0 C r under strong torsion conditions[J]. Material Heat Treatment Technology, 2008, 37(22): 26-31. [段红燕,李有堂,田利,等. 强扭转条件下4 0 C r的超低周疲劳断裂研究[J]. 材料热处理技术, 2008, 37(22): 26-31.] |
| [8] |
Luo Yunrong,Wang Qinyuan,Fu Lei,et al. Low cycle fatigue performance of Q235 steel structure material[J]. Journal of Steel Research, 2016, 28(12): 47-51. [罗云蓉,王清远,付磊,等. Q235钢结构材料的超低周疲劳性能[J]. 钢铁研究学报, 2016, 28(12): 47-51.] |
| [9] |
Wang Shiyue,Lin Mojun,Shao Jianfei. The effect of torsion prestrain on the low cycle fatigue property of 45 steel[J]. Mechanical Strength, 1998, 20(4): 300-302. [王时越,林茉君,邵剑飞. 扭转预应变对45钢低周疲劳性能的影响[J]. 机械强度, 1998, 20(4): 300-302.] |
| [10] |
Wu Zhiyu,Wang Shiyue,Yang Xijie,et al. Effect of torsion prestrain on low cycle fatigue performance of 35CrMo steel[J]. Experimental Mechanics, 2013, 28(4): 511-516. [吴志煜,王时越,杨锡阶,等. 扭转预应变对35CrMo钢低周疲劳性能的影响[J]. 实验力学, 2013, 28(4): 511-516.] |
| [11] |
Zheng Jialiang,Sheng Guangmin,Wang Lijuan,et al. Study on high strain and low cycle fatigue performance of HRB500E reinforcement[J]. Steel Vanadium and Titanium, 2014, 35(5): 129-135. [郑家良,盛光敏,王丽鹃,等. HRB500E钢筋高应变低周疲劳性能研究[J]. 钢铁钒钛, 2014, 35(5): 129-135.] |
| [12] |
Santner J S.Fine M E.The hysteretic plastic work as a failure criterion in a coffin-manson type relation[J].Scripta Metallurgica,1977(11):159-162.
|
| [13] |
Wang Yonglian. Mathematical expression of fatigue toughness[J]. Journal of Aviation, 1995, 16(3): 110-114. [王永廉. 疲劳韧性的数学表达式[J]. 航空学报, 1995, 16(3): 110-114.] |
| [14] |
Sheng Guangmin,Lv Yukun,Huang Zhenhua. Analysis of high strain and low cycle fatigue behavior of seismic reinforcement with fine crystallization and residual heat treatment[J]. Functional Materials, 2014, 45(15): 127-131. [盛光敏,吕煜坤,黄振华. 细晶化和余热处理抗震钢筋的高应变低周疲劳行为分析[J]. 功能材料, 2014, 45(15): 127-131.] |
| [15] |
Singh V, Pandey V,Kumar S,et al. Effect of ultrasonic shot peening on surface microstructure and fatigue behavior of structural alloys[J]. Transactions of the Indian Institute of Metals, 2016,69(2):295-301.
|
 2018, Vol. 50
2018, Vol. 50


