2. 德国克劳斯塔尔工业大学 石油天然气工程研究所,克劳斯塔尔 38678;
3. 德国下萨克森州能源研究中心,哥斯拉尔 38640
2. Inst. of Petroleum Eng., Clausthal Univ. of Technol., Clausthal 38678, Germany;
3. Energy Research Center of Lower Saxony (EFZN), Goslar 38640, Germany
盐岩由于其极低的渗透率、良好的蠕变性能与损伤恢复特性,成为国际上公认的能源储存和核废料处置的理想介质[1–2],对其力学特性的研究日益受到重视。盐岩地下储库在国外建造与运营的经验表明,盐岩地下储库在长期服务年限内,常发生储库失稳、围岩变形大、有效容积率丧失严重等不利情形,其根本原因除储库压力波动、顶板盖层垮塌之外,还与盐岩自身的蠕变特性密切相关,因此对盐岩蠕变特性的研究是一个十分重要的课题[3]。
实际工程中,地下储库的盐岩在原始应力状态被开挖扰动后,首先经历一期蠕变过程,而后进入并长期处于二期蠕变状态,该阶段蠕变速率保持定值,又称为稳态蠕变阶段。在偏应力水平不高的情况下,稳态蠕变将持续数十年直到储库废弃。也即盐岩稳态蠕变的特性对地下能源储库的安全营建和运营至关重要。故如何确定盐岩的长期稳态蠕变率,成为盐岩蠕变本构模型的研究重点之一。
工程现场的盐岩在极低的偏应力作用下,晶体内部的离子扩散等促成了蠕变变形,其蠕变率很低,难以测得[4],盐岩完全进入稳态蠕变所需时间为1~10年[5];在室内试验中,盐岩完全进入稳态蠕变也需要1年以上的时间。实际情况是,室内蠕变试验受试验条件所限持续时间往往较短,一般每个加载阶段约30 d,由此得到的稳态蠕变率远高于现场实测值。图1为德国联邦地质和原材料研究院(BGR)2006年对德国Morsleben地区的两个高纯度盐样进行室内单轴蠕变试验的结果分析曲线[6]。
 |
| 图1 德国室内盐岩单轴蠕变曲线 Fig. 1 Uniaxial creep curve of rock salt in Germany |
由图1可知,在试验进行至30 d,蠕变率似乎减小到了恒定值,但当试验继续进行,200 d后蠕变率依然在减小。根据相关研究,盐岩现场实测的二期蠕变率比室内较短试验时间得到的值低5~50倍[7]。工程实践中,没有太长的时间留给实验室进行长达数年的蠕变试验,故如何由盐岩的一期蠕变数据推求长期稳态蠕变率,成为亟待解决的难题。
针对上述问题,一方面,通过试验手段解决,如德国学者[8]通过提高试验温度在合理的时间内获得可靠的盐岩稳态蠕变率;另一方面,通过理论研究,建立新的蠕变本构模型。本文旨在基于对一些典型盐岩蠕变本构模型的研究,提出能够描述盐岩从一期蠕变自动进入二期蠕变的本构模型,且能够通过实验室所得一期蠕变的数据推求盐岩稳态蠕变率,即达到用数学方法解决试验难题的目的。
1 典型盐岩蠕变本构模型对于盐岩这种软弱岩石,在恒定应力作用瞬间产生弹性应变,随后发生蠕变,其典型蠕变曲线可分为3个阶段,如图2所示[9]。图2中:
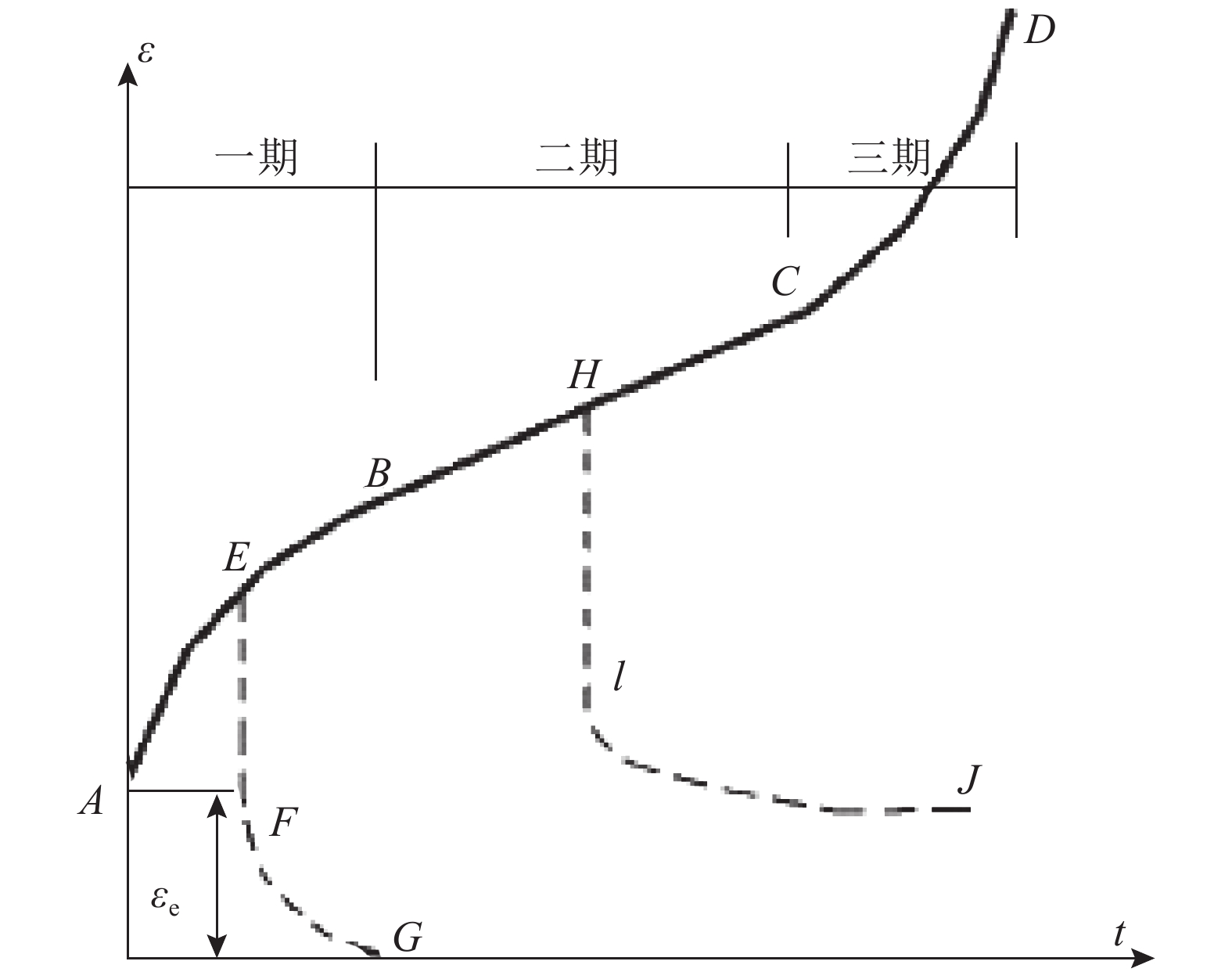 |
| 图2 典型盐岩蠕变曲线 Fig. 2 Typical creep curve of salt rock |
蠕变变形是常荷载或变荷载作用下产生的与时间、温度相关的黏性变形。总的应变是弹性应变、温度应变、塑性应变及黏性应变四者之和。
| $\varepsilon = {\varepsilon ^{\rm{e}}} + {\varepsilon ^t} + {\varepsilon ^{\rm{p}}} + {\varepsilon ^{\rm{v}}}$ | (1) |
由于盐穴埋深固定,其温度也恒定,室内试验在等温条件下进行,故不考虑温度应变;塑性应变相对较小可以忽略,则有:
| $\varepsilon = {\varepsilon ^{\rm{e}}} + {\varepsilon ^{\rm{v}}}$ | (2) |
式中,弹性应变由胡克定律给出,黏性应变由蠕变本构方程给出。
具体模型参数见表1。
| 表1 符号列表 Tab. 1 Nomenclature |
 |
1.1 Lubby2模型
Lubby2模型属于元件组合模型,建立在Burgers模型[10]之上。Burgers模型由描述瞬态蠕变的Kelvin模型和描述稳态蠕变的Maxwell模型串联而成,其本构方程为:
| $\dot \varepsilon = {\dot \varepsilon _{{\rm{tr}}}} + {\dot \varepsilon _{\rm{s}}} = \frac{{{\sigma _{\rm{v}}}}}{{{{\overline \eta }{\rm _k}}}} \cdot {{\rm{e}}^{ - \textstyle\frac{{{{\overline G}\rm_k}}}{{{{\overline \eta }\rm_k}}}t}} + \frac{1}{{{{\overline \eta }{\rm _m}}}} \cdot {\sigma _{\rm{v}}}$ | (3) |
Lubby2模型在Burgers模型基础上假设参数
| $\dot \varepsilon = \left[ {\frac{1}{{{{\overline \eta }_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}} \cdot \left( {1 - \frac{{{\varepsilon _{{\rm{tr}}}}}}{{{\rm{max}}\left( {{\varepsilon _{{\rm{tr}}}}} \right)}}} \right) + \frac{1}{{{{\overline \eta }_{\rm m}}\left( {{\sigma _{\rm{v}}}} \right)}}} \right] \cdot {\sigma _{\rm{v}}}$ | (4) |
其张量形式如下:
| $ \dot{\varepsilon }_{ij}^{\rm{v}}=\frac{3}{2}\cdot\Bigg[\frac{1}{{{{\overline{\eta }}}_{{\rm k}}}\left( {{\sigma }_{\rm{v}}} \right)}\cdot \left( 1-\frac{{{\varepsilon }_{\rm{tr}}}}{\max ({{\varepsilon }_{\rm{tr}}})} \right)+ \frac{1}{{{{\overline{\eta }}}_{{\rm m}}}\left( {{\sigma }_{\rm{v}}} \right)}\Bigg]\cdot {{S}_{ij}} $ | (5) |
| ${\rm{max}}\left( {{\varepsilon _{{\rm{tr}}}}} \right) = \frac{{{\sigma _{\rm{v}}}}}{{{{\overline G}_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}}$ | (6) |
| ${\overline G_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \overline G_{\rm k}^* \cdot {\rm{exp}}\left( {{k_1} \cdot {\sigma _{\rm{v}}}} \right)$ | (7) |
| ${\overline \eta _{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \overline \eta _{\rm k}^* \cdot {\rm{exp}}\left( {{k_2} \cdot {\sigma _{\rm{v}}}} \right)$ | (8) |
| ${\overline \eta _{\rm m}}\left( {{\sigma _{\rm{v}}}} \right) = \overline \eta _{\rm m}^* \cdot {\rm{exp}}\left( {m \cdot {\sigma _{\rm{v}}}} \right) \cdot {\rm{exp}}\left( {l \cdot T} \right)$ | (9) |
Lubby2模型共有7个参数需要确定,即
由式(6)可得:
| ${\overline G_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \frac{{{\sigma _{\rm{v}}}}}{{{\rm{max}}\left( {{\varepsilon _{{\rm{tr}}}}} \right)}}$ | (10) |
由式(6)及(3)可得:
| ${\overline \eta _{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \frac{{{\sigma _{\rm{v}}}}}{{{{\dot \varepsilon }_{{\rm{tr}}}}}} \cdot \left( {1 - \frac{{{\varepsilon _{{\rm{tr}}}}}}{{{\rm{max}}\left( {{\varepsilon _{{\rm{tr}}}}} \right)}}} \right)$ | (11) |
由式(3)可得:
| ${\overline \eta _{\rm m}}\left( {{\sigma _{\rm{v}}}} \right) = \frac{{{\sigma _{\rm{v}}}}}{{{{\dot \varepsilon }_{\rm{s}}}}}$ | (12) |
根据蠕变试验结果及式(10)~(12)即求出某一固定应力状态下
根据式(7)~(9)可知除
IfG-G&S模型为经验模型,是通过大量的蠕变试验,利用试验曲线拟合而成的。该模型分为两种情况[7,11–12]:当瞬态蠕变
| $\left\{\begin{aligned}&\dot \varepsilon = A \cdot {\left( {\frac{{{\sigma _{\rm{v}}}}}{{{\sigma ^*}}}} \right)^\beta }/{\varepsilon _{{\rm{tr}}}}^\mu,\;\;{\dot \varepsilon _{\rm{s}}} = \frac{{{\varepsilon _{{\rm{tr}}}}}}{{{t_0}}};\\& {\dot \varepsilon _{{\rm{tr}}}} = \dot \varepsilon - {\dot \varepsilon _{\rm{s}}} = A \cdot {\left( {\frac{{{\sigma _{\rm{v}}}}}{{{\sigma ^*}}}} \right)^\beta }/{\varepsilon _{{\rm{tr}}}}^\mu - \frac{{{\varepsilon _{{\rm{tr}}}}}}{{{t_0}}};\\& {\varepsilon _{{\rm{tr}}}} < {\rm{max(}}{\varepsilon _{{\rm{tr}}}})\end{aligned}\right.$ | (13) |
| $\left\{\begin{aligned}& \dot \varepsilon = {\dot \varepsilon _{\rm{s}}} = {A_2} \cdot {\left( {\frac{{{\sigma _{\rm{v}}}}}{{{\sigma ^*}}}} \right)^n},{\dot \varepsilon _{{\rm{tr}}}} = 0;\\& {A_2} = A \cdot {\left( {A{t_0}} \right)^{ - \textstyle\frac{\mu }{{\mu + 1}}}}n = \frac{\beta }{{\mu + 1}};\\& {\varepsilon _{{\rm{tr}}}} = {\rm{max(}}{\varepsilon _{{\rm{tr}}}})\end{aligned}\right.$ | (14) |
式中,现场试验取
不同于Lubby2模型分别用两个元件组合模型表现一期、二期蠕变过程,IfG-G&S模型在瞬态蠕变应变量达到最大值后自动进入二期稳态蠕变,具体表现在:当
IfG-G&S模型共有3个未知参数,即
| $\ln\,\, \dot \varepsilon = \ln\,\, A{\rm{ + }}\beta \cdot \ln \,\,{\sigma _{\rm{v}}}{\rm{ - }}\mu \cdot {\rm{ln}}\,\,{\varepsilon _{{\rm{tr}}}}$ | (15) |
当
需要说明的是,当参数获得后若要使用该模型计算蠕变率,需根据试验值给定一个很小的蠕变初值,否则式(13)第一个式子在
另外,与Lubby2模型一样,IfG-G&S模型所描述的蠕变率也可以推广到3维情况,通过偏应力张量表达。
2 基于室内试验能够推求长期稳态蠕变率的Lubby2_Ⅰ-Ⅱ模型Lubby2模型基于元件组合模型,分别使用非线性Kelvin模型和非线性Maxwell模型描述了一期和二期蠕变,参数物理意义明确,且时间不是直接参数(这有利于模拟较为复杂的岩腔运营过程),与试验数据吻合度高;而基于Lubby2模型,Hou等[13]考虑了盐岩的延展性变形、变位、变形硬化和变形恢复、损伤及损伤复原机制,进而提出Hou/Lux本构模型,且应用广泛。IfG-G&S模型是现有可查文献提到的唯一一个能够描述盐岩从一期蠕变自动进入二期蠕变的本构模型,且能通过实验室试验测得的一期蠕变数据推求出二期稳态蠕变率。
基于Lubby2模型精确度高和能发展为蠕变损伤模型的优点,以及IfG-G&S模型能够通过实验室数据推求盐岩二期稳态蠕变率的优势,结合两种模型的特点,提出新的能够通过实验室数据推求盐岩二期稳态蠕变率并且能够延伸到Hou/Lux模型中的本构模型,即Lubby2_Ⅰ-Ⅱ模型:
| $\left\{\begin{aligned}& {\dot \varepsilon _{{\rm{tr}}}} = \frac{{{\sigma _{\rm{v}}}}}{{{{\overline \eta }_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}} \cdot \left( {1 - \frac{{{\varepsilon _{{\rm{tr}}}}}}{{\max \left( {{\varepsilon _{{\rm{tr}}}}} \right)}}} \right),\;\;\;\;{\dot \varepsilon _{\rm{s}}} = \frac{{{\varepsilon _{{\rm{tr}}}}}}{{{t_0}}};\\& \dot \varepsilon = {\dot \varepsilon _{{\rm{tr}}}} + {\dot \varepsilon _{\rm{s}}}{\rm{ = }}\frac{{{\sigma _{\rm{v}}}}}{{{{\overline \eta }_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}} \cdot \left( {1 - \frac{{{\varepsilon _{{\rm{tr}}}}}}{{\max \left( {{\varepsilon _{{\rm{tr}}}}} \right)}}} \right){\rm{ + }}\frac{{{\varepsilon _{{\rm{tr}}}}}}{{{t_0}}};\\& {\varepsilon _{{\rm{tr}}}} < {\rm{max(}}{\varepsilon _{{\rm{tr}}}})\end{aligned}\right.$ | (16) |
| $\dot \varepsilon = {\dot \varepsilon _{\rm{s}}} = \frac{{\max \left( {{\varepsilon _{{\rm{tr}}}}} \right)}}{{{t_0}}},\;\;\;\;{\dot \varepsilon _{{\rm{tr}}}} = 0\\({\varepsilon _{{\rm{tr}}}} = {\rm{max(}}{\varepsilon _{{\rm{tr}}}}{\rm{)}})$ | (17) |
| ${\rm{max}}\left( {{\varepsilon _{{\rm{tr}}}}} \right) = \frac{{{\sigma _{\rm{v}}}}}{{{{\overline G}_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}}$ | (18) |
| $\quad \quad \quad \quad\quad \quad\;\; {\overline G_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \overline G_{\rm k}^* \cdot {\rm{exp}}\left( {{k_1} \cdot {\sigma _{\rm{v}}}} \right)$ | (19) |
| ${\overline \eta _{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) = \overline \eta _{\rm k}^* \cdot {\rm{exp}}\left( {{k_2} \cdot {\sigma _{\rm{v}}}} \right)$ | (20) |
式中,所有符号含义同Lubby2模型。
式(16)和(17)分别描述盐岩的一期和二期蠕变阶段。式(16)中,瞬态蠕变本构方程借鉴Lubby2模型,以非线性Kelvin模型为基础建立,瞬态蠕变率随时间逐渐减小。式(16)中稳态蠕变率的变化规律与IfG-G&S模型一致,即通过参数
式(16)和(17)中参数
根据式(16)及一期蠕变试验数据,可求得瞬态蠕变率
| ${\dot \varepsilon _{{\rm{tr}}}} = \frac{{{\sigma _{\rm{v}}}}}{{{{\overline \eta }_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right)}} - \frac{{{\sigma _{\rm{v}}}}}{{{{\overline \eta }_{\rm k}}\left( {{\sigma _{\rm{v}}}} \right) \cdot \max \left( {{\varepsilon _{{\rm{tr}}}}} \right)}} \cdot {\varepsilon _{{\rm{tr}}}}$ | (21) |
当
Lubby2_Ⅰ-Ⅱ模型共有4个参数,即
对式(20)两边取对数,得:
| ${\rm{ln}}\;{\overline \eta _{\rm k}} = {\rm{ln}}\;\overline \eta _{\rm k}^* + {k_2}{\sigma _{\rm{v}}}$ | (22) |
由于
同理
根据Von Mises应力的定义及蠕变流动法则,Lubby2_Ⅰ-Ⅱ模型描述的蠕变率可通过式(23)推广到3维状态:
| ${\dot \varepsilon _{ij}} = {\dot \varepsilon _{{\rm{cr}}}} \cdot \frac{{\partial {\sigma _{\rm{v}}}}}{{\partial {S_{ij}}}} = \frac{3}{2} \cdot {\dot \varepsilon _{{\rm{cr}}}} \cdot \frac{{{s_{ij}}}}{{{\sigma _{\rm{v}}}}}$ | (23) |
根据针对中国金坛盐岩试件进行的三轴压缩蠕变的试验数据,计算上述3种模型的参数,并运用所得参数和相应模型计算蠕变和蠕变率,与试验数据进行对比。蠕变试验数据来自谢凌志[14],该蠕变试验是在围压20 MPa、温度45℃的条件下,分别对盐样K1、K2、K3进行了4阶段三轴压缩,试验测得盐样弹性模量为18 000 MPa,泊松比为0.3。
3.1 模型参数根据蠕变试验数据和第1、2节中介绍的模型参数求解方法,即可得到中国金坛盐岩试件的蠕变参数。中国金坛盐岩试件Lubby2模型的6个参数:
| $\overline \eta _{\rm m}^* = 6.14 \times {10^5}\;\;{\rm{ MPa}} \cdot {\rm{d}},\;\;\;\;m = - 0.136\;\;{\rm{ MP}}{{\rm{a}}^{ - 1}},$ |
| $\overline \eta _{\rm k}^* = 1.75 \times {10^5}\;\;{\rm{ MPa}} \cdot {\rm{d}},\;\;\;\;{k_2} = - 0.187\;\;{\rm{ MP}}{{\rm{a}}^{ - 1}},$ |
| $\overline G_{\rm k}^* = 1.53 \times {10^4}\;\;{\rm{ MPa}},\;\;\;\;{k_1} = - 0.127\;\;{\rm{ MP}}{{\rm{a}}^{ - 1}}{\text{。}}$ |
中国金坛盐岩试件IfG-G&S模型的3个参数:
| $A = 2.09 \times{10^{ - 24}}\;\;{ }{{\rm{d}}^{ - 1}},\;\;\;\;\beta = 12.132,\;\;\;\;\mu = 2.957{\text{。}}$ |
中国金坛盐岩试件Lubby2_Ⅰ-Ⅱ模型的4个参数:
| $\overline \eta _{\rm k}^* = 1.36 \times {10^5}\;\;{\rm{ MPa}} \cdot {\rm{d}},\;\;\;\;{k_2} = - 0.151\;\;{\rm{ MP}}{{\rm{a}}^{ - 1}},$ |
| $\overline G_{\rm k}^* = 6.03 \times {10^3}\;\;{\rm{ MPa}},\;\;\;\;{k_1} = - 0.114\;\;{\rm{ MP}}{{\rm{a}}^{ - 1}}{\text{。}}$ |
分别使用Lubby2、IfG-G&S、Lubby2_Ⅰ-Ⅱ模型及其相对应的参数计算金坛盐岩的二期稳态蠕变率和轴向应变。
IfG-G&S和Lubby2_Ⅰ-Ⅱ模型认为盐样的稳态蠕变率的改变是由瞬态蠕变决定,盐样瞬态蠕变率减至0时所对应的总蠕变率就是二期稳态蠕变率。
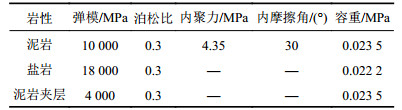
此外,资料显示,金坛储气库西2腔埋深约1 000 m,工作气压为8~13.5 MPa(盐腔围岩偏应力约为15~10 MPa),运行方式为注采气2个月、恒压3个月;运营5年后的腔体体积损失约为1.2%,腔体顶板下沉0.3 m,底板上鼓0.6 m[15]。根据这些数据,使用Flac3D数值模拟软件建立西2腔模型,在数值模拟时使用Norton本构模型反演出蠕变参数
| 表2 不同本构模型求得的金坛盐岩稳态蠕变率 Tab. 2 Calculated stationary creep rates of the salt rock in Jintan with different constitutive models |
 |
| 表3 金坛储气库基本力学参数 Tab. 3 Basic mechanical parameters of rocks from Jintan underground gas storage |
 |
由表2可知,Lubby2模型计算值与每一加载阶段结束时的蠕变率试验值一致;IfG-G&S和Lubby2_Ⅰ-Ⅱ模型计算值都比Lubby2模型计算值小4.0~5.5倍,且都与金坛储气库二期稳态蠕变率反演的现场值接近,尤其是当偏应力为10~15 MPa时。这很好地验证了使用Lubby2_Ⅰ-Ⅱ模型计算盐岩稳态蠕变率的可靠性。
图3~5分别为盐样K1、K2、K3轴向应变试验值与Lubby2、IfG-G&S、Lubby2_Ⅰ-Ⅱ这3个模型计算值的对比。盐样在所有加载阶段都未出现三期蠕变。图3~5中模型计算的应变值包含了蠕变和弹性变形两部分,其中弹性应变由胡克定律计算得出。
由图3~5可知,描述盐样短期蠕变试验的情况时,Lubby2模型准确性最好,其次为Lubby2_Ⅰ-Ⅱ模型,IfG-G&S模型误差最大。进行误差分析:Lubby2模型认定各加载段结束时盐样已经进入稳态蠕变阶段,由此求得参数用以计算蠕变曲线,即由试验推试验,故与试验曲线吻合度最高;Lubby2_Ⅰ-Ⅱ和IfG-G&S模型是根据盐样短期试验数据推导其长期稳态蠕变参数,即由室内推现场,使用长期蠕变参数反算短期试验曲线,因而产生误差。
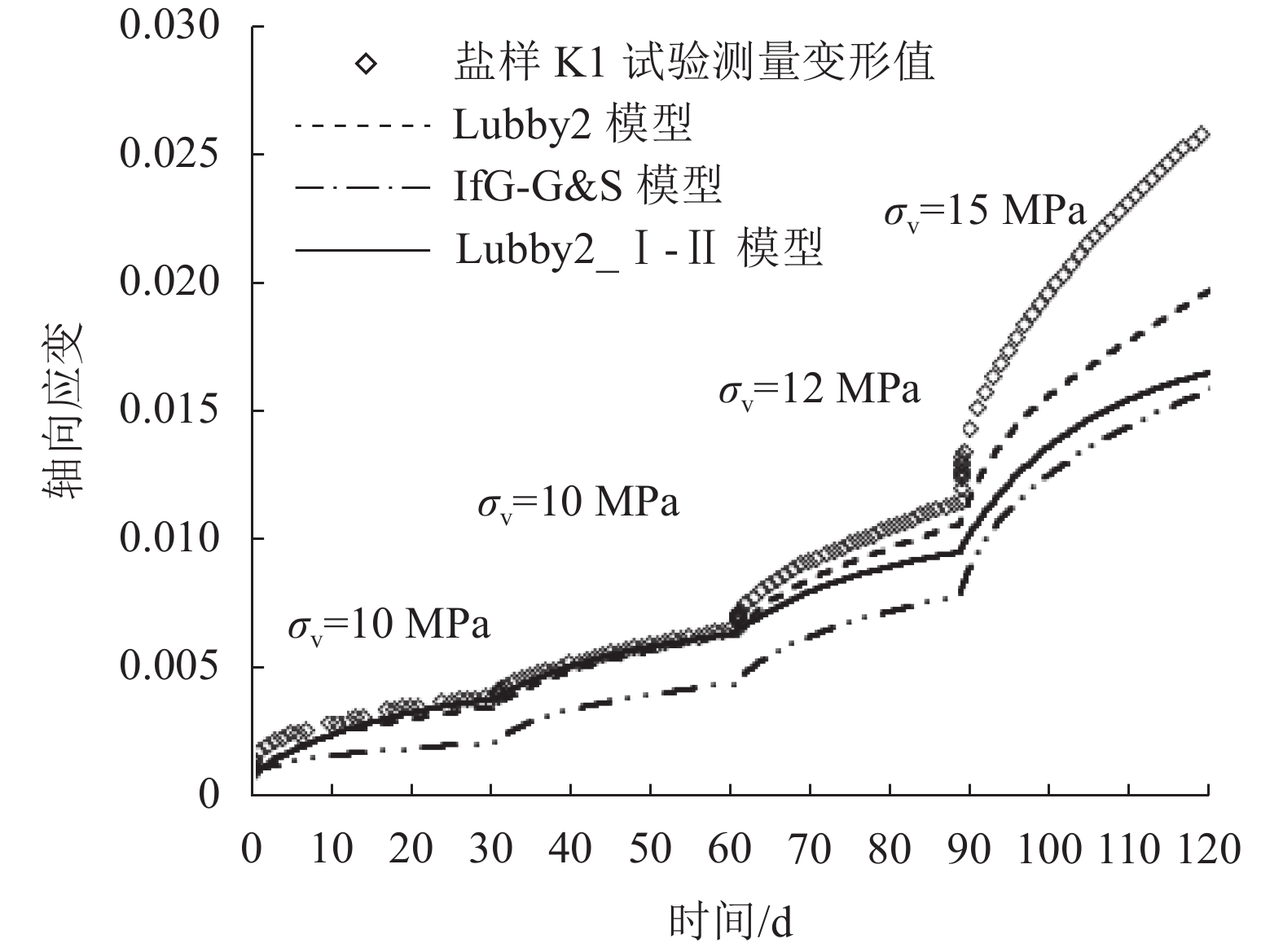 |
| 图3 盐样K1轴向应变的试验值与模型计算值对比 Fig. 3 Comparison between experimental and calculated axial strain of rock salt specimen K1 |
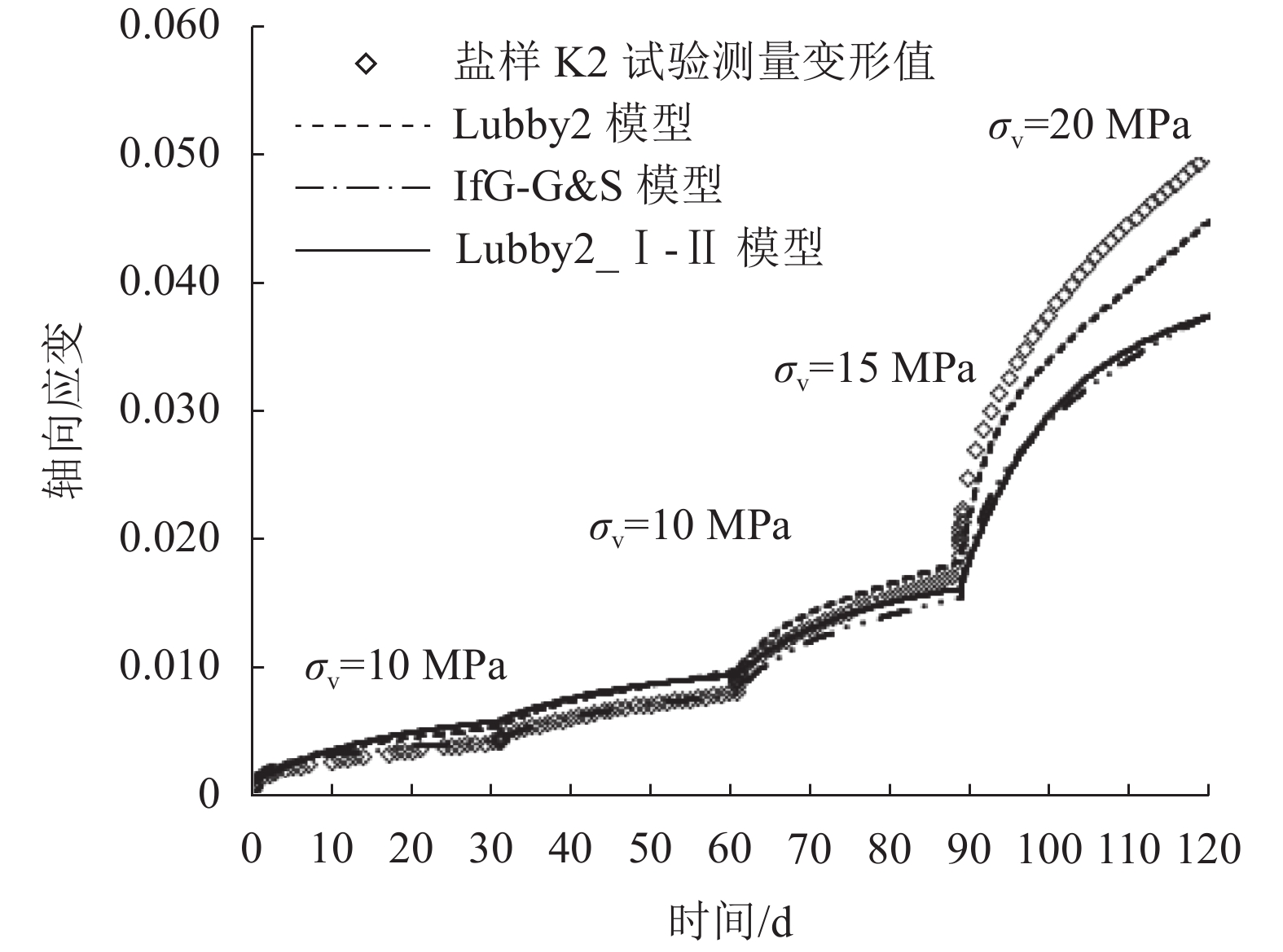 |
| 图4 盐样K2轴向应变的试验值与模型计算值对比 Fig. 4 Comparison of experimental and calculated axial strain of rock salt specimen K2 |
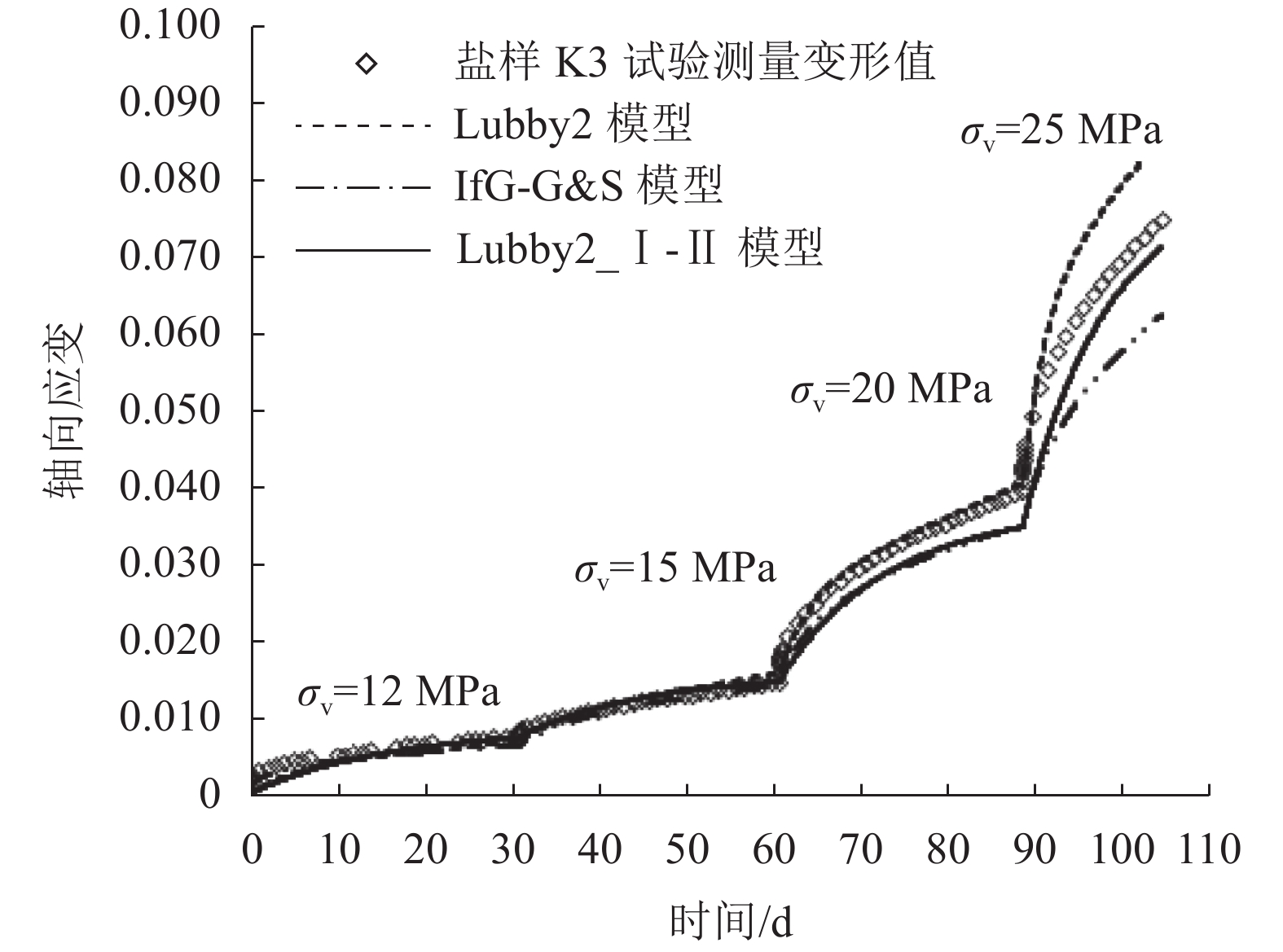 |
| 图5 盐样K3轴向应变的试验值与模型计算值对比 Fig. 5 Comparison of experimental and calculated axial strain of rock salt specimen K3 |
综上可见,Lubby2_Ⅰ-Ⅱ模型在推求盐岩长期稳态蠕变率的方面优于Lubby2模型;作为基于室内试验能够推求长期稳态蠕变率的模型,其在拟合室内试验曲线方面优于IfG-G&S模型。
4 结 论1)Lubby2模型是基于元件组合模型Burgers对参数进行非线性处理得到的。分别用两个元件组合模型反映一期、二期蠕变,既体现了组合模型简单直观的优点,又针对Burgers模型无法描述非线性变形的缺点做出改进。另外,Lubby2模型还可以进一步发展为考虑了盐岩变形硬化、变形恢复、损伤及损伤复原机制的Hou/Lux模型。
2)IfG-G&S是能够描述盐岩由一期蠕变自动进入二期蠕变过程的经验模型,能够估算现场长期稳态蠕变率。
3)Lubby2_Ⅰ-Ⅱ模型兼具Lubby2和IfG-G&S模型的优点:能直观有效地用元件组合模型反映盐岩的瞬态蠕变,具有较高的准确性,且最终可以引入应用广泛的Hou/Lux蠕变损伤模型中;解决了用持续时间较短的室内试验数据推求盐岩的长期稳态蠕变率的关键性问题,达到了用数学方法解决试验难题的目的。
4)使用Lubby2_Ⅰ-Ⅱ和IfG-G&S模型计算出的长期稳态蠕变率比室内试验值小4~5.5倍,且与金坛储气库二期稳态蠕变率的反演现场值接近。这一结果很好地验证了Lubby2_Ⅰ-Ⅱ和IfG-G&S模型在估算盐岩稳态蠕变率方面的可靠性。
5)对于多级加载蠕变试验,用能够由短期试验推导盐岩长期稳态蠕变率的两个蠕变模型拟合实测蠕变曲线,Lubby2_Ⅰ-Ⅱ模型的准确性高于IfG-G&S模型。
总体来说,Lubby2_Ⅰ-Ⅱ模型能够基于盐岩短期室内试验推导其长期稳态蠕变率,并且能够很好地描述盐样的实测蠕变曲线。
| [1] |
Chen Jianwen,Yang Chunhe. Mesoscopic deformation based plastic constitutive model of salt rock[J]. Rock and Soil Mechanics, 2015, 36(1): 117-122. [陈剑文,杨春和. 基于细观变形理论的盐岩塑性本构模型研究[J]. 岩土力学, 2015, 36(1): 117-122.] |
| [2] |
Xing Wei,Zhao Juan,Dusterloh U,et al. Experimental study of mechanical and hydraulic properties of bedded rock salt from the Jintan location[J]. Acta Geotechnica, 2014, 9(1): 145-151. DOI:10.1007/s11440-013-0231-x |
| [3] |
Jing Wenjun,Yang Chunhe,Chen Feng. Risk assessment of salt cavern oil/gas storage based on accident statistical analysis[J]. Rock and Soil Mechanics, 2011, 32(6): 1787-1793. [井文君,杨春和,陈锋. 基于事故统计分析的盐岩地下油/气储库风险评价[J]. 岩土力学, 2011, 32(6): 1787-1793. DOI:10.3969/j.issn.1000-7598.2011.06.031] |
| [4] |
Hunsche U,Hampel A. Rock salt — The mechanical properties of the host rock material for a radioactive waste repository[J]. Engineering Geology, 1999, 52: 271-291. DOI:10.1016/S0013-7952(99)00011-3 |
| [5] |
Lux K H.Gebirgsmechanischer Entwurf und Felderfahrungen im Salzkavernenbau[M].Stuttgart in Germany:Ferdinand Enke Verlag,1984.
|
| [6] |
BGR.Comparison of constitutive models for rock salt.Final report of a research project funded by the German Federal Ministry of Education and Research[R].Hannover:Federal Institute for Geosciences and Natural Resources,2006.
|
| [7] |
Günther R M.Erweiterter Dehnungs-Verfestigungs-Ansatz,Phänomenologisches Stoffmodell für duktile Salzgesteine zur Beschreibung primären,sekundären und tertiären Kriechens[D].Freiberg:Technischen Universität Bergakademie Freiberg,2009.
|
| [8] |
Günther R M,Salzer K,Popp T,et al. Steady-state creep of rock salt:Improved approaches for lab determination and modelling[J]. Rock Mechanics and Rock Engineering, 2015, 48: 2603-2613. DOI:10.1007/s00603-015-0839-2 |
| [9] |
徐志英.岩石力学[M].3版.北京:中国水利水电出版社,2007.
|
| [10] |
Burgers J M. First report on viscosity and plasticity[J]. Protoplasma, 1935, 24(1): 631-632. |
| [11] |
Schulze O,Heemann U,Zetsche F,et al.Comparison of advanced constitutive models for the mechanical behavior of rock salt—Results from a joint research project-I.Modeling of deformation processes and benchmark calculations[C]//Proceedings of 6th Conference on Mechanical Behavior of Salt.Hannover:CRC Press,2007.
|
| [12] |
Hou Z M,Wolters R,Rokahr R,et al.Comparison of advanced constitutive models for the mechanical behavior of rock salt—Results from a joint research project-Ⅱ.Numerical modeling of two in situ case studies and comparison[C]//Proceedings of 6th Conference on Mechanical Behavior of Salt.Hannover:CRC Press,2007.
|
| [13] |
Hou Z M.Untersuchungen zum Nachweis der Standsicherheit für Untertagedeponien im Salzgebirge[D].Clausthal-Zellerfeld:Technical University of Clausthal,1997.
|
| [14] |
Xie Lingzhi.Research on salt caverns for CO2 sequestration geotechnical engineering[D].Chengdu:Sichuan University,2012. 谢凌志.盐穴CO2封存库的基础研究[D].成都:四川大学,2012. |
| [15] |
Yang Haijun,Guo Kai,Li Jianjun. Analysis on long-term operation and interval optimization of pressure for single cavity injection/production in underground salt cavern gas storage — Taking the cavity of Well Xi-2 in salt cavern gas storage in Jintan as an example[J]. Oil & Gas Storage and Transportation, 2015, 34(9): 945-950. [杨海军,郭凯,李建君. 盐穴储气库单腔长期注采运行分析及注采压力区间优化——以金坛盐穴储气库西2井腔体为例[J]. 油气储运, 2015, 34(9): 945-950.] |
| [16] |
Li Mengyao.Creep constitutive model for highly impure rock salt and optimal design for underground energy storages of thin-layered rock salt in China[D].Chengdu:Sichuan University,2017. 李梦瑶.中国高杂质盐岩蠕变模型和薄层状盐岩能源储库的优化设计[D].成都:四川大学,2017. |
 2018, Vol. 50
2018, Vol. 50


