谐振腔天线因结构简洁，易于实现高增益，平面结构等优点得到了广泛的研究与应用^[1–3]。根据射线光学法^[1]，谐振腔天线通过其部分反射层与金属地间的多次反射，在口径面上形成同相口径场，从而获得高增益。但是，射线光学法是一种近似方法^[4–5]。Afzal等^[6–9]指出，谐振腔天线的口径场相位为不均匀分布，其造成谐振腔天线的增益较低。

为了获得高增益谐振腔天线，具有高透射系数幅值，且可以改变入射电磁波相位的相移层被设计并用于修正谐振腔天线的不均匀口径场相位分布^[6–9]。Afzal等^[6]设计了一款连续介质相移层，并加载于一个直径为6个波长的圆柱形谐振腔天线上，该研究结果表明谐振腔天线加载相移结构后，获得了一个更加均匀的口径场相位分布，天线增益由原有的13.4 dB增加到了20.8 dB。此外，Afzal等^[7]还设计了一款阶梯状介质相移层，也成功提高了谐振腔天线的增益。但是，两种相移层^[6–7]均采用介质设计，存在着体积大，重量重，加工制作困难等缺点。

近些年来，拥有优良性能的电磁超材料被提出，并得到广泛研究^[10]。通过改变电磁超材料的形状和尺寸，可以得到不同的透射系数，从而实现超材料相移层^[11]。Afzal等^[8]设计了一款超材料相移层，其相移层单元由印刷在双层印刷电路板（printed circuit board，PCB）上的3层金属块组成；通过调节金属块的边长，实现不同的相移角度。但是，该超材料相移层^[8]仅仅依靠全波仿真和参数扫描进行设计，需要大量的计算时间，不利于工程实现。Zhou等^[9]提出了基于全波仿真和等效电路法的混合设计方法，实现了超材料相移层的快速设计。但是，为了避免金属层之间的强互耦，其金属层间的间距较大，该相移层的高度较高。

惠更斯超表面^[12–13]是一种新型的超材料，可以同时与入射电磁波的电场与磁场进行谐振响应，拥有更加优良的电磁性能。作者采用惠更斯超表面设计了一款相移层，并将其应用于谐振腔天线上，提高天线口径场相位分布的均匀性，实现高增益。该超表面相移层由独立与磁场和电场谐振的两组开口谐振环组成，通过分别设计电场谐振和磁场谐振强度，实现相移层的快速设计。该相移层采用PCB板制备，具有重量轻，厚度薄，加工制备简单等优势。作者设计、加工、实测了一款工作频率5.8 GHz的加载惠更斯超表面相移层的谐振腔天线，验证了设计方法的有效性。

惠更斯超表面是一种同时拥有电谐振与磁谐振的新型超材料^[12]。该超表面的电磁性能可以通过表面电导纳 ${Y_{{\rm{se}}}}$ 与磁阻抗 ${{\textit{Z}}_{{\rm{sm}}}}$ 描述。

如图1所示，当惠更斯超表面受到平行于 ${\textit{z}} $ 轴入射的电磁波照射时，入射电磁波与透射电磁波满足以下方程：

图1(Fig. 1)

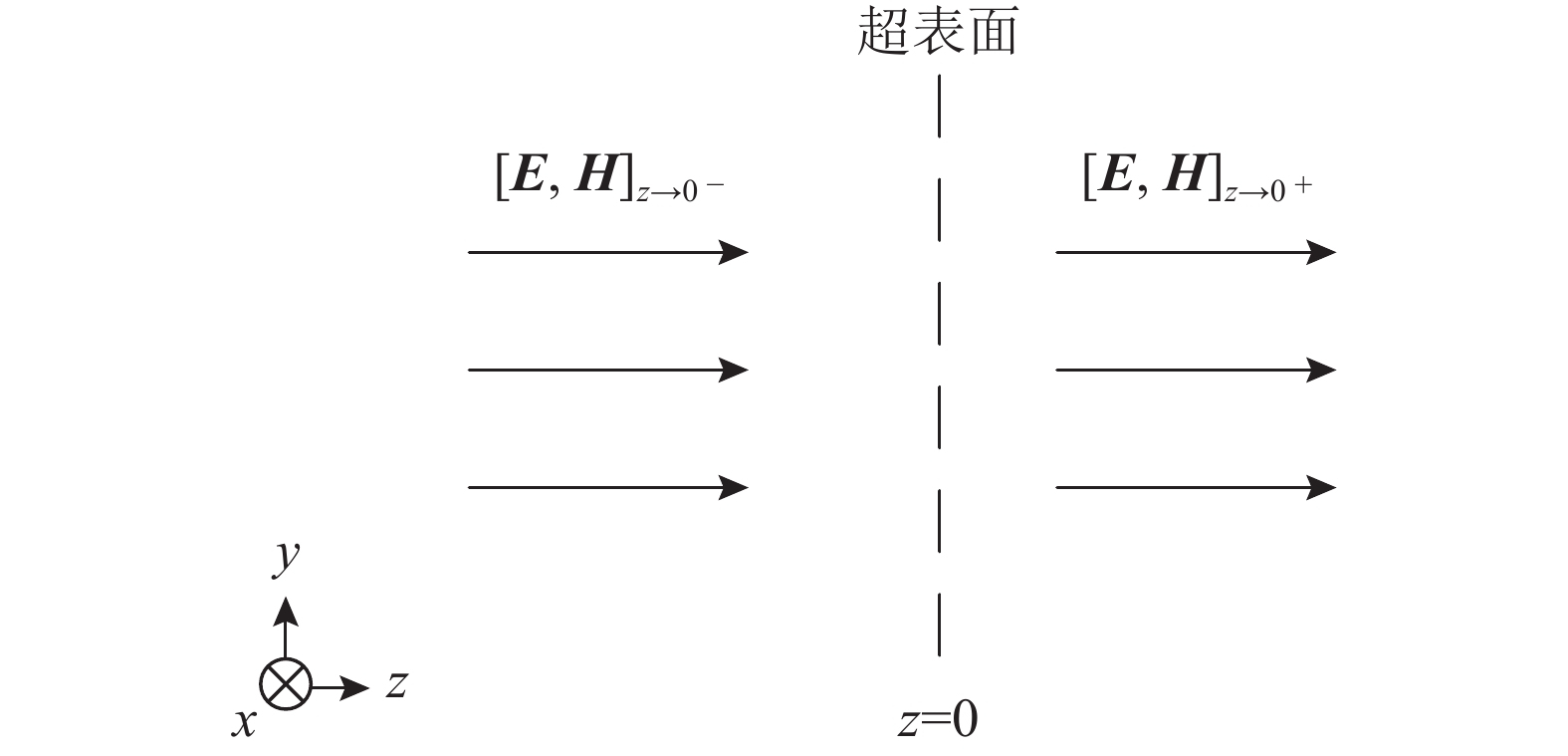图1 在电磁波入射下的超表面示意图 Fig. 1 Schematic of the metasurface under the incident electromagnetic wave

式（1）～（2）中， ${{{E}}_{{\rm{tan}}}}$ 和 ${{{H}}_{{\rm{tan}}}}$ 是垂直于 ${\textit{z}} $ 轴的电场和磁场分量。当超表面的入射电磁波与透射电磁波满足以下方程：

式中， $\theta $ 为电磁波的相移角度。此时，超表面即是一个理想的相移层。将方程（3）和（4）代入（1）和（2）中，可以得到惠更斯超表面相移层的 ${Y_{{\rm{se}}}}$ 、 ${{\textit{Z}}_{{\rm{sm}}}}$ 和 $\theta $ 的关系，如下：

由方程（5）可以看出，通过改变超表面的 ${Y_{{\rm{se}}}}$ 和 ${{\textit{Z}}_{{\rm{sm}}}}$ ，实现期望的相移角度 $\theta $ 。

图2为作者采用的惠更斯相移层单元的结构图^[13]，其由印制于双层PCB板上的两组开口谐振环^[14]组成，两组分别位于 $xy$ 平面和 $y{\textit{z}}$ 平面，每组包含两个开口谐振环。每层PCB板的厚度为2 mm，PCB板的介电常数为2.65。当入射电磁波的电场极化方向平行 $y$ 轴时， $xy$ 平面的开口谐振环与电场谐振， $y{\textit{z}}$ 平面的开口谐振环与磁场谐振。因为磁场谐振与电场谐振分别由不同的开口谐振环引起，故而 ${Y_{{\rm{se}}}}$ 和 ${{\textit{Z}}_{{\rm{sm}}}}$ 之间没有强耦合，可以分开调节。通过调节 $L_1$ ，可以实现不同的 ${{\textit{Z}}_{{\rm{sm}}}}$ ；通过调节 $L_2$ 和 $L_3$ ，可以实现不同的 ${Y_{{\rm{se}}}}$ 。通过适当的 ${Y_{{\rm{se}}}}$ 和 ${{\textit{Z}}_{{\rm{sm}}}}$ 组合，就可以得到期望相移角度的惠更斯超表面相移层单元。将相移层单元组成阵列，即可得到期望的相移层。

图2(Fig. 2)

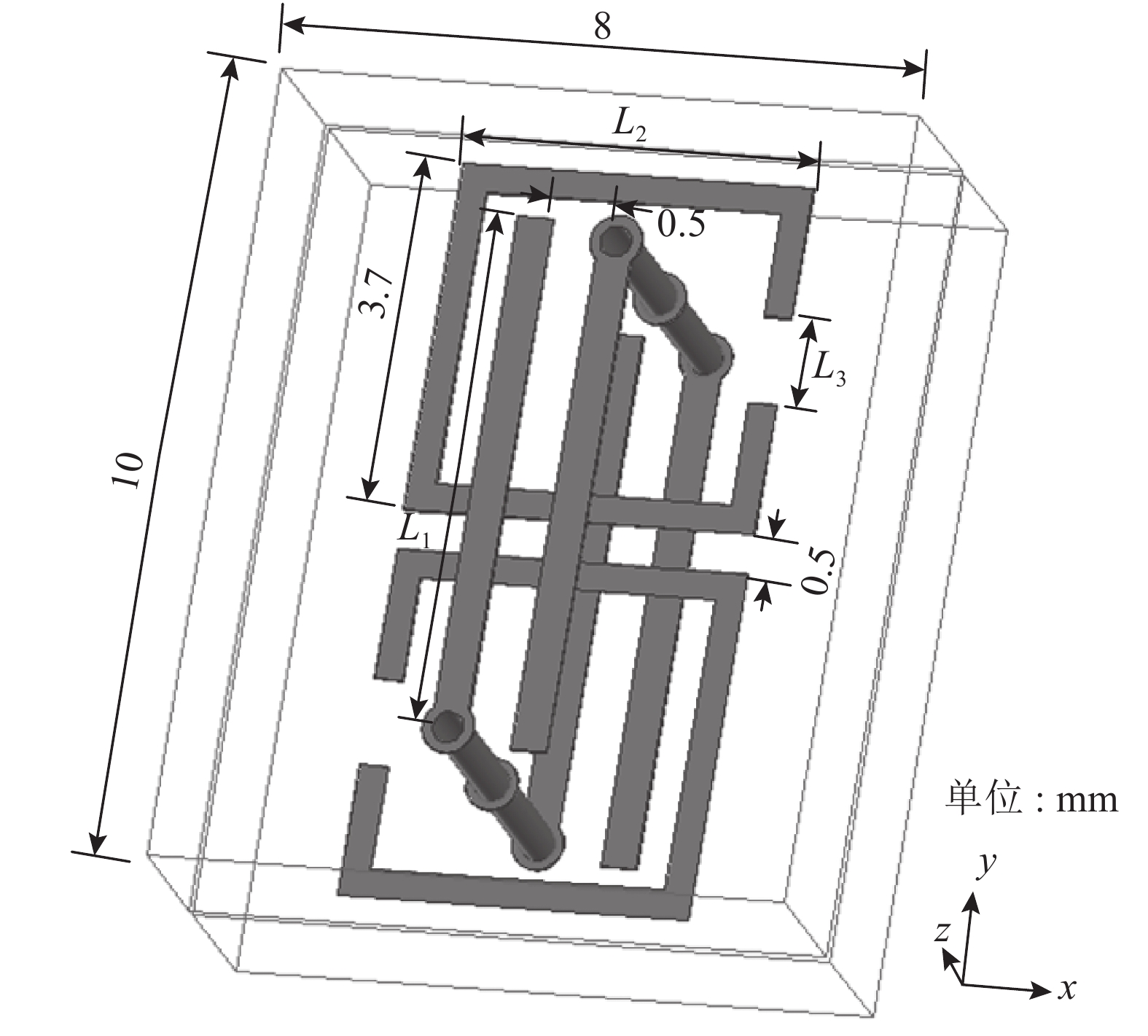图2 惠更斯超表面的单元模型图 Fig. 2 Configuration of the unit cell of the Huygens’ metasurface

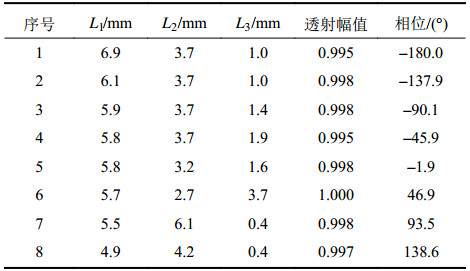
基于上述方法，作者设计了一系列工作于5.8 GHz的惠更斯超表面相移层单元。表1列出了其中一部分相移层单元的尺寸参数与其所具有的透射系数幅值和相位。从表1可以看出，惠更斯超表面相移层可以实现360°相移，并保持透射系数幅值大于0.99。

表1(Tab. 1)

表1 部分相移层单元的尺寸参数和透射系数幅值相位 Tab. 1 Dimensions and transmission magnitudes and phases of some PSS unit cells

表1 部分相移层单元的尺寸参数和透射系数幅值相位 Tab. 1 Dimensions and transmission magnitudes and phases of some PSS unit cells 序号 $L_1$ /mm $L_2$ /mm $L_3$ /mm 透射幅值 相位/(°) 1 6.9 3.7 1.0 0.995 –180.0 2 6.1 3.7 1.0 0.998 –137.9 3 5.9 3.7 1.4 0.998 –90.1 4 5.8 3.7 1.9 0.995 –45.9 5 5.8 3.2 1.6 0.998 –1.9 6 5.7 2.7 3.7 1.000 46.9 7 5.5 6.1 0.4 0.998 93.5 8 4.9 4.2 0.4 0.997 138.6

加载惠更斯超表面相移层的谐振腔天线的结构如图3所示。其中，谐振腔天线为圆柱形，直径 $D_{\rm c}$ 为180 mm，主要由贴片天线、金属地和部分反射层3部分组成^[1–2]。谐振腔天线的工作频率为5.8 GHz。部分反射层采用的是介电常数10.2、厚度2 mm的介质板。贴片天线的介质基板介电常数为2.65，厚度为1 mm。利用CST全波仿真软件^[15]，对谐振腔天线进行仿真优化，得到谐振腔高度 $h_1$ 为28 mm时，天线增益达到最大，即14.90 dB。

图3(Fig. 3)

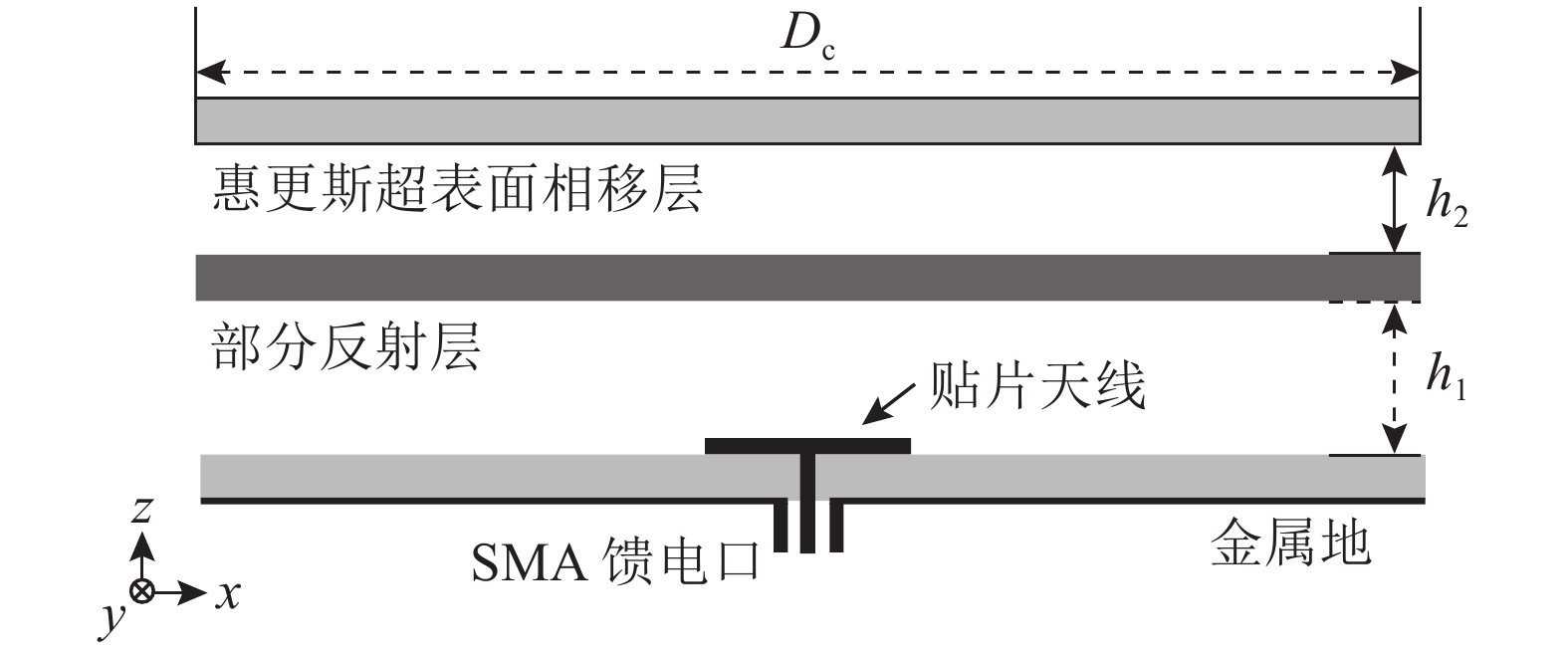图3 加载惠更斯超表面相移层的谐振腔天线的结构图 Fig. 3 Configuration of the resonant cavity antenna with the Huygens’ metasurface as the phase shift surface

惠更斯超表面相移层位于谐振腔天线口径正上方，相移层与部分反射层间的距离 $h_2$ 为20 mm。相移层所需的相移分布等于谐振腔天线的口径场相位分布的互补值^[6–9]，可通过CST全波仿真得到。根据所需相移分布，利用第1节所设计的惠更斯超表面相移层单元组阵，即可形成相移层。

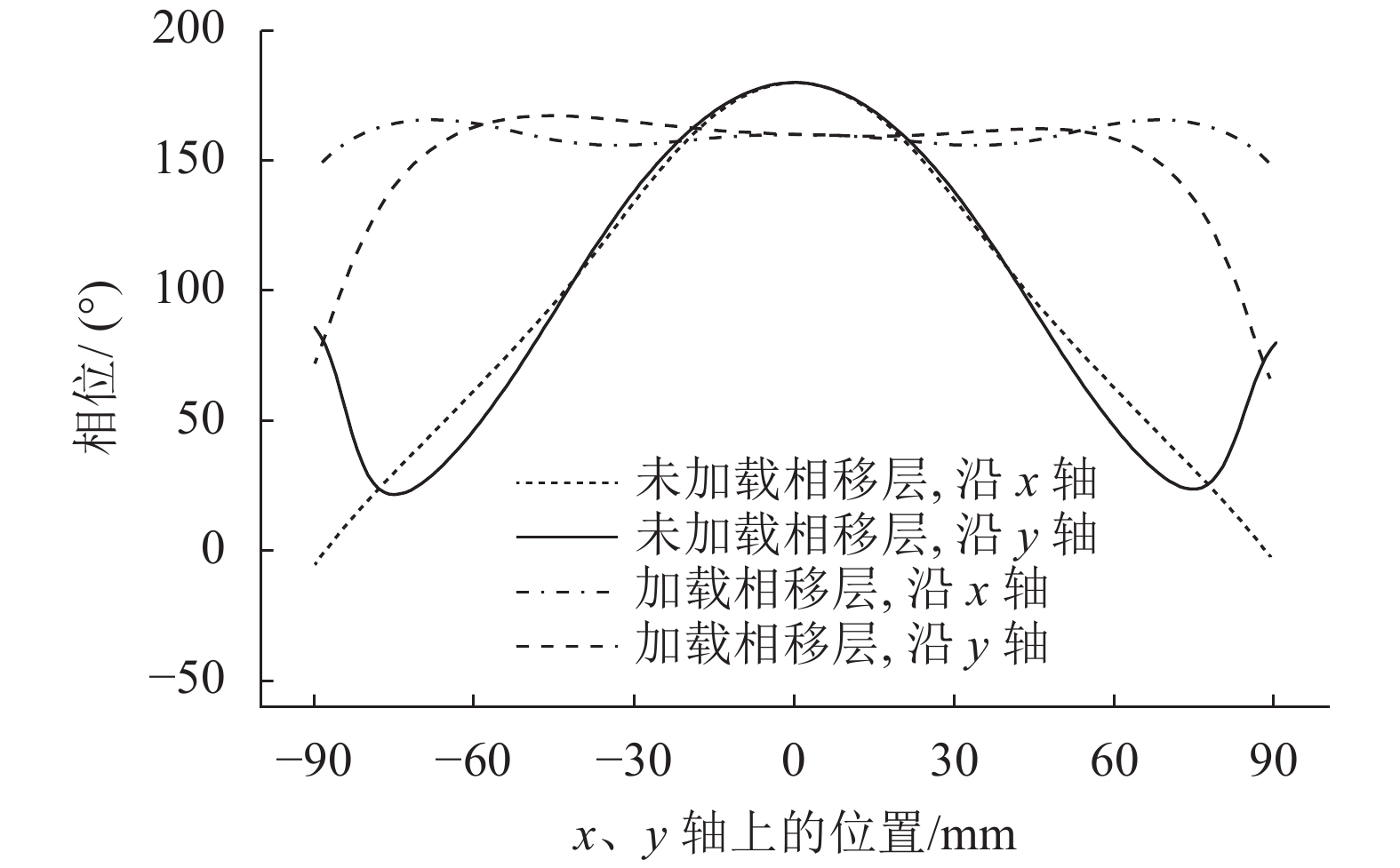
对加载了相移层的谐振腔天线进行CST全波仿真，得到了其口径场相位分布。图4为加载和未加载相移层情况下，谐振腔天线口径场沿 $x$ 和 $y$ 轴的相位分布。对比图4中两组曲线可以看出，加载相移层后，天线口径场相位分布明显更加均匀。

图4(Fig. 4)

图4 加载和未加载相移层的谐振腔天线口径场沿 ${ x}$ 和 ${ y}$ 轴的相位分布 Fig. 4 Aperture field phase distributions of the RCA with or without the PSS along ${ x}$ and ${ y}$ axes

图5给出了加载和未加载相移层的谐振腔天线的仿真方向图。从图5可以看出，加载相移层后，谐振腔天线增益有明显的升高，由原来的14.90 dB升高到18.31 dB，其对应的口径效率由原来的25.9%提高到了56.7%。

图5(Fig. 5)

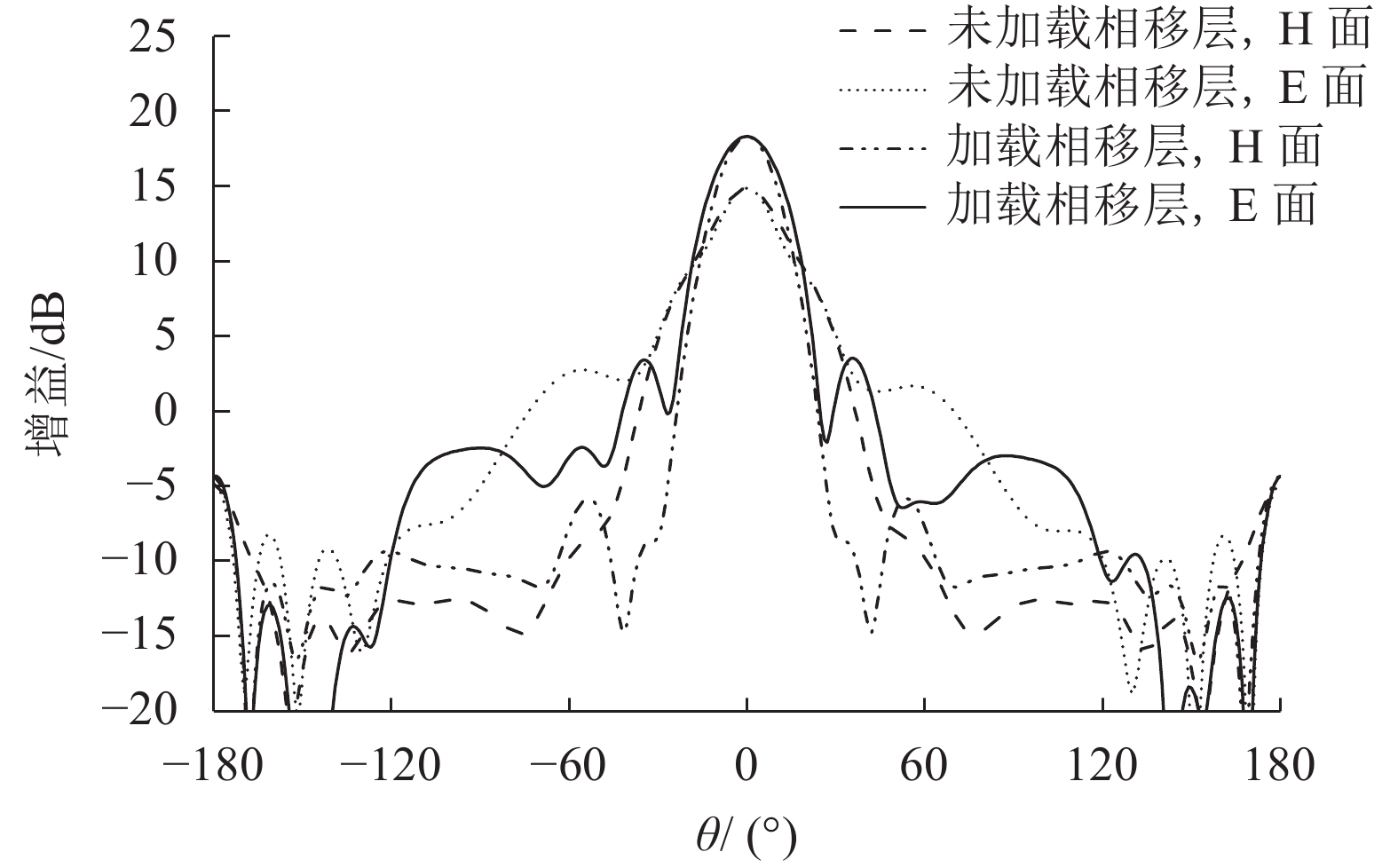图5 加载和未加载相移层的谐振腔天线仿真方向图 Fig. 5 Simulated radiation patterns of the RCA with or without the PSS

对设计的加载惠更斯超表面相移层的谐振腔天线进行了加工，其实物图如图6所示。

图6(Fig. 6)

图6 加载相移层的谐振腔天线的实物图 Fig. 6 Prototype of the RCA with the PSS

对加工的天线进行测试，并与仿真结果进行对比。天线的输入反射系数由安捷伦E8362B测得，结果如图7所示。从图7可以看到，测试结果和仿真结果吻合良好。加载相移层的谐振腔天线的实测| $S\!\!_{11}$ |在5.8 GHz时为–15.96 dB，在5.75～5.90 GHz频段内满足| $S\!\!_{11}$ |<–10 dB。

图7(Fig. 7)

图7 天线的仿真和实测输入反射系数| ${ S}\!_{{11}}$ | Fig. 7 Simulated and measured input reflection coefficients | ${ S}\!_{{11}}$ | of the antenna

天线的辐射特性在微波暗室中测得。图8绘制了加载相移层的谐振腔天线在5.8 GHz时的仿真和实测辐射方向图。

从图8可以看出，实测结果与仿真值吻合良好，天线具有高增益。同时，天线的实测主旁瓣比大于15 dB，半功率波束角内交叉极化比大于20 dB。

图8(Fig. 8)

图8 天线5.8 GHz时的仿真和实测辐射方向图 Fig. 8 Simulated and measured radiation patterns of the antenna at 5.8 GHz

为了获得高增益谐振腔天线，作者设计了一款惠更斯超表面相移层，将其加载于谐振腔天线表面，用于修正天线的口径场相位分布。该惠更斯超表面的电场谐振与磁场谐振相互独立，可以分别调节，从而实现了相移层的快速设计。为验证方法的正确性，采用该结构设计了一款工作频率5.8 GHz的相移层，并将其加载于直径180 mm的谐振腔天线上。CST全波仿真和加工实测结果表明，通过加载惠更斯超表面相移层，谐振腔天线的口径场相位分布变得更加均匀，增益也获得了显著提高。虽然本研究仅将惠更斯超表面相移层应用于谐振腔天线，但其同样可以应用于具有不均匀口径场相位分布的其他天线类型。下一步研究中，作者将把所设计的相移层应用于微带阵列天线和波导缝隙天线，以提高天线的辐射性能。