2. 昆士兰大学 土木工程系,布里斯班 4072;
3. 南昌工程学院 江西省水利土木特种加固与安全监控工程研究中心,江西 南昌 330099;
4. 同济大学 地下建筑与工程系,上海 200092
2. School of Civil Eng., The Univ. of Queensland, Brisbane 4072, Australia;
3. Jiangxi Provincial Eng. Research Center of the Special Reinforcement and Safety Monitoring Technol. in Hydraulic & Civil Eng., Nanchang Inst. of Technol., Nanchang 330099, China;
4. Dept. of Geotechnical Eng., Tongji Univ., Shanghai 200092, China
随着国民经济的蓬勃发展,道路、水利、采矿、建筑以及国防建设等各个领域中都会遇到边坡稳定性问题,边坡加固方法优化和相应的稳定性分析成为了工程实践和学科研究的热点。抗滑桩作为常用的加固手段,因其抗滑作用显著、桩位灵活、施工安全方便、适用范围广等特点,被广泛应用于边坡工程当中。抗滑桩凭借桩–土共同作用把滑坡推力传递到稳定地层,利用稳定地层的锚固作用和被动抗力来平衡滑坡推力,从而提高了边坡的抗滑稳定安全系数,工程实践证明其对于边坡加固非常有效[1]。因此,开展抗滑桩加固边坡整体稳定性的理论解析研究,进一步完善边坡稳定性分析理论和方法,具有重大的理论和现实意义。
近年来,对于边坡在抗滑桩加固后稳定性及抗滑桩设计理论的研究已取得了一些进展。古浩[2]提出了一种把抗滑桩和滑坡体作为整体分析的有限元内力分析方法。郑轶轶[3]将独创的滑面应力法拓展运用到抗滑桩加固边坡的稳定性分析。李荣建等[4]利用考虑基质吸力的有限元程序,探讨了抗滑桩加固前后边坡整体稳定性。张晓曦[5]采用基于极限分析的扇形条分法,对可能出现的次级滑面形状及其稳定性进行了预测研究。王聪聪等[6]利用数值方法分析了抗滑桩在边坡中的加固效果,探讨了桩、坡参数对边坡稳定及桩体内力等的影响规律。
极限分析法根据能量耗散情况直接研究结构最终达到塑流状态时的极限荷载。与其他岩土工程稳定性分析的常用方法相比,其理论基础严密、求解过程简单、适用性广,在实践和研究中的应用也越发广泛。Chen[7]发表专著将极限分析应用于岩土结构的稳定性分析,并详细论述了其在岩土边坡稳定性方面的应用。Michalowski等[8]采用牛角状对数螺旋圆锥体对3维边坡的破坏进行模拟。孙志彬[9]给出了基于上限定理的简单均质土坡潜在滑动面的确定方法。Gao等[10]对3维破坏机构的类型进行了拓展研究,细分出3类破坏机构。饶平平等[11]对坡面沉桩过程中边坡的稳定性进行了极限上限分析。
亦有学者应用极限分析法研究了抗滑桩加固边坡的稳定性问题。Hassiotis[12]和Li[13]等分别采用圆弧和对数螺旋线进行模拟,研究了桩体横向力对边坡稳定性和破坏面形状的影响。Ausilio等[14]对采用极限平衡法和极限分析上下限法的计算结果进行了比较分析,考察了桩对土坡的影响规律及最佳抗滑桩位置。年廷凯[15]围绕组合荷载模式下承重阻滑桩–土–边坡体系的变形与稳定性问题进行了比较系统而深入的研究。吴永等[16]研究了地震荷载作用下滑坡锚固体系的能量输入与耗散机制,分析了导致体系失稳的震波特征和临界值。赵炼恒[17]采用线性和非线性规划方法,发展和完善了复杂条件下边坡稳定性分析和设计的能量方法。谭捍华等[18]分析了单桩加固边坡的局部稳定性,并由此推导了多桩加固边坡的稳定性分析算式。Gao等[19]通过建立3维模型研究桩加固边坡的稳定性并进行了参数分析。
目前,应用3维破坏机构进行抗滑桩加固边坡稳定性极限上限分析的成果很少,相关计算模型类型单一,研究结论的细化工作也较为不足。作者在已有研究的基础上,通过引进新的几何优化参数拓展了3维转动破坏机构的类型,将其应用于抗滑桩加固后边坡稳定性的极限上限分析中,并分析了抗滑桩位置、桩距等参数的影响规律。基于拓展后的边坡破坏机构考察抗滑桩对边坡稳定性的影响,在理论上其结果更加科学合理。
1 计算模型和计算方法 1.1 拓展的3维转动破坏机构应用极限分析上限法研究机构的稳定性,需构建一系列运动许可的速度场,Michalowski等[8]提出用一种牛角状对数螺旋圆锥体模拟3维边坡的转动破坏。然而,该机构的破坏面通过边坡坡趾,但实际的破坏面并不一定通过坡趾,因此机构的几何模型有待改进和拓展,以得到更危险的潜在破坏机构及其对应的更接近真实解的上限解。参考Gao等[10]对未加固边坡的拓展分析方法,作者在抗滑桩加固后边坡稳定性的3维极限上限分析中,对破坏面通过坡趾的3维转动破坏机构(坡趾破坏)进行了类似拓展,考虑破坏面通过坡面(坡面破坏)和破坏面通过坡趾下方(坡底破坏)的情况,如图1所示。
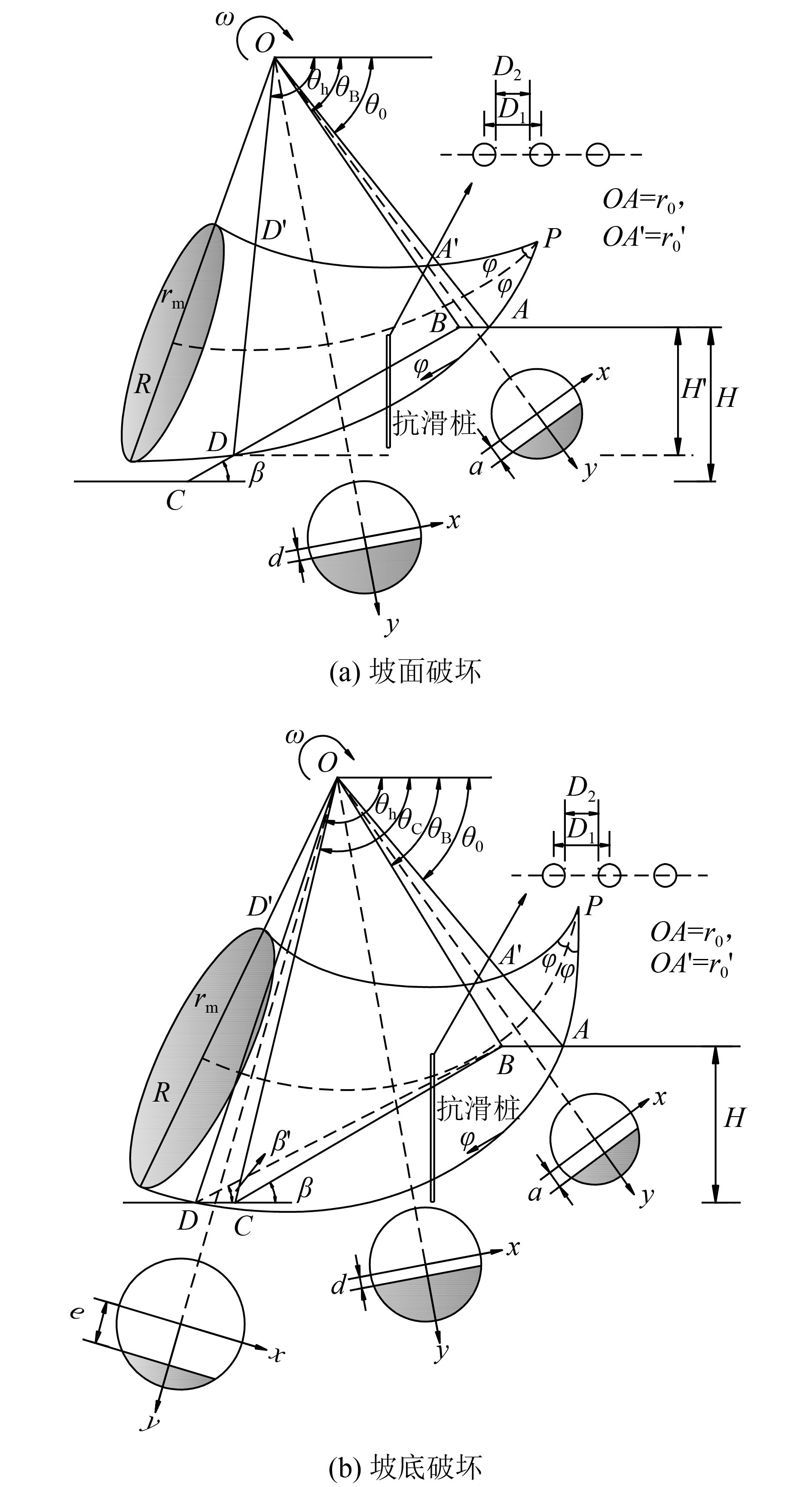 |
| 图1 拓展的3维转动破坏机构 Fig. 1 Extended 3D rotational failure mechanism |
本文计算模型选取单一土层边坡,假设土体满足理想弹塑性模型,服从库仑屈服准则和相关联流动法则。边坡高度为H,坡角为
如图1所示,在坡面破坏和坡底破坏中,分别引进几何参数
在分析过程中,作者认为整体破坏机构被限定在一个确定的宽度
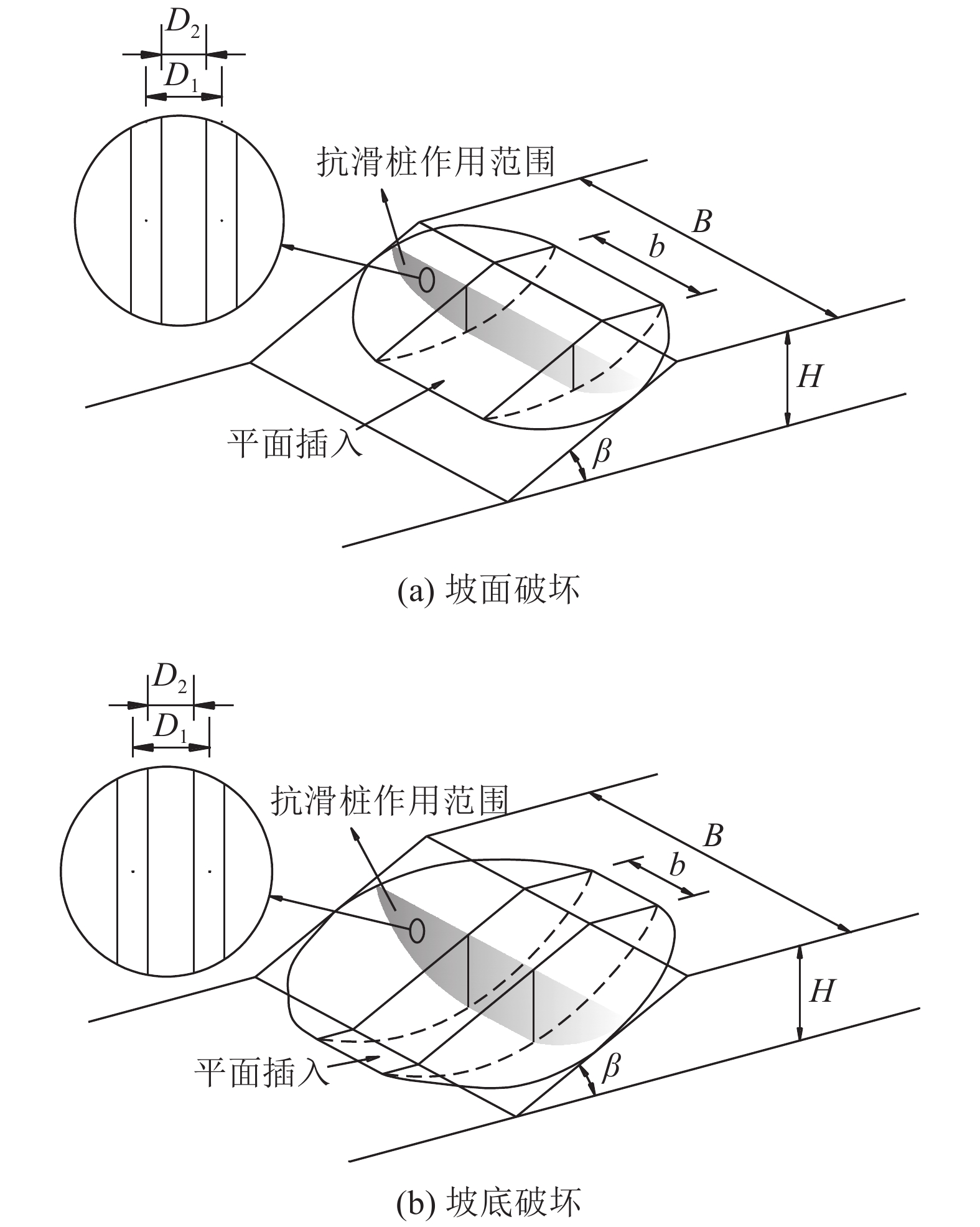 |
| 图2 整体3维破坏机构 Fig. 2 3D failure mechanism with plane insert |
1.2 抗滑稳定安全系数
Fs表征边坡机构稳定性的抗滑稳定安全系数,其定义为:实际土体强度参数与维持边坡稳定所需的最小土体强度参数的比值。其表达式为:
| ${F_{\rm{s}}} = \frac{c}{{{c_{\rm{m}}}}} = \frac{{\tan\; \varphi }}{{\tan \;{\varphi _{\rm{m}}}}}$ | (1) |
式中,
在安全系数
| $\begin{aligned}{F_{\rm{s}}} = \min f({F_{\rm{s}}},{\theta _0},{\theta _{\rm{h}}},{{r'}_0}/{r_0},b,(n,\beta ') |c,\varphi ,\gamma ,H,B,\beta )\end{aligned}$ | (2) |
式中,
根据上述极限分析上限法的计算原理,需在运动许可的变形机构中,通过内外功率的相等关系建立方程,得到安全系数的上限解,并通过机构优化搜索最小上限解。计算中,外功率只包含滑动体重力做功功率
| $W_\gamma ^e + W_\gamma ^c = {D^e} + {D^c} + D_{\rm{p}}^e + D_{\rm{p}}^c$ | (3) |
式中,上标
坡趾破坏的内外功率
如图3所示,可将坡面破坏视为坡高是H'的坡趾破坏,将后者公式中坡高H替换为H'即可得到前者内外功率
 |
| 图3 坡面破坏对称面几何关系示意图 Fig. 3 Geometry of maximum cross section of face-failure mechanism |
考虑单排抗滑桩的加固作用,还需计算克服抗滑桩横向抗力做功的内能耗散率
| $\begin{aligned}[b] p({\textit{z}}) = & c{D_1}{\left( {\frac{{{D_1}}}{{{D_2}}}} \right)^{N_\varphi ^{1/2}\tan \;\varphi + {N_\varphi } - 1}}\left\{ {\frac{1}{{{N_\varphi }\tan \;\varphi }}}\cdot \right.\\& \Bigg[ {\exp } \left( {\frac{{{D_1} - {D_2}}}{{{D_2}}}{N_\varphi }\tan \;\varphi \tan \left( {\frac{{\text{π}} }{8} + \frac{\varphi }{4}} \right)} \right) - \\&\left. { {2N_\varphi ^{1/2}\tan \;\varphi - 1} \Bigg] + \frac{{2\tan \;\varphi + 2N_\varphi ^{1/2} + N_\varphi ^{ - 1/2}}}{{N_\varphi ^{1/2}\tan \;\varphi + {N_\varphi } - 1}}} \right\} - \\ &c\left[ {{D_1}\frac{{2\tan \;\varphi + 2N_\varphi ^{1/2} + N_\varphi ^{ - 1/2}}}{{N_\varphi ^{1/2}\tan \;\varphi + {N_\varphi } - 1}} - 2{D_2}N_\varphi ^{ - 1/2}} \right] + \\& \qquad\qquad\frac{{\gamma {\textit{z}}}}{{{N_\varphi }}}\left[ {{D_1}{{\left( {\frac{{{D_1}}}{{{D_2}}}} \right)}^{N_\varphi ^{1/2}\tan \varphi + {N_\varphi } - 1}} \cdot } \right.\\& \left. {\exp \left( {\frac{{{D_1} - {D_2}}}{{{D_2}}}{N_\varphi }\tan \;\varphi \tan \left( {\frac{{\text{π}} }{8} + \frac{\varphi }{4}} \right)} \right) - {D_2}} \right]\end{aligned}$ | (4) |
式中,
破坏机构对称面内的几何关系如图3所示,其中,
3维转动破坏机构中克服桩土间横向力做功功率
| $D_{\rm{p}}^e = 2\omega \int_0^h {\frac{{p({\textit{z}})}}{{{D_1}}}x({\textit{z}})l({\textit{z}})} {\rm d}{\textit{z}}$ | (5) |
| $D_{\rm{p}}^c = \omega \int_0^h {\frac{{p({\textit{z}})}}{{{D_1}}}bl({\textit{z}})} {\rm d}{\textit{z}}$ | (6) |
式(5)~(6)中,
| $x({\textit{z}}) = \sqrt {R_{\rm{e}}^2 - {{\left( {\sqrt {{l^2} + {{({r_{\rm{p}}}\cos {\theta _{\rm{p}}})}^2}} - {r_{{\rm{me}}}}} \right)}^2}} ,$ |
| $l({\textit{z}}) = {r_{\rm{h}}}\sin \;{\theta _{\rm{h}}} - {X_{\rm{F}}}\tan \;\beta + {\textit{z}},$ |
| $h = {r_{\rm{p}}}\sin \;{\theta _{\rm{p}}} - {r_{\rm{h}}}\sin \;{\theta _{\rm{h}}} + {X_{\rm{F}}}\tan \;\beta{\text{。}}$ |
其中,
| ${\theta _{\rm{e}}} = \arccos \left( {\frac{{{r_{\rm{p}}}\cos \;{\theta _{\rm{p}}}}}{{\sqrt {{{({r_{\rm{p}}}\cos \;{\theta _{\rm{p}}})}^2} + {l^2}} }}} \right)$ | (7) |
如图3所示,由于几何关系的变化,坡面破坏的计算中不仅需要将上述公式中的H替换为H',还需将
由于模型几何形状的改变,坡底破坏的内外功率计算公式与坡趾破坏有所不同。按照Michalowski等[8]的积分推导方法,Gao等[10]给出了端部螺旋圆锥体重力做功功率
| $\begin{aligned} W_\gamma ^e = & 2\omega \gamma \left[ {\int_{{\theta _0}}^{{\theta _{\rm{B}}}} {\int_0^{\sqrt {{R^2} - {a^2}} } {\int_a^{\sqrt {{R^2} - {x^2}} } {{{({r_{\rm{m}}} + y)}^2}\cos \;\theta {\rm{d}}y{\rm{d}}x{\rm{d}}\theta } } } } \right. + \\& \int_{{\theta _{\rm{B}}}}^{{\theta _{\rm{C}}}} {\int_0^{\sqrt {{R^2} - {d^2}} } {\int_d^{\sqrt {{R^2} - {x^2}} } {{{({r_{\rm{m}}} + y)}^2}\cos \;\theta {\rm{d}}y{\rm{d}}x{\rm{d}}\theta } } } + \\& \left. {\int_{{\theta _{\rm{C}}}}^{{\theta _{\rm{h}}}} {\int_0^{\sqrt {{R^2} - {e^2}} } {\int_e^{\sqrt {{R^2} - {x^2}} } {{{({r_{\rm{m}}} + y)}^2}\cos \;\theta {\rm{d}}y{\rm{d}}x{\rm{d}}\theta } } } } \right]\end{aligned}$ | (8) |
| $\begin{aligned}[b]{D^e} = & \frac{{ - 2c\omega r_0^2}}{{\tan \;\varphi }}\left[ {{{\sin }^2}{\theta _0}\int_{{\theta _0}}^{{\theta _{\rm{B}}}} {\frac{{\cos \;\theta }}{{{{\sin }^3}\;\theta }}} \sqrt {{R^2} - {a^2}} {\rm{d}}\theta + } \right.\\& {{\rm e}^{2({\theta _{\rm{h}}} - {\theta _0})\tan \varphi }}\frac{{{{\sin }^2}(\beta + {\theta _{\rm{C}}}){{\sin }^2}{\theta _{\rm{h}}}}}{{{{\sin }^2}\;{\theta _{\rm{C}}}}} \times \\& \int_{{\theta _{\rm{B}}}}^{{\theta _{\rm{C}}}} {\frac{{\cos (\theta + \beta )}}{{{{\sin }^3}(\theta + \beta )}}} \sqrt {{R^2} - {d^2}} {\rm{d}}\theta + \\& \left. {{{\rm e}^{2({\theta _{\rm{h}}} - {\theta _0})\tan \varphi }}{{\sin }^2}{\theta _{\rm{h}}}\int_{{\theta _{\rm{C}}}}^{{\theta _{\rm{h}}}} {\frac{{\cos \;\theta }}{{{{\sin }^3}\;\theta }}} \sqrt {{R^2} - {e^2}} {\rm{d}}\theta } \right]\end{aligned}$ | (9) |
式中,
| $a = \frac{{\sin \;{\theta _0}}}{{\sin \;\theta }}{r_0} - {r_{\rm{m}}},$ |
| $d = \frac{{\sin (\beta + {\theta _{\rm{C}}})\sin \;{\theta _{\rm{h}}}}}{{\sin (\beta + \theta )\sin \;{\theta _{\rm{C}}}}}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}{r_0} - {r_{\rm{m}}},$ |
| $e = \frac{{\sin \;{\theta _{\rm{h}}}}}{{\sin \;\theta }}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}{r_0} - {r_{\rm{m}}},$ |
| ${\theta _{\rm{B}}} = \arctan \frac{{\sin \;{\theta _0}}}{{\cos \;{\theta _0} - A'}},$ |
| ${\theta _{\rm{C}}} = \arctan \frac{{\sin \;{\theta _{\rm{h}}}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}}}{{\cos \;{\theta _0} - A' - (\sin \;{\theta _{\rm{h}}}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }} - \sin \;{\theta _0})/\tan \;\beta }},$ |
其中,
| $A' = \frac{{\sin ({\theta _{\rm{h}}} - {\theta _0})}}{{\sin \;{\theta _{\rm{h}}}}} - \frac{{{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan\;\varphi }}\sin \;{\theta _{\rm{h}}} - \sin \;{\theta _0}}}{{\sin \;{\theta _{\rm{h}}}\sin \;\beta '}} \sin ({\theta _{\rm{h}}} + \beta '){\text{。}}$ |
平面插入部分重力做功功率
| $W_\gamma ^c = b \omega \gamma r_0^3({f_1} - {f_2} - {f_3} - {f_4})$ | (10) |
| ${D^c} = \frac{{b c\omega r_0^2}}{{2\tan \;\varphi }}\left[ {{{\rm e}^{2({\theta _{\rm{h}}} - {\theta _0})\tan\; \varphi }} - 1} \right]$ | (11) |
式(10)~(11)中,
| $\begin{aligned}{f_1} = & \frac{1}{{3(1 + 9{{\tan }^2}\varphi )}}\left[ {(3\tan \;\varphi \cos \;{\theta _{\rm{h}}} + \sin \;{\theta _{\rm{h}}})} \cdot \right.\\& \left. {{{\rm e}^{3({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }} - (3\tan \varphi \cos {\theta _0} + \sin {\theta _0})} \right],\end{aligned}$ |
| ${f_2} = \frac{1}{6}\frac{L}{{{r_0}}}\left( {2\cos \;{\theta _0} - \frac{L}{{{r_0}}}} \right)\sin \;{\theta _0},$ |
| $\begin{aligned}{f_3} = & \frac{1}{6}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}\left[ {\sin ({\theta _{\rm{h}}} - {\theta _0}) - \frac{L}{{{r_0}}}\sin \;{\theta _{\rm{h}}}} \right]\cdot\\& \left[ {\cos \;{\theta _0} - \frac{L}{{{r_0}}} + \cos \;{\theta _{\rm{h}}}{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \varphi }}} \right],\end{aligned}$ |
| $\begin{aligned}{f_4} = & {\left( {\frac{H}{{{r_0}}}} \right)^2}\frac{{\sin (\beta - \beta ')}}{{2\sin \;\beta \sin \;\beta '}}\cdot \\& \left[ {\cos \;{\theta _0} - \frac{L}{{{r_0}}} - \frac{1}{3}\frac{H}{{{r_0}}}(\cot \;\beta ' + \cot \;\beta )} \right],\end{aligned}$ |
其中,
| $\begin{aligned}\frac{L}{{{r_0}}} = & \frac{{\sin ({\theta _{\rm{h}}} - {\theta _0})}}{{\sin \;{\theta _{\rm{h}}}}} - \frac{{\sin ({\theta _{\rm{h}}} + \beta ')}}{{\sin \;{\theta _{\rm{h}}}\sin \;\beta '}}\cdot \\& \left[ {{{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}\sin \;{\theta _{\rm{h}}} - \sin \;{\theta _0}} \right],\end{aligned}$ |
| $\frac{H}{{{r_0}}} = {{\rm e}^{({\theta _{\rm{h}}} - {\theta _0})\tan \;\varphi }}\sin \;{\theta _{\rm{h}}} - \sin \;{\theta _0}{\text{。}}$ |
在坡底破坏的计算中,克服抗滑桩横向抗力做功的功率可由式(5)~(7)计算得到,仅需将公式中的
计算图1和2所示3维边坡破坏机构的抗滑稳定安全系数,并对抗滑桩位置
| 表1 土坡参数 Tab. 1 Parameters of soil and slope |
 |
为验证方法和所编优化程序的正确性,本文在第3.1节和第3.2节中将
对于3种破坏机构类型,坡趾破坏可以看作坡面破坏和坡底破坏的特殊情况。因此在优化过程中,计算结果所对应的破坏机构类型没有规避坡趾破坏。换言之,如果出现坡面破坏和坡底破坏的计算结果,说明对破坏机构类型的拓展是有意义的,从而实现了计算结果的进一步优化。
3.1 抗滑桩位置的影响为研究抗滑桩位置对边坡破坏模式及稳定性的影响,相对桩距
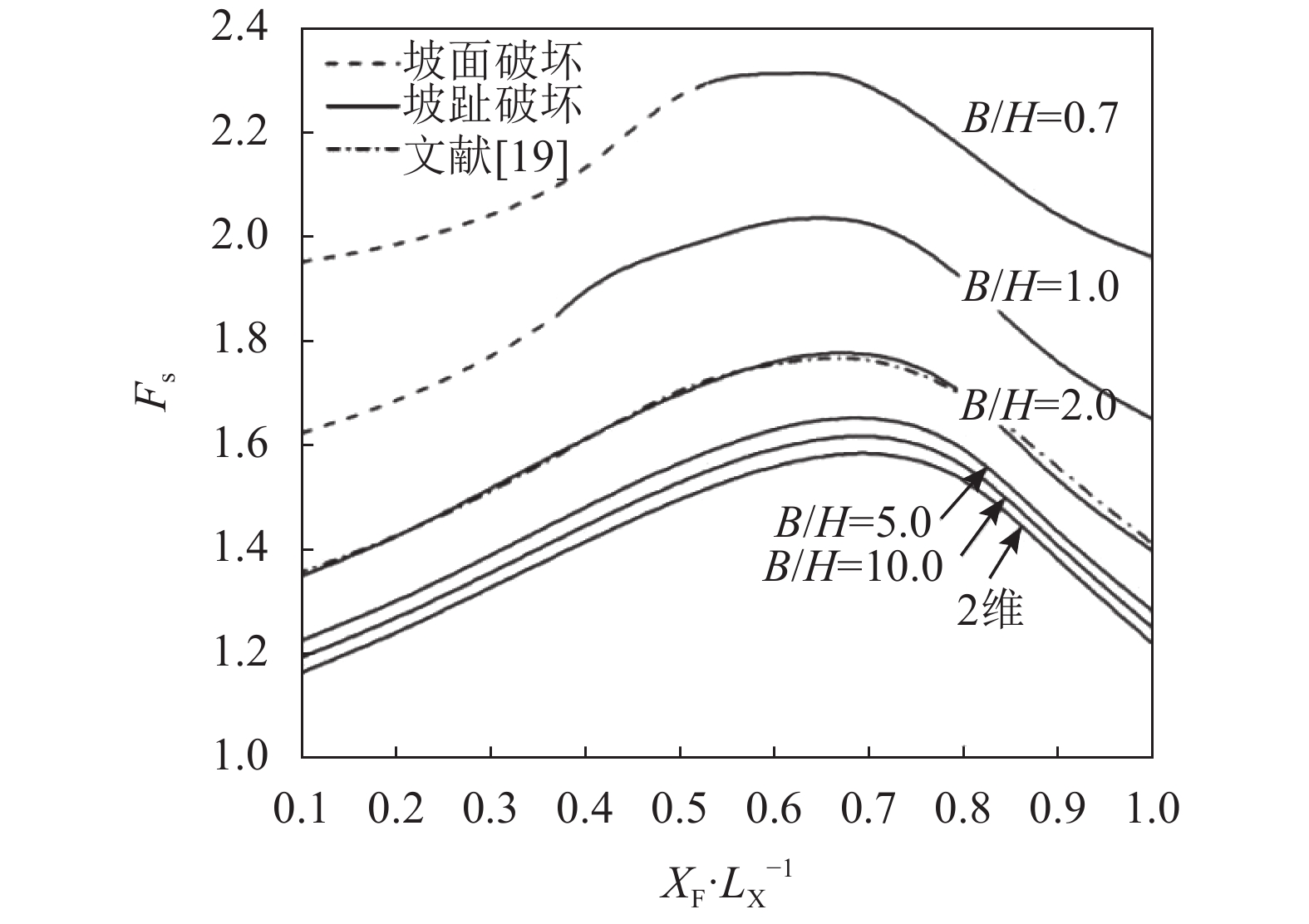 |
| 图4 抗滑桩位置对边坡抗滑稳定安全系数的影响 Fig. 4 Effect of pile location on the anti-slide safety factor of slope stability |
从图4中可以看出,当机构限宽较小且抗滑桩位置较靠近坡趾时,边坡的潜在最危险破坏模式为坡面破坏,其余情况下,边坡仍倾向于在坡趾破坏模式下发生破坏。另外,虽然
图5为
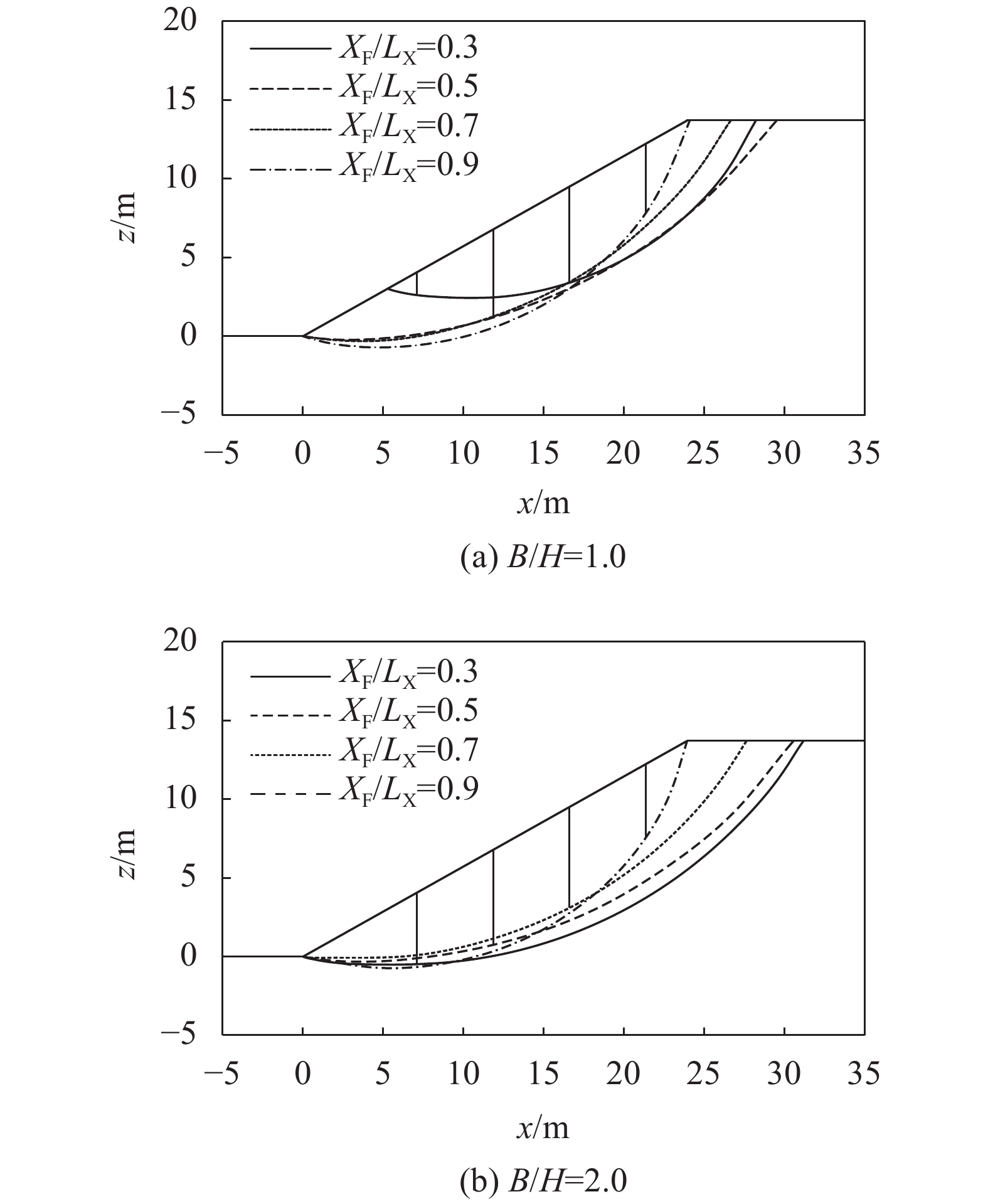 |
| 图5 抗滑桩位置对破坏面形状的影响 Fig. 5 Effect of pile location on the critical failure surface |
与单独考察端部即螺旋圆锥体3维模型的稳定性相比,采用2维模型即插入部分分析边坡稳定性得到的结果更加保守,因此,作者采用的组合模型将优化2维模型过分保守的稳定性评估,将端部对于整体破坏机构安全系数的影响称为“端部效应”。
考察抗滑桩加固后3维边坡的破坏模式和稳定性时,主要考虑3维破坏机构端部效应和抗滑桩横向抗力的影响。用端部的宽度
 |
| 图6 端部效应和横向抗力影响随抗滑桩位置的变化 Fig. 6 Variation of end effect and lateral force with pile location |
从图6(b)可以看出,抗滑桩横向抗力的影响是边坡安全系数变化的主要原因,该部分功率对于边坡安全贡献率的变化规律与边坡安全系数的变化规律契合度较高,抗滑桩加固作用最显著的位置即为安全系数最高的位置。而图6(a)显示,破坏机构端部宽度除去在
为研究桩距对边坡破坏模式及稳定性的影响,抗滑桩位置
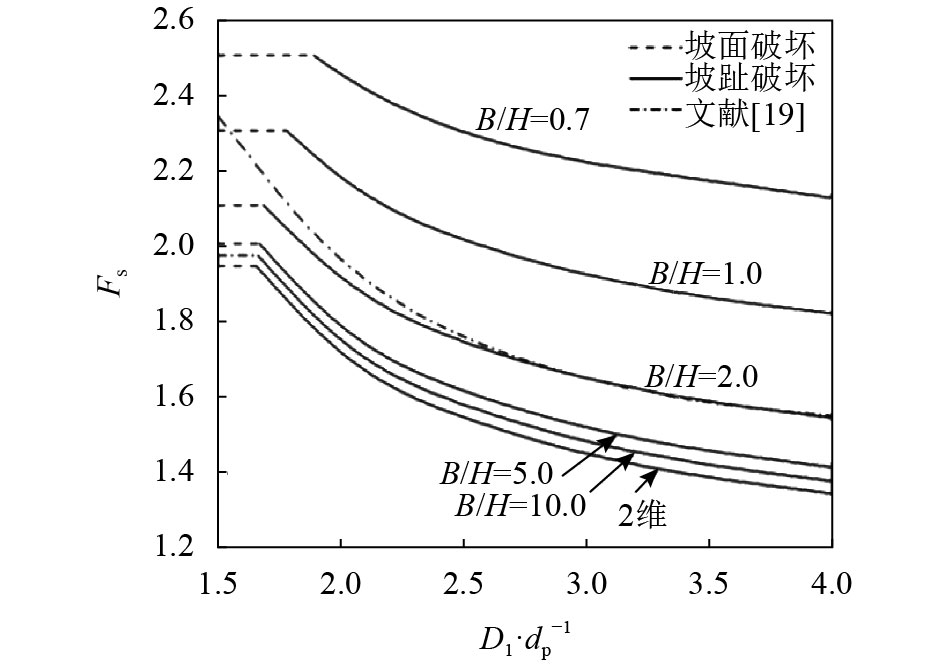 |
| 图7 桩距对边坡抗滑稳定安全系数的影响 Fig. 7 Effect of pile spacing on the anti-slide safety factor of slope stability |
从图7中可以看出:不同机构限宽的条件下,桩距对安全系数的影响规律相似。除
不同
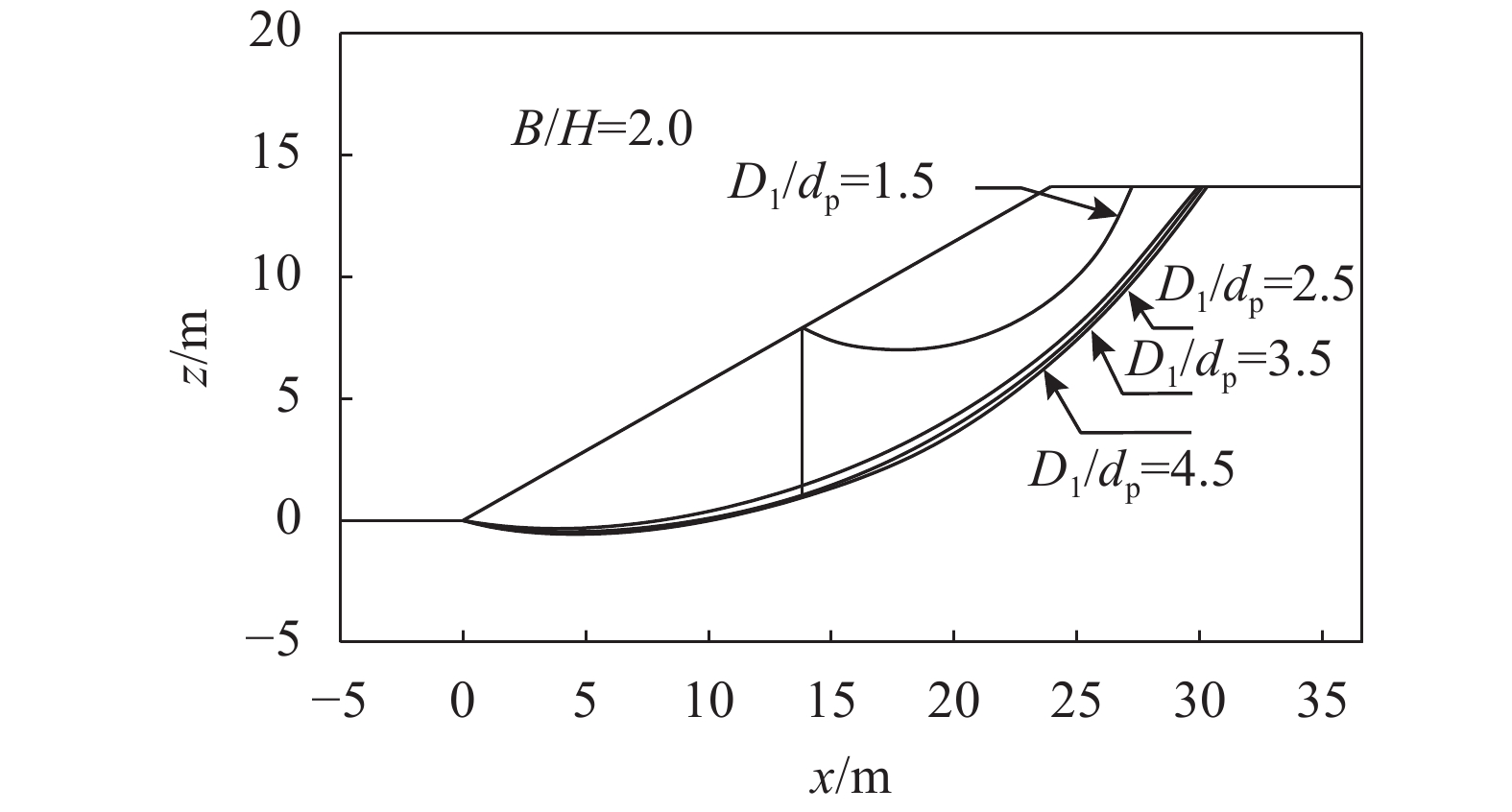 |
| 图8 桩距对破坏面形状的影响 Fig. 8 Effect of pile spacing on the critical failure surface |
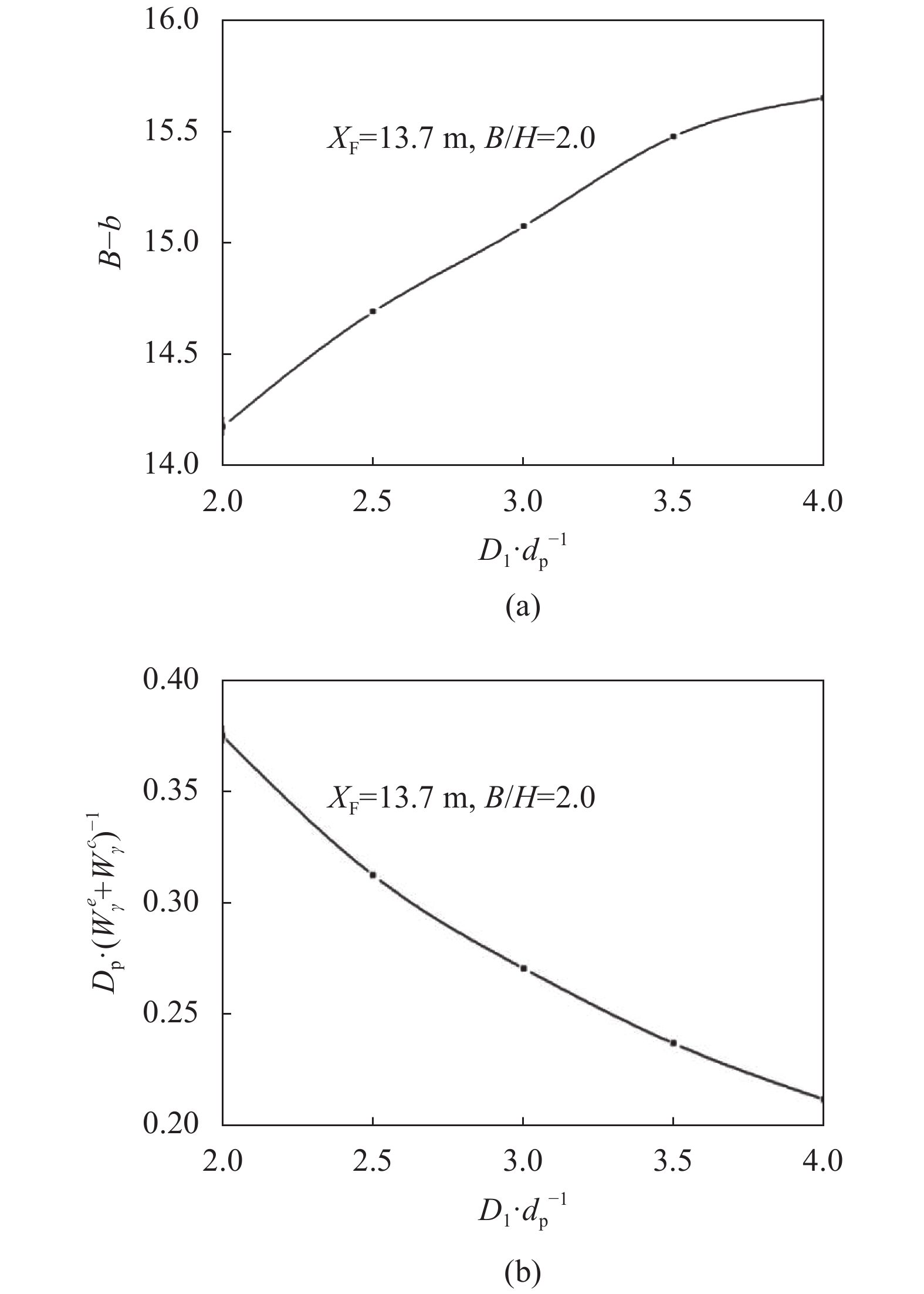 |
| 图9 端部效应和横向抗力影响随桩距的变化 Fig. 9 Variation of end effect and lateral force with pile spacing |
从图8、9可以看出,坡趾破坏的破坏机构受
将图4和7中的曲线进行纵向比较,可以得到
图10反映了
 |
| 图10 机构限宽对破坏面形状的影响 Fig. 10 Effect of slope width on the critical failure surface |
3.4 坡角的影响
对于边坡的稳定性,其坡角是最重要的影响因素之一,因此在沉桩条件一定(
如图11所示,边坡安全系数随坡角
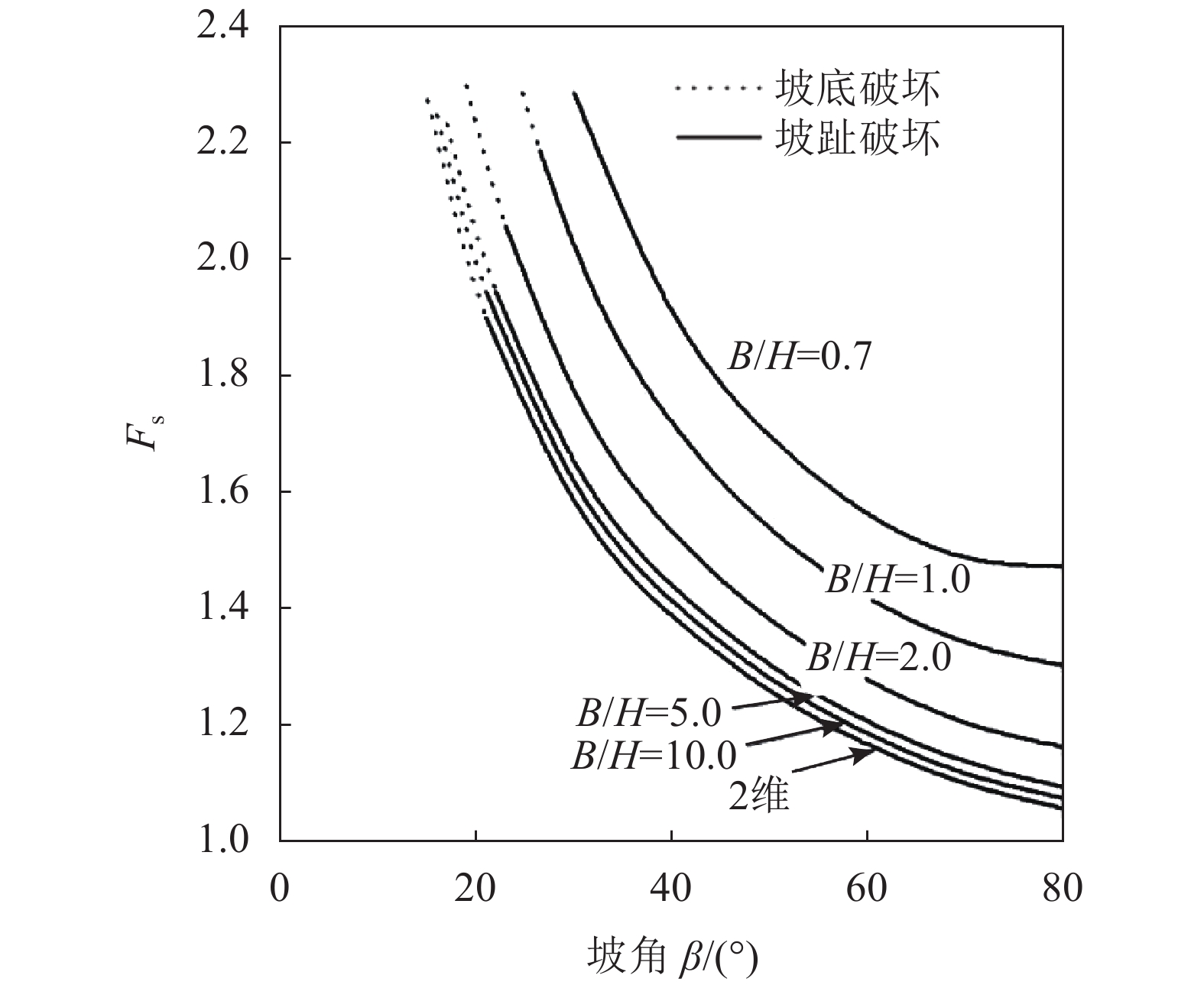 |
| 图11 坡角对边坡抗滑稳定安全系数的影响 Fig. 11 Effect of slope angle on the anti-slide safety factor of slope stability |
4 结 论
通过对不同参数下边坡的3维破坏机构和抗滑稳定安全系数进行拓展研究,得出以下结论:
1)最安全抗滑桩位置不受机构限宽影响,位于坡面中点与坡顶间的某一位置;当机构限宽较小且抗滑桩位置靠近坡趾时,边坡破坏模式为坡面破坏。
2)坡趾破坏模式下,随着抗滑桩位置远离坡趾,破坏面逐渐靠近坡面且曲率增大;当抗滑桩处于横向抗力影响较大的位置时,其是影响边坡稳定性的主因,而非3维破坏机构的端部效应。
3)当抗滑桩桩距较小时,边坡倾向于在抗滑桩位置上方发生次级滑动;边坡整体安全系数随桩距的增大而降低,并逐渐接近未加固边坡的安全系数;坡趾破坏模式下,破坏机构随桩距的增大发生小幅增厚。
4)随着机构限宽的增大,边坡安全系数逐渐降低,破坏机构逐渐增厚,并逐渐接近2维破坏机构的安全系数和破坏面形状。
5)当坡角较小时,抗滑桩加固边坡的破坏模式为坡底破坏。通过对边坡破坏模式类型的拓展,搜寻到了更危险的破坏面和更小的安全系数上限解,实现了计算结果的优化。
| [1] |
孙遇祺,马骥,弗·帕·季托夫,等.铁路公路灾害防治[M].北京:中国铁道出版社,1998:120–121.
|
| [2] |
Gu Hao.Research on slope stability and anti-sliding Piles[D].Nanjing:Hohai University,2006. 古浩.边坡稳定及抗滑桩加固研究[D].南京:河海大学,2006. |
| [3] |
Zheng Yiyi.Stability analysis of slopes with anti-sliding Piles[D].Dalian:Dalian University of Technology,2008. 郑轶轶.抗滑桩加固边坡的稳定性分析[D].大连:大连理工大学,2008. |
| [4] |
Li Rongjian,Yu Yuzhen,Li Guangxin. 3D global stability analysis of unsaturated soil slope reinforced with piles[J]. Rock and Soil Mechanics, 2008, 29(4): 968-972. [李荣建,于玉贞,李广信. 抗滑桩加固非饱和土边坡三维稳定性分析[J]. 岩土力学, 2008, 29(4): 968-972. DOI:10.3969/j.issn.1000-7598.2008.04.021] |
| [5] |
Zhang Xiaoxi.The limit analysis of slope engineering stability[D].Chengdu:Southwest Jiaotong University,2011. 张晓曦.边坡工程稳定性极限分析[D].成都:西南交通大学,2011. |
| [6] |
Wang Congcong,Li Jiangteng,Liao Jun,et al. Stability analysis of slope reinforced with piles and optimization[J]. Journal of Central South University (Science and Technology), 2015, 46(1): 231-237. [王聪聪,李江腾,廖峻,等. 抗滑桩加固边坡稳定性分析及其优化[J]. 中南大学学报(自然科学版), 2015, 46(1): 231-237. DOI:10.11817/j.issn.1672-7207.2015.01.031] |
| [7] |
Chen W F.Limit analysis and soil plasticity[M].Amsterdam: Elsevier,1975.
|
| [8] |
Michalowski R L,Drescher A. Three-dimensional stability of slopes and excavations[J]. Geotechnique, 2009, 59(10): 839-850. DOI:10.1680/geot.8.P.136 |
| [9] |
Sun Zhibin.Upper bound analysis of slope stability and approaches to parameter back analysis[D].Changsha:Central South University,2013. 孙志彬.边坡稳定性上限分析方法及参数反演研究[D].长沙:中南大学,2013. |
| [10] |
Gao Y F,Zhang F,Lei G H,et al. An extended limit analysis of three-dimensional slope stability[J]. Geotechnique, 2013, 63(6): 518-524. DOI:10.1680/geot.12.T.004 |
| [11] |
Rao Pingping,Zhao Linxue,Li Lin,et al. Three-dimensional transient stability of slopes during pile driving using upper-bound limit analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 697-704. [饶平平,赵琳学,李林,等. 坡面沉桩边坡动态稳定性三维极限上限分析[J]. 岩石力学与工程学报, 2017, 36(3): 697-704. DOI:10.13722/j.cnki.jrme.2016.0127] |
| [12] |
Hassiotis S,Chameau J L,Gumnaratne M. Design method for stabilization of slopes with piles[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE, 1997, 123(4): 314-323. DOI:10.1061/(ASCE)1090-0241(1997)123:4(314) |
| [13] |
Li X P,He S M,Wang C H. Stability analysis of slopes reinforced with piles using limit analysis method[J]. Advances in Earth Structures(Research to Practice), 2006, 151: 105-112. DOI:10.1061/40863(195)8 |
| [14] |
Ausilio E,Conte E,Dente G. Stability analysis of slopes reinforced with piles[J]. Computers and Geotechnics,ASCE, 2001, 28(8): 591-611. DOI:10.1016/S0266-352X(01)00013-1 |
| [15] |
Nian Tingkai.Numerical analysis of pile-soil-slope interact system and simplified design method of anti-slide piles[D].Dalian:Dalian University of Technology,2005. 年廷凯.桩–土–边坡相互作用数值分析及阻滑桩简化设计方法研究[D].大连:大连理工大学,2005. |
| [16] |
Wu Yong,He Siming,Li Xinpo. Failure mechanism of anti-slide pile under seismic wave[J]. Journal of Sichuan University (Engineering Science Edition), 2009, 41(3): 284-288. [吴永,何思明,李新坡. 地震波作用下抗滑桩的失效机理[J]. 四川大学学报(工程科学版), 2009, 41(3): 284-288.] |
| [17] |
Zhao Lianheng.Energy analysis study on slope stability and reinforcing design[D].Changsha:Central South University,2009. 赵炼恒.边坡稳定性与加固设计的能量分析方法[D].长沙:中南大学,2009. |
| [18] |
Tan Hanhua,Zhao Lianheng,Li Liang,et al. Energy analysis method for pre-reinforcing slopes with anti-slide piles[J]. Rock and Soil Mechanics, 2011, 32(增刊2): 190-197. [谭捍华,赵炼恒,李亮,等. 抗滑桩预加固边坡的能量分析方法[J]. 岩土力学, 2011, 32(增刊2): 190-197.] |
| [19] |
Gao Y F,Ye M,Zhang F. Three-dimensional analysis of slopes reinforced with piles[J]. Journal of Central South University, 2015, 22(6): 2322-2327. DOI:10.1007/s11771-015-2757-6 |
| [20] |
Ito T,Matsui T. Methods to estimate lateral force acting on stability piles[J]. Soils and Foundations, 1975, 15(4): 43-59. DOI:10.3208/sandf1972.15.4_43 |
 2018, Vol. 50
2018, Vol. 50

