2. 交通运输部公路科学研究院,北京 100088
2. Research Inst. of Highway Ministry of Transport, Beijing 100088, China
受混凝土收缩徐变、预应力损失、施工质量和超载等各种因素的影响,大跨径预应力混凝土(prestressed concrete,PC)连续梁桥普遍出现了不同程度的跨中下挠和梁体开裂问题,严重影响桥梁的正常使用,甚至造成桥梁的坍塌[1–2]。采用斜拉体系加固能够较好地解决此类桥梁的病害问题,逐渐引起了工程界的关注[3]。然而,既有桥梁的变形机理极为复杂,呈现出模糊性和不确定性[4],由此给斜拉体系加固主梁变形的预报带来了极大困难。
目前,预报主梁变形较为实用的方法是根据实测的主梁变形监控数据建立智能预测模型对其进行分析,一方面可以提高计算效率,另一方面可以提高计算精度[5]。斜拉体系加固主梁系统是部分信息已知,部分信息未知的复杂灰色系统。因此,采用灰色系统理论[6]对主梁变形预测是合理可行的,该模型优点在于“少数据建模”。但是,通常的灰色预测模型只适应于严格的等间隔序列[7–8],这给工程的应用带来了诸多不便,如斜拉体系加固张拉阶段的控制索力往往采用非等间隔的索力差对斜拉索进行张拉控制,以达到经济、合理地控制主梁变形量的目的。传统非等间隔灰色模型(traditional unequal interval gray model,TUIGM)对原始数据的一次累加和累减过程中,非等间隔权重直接采用了传统非等间隔序列建立的灰色模型,或者给定某一特定的非等间隔权重分配系数[9]。然而,在累加和累减过程中生成的序列并非最优,使预测模型存在预测精度偏低、误差逐渐偏大等缺点。另外,残差序列往往随机性较强,规律性不明显,单一模型不利于解决多样性问题,因此,还需选择合理的残差修正模型进行组合预测,以便进一步提高预测精度和增强随机灵动性。李欣然等[10]采用傅里叶–马尔科夫组合修正模型,对等间隔年份的售电量进行预测。Ye等[11]通过优化等间隔灰色模型的背景值减小系统误差后,继续利用马尔科夫链法对河南省年粮食产量进行预测,并取得了较高的预测精度。
因此,作者利用斜拉体系加固大跨径PC连续箱梁桥主梁的变形数据,找出变形规律与灰色理论的对应关系,提出了一种马尔科夫链残差修正的改进非等间隔权重灰色(improved unequal interval weight gray model-Markov,IUIWGM-M)主梁变形预测模型。一方面,利用改进非等间隔权重灰色模型解决“不确定性”“贫信息”“成本高”“非等间隔”的问题;另一方面,利用马尔可夫链法反映出状态的随机过程,进一步提高模型的预测精度及随机灵动性。
1 改进非等间隔权重灰色模型在主梁变形预测中的构建与求解将张拉阶段对应的累积索力数据视为非等间隔灰色模型[12]的原始时间序列,主梁桥面测点的竖向累积变形量视为原始非等间隔序列,从而构建斜拉体系加固施工张拉阶段主梁变形预测模型。
1.1 加固主梁变形预测模型的构建设主梁某测点对应的变形量序列为:
| ${X^{(0)}}({F_k}) = ({X^{(0)}}({F_1}),\;{X^{(0)}}({F_{\rm{2}}}), \cdot \cdot \cdot ,{X^{(0)}}({F_n}))$ | (1) |
式中,
设第
| $\Delta {F_k} = {F_k} - {F_{k - 1}} \ne {\rm{const, }}\;k{\rm{ = 2,3,}} \cdot \cdot \cdot {\rm{,}}\;n$ | (2) |
令初始值
对TUIGM的原始序列构造一次累加生成式为:
| ${X^{(1)}}({F_k}) = {X^{(1)}}({F_{k - 1}}) + \Delta {F_k}{X^{(0)}}({F_k})$ | (3) |
然而,将
| $\begin{gathered} {X^{(1)}}({F_k}) = {X^{(1)}}({F_{k - 1}}) + \alpha \Delta {F_k}{X^{(0)}}({F_{k - 1}}) + (1 - \alpha )\Delta {F_k}{X^{(0)}}({F_k}) \\ \end{gathered} $ | (4) |
令
经式(4)进行一次累加后,得到的序列记为:
| ${X^{(1)}}({F_k}) = ({X^{(1)}}({F_1}),\;{X^{(1)}}({F_{\rm{2}}}), \cdot \cdot \cdot ,{X^{(1)}}({F_n}))$ | (5) |
然后,由1阶生成模块
| $\frac{{{\rm d}{X^{(1)}}}}{{{\rm d}F}} + a{X^{(1)}} = u$ | (6) |
式中,
式(6)的解为:
| ${\hat X^{(1)}}({F_k}) = [{X^{(1)}}({F_1}) - \frac{u}{a}]{{\rm{e}}^{ - a({F_k} - {F_1})}} + \frac{u}{a}$ | (7) |
由于
| ${\hat X^{(1)}}({F_k}) = q[{{\rm{e}}^{ - a({F_k} - {F_1})}} - 1] + {X^{(1)}}({F_1})$ | (8) |
按照式(4)进行累减还原,得到的拟合值为:
| $\begin{aligned}[b] {{\hat X}^{(0)}}({F_k}) = & \frac{{{{\hat X}^{(1)}}({F_k}) - {{\hat X}^{(1)}}({F_{k - 1}}) - \alpha \Delta {F_k}{{\hat X}^{(0)}}({F_{k - 1}})}}{{(1 - \alpha )\Delta {F_k}}} \end{aligned}\!\!\!\!\!\!\!$ | (9) |
式中,
由于式(4)和(9)中的权重系数
| ${e_{\min }} = \min \left\{ {{e_1},\;{e_2},\; \cdot \cdot \cdot ,{e_i}, \cdot \cdot \cdot ,{e_n}} \right\}$ | (10) |
式中,
假设期望值
| $\left\{\begin{aligned}& {{X^{(1)}}({F_2}) = {{\hat X}^{(1)}}({F_2}) = q[{{\rm{e}}^{ - a({F_2} - {F_1})}} - 1] + {X^{(1)}}({F_1})},\\& {{X^{(1)}}({F_3}) = {{\hat X}^{(1)}}({F_3}) = q[{{\rm{e}}^{ - a({F_3} - {F_1})}} - 1] + {X^{(1)}}({F_1})},\\ & \quad\quad\quad\quad\quad\quad\quad\quad\vdots \\& {{X^{(1)}}({F_n}) = {{\hat X}^{(1)}}({F_n}) = q[{{\rm{e}}^{ - a({F_n} - {F_1})}} - 1] + {X^{(1)}}({F_1})} \end{aligned}\right.\!\!\!\!\!\!\!\!\!\!$ | (11) |
求解式(11)方程组,共得到
| $\begin{array}{l}\displaystyle\bar a = \frac{2}{{(n - 1)(n - 2)}}\sum\limits_{i = 2}^{n - 1} {\sum\limits_{j = i + 1}^n {{a_{ij}}} } = \\\displaystyle\frac{2}{{(n - 1)(n - 2)}}\sum\limits_{i = 2}^{n - 1} {\sum\limits_{j = i + 1}^n {\left\{ {\frac{{\ln \displaystyle \left[ {\frac{{{F_j} - {F_1}}}{{{F_i} - {F_1}}} \cdot \frac{{{X^{(1)}}({F_i}) - {X^{(1)}}({F_1})}}{{{X^{(1)}}({F_j}) - {X^{(1)}}({F_1})}}} \right]}}{{{F_j} - {F_i}}}} \right\}} } \end{array}$ | (12) |
将平均值
| $\bar q = \frac{1}{{n - 1}}\sum\limits_{i = 2}^n {{q_i}} = \frac{1}{{n - 1}}\sum\limits_{i = 2}^n {\left[ {\frac{{{X^{(1)}}({F_i}) - {X^{(1)}}({F_1})}}{{{{\rm{e}}^{ - \bar a({F_i} - {F_1})}} - 1}}} \right]} $ | (13) |
最后,将平均值
| $\begin{aligned}\!\!\!\!\!\! {{\hat X}^{(0)}}({F_k}) \!\!= \!\!\frac{{\bar q({{\rm{e}}^{ - \bar a{F_k}}} - {{\rm{e}}^{ - \bar a{F_{k - 1}}}}) - \alpha {{\rm{e}}^{ - \bar a{F_1}}}\Delta {F_k}{{\hat X}^{(0)}}({F_{k - 1}})}}{{(1 - \alpha ){{\rm{e}}^{ - \bar a{F_1}}}\Delta {F_k}}}\end{aligned}$ | (14) |
式中,
设残差序列为:
| ${E^{(0)}}({F_k}) = {X^{(0)}}({F_k}) - {\hat X^{(0)}}({F_k})$ | (15) |
那么,将
按照一次累加和累减过程生成序列的不同,采用4种模型对主梁变形量进行预测,不同计算模型如表1所示。
| 表1 不同计算模型 Tab. 1 Different calculation models |
 |
表1中:模型1表示预测模型按照TUIGM进行累加和累减;模型2表示按照TUIGM累加生成数列,累减还原时采用IUIWGM;模型3表示按照IUIWGM对原始序列进行累加,采用TUIGM进行累减还原;模型4表示按照IUIWGM进行累加和累减。
主梁变形残差序列具有很强的随机性,采用Markov 链法对预测模型的残差序列进行预测,以弥补灰色模型预测精度不高的缺陷。
2 马尔科夫链修正模型利用马尔科夫链(Markov chain)[16]进行预测是根据系统变量的现在状态及其变化趋势,预测其在未来某一特定时间可能出现的状态,从而为决策提供依据。主梁变形量受诸多因素的影响,其增长与否是不能完全确定的,表现出马尔科夫残差预测的性质,具有较强的随机特征,采用马尔科夫残差预测可改善序列的随机特征,优化预测结果。
按照自定义的合理标准将残差序列
| $p_{ik}^{(f)} = \frac{{N_{ik}^{(f)}}}{{\displaystyle\sum\limits_{k = 1}^n {N_{ik}^{(f)}} }}$ | (16) |
式中,
设状态转移矩阵为:
| ${{ P}^{(f)}} = \left[ {\begin{array}{*{20}{l}}{p_{11}^{(f)}}&{p_{12}^{(f)}}& \cdots &{p_{1n}^{(f)}}\\{p_{21}^{(f)}}&{p_{22}^{(f)}}& \cdots &{p_{2n}^{(f)}}\\ \;\;\vdots &\;\; \vdots && \;\;\;\vdots \\{p_{n1}^{(f)}}&{p_{n2}^{(f)}}& \cdots &{p_{nn}^{(f)}}\end{array}} \right]$ | (17) |
式中,
一般地,状态区间的划分依据数据序列的平均数和标准差[14],区间两端点值的平均值
| $\hat M({F_{k + 1}}) = \sum\limits_{i = 1}^n {{\omega _i}{\chi _i}} $ | (18) |
式中,
| ${\omega _i} = \frac{{{\eta _i}}}{{\displaystyle\sum\limits_{i = 1}^n {{\eta _i}} }}$ | (19) |
式中,
因此,经过Markov修正后的非等间隔灰色修正模型预测值为:
| $\hat X_1^{(0)}({F_{k + 1}}) = {\hat X^{(0)}}({F_{k + 1}}) + \hat M({F_{k + 1}})$ | (20) |
东明黄河公路大桥主桥采用斜拉体系进行加固,为国内首座采用该加固体系改造的大跨径PC连续箱梁桥。桥塔、主梁与斜拉索的具体连接构造为:桥塔顶部通过安装钢锚箱和滑动索鞍设置斜拉索固定端,在主梁下部横向增设托梁,托梁与主梁之间采用托架在箱梁底面处连接,斜拉索力通过托梁与托架配合传递到主梁上[3]。短、长索设计索力值分别为2 100 kN和2 700 kN。斜拉索张拉采用8台千斤顶由中塔(61#和62#)到边塔(58#和65#),从长索到短索的张拉顺序分级对称张拉。东明黄河公路大桥斜拉体系加固示意图如图1所示。
 |
| 图1 东明黄河公路大桥斜拉体系加固示意图 Fig. 1 Drawing of Dongming Huanghe River Highway Bridge strengthening by the stay cable system |
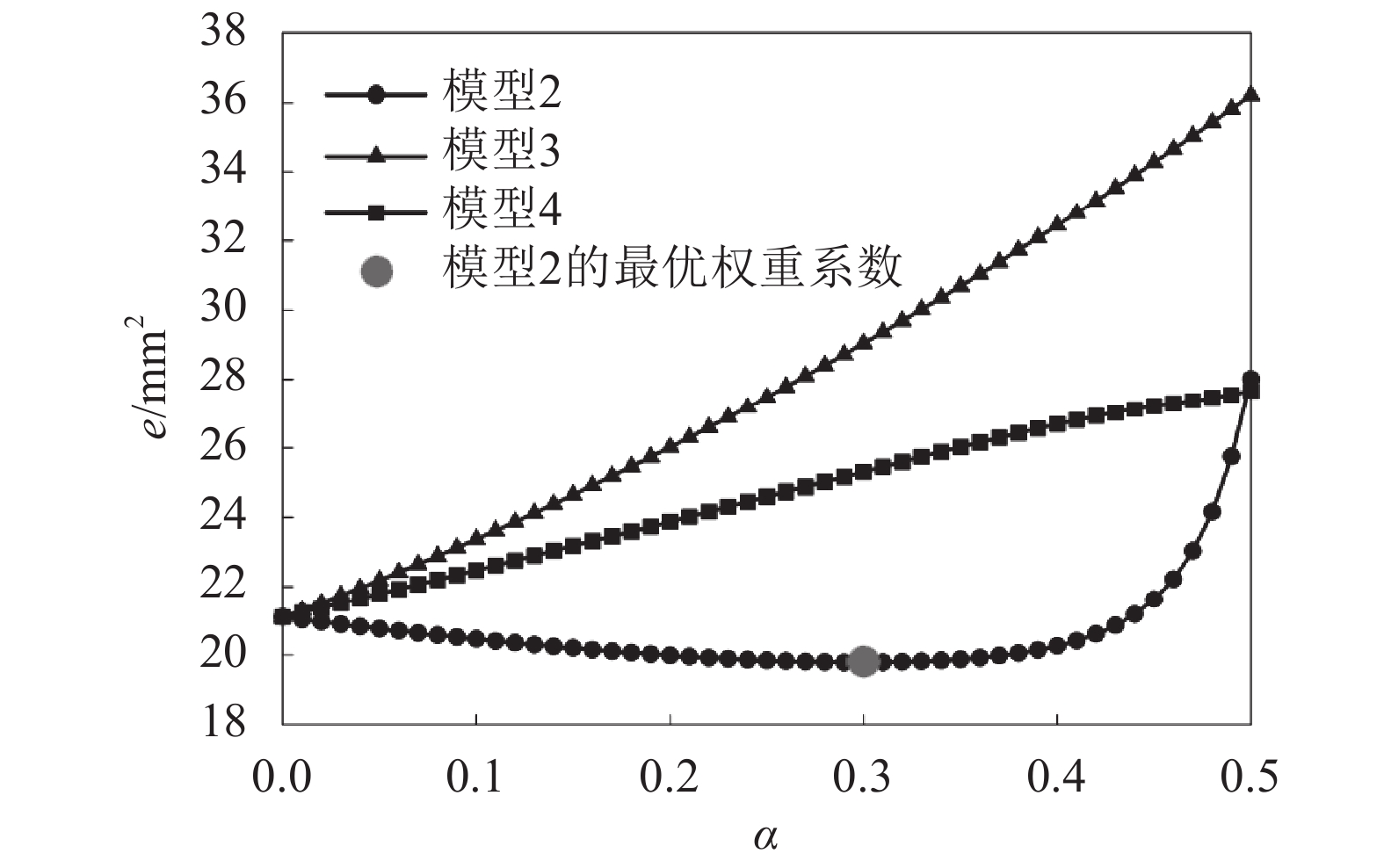
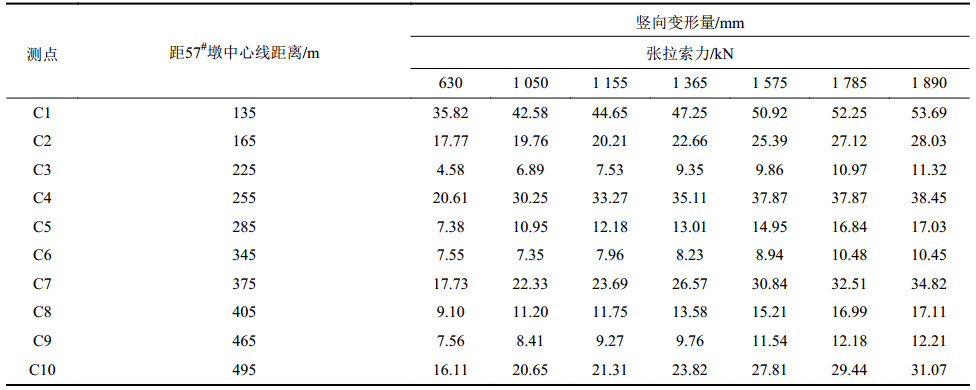
列举了58#跨中到61#跨中桥面测点在不同张拉索力下的竖向变形量(桥面抬升为正),如表2所示。选取C2测点前6个张拉阶段(即对应的张拉索力为630~1 785 kN)的实测变形量组成原始序列,分别建立上述4种模型对第7个张拉阶段(即
 |
|
图2 不同模型下的权重系数
|
| 表3 不同模型下C2测点的变形量计算结果 Tab. 3 Calculation results of deformation for C2 measuring point with the different models |
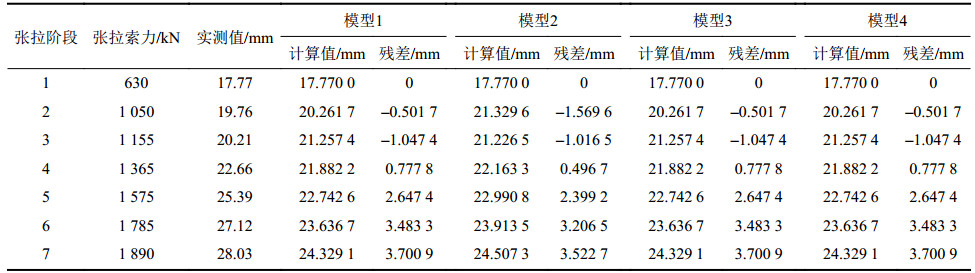 |
由表3可知,实测值>模型 2预测值>模型1预测值
模型2的预测精度虽有提高,但相对误差高达12.57%。另外,从表3可以看出,残差序列随机性较强,且规律性不明显。为了进一步提高该预测模型的预测精度,作者采用Markov链法对其预测值
根据残差的Markov 链进行状态划分,求解残差的状态转移矩阵
根据残差序列的平均值
| 表4 主梁变形量残差序列状态 Tab. 4 State of residual series for main girder deformation |
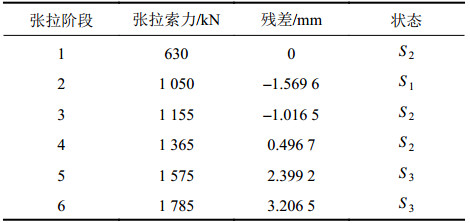 |
状态转移矩阵为:
| ${{ P}^{(1)}} = \left[ \begin{gathered} \;\;0\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;0 \\ \;\;\frac{1}{3}\;\;\;\;\;\;\frac{1}{3}\;\;\;\;\;\;\;\frac{1}{3} \\ \;\;0\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;1 \\ \end{gathered} \right],$ |
| ${{ P}^{(2)}} = \left[ \begin{gathered} 0\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;0 \\ \;0\;\;\;\;\;\;\;\frac{1}{3}\;\;\;\;\;\;\;\frac{2}{3} \\ 0\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;0 \\ \end{gathered} \right],$ |
| ${{ P}^{(3)}} = \left[ \begin{gathered} \;\;0\;\;\;\;\;\;\;0\;\;\;\;\;\;\;1\; \\ \;\;0\;\;\;\;\;\;\frac{1}{2}\;\;\;\;\;\;\frac{1}{2} \\ \;\;0\;\;\;\;\;\;\;0\;\;\;\;\;\;\;0 \\ \end{gathered} \right]{\text{。}}$ |
采用前6个张拉阶段的状态转移预测第7张拉阶段的残差值,共3步转移,转移概率如表5所示。
| 表5 主梁变形量状态转移表 Tab. 5 State transition table for main girder deformation |
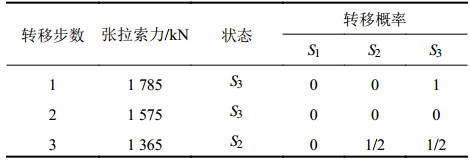 |
计算状态中心
| $\begin{aligned} \hat M(1\;890) = & {\omega _1} \cdot {\chi _1} + {\omega _2} \cdot {\chi _2} + {\omega _3} \cdot {\chi _3} = \\&0 \times ( - 3.087\;4) + \frac{1}{4} \times 0.586\;0 + \frac{3}{4} \times 4.259\;5 = \\ &3.341\;2 {\text{。}}\end{aligned} $ |
那么,由式(20)得到第7个张拉阶段的主梁变形量为:
| $\begin{aligned} \hat X_1^{(0)}(1\;890) = & {{\hat X}^{(0)}}(1\;890) + \hat M(1\;890)= 24.507\;3 + \\& 3.341\;2 = 27.848\;5 {\text{。}}\end{aligned} $ |
同理,对模型1(即TUIGM)的预测值进行Markov残差修正,得到修正后的计算结果为:
| $\begin{aligned} \hat X_1^{(0)}(1\;890) = &{{\hat X}^{(0)}}(1\;890) + M(1\;890)= 24.329\;2 + \\& 1.941\;4 = 26.270\;6{\text{。}}\end{aligned} $ |
从预测结果来看,模型1和模型2经Markov残差修正后预测精度明显提高,前者的相对误差仅为0.65%,预测值更加接近真实值。
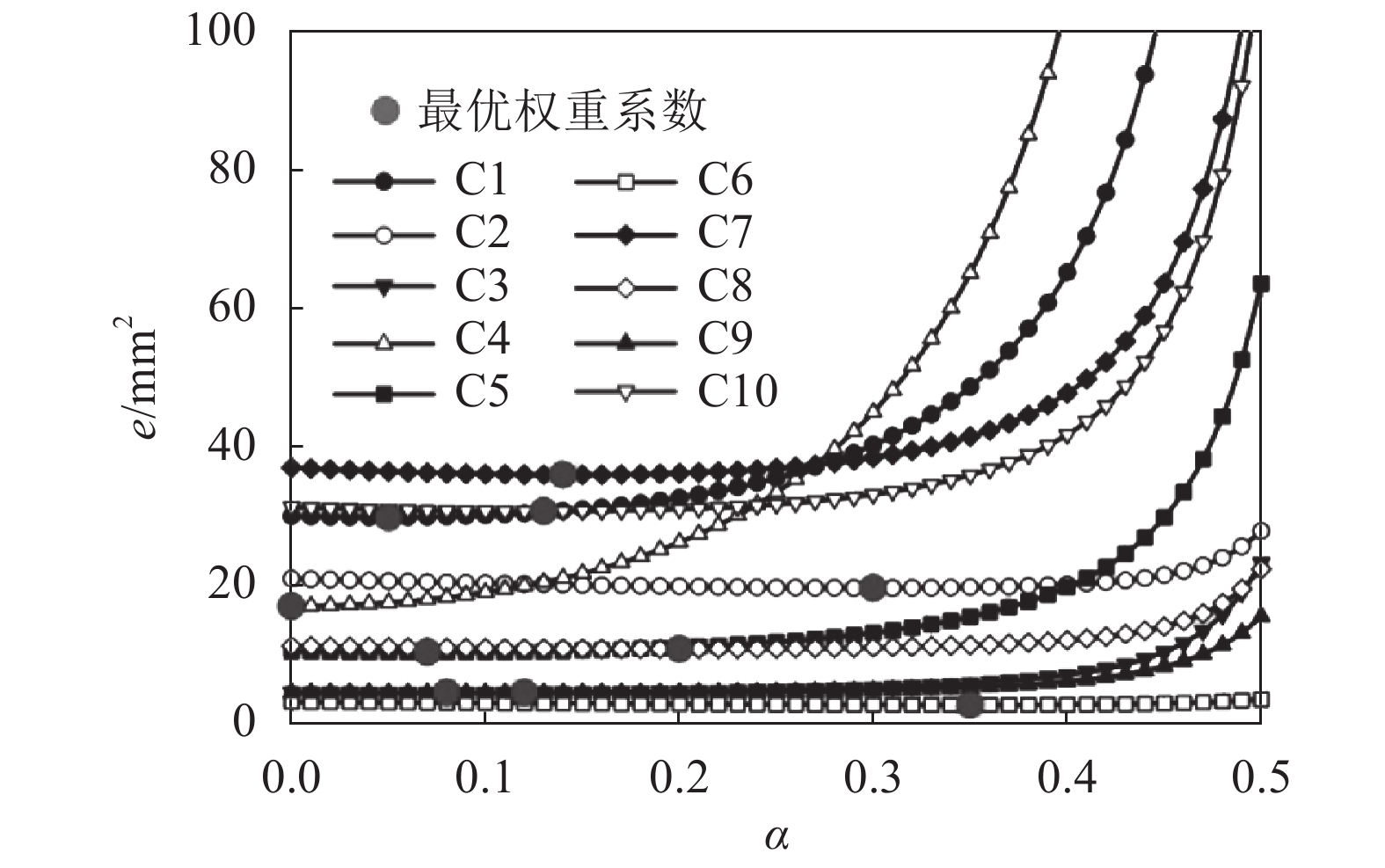
为了进一步验证该模型的预测精准度和可靠性,对表2中其余测点的第7个张拉阶段的变形量进行预测分析。不同权重系数对应的拟合值残差平方和关系曲线如图3所示,拟合值残差平方和最小值与最优权重系数见表6。
 |
|
图3 不同测点的权重系数
|
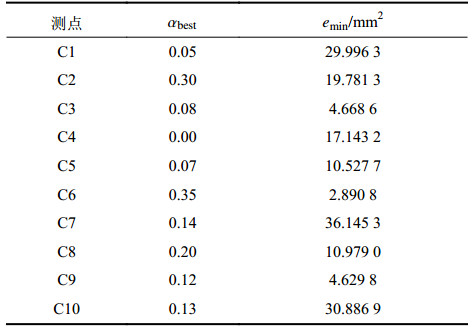
| 表6 不同测点的最优权重系数及拟合值残差平方和最小值 Tab. 6 Optimal weight coefficient and minimum quadratic sum of the fitting values residual with the different measuring points |
 |
| 表2 不同张拉阶段下测点的竖向变形量 Tab. 2 Vertical deformations of measuring points under the different tensioning stages |
 |
从表6中可以看出,原始数据列不同,得到的最优权重系数也不同,并非为给定的某一特定权重系数。
表7为不同预测模型下C1~C10测点的预测结果和相对误差。
| 表7 不同预测模型下C1~C10测点的预测值及相对误差 Tab. 7 Predicted results and relative errors of C1~C10 measuring point based on different prediction models |
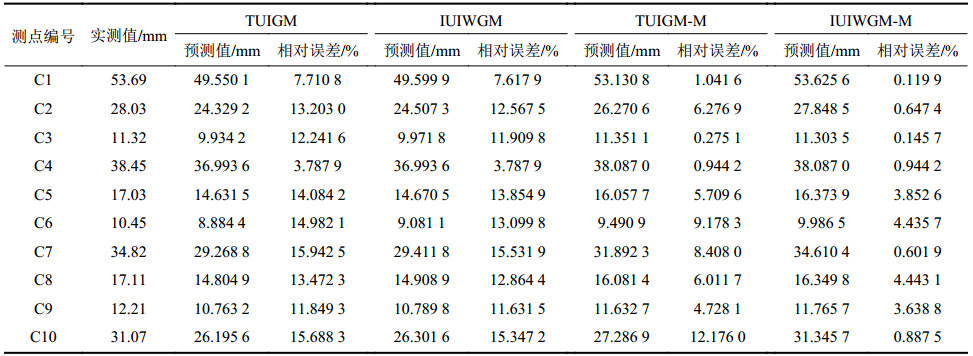 |
由表7可知:IUIWGM预测精度高于TUIGM,经Markov链法对残差进行修正后,2种模型的预测精度均有较大程度提高,TUIGM-M的相对误差平均值为5.47%,IUIWGM-M为1.97%,后者提高幅度更大。
为了更加直观地反映出表7中预测模型的实测值和预测值,将表7中数据表示成图4和5所示的图形,其中图4中的预测值相对于实测值的绝对偏差放大了5倍。
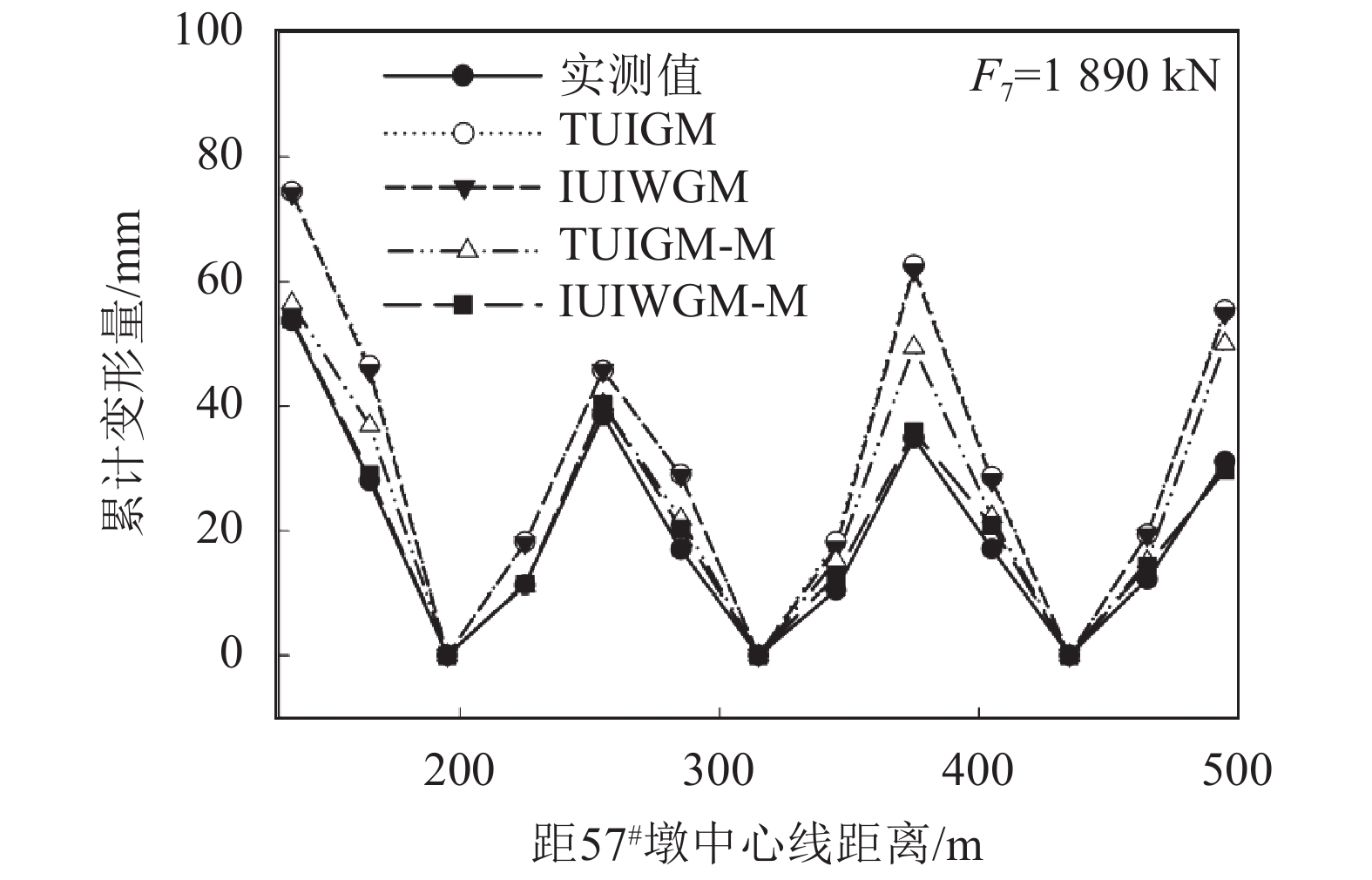 |
| 图4 预测值对比 Fig. 4 Contrast diagram of prediction results |
 |
| 图5 相对误差对比 Fig. 5 Contrast diagram of relative error |
3.2 建筑物沉降量预测
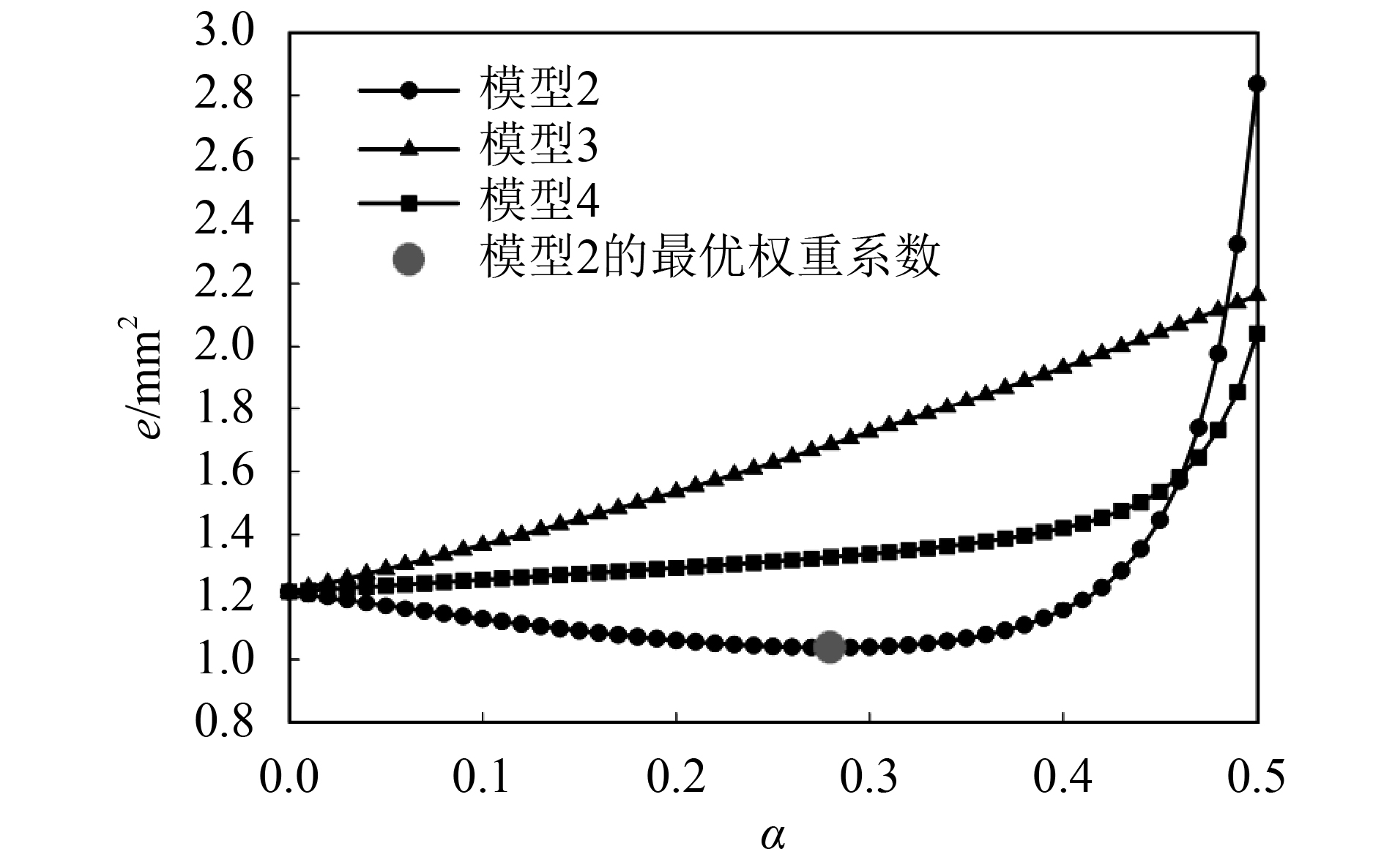
根据文献[17−18]中建筑物某测点前8次沉降量实测数据,采用前述的4种模型对第9和第10次(即第140和154 d)的沉降量进行预测。其中,模型2、模型3和模型4的权重系数
 |
|
图6 不同模型的权重系数
|
由图6可知:模型3和模型4的拟合值残差平方和最小值
| 表8 不同模型下某测点沉降量的计算结果 Tab. 8 Calculation results of settlement of a measuring point with the different models |
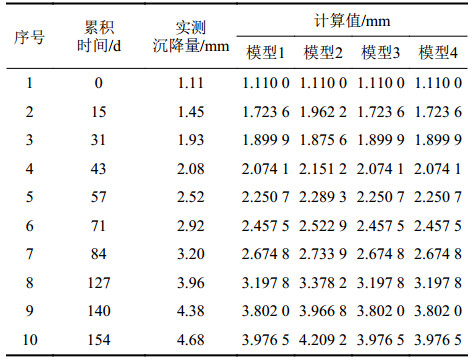 |
由表8可知:实测值>模型 2预测值>模型1预测值=模型3预测值=模型4预测值;模型2的预测值精度最高,相对误差平均值为9.75%,与模型1、模型3及模型4相比,其值下降了4.36%。
然后,采用Markov链法分别对模型2和模型1的预测值
| 表9 建筑物沉降量残差序列状态 Tab. 9 State of residual series for building settlement |
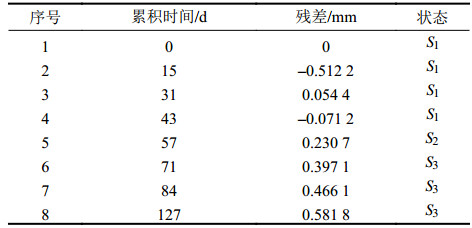 |
状态转移矩阵为:
| ${{ P}^{(1)}} = \left[ \begin{gathered} \frac{3}{4}\;\;\;\;\;\;\frac{1}{4}\;\;\;\;\;\;0 \\ \;\;0\;\;\;\;\;\;\;0\;\;\;\;\;\;\;1 \\ \;\;0\;\;\;\;\;\;\;0\;\;\;\;\;\;\;1 \\ \end{gathered} \right],\;{{ P}^{(2)}} = \left[ \begin{array}{l}\;\displaystyle\frac{1}{2}\;\;\;\;\;\frac{1}{4}\;\;\;\;\;\;\frac{1}{4}\\\;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;1\\\;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;1\end{array} \right],$ |
| ${{ P}^{(3)}} = \left[ \begin{gathered} \; \frac{1}{4}\;\;\;\;\;\frac{1}{4}\;\;\;\;\;\;\frac{1}{2} \\ \;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;1 \\ \;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;0 \\ \end{gathered} \right]{\text{。}}$ |
采用前8次沉降量的状态转移来预测第9和第10次沉降量的残差值,共3步转移,转移概率如表10所示。
| 表10 建筑物沉降量状态转移表 Tab. 10 State transition table for building settlement |
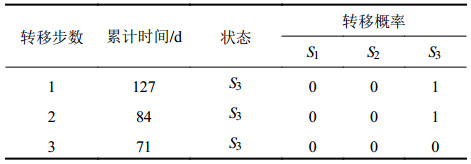 |
那么,第9次建筑物沉降量的Markov链法残差预测值为:
| $\begin{aligned} \hat M(140) = & {\omega _1} \cdot {\chi _1} + {\omega _2} \cdot {\chi _2} + {\omega _3} \cdot {\chi _3}\; = 0 \times ( - 0.204\;6) + \\& 0 \times 0.143\;3 + 1 \times 0.491\;3 = 0.491\;3{\text{。}}\end{aligned} $ |
最终,得到的第9次建筑物沉降量预测值为:
| $\begin{aligned} \hat X_1^{(0)}(140) = & {{\hat X}^{(0)}}(140) + \hat M(140) = \\& 3.966\;8 + 0.491\;3 = 4.458\;1{\text{。}}\end{aligned} $ |
同理,经Markov链法修正后的第10次建筑物沉降量预测值为:
| $\begin{aligned} \hat X_1^{(0)}(154) = & {{\hat X}^{(0)}}(154) + \hat M(154) = \\& 4.209\;2 + 0.491\;3 = 4.700\;5{\text{。}}\end{aligned} $ |
另外,对模型1的预测值也进行Markov链法残差修正。各模型的预测结果如表11所示。
| 表11 预测结果对比 Tab. 11 Comparison of predicted results |
 |
由表11可知,经Markov链法对残差进行修正后,2种模型的预测精度均有较大程度提高,后者提高幅度更大,与文献[17–18]预测模型相比,本文所提模型也具有更高的预测精度。
改进非等间隔权重灰色修正模型的核心理论是灰色系统理论,是一种研究“小样本”“贫信息”及“非等间隔”不确定性问题的新方法,对实测数据并无特殊要求和限制,同样适应于其他工程领域的变形预测。
4 结 论传统非等间隔灰色模型对斜拉体系加固主梁变形进行预测,预测值与实测值偏差较大,预测精度较低。通过引入非等间隔权重系数,优化累减过程的生成序列,可提高模型的预测精度。马尔科夫链法克服了非等间隔灰色模型对采集样本数据随机波动适应能力的不足,经状态转移矩阵对预测结果进行修正,能明显提高了预测模型的精度。与马尔科夫链修正后的传统灰色模型预测结果相比,经累减还原优化后的模型预测精度更高,能够较好地反映斜拉体系加固主梁变形的发展趋势。通过对建筑物沉降量进行预报分析,同样验证了该模型具有较高的预测精度,对各领域的非等间隔序列建模预测问题有一定参考价值。
| [1] |
Sousa H,Bento J,Figueiras J. Construction assessment and long-term prediction of prestressed concrete bridges based on monitoring data[J]. Engineering Structures, 2013, 52(9): 26-37. DOI:10.1016/j.engstruct.2013.02.003 |
| [2] |
Xu Xiangfeng,Zhang Feng,Wei Chenglong. Stiffness damage assement of prestressed concrete box-girder after cracking[J]. Engineering Mechanics, 2015, 32(7): 95-102. [徐向锋,张峰,韦成龙. 预应力混凝土箱梁开裂后的刚度损伤评估[J]. 工程力学, 2015, 32(7): 95-102. DOI:10.6052/j.issn.1000-4750.2013.12.1161] |
| [3] |
Xu Gangnian,Wang Youzhi,Wang Shimin,et al. Key construction techniques for strengthening of main girder of Dongming Huanghe River Highway Bridge[J]. Bridge Construction, 2017, 47(5): 101-106. [徐刚年,王有志,王世民,等. 东明黄河公路大桥主梁加固关键施工技术[J]. 桥梁建设, 2017, 47(5): 101-106. DOI:10.3969/j.issn.1003-4722.2017.05.018] |
| [4] |
Li Yuan,He Shuanhai,Hou Wei,et al. Bridge long-term deformation based on structure degradation[J]. Journal of Chang’an University(Natural Science Edition), 2014, 34(3): 53-59. [李源,贺拴海,侯炜,等. 基于结构退化分析的桥梁长期挠度计算[J]. 长安大学学报(自然科学版), 2014, 34(3): 53-59. DOI:10.3969/j.issn.1671-8879.2014.03.009] |
| [5] |
Huang Teng,Chen Xifeng,Liu Ling. Deflection prediction of long span prestressed concrete beam bridge based on ant colony optimization algorithm[J]. Journal of Southeast University(Natural Science Edition), 2013, 43(增刊2): 235-240. [黄腾,陈喜凤,刘岭. 基于蚁群优化算法的大跨度预应力混凝土桥梁挠度预测[J]. 东南大学学报(自然科学版), 2013, 43(增刊2): 235-240. DOI:10.3969/j.issn.1001-0505.2013.S2.004] |
| [6] |
Wan Shuting,Wan Jie,Zhang Chengjie. Comprehensive evaluation of wind power unit performance evaluation based on grey theory and variable weight fuzzy mathematics[J]. Acta Energiae Solaris Sinica, 2015, 36(9): 2285-2291. [万书亭,万杰,张成杰. 基于灰色理论和变权模糊综合评判的风电机组性能评估[J]. 太阳能学报, 2015, 36(9): 2285-2291. DOI:10.3969/j.issn.0254-0096.2015.09.037] |
| [7] |
Di Yi,Gu Xiaohui,Long Fei. Target track prediction method based on grey residual modification theory[J]. Acta Armamentarii, 2017, 38(3): 454-459. [邸忆,顾晓辉,龙飞. 基于灰色残差修正理论的目标航迹预测方法[J]. 兵工学报, 2017, 38(3): 454-459. DOI:10.3969/j.issn.1000-1093.2017.03.006] |
| [8] |
Yang Qi,Yang Yunfeng,Feng Zhongxiang,et al. Prediction method for passenger volume of city public transit based on grey theory and Markov model[J]. China Journal of Highway and Transport, 2013, 26(6): 169-175. [杨琦,杨云峰,冯忠祥,等. 基于灰色理论和马尔科夫模型的城市公交客运量预测方法[J]. 中国公路学报, 2013, 26(6): 169-175. DOI:10.3969/j.issn.1001-7372.2013.06.023] |
| [9] |
Zhang Dongming,Chen Jiang,He Hongfu,et al. Unequal interval grey model based on dynamic correction of time-distance weight[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1137-1141. [张东明,陈江,何洪甫,等. 动态修正时距权重的不等时距灰色模型及应用[J]. 岩土工程学报, 2012, 34(6): 1137-1141.] |
| [10] |
Li Xinran,Chen Honglin,Leng Hua,et al. Mid-long term load forecasting model with Fourier series and Markov theory residual error correction[J]. Journal of Hunan University(Natural Sciences), 2016, 43(10): 62-69. [李欣然,陈鸿琳,冷华,等. 中长期电量预测的傅里叶-马尔科夫修正模型[J]. 湖南大学学报(自然科学版), 2016, 43(10): 62-69. DOI:10.16339/j.cnki.hdxbzkb.2016.10.008] |
| [11] |
Ye Jing,Dang Yaoguo,Li Bingjun. Grey-Markov prediction model based on background value optimization and central-point triangular whitenization weight function[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 54: 320-330. DOI:10.1016/j.cnsns.2017.06.004 |
| [12] |
Wang Yuhong,Dang Yaoguo,Pu Xujin. Improved unequal interval grey model and its applications[J]. Journal of Systems Engineering and Electronics, 2011, 22(3): 445-451. DOI:10.3969/j.issn.1004-4132.2011.03.012 |
| [13] |
Jiang Zhongxin. An unequal interval gray forecast to the development of debris flow valley[J]. Geographical Research, 1994, 13(3): 53-59. [蒋忠信. 泥石流沟谷演化的不等时距灰色预测[J]. 地理研究, 1994, 13(3): 53-59. DOI:10.3321/j.issn:1000-0585.1994.03.006] |
| [14] |
Guo Yi,Gao Jianmin. Track irregularity evolution prediction for high speed railways in frozen ground region based on GM(1,1) power model[J]. Journal of Railway Science and Engineering, 2016, 13(5): 791-799. [郭毅,高建敏. 基于GM(1,1)幂模型的冻胀区高速铁路轨面不平顺发展预测[J]. 铁道科学与工程学报, 2016, 13(5): 791-799. DOI:10.3969/j.issn.1672-7029.2016.05.001] |
| [15] |
Li Kegang,Xu Jiang,Huang Guoyao. Prediction for slope displacement based on unequal interval GM(1,1) model[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(6): 988-992. [李克钢,许江,黄国耀. 基于不等时距GM(1,1)模型预测边坡失稳变形[J]. 地下空间与工程学报, 2006, 2(6): 988-992. DOI:10.3969/j.issn.1673-0836.2006.06.024] |
| [16] |
Chen Dongming,Wang Yang,Zhang Jiliang,et al. Modeling of wireless link connectivity on high order Markov chain[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 36-41. [陈冬明,汪洋,张继良,等. 高阶马尔科夫链无线链路连通性建模[J]. 哈尔滨工业大学学报, 2015, 47(3): 36-41. DOI:10.11918/j.issn.0367-6234.2015.03.006] |
| [17] |
Li Bin,Zhu Jian. Application of unequal interval grey model in analysis of settlement data[J]. Science of Surveying and Mapping, 2007, 32(4): 52-55. [李斌,朱健. 非等间隔灰色GM(1,1)模型在沉降数据分析中的应用[J]. 测绘科学, 2007, 32(4): 52-55. DOI:10.3771/j.issn.1009-2307.2007.04.019] |
| [18] |
Chi Qicai,Zhou Shijian,Wang Fengwei. Re-optimization of non-equilditant gray model[J]. Journal of Liaoning Technical University(Natural Science), 2017, 36(5): 523-527. [池其才,周世健,王奉伟. 非等间隔灰色预测模型的二次优化[J]. 辽宁工程技术大学学报(自然科学版), 2017, 36(5): 523-527. DOI:10.11956/j.issn.1008-0562.2017.05.014] |
 2018, Vol. 50
2018, Vol. 50


