普通钢板剪力墙结构在侧向荷载作用下容易产生较大的面外屈曲，延性较差，同时，内嵌钢板产生的拉力带会对框架产生附加弯矩，对整体结构的受力状况造成不利影响。Guo等^[1]对钢板剪力墙的加劲肋形式进行了研究，对无加劲肋、对角加劲肋和十字形加劲肋这3类钢板剪力墙滞回性能进行了分析，结果表明带加劲肋试件的极限承载力最高可比无加劲肋试件提高20%。Purba等^[2]对开洞钢板剪力墙进行弹塑性屈曲分析，结果表明开洞钢板剪力墙相较于传统钢板剪力墙削弱了拉力带对框架柱附加弯矩的影响，但抗侧刚度和极限承载力有明显的降低^[3–5]。Hitaka等^[6]提出了开缝钢板剪力墙，并对缩尺比例为1∶3的42个试件进行低周往复试验，结果表明所有墙板均具有较好的延性，滞回曲线饱满，墙肢宽厚比小于20时能基本保证试件在3%侧移角内具有较高的承载力。赵作周等^[7]对带缝钢板剪力墙缩尺试件进行低周往复加载试验，认为墙板刚度和极限承载力随缝间墙肢高度增大而减小。陈勇豪^[8]利用有限元分析指出，增大缝间墙肢高度将减小墙板抗侧刚度和极限承载力。蒋路等^[9]通过试验分析指出，竖缝的开设改变了钢板剪力墙的传力途径，有效地提高了钢板剪力墙的耗能性能和延性，但同时也降低了墙板的抗侧刚度和极限承载力，使得其在低周往复荷载作用下的滞回环面积较小。陆金钰等^[10]对侧边加劲的开缝钢板剪力墙进行了数值模拟并提出了承载力计算公式，增强了其适用性和准确性。针对开设竖缝后大幅削弱钢板剪力墙抗侧刚度和极限承载力的问题，陆金钰等^[11]提出了蝶型和梭型两种不等高开缝形式，并采用数值模拟的方法对其进行了弹塑性屈曲性能及滞回性能研究，结果表明不等高开缝形式显著提高了钢板剪力墙的抗侧刚度和极限承载力，抗侧刚度能力的增幅能达到40%以上，极限承载力的增幅能达到15%以上。Zirakian等^[12]对低屈服点钢板剪力墙进行研究，结果表明低屈服点钢板剪力墙能在地震发生的早期进行耗能，从而保证结构的整体安全性。

目前，折纸艺术已经和工程应用联系得越来越紧密，刘珂^[13]分析了折纸设计的典型案例，认为建立有限元模型可以较为详细地反映出折纸结构的应力分布和变形特点，并指出可以利用带可3维旋转喷头的3D打印机制作此类折纸结构。通过引入折纸原理，Yang等^[14]使用3D打印技术制造了带有折痕图案的黄铜管，研究了折痕对单轴加载下管的能量吸收和变形机理的影响，结果表明，带折痕黄铜管的初始峰值力显著降低，而其能量吸收能力得到了提高。Ma等^[15]基于折纸原理提出了耗能薄壁梁等构件，研究其折纸机构的参数对薄壁梁的耗能性能及破坏模式的影响，认为折痕能够引导塑性铰的开展，使构件表现出优越的抗冲击和耗能性能。李峰等^[16]在竖直折板剪力墙的基础上提出一种将整片折板斜置的钢板剪力墙，进一步分析表明随着折板平段宽度、斜段宽度的增加使结构的承载力反而减小，而折板高度的增加会导致承载力先增大然后小幅度减小。陆金钰等^[17]借鉴折纸原理，提出了一种新型带预折痕钢板剪力墙，钢板由若干折痕单元构成，详细分析了折痕单元几何尺寸及放置角度对钢板剪力墙延性及滞回性能的影响，结果表明带预折痕钢板剪力墙比平板式钢板剪力墙具有更好的延性，且钢板剪力墙的塑性带均沿折痕处开展，可吸收大量能量。

作者在文献[17]的基础上进一步提出了3种具有塑性铰引导机制的新型钢板剪力墙，分析剪力墙上折痕单元的受力机理和变形趋势。剪力墙的折痕单元可通过冲压的方式实现，并在制作过程中采取退火工序以消除或降低折痕处冷作硬化带来的不利影响。另基于ABAQUS有限元软件对这3种类型的折痕钢板剪力墙进行弹塑性屈曲分析，给出了不同种类折痕单元对钢板剪力墙屈曲性能的影响，系统分析了极限承载力、初始刚度、延性等指标，且与平钢板剪力墙以及压型钢板剪力墙进行对比，提出合理的建议。

图1所示的折痕钢板剪力墙由若干凹凸折痕单元根据一定规律排列组成。模型几何参数包括：折痕钢板高度 $ H$ 、跨度 $ B$ 以及厚度 $ t$ 。为防止侧边在加载中过早出现较大的面外变形，提高其极限承载力，在墙板两侧分别设置尺寸为 $ {H_{\rm s}} \times {B_{\rm s}} \times {t_{\rm s}} $ 的加劲肋。作者提出3种不同类型折痕单元的几何构型（图2～4），折痕单元在钢板剪力墙中均以 $\theta$ =45°排列布置（角度 $\theta$ 为折痕单元局部坐标系与整体坐标系夹角），折痕单元2个方向尺寸分别为 $ a$ 和 $ b$ ，矢高为 $ h$ 。

图1(Fig. 1)

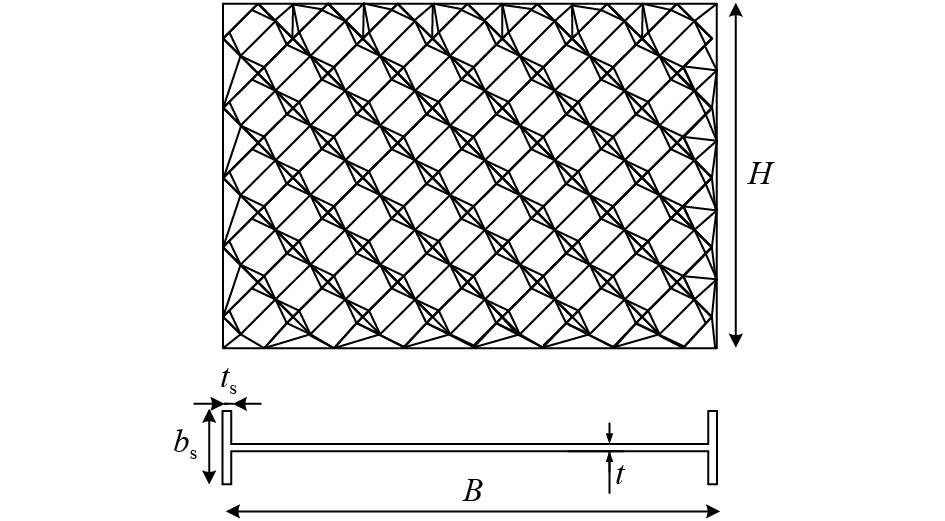图1 折痕钢板剪力墙几何模型 Fig. 1 Geometrical model of pre-folded steel plate shear wall

图2所示的A型折痕单元主要由对称的2个梯形面和2个三角形面构成，其立面如图2（c）所示，梯形面的上底为 $d=a-2h/\!\tan \,\beta$ （ $\beta$ 为三角形面和水平面之间的夹角），梯形面和水平面之间夹角为 $\alpha$ ，调整 $ d$ 的大小可控制构成子单元各个面的大小。

图2(Fig. 2)

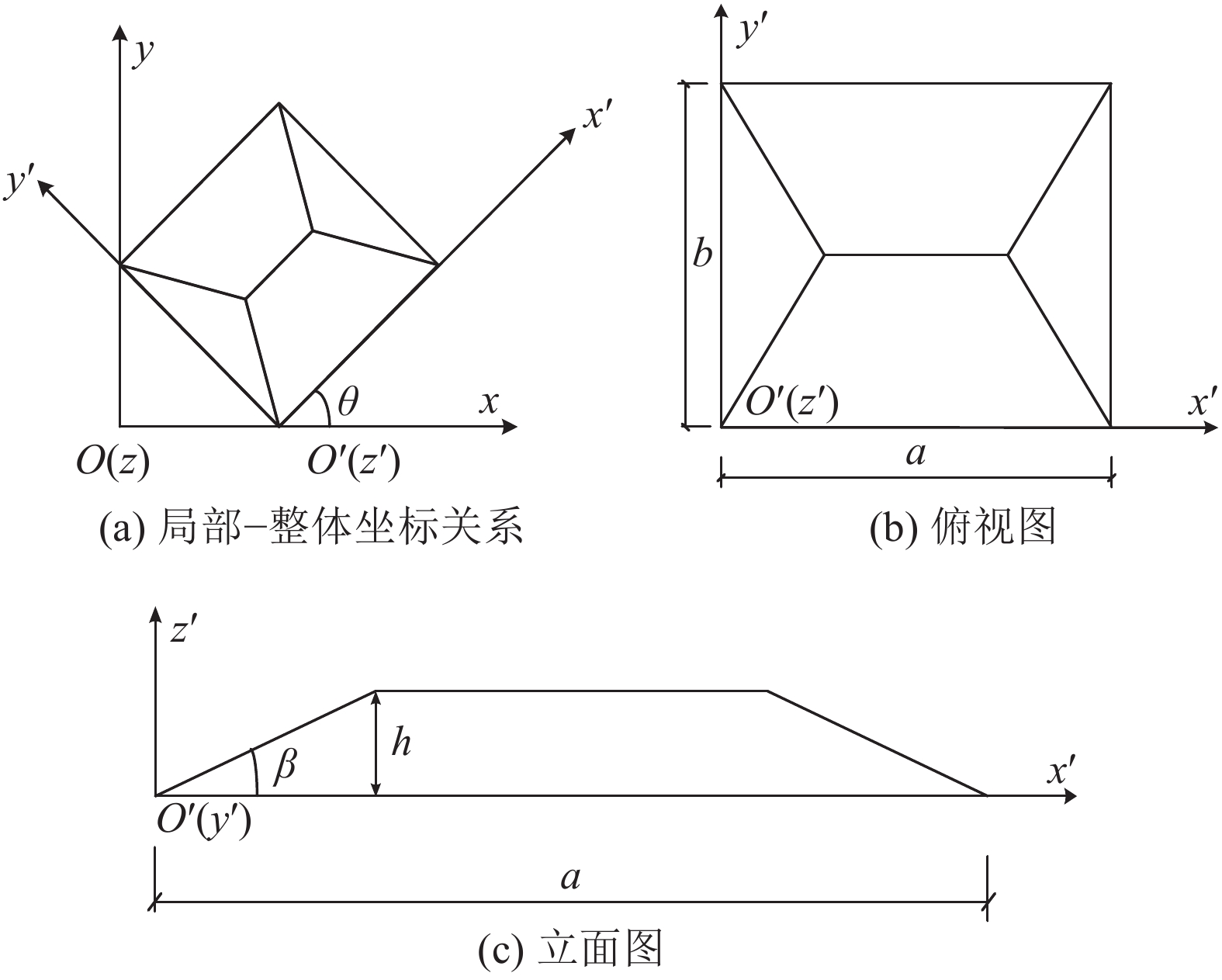图2 A型折痕单元构型 Fig. 2 Configuration of origami pattern A

图3为B型折痕单元的几何构型，该折痕单元由2个长边相连的梯形面和4个三角形面组成，梯形面中多余2个长边与水平面之间的距离为 $ h$ 。图3（a）中，与x′轴重合的三角形面的边和水平面之间的夹角为 $\alpha$ ，该边长度为 $h/\!\!\tan\,\alpha$ ，与其相邻的梯形上底（短边）为 $a-2h/\!\!\tan\,\alpha$ 。图3（b）、（c）分别为B型折痕单元的轴测图和立面图。

图3(Fig. 3)

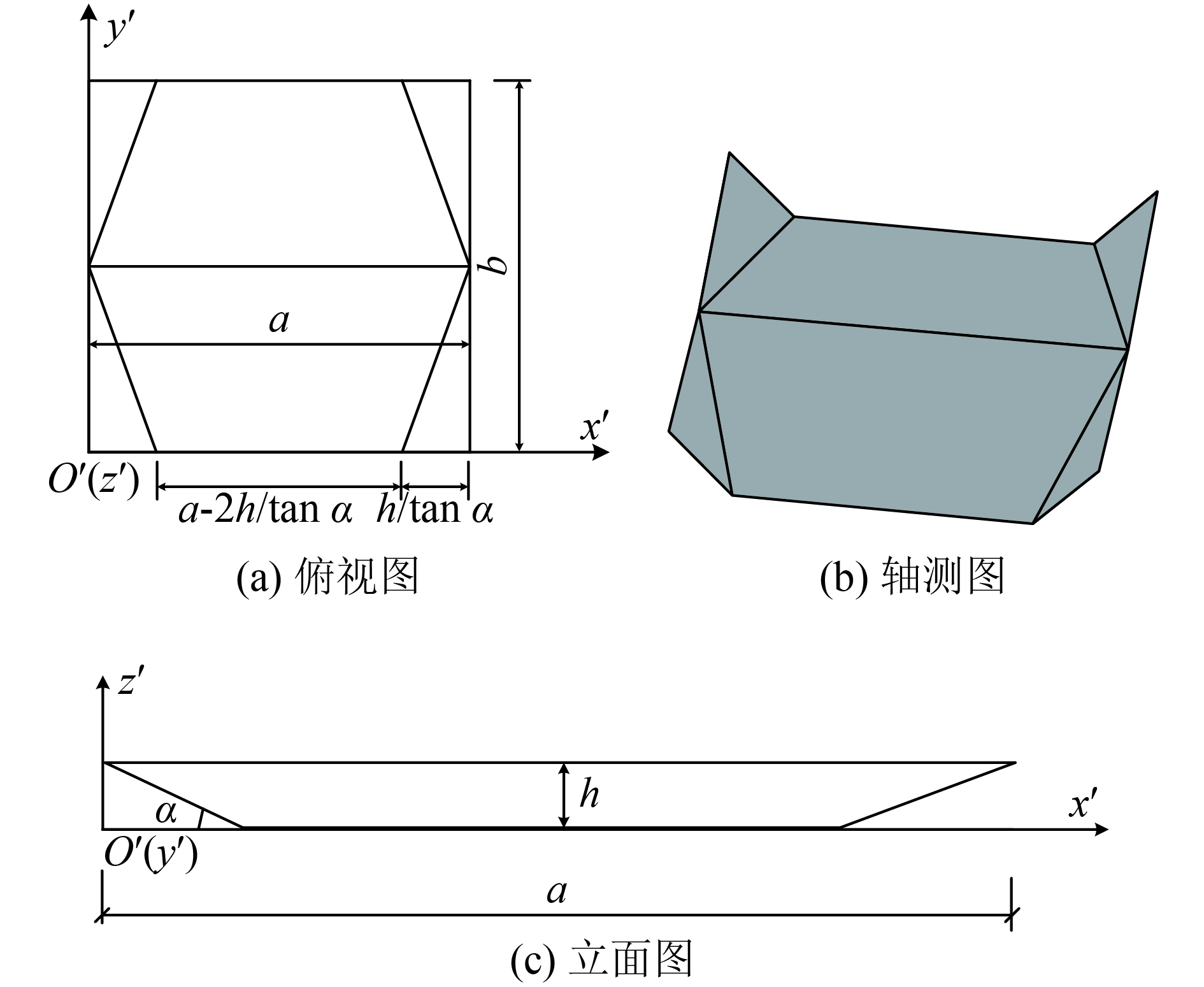图3 B型折痕单元构型 Fig. 3 Configuration of origami pattern B

图4为C型折痕单元的构型，由A型折痕单元与B型折痕单元组合形成。图4（b）、（c）为C型折痕单元受力变形示意图，对其进行形态分析可以看出，在主应力方向上，钢材会率先在预先经过冲压形成凹凸折痕处进入塑性并形成塑性铰线，使折痕单元的梯形和三角形面绕着塑性铰线转动，且由于凹凸折痕的交错布置，相邻的折痕单元变形趋势一致，能够形成较为理想的折叠式变形，钢板不易发生单向的面外屈曲，可见折痕的引入能够有效引导钢板剪力墙的塑性开展，使结构能够较早进入耗能阶段。

图4(Fig. 4)

图4 C型折痕单元构型 Fig. 4 Configuration of origami pattern C

各有限元模型详细尺寸如表1所示，其中，W0为平钢板剪力墙，W1～W3分别为A、B、C型折痕单元构成的钢板剪力墙，W4为压型钢板剪力墙。钢板尺寸H $\times $ B $\times $ t为2 500 mm $\times $ 3 000 mm $\times $ 12 mm。墙板两侧设置尺寸H_s $\times $ B_s $\times $ t_s为2 500 mm $\times $ 100 mm $\times $ 12 mm的加劲肋。加劲肋与墙板的面外刚度比满足文献[18]对加劲肋设置的要求，且符合《钢结构设计规范》中对板件宽厚比的要求。为使计算结果具有可比性，以上3种折痕钢板剪力墙的折痕单元参数（边长、矢高）均保持一致，边长a=b=250 mm，矢高h=25 mm，压型钢板波长取250 mm，矢高与折痕钢板剪力墙相同，并也按45°布置（图5）。

图5(Fig. 5)

图5 压型钢板尺寸 Fig. 5 Detailed sizes of profiled steel sheet

表1(Tab. 1)

表1 试件详细尺寸 Tab. 1 Detailed sizes of specimens

表1 试件详细尺寸 Tab. 1 Detailed sizes of specimens 编号 内嵌钢板 $ H\times B\times t$ / （mm $\times$ mm $\times$ mm） 加劲肋 $ {H_{\rm s}} \times {B_{\rm s}} \times {t_{\rm s}} $ / （mm $\times$ mm $\times$ mm） 折痕单元 子单元尺寸 $ a\times b$ / （mm $\times$ mm） $ h$ /mm W0 平板 — — W1 A型 W2 2 500 $\times $ 3 000 $\times $ 12 2 500 $\times $ 100 $\times $ 12 B型 250 $\times $ 250 25 W3 C型 W4 波形 — —

利用ABAQUS对两边连接的各试件进行了分析，试件的内嵌钢板和加劲肋均采用四节点通用壳单元（S4R）模拟^[19]，采用双线性模型本构关系，材料定义为各向同性，屈服强度为σ_y=235 N/mm ²，弹性模量E=2.06 $\times $ 10⁵ N/mm²。钢板剪力墙下端固定约束，上端约束转动自由度及平面外的平动自由度。各试件缺陷的幅值均参考文献[20]对钢板剪力墙的缺陷幅值建议，取为试件长边尺寸的1/1 000。

为验证有限元模型的正确性和边界条件的适用性，对文献[21]中的W试件进行模拟对比（图6）^[21]。剪力墙试件边界条件为两边连接，采用摩擦型高强螺栓通过角钢和铰接框架进行连接。试件尺寸H $\times $ B $\times $ t=1 100 mm $\times $ 1 100 mm $\times $ 2.75 mm，材性试验的数据表明，钢材具有明显的屈服平台，其屈服强度为σ_y=294.64 N/mm²，弹性模量E=2.15 $\times $ 10⁵ N/mm²。

图6(Fig. 6)

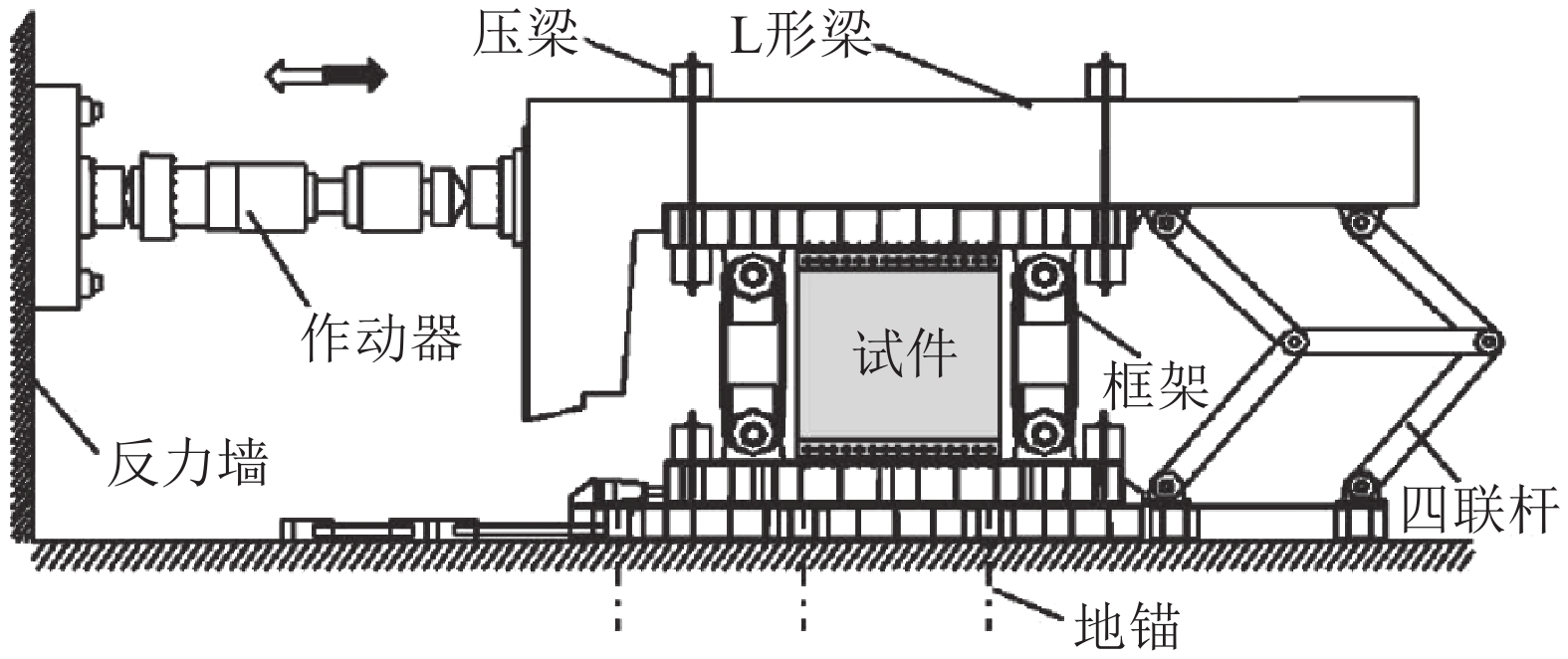图6 试验装置示意图 Fig. 6 Testing setup

基于ABAQUS对试件进行数值模拟，分析其在侧向荷载作用下的荷载–位移曲线并与试验结果曲线对比（图7），可以看出数值模拟得到的初始刚度、极限承载力以及延性这3种主要的力学特征参数的取值均比试验值略高，主要因为试验装置存在偏差，试件存在初始缺陷以及试验测量误差等。误差较大的是延性系数，因为延性系数的计算不仅涉及到试验误差，且与引材性试验数据的引入有着较大的关系。总体上两曲线的变化趋势基本吻合，验证了有限元模型的适用性。

图7(Fig. 7)

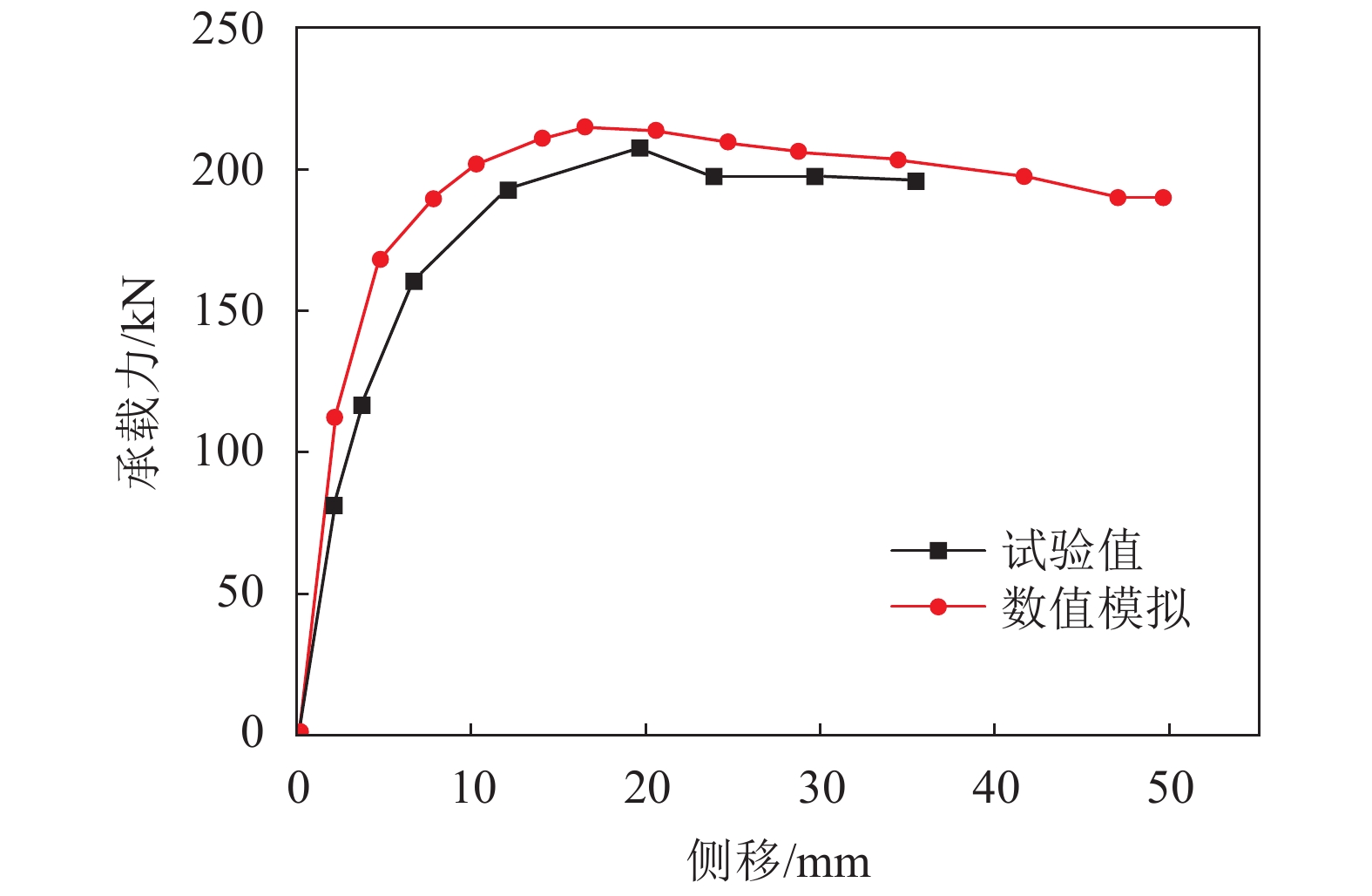图7 试件W荷载–位移曲线 Fig. 7 Load–deflection curves of specimen W

对某波形钢板试件（SPSW–3）^[22]进行数值模拟对比，试验模型采用四边连接方式，钢板总尺寸H $\times $ B $\times $ t=1 500 mm $\times $ 2 000 mm $\times $ 1.25 mm，钢材屈服强度为σ_y=207 N/mm²，弹性模量E=2.10 $\times $ 105 N/mm²。详细几何尺寸见文献[22]。

通过建立有限元模型将侧向位移缓慢加载至80 mm并进行荷载–位移曲线的对比。如图8所示，ABAQUS数值模拟结果与试验结果曲线以及文献[22]中的数值模拟曲线基本吻合，说明采用壳单元及双线性本构模型模拟钢板剪力墙较为准确，这种建模计算方法可用于新型钢板剪力墙弹塑性屈曲分析。

图8(Fig. 8)

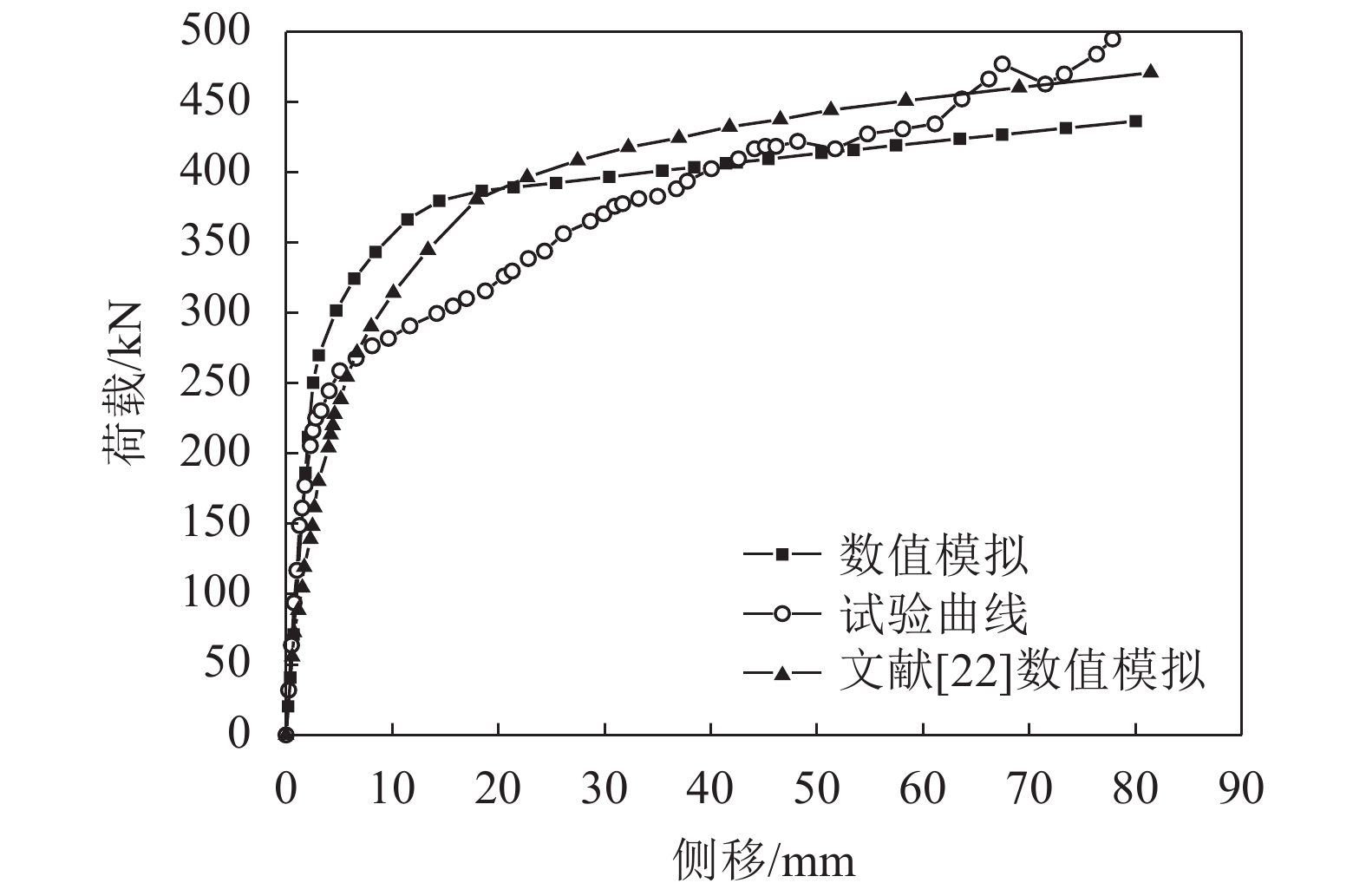图8 试件SPSW–3荷载–位移曲线 Fig. 8 Load–deflection curves of specimen SPSW–3

图9（a）、（b）、（c）分别为试件W1、W2、W3在侧移角为2.0%时的等效塑性应变分布。从图9（a）中可以看出，由A型折痕单元构成的试件W1的塑性主要沿着拉力带区域的折痕单元连接处开展，并没有改变钢板剪力墙的传力机制，与对角线平行的折痕出现了少许的塑性开展区，不能大幅提升折痕钢板剪力墙的耗能性能。主要原因是在侧向荷载的作用下在对角线上出现了类似于拉压杆的连接带。荷载传递路径具有简捷性，故塑性开展也是主要沿对角线附近区域开展，而其余部分折痕单元由于折痕的存在阻碍了拉力带的发展，不能形成完整的折叠变形趋势，故塑性开展部位没有增加太多也不可预测，因此不能构成力学性能相对较好的折痕钢板剪力墙。

如图9（b）所示，对于试件W2，除了对角线区域的塑性开展比较充分外，在内嵌钢板的两侧与拉力带垂直的方向上出现了较为均匀的零星塑性开展处，一定程度上符合折纸原理在钢板剪力墙上提升耗能性能的理念。此外，拉力带的两端应力集中现象较为严重，与其不能形成完整的折叠变形趋势以及边界空缺时填充的三角形面有一定关系，剪力墙在最后发生类似于普通钢板剪力墙的整体面外屈曲破坏模式。

从图9（c）中发现，试件W3塑性主要沿着各折痕单元的折痕处以及折痕单元之间的连接处开展，塑性开展较为均匀，折痕钢板的大部分折痕均进入了塑性。该折痕钢板剪力墙能产生较多的塑性开展区，主要的原因是C型折痕单元的折痕布局较为合理，能够形成完整的折叠式变形，在钢板剪力墙的对角线上阻碍了拉力带的传递。同时由于A型和B型折痕单元的变形互为反对称，其受到荷载时边界上的位移不发生冲突，因此，由C型折痕单元所组成的折痕钢板剪力墙在侧向荷载的作用下主要发生折叠式的变形趋势，而非普通钢板剪力墙的面外屈曲模式，其耗能性能和延性可得到显著提高。

图9(Fig. 9)

图9 各试件等效塑性应变分布 Fig. 9 Equivalent plastic strain distribution of specimens

屈曲分析能反映结构或构件的临界载荷、初始刚度及延性等特征。图10为各试件荷载–侧移变化曲线。由图10可以看出，当侧移角较小时这4个试件的承载力都随侧移角线性增加，而当试件进入塑性时承载力增加较为缓慢，直到其达到试件的极限承载力时，曲线迅速下降。从图10中明显可以看出，试件W1～W3与W0和W4相比初始刚度较小，说明折纸原理的引入一定程度上削弱了钢板剪力墙的初始刚度，且折痕数越多的剪力墙初始刚度越小。试件W1和W2的子单元能够形成折叠变形的趋势，只是在形成折痕钢板剪力墙后相邻子单元的变形与其变形发生冲突，同时W1、W2折痕相对较多，故两者的承载力比试件W0略低，但试件W2由于折痕数较多，对其承载力削弱程度较大，承载力与压型钢板剪力墙相差14.20%。

图10(Fig. 10)

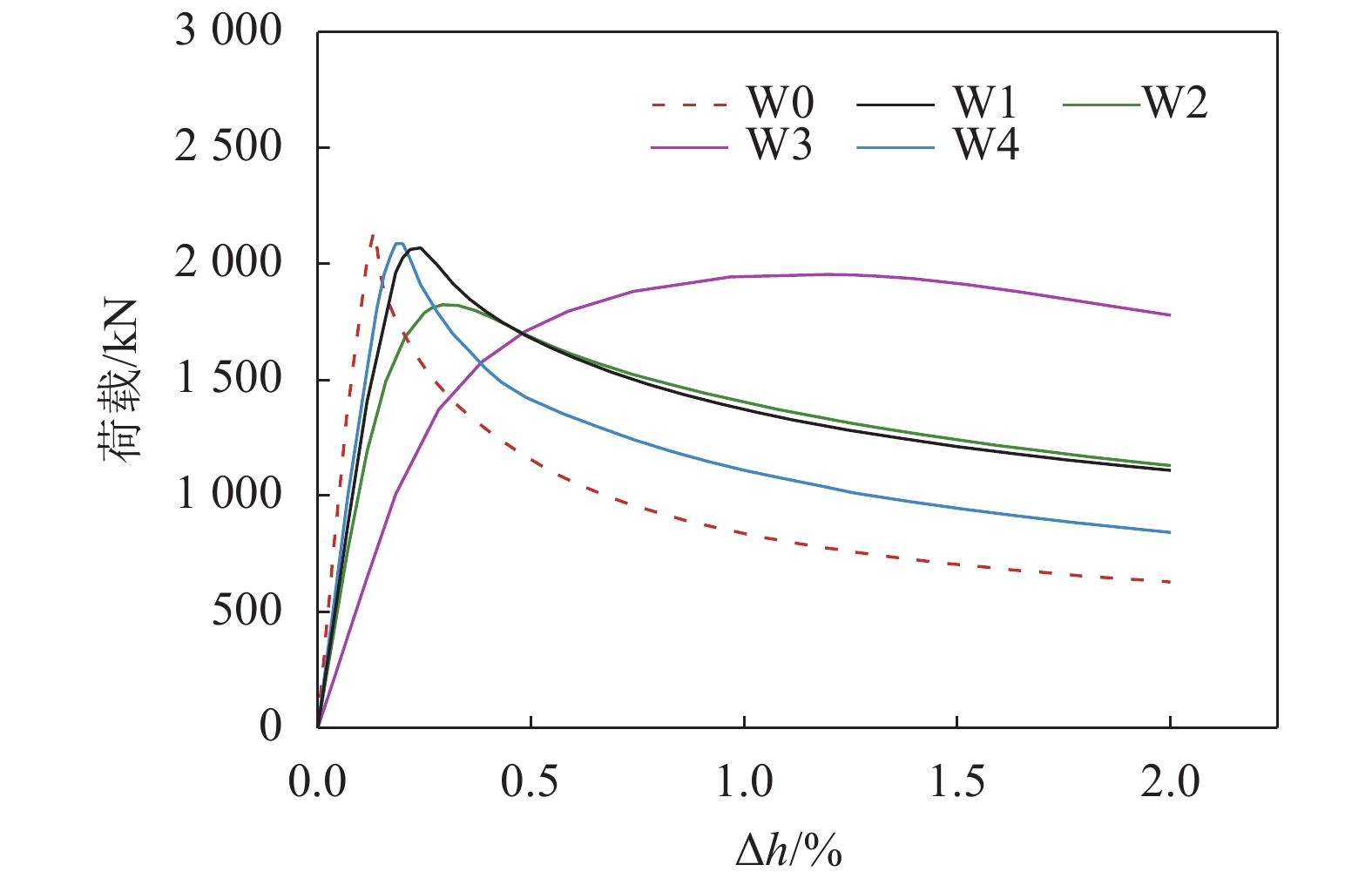图10 各试件荷载–侧移曲线 Fig. 10 Load–deflection curves of specimens

试件W3的初始刚度比其他两个折痕钢板剪力墙试件都低，主要的原因是C型折痕单元的折痕比A型和B型都要多，对刚度的削弱作用更加明显，但可以通过增加板厚或加劲肋等方式改善。W3的极限承载能力和其他试件相差不大，介于W1和W2之间，但荷载–侧移曲线在达到极限承载力后下降得较为缓慢，且下降段更为平滑，相较于其他3个试件拥有更良好的延性，这是因为C型折痕单元的折痕布局比A型和B型更加合理，结合等效塑性应变云图可知，在侧向荷载下钢板的塑性开展更加均匀和充分。

表2为根据图10中曲线所计算出的各试件力学特征参数。由表2可以看出，压型钢板剪力墙和平钢板剪力墙的抗侧刚度和极限承载力较大，但延性相对较差，引入折纸原理后，折痕钢板剪力墙的抗侧刚度有了一定的削弱，但延性有了较明显的提升，是压型钢板剪力墙的2～3倍；而引入可以发生完整折叠式变形的折纸机构（W3）后，折痕钢板剪力墙的延性比压型钢板剪力墙有大幅提升，是压型钢板剪力墙的5.2倍、平钢板剪力墙的8.2倍。因此，将折纸概念应用于钢板剪力墙，能有效地提升其延性，并且C型折痕单元相对于其他两种折痕单元，对钢板剪力墙延性的提升更显著。

表2(Tab. 2)

表2 各试件特征参数 Tab. 2 Characteristic parameters of specimens

表2 各试件特征参数 Tab. 2 Characteristic parameters of specimens 试件编号 抗侧刚度/(kN·mm–1) 极限承载力/kN 延性 μ W0 843.26 2 138.27 1.5 W1 499.52 2 068.63 3.58 W2 443.42 1 824.49 4.31 W3 224.79 1 954.30 12.34 W4 552.92 2 088.75 2.39

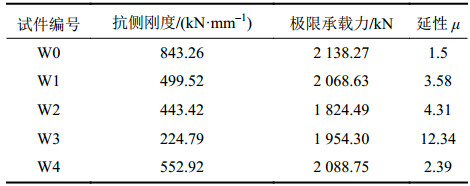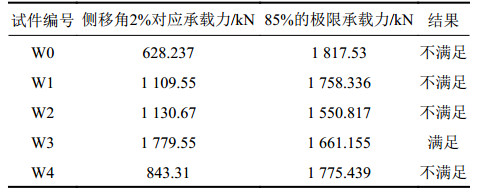
表3列出了各试件的侧移角为2.0%时的承载力及85%的极限承载力。为了保证墙板具有良好的延性，使结构具备优越的抗震性能，试件在侧移角为2.0%时的承载力不应低于极限承载力的85%。从表3中还可以看出，平钢板剪力墙和压型钢板剪力墙的承载力远达不到此项要求，引入不完整折叠式变形的折纸机构（W1、W2）后，有了一定程度的改善。在同等情况下（钢板厚度及加劲肋的尺寸相等），当引入可完整折叠的折痕形式（W3）后，折痕钢板剪力墙在侧移角为2.0%时的承载力要大于85%的极限承载力，这就说明由C型折痕单元组成的剪力墙在相同条件下更易满足结构抗震要求，即保证了此类型钢板剪力墙具有较好的延性，在地震后期仍具有较高的承载力，为结构提供耗能性能的同时持续为结构提供抗侧力。

表3(Tab. 3)

表3 各试件承载力对比 Tab. 3 Comparison of bearing capacity of each specimen

表3 各试件承载力对比 Tab. 3 Comparison of bearing capacity of each specimen 试件编号 侧移角2%对应承载力/kN 85%的极限承载力/kN 结果 W0 628.237 1 817.53 不满足 W1 1 109.55 1 758.336 不满足 W2 1 130.67 1 550.817 不满足 W3 1 779.55 1 661.155 满足 W4 843.31 1 775.439 不满足

目前，新型钢板剪力墙形式已不断被应用到实际的工程结构中，不同形式的钢板剪力墙各有优势，但是，均难同时满足力学性能和耗能性能均较高的要求。作者提出的基于折纸理念的折痕钢板剪力墙可在一定程度上解决这个问题。作者基于折纸理念，提出了3种具有塑性铰引导机制的新型钢板剪力墙，分析了折痕单元的受力机理和变形趋势，并利用ABAQUS有限元分析软件分别对折痕钢板剪力墙进行了弹塑性屈曲性能研究，给出了塑性铰开展机制，分析了初始刚度、极限承载力、延性系数等各项指标，并与平钢板剪力墙和压型钢板剪力墙进行了对比，得出以下结论：

1）折痕钢板剪力墙在侧向荷载作用下能够形成折叠式变形，由于折痕的存在，其抗侧刚度相较于平钢板剪力墙和压型钢板剪力墙有较为明显的削弱，但极限承载力削弱程度较小，其中，B型折痕单元对钢板剪力墙极限承载力的削弱影响最大，与压型钢板剪力墙相差12.65%。

2）引入折纸原理后，有效避免了钢板剪力墙的整体面外失稳。塑性铰率先出现在钢板剪力墙折痕处，且折痕引导了塑性开展过程。3种折痕钢板剪力墙的延性比压型钢板剪力墙均有不同程度的提高，最高可达到压型钢板剪力墙的5.2倍，平钢板剪力墙的8.2倍。

3）不同类型的折痕单元对所构成的折痕钢板剪力墙的各项性能会产生不同的影响，C型折痕单元所组成的折痕钢板剪力墙在侧向荷载作用下能够形成完整的折叠变形模式，塑性开展得更为均匀和充分，其对试件延性的提升相较于其他两种折痕钢板剪力墙更大，是其他两种折痕钢板剪力墙的2倍左右，且在地震后期仍具有较高的承载力，为结构提供耗能性能的同时持续为结构提供抗侧力，也说明了所提出的折痕钢板剪力墙尤其是由C型折痕单元组成的剪力墙在结构抗震方面具有较好的利用前景。

4）具有塑性铰引导机制的新型钢板剪力墙的加工工艺有待进一步研究，建议其折痕单元可通过冲压的方式实现，并采取退火工序以消除或降低冷作硬化带来的不利影响。