火灾、爆炸、撞击等突发事件可能使建筑物局部构件失效,失效构件相邻梁柱体系通过拉结作用形成新的传力路径并进行力和变形的重新分配。在中柱失效的情况下,梁柱节点作为重要传力构件对剩余结构的传力机制影响甚大,是建筑结构抵抗连续性倒塌的关键。二十世纪以来,随着国际上恐怖活动逐年增多,各国开始重视建筑抗倒塌规范的制定,美国总务局(GSA)出台针对联邦政府等重要建筑的抵抗连续倒塌设计指南GSA[1],美国国防部(DoD)出台结构防连续性倒塌准则DoD[2]。近年来,学者们开始从结构体系的抗倒塌机理研究拓展到节点抵抗连续倒塌能力研究。Lee等[3]通过对不同跨高比的钢节点进行静力倒塌试验,得到刚性节点弯曲铰模型;Sadek等[4]对普通钢节点和翼缘削弱型钢节点进行抗倒塌对比试验,分析削弱翼缘后塑性铰外移对节点抗倒塌性能的影响;王伟等[5–6]对不同构造的钢管柱–H形钢梁节点进行拟静力加载试验及数值模拟,考察不同节点形式、构造在连续性倒塌工况下的传力模式和抗力机理;Wang等[7]采用ABAQUS多尺度建模的方法建立突出反应节点的钢管混凝土框架有限元模型,研究其在静力荷载和动力荷载下的抗倒塌性能;李天昊[8]进行了钢管混凝土外环板式梁柱节点的连续倒塌试验,对该类节点在静力荷载下的变形模式和破坏机理进行探究。
随着中国经济建设快速发展,钢与混凝土组合结构不断出现在超高层建筑中,由于钢管混凝土柱具有截面小、刚度大、延性好、可用高强度混凝土等优点,钢管混凝土框架结构已经成为强风、强震地区高层及超高层建筑的一种主导结构类型[9]。目前,钢管混凝土柱–钢梁外加强环板式节点已被广泛应用于工程实例中,但其因在钢管外壁焊接外加强环板占用大量建筑空间,影响建筑物使用功能。而钢管混凝土柱–钢梁穿心式节点即钢梁整体或部分穿过钢管及钢管内填充的混凝土,大大节省建筑使用空间同时具有良好的传力性能。针对此类节点的抗连续性倒塌研究,主要集中在穿心腹板和内隔板两种形式上。王来等[10]利用ANSYS有限元软件对二层二跨平面钢管混凝土框架进行抗连续性倒塌能力模拟研究,着重分析了钢管混凝土柱–钢梁节点的穿心腹板构造对框架抗连续性倒塌能力的影响;史艳莉等[11]利用ABAQUS有限元软件对圆钢管混凝土柱–钢梁内隔板式节点进行抗连续性倒塌工作机理的模拟研究,考察其在连续性倒塌工况下承载力曲线、破坏形态及抗力机制。
针对不同穿心构造形式的钢管混凝土柱–H形钢梁节点,作者利用ABAQUS有限元软件对其进行抗连续性倒塌性能研究,考察节点在中柱失效工况下的破坏模式、传力途径及抗力机理,对比分析不同穿心构造对节点抵抗连续倒塌能力的影响,并提出可提高结构抗倒塌性能的新型穿心构造梁柱节点。
1 穿心构造节点设计结构中某关键竖向承力构件失效后,剩余结构通过改变结构传力途径抵抗连续性倒塌,GSA[1]和DoD[2]均通过考察关键柱失效后剩余结构的冗余性能判断结构抗连续倒塌能力,即备用荷载路径法。在如图1所示的典型连续倒塌工况下,框架结构中柱失效后,其余梁柱结构产生大变形,失效柱上方柱通过节点带动两侧梁发生位移,为简化分析,在梁跨中
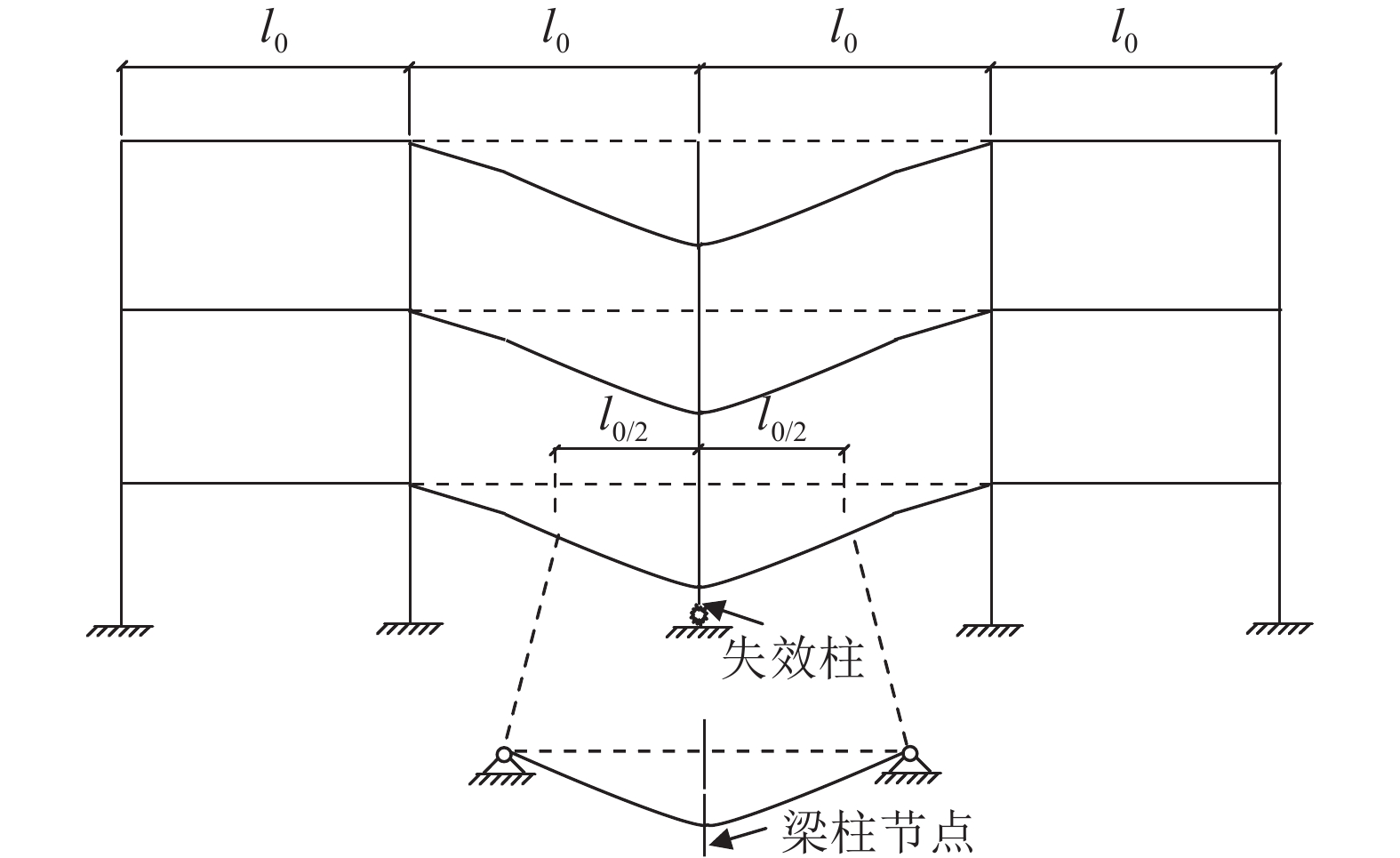 |
| 图1 “双半跨单柱子结构”简化模型 Fig. 1 Simplified assembly with double-half beam and column |
作者设计5个不同形式穿心构造的钢管混凝土柱–钢梁节点,构造形式包括穿心钢梁、穿心腹板、穿心翼缘、内加强隔板及新型穿心构造,节点编号分别为SJ–PSB、SJ–PW、SJ–PF、SJ–ID及SJ–NT,并设计钢管混凝土柱–钢梁全焊接节点SJ–W与以上5种穿心型节点进行对比。方钢管柱截面为400 mm
| 表1 梁柱节点参数 Tab. 1 Parameters of beam-to-column joints |
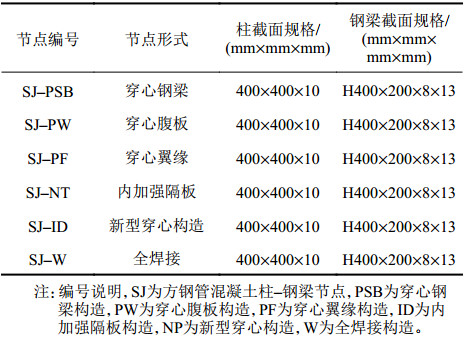 |
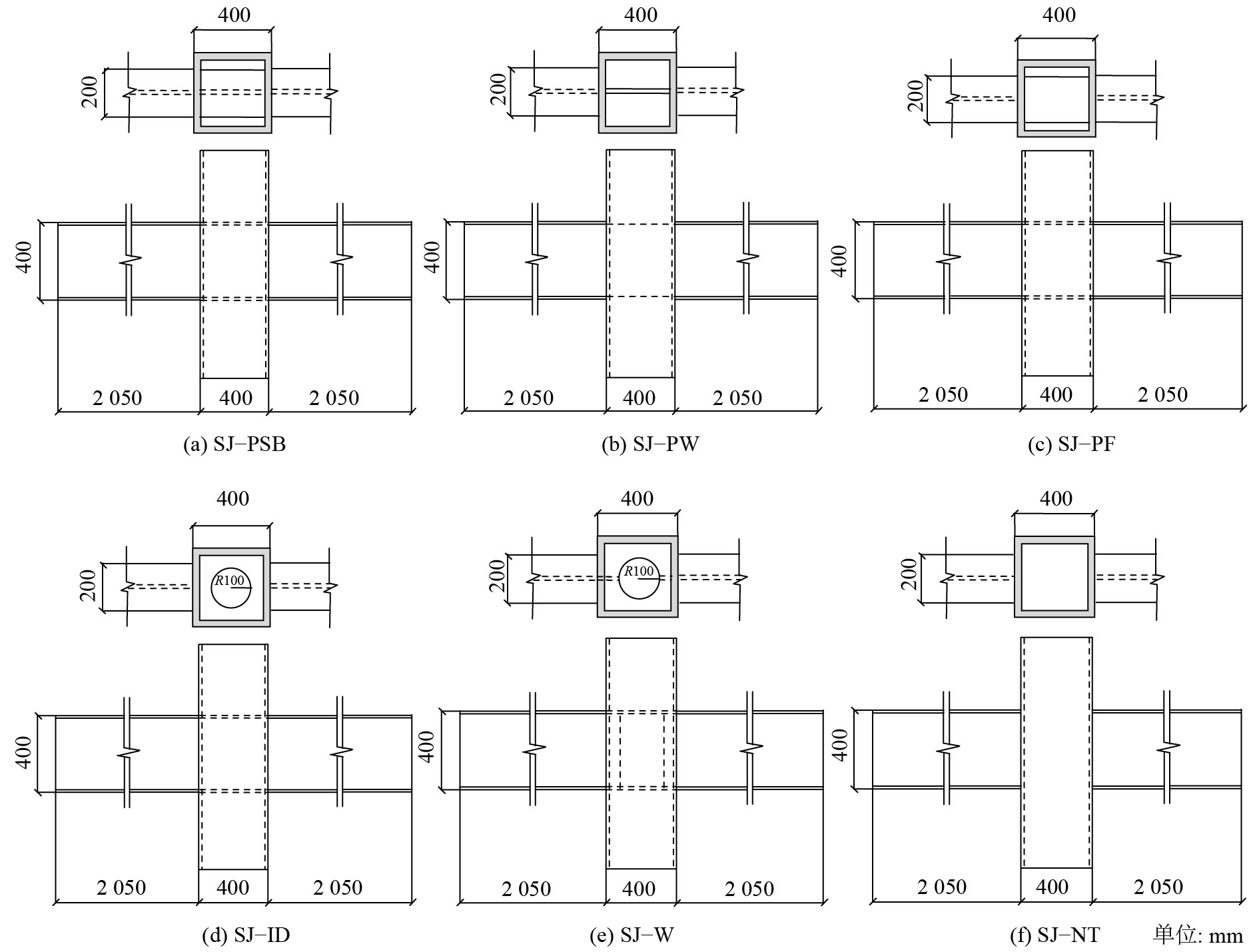 |
| 图2 节点具体尺寸及穿心构造详图 Fig. 2 Specific sizes of joints and details of through-center construct |
2 有限元模拟方法 2.1 材料本构模型
梁柱节点试件均使用钢管混凝土柱,即在空钢管内填充核心混凝土,此类混凝土受力复杂,需考虑钢管内壁对其约束作用。因此,参考韩林海[9]提出的考虑钢管约束效应的核心混凝土本构模型,该模型核心混凝土应力–应变关系如式(1)所示,其中,具体参数选取方法见文献[9]。
| $y = \left\{ \begin{aligned}&2x - {x^2} \text{,} {x \le 1} \text{;}\\&\frac{x}{{{\beta _0} \cdot {{\left( {x - 1} \right)}^\eta } + x}}, \quad {x > 1} \end{aligned} \right.$ | (1) |
式中,
而本文梁柱节点试件中方钢管、H形钢梁及穿心构件均采用强度等级为Q345b的低碳合金钢,在建立节点有限元模型时,应充分考虑钢材大变形及断裂带来的难收敛问题,因此,选取合理的钢材本构模型至关重要。提出的钢材本构模型参考Esmaeily和Xiao[12]提出的拉压不等强钢材本构关系,该模型通过设置
| $\sigma = \left\{ \begin{aligned}&{E}_{\rm{s}}\varepsilon , \varepsilon \le {\varepsilon _{\rm y}};\\&{f_{\rm y}},{\varepsilon _{\rm y}} < \varepsilon \le {k_1}{\varepsilon _{\rm y}};\\&{k_3}{f_{\rm y}} + \frac{{{E_{\rm s}}\left( {1 - {k_3}} \right)}}{{{\varepsilon _{\rm y}}{{\left( {{k_2} - {k_1}} \right)}^2}}}{\left( {\varepsilon - {k_2}{\varepsilon _{\rm y}}} \right)^2} ,\varepsilon > {k_1}{\varepsilon _{\rm y}}\end{aligned} \right.$ | (2) |
式中,
梁柱节点有限元模型中钢管内核心混凝土及柱顶加载板采用八结点实体单元,其余构件采用四结点薄壳单元。本模型为模拟真实焊接连接,将柱顶加载板与钢管和核心混凝土上表面、钢梁与钢管柱外壁、穿心构件与钢管柱内壁分别设置为接触对,并定义为绑定接触。定义穿心构件嵌入于核心混凝土中。节点中钢管柱与核心混凝土的接触关系选择表面与表面接触。边界条件为节点钢梁两端插入铰接装置,节点柱底设置为仅可竖向滑移。通过在柱顶加载板施加位移控制的均布荷载,以实现连续性倒塌工况下节点子结构所承受的失效荷载。节点网格划分、边界条件及加载方式如图3所示。
 |
| 图3 节点网格划分、边界条件及加载方式 Fig. 3 Hypermesh, boundary condition and loading method of joint |
梁柱节点连续倒塌过程的变形模式为大变形,钢材断裂情况严重影响节点竖向承载能力,建立有限元模型时在材性模块中对所有钢材赋予延性金属断裂属性,并在后处理中利用“单元删除法”对达到断裂应变的壳体单元进行删除。
2.3 节点试验验证 2.3.1 外环板式节点抗连续倒塌试验为探究钢管混凝土外环板式梁柱节点的抗连续倒塌性能,李天昊[8]针对方钢管混凝土柱–钢梁外环板式节点进行倒塌静力试验。其中,试件梁跨为3 m,柱高为1 m,外环板厚度为5.5 mm,节点具体参数见表2。外环板与薄壁钢管柱采用焊接连接,试件钢材材性为Q235b,钢管内浇筑C50自密实商砼。钢梁梁端设置铰接装置,加载方式为在钢管砼柱顶施加竖向荷载。
| 表2 外环板式节点参数 Tab. 2 Parameters of joint with outer-ring plate contruct |
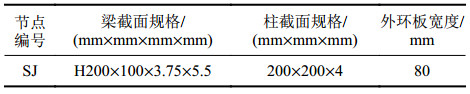 |
试验中,方钢管砼柱外环板式节点在柱顶位移达到30 mm之前呈现出整体受弯态,其刚度较大;随着荷载持续施加,试件钢管柱竖向位移加大,两侧钢梁弯曲变形加大,靠近环板的钢梁上翼缘出现微小屈曲;位移加载至195 mm及240 mm时,两侧钢梁下翼缘相继发生受拉开裂,随后两侧钢梁断裂裂缝发展趋势逐渐一致,试件达到极限承载力后节点失效。
图4为外环板式节点试验结果与模拟结果对比。由图4(a)可以看出,试验与模拟曲线在梁机制阶段以及悬链线效应阶段吻合较好,而在混合机制阶段有一定差异,这是由于有限元模型未考虑真实试验试件中的初始损伤以及残余应力;试验曲线在加载后期存才2~3个下降拐点是由于两侧钢梁开裂时间不同。由图4(b)可见,有限元模型与试验试件在倒塌时整体变形形态一致,钢管砼柱下移引起的钢梁变形趋势相同。由图4(c)可知,二者破坏模式也均相同,其钢梁下翼缘断裂位置均发生在环板与翼缘变截面处,下翼缘裂缝贯穿后,开裂裂缝均由下翼缘断裂位置展开并延伸至腹板处。
 |
| 图4 外环板式节点试验结果与模拟结果对比 Fig. 4 Comparison of experimental results and simulation results of joint with outer-ring plate contruct |
2.3.2 全螺栓连接节点抗连续倒塌试验
王伟等[5]对空钢管柱–钢梁全螺栓连接节点进行抗连续倒塌试验,H形钢梁截面尺寸为H300 mm
从图5不难看出,本文数值建模结果与试验抗力曲线吻合良好,有限元模拟出的承载力略微高于试验结果,曲线走势、节点域刚度与实际相符。
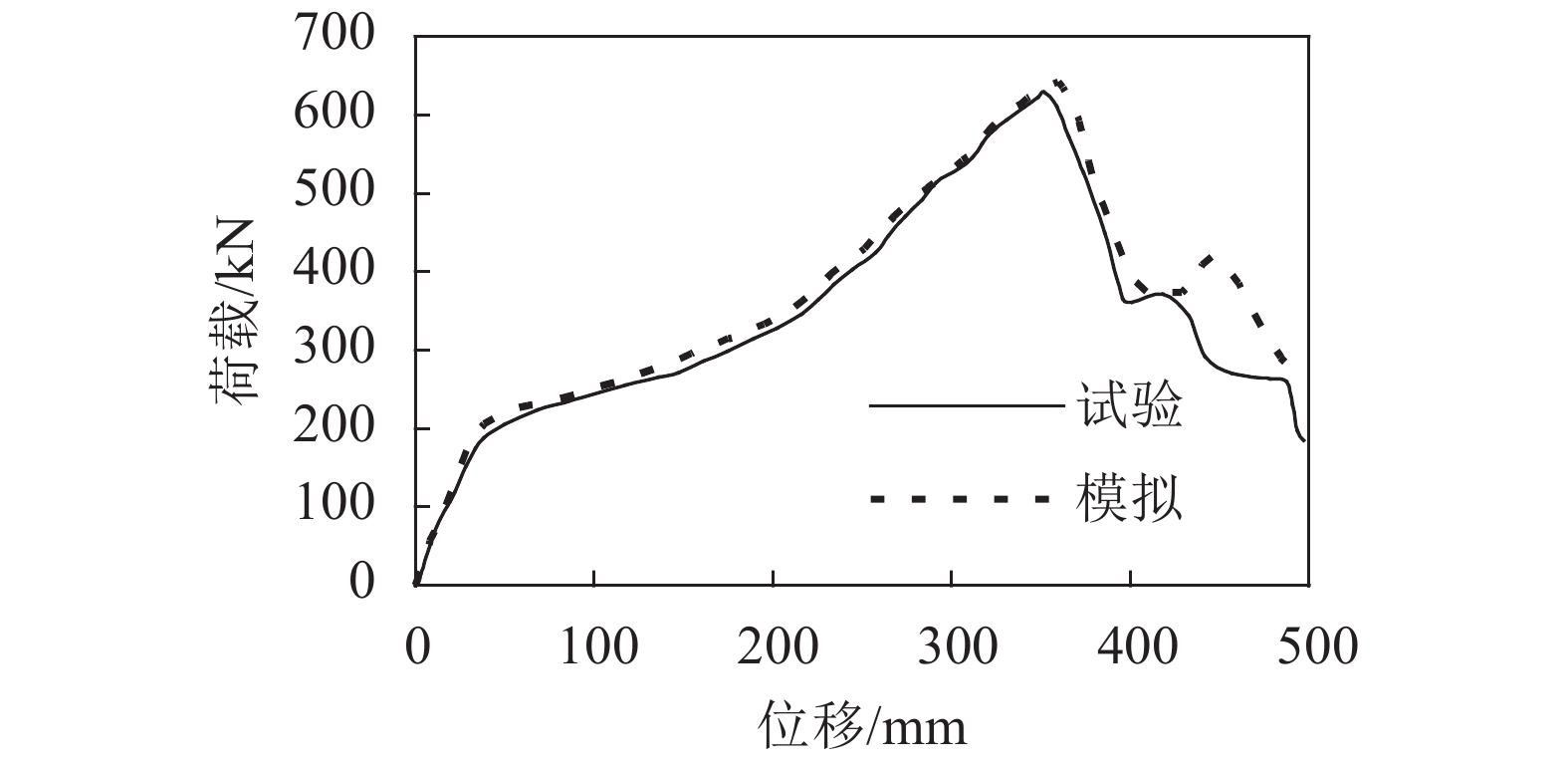 |
| 图5 全螺栓连接节点荷载–位移曲线对比 Fig. 5 Comparison of load–displacement curves of joint with bolt connections |
2.3.3 不同破坏模式节点抗连续倒塌试验
王伟等[6]对不同构造的钢管柱–钢梁节点进行抗连续倒塌试验,结果表明,内隔板式节点SI–W和狗骨式钢梁–内隔板式节点SI–W–RBS在连续倒塌工况下分别呈现梁端破坏和柱身破坏两种破坏模式。作者对以上两个试件进行有限元模拟验证,试验与模拟荷载–位移曲线对比如图6所示,两个试件总体模拟效果较好。其中:梁端破坏试件SI–W的模拟曲线更为吻合;柱身破坏试件SI–W–RBS的有限元模拟曲线并未计算出第1次柱身破坏,主要由于未考虑试件焊接初始缺陷,而有限元模拟出第2次柱身破坏,即节点失效处,且极限承载力相差仅为4.47%,验证了有限元建模策略的准确性。
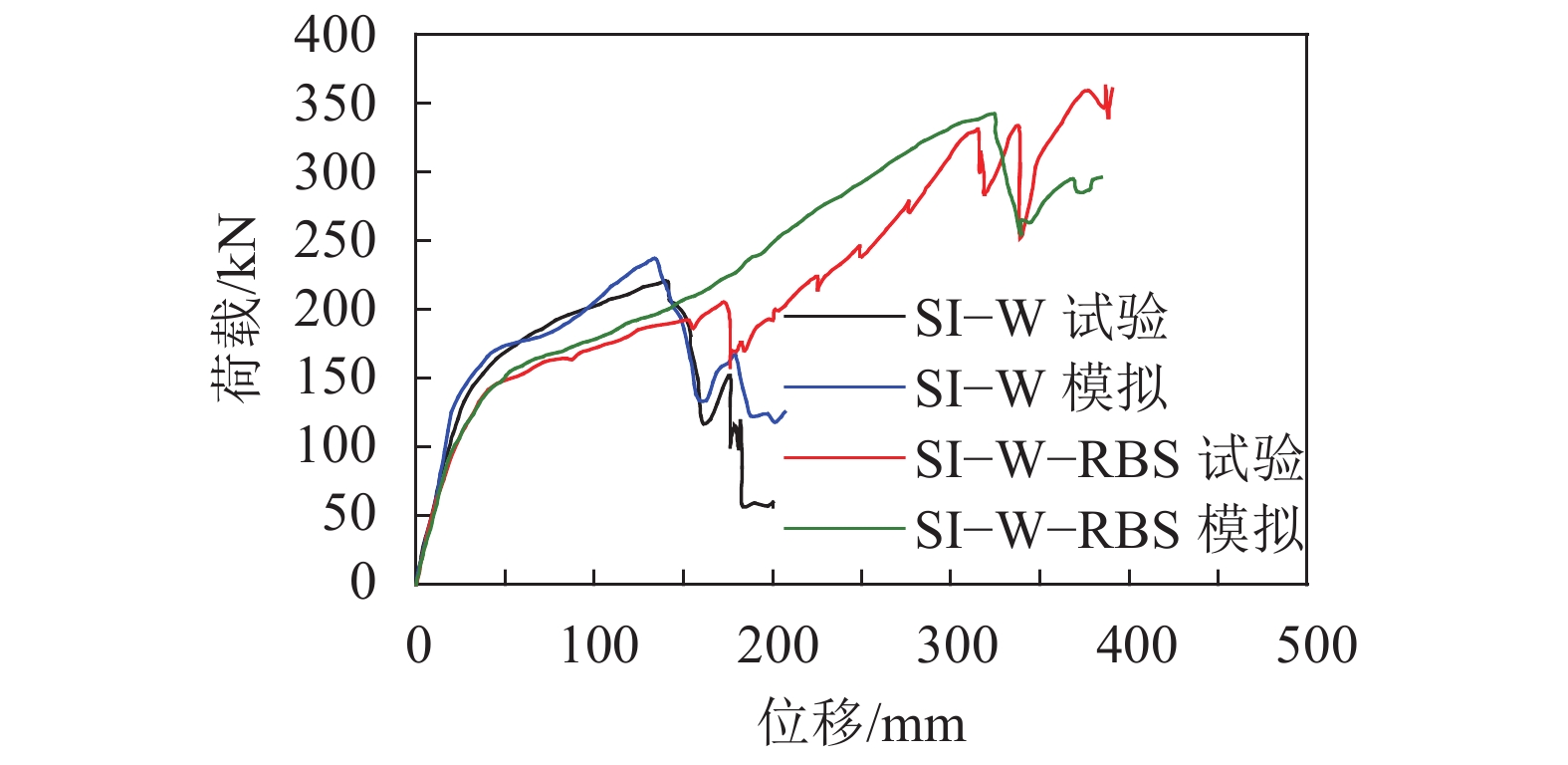 |
| 图6 不同破坏模式节点荷载–位移曲线对比 Fig. 6 Comparison of load–displacement curves of joint with different failure modes |
3 穿心构造节点倒塌过程与分析 3.1 节点荷载–位移曲线与变形过程
图7给出了节点柱顶荷载–位移曲线。由图7不难看出,6个节点试件在连续倒塌工况下的抗力曲线趋势基本一致,可分为4个阶段:受弯机制阶段、混合机制阶段、悬链线机制阶段及破坏阶段。图7中,A1~A6点均为受弯机制阶段的终点,B1~B6点均为悬链线机制阶段的终点及破坏阶段的起点,而C1~C6点为各个节点在破坏阶段中钢梁或柱壁发生明显断裂的破坏点。
由6个节点试件的数值模拟对比结果可知,穿心型钢管混凝土柱–H形钢梁节点的连续倒塌变形破坏模式分为两种,即钢梁倒塌破坏和柱壁倒塌破坏,作者选取节点SJ–PSB为钢梁倒塌破坏典型节点,节点SJ–PW为柱壁倒塌破坏典型节点。
图7(a)为节点SJ–PSB柱顶荷载–位移曲线,图8为钢梁倒塌破坏典型节点SJ–PSB变形模式,由图7(a)及8可知:节点SJ–PSB在加载初期,柱顶抗力与竖向位移呈线性增长关系;竖向位移到达22 mm(A1点)时,节点竖向抗力达到453 kN,曲线出现拐点刚度骤然下降,节点靠近中柱的钢梁由全截面受弯逐渐转变为受拉状态,上下翼缘应力均达到345 MPa,即钢材受拉屈服极限应力;随着竖向位移增大,曲线刚度有所回升,节点域钢梁下翼缘应力由于拉力增大而急剧增大;当柱顶位移增大到533 mm(B1点)时,穿心钢梁型节点竖向抗力达到最大值1 683 kN,紧接着节点域钢梁下翼缘出现断裂,加载到577 mm(C1点)时竖向抗力下降47.5%,钢梁腹板沿着下翼缘破坏位置由下至上开始断裂,此时节点梁弦转角为
 |
| 图8 钢梁倒塌破坏典型节点SJ–PSB变形模式 Fig. 8 Deformation mode of SJ–PSB with the collapse failure at the beam |
图7(b)为节点SJ–PW柱顶荷载-位移曲线,图9为柱壁倒塌破坏典型节点SJ–PW变形模式,由图7(b)及9可知,节点SJ–PW在倒塌工况初始阶段竖向荷载随柱顶竖向位移线性增长,节点域处于受弯状态;竖向位移加载到24 mm(A2点)时,节点柱顶抗力为300 kN,抗力曲线斜率突然降低,靠近中柱的钢梁上翼缘,与钢梁下翼缘焊接处对应的钢管外壁率先屈服;随着柱顶竖向位移持续增大,与下翼缘焊接位置对应的薄壁钢管出现鼓曲变形,两侧钢梁抗力机制从受弯机制逐渐转变为悬链线机制;当竖向位移加载到697 mm(B2点)时,节点竖向抗力达到最大值2 208 kN,此时穿心腹板型节点应力极值位于钢梁下翼缘与钢管壁焊接处;对柱顶继续加载,钢梁下翼缘、腹板与钢管壁焊接处接连发生断裂,位移达到720 mm(C2点)时,节点梁弦转角为
 |
| 图9 柱壁倒塌破坏典型节点SJ–PW变形模式 Fig. 9 Deformation mode of SJ–PW with the collapse failure at the column |
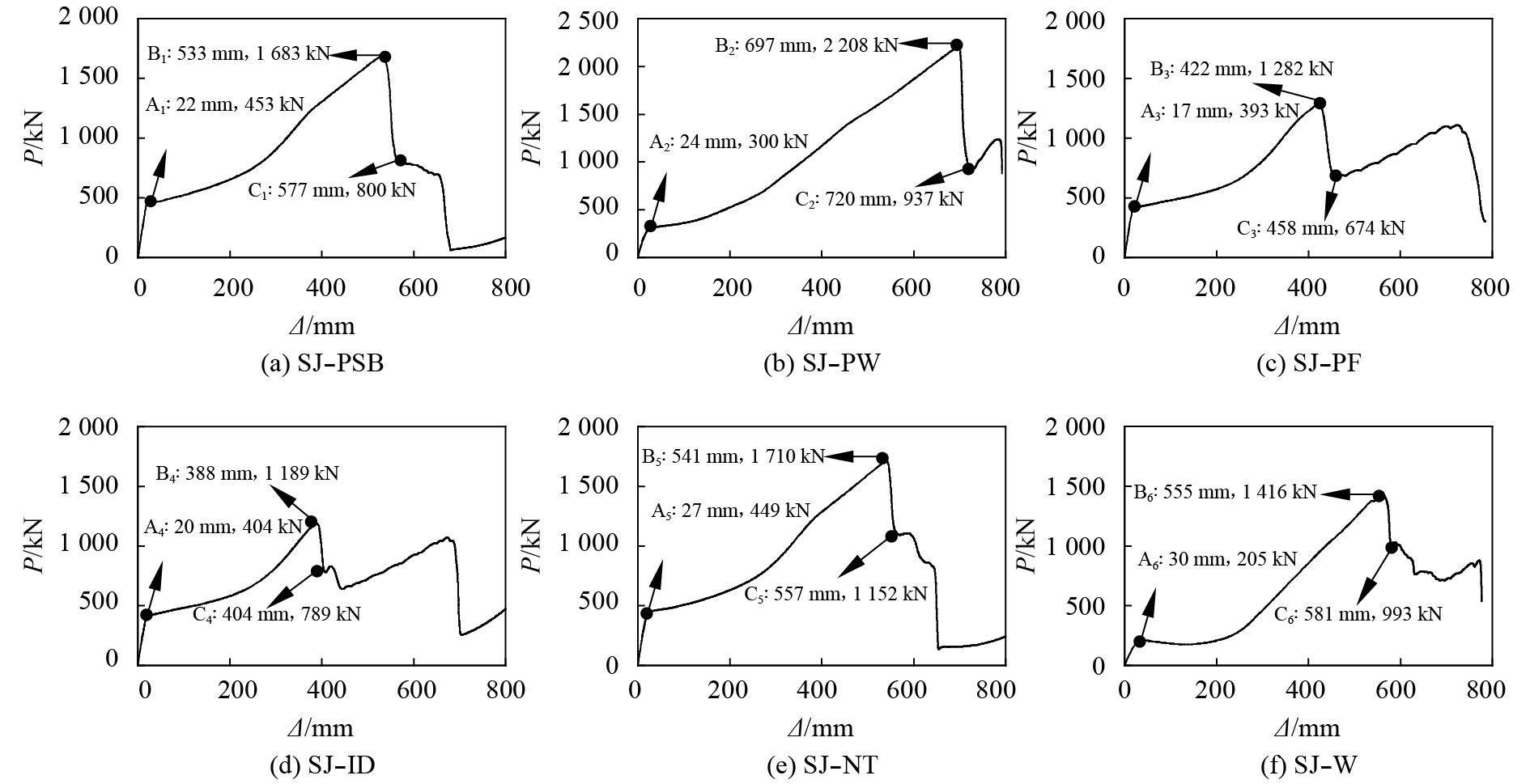 |
| 图7 节点柱顶荷载–位移曲线 Fig. 7 Load–displacement curves of the top of column of joints |
3.2 破坏模式分类与分析 3.2.1 钢梁倒塌破坏模式
破坏模式为如图10所示的钢梁倒塌破坏节点,两侧钢梁在受弯机制阶段结束后达到塑性极限弯矩,并在靠近钢管柱的钢梁最不利截面处形成塑性铰;随着梁弦转角持续增大,节点进入混合机制阶段及悬链线机制阶段,两侧钢梁绕此塑性铰发生转动,钢梁的拉结力随之增大,钢梁最不利截面下翼缘及下翼缘上方腹板部分形成应力集中区;当荷载加载到节点抗力最大值时,最不利截面下翼缘断裂;在轴力作用下,裂缝迅速向上延伸至腹板,钢梁由于有效截面面积持续减小,其抗力迅速降低,直至节点完全失效。
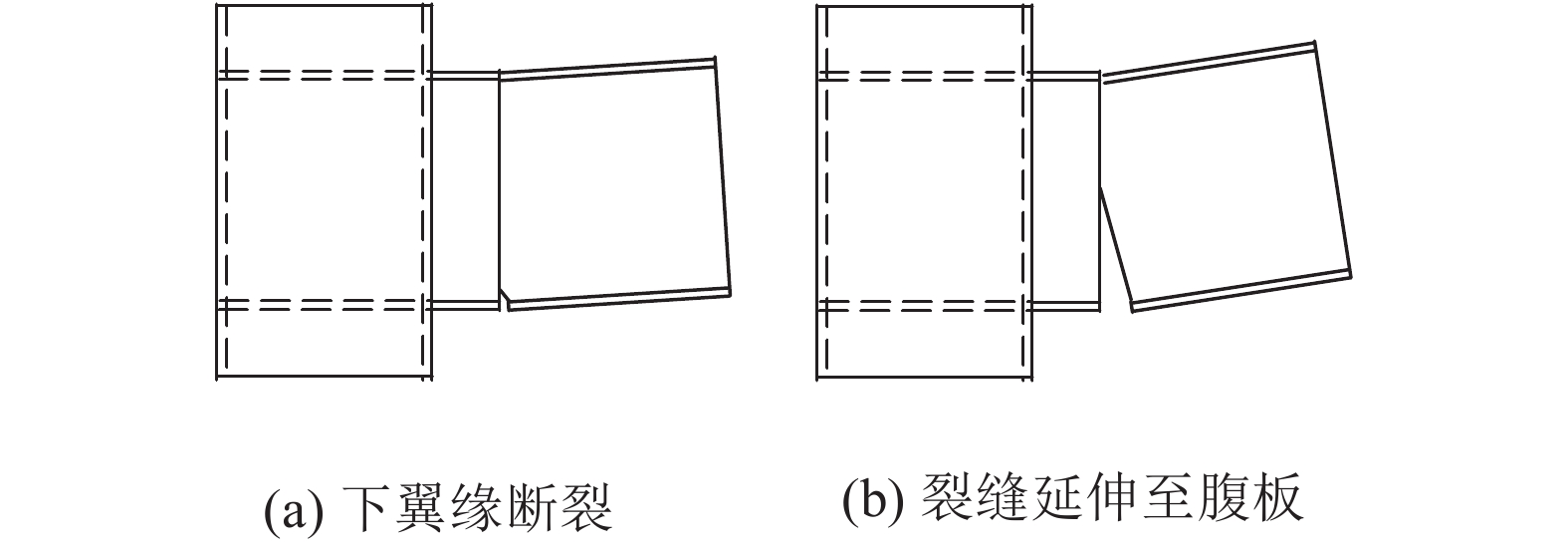 |
| 图10 钢梁倒塌破坏模式 Fig. 10 Collapse failure mode at the beam |
3.2.2 柱壁倒塌破坏模式
破坏模式为如图11所示的柱壁倒塌破坏节点,其最不利截面位于钢梁与钢管柱焊接处,在加载前期节点主要承受弯矩作用,此时与下翼缘焊接位置对应的钢管柱外壁出现正应力集中区,而靠近钢管柱的钢梁上翼缘出现负应力集中区;随着竖向位移不断增大,节点进入混合机制阶段及悬链线机制阶段,两侧钢梁绕最不利截面转动,与钢梁下翼缘焊接处对应的钢管柱外壁发生明显鼓曲;当位移达到极限竖向位移时,钢管柱外壁鼓曲变形不再增大,钢梁与钢管柱连接处发生开裂,裂缝从下翼缘迅速扩散至腹板及上翼缘,加载后期节点承载力持续减小至零。
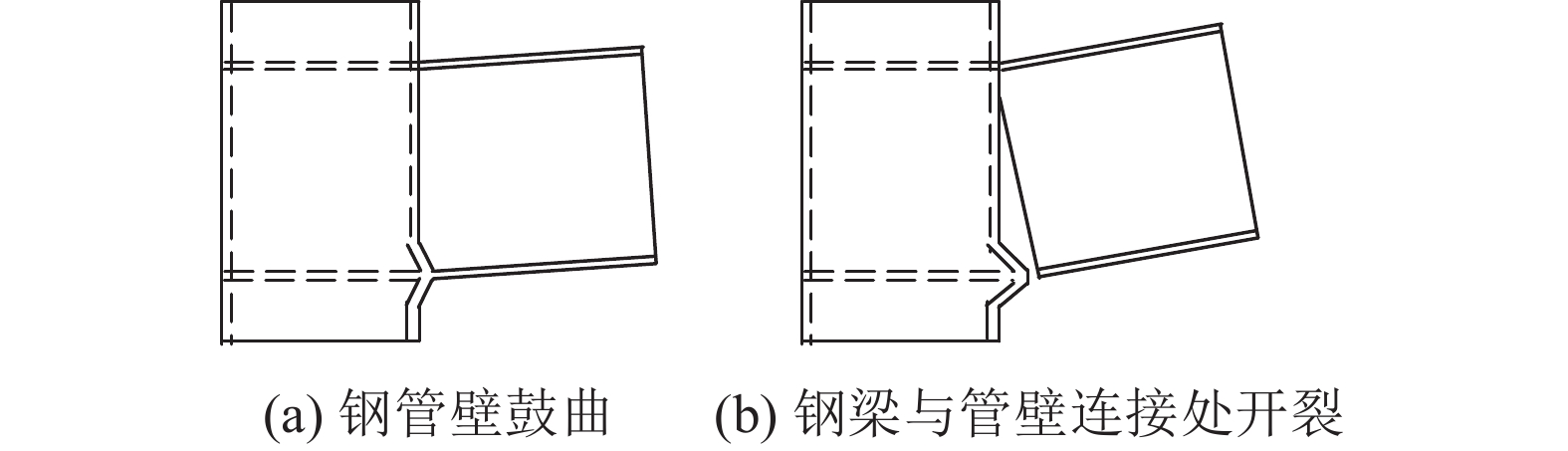 |
| 图11 柱壁倒塌破坏模式 Fig. 11 Collapse failure mode at the column |
3.3 最不利截面应力及应变分析
以穿心钢梁构造节点SJ–PSB为例,选取其最不利截面(如图12所示)进行应力及应变分析。
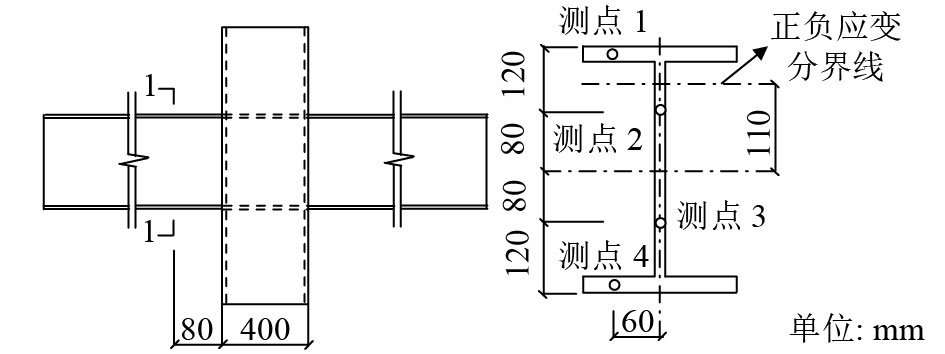 |
| 图12 最不利截面示意 Fig. 12 Schematic of the most adverse section |
图13为节点SJ–PSB最不利截面S11应力发展曲线。由图13可以看出:节点在加载初期,上翼缘(测点1)及靠近上翼缘处腹板(测点2)受压应力作用,下翼缘(测点4)及靠近下翼缘处腹板(测点3)受拉应力作用,正负应力均呈线性发展且斜率绝对值相等;节点抗力模式进入混合机制阶段后,中性轴开始向上发展,靠近上翼缘处腹板开始由受压状态转变为受拉状态,测点2应力由负值逐渐向零靠近并转为正值,上翼缘(测点1)、靠近下翼缘处腹板(测点3)及下翼缘(测点4)应力均缓慢增长;节点进入悬链线机制阶段后,上翼缘(测点1)应力快速降为零并达到正值,此时钢梁全截面为受拉状态,当下翼缘应力水平达到断裂应力时,下翼缘(测点4)及靠近下翼缘处腹板(测点3)应力瞬间减小至0,钢梁从下翼缘开始断裂,裂缝从下至上延伸至腹板。
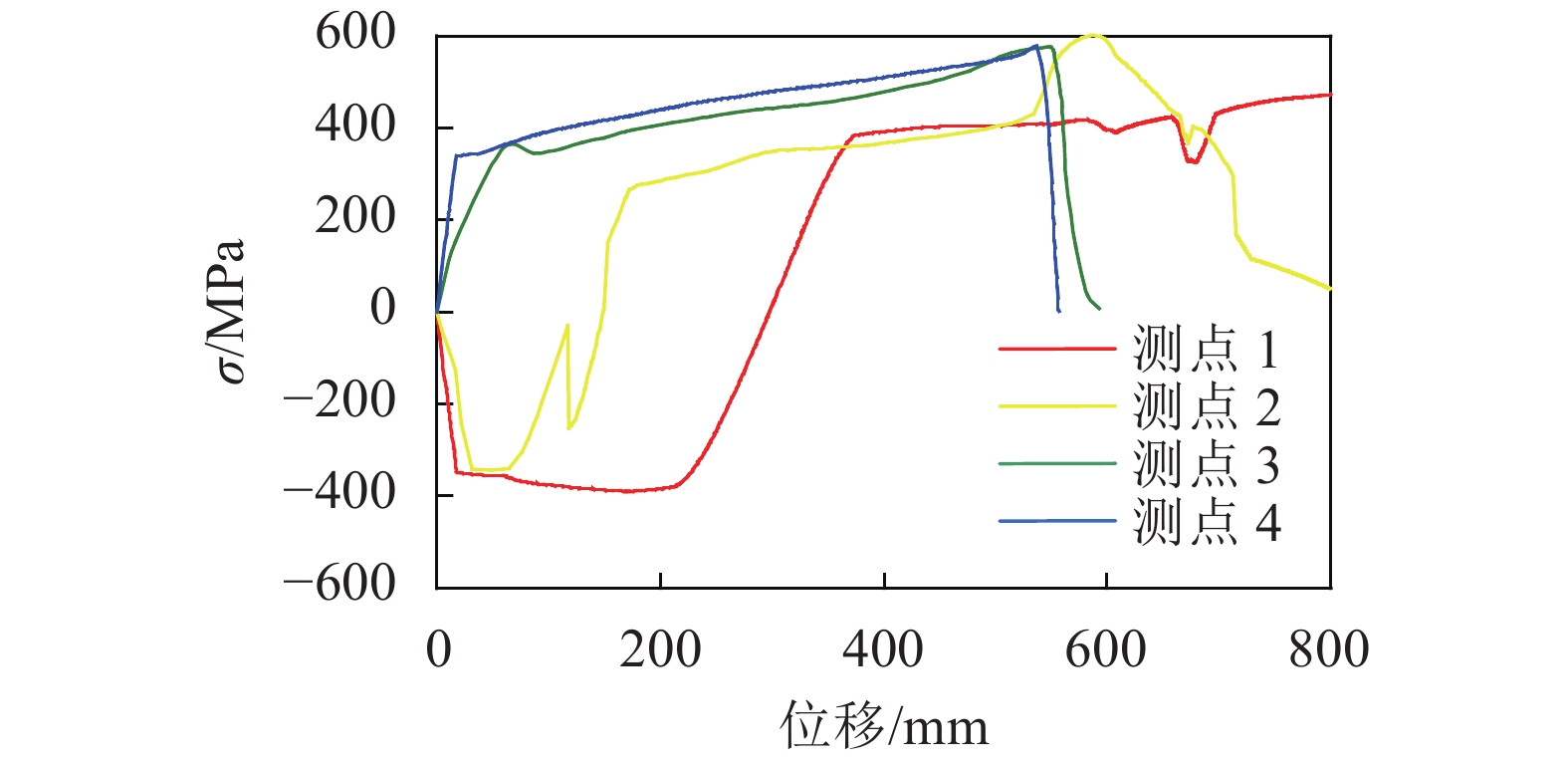 |
| 图13 最不利截面S11应力发展曲线 Fig. 13 S11 stress curves of the most adverse section |
图14为节点SJ–PSB最不利截面PE11应变发展曲线。由图14可以看出:节点在受弯机制阶段,钢梁处于弹性状态,其应变水平较小;节点进入混合机制阶段后,钢梁上翼缘及靠近上翼缘处腹板进入负应变状态,钢梁下翼缘及靠近下翼缘处腹板进入正应变状态;节点进入混合机制阶段后,钢梁最不利截面拉压应变水平持续增大,并呈现塑性变形的特点;随着柱顶荷载持续增长,钢梁最不利截面正负应变分界线(图12)趋于明显,分界线上方截面处于压应变状态,分界线下方截面拉应变状态。
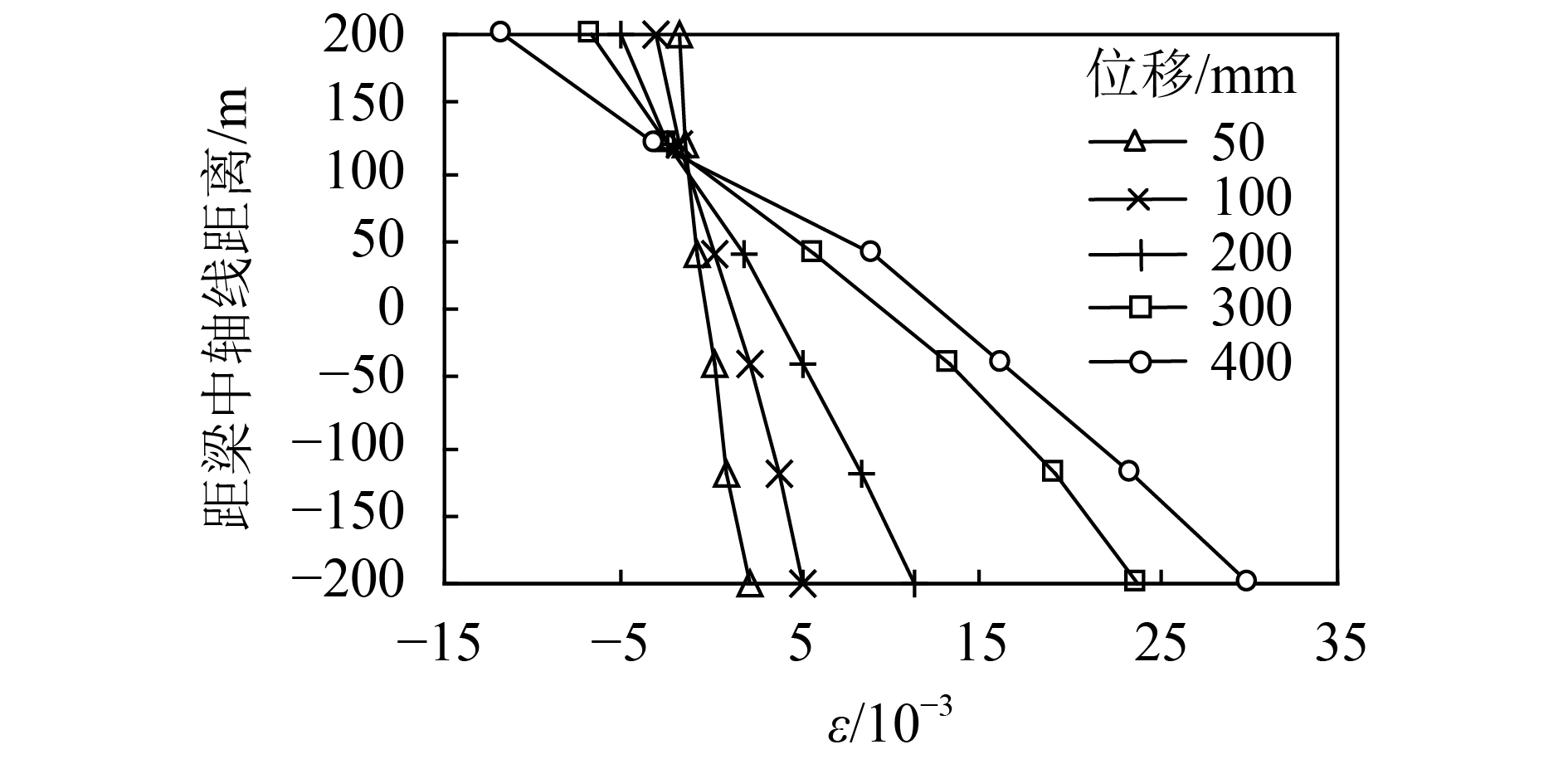 |
| 图14 最不利截面PE11应变发展曲线 Fig. 14 PE11 strain curves of the most adverse section |
3.4 节点抗倒塌机制分析
节点竖向抗力
| ${F}_{\rm{P}} = {F}_{\rm{f}} + {F}_{\rm{a}}$ | (3) |
| ${F}_{\rm{f}} = \left( {{V_1} + {V_2}} \right){\rm{cos}}\;\theta $ | (4) |
| ${F}_{\rm{a}} = \left( {{N_1} + {N_2}} \right){\rm{sin}}\;\theta $ | (5) |
由节点SJ–PSB抗力机制(图15)可知:穿心型钢管混凝土柱–钢梁节点在抗弯机制阶段的抗力完全由
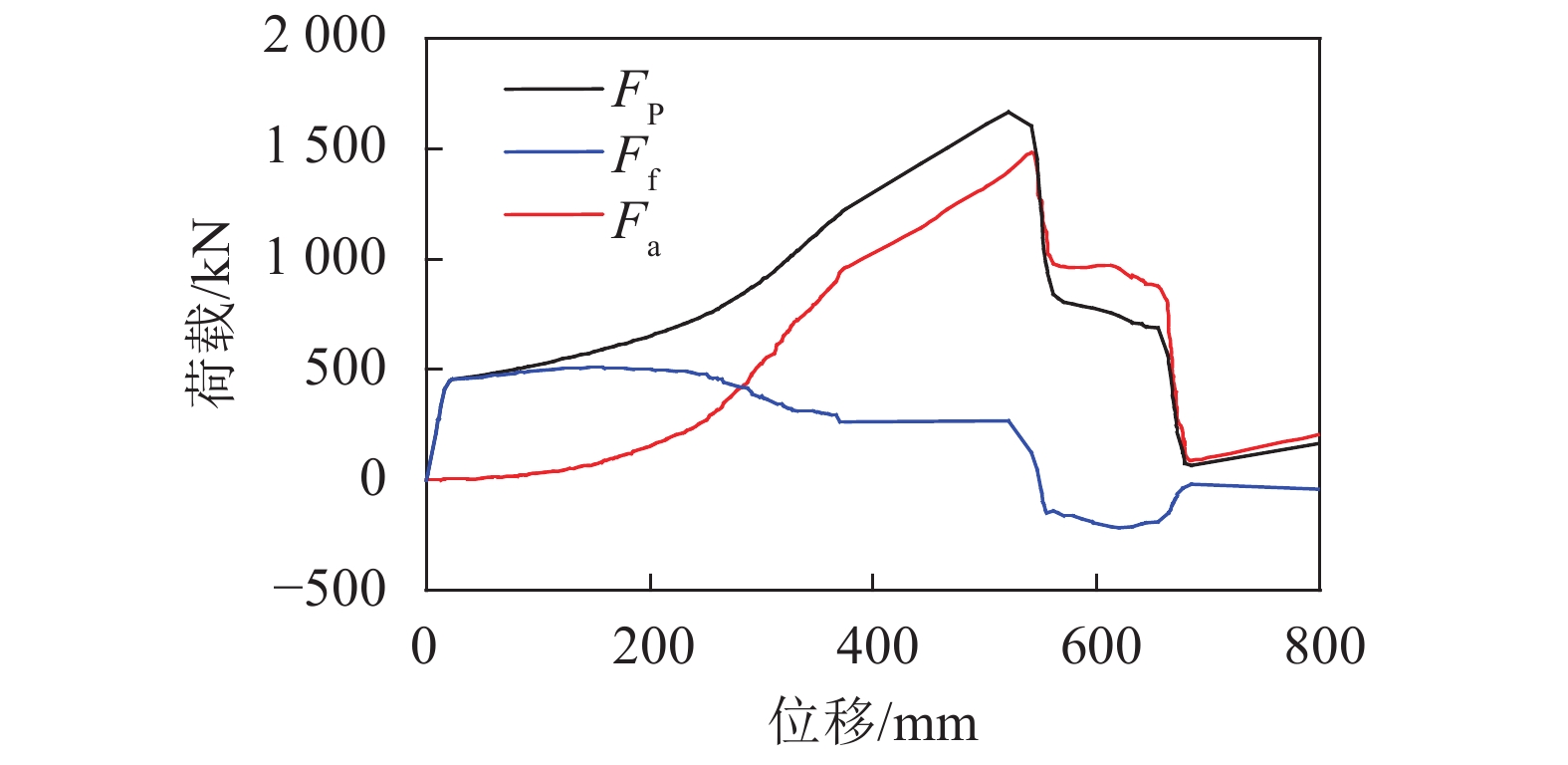 |
| 图15 节点SJ–PSB抗力机制 Fig. 15 Resistance mechanism of SJ–PSB |
3.5 穿心构造节点抗倒塌性能评估 3.5.1 节点抗连续倒塌性能评估指标
综上所述,节点的抗力由抗弯机制和悬链线机制提供,其中,抗弯机制主要提供前期抗力,悬链线机制控制节点极限承载力,作者提出节点抗连续倒塌性能评估指标
| $\eta = \frac{{F_{{\rm{a}}\max} }}{{F_{{\rm{P}}\max} }} \times 100{\text{%}} $ | (6) |
式中,
表3为穿心构造节点抗倒塌性性能评估。表3中节点SJ–PW和节点SJ–W破坏模式为柱壁倒塌破坏。节点SJ–PW和节点SJ–W极限位移
| 表3 穿心构造节点抗倒塌性能评估 Tab. 3 Resistance to progressive collapse performance assessment of joints with through-center construct |
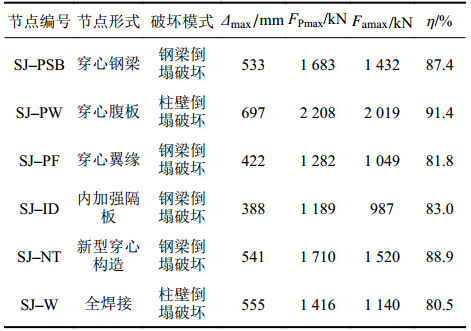 |
节点SJ–PSB、节点SJ–PF、节点SJ–ID及节点SJ–NT破坏模式为钢梁倒塌破坏。其中,新型穿心构件节点SJ–NT极限位移
设计了5个穿心型钢管混凝土柱–钢梁节点及1个全焊接节点计算模型,对其进行抗连续倒塌的有限元模拟及分析,结论如下:
1) 穿心型钢管混凝土柱–钢梁节点的连续倒塌破坏模式可分为两种类型:钢梁倒塌破坏模式和柱壁倒塌破坏模式。当节点发生柱壁倒塌破坏时,虽具有更好的延性及承载力,但钢管壁鼓曲具有不稳定性。
2) 穿心型节点的竖向承载力主要由抗弯机制及悬链线机制提供,其中,抗弯机制提供前期抗力,悬链线机制决定后期极限承载力。
3) 新型穿心构造的钢管混凝土柱–钢梁节点具有良好的抗连续倒塌能力,其节点抗连续倒塌性能评估指标
| [1] |
Alternate path analysis and design guidelines for progressive collapse resistance:GSA2013[S].Washington:US General Service Administration,2013.
|
| [2] |
Design of building to resist progressive collapse:UFC 4-023-03[S].Washington:Unified Facilities Criteria,2013.
|
| [3] |
Lee C H,Kim S,Han K H,et al. Simplified nonlinear progressive collapse analysis of welded steel moment frames[J]. Journal of Constructional Steel Research, 2009, 65(5): 1130-1137. DOI:10.1016/j.jcsr.2008.10.008 |
| [4] |
Sadek F,Main J A,Lew H S,et al. Testing and analysis of steel and concrete beam-column assemblies under a column removal scenario[J]. Journal of Structural Engineering, 2011, 137(9): 881-892. DOI:10.1061/(ASCE)ST.1943-541X.0000422 |
| [5] |
Qin Xi,Wang Wei. Numerical simulation for progressive collapse behavior of through diaphragm bolted beam-column joints[J]. Journal of Vibration and Shock, 2015, 34(10): 68-75. [秦希,王伟. 隔板贯通式全螺栓节点抗连续性倒塌性能数值模拟分析[J]. 振动与冲击, 2015, 34(10): 68-75. DOI:10.13465/j.cnki.jvs.2015.10.012] |
| [6] |
Li Ling,Wang Wei,Chen Yiyi. Failure modes and robustness of beam-to-column joints for steel tubular frame resisting progressive collapse[J]. Journal of Building Structures, 2015, 36(4): 9-15. [李玲,王伟,陈以一. 连续性倒塌工况下钢管柱框架节点的破坏模式与鲁棒性[J]. 建筑结构学报, 2015, 36(4): 9-15. DOI:10.14006/j.jzjgxb.2015.04.002] |
| [7] |
Wang Wenda,Li Huawei,Wang Jingxuan. Progressive collapse analysis of concrete-filled steel tubular column to steel beam connections using multi-scale model[J]. Structures, 2017, 9: 123-133. DOI:10.1016/j.istruc.2016.10.004 |
| [8] |
Li Tianhao. Progressive collapse performance experimental research and analysis of concrete-filled steel tube column to steel beam with outer-ring plate connections[D].Lanzhou:Lanzhou University of Technology, 2017. 李天昊.钢管混凝土柱–钢梁外环板式节点抗连续性倒塌性能试验研究与分析[D].兰州:兰州理工大学,2017. |
| [9] |
韩林海.钢管混凝土结构–理论与实践[M].3版.北京:科学出版社,2016.
|
| [10] |
Wang Lai,Yang Hongyan,Chen Haitao. Numerical simulation of progressive collapse of concrete-filled steel tube frame with continuous web plate joint[J]. Journal of Guangxi University(Natural Science Edition), 2016, 41(1): 44-52. [王来,杨红燕,陈海涛. 钢管混凝土框架穿心节点连续倒塌数值模拟[J]. 广西大学学报(自然科学版), 2016, 41(1): 44-52. DOI:10.13624/j.cnki.issn.1001-7445.2016.0044] |
| [11] |
Shi Yanli,Shi Xiaofei,Wang Wenda,et al. Progressive collapse mechanism for H-beam to concrete-filled steel tubular column connections with steel inner-diaphragm joints[J]. Journal of Vibration and Shock, 2016, 35(19): 148-155. [史艳莉,石晓飞,王文达,等. 圆钢管混凝土柱–H钢梁内隔板式节点抗连续倒塌机理研究[J]. 振动与冲击, 2016, 35(19): 148-155. DOI:10.13465/j.cnki.jvs.2016.19.025] |
| [12] |
Esmaeily A,Xiao Y. Behavior of reinforced concrete columns under variable axial loads:analysis[J]. ACI Structure Journal, 2005, 102(5): 736-744. |
 2018, Vol. 50
2018, Vol. 50

