IPCC第5次气候变化评估报告指出:20世纪以来,全球大部分地区经历了以升温为主要特征的气候变化过程。1880—2012年,全球海陆表面平均温度升高了0.85 ℃,且近三十年来地表温度的增幅高于1850年以来的任何时期[1]。气温的增加将加速大气环流和水文循环过程,导致全球不同尺度水资源的重新分配,进而影响地球的生态环境和人类社会的经济发展[2]。因此,预估气候变化背景下地表径流的演变趋势可为水资源的规划管理与开发利用、生态环境保护等提供科学依据[3],已成为当前全球变化研究的热点和前沿问题[4]。
气候变化背景下地表径流演变预估的研究基本上遵从“未来气候情景设计–水文模型–影响评估”的模式[5]。水文模型是未来地表径流预估的关键工具。目前,基于精细化水文模拟的方法在大尺度地表径流演变预估中存在2个突出的难题:技术层面,由于中国不同流域气候、下垫面等特征差异显著,建立在全国范围内较为通用且能反映区域特性的水文模型存在很大困难[6];应用层面,精细化水文模型的构建对数据和计算量的要求较高,需要详尽的流域气候、下垫面、取用水、工程调度等信息[7],适用于典型流域和区域的分析,但难以在大区域上推广应用。
选取抚河流域作为研究区,从地表径流形成的宏观机理出发,建立能够描述大尺度上气候要素、下垫面要素和地表径流三者之间定量关系的流域尺度水文模型,评估抚河流域对气候变化的敏感性,并利用CMIP5气候变化预估成果,对抚河流域未来地表径流进行预估,以期为抚河流域未来水资源系统的规划设计、开发利用和运行管理提供可靠的科学依据。
1 研究区概况抚河为鄱阳湖流域第2大水系,全长约348 km,河流自南向北,流经广昌、南丰、南城,右汇黎滩河,经浒湾进入下游平原,至抚州左纳抚河最大支流临水,西北向流经南昌县境,在荏港改道由青岚湖入鄱阳湖。抚河流域位于江西省东部,涉及抚州市11个县(区)和南昌市的南昌县、进贤县及宜春市区丰城县部分地区。流域地理坐标为115°30′~117°10′E和26°30′~28°37′N,总面积16 493 km2[8]。其中,李家渡以上流域面积15 811 km2,约占流域面积的95.9%(图1)。
 |
| 图1 研究区概况 Fig. 1 Overview of Fu River basin |
流域地处中亚热带湿润季风区,四季分明,雨量充沛,年均降水量为1 790 mm[9]。李家渡水文站以上平水年、偏枯水年和枯水年地表水资源量分别为164.65 亿m3、136.47 亿m3和102.21 亿m3。
2 资料与方法 2.1 数据来源所选用的气象观测数据源于国家气象信息中心提供的中国地面气候资料日值数据集(V3.0)。该数据集涵盖中国824个国家级地面站数据,涉及到的气象要素包括气压、气温、相对湿度、降水、蒸发、风向风速、日照等。选取1956—2013年抚河流域及周边共10个气象站点的数据(图2)。径流数据为李家渡水文站1956—2013年逐日流量数据,经处理后得到抚河流域历年地表径流深数据。
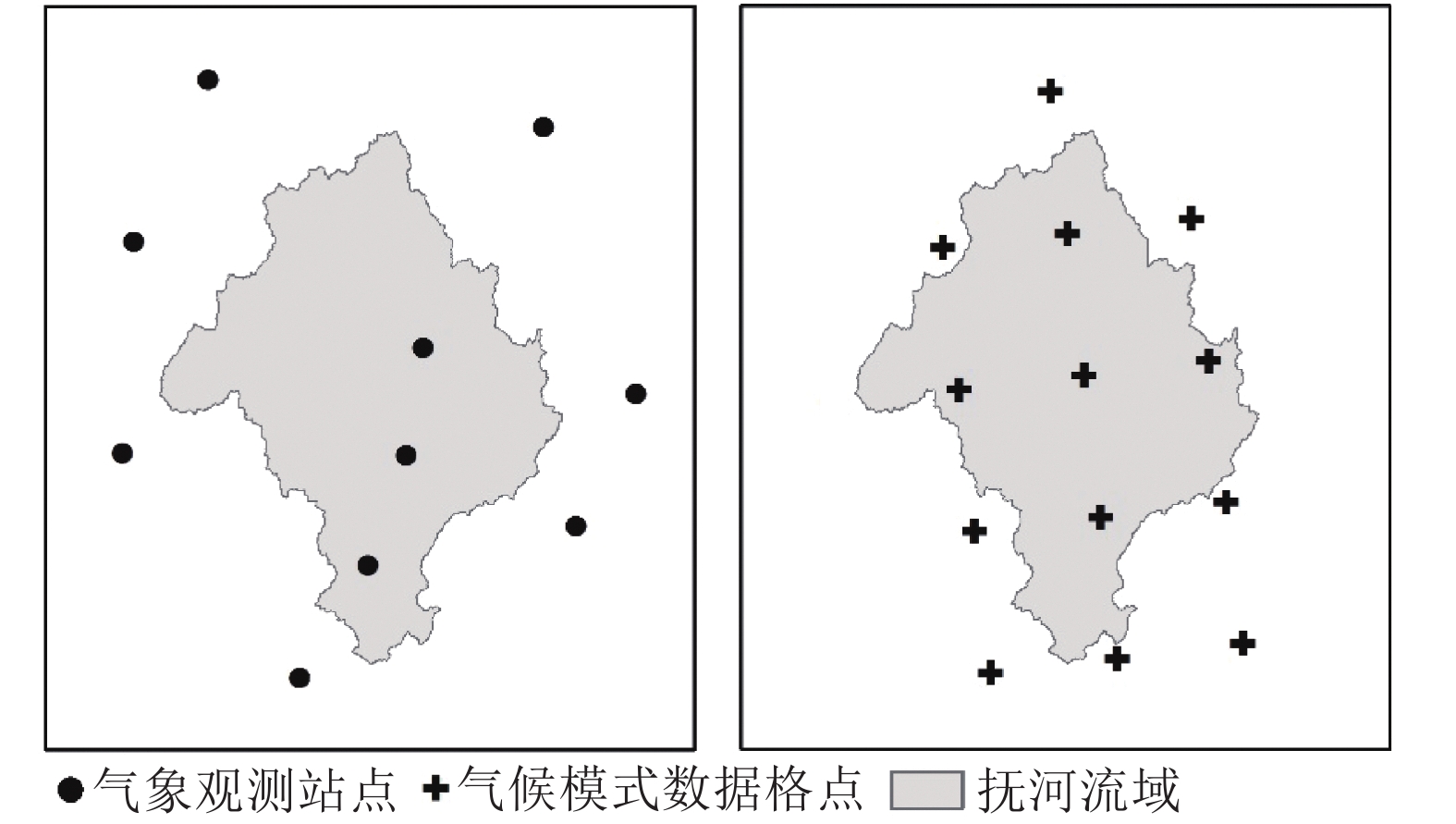 |
| 图2 气象站点和气候模式格点分布 Fig. 2 Location of meteorological stations and grid boxes |
气候模式是由ISI-MIP(the Inter-Sectoral Impact Model Intercomparison Project)提供的5套全球气候模式插值、订正结果。插值和订正方法分别为双线性插值和基于概率分布的统计偏差订正[10–12]。ISI-MIP中5套全球气候模式分别为GFDL-ESM2M、HadGEM2-ES、IPSL-CM5A-LR、MIROC-ESM-CHEM、NorESM1-M。模式提供的气象要素包括气温和降水等,分辨率为0.5°×0.5°,涉及到的情景分别为RCP2.6、RCP4.5、RCP6.0、RCP8.5,时间范围为1960年1月1日—2099年12月31日。研究中,选取其中的RCP2.6、RCP4.5和RCP8.5分别表示低、中、高情景,研究区内及周边共计有14个格点(图2)。研究时段选取2050年以前,对未来2020—2050年的地表径流深进行预估。
2.2 流域尺度水热平衡模型对于任意一个封闭流域,其水文气候特征满足流域水量平衡原理和能量平衡原理。在水文学研究中通常采用水量平衡分析方法和能量平衡法构建流域水均衡模型模拟流域水循环规律。
根据水量平衡原理、能量平衡原理建立降水、蒸发、土地利用和径流量之间的相关关系,构建流域尺度水热平衡模型。
| $R = P - E + \Delta W$ | (1) |
| ${R_{\rm n}} = \lambda E + H + G$ | (2) |
| $E = f\left( {{E_0},P} \right)$ | (3) |
式(1)~(3)中:P为降水;E为实际蒸发量;ΔW为土壤含水量的蓄变量,从较长的时间尺度分析,ΔW接近于0;Rn为到达地表面的净辐射通量;G为土壤热通量;λE为汽化潜热通量;H为显热输送通量;E0为蒸发能力,可根据国际粮农组织(FAO)推荐的Penman−Monteith方法计算。
E可通过基于Budyko曲线获取。Budyko假设认为流域水分和能量之间存在一个耦合平衡关系(称为水热平衡关系),并给出了一条经验关系曲线描述流域多年平均降水量、潜在蒸散发量和实际蒸散发量之间的定量关系。主要的Budyko曲线不同表达式[13–20]:
| ${E / P} = 1 - {\exp ^{ - \theta }}$ | (4) |
| ${E / P} = \phi \tanh \left( {{1 / \phi }} \right)$ | (5) |
| ${E / P} = {\left[ {0.9 + {{\left( {{1 / \phi }} \right)}^2}} \right]^{ - 0.5}}$ | (6) |
| ${E / P} = {\left[ {1 + {{\left( {{1 / \phi }} \right)}^2}} \right]^{ - 0.5}}$ | (7) |
| ${E / P} = {\left[ {1 + \tanh \left( {{1 / \phi }} \right)\left( {1 - {{\exp }^{ - \phi }}} \right)} \right]^{ - 0.5}}$ | (8) |
| ${E / P} = 1 + \phi - {\left( {1 + {\phi ^\omega }} \right)^{{1 / \omega }}}$ | (9) |
| ${E / P} = 1 - \left( {\phi {\gamma ^{\frac{\gamma }{\phi } - 1}}{{\exp }^{ - \gamma }}} \right){\left[ {\Gamma \left( {\frac{\gamma }{\phi }} \right) - \Gamma \left( {\frac{\gamma }{\phi },\gamma } \right)} \right]^{ - 1}}$ | (10) |
鉴于在众多的Budyko曲线形式中,式(9)为具有数学物理意义的解析表达式[21],对降水、蒸发能力和实际蒸发之间的函数关系描述如下:
| $\frac{E}{{{E_0}}} = 1 + \frac{P}{{{E_0}}} - {\left[ {1 + {{\left( {\frac{P}{{{E_0}}}} \right)}^\omega }} \right]^{1/\omega }}$ | (11) |
式中,ω为经验参数,与土地利用类型有关。
根据式(11)和(1)可得,基于式(9)的流域尺度水热平衡模型可用于径流量的模拟和预估[22]:
| $R = {E_0}\left\{ {{{\left[ {1 + {{\left( {\frac{P}{{{E_0}}}} \right)}^\omega }} \right]}^{{1 / \omega }}} - 1} \right\}$ | (12) |
式中,参数ω可通过给定时段的径流R、降水P和蒸发能力E0数据率定得到。
模型效果的评价选用决定系数R2、Nash−Sutcliffe效率系数NSE和相对误差RE这3个指标,具体计算式为:
| ${R^2} = \frac{{{{\left[ {\displaystyle\sum\limits_{t = 1}^N {\left( {{q_{\rm obs}}\left( t \right) - {{\overline q_{\rm obs}}} } \right)\left( {{q_{\rm sim}}\left( t \right) - {{\overline q_{\rm sim}}} } \right)} } \right]}^2}}}{{\displaystyle\sum\limits_{t = 1}^N {{{\left( {{q_{\rm obs}}\left( t \right) - {{\overline q_{\rm obs}}} } \right)}^2}\displaystyle\sum\limits_{t = 1}^N {{{\left( {{q_{\rm sim}}\left( t \right) - {{\overline q_{\rm sim}}} } \right)}^2}} } }}$ | (13) |
| $NS\!E = 1 - \frac{{\displaystyle\sum\limits_{t = 1}^N {{{\left[ {{q_{\rm obs}}\left( t \right) - {q_{\rm sim}}\left( t \right)} \right]}^2}} }}{{\displaystyle\sum\limits_{t = 1}^N {{{\left[ {{q_{\rm obs}}\left( t \right) - {{\overline q_{\rm obs}}} } \right]}^2}} }}$ | (14) |
| $RE = \frac{{{{\overline q_{\rm sim}}} - {{\overline q_{\rm obs}}} }}{{{{\overline q_{\rm obs}}} }} \times 100 {\text%}$ | (15) |
式中,
从2个方面分析气候变化对径流的影响:1)建立假定的气候变化情景,分析径流对于气候变化的敏感性;2)利用未来气候模式输出数据,驱动水热平衡模型,预估未来气候变化对径流的影响。具体过程如下:
假设降水和气温按一定幅度变化(ΔP和ΔT),构建假定的气候变化情景,结合所构建的水热平衡模型,利用式(16)分析径流量对气候变化的敏感性:
| $\delta \left( {\Delta P,\Delta T} \right) = \frac{{f\left( {P + \Delta P,T + \Delta T} \right) - f\left( {P,T} \right)}}{{f\left( {P,T} \right)}} \times 100{\text{%}}$ | (16) |
式中:P和T分别表示降水和气温;ΔP和ΔT分别为假定的降水和气温变幅,表示径流与降水、气温的响应函数;δ(ΔP,ΔT)表示径流对气候变化的敏感性。研究将1961—1990年作为基准期,基于此,假定降水变化为30%、20%、10%、0、–10%、–20%,气温变化为3、2、1、0、–1、–2和–3 ℃[24]。
为消除气候模式模拟系统偏差对未来径流预估带来的影响,采用气候模式模拟的降水和气温驱动水热平衡模型,利用模拟径流的相对变化表征径流未来演变趋势。其中:基准期同上,为1961—1990年;未来预估时段取2020—2050年。
3 结果分析 3.1 流域尺度水热平衡模型效果评价采用1956—2013年抚河流域径流深对模型进行率定和验证。其中,1956—2000年为模型参数率定期,2001—2013年为模型验证期。率定得到的参数ω取值为2.756,率定期和验证期内NSE大于0.65,R2大于0.7,RE不超过7%(图3和表1)。模拟结果表明应用流域尺度水热平衡模型进行抚河流域地表径流深模拟可行,适用于后续抚河流域地表径流深的预估。
 |
| 图3 抚河流域地表径流深模拟值与实测值对比 Fig. 3 Observation and simulation of surface runoff depth in Fu River basin |
| 表1 流域尺度水热平衡模型模拟效果评价结果 Tab. 1 Performance of the hydrological model based on water-energy balance |
 |
3.2 抚河流域地表径流深演变对气候因子的敏感性分析
利用1961—2010年抚河流域月均气温数据Tm和逐月潜在蒸散发数据ET0,建立Tm与ET0之间的统计关系。经计算统计发现,气温和潜在蒸散发近似符合指数关系,如图4所示。
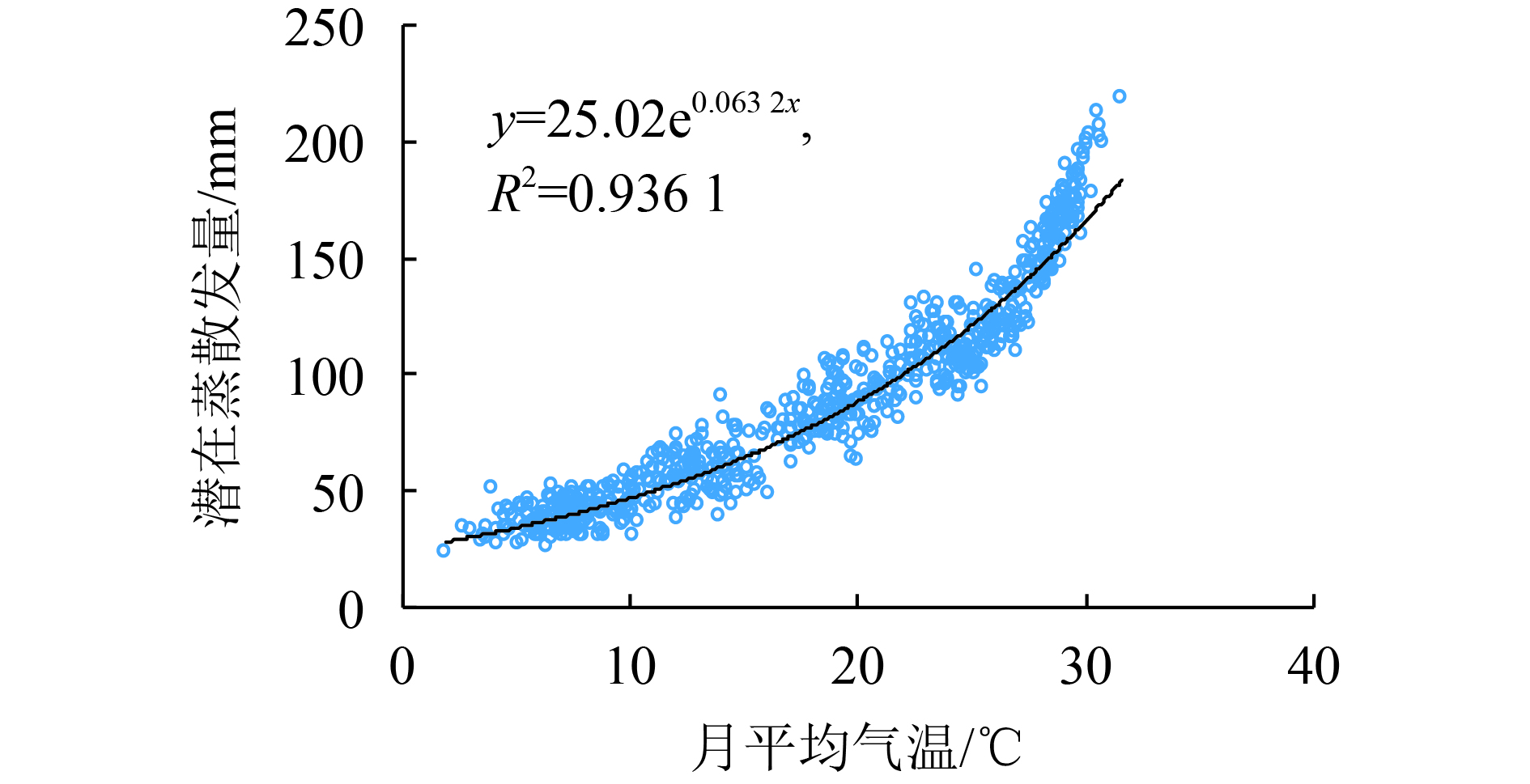 |
| 图4 气温–潜在蒸散发量关系 Fig. 4 Relationship between temperature and potential evapotranspiration |
根据所设置的假定气候变化情景,基于气温和潜在蒸散发统计关系,可得到不同情景下的潜在蒸散发量;进一步结合所构建的抚河流域水热平衡模型,可模拟得到各种气候情景下抚河流域地表径流深,按照式(16)得到降水和气温变化对地表径流深的影响(图5):1)在降水量一定的条件下,气温每升高1.0 ℃,地表径流深减少3.6%~6.3%,即27.8~49.3 mm。其中:降水量增加30%的情景下,温度每变化1 ℃,径流变化幅度最大;降水量减少30%的情景下,温度每变化1 ℃,径流变化幅度最小。主要是因为在暖湿条件下,区域实际蒸发量较大,因而在降水一定的条件下,径流对气温更为敏感。2)在气温一定的条件下,降水每增加1%,地表径流深增加1.7%~1.9%,即13.0~15.1 mm。
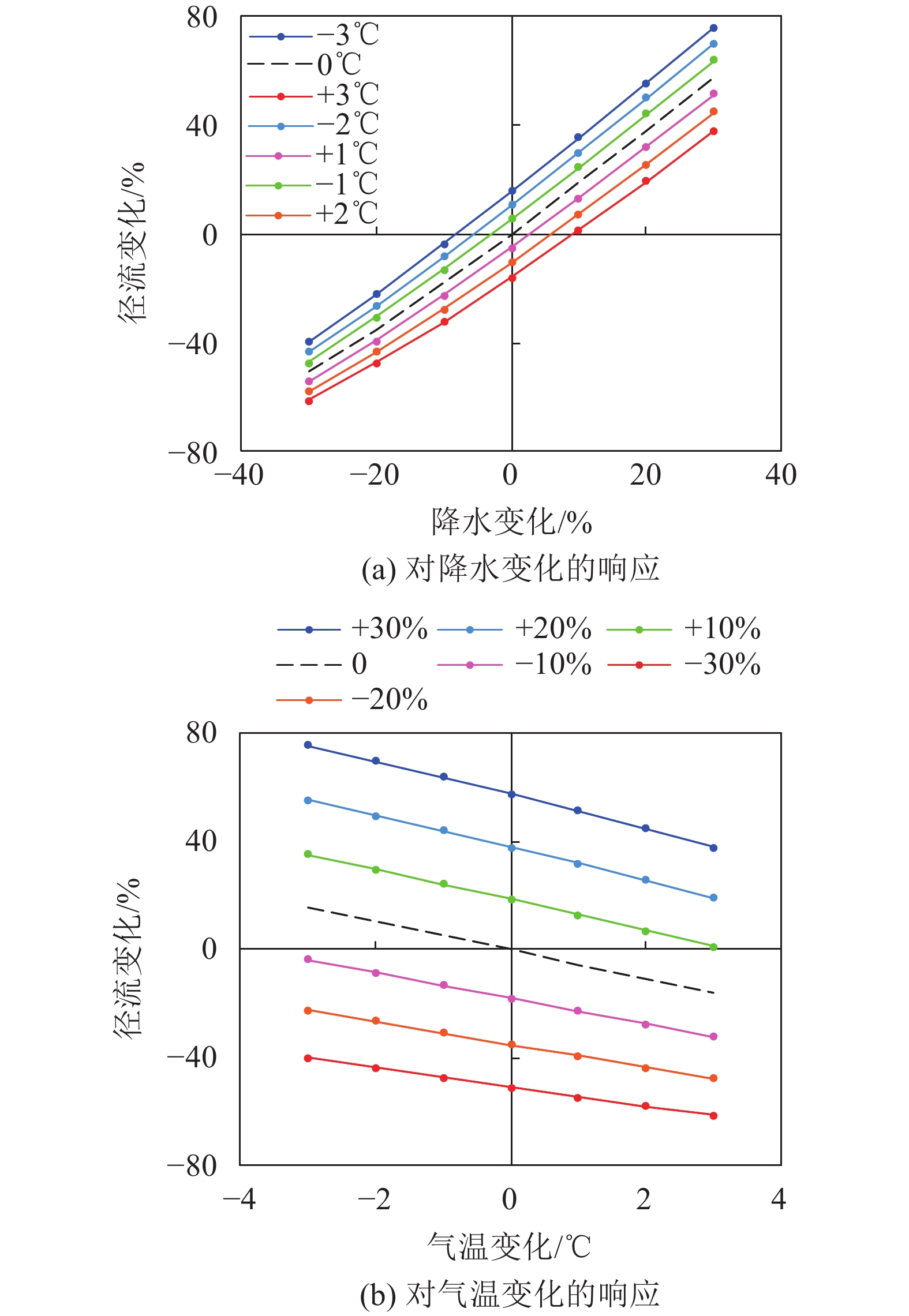 |
| 图5 抚河流域地表径流深对降水和气温变化的响应 Fig. 5 Relationship between runoff depth and precipitation/temperature of Fu River basin |
Chiew[25]的研究表明,一般情况下,流域径流系数越大,对气候变化越不敏感。研究区多年平均降水量和地表径流深分别为1 790.0和771.6 mm,其径流系数为0.43,依据Chiew的研究成果,抚河流域对于气候变化并不敏感。基于水热平衡模型的分析结果与之较为一致。
3.3 气候变化下抚河流域地表径流深演变预估图6和7为1961—2050年抚河流域气温和年降水年际变化过程。基于图6、7,得到2020—2050年抚河流域气温,降水和地表径流相对于基准期的变化,如图8所示。如未来气温的变化具有明显的一致性,在RCP2.6、RCP4.5和RCP8.5下,变化期(2020—2050年)多年平均气温相对于基准期(1961—1990年)分别增加了1.1~2.3、1.1~1.9和1.5~2.6 ℃(图8(a))。未来降水的变化存在一定的不确定性,变化期多年平均降水相对于基准期变化了–5.4%~13.8%(RCP2.6)、–3.3%~10.2%(RCP4.5)和–7.7%~5.6%(RCP8.5)。其中:GFDL-ESM2M、HadGEM2-ES和NorESM1-M模式降水增加,变化期降水量分别增加了5.3%~13.8%、0.3%~5.6%和1.7%~5.2%;IPSL-CM5A-LR和MIROC-ESM-CHEM模式降水减少,变化期降水量分别减少了2.1%~4.3%和3.3%~7.7%。可以看出,除GFDL-ESM2M模式外,其他模式预估的未来降水变化均较小(图8(b))。
 |
| 图6 1961—2050年抚河流域气温变化过程 Fig. 6 Temperature of Fu River basin from 1961 to 2050 |
 |
| 图7 1961—2050年抚河流域降水变化过程 Fig. 7 Precipitation of Fu River basin from 1961 to 2050 |
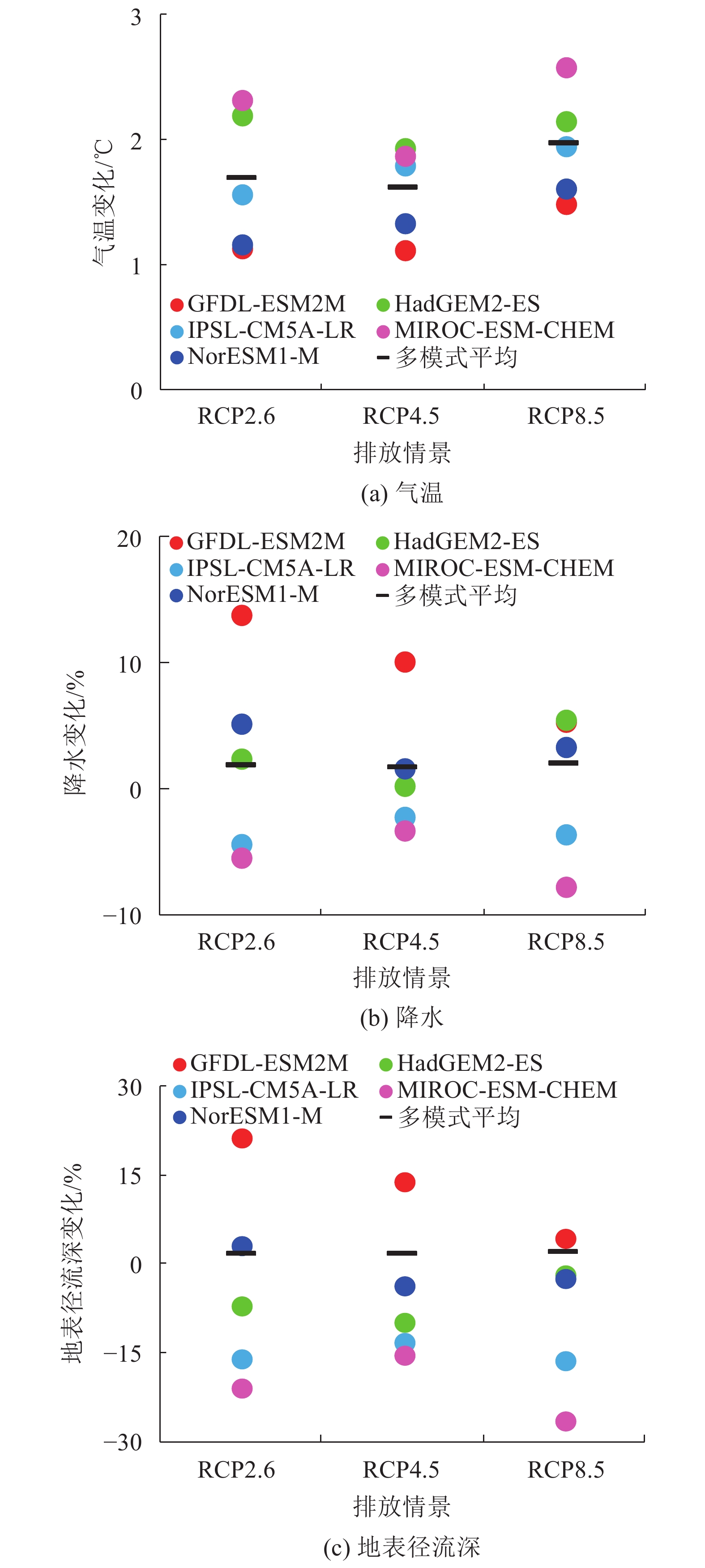 |
| 图8 2020—2050年抚河流域气温、降水和地表径流相对于基准期的变化 Fig. 8 Change of temperature, precipitation and runoff depth compared to the baseline |
图9为1961—2050年期间抚河流域地表径流深年际变化过程。由于模式之间存在差异,因此未来径流变化存在一定的不确定性,但所选取的3×5=15种情景中,有11种情景预估未来地表径流深呈减少态势。结合图8,预估地表径流深呈增加趋势的模式主要为GFDL-ESM2M,在RCP2.6、RCP4.5和RCP8.5情景下,变化期地表径流深分别增加21.5%、13.9%和4.5%;其次为NorESM1-M,在RCP2.6情景下,变化期地表径流深增加3.3%。其余气候变化情景下,地表径流深均呈减少态势,变化期地表径流深减少1.8%~26.5%,不同模式和情景下存在一定的差异。其中,IPSL-CM5A-LR和MIROC-ESM-CHEM模式地表径流减少趋势较明显,分别为13.1%~16.1%和15.3%~26.5%。多模式集合平均结果表明:未来地表径流深在RCP2.6、RCP4.5和RCP8.5情景下,分别减少3.8%、5.3%和8.5%;若不考虑与其余4种模式差别较大的GFDL-ESM2M,未来地表径流深将减少10.1%(RCP2.6)、10.5%(RCP4.5)和11.7%(RCP8.5)。王乐等[26]在赣江流域的研究成果表明:2020年代和2050年代年径流量均比近期减少约2%~8%,同本研究类似,亦得出了径流减少的结果,但由于所选研究区的地理位置和气候模式的差异,减少幅度并不相同。
 |
| 图9 1961—2050年抚河流域地表径流深变化过程 Fig. 9 Runoff depth of Fu River basin from 1961 to 2050 |
4 结 论
构建了抚河流域水热平衡模型,并结合5套气候模式预估了RCP2.6、RCP4.5和RCP8.5这3种情景下抚河流域地表径流深未来变化趋势。结果表明:
1)所构建的抚河流域水热平衡模型对年尺度径流模拟效果较好,率定期和验证期内,决定系数R2和Nash−Sutcliffe效率系数NSE均大于0.69,模型相对误差RE不超过7%,可用于分析未来气候变化对抚河流域地表径流的影响。且与其他分布式水文模型相比,本文模型参数少,计算简单,在大尺度水文模拟和预测中,具有一定的优势。
2)地表径流深对气候变化的响应幅度与流域干湿状况有关。抚河流域径流系数为0.43,属于较湿润地区,因此对气候变化敏感性相对较低;气温每升高1.0 ℃,地表径流深减少3.6%~6.3%;降水每增加1%,地表径流深增加1.7%~1.9%。
3)气候模式预估结果表明:未来抚河流域表现出增温的特点,2020—2050年多年平均气温相对于1961—1990年增加1.1~2.6 ℃;降水的变化表现出较大的不确定性,2020—2050年多年平均降水量相对于1961—1990年变化–7.7%~13.8%。在这种背景下,抚河流域地表径流深呈一定的减少态势,其主要原因在于:预估时段内,降水变化幅度相对较小,对地表径流的影响程度相对较小;气温增幅相对较大,对地表径流的影响程度相对较大。除GFDL-ESM2M模式外,其余各模式对地表径流的预估较为一致,若不考虑与其余4种模式差别较大的GFDL-ESM2M,未来地表径流深将减少10%~11%。
未来气候预测模式较多,然而限于资料条件,本研究仅选择了其中部分模式,而对未来地表径流深演变预估均是建立在模式数据的基础之上,故所得结果的合理性和正确性受到所选模式的预测精度和合理性的直接影响,采用不同未来气候模式,可能得到不同结论。
| [1] |
IPCC.Working Group I Contribution to the IPCC Fifth Assessment report,Climate change 2013:The physical science basis:Summary for policymakers[M].New York:Cambridge University Press,2013.
|
| [2] |
Zhang Liping,Chen Xiaofeng,Zhao Zhipeng,et al. Progress in study of climate change impacts on hydrology and water resource[J]. Advances in Earth Science, 2010, 27(3): 60-67. [张利平,陈小凤,赵志鹏,等. 气候变化对水文水资源影响的研究进展[J]. 地理科学进展, 2010, 27(3): 60-67.] |
| [3] |
Narsimlu B,Gosain A K,Chahar B R. Assessment of future climate change impacts on water resources of upper sind river basin,India using SWAT model[J]. Water Resources Management, 2013, 27(10): 3647-3662. DOI:10.1007/s11269-013-0371-7 |
| [4] |
Liquete C,Arnau P,Canals M,et al. Mediterranean river systems of Andalusia,southern Spain,and associated deltas:A source to sink approach[J]. Marine Geology, 2005, 222/223: 471-495. DOI:10.1016/j.margeo.2005.06.033 |
| [5] |
Thompson J R,Green A J,Kingston D G,et al. Assessment of uncertainty in river flow projections for the Mekong River using multiple GCMs and hydrological models[J]. Journal of Hydrology, 2013, 486: 1-30. DOI:10.1016/j.jhydrol.2013.01.029 |
| [6] |
Qiao Juan,Zhang Qiang,Zhang Jie. Preliminary summary on parameterization of heterogeneous land surface process and remote sensing technology research[J]. Arid Meteorology, 2008, 26(1): 73-77. [乔娟,张强,张杰. 非均匀下垫面陆面过程参数化问题研究进展[J]. 干旱气象, 2008, 26(1): 73-77. DOI:10.3969/j.issn.1006-7639.2008.01.014] |
| [7] |
Xu Zongxue,Cheng Lei. Progress on studies and applications of the distributed hydrological models[J]. Journal of Hydraulic Engineering, 2010, 41(9): 1009-1017. [徐宗学,程磊. 分布式水文模型研究与应用进展[J]. 水利学报, 2010, 41(9): 1009-1017.] |
| [8] |
Deng Xiaoyu,Zhang Qiang,Chen Xiaohong. Assessment of impacts of climate change and human activities on runoff with HSPF for the Fuhe River basin[J]. Journal of Wuhan University (Natural Science Edition), 2015, 61(3): 262-270. [邓晓宇,张强,陈晓宏. 气候变化和人类活动综合影响下的抚河流域径流模拟研究[J]. 武汉大学学报(理学版), 2015, 61(3): 262-270.] |
| [9] |
Xiao Juncang,Luo Dinggui,Wang Zhongzhong. Soil erosion simulation in Fuhe basin based on SWAT model[J]. Research of Soil and Water Conservation, 2013, 20(1): 14-18. [肖军仓,罗定贵,王忠忠. 基于 SWAT 模型的抚河流域土壤侵蚀模拟[J]. 水土保持研究, 2013, 20(1): 14-18.] |
| [10] |
Piani C,Weedon G P,Best M,et al. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models[J]. Journal of Hydrology, 2010, 395(3/4): 199-215. |
| [11] |
Hagemann S,Chen C,Haerter J O,et al. Impact of a statistical bias correction on the projected hydrological changes obtained from three GCMs and two hydrology models[J]. Journal of Hydrometeorology, 2011, 12(4): 556-578. DOI:10.1175/2011JHM1336.1 |
| [12] |
Warszawski L,Frieler K,Huber V,et al. The inter-sectoral impact model intercomparison project (ISI-MIP):Project framework[J]. Proceedings of the National Academy of Sciences, 2014, 111(9): 3228-3232. DOI:10.1073/pnas.1312330110 |
| [13] |
Schreiber P. Über die Beziehungen zwischen dem Niederschlag und der Wasserführung der Flüsse in Mitteleuropa[J]. Zeitschrift für Meteorologie, 1904, 21(10): 441-452. |
| [14] |
Ol’Dekop E M. On evaporation from the surface of river basins[J]. Transactions on Meteorological Observations, 1911, 4: 200. |
| [15] |
Turc L.Le bilan d’eau des sols:Relations entre les précipitations,l’évaporation et l’écoulement[D].Paris:Institute National de la Recherche Agronomique,1953.
|
| [16] |
Pike J G. The estimation of annual run-off from meteorological data in a tropical climate[J]. Journal of Hydrology, 1964, 2(2): 116-123. DOI:10.1016/0022-1694(64)90022-8 |
| [17] |
Budyko M I.Climate and life[M].New York:AcademicPress, 1974.
|
| [18] |
Fu Baopu. On the calculation of the evaporation from land surface[J]. Scientia Atmospherica Sinica, 1981, 5(1): 23-31. [傅抱璞. 论陆面蒸发的计算[J]. 大气科学, 1981, 5(1): 23-31. DOI:10.3878/j.issn.1006-9895.1981.01.03] |
| [19] |
Zhang L,Hickel K,Dawes W R,et al. A rational function approach for estimating mean annual evapotranspiration[J]. Water Resources Research, 2004, 40: W02502. |
| [20] |
Porporato A,Daly E,Rodriguez-Iturbe I. Soil water balance and ecosystem response to climate change[J]. The American Naturalist, 2004, 164(5): 625-632. DOI:10.1086/424970 |
| [21] |
Sun Fubao.Study on watershed evapotranspiration based on the Budyko hypothesis[D].Beijing:Tsinghua University,2007. 孙福宝.基于Budyko水热平衡平衡假设的流域蒸散发研究[D].北京:清华大学,2007. |
| [22] |
Yuan Z,Yan D,Yang Z,et al. Projection of surface water resources in the context of climate change in typical regions of China[J]. Hydrological Sciences Journal, 2017, 62(2): 283-293. DOI:10.1080/02626667.2016.1222531 |
| [23] |
Kumar S,Merwade V. Impact of watershed subdivision and soil data resolution on SWAT model calibration and parameter uncertainty[J]. Journal of the American Water Resources Association, 2009, 45(5): 1179-1196. DOI:10.1111/jawr.2009.45.issue-5 |
| [24] |
Wang Guoqing,Zhang Jianyun,Liu Jiufu,et al. The sensitivity of runoff to climate change in different climatic regions in China[J]. Advances in Water Science, 2011, 22(3): 307-314. [王国庆,张建云,刘九夫,等. 中国不同气候区河川径流对气候变化的敏感性[J]. 水科学进展, 2011, 22(3): 307-314.] |
| [25] |
Chiew F H S. Estimation of rainfall elasticity of streamflow in Australia[J]. Hydrological Sciences Journal, 2006, 51: 613-625. DOI:10.1623/hysj.51.4.613 |
| [26] |
Wang Le,Guo Shenglian,Hong Xingjun,et al. Simulation and prediction of future precipitation and runoff change in the Ganjiang basin[J]. Journal of Water Resources Research, 2014, 3(6): 522-531. [王乐,郭生练,洪兴骏,等. 赣江流域未来降雨径流变化模拟预测[J]. 水资源研究, 2014, 3(6): 522-531.] |
 2019, Vol. 51
2019, Vol. 51


