近年来,随着航空航天、武器装备等尖端领域的发展,行星滚柱丝杠(planetary roller screw,PRS)由于承载能力大、传动精度高、额定寿命长、结构体积小、运转噪声低等优点受到了广泛关注。反向式行星滚柱丝杠(inverted planetary roller screw,IPRS)作为PRS的一种变种,因其可将螺母作为电机转子实现电机和直线传动机构融合设计的特点,在要求空间紧凑的机电伺服系统中得到了越来越多的应用[1–2]。
图1所示为反向式行星滚柱丝杠的基本结构,A、B、C、D、E分别为螺母、滚柱、丝杠、滚柱保持架和弹性挡圈。通常情况下,该机构由螺母旋转作为主动输入,丝杠直线运动作为被动输出。螺母旋转时,滚柱既绕着螺母轴线公转,又绕着自身轴线自转。丝杠及滚柱两端加工直齿以保证滚柱与丝杠轴线平行;滚柱丝杠圆周均匀分布,由滚柱保持架约束其相对位置;为了保证滚柱与丝杠无轴向相对位移,丝杠及螺母头数与结构参数具有独特的匹配关系[3–4]。
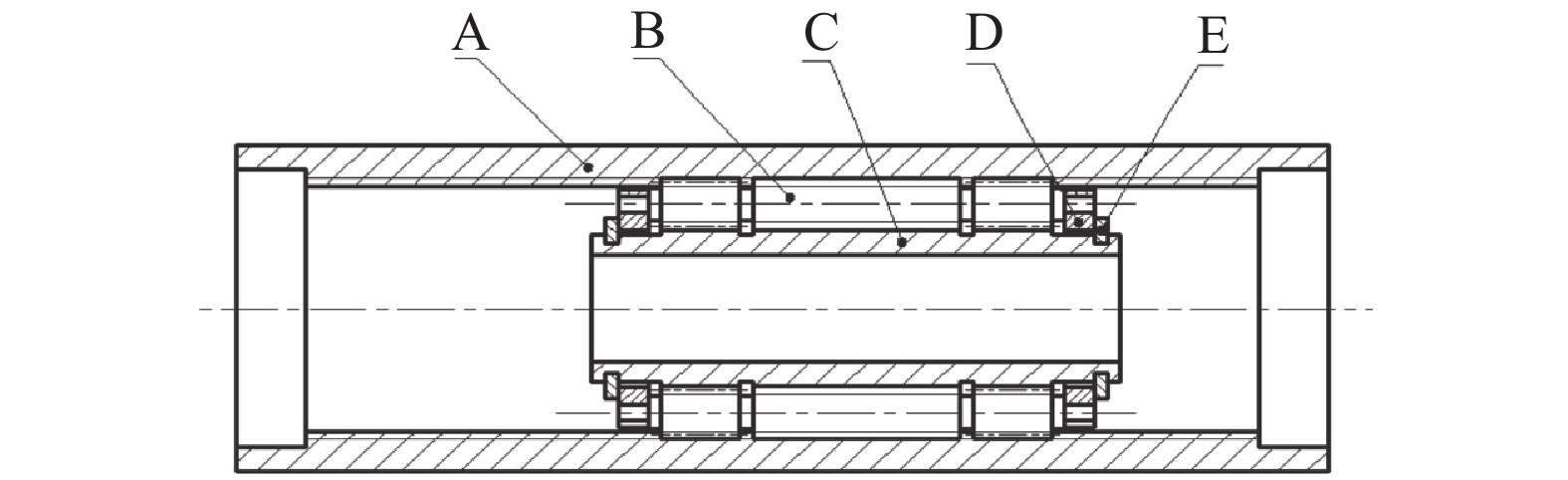 |
| 图1 IPRS基本结构 Fig. 1 Basic structure of IPRS |
由于IPRS滚柱上所有螺纹同时参与啮合,接触点多,在承受轴向载荷时会产生载荷分布不均的问题。当IPRS载荷分布不均现象严重时,会导致其传动精度及使用寿命大大降低,故深入研究该机构的承载分布特性是必要的。靳谦忠等[5]基于滚珠丝杠载荷分布的计算方法将PRS滚柱分解为多个滚珠建立了PRS载荷分布的模型,存在较大误差。杨家军等[6]基于等效圆理论将滚柱啮合曲面近似为球面建立了PRS载荷分布及刚度模型。但该模型沿用的将接触曲面近似为球面的方法并不能得出接触变形的准确值。并且该理论假设在半个节距的标定长度内滚柱受丝杠和螺母的法向压力相等,该假设仅在PRS机构承载端相同时近似成立。故该理论不能真实反映PRS机构内部的载荷分布情况。Jones等[7]利用直接刚度法得出了PRS的载荷分布及承载端变形的计算模型,但由于该方法将赫兹变形进行了线性化的近似处理,与赫兹变形的非线性特性并不符合,故该模型的精度还有待提高。
近些年,随着对PRS啮合机理研究的深入,Jones等[8]及付晓军等[9]基于啮合曲面的连续相切接触条件,得出了PRS啮合点位置的计算模型。该模型对精确计算PRS赫兹接触变形提供了依据。
相对于承载特性及啮合特性研究的深入,目前针对PRS使用寿命及可靠性的研究还鲜见报道。已有模型基于滚珠丝杠寿命公式得出工程计算模型[2],该模型并无足够的理论支持其正确性。
作者以IPRS为研究对象,建立了赫兹变形精确解的求解模型,IPRS的载荷分布及刚度模型以及IPRS寿命的评估模型。基于以上模型对IPRS进行了分析,为IPRS结构理论计算及优化设计提供了依据。
1 赫兹变形以各组件轴心为z轴、丝杠轴心到滚柱轴心方向为r轴建立圆柱坐标系,则各组件的牙型轮廓如图2所示。其中,
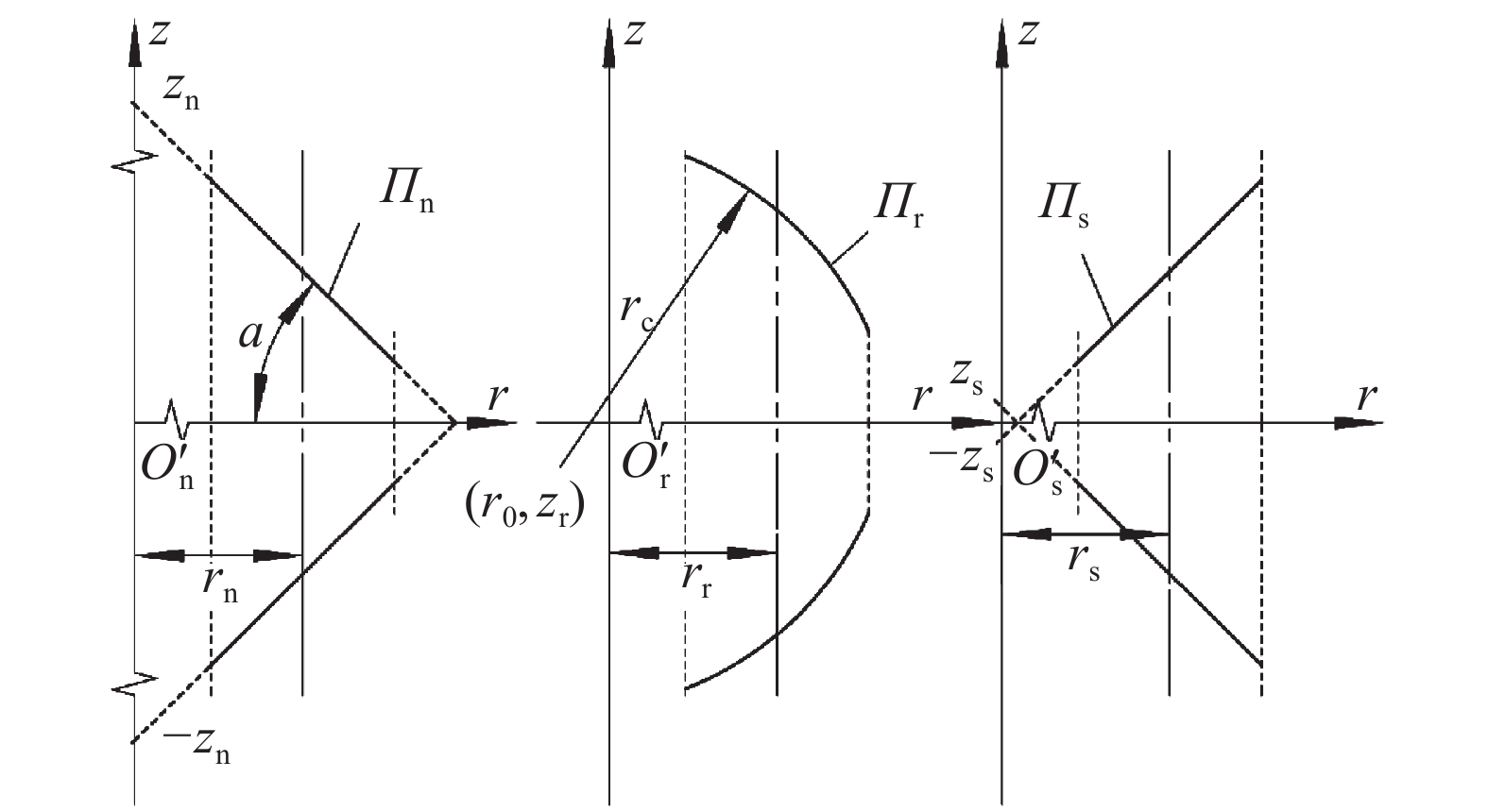 |
| 图2 丝杠、滚柱和螺母螺纹的牙型轮廓 Fig. 2 Thread profile of screw, roller and nut |
| $ \begin{aligned}[b] {{{\varPi }}_{\rm{n}}}\left( {\theta ,r} \right)= &\left\{ { r\cos\; \theta ,\;r\sin\; \theta ,} \right.\\ &\left. {\theta {r_{\rm{n}}}\tan\; {\beta _{\rm{n}}} \mp \left( {{{\textit{z}}_{\rm{n}}} - r\tan\; a} \right)} \right\} \end{aligned} $ | (1) |
| $ \begin{aligned}[b] {{{\varPi }}_{\rm{r}}}\left( {\theta ,r} \right) = & \left\{ { r\cos\; \theta ,\;r\sin\; \theta ,\;\; } \right.\\ &\pm \left( {{{\textit{z}}_{\rm{r}}} + \sqrt {r_{\rm{c}}^2 - {{\left( {r - {r_0}} \right)}^2}} } \right) -\theta {r_{\rm{r}}}\tan\; {\beta _{\rm{r}}}\} \end{aligned} $ | (2) |
| $ \begin{array}{l} {{{\varPi }}_{\rm{s}}}\left( {\theta ,r} \right) = \left\{ { r\cos\; \theta ,\;r\sin\; \theta ,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left. {\theta {r_{\rm{s}}}\tan\; {\beta _{\rm{s}}} \pm \left( {{{\textit{z}}_{\rm{s}}} - r\tan\; a} \right)} \right\} \end{array} $ | (3) |
用
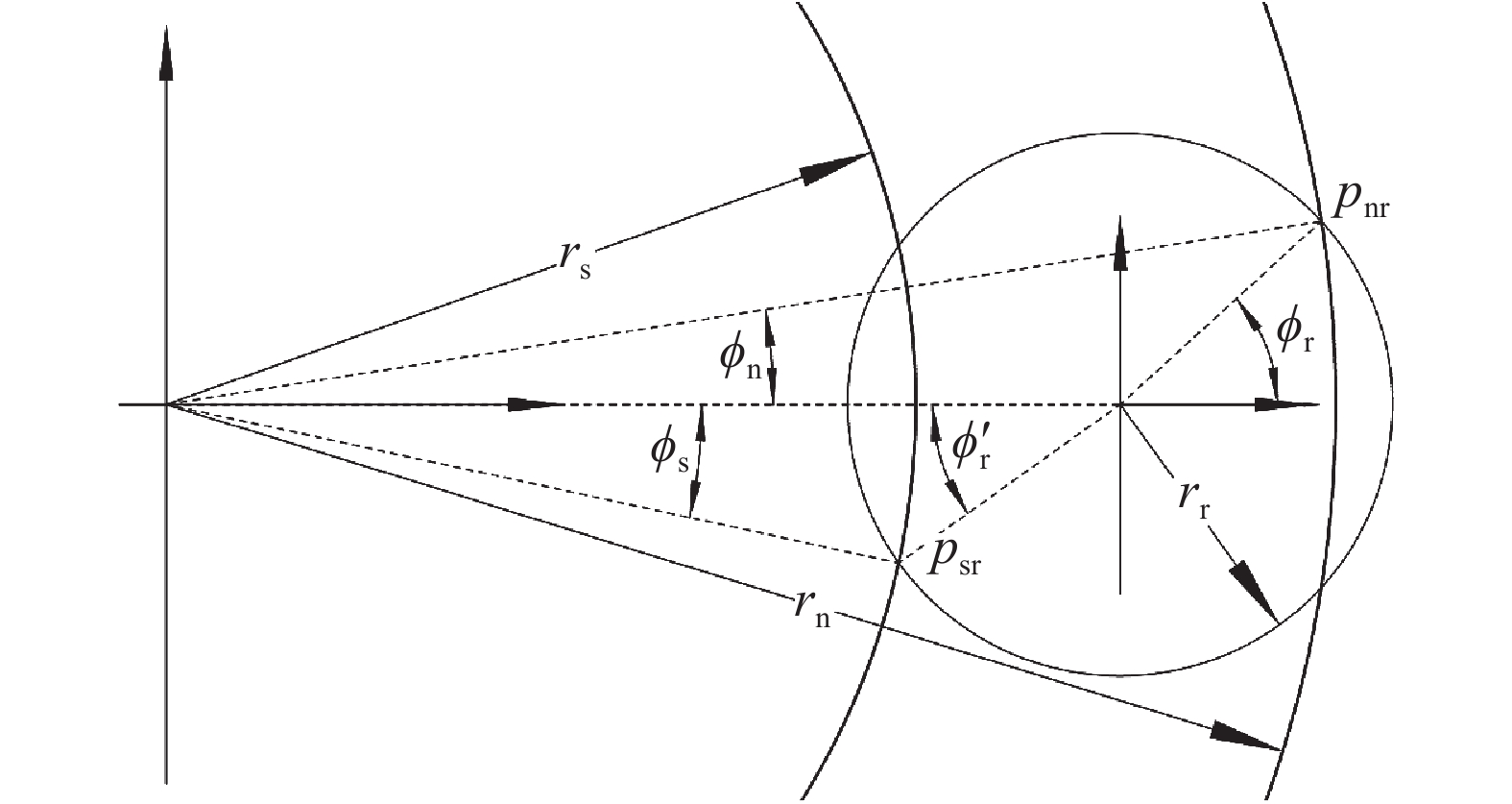 |
| 图3 接触点相对位置示意 Fig. 3 Relative position of contact point |
| $ {\phi _{\rm{n}}} = {{\rm arc}\sin ^{ }}\frac{{{r_{\rm{r}}}\left( {\sin \;{\beta _{\rm{r}}} + \sin \;{\beta _{\rm{n}}}} \right)}}{{{r_{\rm{n}}} - {r_{\rm{r}}}}} $ | (4) |
| $ {\phi _{\rm{r}}} = {{\rm arc}\sin ^{ }}\frac{{{r_{\rm{n}}}\left( {\sin\; {\beta _{\rm{r}}} + \sin \;{\beta _{\rm{n}}}} \right)}}{{{r_{\rm{n}}} - {r_{\rm{r}}}}} $ | (5) |
| $ {\phi _{\rm{s}}} = {{\rm arc}\sin ^{ }}\frac{{{r_{\rm{r}}}\left( {\sin\; {\beta _{\rm{r}}} - \sin\; {\beta _{\rm{s}}}} \right)}}{{{r_{\rm{s}}} + {r_{\rm{r}}}}} $ | (6) |
| $ {\phi '_{\rm{r}}} = {{\rm arc}\sin ^{ }}\frac{{{r_{\rm{s}}}\left( {\sin \;{\beta _{\rm{r}}} - \sin \;{\beta _{\rm{s}}}} \right)}}{{{r_{\rm{s}}} + {r_{\rm{r}}}}} $ | (7) |
对于机构中任一接触曲面,其在啮合点处的曲面主方向
| $ {\left( {{\rm d}{{\varPi }}} \right)_1} {\left( {{\rm d}{{\varPi }}} \right)_2} = \frac{{\partial {{\varPi }}}}{{\partial \theta }}{\rm d}\theta + \frac{{\partial {{\varPi }}}}{{\partial r}}{\rm d}r $ | (8) |
式中,
| $\begin{aligned} & {\rm{d}}\theta /{\rm{d}}r = \\ & \frac{{[ - \left( {EN - GL} \right) \pm \sqrt {{{\left( {EN - GL} \right)}^2} - 4\left( {EM - FL} \right)\left( {FN - GM} \right)} ]}}{{2\left( {EM - FL} \right)}}\end{aligned}$ | (9) |
式中:
接触点的主曲率:
| $ {\rho _1} 、{\rho _2} = H \pm \sqrt {{H^2} - K} $ | (10) |
式中,H和K分别指曲面的平均曲率和高斯曲率,表示如下:
| $ K = \frac{{LN - {M^2}}}{{EG - {F^2}}} $ | (11) |
| $ H = \frac{{LG - 2MF + NE}}{{2\left( {EG - {F^2}} \right)}} $ | (12) |
基于Hertz接触理论,假设接触区域为椭圆。引入主曲率函数[10]:
| $f\left( \rho \right) \!=\! \frac{{\sqrt {{{\left( {{\rho _1} \!-\! {\rho _2}} \right)}^2} \!+\! {{\left( {\rho '\!\!{_1} \!-\! \rho '\!\!{_2}} \right)}^2} \!+\! 2\left( {{\rho _1} \!-\! {\rho _2}} \right)\left( {\rho '\!\!{_1} \!-\! \rho '\!\!{_2}} \right)\cos \; \omega } }}{{\displaystyle\sum \rho \!=\! \left[ {\left( {2 - {e^2}} \right)L\left( e \right) - 2\left( {1 - {e^2}} \right)K\left( e \right)} \right]/\left[ {{e^2}L\left( e \right)} \right]}}$ | (13) |
式中:
| $\delta \left( {{N_{\rm n}}} \right) \!=\! \left( {1 \!-\! {\nu ^2}} \right)K\left( e \right){\left( {\sum \rho } \right)^{\left( {1/3} \right)}}{{N_{\rm n}^{\left( {2/3} \right)}} \Big/ {\left[ {{\text{π}} {m_{\rm a}}EE_0^{\left( {1/3} \right)}} \right]}} \!\!\!\!\!\!\!$ | (14) |
式中:
螺母机构通常由轴承两端固定,当丝杠承受压力或拉力时,作用在螺母上的平衡力既可能与拉力或压力同侧,又可能与之异侧。将机构的两种承载情况简称为同侧承载与异侧承载。考虑单滚柱简化模型,并作如下假设:1)滚柱和丝杠端齿轮不承受轴向力,2)滚柱丝杠侧和滚柱螺母侧的螺纹接触对数目相等,3)接触角在承载条件下保持恒定,4)相邻螺母侧啮合点与丝杠侧啮合点在滚柱轴向上的距离为滚柱节距的一半。
图4为IPRS螺纹啮合段变形状态。
 |
| 图4 IPRS螺纹啮合段变形状态 Fig. 4 IPRS deformation conditions of thread meshing section |
图4中:下标
将丝杠和滚柱近似作为实心圆柱,将螺母近似为空心圆柱,考虑各组件在整个长度上的承载状态,求得轴段轴向变形的表达式如下:
| ${l_{{\rm {n}}i}} = 4pn\cos\; a\cos\; {\beta _{\rm{r}}} \div \left\{\left[ {{\text{π}} \left( {D_0^2 - d_{{\rm{ne}}}^2} \right){E_{\rm{n}}}} \right]\sum\limits_{j = i + 1}^m {{N\!\!_j}}\right\} $ | (15) |
| ${l_{{\rm{rn}}i}} = 2p\cos \;a\cos \;{\beta _{\rm{r}}} \div \left\{ {\left( {{\text{π}} d_{{\rm{re}}}^2{E_{\rm{r}}}} \right)\left[ {2\sum\limits_{j = 1}^i {\left( {N{\!\!_j} - N'{\!\!\!_j}} \right)} + {N_i}^\prime } \right]} \right\}$ | (16) |
| ${l_{{\rm{rs}}i}} = 2p\cos \;a\cos \;{\beta _{\rm{r}}} \div \left\{ {\left( {\text{π} d_{{\rm{re}}}^2{E_{\rm{r}}}} \right)\left[ {2\sum\limits_{j = 1}^i {\left( {N{\!\!_j} - N'{\!\!\!_j}} \right)} + {N_{{i + 1} }}} \right]} \right\} $ | (17) |
| $ {l_{{\rm{s}}i}}\left| {_{{\text{异侧承载}}}} \right. = 4pn\cos\; a\cos\; {\beta _{\rm{r}}} \div \left\{ {\left( {\text{π} d_{{\rm{se}}}^2{E_{\rm{s}}}} \right)\sum\limits_{j = 1}^i {N'{\!\!\!_j}} } \right\} $ | (18) |
| ${l_{{\rm{s}}i}}\left| {_{{\text{同侧承载}}}} \right. = 4pn\cos\; a\cos\; {\beta _{\rm{r}}} \div \left\{ {\left( {\text{π} d_{{\rm{se}}}^2{E_{\rm{s}}}} \right)\sum\limits_{j = i + 1}^m {N'{\!\!\!_j}} } \right\} $ | (19) |
式中,
IPRS螺牙变形指各组件螺牙受到法向载荷时由于弯矩、剪切、根部倾斜、根部剪切、丝杠及滚柱径向收缩、螺母径向扩大等因素而产生的变形。该变形与所受法向载荷呈线性关系,计算方式见文献[11]。
由轴段轴向变形、赫兹变形和螺牙变形的几何关系得:
| $ \begin{aligned}[b] & {l_{{\rm{n}}i}} - {\delta _{{\rm{n}}i}} - {\varepsilon _{{\rm{n}}i}} + {\delta _{{\rm{n}}\left( {i + 1} \right)}} + {\varepsilon _{{\rm{n}}\left( {i + 1} \right)}}=\\ & \quad {l_{{\rm{r}}i}} + {\delta _{{\rm{r}}i}} + {\varepsilon _{{\rm{r}}i}} - {\delta _{{\rm{r}}\left( {i + 1} \right)}} - {\varepsilon _{{\rm{r}}\left( {i + 1} \right)}} \end{aligned} $ | (20) |
| $ \begin{aligned}[b] &{{l'}\!\!_{{\rm{r}}i}} - {{\delta '}\!\!_{{\rm{r}}i}} - {{\varepsilon '}\!\!_{{\rm{r}}i}} + {{\delta '}\!\!_{{\rm{r}}\left( {i + 1} \right)}} + {{\varepsilon '}\!\!_{{\rm{r}}\left( {i + 1} \right)}}=\\ & \quad{l_{{\rm{s}}i}} + {\delta _{{\rm{s}}i}} + {\varepsilon _{{\rm{s}}i}} - {\delta _{{\rm{s}}\left( {i + 1} \right)}} + {\varepsilon _{{\rm{s}}\left( {i + 1} \right)}} \end{aligned} $ | (21) |
螺纹牙法向载荷与总轴向载荷之间的关系:
| $ F = n\sum\limits_{i = 1}^m {{N_i}\cos\; a\cos\; {\beta _{\rm{s}}}}= n\sum\limits_{i = 1}^m {{{N'}\!\!_i}\cos\; a\cos\; {\beta _{\rm{s}}}} $ | (22) |
IPRS的载荷分布可由式(20)~(22)联立求得。以
| $ \begin{aligned}[b] \varDelta = & \sum\limits_{i = 1}^{m - 1} {{l_{{\rm{r}}i}}} + {\delta _{{\rm{nm}}}} + {\delta _{{\rm{sm}}}} + {\delta _{{\rm{rm}}}} + {{\delta '}\!\!_{{\rm{rm}}}} +\\ & {\varepsilon _{{\rm{nm}}}} + {\varepsilon _{{\rm{sm}}}} + {\varepsilon _{{\rm{rm}}}} + {{\varepsilon '}\!\!_{{\rm{rm}}}} \end{aligned} $ | (23) |
| $ \begin{aligned}[b] \varDelta ' = & \; {\delta _{{\rm{nm}}}} + {\delta _{{\rm{sm}}}} + {\delta _{{\rm{rm}}}} + {{\delta '}\!\!_{{\rm{rm}}}} + \quad \\ & {\varepsilon _{{\rm{nm}}}} + {\varepsilon _{{\rm{sm}}}} + {\varepsilon _{{\rm{rm}}}} + {{\varepsilon '}\!\!_{{\rm{rm}}}} \end{aligned} $ | (24) |
IPRS的失效形式分为3种:偶然失效,磨损失效及疲劳失效[2]。在润滑良好的情况下,接触表面疲劳失效是机构失效的主要原因[12]。从断裂力学的角度来看,表面疲劳破坏通常经历裂纹萌生和裂纹拓展两个阶段。通常裂纹的萌生寿命是构成接触面全寿命的主要部分[13]。为了建立IPRS接触疲劳寿命的计算模型,有以下假设:1)IPRS机构在稳定运转时,螺纹牙间载荷分布与静压力下的分布相同;2)IPRS机构裂纹扩展寿命在全寿命中很小,在寿命预测时可忽略不计;3)接触椭圆长半轴位于滚道法平面上。
基于Lundberg–Palmgren方程,接触表面疲劳预测寿命表示如下[14]:
| $M = A\sqrt[f]{{ - {{\textit{z}}_0^h}\left( {\frac{{{\rm ln}\left( S \right)}}{{V{\tau _0^c}}}} \right)}}\quad $ | (25) |
式中:
| $ V = 4a{{\textit{z}}_0}\left( {{\text{π}} r\sec\; \beta } \right) \quad $ | (26) |
| $ {{\textit{z}}_0} = \frac{b}{{\left( {t + 1} \right)\sqrt {2t - 1} }} \quad$ | (27) |
| $ {\tau _0} = \frac{{3{N_{\rm{n}}}\sqrt {2t - 1} }}{{4{\text{π}} abt\left( {t + 1} \right)}}\quad $ | (28) |
式中:
| $ a = {m_a}{\left[ {{{3{N_{\rm{n}}}{E_0}} / {\left( {2\sum \rho } \right)}}} \right]^{{1 / 3}}} $ | (29) |
| $ b = {m_b}{\left[ {{{3{N_{\rm{n}}}{E_0}} / {\left( {2\sum \rho } \right)}}} \right]^{{1 / 3}}} $ | (30) |
| $ {m_b} = {\left\{ {{{2\sqrt {1 - {e^2}} L\left( e \right)} / {\text{π}} }} \right\}^{1/3}} $ | (31) |
基于IPRS运动原理[3],每当螺母转过一圈时,螺母、滚柱、丝杠上的接触点在对应的滚道上分别转过
| $ {\gamma _{\rm{n}}} = {{{k^2}} / {\left( {2k + 2} \right)}} \quad$ | (32) |
| $ {\gamma _{\rm{r}}} = {{\left( {k - 1} \right)\left( {k + 2} \right)} / {\left( {2k + 2} \right)}} $ | (33) |
| $ {\gamma _{\rm{s}}} = {{k\left( {k + 2} \right)} / {\left( {2k + 2} \right)}} \quad$ | (34) |
式中,
| ${S\!\!_{\rm{n}}} = \exp \left[ { - k{{\left( {{{{\gamma _{\rm{n}}}M} / A}} \right)}^f}\sum {{V_{{\rm{n}}i}}} \times }{{{{\tau _{{\rm{n}}i}}\!\!\!\!^c} / {{{\textit{z}}_{{\rm{n}}i}}\!\!\!\!^h}}} \right]$ | (35) |
| $ \begin{aligned}[b] {S\!_{\rm{r}}} = & \exp \left[ { - {{\left( {{\gamma _{\rm{r}}}{M / A}} \right)}^f}\left( {\sum {{V_{{\rm{r}}i}}} \times } \right.} \right.\\ & \left. \displaystyle{\left. {{{{\tau _{{\rm{r}}i}}\!\!\!\!^c} / {{{\textit{z}}_{{\rm{r}}i}}\!\!\!\!^h}} + \sum {{{V'}\!\!\!_{{\rm{r}}i}}} {{{{\tau '}\!\!_{{\rm{r}}i}}\!\!^c} / {{{{\textit{z}}'}\!\!_{{\rm{r}}i}}\!\!^h}}} \right)} \right] \end{aligned} $ | (36) |
| ${S\!_{\rm{s}}} = \exp \left[ { - k{{\left( {{{{\gamma _{\rm{s}}}M} / A}} \right)}^f}\sum {{V_{{\rm{s}}i}}} \times }{{{{\tau _{{\rm{s}}i}}\!\!\!^c} / {{{\textit{z}}_{{\rm{s}}i}}\!\!\!^h}}} \right]$ | (37) |
式中:
| $\begin{aligned}[b] M' = & A\left[ {n\gamma _{\rm{n}}^f\sum {\left( {{{{V_{{\rm{n}}i}}\tau _{{\rm{n}}i}^c} / {{\textit{z}}_{{\rm{n}}i}^h}}} \right)} } \right. + n\gamma _{\rm{s}}^f \times \\ & \sum {\left( {{{{V_{{\rm{s}}i}}\tau _{{\rm{s}}i}^c} / {{\textit{z}}_{{\rm{s}}i}^h}}} \right)} + \gamma _{\rm{r}}^f\sum {\left( {{{{V_{{\rm{r}}i}}\tau _{{\rm{r}}i}^c} / {{\textit{z}}_{{\rm{r}}i}^h}}} \right)} + \\ & {\left. {{\gamma '}\!\! _{\rm{r}}\!\!^{f}\sum {\left( {{{{{V'}\!\!\!_{{\rm{r}}i}}{\tau '} \!\!_{{\rm{r}}i}\!\!^{c}} / {{{\textit{z}}'}\!\!_{{\rm{r}}i}\!\!^{h}}}} \right)} } \right]^{{{ - 1} / f}}}{\left[ { - \ln \left( S \right)} \right]^{{1 / f}}} \end{aligned}$ | (38) |
对丝杠节径为21 mm,头数为3,导程为5 mm,螺母外径为80 mm,滚柱个数为11,接触角为45°的IPRS的承载端轴向变形进行数值计算,得出其轴向变形曲线,并与文献[15]实验数据进行对比,如图5所示。由于IPRS的制造误差和定位误差,在轴向载荷较低时,并非所有滚柱均承载,故实验数据在该范围内增长较快。经过对比:基于本文理论得出的轴向变形与实验结果之间的误差在机构不承受预紧力时小于20%,在机构承受不小于5 kN预紧力时小于10%。
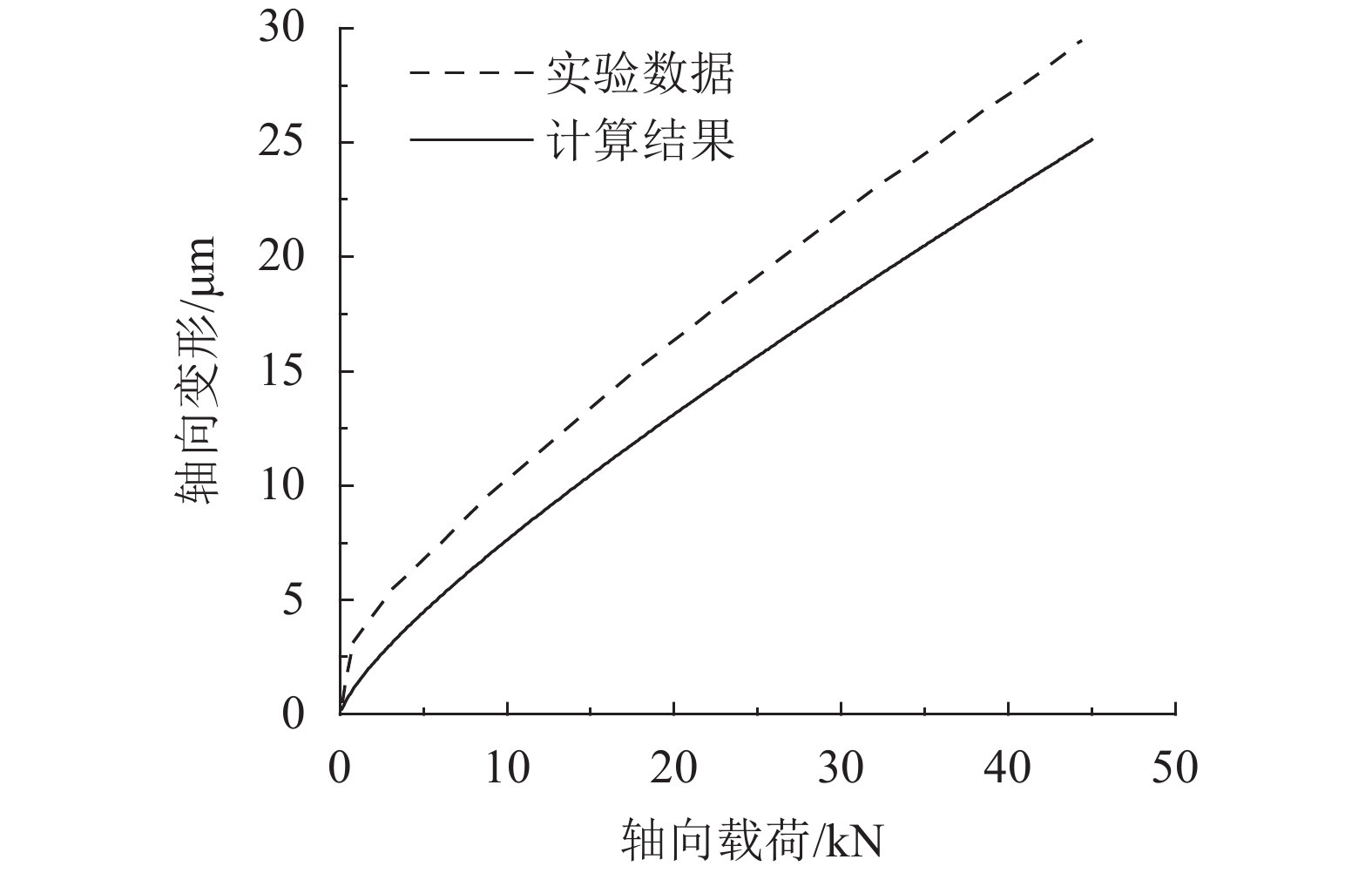 |
| 图5 承载端轴向变形 Fig. 5 Axial deformation between working sides |
4.2 结构参数对偏载率的影响
图6为异侧承载条件下各参数的改变对偏载率的影响。从图6可知:偏载率受螺牙数目、滚柱数目和螺旋角的影响显著,且偏载率随之增加而增大;与此同时,较小的牙型半径和较大的螺母外径对降低机构的偏载率也有一定作用。
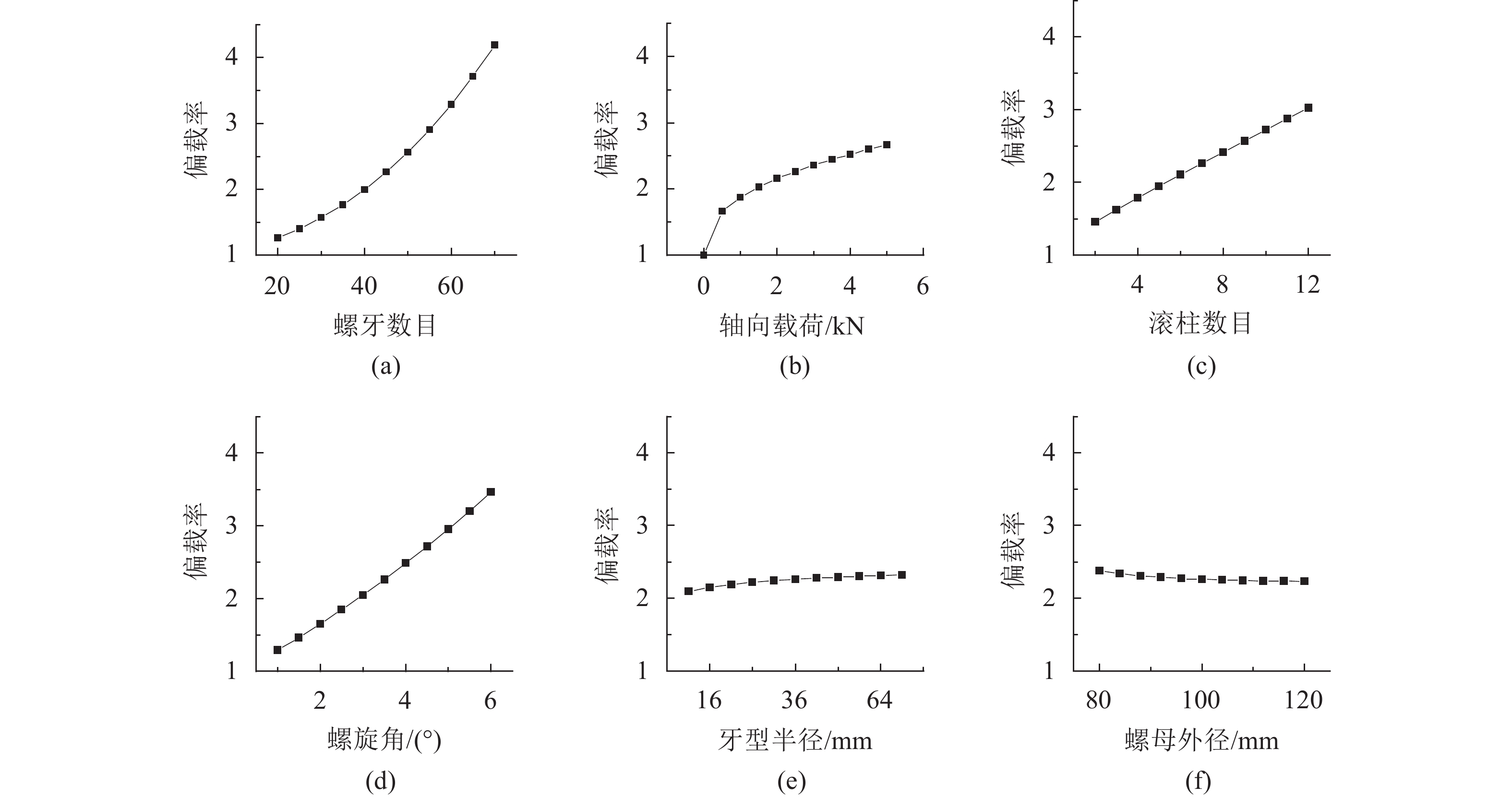 |
| 图6 各参数对偏载率的影响 Fig. 6 Influence of various parameters on load distribution rate |
4.3 承载形式对载荷分布的影响
根据载荷分布模型,分别计算某型号IPRS在异侧承载及同侧承载条件下的载荷分布。为了量化载荷分布,引入偏载率
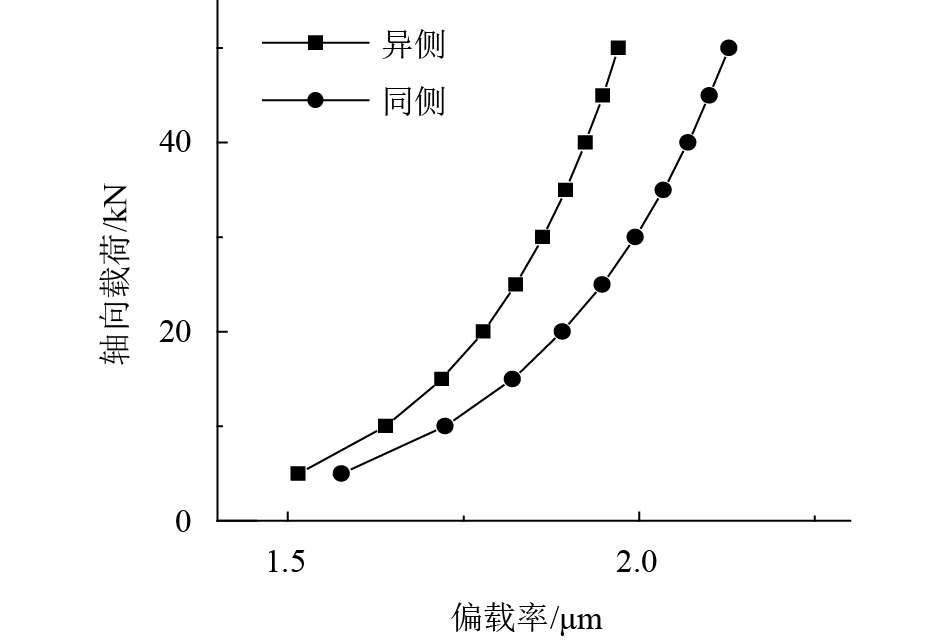 |
| 图7 承载形式对偏载率的影响 Fig. 7 Influence of loading forms on eccentric load ratio |
4.4 结构参数对轴向变形的影响
图8为异侧承载条件下结构参数对轴向变形的影响。从图8可知,IPRS机构刚度随着滚柱数目的影响最为显著。由于IPRS机构通常对刚度及承载能力要求较高,故滚柱数目一般都取满足可安装性的最大值。此外,适当的螺牙数目、螺旋角及较大的螺母外径对提高机构刚度有益。
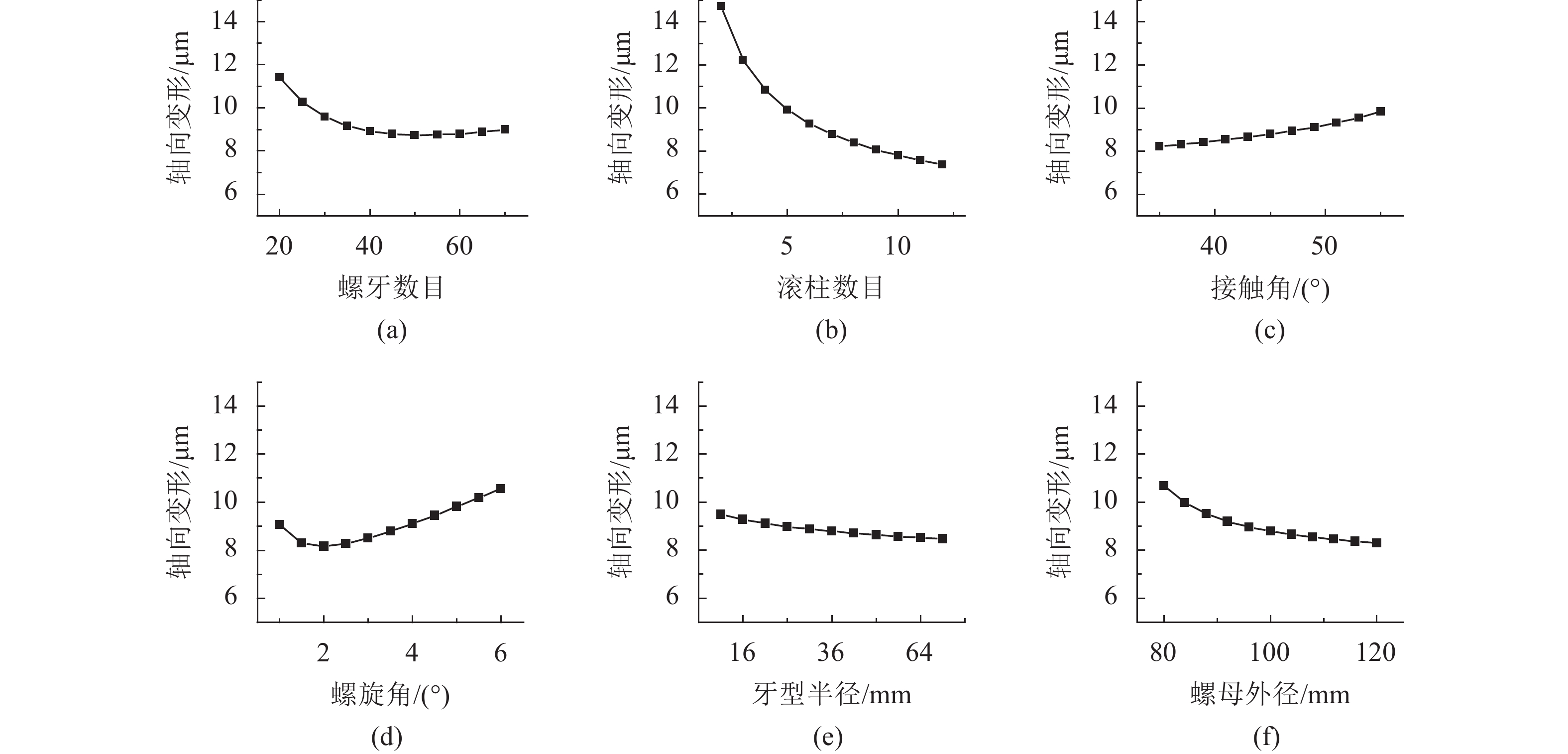 |
| 图8 各参数对轴向变形的影响 Fig. 8 Influence of various parameters on axial deformation |
4.5 结构参数对接触疲劳寿命的影响
图9为异侧承载时各参数对机构疲劳寿命的影响。为了消去实验常数
 |
| 图9 各参数对接触疲劳寿命的影响 Fig. 9 Influence of various parameters on contact fatigue life |
为了进一步研究接触疲劳失效的形式,提取出机构可靠性为0.9时,丝杠、螺母的可靠性及所有滚柱的总可靠性如图10所示。从图10可知,IPRS的接触疲劳破坏主要发生在滚柱上,其次发生在丝杠上。
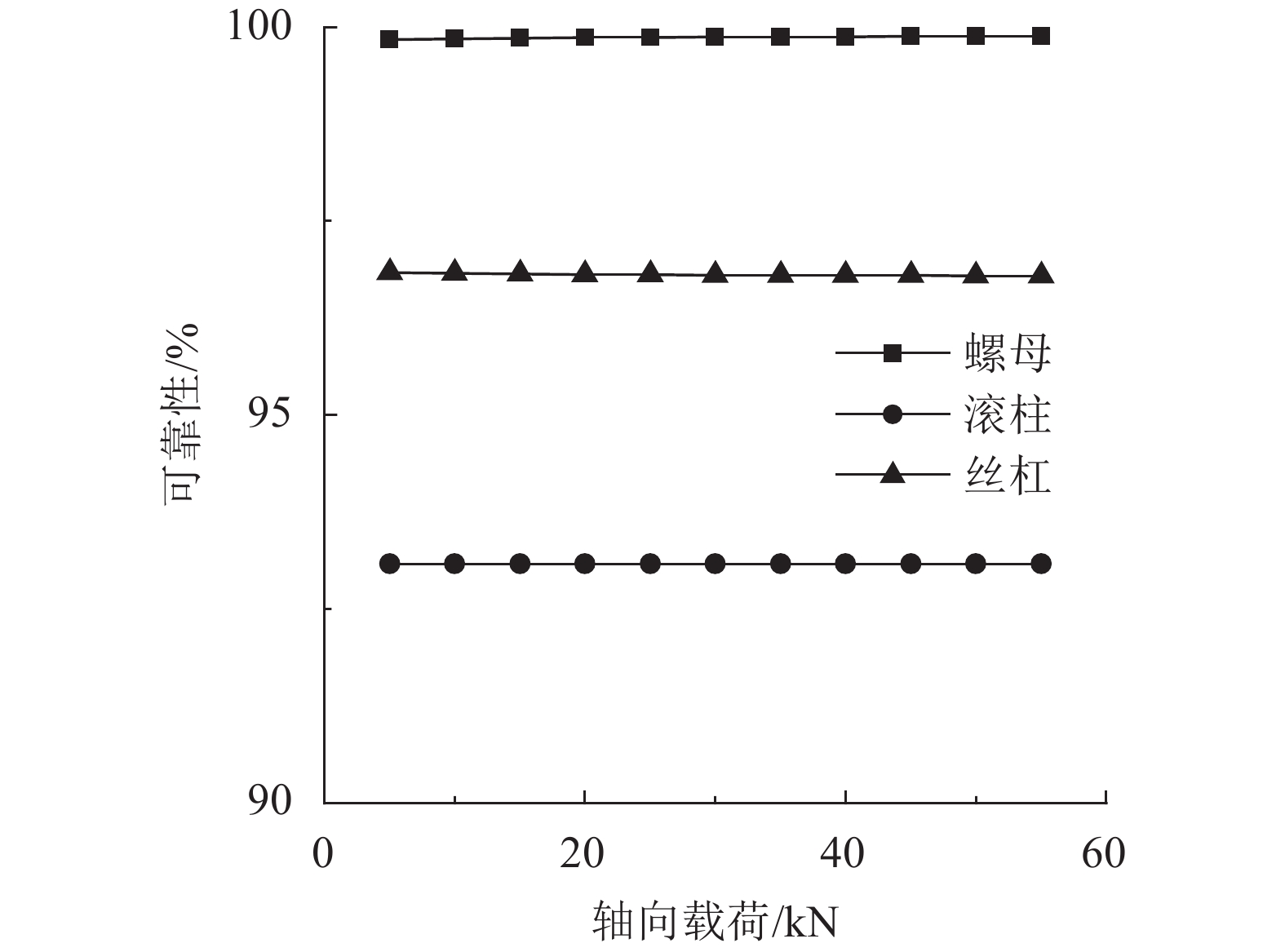 |
| 图10 丝杠、螺母及所有滚柱的可靠性 Fig. 10 Reliability of the screw, nut and all rollers |
5 结 论
对IPRS的载荷分布及寿命开展研究,建立了IPRS载荷分布及寿命模型,为IPRS理论计算及优化设计提供了依据。研究了IPRS机构载荷分布特性,刚度特性和疲劳寿命的影响因素,得到以下主要结论:1)由于牙数增大,分配给每个螺牙的载荷减小。故:虽然螺牙数目的增加导致偏载率变大,但较多的牙数对机构刚度及寿命有益。2)滚柱数目增大能显著提高机构轴向刚度及疲劳寿命。3)在螺牙数目不变的条件下,适当的螺旋角有利于减小轴向变形。
| [1] |
Liu Geng,Ma Shangjun,Tong Ruiting,et al. New development and key technology of planetary roller screw[J]. Journal of Mechanical Transmission, 2012(5): 103-108. [刘更,马尚君,佟瑞庭,等. 行星滚柱丝杠副的新发展及关键技术[J]. 机械传动, 2012(5): 103-108. DOI:10.3969/j.issn.1004-2539.2012.05.031] |
| [2] |
Lemor P C.The roller screw,an efficient and reliable mechanical component of electro-mechanical actuators[C]//Energy Conversion Engineering Conference.New York:IEEE,2002.
|
| [3] |
Dang Jinliang,Liu Geng,Ma Shangjun. Motion principle and simulation analysis of inverted planetary roller screw mechanism[J]. Journal of System Simulation, 2013, 25(7): 1646-1651. [党金良,刘更,马尚君,等. 反向式行星滚柱丝杠机构运动原理及仿真分析[J]. 系统仿真学报, 2013, 25(7): 1646-1651.] |
| [4] |
Ma Shangjun,Liu Geng,Tong Ruiting,et al. Kinematic analysis of an inverted planetary roller screw considering roller pitch circle mismatch[J]. China Mechanical Engineering, 2014, 25(11): 1421-1426. [马尚君,刘更,佟瑞庭,等. 考虑滚柱节圆偏移的反向式行星滚柱丝杠副运动学分析[J]. 中国机械工程, 2014, 25(11): 1421-1426. DOI:10.3969/j.issn.1004-132X.2014.11.001] |
| [5] |
Jin Qianzhong,Yang Jiajun,Sun Jianli. A comparative study of static stiffness between ball screw and planetary roller screw[J]. Mechanical Science and Technology for Aerospace Engineering, 1999(2): 230-232. [靳谦忠,杨家军,孙健利. 滚珠丝杠副和行星式滚柱丝杠副静刚度的比较研究[J]. 机械科学与技术, 1999(2): 230-232. DOI:10.3321/j.issn:1003-8728.1999.02.019] |
| [6] |
Yang Jiajun,Wei Zhenxing,Zhu Jisheng,et al. Calculation of load distribution of planetary roller screws and static rigidity[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011(4): 1-4. [杨家军,韦振兴,朱继生,等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报(自然科学版), 2011(4): 1-4.] |
| [7] |
Jones M H,Steven A V. Stiffness of the roller screw mechanism by the direct method[J]. Mechanics Based Design of Structures & Machines, 2014, 42(1): 17-34. |
| [8] |
Jones M H,Velinsky S A.Contact kinematics in the roller screw mechanism[C]//Proceedings of ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.Chicag:ASME 2013:451–459.
|
| [9] |
Fu Xiaojun,Liu Geng,Ma Shangjun,et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2016, 52(3): 26-33. [付晓军,刘更,马尚君,等. 行星滚柱丝杠副螺旋曲面啮合机理研究[J]. 机械工程学报, 2016, 52(3): 26-33.] |
| [10] |
万长森.滚动轴承的分析方法[M].北京:机械工业出版社,1987.
|
| [11] |
山本晃,郭可谦.螺纹联接的理论与计算[M].上海:上海科学技术文献出版社,1984.
|
| [12] |
Aurégan G,Fridrici V,Kapsa P,et al. Experimental simulation of rolling–sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332: 1176-1184. DOI:10.1016/j.wear.2015.01.047 |
| [13] |
Zhao Guoping,Dong Huili,Wang Chunming,et al. Whole fatigue life of helical gear covering crack initiation stage and propagation process[J]. Tribology, 2016, 36(5): 643-649. [赵国平,董辉立,王春明,等. 斜齿轮疲劳裂纹萌生及扩展过程全寿命研究[J]. 摩擦学学报, 2016, 36(5): 643-649.] |
| [14] |
Harris T A,Yu W K. Lundberg–Palmgren fatigue theory:Considerations of failure stress and stressed volume[J]. Journal of Tribology, 1999, 121(1): 85-89. DOI:10.1115/1.2833815 |
| [15] |
Abevi F K,Daidie A,Chaussumier M,et al. Static analysis of an inverted planetary roller screw mechanism[J]. Journal of Mechanisms & Robotics, 2016, 8(4): 56-61. |
 2019, Vol. 51
2019, Vol. 51


