2. 北京市水土保持工程技术研究中心,北京 100083
2. Beijing Eng. Research Center of Soil and Water Conservation, Beijing Forestry Univ., Beijing 100083, China
水流流经柱体时,受压力梯度作用在近柱体端减速并向床面流动继而回流,逆向射流与来流相互作用会在柱体基部前端产生涡旋[1],涡旋具有较大的剪切力致使柱体基部产生局部冲刷、侵蚀[2],该涡旋的运动形状似马蹄形,因而称之为马蹄涡[3]。浅薄层低雷诺数水流绕流圆柱体模型常见于河岸消落带、侵蚀沟、坡面漫流下水流绕植被运动,对该水流条件下柱体前端马蹄涡的研究可为相应工程科学布设防冲措施、测算侵蚀提供科学依据。
由于马蹄涡对实际工程的重要性,早在1989年Dargahi[4]利用氢气泡显示技术开展了柱体前端马蹄涡的研究,并提出了水流经过柱体前端时马蹄涡的发生发展过程,其发展由开始阶段的5个涡旋变成稳定阶段的3个涡旋,并对前端流速、压力系数等进行了测量。随着测量手段及计算技术的大幅提升,研究者们对马蹄涡进行了更加深入及细致的观测。Graf等[5]采用AVD测量了两组水流条件下上游流速特征、流动分离点及马蹄涡位置进行了测量;Ozturk等[6]使用PIV对雷诺数变化范围为750~9 600的3组试验,通过对时均流场的分析阐述马蹄涡位置、形态随柱体雷诺数变化关系;陈启刚等[7–9]使用高频PIV系统测量了6组水流条件下柱体前端来流的流速、水位及马蹄涡运动学特征。受技术限制目前对浅薄层低雷诺数(水深小于柱体直径)条件下柱体绕流的研究报道较少。Akilli等[10]采用流动显示技术测量浅层水流绕柱体流动对背水部分的涡旋特征;Fu等[11]采用PIV测量了3组水流条件下展向的水流特征,对背水部的涡街进行了详细的测量。这些浅层水流的研究尚未关注柱体前端马蹄涡的运动学特征,因此仍需要进一步的试验认识该种水流条件下马蹄涡的运动状态。
作者通过在明渠水槽中开展柱体绕流试验,控制上游来流水深在5 mm范围内,使来流水深h小于柱体直径D。通过增加PIV镜头的接圈构建一套高分辨率的PIV测量柱体前端的流场,并对大量流场进行时均,进而计算出柱体前端马蹄涡的时均特征,重点关注马蹄涡的位置、半径及强度等运动学特征,以期补充在浅薄层水流下对马蹄涡的认识。
1 试验与方法 1.1 试验系统试验于北京林业大学水土保持学院水蚀机理与过程实验室的高精度明渠水槽中开展,玻璃水槽长为12 m,宽0.3 m,深0.3 m,坡度可调范围为0~1.5%。水槽系统由供水段、试验段及集水段组成,流量的控制与测量由供水段的变频器、水泵、电磁流量计完成。水槽出水口放置有蜂窝状PVC管,以稳定水流。水槽沿程等间距分布6个超声波水位计测量水槽沿程的水位变化,并在水槽尾端设置尾门,调节尾门可以使水流达到均匀流条件。本试验采用直径D为1 cm和2 cm的黑色聚乙烯管作为柱体,该种材料柱体能够有效避免片光在柱体表面形成高光溢出从而影响图像质量,柱体高10 cm以保证圆柱高于水面。测量位置为保证来流稳定且不受出口影响,垂直粘于距水槽入口7 m处并处于横断面的中点位置。如图1所示,为观测来流特征,观测窗口的选取参照前人试验[4,7],选取前方柱体对称面(即柱体中轴的纵垂面),并定义柱体上游端点为坐标零点(图1中“O”),顺水流方向为
 |
| 图1 试验示意图 Fig. 1 Schematic diagram of experimental set-up |
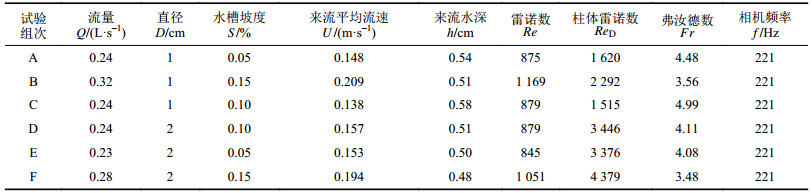
| 表1 水流条件及PIV参数 Tab. 1 Flow conditions and parameters of PIV |
 |
流场的拍摄采用高频粒子图像测速仪进行测量,本试验拍摄的水流水深为毫米量级,因此需要高分辨率的摄像系统。作者利用微距摄像技术,即增加近摄接圈,放大所测流场,构建了高分辨率粒子示踪测速技术(HR-PIV)[13],图1为本试验的装置示意图。实际图像的分辨率达63 像素/mm。HR-PIV由8W Nd:YAG半导体连续激光器和像素为640
柱体前端存在侵蚀力较强的涡旋,通常涡量按照定义进行计算为
| ${M}{\text{ = }}\left[\!\!\! {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial u}}{{\partial x}}}&{\displaystyle\frac{{\partial u}}{{\partial y}}}\\ {\displaystyle\frac{{\partial v}}{{\partial x}}}&{\displaystyle\frac{{\partial v}}{{\partial y}}} \end{array}}\!\!\!\right]$ | (1) |
| ${\lambda _{{\rm ci}}} = \left\{ {\begin{aligned} & {\sqrt {Q - \frac{{{P^2}}}{4}} }{\text{,}}{Q - \frac{{{P^2}}}{4} < 0}{\text{;}}\\ & {0,}\qquad\qquad\;\,{Q - \frac{{{P^2}}}{4} < 0} \end{aligned}} \right.$ | (2) |
式中,P、Q分别为第1不变量和第2不变量:
| $P = - \frac{{\partial u}}{{\partial x}} - \frac{{\partial v}}{{\partial y}}$ | (3) |
| $Q = \frac{{\partial u}}{{\partial x}}\frac{{\partial v}}{{\partial y}} - \frac{{\partial u}}{{\partial y}}\frac{{\partial v}}{{\partial x}}$ | (4) |
当2维流场中任意一点
由于涡结构与背景流动之间关系的复杂性,受流体黏性的影响,难以明确区分涡结构与背景流动之间的界限,因此目前尚未有统一的方法确定涡旋尺度。关于涡旋尺度的提取方法,目前的一种方法是根据涡旋特征(涡量、旋转强度)的等值线代表涡旋的尺度[5,8,18],即选取涡旋特征量的一定值作为阈值确定涡旋与背景流动间的界限,然而该方法在选取阈值时,具有主观性;另一种涡旋尺度提取方法是寻找涡旋中心至边界范围速率增加的最大点处作为涡旋与背景流动的界限[17],该方法具有一定的局限性,即流动只受涡旋的影响,而当具有其他因素(例如圆柱)影响流动时难以找到临界点。
为了提取马蹄涡的尺度,作者参照前人的研究思路[19–20],使用标准模式的涡旋与涡核附近流场进行拟合,通过拟合后的流动方程参数获得涡旋的尺度信息。在浅薄层水流绕流圆柱时,柱体前端马蹄涡受床面剪切力影响较大,因此作者选择标准Oseen涡叠加纯剪切流动模拟实际流动[8]。
根据Oseen涡在笛卡尔坐标系下的表达和与床面相交角度为
| $\begin{aligned}[b] & {u = \frac{\varGamma }{{2{\text{π}} }} \cdot \left[ {1 - \exp \left( - \frac{{{x^2} + {y^2}}}{{{R^2}}}\right)} \right] \cdot \left( - \frac{y}{{{x^2} + {y^2}}}\right)}+\\ & {\;\;\; k{{\cos }^2}\theta y - k\cos \theta \sin x} \end{aligned}$ | (5) |
| $\begin{aligned}[b] & {v = \frac{\varGamma }{{2{\text{π}} }} \cdot \left[ {1 - \exp \left( - \frac{{{x^2} + {y^2}}}{{{R^2}}}\right)} \right] \cdot \frac{x}{{{x^2} + {y^2}}}}+\\ & {\;\;\; k\sin \theta \cos \theta y - k{{\sin }^2}\theta x} \end{aligned}$ | (6) |
式(5)、(6)中,
 |
| 图2 实测流场与拟合流场对比 Fig. 2 Compared of simulated and measured fields |
2 试验结果与讨论 2.1 流动分离点
由于柱体与边界层的逆压作用,导致柱体前端的流体回流,与上游来流间形成流向流速为0的流动分离点,柱体前端的马蹄涡被限制在流动分离点下游范围,鉴于马蹄涡对床面的冲刷作用[21–22],找到流动分离点可为实际工程防冲设施的布设提供科学依据。由于流动分离点极靠近床面,采用以下方法获得流动分离点位置:根据实际所测得的流场,记录第1层测点与第2层测点
图3为无量纲化的流动分离点
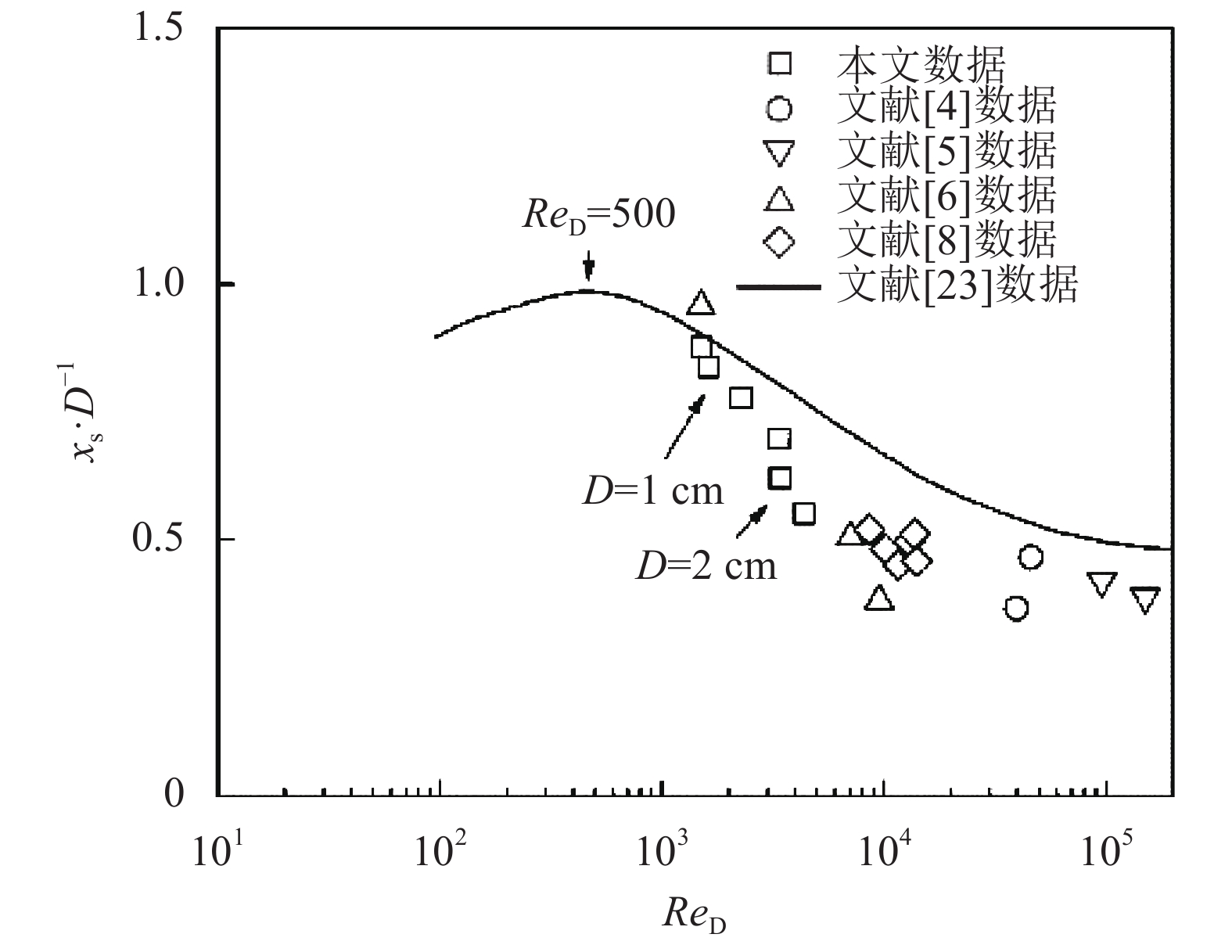 |
| 图3 流动分离点位置随柱体雷诺数变化关系 Fig. 3 Relationship between location of separation point and cylinder Reynolds number |
水深是影响流动分离点的重要因素。
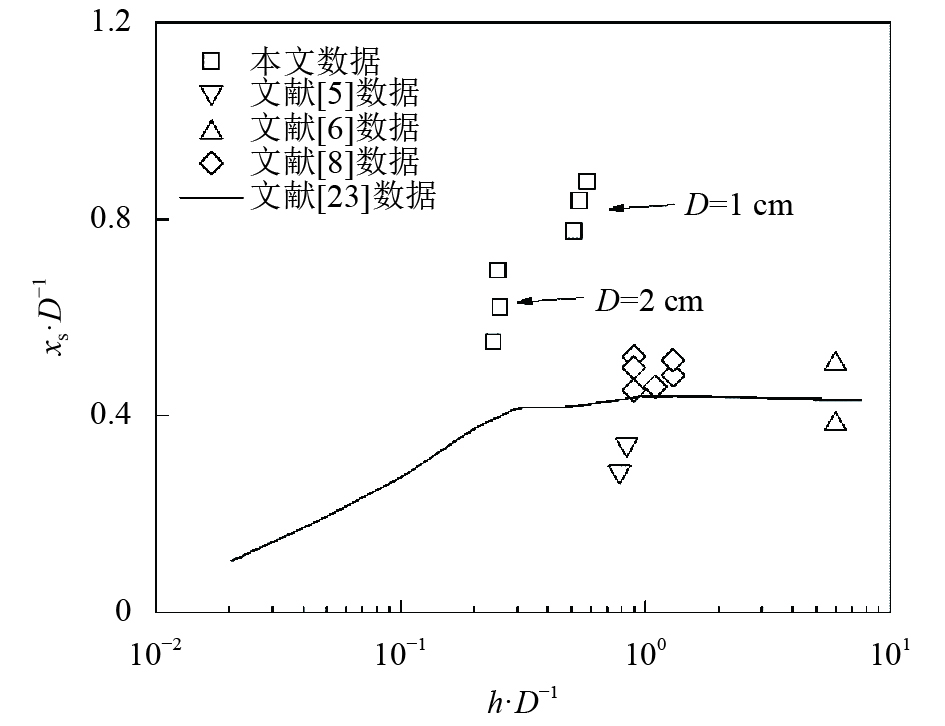 |
| 图4 流动分离点位置随水深的变化关系 Fig. 4 Relationship between location of separation point and depth |
2.2 马蹄涡的特征
通过
 |
| 图5 马蹄涡识别 Fig. 5 Horseshoe vortex system extraction |
根据旋转强度的
 |
| 图6 马蹄涡纵向及垂向位置随柱体雷诺数变化关系 Fig. 6 Relationship between location of horseshoe voretex and cylinder Reynolds number |
从马蹄涡半径与柱体雷诺数的变化关系来看(图7),次生马蹄涡V2的影响范围显著小于主马蹄涡V1的影响范围。两个涡旋的半径与其位置表现出同样的现象:当
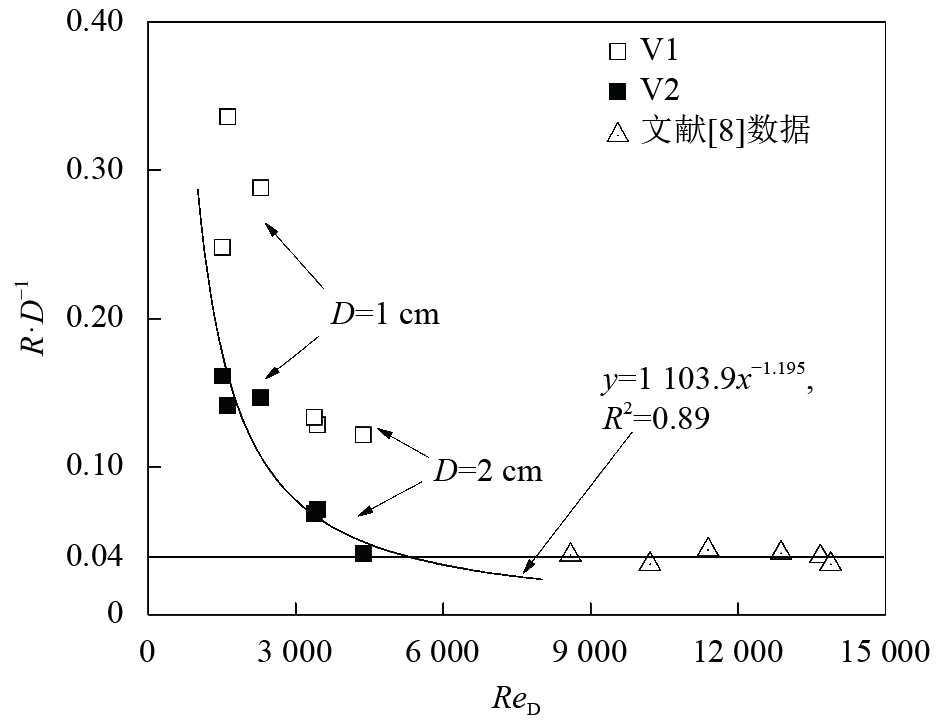 |
| 图7 马蹄涡半径随柱体雷诺数的变化关系 Fig. 7 Relationship between radius of horseshoe vortex and cylinder Reynolds number |
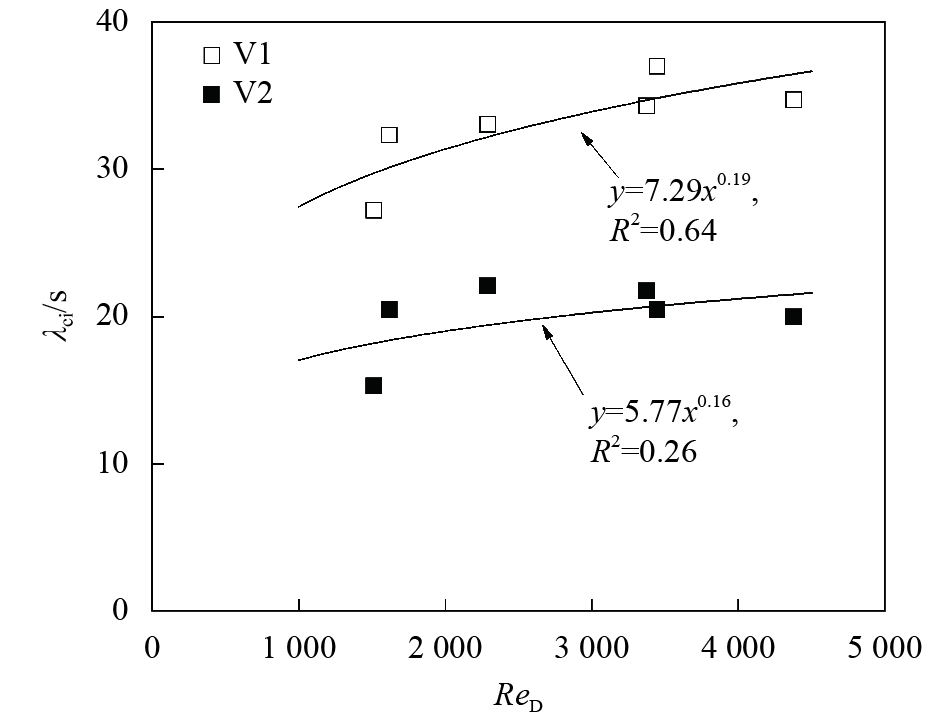 |
| 图8 旋转强度随柱体雷诺数的变化关系 Fig. 8 Relationship between swirling rate of horseshoe voretex and cylinder Reynolds |
图9为主马蹄涡V1的
 |
| 图9 主马蹄涡位置及半径随水深变化关系 Fig. 9 Relationship between both location and radius of horseshoe vortex and cylinder Reynolds number |
2.3 流动过程
水流流经圆柱体,其前端会产生冲刷床面的马蹄涡,在流动过程中该涡旋是动态变化的。参照文献[4]对马蹄涡产生的阐述,作者认为在浅薄层水流稳定后,发生如图10所示的马蹄涡模型。水流达到柱体前端时由于逆压作用,来流流速减小并在柱体前端改变方向,会产生向上流动的流体致使水面抬升,以及冲向床面的流体并向上游回流,在回流的过程中受来流的影响流速逐渐减小至0产生
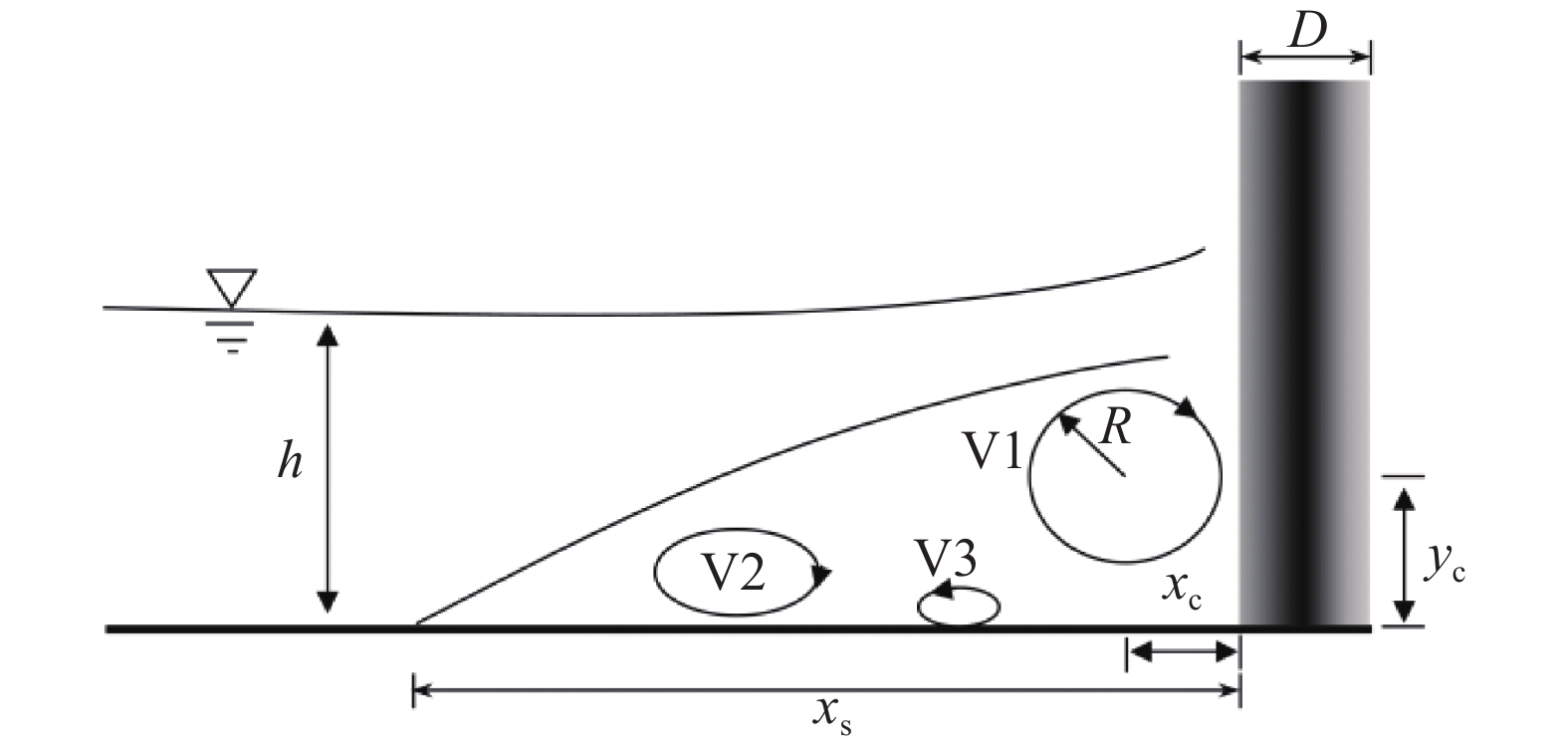 |
| 图10 柱体前端马蹄涡模型 Fig. 10 Model of horseshoe vortex |
作者从时间平均的角度分析了低柱体雷诺数条件到高柱体雷诺数下前端流动分离区、马蹄涡的位置、形状及强度的变化特征,实测点数据表明流动分离点及马蹄涡特征的变化呈现两个阶段,在
作者在明渠水槽中开展浅薄层水流条件下圆柱绕流试验,共开展6组次且所有试验组次的水深在5 mm左右,柱体直径皆小于水深,且柱体雷诺数变化范围在1 600~4 400。为研究该种条件下柱体前端马蹄涡的特征,构建了高分辨率高频PIV对柱体前端的流场进行测量,共测得1 000对独立流场。通过对瞬时流场时间平均测得流动分离点和马蹄涡的结构,进而通过旋转强度计算、涡旋模拟,提取了马蹄涡的位置、半径、旋转强度等特征,得出如下结论:
1)在低柱体雷诺数条件下(1 600<
2)在浅薄层水流条件下(0.48<
3)与前人的研究数据对比,发现马蹄涡的运动状态呈3个阶段:500<
| [1] |
Gossler A A,Marshall J S. Simulation of normal vortex cylinder interaction in a viscous fluid[J]. Journal of Fluid Mechanics, 2001, 431: 371-405. DOI:10.1017/S0022112000003062 |
| [2] |
Kairouz K A,Rahai H R. Turbulent junction flow with an upstream ribbed surface[J]. International Journal of Heat & Fluid Flow, 2005, 26(5): 771-779. DOI:10.1016/j.ijheatfluidflow.2005.02.002 |
| [3] |
Kirkil G,Constantinescu G. A numerical study of the laminar necklace vortex system and its effect on the wake for a circular cylinder[J]. Physics of Fluids, 2012, 24(7): 415-443. DOI:10.1063/1.4731291 |
| [4] |
Dargahi B. The turbulent flow field around a circular cylinder[J]. Experiments in Fluids, 1989, 8(1): 1-12. |
| [5] |
Graf W H,Yulistiyanto B. Experiments on flow around a cylinder; the velocity and vorticity fields[J]. Journal of Hydraulic Research, 1998, 36(4): 637-654. DOI:10.1080/00221689809498613 |
| [6] |
Ozturk N A,Akkoca A,Sahin B. Flow details of a circular cylinder mounted on a flat plate[J]. Journal of Hydraulic Research, 2008, 46(3): 344-355. DOI:10.3826/jhr.2008.3126 |
| [7] |
Chen Qigang,Qi Meilan,Li Jinzhao,et al. Study on the features of approaching flow upstream of a circular cylinder inopen channel flows based on PIV measurement[J]. Journal of Hydraulic Engineering, 2015, 46(8): 967-973. [陈启刚,齐梅兰,李金钊,等. 基于粒子图像测速技术的明渠圆柱上游行近流特征研究[J]. 水利学报, 2015, 46(8): 967-973. DOI:10.13243/j.cnki.slxb.20141253] |
| [8] |
Chen Qigang,Qi Meilan,Li Jinzhao. Kinematic characteristics of horseshoe vortex upstreamof circular cylinders in open channel flow[J]. Journal of Hydraulic Engineering, 2016, 47(2): 158-164. [陈启刚,齐梅兰,李金钊. 明渠柱体上游马蹄涡的运动学特征研究[J]. 水利学报, 2016, 47(2): 158-164. DOI:10.13243/j.cnki.slxb.20150528] |
| [9] |
Chen Qigang,Qi Meilan,Zhang Qiang,et al. Experimental study on the multimodal dynamics of the turbulent horseshoe vortex system around a circular cylinder[J]. Physics of Fluids, 2017, 29(1): 015106. DOI:10.1063/1.4974523 |
| [10] |
Akilli H,Rockwell D. Vortex formation from a cylinder in shallow water[J]. Physics of Fluids, 2002, 14(9): 2957-2967. DOI:10.1063/1.1483307 |
| [11] |
Fu H,Rockwell D. Shallow flow past a cylinder:Transition phenomena at low Reynolds number[J]. Journal of Fluid Mechanics, 2005, 540: 75-97. DOI:10.1017/S0022112005003381 |
| [12] |
Nezu I. Open-channel flow turbulence and its research prospect in the 21st century[J]. Journal of Hydraulic Engineering, 2005, 131(4): 229-246. DOI:10.1061/(ASCE)0733-9429(2005)131:4(229) |
| [13] |
Zhong Qiang,Wang Xingkui,Miao Wei,et al. High resolution PTV system and its application in the measurement inviscous sub layer in smooth open channel flow[J]. Journal of Hydraulic Engineering, 2014, 45(5): 513-520. [钟强,王兴奎,苗蔚,等. 高分辨率粒子示踪测速技术在光滑明渠紊流黏性底层测量中的应用[J]. 水利学报, 2014, 45(5): 513-520. DOI:10.13243/j.cnki.slxb.2014.05.002] |
| [14] |
Zhou J,Adrian R J,Balachandar S,et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. Journal of Fluid Mechanics, 1999, 387(10): 353-396. DOI:10.1017/S002211209900467X |
| [15] |
Gao Q,Ortiz-Dueñas C,Longmire E K. Analysis of vortex populations in turbulent wall-bounded flows[J]. Journal of Fluid Mechanics, 2011, 678: 87-123. DOI:10.1017/jfm.2011.101 |
| [16] |
Tomkins C D,Adrian R J. Spanwise structure and scale growth in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2003, 490: 37-74. DOI:10.1017/S0022112003005251 |
| [17] |
Zhong Qiang,Chen Qigang,Li Danxun,et al. The scale and eirculation characteristics of spanwise vortexes in open channel flows[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(增刊2): 66-70. [钟强,陈启刚,李丹勋,等. 明渠湍流横向涡旋的尺度与环量特征[J]. 四川大学学报(工程科学版), 2013, 45(增刊2): 66-70.] |
| [18] |
Varun A V,Balasubramanian K,Sujith R I. An automated vortex detection scheme using the wavelet transform of the d2 field[J]. Experiments in Fluids, 2008, 45(5): 857-868. DOI:10.1007/s00348-008-0505-5 |
| [19] |
Carlier J,Stanislas M. Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry[J]. Journal of Fluid Mechanics, 2005, 535(535): 143-188. DOI:10.1017/S0022112005004751 |
| [20] |
Herpin S,Stanislas M,Soria J. The organization of near-wall turbulence:A comparison between boundary layer SPIV data and channel flow DNS data[J]. Journal of Turbulence, 2010, 11(47): 1-30. DOI:10.1080/14685248.2010.508460 |
| [21] |
Qi Meilan. Riverbed scouring around bridge piers in river section with sand pits[J]. Journal of Hydraulic Engineering, 2005, 36(7): 835-839. [齐梅兰. 采沙河床桥墩冲刷研究[J]. 水利学报, 2005, 36(7): 835-839. DOI:10.3321/j.issn:0559-9350.2005.07.012] |
| [22] |
Unger J,Hager W H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers[J]. Experiments in Fluids, 2007, 42(1): 1-19. DOI:10.1007/s00348-006-0209-7 |
| [23] |
Roulund A,Sumer B M,Fredsøe J,et al. Numerical and experimental investigation of flow and scour around a circular pile[J]. Journal of Fluid Mechanics, 2005, 534(534): 351-401. DOI:10.1017/S0022112005004507 |
| [24] |
Wei Q D,Chen G,Du X D. An experimental study on the structure of juncture flows[J]. Journal of Visualization, 2001, 3(4): 341-348. |
 2019, Vol. 51
2019, Vol. 51


