黏聚力是土的重要力学性能参数之一,直接影响着土体的剪切与压缩强度。在基坑、边坡与隧道等岩土工程中,黏聚力是确定一些施工参数与工程安全性的重要依据。如:在采用朗肯与库伦主动(被动)土压力理论计算黏性土层的主动与被动土压力[1]时,黏聚力是反映土层自身性能的2个力学参数之一(另一个为内摩擦角);在岩土工程的锚喷与土钉支护中,黏聚力是确定锚杆、土钉抗拔力的重要参数[2];黏聚力还被广泛应用在评价边坡[3]与隧道掌子面[4]稳定性等方面。但岩土工程是一个动态发展的过程,如地基的夯实过程[5]、边坡的滑移发展过程[6–7]、隧道围岩的变形过程[8]等。伴随着岩土工程的动态发展,土体性质最直观的变化是干密度与孔隙比的改变,进而影响黏聚力与土体稳定性。因此,根据干密度、孔隙比的变化确定黏聚力动态值具有重要的工程应用价值。
目前,对土体黏聚力的研究主要是通过十字板剪切试验(可用于工程现场)[9]、直剪试验与三轴压缩试验等方法测定土体黏聚力,进而分析含水率[10]、密度[11–12]、颗粒级配[13–14]等物理参数对黏聚力的影响规律。大量的剪切试验研究得出了部分定性结论:土体黏聚力与其干密度正相关,与含水率及无黏性颗粒的含量负相关。利用大量的试验数据并结合数学方法,可以拟合出一些黏聚力与其影响因素间的函数关系式[15]。但以上研究中,黏聚力都是通过在一定几何尺度的土体(或土块)上进行剪切试验间接计算得出的。也可以认为以上研究内容都是在宏观尺度上开展的。这就导致,通过试验方法得出的黏聚力变化规律只能停留在定性描述层面,不能从本质上解释干密度、孔隙比等因素对黏聚力产生影响的原因,更无法建立科学有效的黏聚力计算方法用于分析黏聚力随干密度、孔隙比等因素的变化规律。
根据表面物理化学理论[16],当固体颗粒净距减小到分子间力的作用范围时,颗粒间会表现出吸引力作用,但土体黏聚力的本质是土颗粒间吸引力的宏观表现。程昌炳等[17–18]认为针铁矿高岭土的黏聚力本质是高岭土分子间存在的氢键,黏聚力仅是大量氢键在宏观上的一种表现;并据此建立了土中胶结键的微观赋存模型,对比计算得出的胶结强度值与直剪试验得出的黏聚力值验证了其研究方法的正确性。但应用此方法计算黏聚力首先需要确定氢键的强度与数量,这就给该方法的普遍运用带来一定的难度。
Lifshitz[19]对微观固体颗粒间分子吸引力的理论研究表明:相邻固体颗粒间的分子吸引力与其净距的4次方负相关。土体作为由大量固体颗粒胶结成的组合体,土颗粒间相互作用力同样应符合Lifshitz的研究结论。以Lifshitz的研究为依据,以均匀土体为研究对象,建立均匀土黏聚力计算方法,可用于计算土体干密度、孔隙比变化后的黏聚力值;并与直剪试验结果进行了对比,证明了该方法的正确性。
1 均匀黏性土黏聚力计算方法 1.1 均匀黏性土的孔隙结构模型土体是由固体土颗粒、水、气3相共同组成的,土的水、气两相都赋存于土颗粒间的孔隙中。因此,可认为土体包含土颗粒胶结形成的土体骨架与粒间孔隙2个部分;土颗粒的净距与孔隙体积所占的比例直接相关。对于均匀的黏性土,可认为是由形状、大小相近的土颗粒形成的骨架与均匀分布在土颗粒骨架间的孔隙组合而成。为建立均匀土体的孔隙结构模型,分析均匀细粒土中土颗粒净距与孔隙比之间的关系,对均匀的细粒土进行如下假设:
1)土体中所有土颗粒均为边长为l的正方体,且土颗粒排列有序,如图1所示;2)土体中存在孔隙时,孔隙在土颗粒间均匀分布,即任意2个相邻土颗粒的净距d相等。
 |
| 图1 均匀黏性土孔隙结构模型 Fig. 1 Conceptual model of pore structure in uniform cohesion soil |
在均匀黏性土孔隙结构模型中选取特征单元体(图1中右上虚线表示的土颗粒部分),特征单元体包括一个正方体的土颗粒及其周围厚度为
分析图2中特征单元体的几何特征,其体内孔隙体积可用颗粒净距表示为:
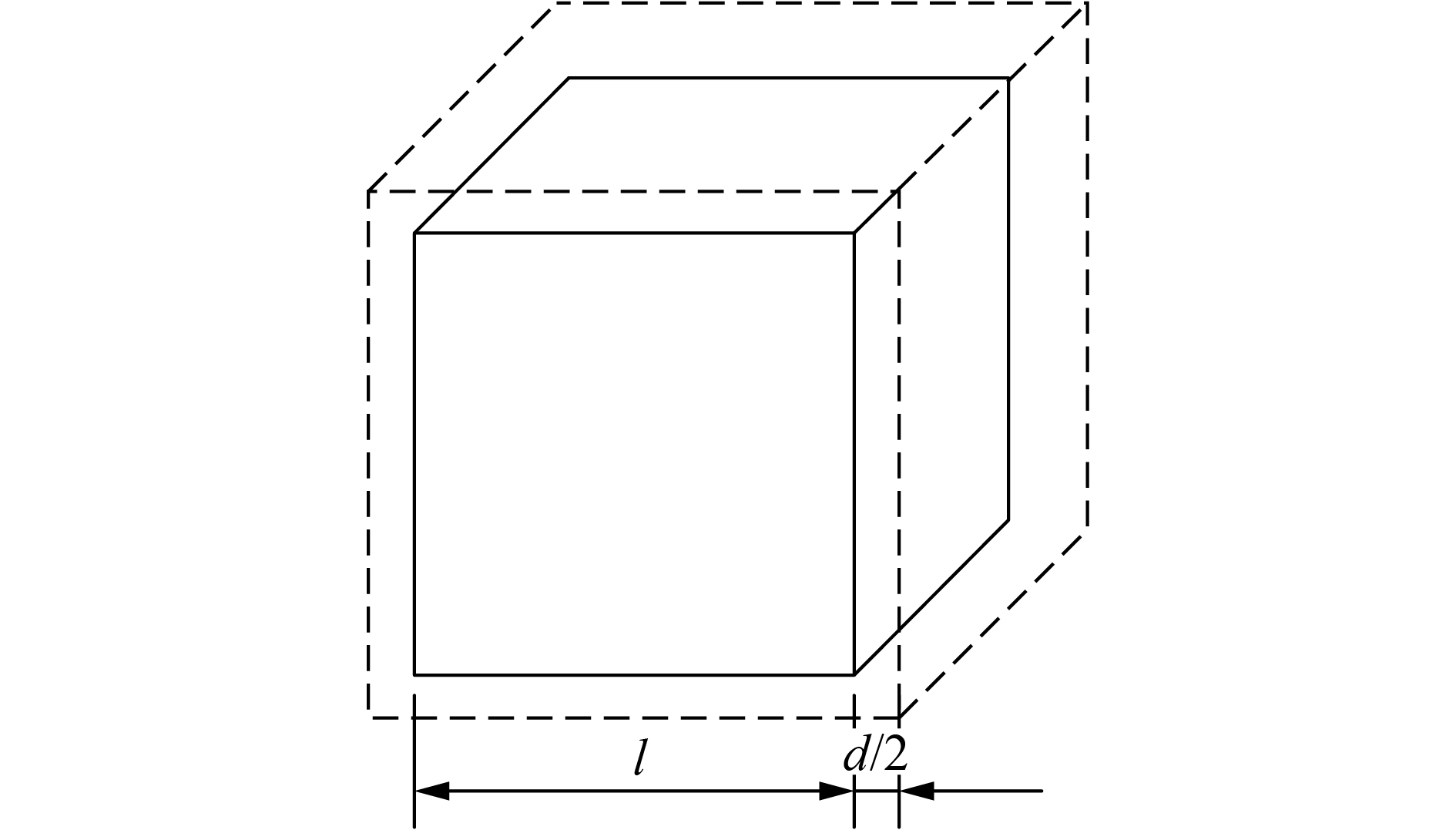 |
| 图2 均匀黏性土特征单元体 Fig. 2 Feature element of the uniform cohesion soil |
| $ {V_{\rm{v}}} = {(d + l)^3} - {l^3} $ | (1) |
式中,Vv为孔隙体积,d为土颗粒净距,l为土颗粒边长。式(1)化简后可得:
| $ {V_{\rm{v}}} = {d^3}{\rm{ + }}3l{d^2} + 3{l^2}d $ | (2) |
土颗粒体积为:
| $ {V_{\rm{s}}} = {l^3} $ | (3) |
式中,Vs为土颗粒体积。根据式(2)~(3),可得出特征单元体的孔隙比e为:
| $ e = \frac{{{V_{\rm{v}}}}}{{{V_{\rm{s}}}}} = \frac{{{d^3}{\rm{ + }}3l{d^2} + 3{l^2}d}}{{{l^3}}} $ | (4) |
若将正方体土颗粒的边长l作为土的固有性质,即对于特定种类的土l可作为常数,根据式(4),可将土颗粒净距d化简为孔隙比e的函数:
| $ d = l(\sqrt[3]{{e + 1}} - 1) $ | (5) |
式(5)表明,土颗粒净距与孔隙比正相关。为进一步分析土颗粒净距的变化规律,分别绘制l=5、15、25 μm时,土颗粒净距变化趋势(图3)。由图3可知,曲线斜率随孔隙比的增大有缓慢减小趋势,即随孔隙比增大,其对土颗粒净距的影响逐渐减小。
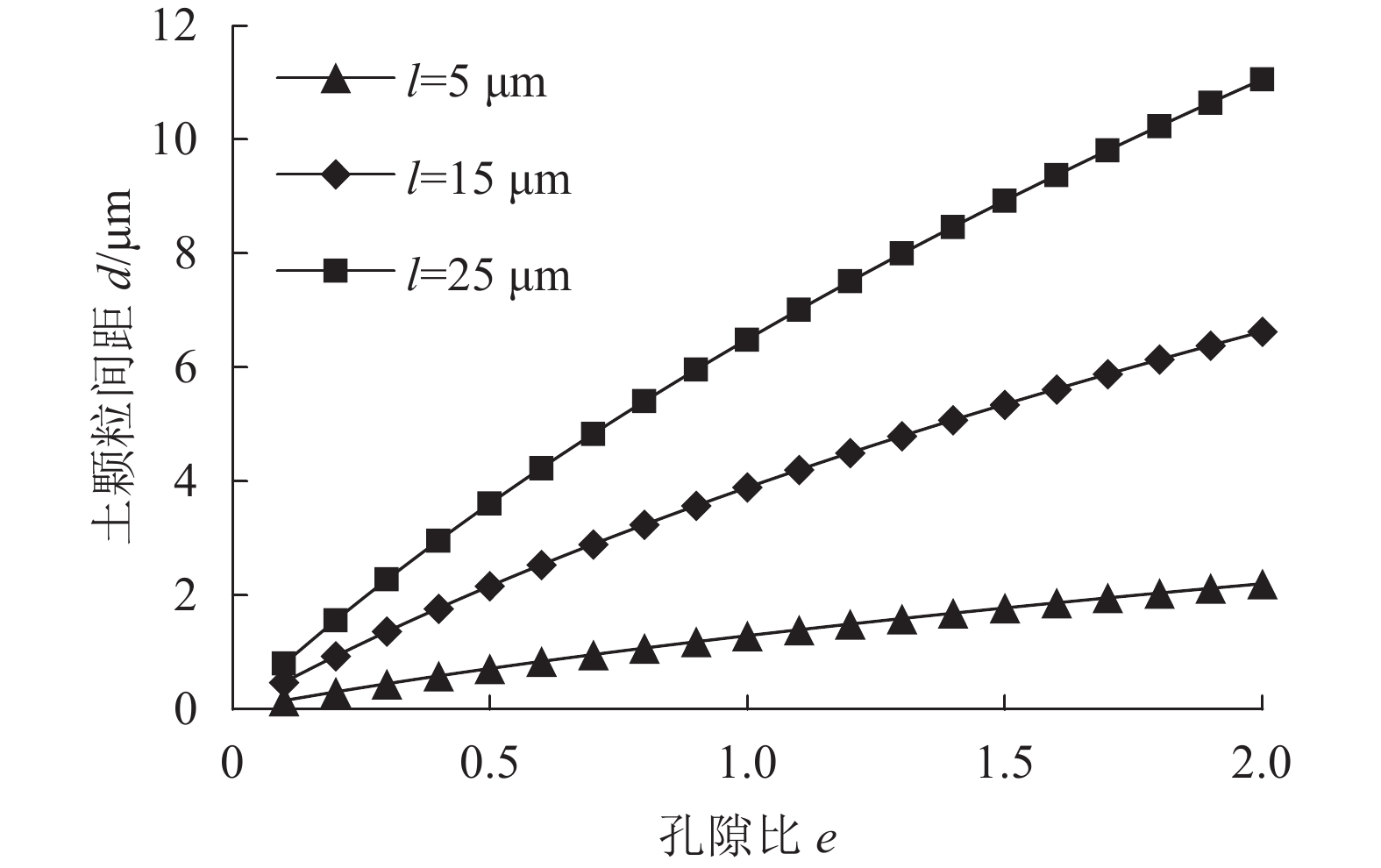 |
| 图3 土颗粒净距随孔隙比的变化趋势 Fig. 3 Variation of soil particle spacing with the void ratio |
1.1.2 土体内任意截面上的有效面积率
由于土体内同时包含土颗粒与粒间孔隙,沿任意方向切割土体产生的截面,也是由土颗粒截面与孔隙2个部分组成。影响土体截面力学性能的决定性因素主要有土颗粒截面所占比例及其力学性质,因此可认为:土体截面上只有被土颗粒截面所占据的部分对土体性能产生有效影响。综上所述,定义:土体任意截面上土颗粒截面所占据的部分为有效面积,土颗粒截面面积与土体截面面积之比为该截面的有效面积率。
为分析均匀土体内任意截面上的有效面积率与孔隙比之间的关系,根据均匀细粒土孔隙结构模型,在土体内任取一矩形截面,如图4所示。截面内包含a×b个土颗粒;边界尺寸为土颗粒长度与孔隙宽度之和,即横向长度为a(l+d),纵向宽度为b(l+d)。
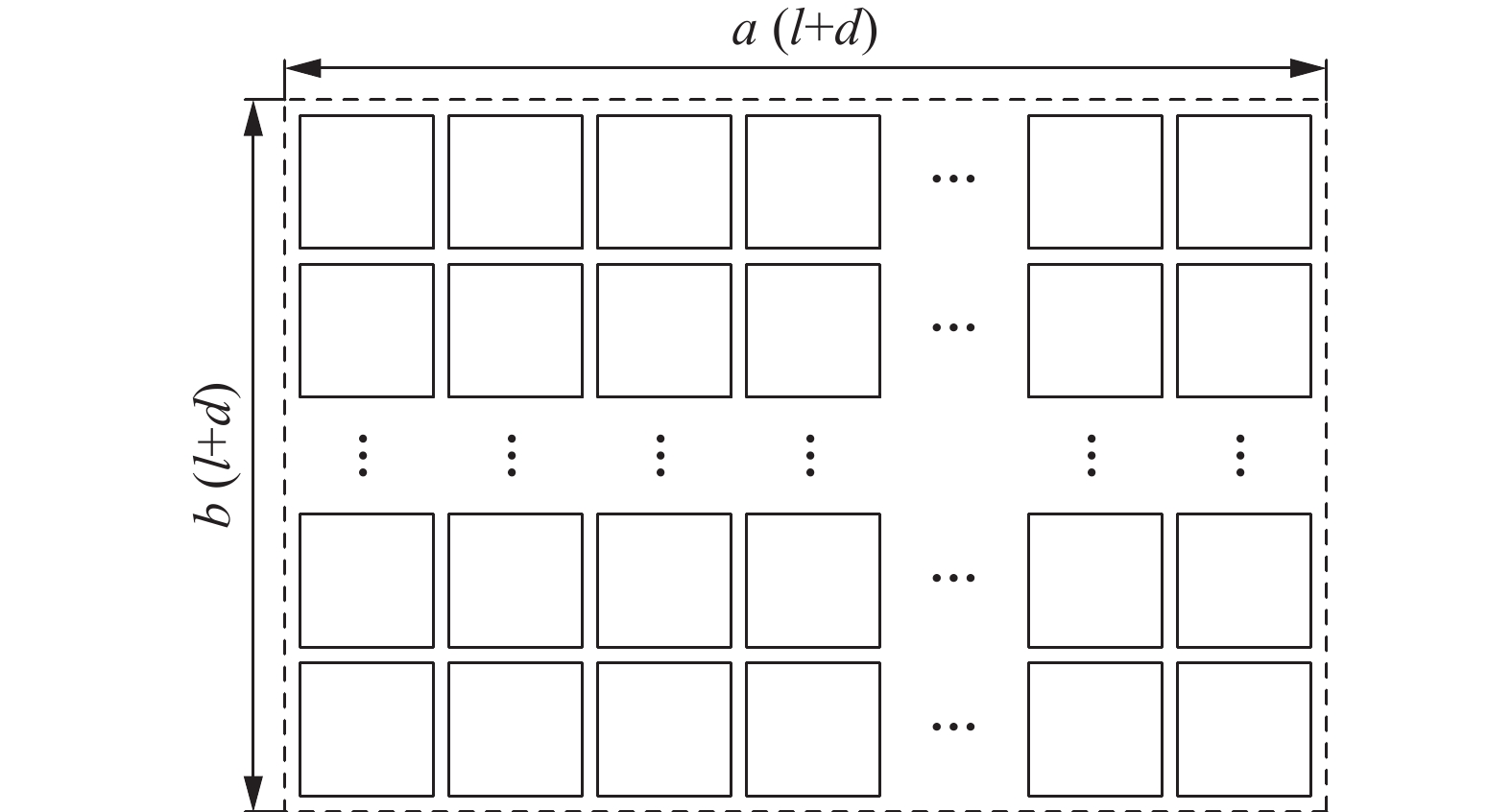 |
| 图4 土体矩形截面示意图 Fig. 4 Plan sketch of rectangular section in soil |
因此,可确定土体截面面积为:
| $ S = ab{(l + d)^2} $ | (6) |
式中,S为土体截面面积。土颗粒截面面积,即有效面积为:
| $ {S\!_{\rm{s}}} = ab{l^2} $ | (7) |
式中,Ss为土颗粒截面面积。因此,该截面上有效面积率为:
| $ \eta = \frac{{{S\!_{\rm{s}}}}}{S} = \frac{{ab{l^2}}}{{ab{{(l + d)}^2}}} = {\left(\frac{l}{{l + d}}\right)^2} $ | (8) |
式中,η为土体截面的有效面积率。为建立有效面积率与孔隙比间的关系,将式(5)代入式(8)可得:
| $ \eta = {\left[\frac{l}{{l + l(\sqrt[3]{{e + 1}} - 1)}}\right]^2} = {(e + 1)^{ - \textstyle\frac{2}{3}}} $ | (9) |
式(9)表明:均匀黏性土截面的有效面积率只受孔隙比影响,且与孔隙比存在负相关关系。为直观分析孔隙比对土体有效面积率的影响,根据式(9)绘制有效面积率随孔隙比的变化趋势图(图5)。
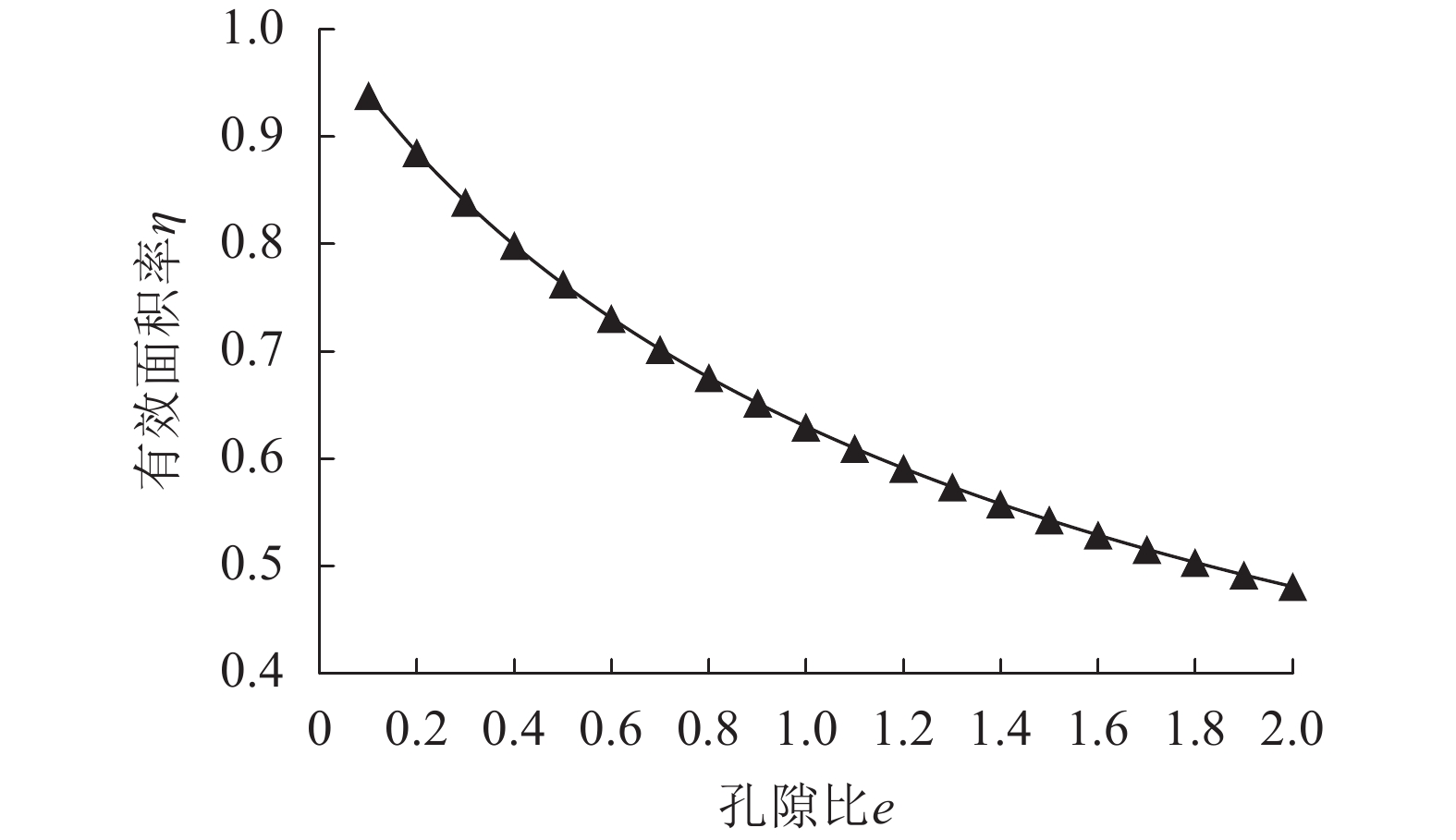 |
| 图5 土体截面有效面积率随孔隙比e的变化趋势 Fig. 5 Variation of effective area rate of soil section with the void ratio |
图5表明:有效面积率曲线随孔隙比的增大迅速减小,即随孔隙比增大,其对土体有效面积率的影响迅速减小。
1.2 均匀细粒土的黏聚力 1.2.1 均匀细粒土的黏聚力本质根据程昌炳等[18]的研究结论:土体的黏聚力等于单位面积A上土体内胶结键的合力。若把均匀土体简化为图1中所示的孔隙结构模型,以土颗粒间的吸引力等效代替土分子间的胶结键(图6),则土的黏聚力可以概括为单位面积A上土颗粒间吸引力F的合力(式(10)):
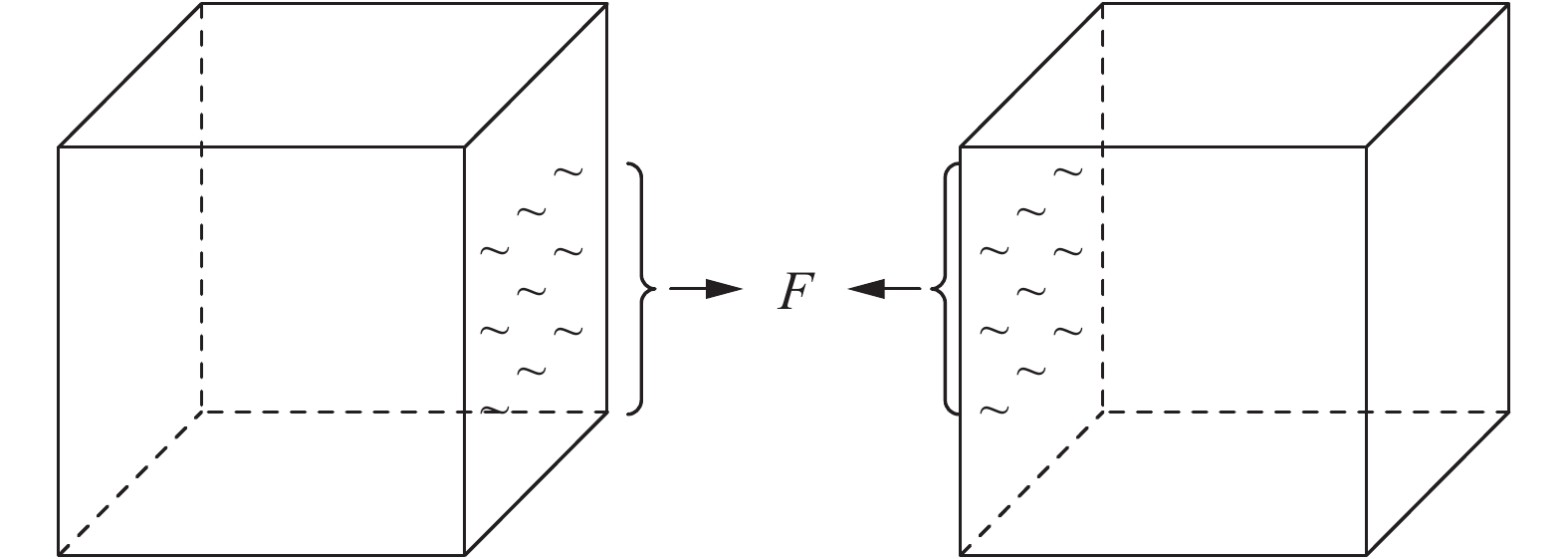 |
| 图6 土颗粒间吸引力作用示意图 Fig. 6 Schematic diagram of molecular attractive force between two soil particles |
| $ C = \sum F {\rm{ = }}n \cdot F $ | (10) |
式中:C为土的黏聚力;F为2个相邻土颗粒间的吸引力;n为单位截面面积上土颗粒的数量,可由土体截面的有效面积率求得:
| $ n{\rm{ = }}\frac{{\eta \cdot A}}{{{l^2}}}{\rm{ = }}\frac{A}{{{l^2}}}{(e + 1)^{ - \textstyle\frac{2}{3}}} $ | (11) |
将式(11)代入式(10)可得以土颗粒间吸引力与孔隙比表示的土体黏聚力:
| $ C{\rm{ = }}\frac{A}{{{l^2}}}{(e + 1)^{ - \textstyle\frac{2}{3}}} \cdot F $ | (12) |
由于现阶段无法实现对土颗粒间吸引力F的准确测量与计算,因此无法通过式(12)直接得出土体的黏聚力。但是,Lifshitz[19]通过理论推导建立了固体颗粒间吸引力F与其净距d的关系,为估算与分析土体黏聚力的变化规律提供了另外一种可能。根据Lifshitz固体颗粒间分子吸引力理论:在一定条件下,相邻的2个土颗粒间吸引力F为其净距
| $ F(d) \propto \frac{1}{{{d^4}}} $ | (13) |
式中,F(d)为净距为d时的土颗粒间吸引力。因此,当颗粒净距由
| $ \frac{{F({d_1})}}{{F({d_0})}} = \frac{{d_0^4}}{{d_1^4}} = {\left(\frac{{\sqrt[3]{{{e_0} + 1}} - 1}}{{\sqrt[3]{{{e_1} + 1}} - 1}}\right)^4} $ | (14) |
式中,d0为初始土颗粒净距,d1为变化后的土颗粒净距,e0为初始孔隙比,e1为变化后孔隙比。式(14)化简可得:
| $ F({d_1}) = {\left(\frac{{\sqrt[3]{{{e_0} + 1}} - 1}}{{\sqrt[3]{{{e_1} + 1}} - 1}}\right)^4} \cdot F({d_0}) $ | (15) |
随着土颗粒净距的变化,单位土体上土颗粒的数量n与土体孔隙率e必然会发生改变。因此,当土颗粒净距由
| $ \frac{{{C_1}}}{{{C_0}}} = \frac{{{{A{{({e_1} + 1)}^{ - \textstyle\frac{2}{3}}}} / {{l^2}}}}}{{{{A{{({e_0} + 1)}^{ - \textstyle\frac{2}{3}}}} / {{l^2}}}}} \cdot \frac{{F({d_1})}}{{F({d_0})}} $ | (16) |
式中,C0为初始黏聚力,C1为变化后的黏聚力。将式(15)代入式(16),化简得:
| $ {C_1} = {\left( {\frac{{{e_0} + 1}}{{{e_1} + 1}}} \right)^{\textstyle\frac{2}{3}}} \cdot {\left( {\frac{{\sqrt[3]{{{e_0} + 1}} - 1}}{{\sqrt[3]{{{e_1} + 1}} - 1}}} \right)^4} \cdot {C_0} $ | (17) |
根据式(17),在已知土的初始黏聚力与孔隙比的情况下,可以计算出孔隙比变化后的黏聚力值,用于分析黏聚力随孔隙比的变化规律。但在工程中土的干密度更加常用,且孔隙比与土体干密度间存在关系:
| $ e = \frac{{{G_{\rm{s}}}}}{{{\rho _{\rm{d}}}}} - 1 $ | (18) |
式中,Gs为土粒比重,ρd为土的干密度。因此,以式(18)替换孔隙比e,可将式(17)化简为:
| $ {C_1} = {\left( {\frac{{{\rho _{{\rm d}1}}}}{{{\rho _{{\rm d}0}}}}} \right)^{\textstyle\frac{2}{3}}} \cdot {\left( {\frac{{\sqrt[3]{{{{{G_{\rm{s}}}} / {{\rho _{{\rm d}0}}}}}} - 1}}{{\sqrt[3]{{{{{G_{\rm{s}}}} / {{\rho _{{\rm d}1}}}}}} - 1}}} \right)^4} \cdot {C_0} $ | (19) |
式(19)建立了一种黏聚力随干密度变化的函数表达式。在土粒比重、初始黏聚力与干密度已知的情况下,通过式(19)可研究土的黏聚力随干密度的变化规律。
2 试验验证 2.1 均匀细粒土直剪试验为验证均匀黏性土孔隙结构模型的合理性及式(19)计算土体黏聚力的正确性,设计并开展了均匀细粒重塑土的直剪试验。试验用土为济南市地表土,并利用土壤筛分仪筛除了0.075 mm以上的固体颗粒,保障土体颗粒尽量均匀。用于直剪试验的重塑土试样依据《土工试验方法标准》[20],采用压样器制作。试验首先测定了土粒比重为2.71;同时,为探究不同含水量条件下式(19)的适用性,试样制备时考虑了含水量的变化,按不同含水量分为5组;每组试验分别测定干密度1.4~1.8 g/cm3的土样黏聚力,试样干密度梯度为0.05 g/cm3。均匀细粒土部分性能参数及试验分组见表1。
| 表1 均匀细粒土性能参数与直剪试验分组 Tab. 1 Property of uniform fine-grained soil and the direct shear test groupings |
 |
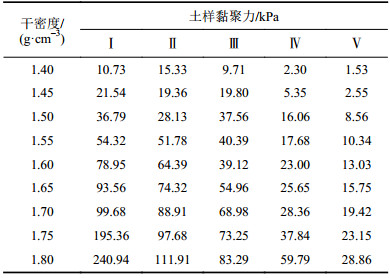
通过200余个重塑土试样的直剪试验,测得了5组共45种土样的直剪试验数据。根据莫林利等[21]提出的直剪试验数据处理方法,利用Excel内置trend函数,对试验数据求解土样黏聚力,结果见表2。
| 表2 均匀细粒土黏聚力直剪试验测定结果 Tab. 2 Cohesive forces of uniform fine-grained soil tested by direct shear test |
 |
2.2 均匀细粒土的黏聚力计算结果验证
由于直剪试验过程存在正应力不稳定[22]、剪应力分布不均匀等问题,试验结果不可避免地存在一定的绝对误差。对于特定的一台直剪仪,试验结果的绝对误差可以认为基本稳定,此时土样黏聚力的增大,有助于减小绝对误差对试验结果的影响。因此,采用表2中干密度为1.8 g/cm3的土样参数作为计算土体黏聚力初始值。初始值分别为:土粒比重2.71,初始干密度1.8 g/cm3,初始黏聚力可在表2中查找。结合表2中的土样参数初始值,通过式(19)分别计算出其他干密度下土样黏聚力,并与5组直剪试验结果对比,如图7所示。
 |
| 图7 均匀细粒土黏聚力试验与计算结果对比 Fig. 7 Comparison of test and calculating cohesive forces of uniform fine-grained soil |
对比5组不同含水量的均匀细粒土黏聚力变化趋势可知,试验结果与式(19)计算结果基本吻合。特别是含水量6%与15%土样,2种方法得出的黏聚力吻合程度较好。另外,随干密度的增大,图7中式(19)的黏聚力计算结果曲线斜率不断增大,特别是干密度超过1.6 g/cm3以后,曲线斜率呈加速增长趋势,说明土体干密度越大,对黏聚力的影响越显著。
含水量9%与12%的土样,通过2种方法得出的黏聚力存在较大差异。分析其原因可能包括2个方面:1)试验误差,除直剪试验过程与仪器会出现误差外,重塑土直剪试样之间的差异也会导致试验结果产生误差[23]。2)对于非饱和土,干密度的变化会对基质吸力产生影响[24],进而影响土体黏聚力[25];但本文在土体模型建立与公式推导中没有考虑基质吸力的影响,导致公式计算结果与真实值之间必然会存在一定差异。总体而言,式(19)表达的黏聚力随干密度的变化规律与直剪试验结果相符合,验证了第1节中均匀细粒土孔隙结构模型与式(19)的合理性。
3 结 论1)以均匀黏性土为研究对象,通过对土体结构的简化假设,建立了均匀黏性土的孔隙结构模型,推导了土颗粒净距与孔隙比的函数关系。研究表明:土颗粒净距与土体孔隙比正相关,随孔隙比的增大,其对土颗粒净距的影响逐渐减弱。
2)根据Liftshitz固体间分子吸引力理论,将土颗粒之间的相互作用简化为颗粒间吸引力,以单位面积上土颗粒间的吸引力表示土体黏聚力,建立了一种均匀黏性土的黏聚力计算方法,可用于分析土体黏聚力随干密度(或孔隙比)的变化规律。
3)设计开展了均匀细粒土的直剪试验,以干密度为1.8 g/cm3的土样黏聚力为初始值,计算得出了其他干密度下的土体黏聚力;计算结果与试验结果基本符合,验证了所提出的均匀土体孔隙结构模型和黏聚力计算方法的合理性。
| [1] |
Lu Tinghao. A formula of active earth pressure including cohesion and adhesion[J]. Rock and Soil Mechanics, 2002, 23(4): 470-473. [卢廷浩. 考虑黏聚力及墙背黏着力的主动土压力公式[J]. 岩土力学, 2002, 23(4): 470-473. DOI:10.3969/j.issn.1000-7598.2002.04.016] |
| [2] |
Liang Shihua,Ying Hongwei,Xie Kanghe,et al. Analysis of the pseudo-cohesion for the soil-nailed retaining structure[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(3): 64-68. [梁仕华,应宏伟,谢康和,等. 土钉支护结构似黏聚力分析[J]. 浙江大学学报(工学版), 2003, 37(3): 64-68.] |
| [3] |
Wang Dingjian,Tang Huiming,Li Changdong,et al. Stability analysis of colluvial landslide due to heavy rainfall[J]. Rock and Soil Mechanics, 2016, 37(2): 439-445. [汪丁建,唐辉明,李长冬,等. 强降雨作用下堆积层滑坡稳定性分析[J]. 岩土力学, 2016, 37(2): 439-445.] |
| [4] |
Khezri N,Mohamad H,Hajihassani M,et al. The stability of shallow circular tunnels in soil considering variations in cohesion with depth[J]. Tunnelling and Underground Space Technology, 2015, 49: 230-240. DOI:10.1016/j.tust.2015.04.014 |
| [5] |
Ma Zongyuan,Xu Qingqing,Dang Faning. Numerical study of dynamic compacted for gravel foundation using particle flow method[J]. Engineering Mechanics, 2012, 30(6): 184-190. [马宗源,徐清清,党发宁. 碎石土地基动力夯实的颗粒流离散元数值分析[J]. 工程力学, 2012, 30(6): 184-190.] |
| [6] |
Zhou X P,Cheng H. The long-term stability analysis of 3D creeping slopes using the displacement-based rigorous limit equilibrium method[J]. Engineering Geology, 2015, 195: 292-300. DOI:10.1016/j.enggeo.2015.06.002 |
| [7] |
Di Traglia F,Nolesini T,Ciampalini A,et al. Tracking morphological changes and slope instability using spaceborne and ground-based SAR data[J]. Geomorphology, 2018, 300: 95-112. DOI:10.1016/j.geomorph.2017.10.023 |
| [8] |
Gan Penglu.Research on the rules and prediction of ground deformation induced by tunneling and shallow tunneling method under water-rich soft stradium[D].Hangzhou:Zhejiang University,2016. 甘鹏路.富水软弱地层浅埋暗挖隧道地层变形规律及预测研究[D].杭州:浙江大学,2016. |
| [9] |
Li Hongzeng.Study and application of electrical-logging vane shear test[J].Chinese Journal of Rock Mechanical and Engineering,2004,23(Supp 1):4446–4449. 李洪增.电测式十字板剪切试验的研究与应用[J].岩石力学与工程学报,2004,23(增1):4446–4449. |
| [10] |
Lu Li,Wang Huafei,Hu Daiwen. Influence of moisture content and grain composition on shear strength of slightly dense gravel soil and bearing capacity of foundation[J]. Journal of Civil Architectural & Environmental Engineering, 2017, 39(3): 138-144. [卢黎,王华飞,胡岱文. 含水率和颗粒级配对稍密碎石土抗剪性能及地基承载力的影响[J]. 土木建筑与环境工程, 2017, 39(3): 138-144.] |
| [11] |
Jiang Jingshan,Liu Hanlong,Cheng Zhanlin,et al. Influence of density and confining pressure on mechanical properties of coarse-grained soils[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(8): 46-50. [姜景山,刘汉龙,程展林,等. 密度和围压对粗粒土力学性质的影响[J]. 长江科学院院报, 2009, 26(8): 46-50. DOI:10.3969/j.issn.1001-5485.2009.08.011] |
| [12] |
Huang Da,Zeng Bin,Wang Qingle. Study on probabilistic relation between permeability coefficient and void ratio and grain composition of coarse-grained soils using Copula theory[J]. Journal of Hydraulic Engineering, 2015, 46(8): 900-907. [黄达,曾彬,王庆乐. 粗粒土孔隙比及级配参数与渗透系数概率的相关性研究[J]. 水利学报, 2015, 46(8): 900-907.] |
| [13] |
Chang W J,Phantachang T. Effects of gravel content on shear resistance of gravelly soils[J]. Engineering Geology, 2016, 207: 78-90. DOI:10.1016/j.enggeo.2016.04.015 |
| [14] |
Hamidi A,Azini E,Masoudi B. Impact of gradation on the shear strength-dilation behavior of well graded sand-gravel mixtures[J]. ScientiaIranica, 2012, 19(3): 393-402. |
| [15] |
Zhang Zhifeng,Hao Fei,Shen Jianjun,et al. Test on mechanic properties of graded soil[J]. Journal of Chang’an University (Natural Science Edition), 2009, 29(4): 16-19. [张志峰,郝飞,沈建军,等. 级配土的力学性能试验[J]. 长安大学学报(自然科学版), 2009, 29(4): 16-19. DOI:10.3321/j.issn:1671-8879.2009.04.004] |
| [16] |
亚当森 A W.表面的物理化学[M].顾惕人,译.北京:科学出版社,1984.
|
| [17] |
Cheng Changbing,Liu Shaojun,Wang Yuanfa,et al. Microscopic study on cohesion of a cemented soil[J]. Chinese Journal of Rock Mechanical and Engineering, 1999, 18(3): 322-326. [程昌炳,刘少军,王远发,等. 胶结土的凝聚力的微观研究[J]. 岩石力学与工程学报, 1999, 18(3): 322-326. DOI:10.3321/j.issn:1000-6915.1999.03.019] |
| [18] |
Yao Hailin,Liu Shaojun,Cheng Changbing. Scopic essence of cohesion of a natural cemented soil[J]. Chinese Journal of Rock Mechanical and Engineering, 2001, 20(6): 871-874. [姚海林,刘少军,程昌炳. 一种天然胶结土黏聚力的微观本质[J]. 岩石力学与工程学报, 2001, 20(6): 871-874. DOI:10.3321/j.issn:1000-6915.2001.06.026] |
| [19] |
Lifshitz E M. The theory of molecular attractive forces between solids[J]. Soviet Physics, 1956, 2(1): 73-83. |
| [20] |
中华人民共和国建设部.土工试验方法标注:GB/T 50123—1999[S].北京:中国计划出版社,1999.
|
| [21] |
Mo Linli,Zhao Xiushao,Wang Xu,et al. Data processing method of direct shear test based on Excel[J]. Railway Engineering, 2015(9): 102-105. [莫林利,赵秀绍,王旭,等. 基于Excel的直剪试验数据处理方法[J]. 铁道建筑, 2015(9): 102-105. DOI:10.3969/j.issn.1003-1995.2015.09.29] |
| [22] |
Han Jiayong. Discussion on error of parameters in direct shear test[J]. Dam Observation and Geotechnical Tests, 2001, 25(2): 43-44. [韩佳泳. 直剪试验中参数误差原因探讨[J]. 大坝观测与土工测试, 2001, 25(2): 43-44. DOI:10.3969/j.issn.1671-3893.2001.02.013] |
| [23] |
Zou Zongxing,Tang Huiming,Liu Xiao,et al. Quantitative study of structural plane direct shear test results influenced by sample preparation errors[J]. Chinese Journal of Rock Mechanical and Engineering, 2010, 29(8): 1664-1669. [邹宗兴,唐辉明,刘晓,等. 制样误差对结构面直剪试验结果影响定量研究[J]. 岩石力学与工程学报, 2010, 29(8): 1664-1669.] |
| [24] |
Zhang Pengcheng,Tang Liansheng,Jiang Liqun,et al.Research of quantitative relations of matric suction with water content and dry density[J].Chinese Journal of Rock Mechanical and Engineering,2013,31(Supp 1):2792–2797. 张鹏程,汤连生,姜力群,等.基质吸力与含水量及干密度定量关系研究[J].岩石力学与工程学报,2013,31(增1):2792–2797. |
| [25] |
Patil U D,Puppala A J,Hoyos L R,et al. Modeling critical-state shear strength behavior of compacted silty sand via suction-controlled triaxialtesting[J]. Engineering Geology, 2017, 231: 21-33. DOI:10.1016/j.enggeo.2017.10.011 |
 2019, Vol. 51
2019, Vol. 51


