2. 湖南科技大学 土木工程学院,湖南 湘潭 411201
2. College of Civil Eng., Hunan Univ. of Sci. and Technol., Xiangtan 411201, China
桩基础在港口码头及桥梁工程中应用非常广泛。为满足承载、变形及稳定性要求,桩基往往需要嵌入到一定深度的基岩中,从而形成嵌岩桩[1–2]。有关其嵌入深度,一直是学术和工程界均比较关注的问题。因此,自20世纪以来,许多学者对其开展了一些有益的研究,如:Pells等[3]提出了确定嵌岩深度的两种方法;Radhakrishnan等[4]分析了嵌岩桩的荷载传递特性,推导了嵌岩深度计算方法;Dai等[5]根据120根实际工程桩的载荷试验结果,分析了岩石单轴抗压强度对基桩最佳嵌岩深度的影响;Xing等[6]发现嵌岩深度达3.5倍桩径后桩端阻力且桩顶沉降最小;刘树亚等[7]认为满足沉降和承载力的前提下,如果桩岩模量同量级且界面胶结较好,嵌岩深度越浅越有利;宋仁乾等[8]通过试验研究了端阻比与嵌岩深度的关系,认为软土地基中的基桩不存在最大嵌岩深度;雷勇等[9]提出了一种按桩顶沉降量确定嵌岩深度的计算方法;何杰等[10]根据桩身稳定计算方法,分析了风化花岗岩基桩的最佳嵌岩深度。上述研究在确定嵌岩桩嵌固深度时,主要是从基桩竖向承载力和沉降两方面确定基桩的嵌固深度。然而实际工程中,基桩除承受竖向荷载外,还需承受较大的水平荷载。因此,在确定嵌岩深度时,还应考虑嵌岩段的水平极限承载特性。为此,赵明华等[11–12]提出了一种确定桥梁基桩嵌岩深度的新方法,弥补了规范方法过于保守的不足,但其在分析嵌岩段基桩极限承载力时,并未考虑岩体破坏特征;雷勇等[13]基于Hoke–Brown强度准则,分析了嵌岩段桩侧岩石水平极限承载力,获得了嵌岩桩嵌岩深度计算公式。但该计算公式忽略了基岩顶面处水平力,而仅考虑基岩顶面处弯矩作用。为反映嵌岩桩真实受力状况,在确定其嵌固深度时,既要考虑桩侧岩石的破坏特征,还应考虑基岩顶面水平力和弯矩的共同作用。
鉴于Hoek–Brown强度准则可以反映岩体非线性破坏特征以及结构面和应力状态对强度的影响[14–15]。作者拟从嵌岩段桩侧岩石水平极限承载角度出发,根据Hoek–Brown强度破坏准则及静力平衡原理,建立考虑基岩顶面水平力和弯矩的共同作用的嵌岩桩嵌固深度简化计算模型,据此导出嵌岩桩最小嵌岩深度计算公式,进而探讨各设计参数对基桩嵌岩深度的影响。
1 计算模型及破坏准则 1.1 简化计算模型建立对于轴横向受荷嵌岩桩,主要考虑嵌岩段桩侧岩石水平极限承载特性,并忽略轴向荷载对嵌岩段桩身内力与变形的影响,从而可建立如图1所示的简化计算模型,据此分析轴横向受荷嵌岩桩的最小嵌岩深度。
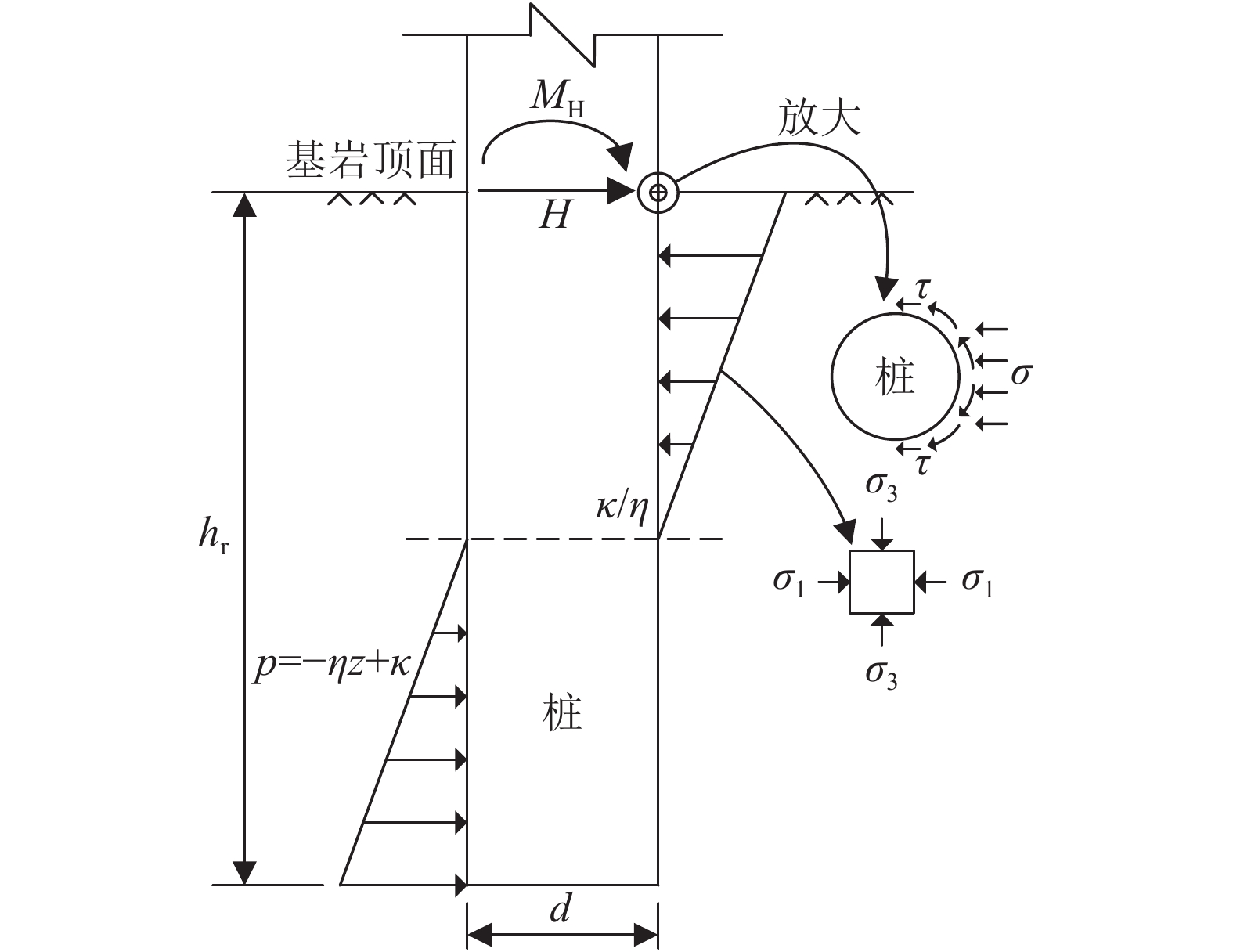 |
| 图1 嵌岩深度计算模型 Fig. 1 Calculation model for rock-socketed depth |
图1中,
1)嵌岩桩由于水平力作用而产生水平转动,嵌岩段桩侧岩石受到桩前法向正应力和桩侧切向剪应力共同作用。假定嵌岩段桩侧岩石水平抗力自上而下随深度呈现线性变化,如图1所示,且满足如下关系:
| $p = - \eta {\textit{z}} + \kappa $ | (1) |
式中:
2)以圆形桩为例,如图2所示,在水平荷载作用下,基岩顶面处桩侧法向应力
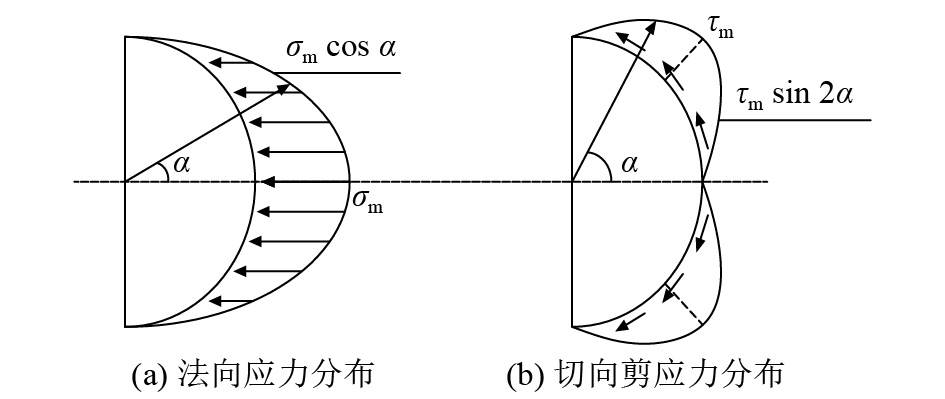 |
| 图2 桩侧法向应力及切向剪应力分布 Fig. 2 Distribution of normal stress and shear stress outside piles |
| $\sigma = {\sigma _{\rm{m}}}\cos \,\alpha $ | (2) |
| $\tau {\rm{ = }}{\tau _{\rm{m}}}\sin\;2\alpha $ | (3) |
式中,
3)根据图1和2中的几何关系,可知基岩顶面处桩侧岩石水平极限抗力是由桩侧总法向应力
| ${p_{\rm{n}}}{\rm{ = 2}}\int_0^{\textstyle\frac{{\text{π}} }{2}} {\frac{d}{2}{\sigma _{\rm{m}}}} {\cos ^2}\;\alpha {\rm{d}}\alpha {\rm{ = }}\frac{{\text{π}} }{4}d{\sigma _{\rm{m}}}$ | (4) |
| ${p_{\rm{\tau }}}{\rm{ = 2}}\int_0^{\textstyle\frac{{\text{π}} }{2}} {\frac{d}{2}{\tau _{\rm{m}}}} \sin (2\alpha )\cos \,\alpha {\rm{d}}\alpha = \frac{2}{3}d{\tau _{\rm{m}}}$ | (5) |
根据式(4)和(5)可得桩侧岩石总水平极限抗力
| ${p_{\rm{u}}} = {p_{\rm{n}}} + {p_{\rm{\tau }}} = d\left( {\frac{{\text{π}} }{4}{\sigma _{\rm{m}}}{\rm{ + }}\frac{2}{3}{\tau _{\rm{m}}}} \right)$ | (6) |
由式(6)可知,要计算桩侧岩石总水平极限抗力
不同围压下所有应力圆的外包络线就是给定正应力下岩石所能承受的最大剪应力,其与所有应力圆均具有相同的切线,如图3所示,其可表示为[15]:
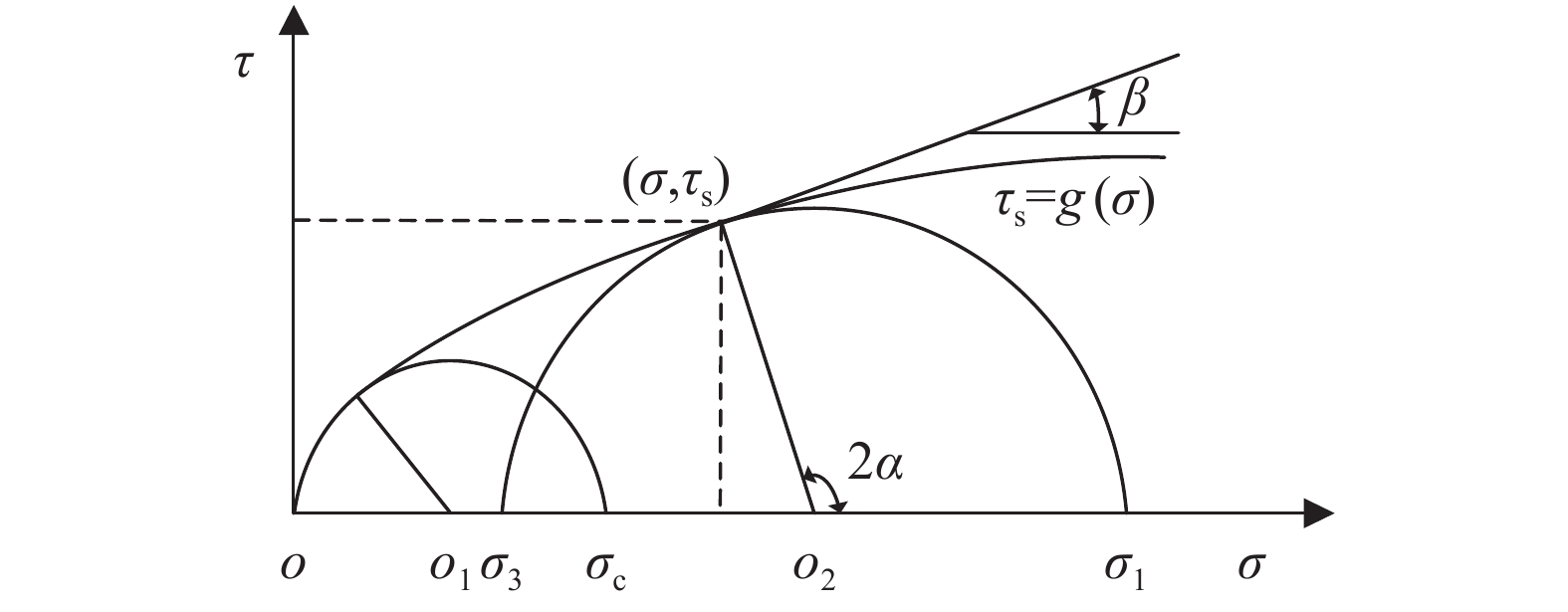 |
| 图3 岩石的强度准则和Mohr应力圆 Fig. 3 Strength criterion for rock and Mohr stress circles |
| ${\tau _{\rm{s}}} = g(\sigma )$ | (7) |
由图3可得到岩石破坏时最大主应力与最小主应力之间的函数关系:
| $\frac{{{\sigma _1} - {\sigma _3}}}{2} = \frac{{{\tau _{\rm{s}}}}}{{\cos \,\beta }}$ | (8) |
| $\frac{{{\sigma _1}{\rm{ + }}{\sigma _3}}}{2} = \sigma {\rm{ + }}{\tau _{\rm{s}}}\tan \,\beta $ | (9) |
Hoek–Brown破坏准则对应的大、小主应力之间的关系为[14–15]:
| ${\left( {{\sigma _1}{\rm{ - }}{\sigma _3}} \right)^2} = {\sigma _3}{\sigma _{\rm{c}}}m + \sigma _{\rm{c}}^2s$ | (10) |
式中,
| $m = {m_0}\exp \frac{{RMR - 100}}{a}$ | (11) |
| $s = \exp \frac{{RMR - 100}}{b}$ | (12) |
式中:
为推导Hoek–Brown破坏准则的摩尔强度外包络线,将Laber变量
| ${\left( {q + \frac{{m{\sigma _{\rm{c}}}}}{8}} \right)^2} = \frac{m}{4}{\sigma _{\rm{c}}}p + \left( {\frac{{{m^2}}}{{64}} + \frac{s}{4}} \right)\sigma _{\rm{c}}^2$ | (13) |
令
| ${(\bar q{\rm{ + }}1)^2} = 2(\bar p + \xi ){\rm{ + }}1$ | (14) |
式中,
定义即时摩擦角
| $\sin \,\rho = \frac{{{\rm{d}}\bar q}}{{{\rm{d}}\bar p}} = \frac{1}{{1 + \bar q}}$ | (15) |
则Hoek–Brown破坏准则的摩尔强度外包络线可以通过即时摩擦角
| $\bar \tau = \frac{\tau }{\lambda } = \frac{{1 - \sin\, \rho }}{{\tan \rho }}$ | (16) |
| $\bar \sigma = \frac{\sigma }{\lambda } + \xi = {\left( {\frac{{1 - \sin \,\rho }}{{\sin\, \rho }}} \right)^2}\frac{{\left( {1 + 2\sin \,\rho } \right)}}{2}$ | (17) |
式中,
联立式(16)和(17)可建立如下方程:
| $2{\sin ^3}\,\rho - (2\bar \sigma + 3){\sin ^2}\,\rho + 1 = 0$ | (18) |
式(18)的解为:
| $\rho {\rm{ = }}\frac{{\text{π}} }{2} - \sqrt[\scriptstyle 4]{{\frac{{8\bar \sigma }}{3}}}$ | (19) |
根据式(16)和(17),通过非线性拟合可建立
| $\bar \tau \approx 1.25{\bar \sigma ^{0.75}}$ | (20) |
将式(16)和(17)代入式(20),即可得岩石破裂面上切向剪应力
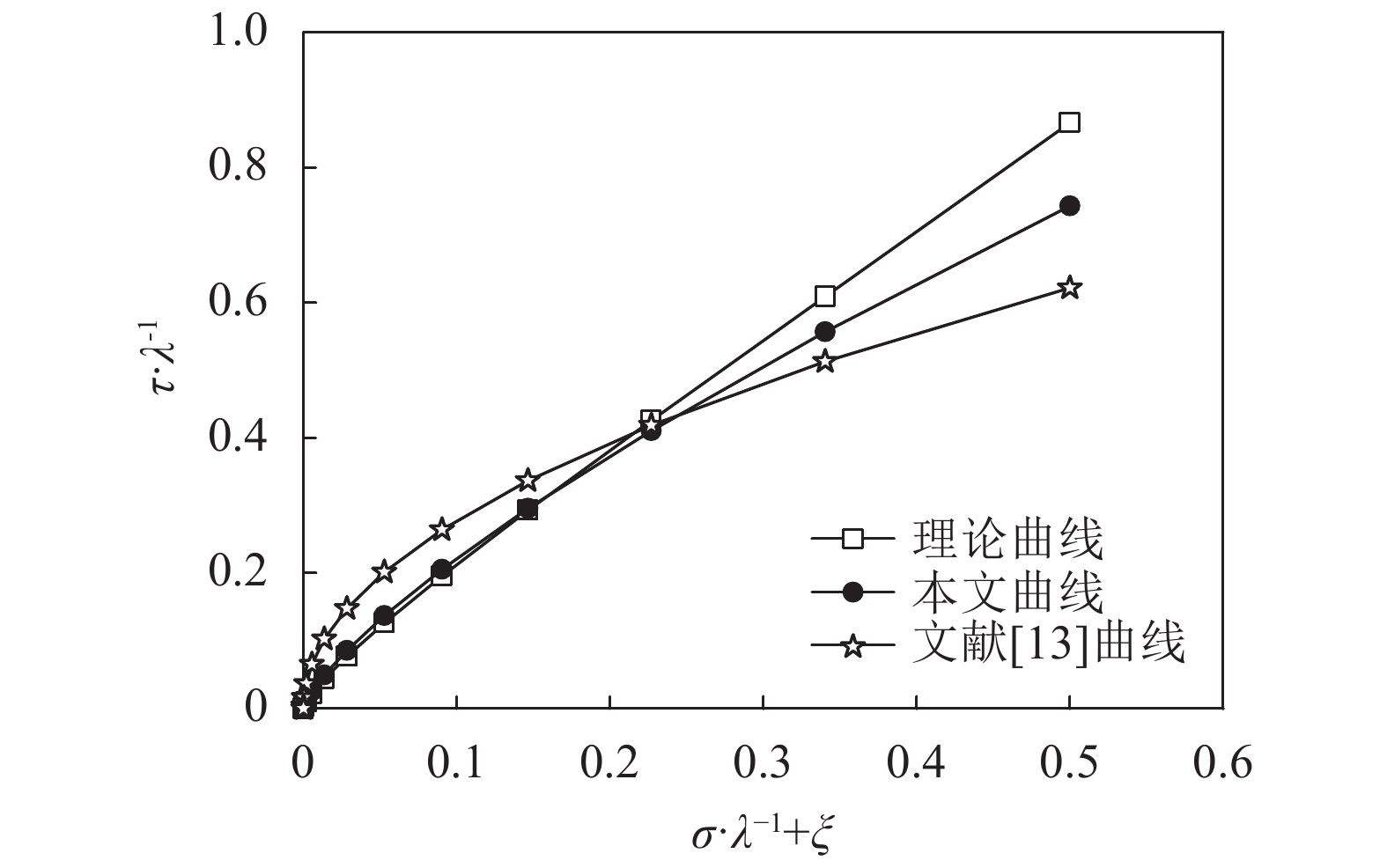 |
| 图4 Hoek–Brown破坏准则的拟合曲线 Fig. 4 Fitting curves of Hoek–Brown strength criterion |
| $\frac{\tau }{\lambda } = 1.25{\left( {\frac{\sigma }{\lambda } + \xi } \right)^{0.75}}$ | (21) |
图4中,理论曲线即为由即时摩擦角
根据图1,当
| ${\sigma _1}{\rm{ = }}{\sigma _{\rm{m}}}$ | (22) |
| ${\sigma _3}{\rm{ = }}{\sigma _{\rm{v}}} = \sum\limits_{i = 1}^n {{l_i}} {\gamma _{{\rm{si}}}}$ | (23) |
式中,
将式(22)和(23)代入式(10)可得桩侧岩石的最大法向应力为:
| ${\sigma _{\rm{m}}} = {\sigma _{\rm{v}}} + \sqrt {{\sigma _{\rm{c}}}m{\sigma _{\rm{v}}} + \sigma _{\rm{c}}^2s} $ | (24) |
当
| $\sigma = {\sigma _{\rm{m}}}\cos \frac{{\text{π}} }{4}{\rm{ = }}\frac{{\sqrt 2 }}{2}{\sigma _{\rm{m}}}{\rm{ = }}\frac{{\sqrt 2 }}{2}\left( {{\sigma _{\rm{v}}} + \sqrt {{\sigma _{\rm{c}}}m{\sigma _{\rm{v}}} + \sigma _{\rm{c}}^2s} } \right)$ | (25) |
将式(25)代入式(21),可得岩石的切向剪应力为:
| $\begin{aligned}[b] {\tau _{\rm{m}}} &= 1.{\rm{25}}\lambda {\left( {\frac{\sigma }{\lambda } + \xi } \right)^{0.75}} = \\ &\,\,\,\,\,\,\,\,\,\,1.25\lambda {\left\{ {\frac{{\sqrt 2 }}{{2\lambda }}\left[ {{\sigma _{\rm{v}}} + \sqrt {{\sigma _{\rm{c}}}m{\sigma _{\rm{v}}} + \sigma _{\rm{c}}^2s} } \right] + \xi } \right\}^{0.75}} \end{aligned}\!\!\!\!\!\!$ | (26) |
将式(24)和(26)代入式(6),即可得到基于Hoek–Brown破坏准则的桩侧岩石水平极限抗力:
| $\begin{aligned}[b]{p_{\rm{u}}} = & d\Bigg\{\frac{{\text{π}} }{4}\left( {{\sigma _{\rm{v}}} + \sqrt {{\sigma _{\rm{c}}}m{\sigma _{\rm{v}}} + \sigma _{\rm{c}}^2s} } \right) + \Bigg. \\ & \left.\frac{{5\lambda }}{6}{{\left[ {\frac{{\sqrt 2 }}{{2\lambda }}\left( {{\sigma _{\rm{v}}} + \sqrt {{\sigma _{\rm{c}}}m{\sigma _{\rm{v}}} + \sigma _{\rm{c}}^2s} } \right) + \xi } \right]}^{0.75}} \right\}\end{aligned}$ | (27) |
根据桩体水平向静力平衡条件,则有:
| $H - \int_0^{\textstyle\frac{\kappa }{\eta }} {( - \eta x + \kappa )} {\rm{d}}x + \int_{\textstyle\frac{\kappa }{\eta }}^{{h_{\rm{r}}}} {(\eta x - \kappa )} {\rm{d}}x = 0$ | (28) |
对基岩顶面桩身中心点取矩,则有:
| ${M_{\rm{H}}} - \int_0^{\textstyle\frac{\kappa }{\eta }} {x( - \eta x + \kappa )} {\rm{d}}x + \int_{\textstyle\frac{\kappa }{\eta }}^{{h_{\rm{r}}}} {x(\eta x - \kappa )} {\rm{d}}x = 0$ | (29) |
联立式(28)和(29),化简可得:
| $\kappa {h_{\rm{r}}}^2 - 4H{h_{\rm{r}}} - 6{M_{\rm{H}}} = 0$ | (30) |
当基岩顶面处岩石发生剪切破坏时,还须满足以下边界条件:
| ${\left. p \right|_{{\textit{z}} = 0}} = \kappa = {p_{\rm{u}}}$ | (31) |
联立式(31)即可对式(30)进行求解,得到基桩最小嵌岩深度
| ${h_{\rm{r}}} = \frac{{2H}}{{{p_{\rm{u}}}}} + \sqrt {\frac{{4{H^2}}}{{{p_{\rm u}^2}}} + \frac{{6{M_{\rm{H}}}}}{{{p_{\rm{u}}}}}} $ | (32) |
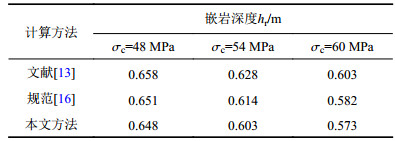
为验证上述解的可行性,现以文献[13]中的嵌岩桩为例,利用规范方法和本文方法进行计算对比。具体计算参数为:桩径
由表1可知,本文计算所得嵌岩深度与规范[16]的结果更为接近,可以验证本文拟合曲线及理论解的合理性。且本文计算结果比文献[13]和规范[16]的结果都小,相对更为经济。
| 表1 基桩嵌岩深度计算结果 Tab. 1 Calculation results of rock-socketed depth of piles |
 |
4 影响因素分析
由式(32)可知基桩嵌岩深度与基岩顶面水平力
| 表2 参数分析方案表 Tab. 2 Scheme of parameters analysis |
 |
4.1 水平力H和桩径d的影响
图5和6分别给出了
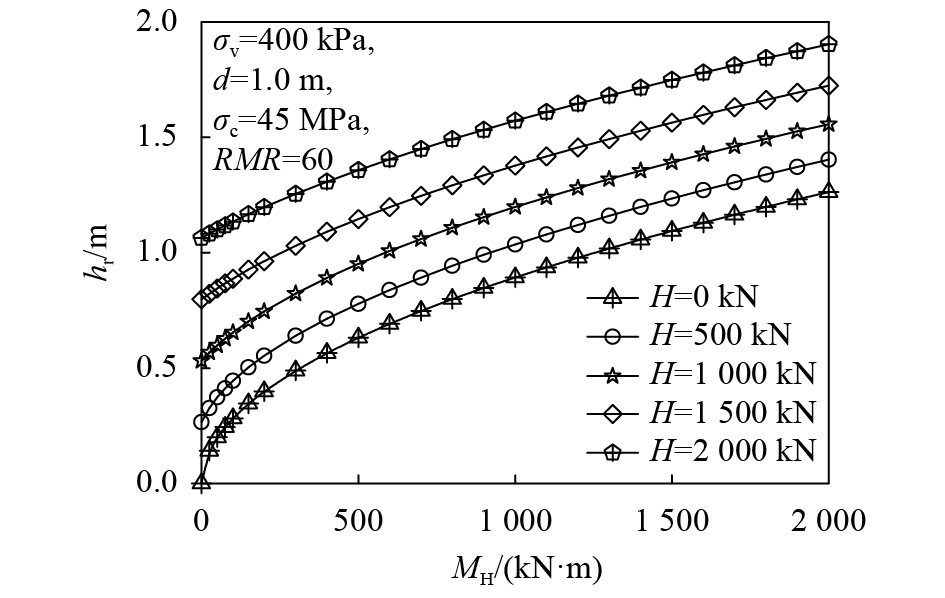 |
| 图5 不同水平荷载H下hr–MH关系曲线 Fig. 5 hr–MH curves with different horizontal load H |
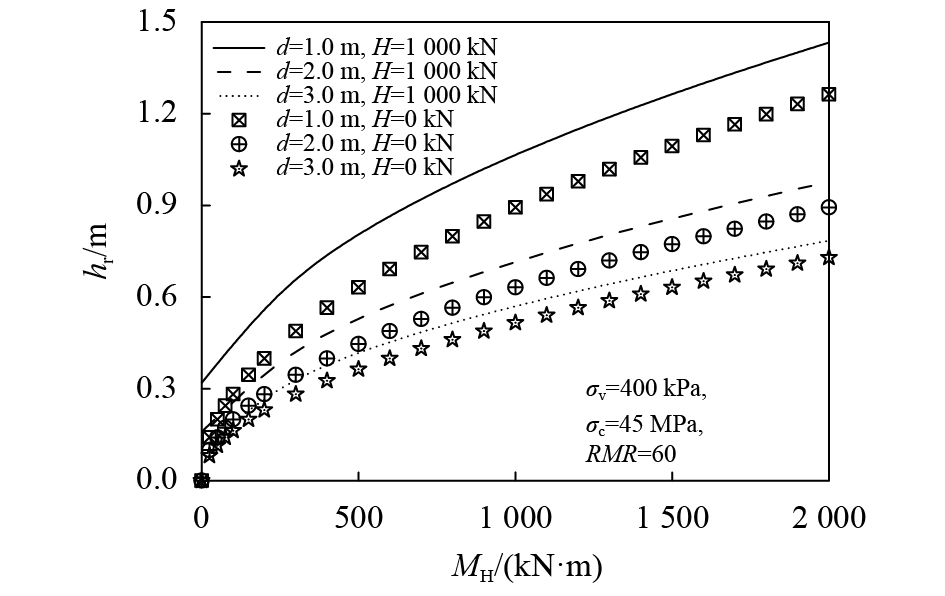 |
| 图6 不同桩径d下hr–MH关系曲线 Fig. 6 hr–MH curves with different pile diameter d |
由图5可知,基桩最小嵌岩深度
图6显示,基桩最小嵌岩深度
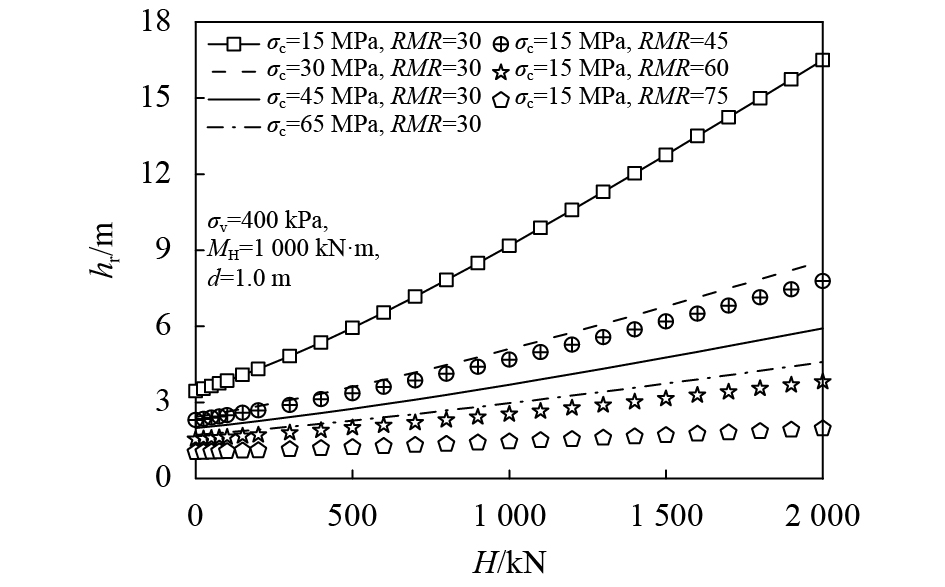
图7为
 |
|
图7 不同
|
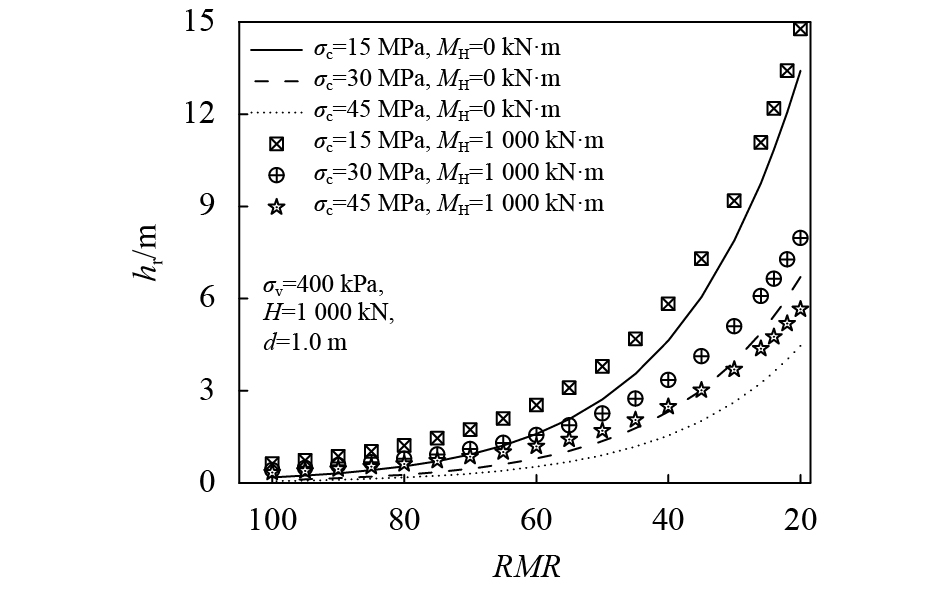
图8为
 |
|
图8 不同
|
由图7和8可知,嵌岩深度
综上所述,岩体地质力学分类指标
基于Hoek–Brown强度准则和静力平衡原理,推导了嵌岩桩嵌岩深度理论计算公式,通过算例验证和影响因素分析,得到如下主要结论:
1)基桩嵌岩深度
2)基桩嵌岩深度
3)其他条件相同时,岩体地质力学分类指标
| [1] |
Zhao Minghua,Luo Weihua,Lei Yong,et al. In-site load-carrying characteristics test of rock-socketed piles of Mishui River bridge[J]. Journal of Hunan University(Natural Sciences), 2014, 41(3): 6-11. [赵明华,罗卫华,雷勇,等. 汨水河特大桥嵌岩桩承载特性试验研究[J]. 湖南大学学报(自然科学版), 2014, 41(3): 6-11. DOI:10.3969/j.issn.1674-2974.2014.03.001] |
| [2] |
Lyu Yaru,Liu Hanlong,Wang Xinquan,et al. A modified Geddes solution for estimating induced stress coefficient of subsoil and settlement of pile foundation[J]. Journal of Sichuan University(Engineering Science Edition), 2013, 45(2): 68-74. [吕亚茹,刘汉龙,王新泉,等. 地基附加应力和桩基沉降计算的修正Geddes应力解[J]. 四川大学学报(工程科学版), 2013, 45(2): 68-74. DOI:10.15961/j.jsuese.2013.02.029] |
| [3] |
Pells P J N,Turner R M. Elastic solutions for the design and analysis of rock-socketed piles[J]. Canadian Geotechnical Journal, 1979, 16(3): 481-487. DOI:10.1139/t79-054 |
| [4] |
Radhakrishnan R,Leung C F. Load transfer behavior of rock-socketed piles[J]. Journal of Geotechnical Engineering, 1989, 115(6): 755-768. DOI:10.1061/(ASCE)0733-9410(1989)115:6(755 |
| [5] |
Dai Guoliang,Gong Weiming,Chen Long. Modified method for shaft resistance of rock-socketed piles based on Hoek-Brown criterion[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1746-1752. [戴国亮,龚维明,陈隆. 基于Hoek-Brown准则嵌岩段桩-岩侧阻力修正计算方法[J]. 岩土工程学报, 2012, 34(9): 1746-1752.] |
| [6] |
Xing H,Zhang Z,Meng M,et al. Centrifuge tests of superlarge-diameter rock-socketed piles and their bearing characteristics[J]. Journal of Bridge Engineering, 2014, 19(6): 4001-4010. DOI:10.1061/(ASCE)BE.1943-5592.0000582 |
| [7] |
Liu Shuya,Liu Zude. Issues on research and design of piles socketed in rock[J]. Rock and Soil Mechanics, 1999, 20(4): 86-92. [刘树亚,刘祖德. 嵌岩桩理论研究和设计中的几个问题[J]. 岩土力学, 1999, 20(4): 86-92. DOI:10.16285/j.rsm.1999.04.016] |
| [8] |
Song Renqian,Zhang Zhongmiao. Study on socket length of rock-socketed piles in soft soil ground[J]. Rock and Soil Mechanics, 2003, 24(6): 1053-1056. [宋仁乾,张忠苗. 软土地基中嵌岩桩嵌岩深度的研究[J]. 岩土力学, 2003, 24(6): 1053-1056. DOI:10.16285/j.rsm.2003.06.044] |
| [9] |
Lei Yong,Zhao Minghua,Ma Binhui. Calculation method of socketed length of rock socketed pile based on requirement of pile top settlement[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 86-91. [雷勇,赵明华,马缤辉. 按桩顶沉降控制的嵌岩桩嵌岩深度计算方法[J]. 公路交通科技, 2011, 28(5): 86-91. DOI:10.3969/j.issn.1002-0268.2011.05.016] |
| [10] |
He Jie,Li Li,Feng Mingwei. The depth calculation of rock-socketed pile in weathered granite region[J]. Highway Engineering, 2012, 37(6): 11-13. [何杰,李力,冯明伟. 风化花岗岩地区嵌岩桩嵌岩深度计算方法[J]. 公路工程, 2012, 37(6): 11-13.] |
| [11] |
Zhao Minghua,Zhang Ling,Liu Jianhua. Calculation method for socketed length of rock-socketed pile[J]. Central South Highway Engineering, 2007, 32(1): 1-4. [赵明华,张玲,刘建华. 公路桥梁嵌岩桩嵌岩深度计算[J]. 中南公路工程, 2007, 32(1): 1-4. DOI:10.3969/j.issn.1674-0610.2007.01.001] |
| [12] |
Zhao Minghua,Feng Mingwei,Liu Meng,et al. A method to calculate socketed depth of large diameter rock socketed piles in soft rock ground[J]. Advances in Science and Technology of Water Resources, 2015, 35(1): 73-77. [赵明华,冯明伟,刘猛,等. 大直径软岩嵌岩桩嵌岩深度计算模型[J]. 水利水电科技进展, 2015, 35(1): 73-77. DOI:10.3880/j.issn.10067647.2015.01.013] |
| [13] |
Lei Yong,Liu Ze. A calculation method for rock-socketed depth of highway bridge pile based on Hoek-Brown strength criterion[J]. Rock and Soil Mechanics, 2015, 36(2): 457-462. [雷勇,刘泽. 基于H-B准则的公路桥梁基桩嵌岩深度计算[J]. 岩土力学, 2015, 36(2): 457-462. DOI:10.16285/j.rsm.2015.02.022] |
| [14] |
Hock E,Brown E T. Empirical strength criterion for rock masses[J]. Journal of Geotechnical Engineering Division ASCE, 1980, 106(GT9): 1013-1035. DOI:10.1016/0148-9062(81)90766-X |
| [15] |
You Mingqing. Study of mathematical equation and parameter determination of strength criteria for rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(11): 2172-2184. [尤明庆. 岩石强度准则的数学形式和参数确定的研究[J]. 岩石力学与工程学报, 2010, 29(11): 2172-2184.] |
| [16] |
公路桥涵地基与基础设计规范:JTG D63—2007[S].北京:人民交通出版社,2007.
|
 2019, Vol. 51
2019, Vol. 51

