机器人技术的发展与运用，推动了全球生产技术的发展，推进了世界各国经济发展进程。在此背景下，世界各国将发展机器人技术上升为国家发展战略。机器人减速器是机器人的核心部件之一，谐波减速器和RV减速器应用最为广泛^[1–2]。两种减速器制造复杂，目前主要依赖进口。包括机器人减速器在内的核心零部件的国产化，是加速国内机器人技术发展的关键。平面蜗轮传动具备啮合齿数多、承载能力大、传动效率高等有点，其蜗轮齿面为平面，齿形简单，易于精确制造^[3]，能够满足机器人减速器传动部件的性能要求。

在平面蜗轮传动设计方面，佐藤申一发明斜齿平面蜗轮传动^[3]。张光辉^[4]发明了侧隙可调式变齿厚平面蜗轮环面蜗杆传动，并且进行理论研究和加工试制^[5–6]。邱昕洋^[7]对钢制变齿厚平面蜗轮包络环面蜗杆传动进行系统研究，通过蜗轮轮齿的楔形结构实现侧隙调整。陈永洪等^[8–9]对平面内齿轮一次包络鼓形蜗杆传动进行研究，此种传动是一种体积小、重量轻的重载蜗杆内啮合传动形式，并进行试验分析传动性能^[10]。王进戈等^[11]结合变齿厚蜗轮和内齿轮的优点，提出侧隙可调式内啮合鼓形蜗杆传动慢驱装置。

结合变齿厚蜗轮^[7]和内齿轮^[8]的优点，在侧隙可调式内啮合鼓形蜗杆传动慢驱装置^[11]的基础上，作者设计变齿厚内齿轮平面包络外转子鼓形蜗杆传动装置。此种装置具有驱动、传动、支撑一体化的结构^[11]，内齿轮与鼓形蜗杆可通过磨削提高制造精度^[7–8]，同时具备传动比大、传动精度高、结构紧凑和侧隙可调等优点。

右旋蜗杆传动标架（甲面标架）如图1所示，固定标架 ${{{\sigma }}_{{m}}}({{{o}}_{{m}}},$ ${{{x}}_{{m}}},{{{y}}_{{m}}},{{{\textit{z}}}_{{m}}})$ 和 ${{{\sigma }}_{{n}}}({{{o}}_{{n}}},{{{x}}_{{n}}},{{{y}}_{{n}}},{{{\textit{z}}}_{{n}}})$ 分别表示蜗杆和内齿轮的初始位置，之间距离为中心距a。建立活动标架 ${{{\sigma }}_{{{1}}}}({{{o}}_{{{1}}}},{{{x}}_{{{1}}}},{{{y}}_{{{1}}}},{{{\textit{z}}}_{{{1}}}})$ 与蜗杆固联，建立活动标架 ${{{\sigma }}_{{{2}}}}({{{o}}_{{{2}}}},{{{x}}_{{{2}}}},$ ${{{y}}_{{{2}}}},{{{\textit{z}}}_{{{2}}}})$ 和 ${{{\sigma }}_{{{3}}}}({{{o}}_{{{3}}}},{{{x}}_{{{3}}}},{{{y}}_{{{3}}}},{{{\textit{z}}}_{{{3}}}})$ 与内齿轮固连，标架 ${{{\sigma }}_{{{2}}}}$ 与 ${{{\sigma }}_{{{3}}}}$ 之间为角度 $\theta $ 。如图1所示，正向转动时，标架 ${{{\sigma }}_{{{2}}}}$ 转动角度记为 ${\varphi _2}$ ，以标架 ${{{\sigma }}_{{{2}}}}$ 为辅助标架确定工作标架 ${{{\sigma }}_{{{3}}}}$ 位置，标架 ${{{\sigma }}_{{{3}}}}$ 转动角度 ${\varphi _3}$ 确定内齿轮工作角度。角度 $\theta $ 、 ${\varphi _2}$ 与 ${\varphi _3}$ 之间满足：

图1(Fig. 1)

图1 甲面标架 Fig. 1 A side’s coordinate frame

式中： ${r_{\rm b}}$ 为基圆半径； ${r_2}$ 为内齿轮分度圆半径； ${{\textit{z}}_2}$ 为内齿轮齿数； ${i_{12}}$ 为传动比， ${i_{12}} = \dfrac{{{{\textit{z}}_2}}}{{{{\textit{z}}_1}}}$ ； ${{\textit{z}}_1}$ 为蜗杆头数。

辅助标架确定蜗杆转角与内齿轮转角的关系，工作标架确定啮合面位置，计算时将内齿轮转角 ${\varphi _2}$ 转换为工作转角 ${\varphi _3}$ ，工作转角 ${\varphi _3}$ 在啮合起始角和啮合终止角之间。

$\omega_1$ 表示蜗杆与标架 $\sigma_1$ 正向转动的角速度， $\omega_2$ 表示内齿轮与标架 ${{{\sigma }}_{{2}}}$ 正向转动的角速度，标架 $\sigma_3$ 与标架 $\sigma_2$ 同步转动，即 $\omega_2$ = $\omega_3$ 。根据平面包络蜗杆传动啮合原理^[12]，啮合点P发生在过基圆锥母线的切平面上，此平面是平面轮齿的工作齿面，记为甲面。 $ {{{{r}}^{({{1}})}}} $ 为啮合点P在标架 ${{{\sigma }}_{{1}}}$ 的位矢， $ {{{{r}}^{(3)}}} $ 为啮合点P在标架 ${{{\sigma }}_{{{3}}}}$ 的位矢。在甲面上建立活动标架 ${{{\sigma }}_{{p}}}({{{o}}_{{p}}},{{{x}}_{{p}}},{{{y}}_{{p}}},{{{\textit{z}}}_{{p}}})$ ，原点 ${{{o}}_{{p}}}$ 在基圆上，坐标轴 ${{{y}}_{{p}}}$ 与基圆锥母线重合，坐标轴 ${{{x}}_{{p}}}$ 指向基圆切线方向，坐标轴 ${{\textit{z}}_{{p}}}$ 与坐标轴 $x_3$ 之间夹角为母平面倾角 $\beta $ 。

通过标架 ${{{\sigma }}_{{1}}}$ 、 ${{{\sigma }}_{{m}}}$ 、 ${{{\sigma }}_{{n}}}$ 、 ${{{\sigma }}_{{3}}}$ 之间的坐标变换与底矢变换，将啮合方程表达在标架 ${{{\sigma }}_{{3}}}$ 中。

如图1所示，以固定标架 ${{{\sigma }\!}_{m}}$ 为参照，蜗杆副正向转动时，相对速度 $ {{{{v}}^{({{31}})}}} $ 表示为：

式中， $ {{{v}}_{{0}}^{(1{{m}})}} $ 、 $ {{{v}}_{{0}}^{(3m)}}$ 为活动标架 ${{{\sigma }}_{{1}}}$ 与 ${{{\sigma }}_{{3}}}$ 分别相对固定标架 ${\sigma_m}$ 的速度， ${\omega }^{(1m)} $ 、 ${\omega }^{(3m)} $ 为活动标架σ₁与σ₃分别相对固定标架σ_m的转速， $ {r^{(1)}}{\text{、}}\!\!\!{r}^{(3)} $ 为啮合点P分别在活动标架 ${{{\sigma }}_{{1}}}$ 与 ${{{\sigma }}_{{3}}}$ 的位矢。

啮合点P在标架 ${{{\sigma }}_{{p}}}$ 中的坐标表示为 $(u,v,0)$ ，i₂₁=1/i₁₂。经坐标变换，在活动标架 ${{{\sigma }}_{{3}}}$ 中蜗杆与内齿轮在啮合点的相对速度 $ {{{v}}_{{3}}^{{({{31}})}}} $ 表达为：

如图1所示，相对速度 $ {{{{v}}^{(31)}}} $ 发生在蜗杆与内齿轮接触面的公切面上，即甲面。根据啮合原理^[12]，相对速度 $ {{{{v}}^{(31)}}} $ 与甲面法矢 $ {{{{n}}^{(3)}}} $ 满足啮合方程 $\varPhi = {{{{v}}^{(31)}}} {{{{n}}^{(3)}}} = 0$ ，将啮合方程在标架 ${\sigma_3}$ 进行表达，整理得出变齿厚内啮合平面包络鼓形蜗杆的甲面啮合方程为：

乙面标架图图2所示。反转时， $ {{\omega_1'}} $ 、 $ {{\omega_2'}} $ 及 $ {{\omega_3'}} $ 分别表示反转时标架 ${{{\sigma }}_1}$ 、 ${{{\sigma }}_2}$ 及 ${{{\sigma }}_3}$ 的角速度，其中 $\omega_2'$ = $ {{\omega_3'}} $ ，以标架 ${{{\sigma }}_3}$ 为辅助标架确定标架 ${{{\sigma }}_2}$ 位置。对应于正转时标架 ${{{\sigma }}_1}$ 转动的角度，在反转时蜗杆转动角度 ${\varphi _1}$ 应满足：

图2(Fig. 2)

图2 乙面标架 Fig. 2 B side’s coordinate frame

图2中，反转时蜗杆与内齿轮的接触面为乙面，啮合点Q在标架 ${{{\sigma }}_1}$ 的坐标记为 $({x_1'},{y_1'},{{\textit{z}}_1'})$ ，在标架 ${{{\sigma }}_2}$ 的坐标记为 $({x_2'},{y_2'},{{\textit{z}}_2'})$ 。 $ {{{{r}}^{(1)}}'} $ 为啮合点Q在标架 ${{{\sigma }}_1}$ 的位矢， $ {{{{r}}^{(2)}}'} $ 为啮合点Q在标架 ${{{\sigma }}_2}$ 的位矢。在乙面上建立活动标架 ${{{\sigma }}_q}({{{o}}_q},{{{x}}_q},{{{y}}_q},{{\textit{z}}_q})$ ，原点 ${{{o}}_q}$ 在基圆上，坐标轴 ${{y}_q}$ 与基圆锥母线重合，坐标轴 ${{x}_q}$ 指向基圆切线方向，坐标轴 $-{{\textit{z}}_q}$ 与坐标轴 ${x_2}$ 之间夹角为母平面倾角 $\,\beta $ 。

以空间固定标架 ${\sigma_m}$ 为参照，蜗杆副反向转动时，蜗杆与内齿轮的相对速度 $ {{{{v}}^{(21)}}} $ ，啮合点Q在标架 ${\sigma\!_q}$ 的坐标为 $(u',v',0)$ ，经坐标变换，在活动标架 ${\sigma\!_2}$ 表达相对速度 $ {{{v}}_2^{^{(21)}}} $ 。相对速度 $ {{{{v}}^{(21)}}} $ 发生在蜗杆与内齿轮接触面的乙面，根据啮合原理^[12]，相对速度 $ {{{{v}}^{(21)}}} $ 与乙面法矢 $ {{{{n}}^{(2)}}} $ 满足啮合方程 $\varPhi = {{{{v}}^{(21)}}} {{{{n}}^{(2)}}} = 0$ ，将啮合方程在标架 ${{{\sigma }}_2}$ 进行表达，整理得出变齿厚内啮合平面包络鼓形蜗杆的乙面啮合方程：

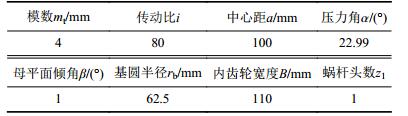
变齿厚内齿轮平面包络外转子鼓形蜗杆传动通过设计甲、乙两齿面的母平面倾角β实现侧隙可调。内啮合传动机构体积更小，结构更为紧凑。鼓形蜗杆内部安装电机，电机型号为U10PLUS KV170，通过电机安装接口与蜗杆进行固定，电机参数如表1所示。依据电机参数及载荷确定蜗杆传动装置设计参数，设计参数如表2所示。

表1(Tab. 1)

表1 电机参数 Tab. 1 Parameters of motor

表1 电机参数 Tab. 1 Parameters of motor 电机尺寸(D×L)/(mm×mm) 最大功率Pm/W 转速r/(r·min–1) 88.6×40 2 000 1 100～9 955

表2(Tab. 2)

表2 设计参数 Tab. 2 Design parameters

表2 设计参数 Tab. 2 Design parameters 模数mt/mm 传动比i 中心距a/mm 压力角 $\alpha$ /(°) 4 80 100 22.99 母平面倾角β/(°) 基圆半径rb/mm 内齿轮宽度B/mm 蜗杆头数z1 1 62.5 110 1

3.2.1 内齿轮设计

在图1和2中，甲面和乙面为内齿轮轮齿两侧齿面所在平面，根据蜗杆传动副设计参数设计内齿轮，其轮齿为对称的楔形轮齿，内齿轮3维造型图3所示。

图3(Fig. 3)

图3 变齿厚内齿轮 Fig. 3 Beveloid internal gear

3.2.2 蜗杆设计

通过标架变换，将甲面啮合方程（式（4））与乙面啮合方程（式（6））表达在标架 ${{{\sigma }}_{{1}}}$ 中。如图（2）所示，正转时蜗杆转动角度 ${\varphi _1}$ 满足 ${\varphi _1} = {i_{12}}{\varphi _2}$ ，蜗杆工作位置由 ${\varphi _3}$ 确定。图2所示，反转时蜗杆转动角度为式（5），工作位置由 ${\varphi _2}$ 确定。蜗杆包容齿数 ${\textit{z}}' = 7$ ，工作半角 ${\varphi _{\rm w}}$ 满足 ${\varphi _{\rm w}} = ({\textit{z}}' + 0.45) $ ${i_{21}}{\text{π}} $ ，工作初始角 ${\varphi _0}$ 满足 ${\varphi _0} = \alpha - {\varphi _{\rm w}}$ ，其中，压力角 $\alpha $ 表达为 $\alpha = {\rm arcsin}\;(2{r_{\rm b}}/{{d_2})}$ ，经计算压力角 $\alpha $ 为22.99º，蜗杆工作角度范围是 $\left( {{\varphi _0},{\varphi _0} + 2{\varphi _{\rm w}}} \right)$ ，蜗杆3维造型图4所示。

图4(Fig. 4)

图4 蜗杆三维造型 Fig. 4 3D model of worm

3.2.3 装　配

变齿厚内齿轮鼓形蜗杆传动可通过改变内齿轮的相对轴向位置实现侧隙可调，提高蜗杆传动利用率。同时，在安装过程中可调整内齿轮的相对轴向位置，实现内齿轮与蜗杆在虚拟环境下无干涉装配。如图5（a）所示，调整后内齿轮轴向移动7 mm时与蜗杆无干涉装配。图5（b）中，相同设计参数的变齿厚环面蜗杆传动的中心距为220 mm，与之比较，鼓形蜗杆传动中心距减小，结构更为紧凑。

图5(Fig. 5)

图5 蜗杆传动 Fig. 5 Worm drive

以甲面为研究对象，图1中，依据齿轮啮合原理^[12]得出蜗杆工作角度范围为 ${\varphi _3} \in \left( {{\varphi _0},{\varphi _0} + 2{\varphi _{\rm w}}} \right)$ ，内齿轮齿距中心角为 ${\theta _\alpha } = 2{\text{π}} /{{\textit{z}}_2}$ 。

观察在同一时刻发生啮合的轮齿，极限啮合对数为8，各啮合齿所对应工作角度为 ${\varphi _{3(i)}} = {\varphi _0} +(i - 1){\theta _\alpha }$ ，其中， $i = 1,2, \cdots ,8$ 。

图1中， $u$ 的范围为内齿轮齿面接触长度，表示为：

式中， ${d_{\rm a2}}$ 为内齿轮齿顶圆直径， ${d_{\rm f2}}$ 为内齿轮齿根圆直径， $ c$ 为顶隙。

在标架 ${{{\sigma }}_{{p}}}$ 中观察接触线在齿宽范围 $v \in \left( { - \dfrac{B}{{2\cos\;\beta }},} \right.$ $\left.{\dfrac{B}{{2\cos\;\beta }}} \right)$ 的分布状态，如图6（a）所示，甲面接触线在 ${{v}}$ 轴方向分布范围为(4.40，26.35)。同理，乙面接触线的分布状态如图6（b）所示，在v轴方向分布范围为(–8.58，–1.44)。综合考虑接触区域和安装尺寸，内齿轮宽度设计为有效工作宽度B'，B' = 75 mm，如图5（a）所示。

图6(Fig. 6)

图6 接触线分布 Fig. 6 Contact line distribution

根据齿轮啮合原理^[12]，二类界限曲线是内齿轮齿面接触线的包络线，二类界限方程 ${\mathit{\Phi} _t}$ 与啮合方程 $\mathit{\Phi} $ 满足：

得到二类界限曲线方程，即：

在标架 ${{{\sigma }}_{{p}}}$ 中观察二类界限曲线与接触线间关系，如图7所示，二类界限曲线与接触线相切。

图7(Fig. 7)

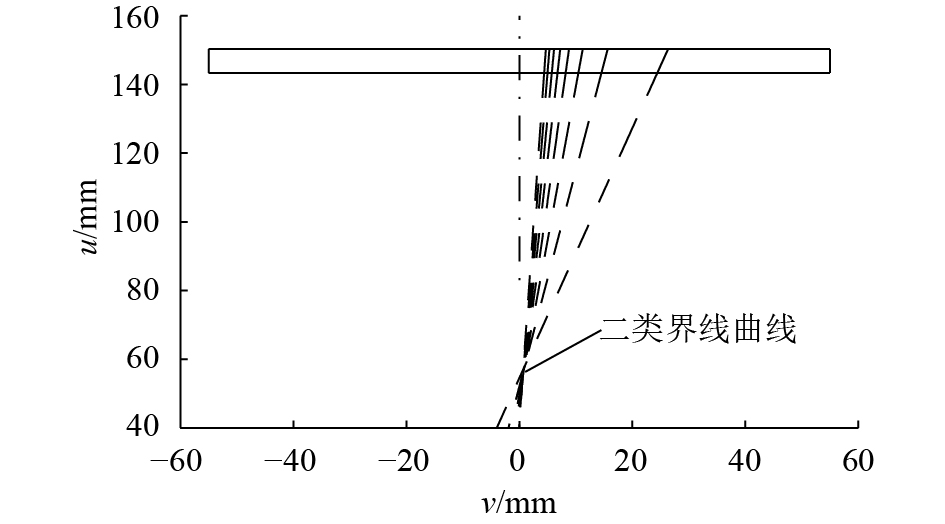图7 二类界限曲线与接触线 Fig. 7 Second boundary curves and contact line distribution

根据齿轮啮合原理^[12]，一类界限曲线是蜗杆齿面啮合线的包络线，一类界限曲线方程 $\psi $ 满足：

接触曲面在标架 ${{{\sigma }}_{{3}}}$ 可表示为：

由式（10）与（11），得到一类界限曲线方程：

在标架 ${{{\sigma }}_{{1}}}$ 中观察一类界限曲线、蜗杆齿根线及内齿轮齿顶接触点运动轨迹之间关系，如图8所示。一类界限曲线在蜗杆齿根边界内部，未超过接触点轨迹边界，蜗杆传动副不会发生根切。

图8(Fig. 8)

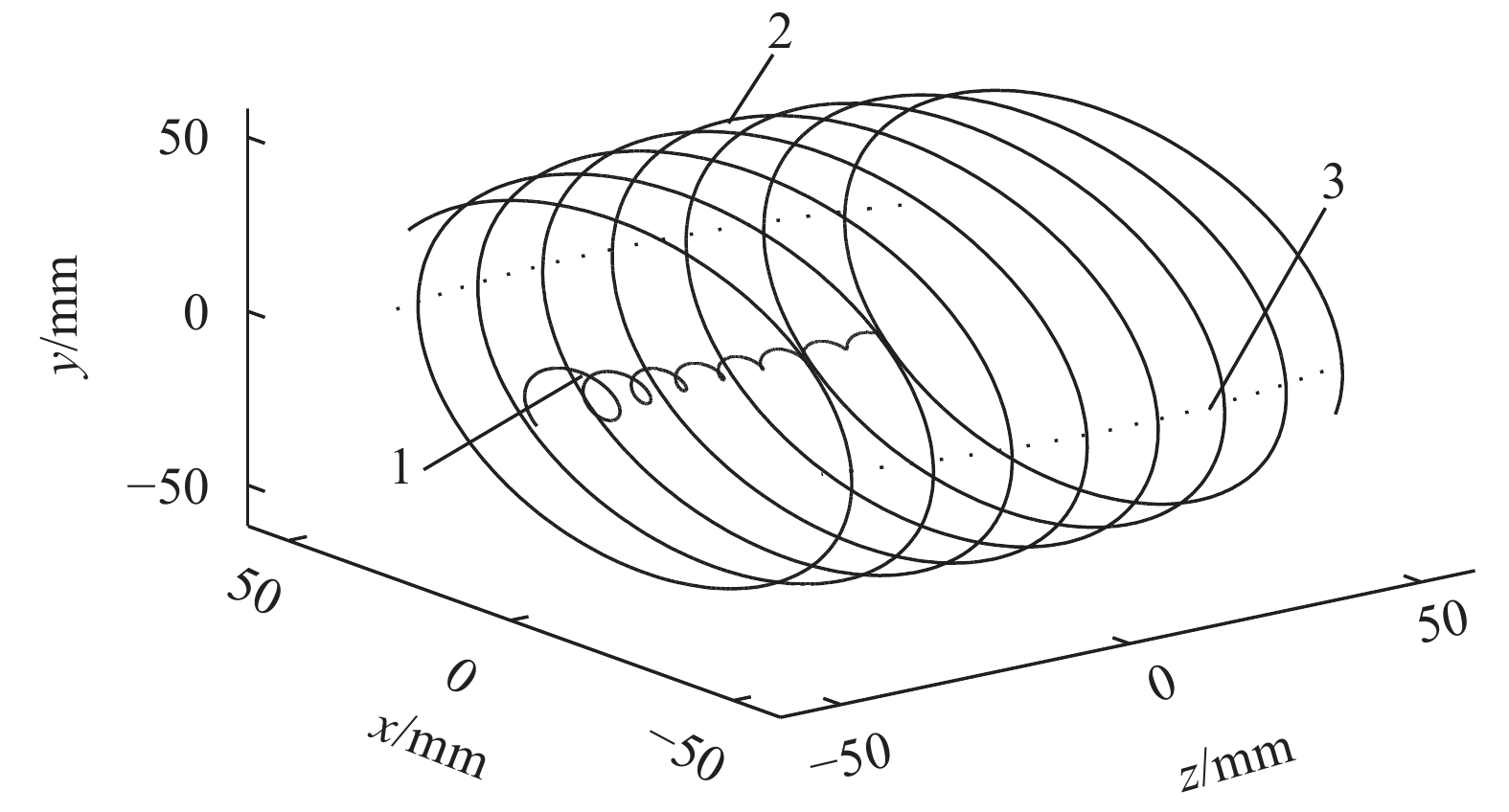1. 一类界限曲线；2. 内齿轮齿顶接触点运动轨迹；3. 蜗杆齿根线。 图8 一类界限曲线 Fig. 8 First boundary curve

如图9所示，变齿厚内齿轮平面包络外转子鼓形蜗杆传动装置具有驱动、传动及支撑一体化的结构。在驱动方面，蜗杆内部安装U10PLUS KV170型电机，与传统外部电机驱动相比，结构更加紧凑。在传动方面，内齿轮具有对称的楔形轮齿，通过紧定螺钉、上齿轮座、上齿轮座固定内齿轮，通过端盖与齿轮座之间的垫片实现内齿轮轴向移动，从而实现侧隙可调。在运动过程中，齿轮座与内齿轮同步转动。在支撑方面，通过支撑轴实现定位安装，无需安装箱体，结构更加紧凑。

图9(Fig. 9)

1. 上齿轮座；2. 内齿轮；3. 支架；4. 电机；5. 蜗杆；6. 固定轴；7. 支板；8. 支撑轴；9. 端盖垫片；10. 端盖；11. 下齿轮座。 图9 设计方案 Fig. 9 Design scheme

依据蜗杆传动副设计参数，将变齿厚内齿轮平面包络外转子鼓形蜗杆传动装置进行3维造型设计，设计模型如图10所示。

图10(Fig. 10)

图10 机器人转动关节 Fig. 10 Robot’s rotation joint

1） 根据内啮合运动规律构建6个标架，依据啮合原理、活动标架法获得鼓形蜗杆副齿面啮合方程，通过MATLAB和CREO进行参数化设计，得到鼓形蜗杆的3维造型。并通过对蜗杆副的接触线、二类界限曲线和一类界限曲线的分析，确定无根切发生。

2） 设计变齿厚内齿轮平面包络外转子鼓形蜗杆副，利用内齿轮轮齿的楔形结构，通过调整内齿轮与蜗杆在内齿轮轴向的相对位置实现侧隙可调。与传统的蜗杆传动相比，安装方便并提高蜗杆传动装置利用率。与相同设计参数的变齿厚平面包络环面蜗杆传动相比，中心距减小，结构紧凑。依据接触线分布区域及内齿轮安装尺寸减小内齿轮宽度尺寸，有利于降低内齿轮制造成本。

3） 对变齿厚内齿轮平面包络外转子鼓形蜗杆传动装置进行结构设计，鼓形蜗杆传动装置具有驱动、传动及支撑一体化的结构特点。

所选用电机型号有限，设计参数受到电机尺寸限制，需进一步研制适合变齿厚内齿轮平面包络外转子鼓形蜗杆传动装置的专用电机，可进一步减少结构尺寸，使鼓形蜗杆传动装置更加紧凑。