2. 武汉大学 水工岩石力学教育部重点实验室,湖北 武汉 430072
2. Key Lab. of Rock Mechanics in Hydraulic Structural Eng. of Ministry of Education, Wuhan Univ., Wuhan 430072, China
随着中国西部大开发战略的持续推进,在西部地区已建、在建和规划了一大批长距离的公路、铁路和输水隧洞。该地区地质构造复杂,活动断裂带多,地震活动频繁。这些长大隧洞在建设过程中往往不可避免地穿越高地震烈度区,面临突出的抗震稳定问题。隧洞大多深埋于地下,一般认为其抗震性能优于地面结构[1–2],然而近年来随着地震灾害的频繁发生,强震区的隧洞结构屡屡遭受破坏[3–5]。长大隧洞作为西部生命线工程的重要组成部分,其抗震减震问题日益得到重视。基于以上背景,研究隧洞结构抗震稳定的定量评价方法,进而评估其抗震性能,对保证工程的长期安全运行具有重要意义。
汶川大地震以来,许多学者围绕长大隧洞地震响应问题展开了行之有效的研究工作。Chen等[6]收集了全世界10次强震下的81条隧道震害资料,分析归纳了隧道地震破坏类型,概括了影响隧道地震破坏的各种因素。徐华等[7]以黄草坪隧道为原型,开展大型振动台模型试验,研究了隧道结构地震响应规律及围岩与结构的动力相互作用。Yu等[8]针对汶川地震灾区的龙溪隧道,基于ABAQUS研究了不同地震动输入组合下衬砌结构的弹塑性力学响应。这些成果多注重隧洞结构的地震响应分析方法和地震响应特性研究,对定量的抗震安全评价方法研究较少涉及,这也正是隧洞结构地震灾害预估的前提。
由于地震动存在较大的不确定性和随机性,故基于性能的结构抗震评估必须建立在概率的基础上,而基于IDA的地震易损性分析方法可弥补单一时程分析在结构性能评估中的不确定性。根据数据来源的不同,地震易损性分析方法可分为4种[9]:专家判断法、经验法、解析法和混合法。专家判断法和经验法是利用已有的震害资料进行易损性分析,需要足够多的数据作为统计样本,会受到专家个人能力的限制,局限性较大;解析法是借助有限元模拟技术,利用地震响应计算结果进行易损性分析,目前已广泛应用于高层结构抗震性能评估中。在隧洞结构地震易损性分析方面,已有学者[10–11]假定混凝土衬砌为线弹性材料进行了初步研究,但忽略了混凝土的动力损伤特性。
作者基于IDA方法,考虑地震动输入的不确定性,以损伤系数为结构的性能参数,确定了隧洞结构地震破坏等级及抗震性能水平,形成了隧洞结构抗震性能评估方法。针对某隧道工程,选取强震记录,进行大量弹塑性有限元动力时程计算,获得了衬砌结构的地震易损性曲线,进而评估了其抗震性能,期望为隧洞结构抗震安全评价提供一种有效的分析思路,并为其抗震减震设计提供有益的参考。
1 基于IDA的地震易损性分析方法 1.1 IDA方法IDA方法是一种基于弹塑性动力时程的参数化分析方法,通过研究结构在不同强度地震作用下的动力响应,评估其抗震性能。IDA方法最早于1977年由Bertero[12]提出,后经Vamvatsikos等[13]进行了系统的研究和总结,现已广泛应用于结构基于性能的抗震评估中。
IDA方法的基本思路是对结构施加一条或多条地震动记录,对每一条地震记录,将其峰值加速度(peak ground acceleration,PGA)乘以一比例因子,逐级放大,从而形成一组具有多重强度的地震动,并分别作用于结构的非线性时程分析。基于此,绘制出结构的性能参数(demand measure,DM)与地震强度参数(intensity measure,IM)之间的关系曲线,即IDA曲线。单条IDA曲线反映了结构在特定地震动作用下,从弹性状态到塑性状态直至失稳破坏的全变化过程。考虑到自然界地震动的随机性,应尽可能选取足够多的地震记录,以覆盖结构将来可能遇到的各种地震动。多条地震动记录形成的IDA曲线簇能更真实地反映结构的抗震性能,可按照一定的统计方法从概率意义上评价其地震安全性。
1.2 地震易损性分析方法地震易损性是指结构在不同强度地震动作用下达到或超过某一极限状态(limit state,LS)的条件概率,是对结构所有极限状态的概率分布描述。在基于性能的抗震设计中,通常称极限状态为性能水准,代表结构在某一特定强度地震作用下可能产生的最大损伤。地震易损性从概率意义上定量刻画了结构的抗震性能,从宏观角度描述了结构破坏程度与地震强度参数之间的关系[14]:
| $ F(x) = P(DM \ge L{S_i}\left| {IM = } \right.x) $ | (1) |
式中,x为地震动强度水平,
研究表明,DM对IM的条件概率分布一般服从对数正态分布[15],即:
| $ \begin{aligned}[b] & P(DM\ge L{S_i}\left|IM\!=\!\right.x) \!=\! 1 \!-\!P(DM{\rm{ < }}L{S_i}\left|IM =\!\right.x)\!=\\ &\quad\quad 1 -\varPhi \left(\dfrac{{{\rm{ln}}\;L{S_i} - {\mu _{{\rm{ln}}\;DM\left|IM = \right.x}}}}{{{\sigma _{{\rm{ln}}\;DM\left|IM = \right.x}}}}\right) \end{aligned}\!\!\!\!\! $ | (2) |
式中,
由于IDA方法是计算结构在不同强度地震动作用下的响应,而地震易损性分析是计算结构在不同强度地震动作用下达到或超过某一极限状态的条件概率,因此可利用IDA方法的计算结果,结合极限状态的定义,得到结构的地震易损性[16],最终建立以IM为横坐标、P为纵坐标的易损性曲线。根据地震易损性曲线,可计算不同设防水准下结构的超越概率,进而评估其抗震性能。
2 性能参数的选取结构的性能参数DM是用于定义结构破坏状态的物理量,标志着结构的抗震能力。DM的选取是进行地震易损性分析的基础,也是量化结构损伤状态的重要指标。目前,对混凝土结构基于IDA的抗震性能评价多是针对复杂高层结构,比如房屋结构、桥梁结构、混凝土坝等,常采用的DM有位移、应变、损伤指数等。
地下结构赋存于周围岩土体中,其位移会受到岩体的约束作用,导致其地震响应特性与地面结构存在诸多差异。位移、应变指标虽然能在一定程度上反映地下结构的动力响应大小,但对于极限状态的定量划分存在困难。损伤指数指标更多地被应用于重力坝地震易损性分析中,能较直观地反映结构的破坏状态,但对于结构子区域的划分、权重系数的确定较主观,最终运用于IDA分析的损伤指数为整体性指标,不能反映局部破损状态。
数值计算表明[17],受地形地质条件、结构空间形态及入射波的影响,地震作用下隧洞结构不同部位的损伤状态是不一样的,损伤系数能较全面地反映外部荷载和内部属性对结构震害的影响。基于上述认识,提出采用震后衬砌结构特征部位的损伤系数作为DM。
衬砌结构特征部位的损伤系数D通过对径向各单元损伤系数进行加权平均的方法得到:
| $ D = \sum\limits_{i = 1}^m {{D_i}{V_i}} /\sum\limits_{i = 1}^m {{V_i}} $ | (3) |
式中,
衬砌结构的损伤是混凝土内部微裂纹扩展的结果。在地震荷载循环作用下,微裂纹反复张开与闭合,使得损伤机制更加复杂。试验表明,当荷载方向变化时,混凝土的部分弹性刚度会恢复。为充分描述这一现象,损伤系数D可以写为[18]:
| $ D = 1 - (1 - {s_{\rm{t}}}{D_{\rm{c}}})(1 - {s_{\rm{c}}}{D_{\rm{t}}}) $ | (4) |
式中:
| $ \left\{ \begin{aligned} & {D_{\rm{t}}} = 1 - \exp ( - R\sqrt {\varepsilon _{\rm{t}}^{\rm{p}}\varepsilon _{\rm{t}}^{\rm{p}}} ),\\ & {D_{\rm{c}}} = 1 - \exp ( - R\sqrt {\varepsilon _{\rm{c}}^{\rm{p}}\varepsilon _{\rm{c}}^{\rm{p}}} ) \end{aligned} \right. $ | (5) |
式中,
在绘制地震易损性曲线时,性能水准的大小直接影响易损性曲线的形状。进行结构的易损性分析需要划分地震破坏等级与抗震性能水平。
Yu等[20]收集了汶川大地震震中区55座山岭隧道震害资料,通过调查分析震中距、地震烈度、埋深、地质条件与隧道震损之间的关系,将隧道震害划分为5个等级:无破坏、轻微破坏、中等破坏、严重破坏和垮塌,详细定义如表1所示。结合地面结构地震破坏等级的划分,本文也将隧洞结构划分为5个破坏等级:基本完好、轻微破坏、中等破坏、严重破坏和垮塌。
| 表1 山岭隧道震害等级划分 Tab. 1 Classification of seismic damage grades of mountain tunnel |
 |
在地下工程领域,采用损伤系数划分结构破坏等级的研究较少。刘国庆等[17]在研究隧洞洞口段结构的地震损伤特性时,通过定义损伤系数大于0.2的区域为震损区,得到了洞口段抗震设防长度,并从数值结果的角度说明了衬砌的脱开、滑移区与严重震损区(损伤系数大于0.5)分布一致。基于该研究成果,结合有关重力坝地震损伤分析成果[21],以0.05、0.20、0.50、0.80作为损伤系数限值,建立基于损伤系数指标的隧洞结构地震破坏等级划分标准,如表2所示。
| 表2 基于损伤系数的隧洞结构地震破坏等级 Tab. 2 Seismic failure grades of tunnel structure based on damage coefficient |
 |
结构的抗震性能水平是一种极限破坏状态,与某一地震强度下结构预期的最大损伤程度相对应,也即结构的抗震性能水平可通过确定不同的性能水准值定义。参照有关高层结构性能水平的划分方法[9,16],将隧洞结构的抗震性能水平划分为4级:正常使用、修复使用、生命安全、接近垮塌,并给出与地震破坏等级相对应的基于损伤系数指标的性能水准,如表3所示。
| 表3 基于损伤系数的隧洞结构抗震性能水平 Tab. 3 Seismic performance levels of tunnel structure based on damage coefficient |
 |
4 实例分析 4.1 计算模型与参数
某公路隧道位于中国西部地区,工程总长度7.6 km,最大埋深115 m。设计采用3车道标准断面形式,隧道拱部采用3心圆,侧墙为大半径圆弧,仰拱与侧墙之间用小半径圆弧连接,最大开挖尺寸15.5 m×10.2 m(宽×高)。工程区岩体以Ⅲ类为主;衬砌结构采用C30混凝土,厚0.6 m;仰拱回填材料采用C20混凝土。
选取0+300~0+360段进行分析。建立该段的3维有限元模型,全部采用8节点6面体单元进行离散,共剖分了26 720个单元和29 546个节点,其中衬砌单元2 400个。模型网格尺寸大小范围为0.2~6.0 m。模型x轴沿水平向与洞轴线垂直,y轴沿洞轴线方向,z轴与大地坐标一致,3个方向尺寸分别为120、60、175 m。有限元模型如图1所示,隧道横断面如图2所示。选取
 |
| 图1 隧道3维有限元模型 Fig. 1 3D finite element model of tunnel |
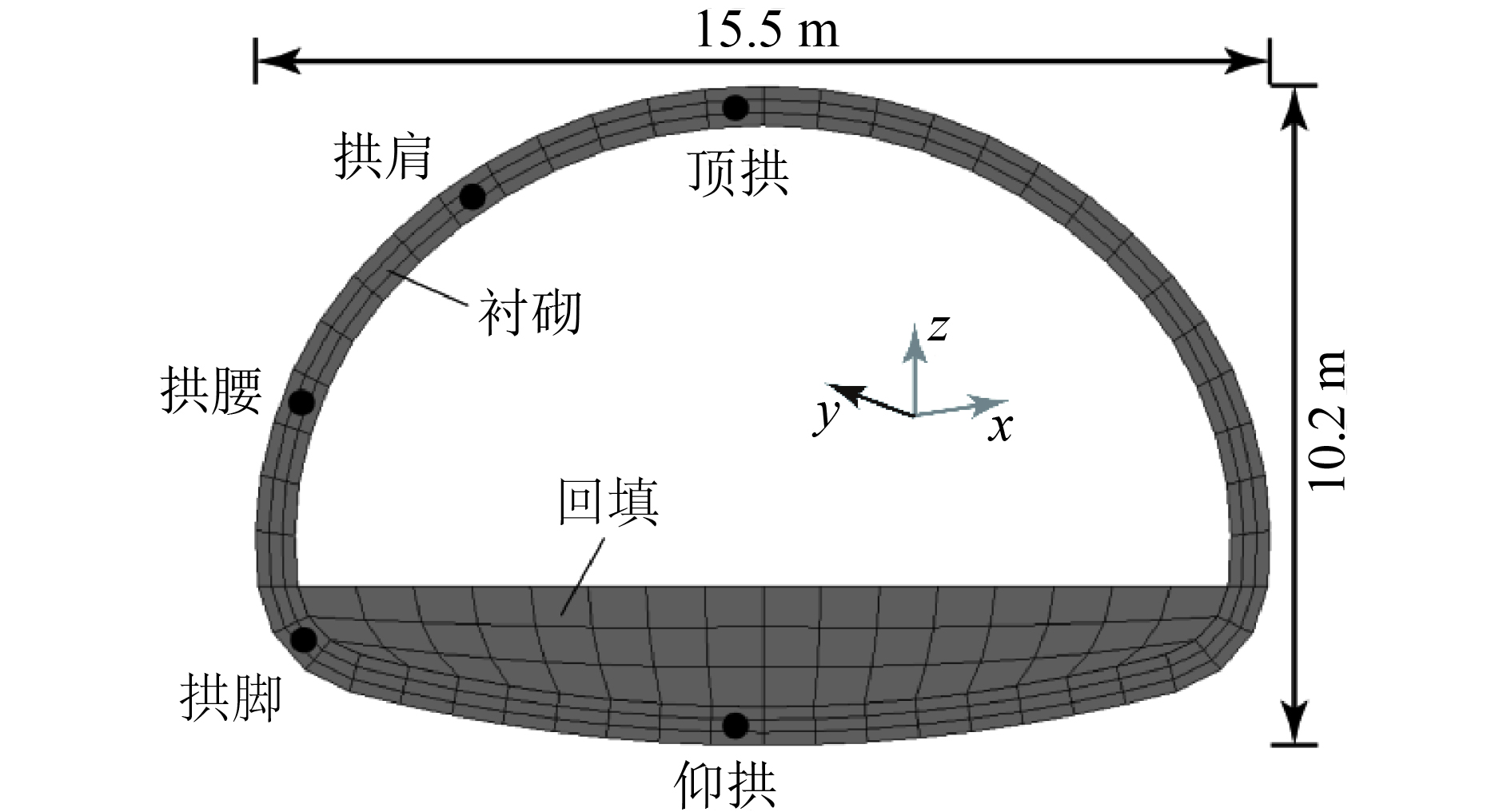 |
| 图2 隧道横断面 Fig. 2 Cross section of tunnel |
工程区3维初始地应力采取自重应力场,侧压力系数取
| 表4 材料力学参数 Tab. 4 Mechanical parameters of materials |
 |
4.2 地震动选取
根据Vamvatsikos等[13]的建议,进行结构的IDA分析时,10~20条地震动记录即可满足计算精度要求。按照来源不同,选取地震记录主要有2种方式:一是基于工程类比法,选取地震地质条件相似的实测强震记录;二是基于设计加速度反应谱,人工合成地震波。地下结构地震动输入应采用实际地震记录和人工合成波的形式,以此考虑地震动的随机性。
根据场地地震危险性分析,工程区50年超越概率10%的水平向地震动峰值加速度为0.2g,相应地震基本烈度为8度;设计反应谱最大值的代表值为2.25,特征周期0.3 s,据此绘制设计加速度反应谱。以设计反应谱为目标谱,在PEER数据库中设置搜索地震记录的限制条件:震级6.0~7.5级,震中距10~30 km,遴选了13条与场地条件吻合良好的实测地震记录。
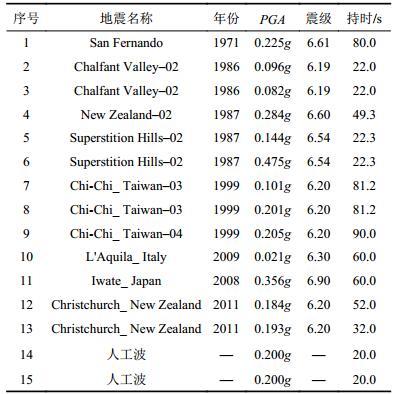
13条地震记录的加速度反应谱如图3所示。为验证所选地震波的合理性,图3中同时画出了目标谱与13条地震波反应谱的平均值(均值谱),可见二者吻合度很好,表明所选地震波能较好地反映隧洞区场地地震特性。另外,根据目标谱人工合成了2条地震波,共计15条地震波用于隧洞的IDA分析,基本信息见表5。
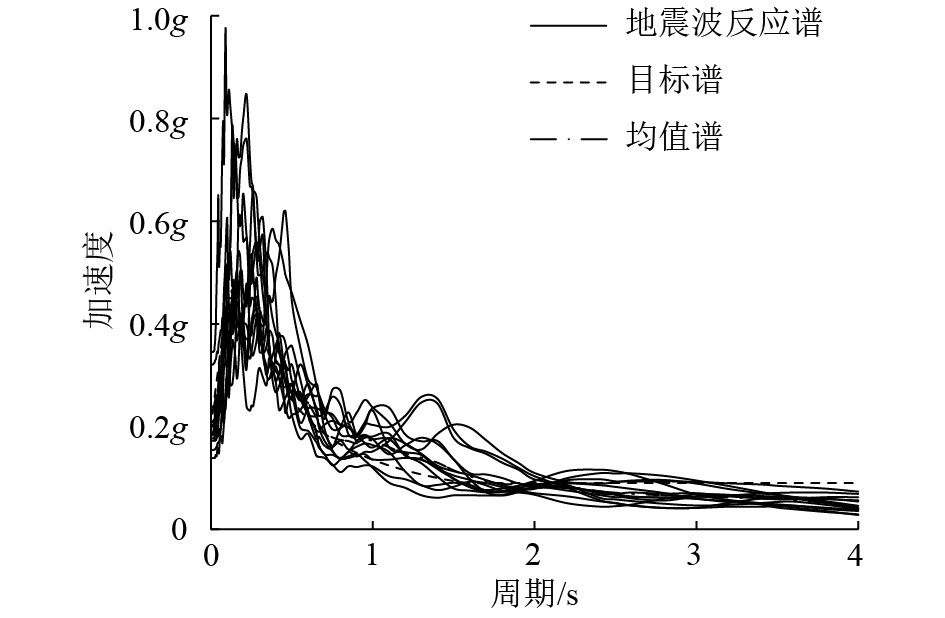 |
| 图3 地震波加速度反应谱 Fig. 3 Response spectrum of seismic wave acceleration |
| 表5 地震动记录信息 Tab. 5 Seismic records information |
 |
4.3 计算条件
IDA分析的本质是对结构进行大量的弹塑性动力时程分析,因此准确而高效的弹塑性动力分析方法是进行IDA分析的基础。计算程序采用课题组自主开发的3维弹塑性损伤动力显示有限元计算平台[19],围岩和混凝土材料采用基于Mohr–Coulomb屈服准则的弹塑性损伤动力本构模型。
有限元模型底部采用黏弹性人工边界,四周采用自由场人工边界。地震波由模型底部垂直入射,鉴于y向地震激励对隧洞结构影响较小[22],计算同时考虑x和z向地震激励,z向输入波加速度取为x向的2/3。
对选取的15条地震波按PGA进行调幅,调幅后的PGA分别为0.1g,0.2g,···,1.2g,共计180种计算方案。
4.4 计算结果分析 4.4.1 IDA分析经过上万机时的冗长计算,得到15条地震波作用下衬砌结构特征部位损伤系数与地震动强度之间的关系曲线,即IDA曲线簇,如图4所示。由图4可知,随着PGA的增加,各特征部位损伤系数呈相似的变化规律:1)当PGA<0.2g~0.4g时,损伤系数为0,表明衬砌在低强度地震作用下没有产生损伤,结构处于弹性应力状态;2)当PGA>0.2g~0.4g时,损伤系数先缓慢增加,而后近似呈指数型增长,表明在中强度地震作用下衬砌损伤的发展速度很快;3)当PGA进一步增加时,损伤系数逐渐趋近于1,衬砌面临完全破坏的风险;4)受地震波频谱特性、持时的影响,不同地震动作用下衬砌的损伤响应特性不一样。
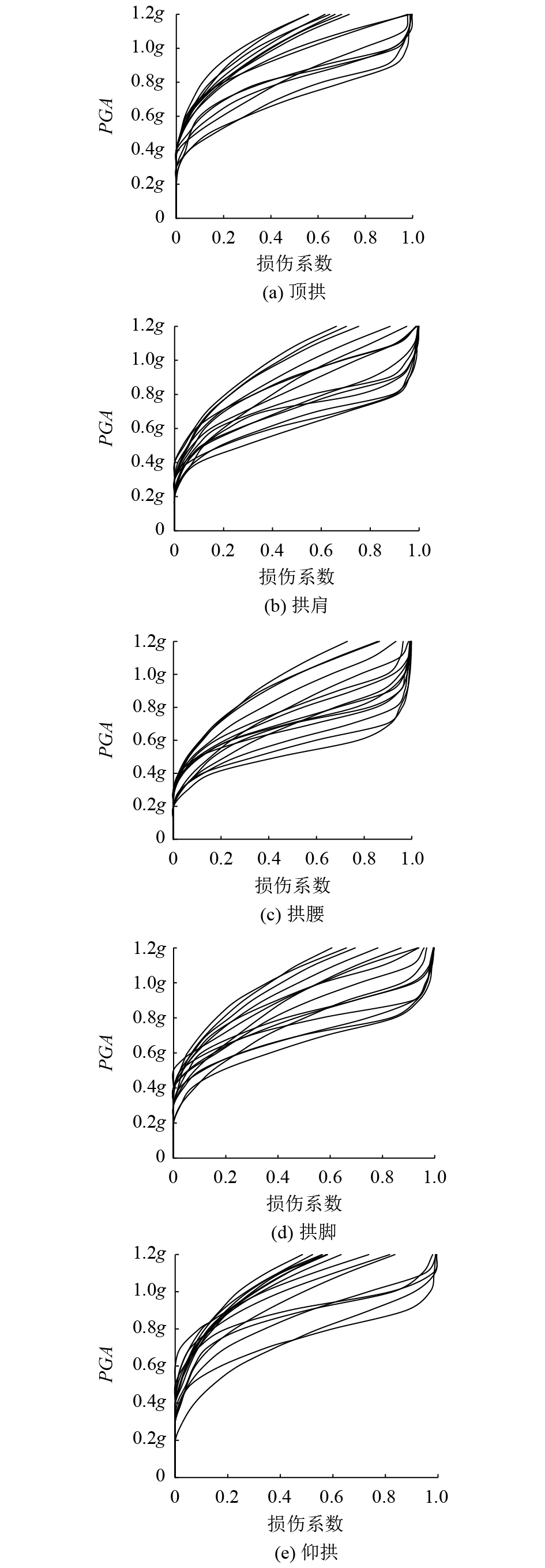 |
| 图4 衬砌特征部位IDA曲线簇 Fig. 4 IDA curves of characteristic parts of lining |
4.4.2 地震易损性分析
根据衬砌结构IDA分析结果,由式(2)计算得到不同地震强度水平下结构超过某一极限状态的概率,从而绘制出不同抗震性能水平下各特征部位的地震易损性曲线,如图5所示。
 |
| 图5 衬砌特征部位地震易损性曲线 Fig. 5 Seismic fragility curves of characteristic parts of lining |
文献[23]规定了建筑物需按照50年超越概率63%的多遇地震、50年超越概率10%的设防地震和50年超越概率5%的罕遇地震进行3级抗震设防。考虑到该隧道工程的重要性,提高一级参数,将其按照50年超越概率10%、50年超越概率5%和100年超越概率2%的3级抗震设防水准进行设防。工程区8度多遇、设防、罕遇地震的峰值加速度分别为0.2g、0.3g、0.5g,由图5可得到3级设防水准下各抗震性能水平对应的超越概率如表6所示。
| 表6 3级设防水准下的超越概率 Tab. 6 Exceeding probability under three–level fortification standards |
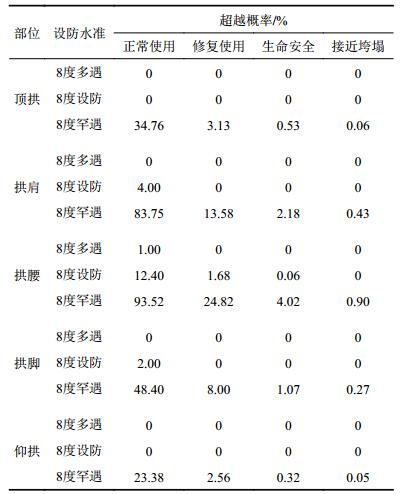 |
以最不利的拱腰为例,由表6可知:在多遇地震作用下,拱腰超越正常使用水平的概率仅为1%;在设防地震作用下,拱腰超越正常使用水平的概率为12.4%,超越修复使用水平的概率仅为1.68%;在罕遇地震作用下,拱腰超越正常使用水平的概率为93.52%,超越修复使用水平的概率为24.82%,超越生命安全水平的概率为4.02%,超越接近垮塌水平的概率仅为0.90%。
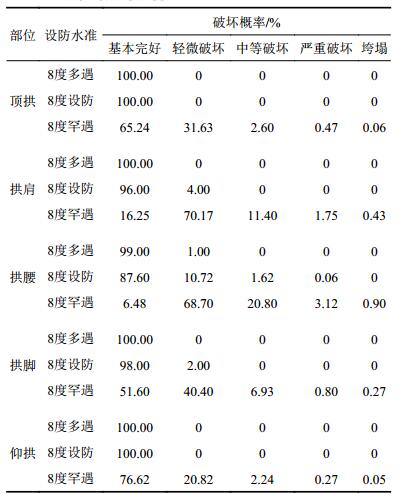
由表6可计算得到3级设防水准下各特征部位处于各破坏等级状态的概率,如表7所示。由表7可知,在多遇地震作用下,各部位基本无破坏,处于基本完好状态。在设防地震作用下,拱腰处于基本完好状态的概率为87.6%,处于轻微破坏状态的概率为10.72%,处于中等破坏状态的概率为1.62%;其他部位处于基本完好状态的概率超过96%,处于轻微破坏状态的概率不超过4%。在罕遇地震作用下,拱腰和拱肩处于基本完好状态的概率为6%~17%,处于轻微破坏状态的概率约为70%,处于中等破坏状态的概率为11%~21%,处于严重破坏状态的概率为1.5%~3.5%,处于垮塌状态的概率不超过1%;其他部位处于基本完好状态的概率为51%~77%,处于轻微破坏状态的概率为20%~41%,处于中等破坏状态的概率为2%~7%。
| 表7 3级设防水准下的破坏概率 Tab. 7 Failure probability under three–level fortification standards |
 |
综上分析可知,在8度多遇地震作用下,衬砌结构基本无破坏。在8度设防地震作用下,衬砌结构处于基本完好状态的概率较大,拱腰会出现一定概率的轻微破坏。在8度罕遇地震作用下,衬砌拱腰和拱肩处于轻微破坏状态的概率较大,仍会出现一定概率的中等破坏;拱脚、顶拱和仰拱处于基本完好和轻微破坏状态的概率均较大。因此,该隧道工程具备良好的抗震性能,地震作用下的安全性是有保障的。
在本文双向地震动输入下,受隧洞空间结构的影响,衬砌结构不同部位的抗震性能大小不同,由小到大依次为拱腰、拱肩、拱脚、顶拱和仰拱。仰拱由于受到回填混凝土的约束作用,其抗震性能略优于顶拱。因此,拱腰、拱肩和拱脚可作为衬砌抗震设计的薄弱部位。
5 结 论1)将IDA方法引入隧洞结构地震动力稳定性评估领域,建立基于损伤系数指标的隧洞结构抗震性能评估方法。该方法较好地考虑了地震动的随机性,能够得到衬砌结构不同部位在不同地震强度、不同抗震性能水平下的超越概率,进而可全面评估隧洞结构的抗震性能,为隧洞结构抗震安全评价提供一种有效途径。
2)探讨了选取损伤系数作为结构性能参数的原则和依据,确定了适用于隧洞结构抗震安全评价的5级破坏划分标准(基本完好、轻微破坏、中等破坏、严重破坏、垮塌)和4级抗震性能水平(正常使用、修复使用、生命安全、接近垮塌),为结构地震易损性分析提供了基础。
3)以某隧道工程为例,研究了衬砌结构的抗震性能特性。结果表明:在8度多遇地震作用下,衬砌结构基本无破坏;在8度设防地震作用下,衬砌结构处于基本完好状态的概率较大;在8度罕遇地震作用下,衬砌结构处于轻微破坏状态的概率较大。
4)衬砌结构不同部位的抗震性能大小不同,在双向地震动输入下,衬砌拱腰、拱肩、拱脚、顶拱、仰拱抗震性能依次增大,因而拱腰、拱肩和拱脚可作为衬砌抗震设计的薄弱部位。
作者建立的基于损伤系数指标的隧洞结构地震破坏等级划分标准,虽然能较直观地反映结构的破坏状态,但对于性能水准的取值有较大的经验性。为使隧洞结构的地震易损性分析更加科学合理,还需结合大量工程案例,从震害调查、模型试验和数值模拟等方面对此进行更深入的研究。
| [1] |
Sharma S,Judd W R. Underground opening damage from earthquakes[J]. Engineering Geology, 1991, 30(3/4): 263-276. DOI:10.1016/0013-7952(91)90063-Q |
| [2] |
He C,Koizumi A. Study on seismic behavior and seismic design methods in transverse direction of shield tunnels[J]. Structural Engineering and Mechanics, 2001, 11(6): 651-662. DOI:10.12989/sem.2001.11.6.651 |
| [3] |
Asakura T,Sato Y. Mountain tunnels damage in the 1995 Hyogoken-Nanbu Earthquake[J]. Quarterly Report of the Railway Technical Research Institute, 1998, 39: 9-16. |
| [4] |
Wang W L,Wang T T,Su J J,et al. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 133-150. DOI:10.1016/S0886-7798(01)00047-5 |
| [5] |
Wang Z Z,Gao B,Jiang Y J,et al. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan Earthquake[J]. Science in China (Series E), 2009, 52(2): 546-558. DOI:10.1007/s11431-009-0054-z |
| [6] |
Chen Z Y,Shi C,Li T B,et al. Damage characteristics and influence factors of mountain tunnels under strong earthquakes[J]. Natural Hazards, 2012, 61(2): 387-401. DOI:10.1007/s11069-011-9924-3 |
| [7] |
徐华,李天斌,王栋,等. 山岭隧道地震动力响应规律的三维振动台模型试验研究[J]. 岩石力学与工程学报, 2013, 32(9): 1762-1771. DOI:10.3969/j.issn.1000-6915.2013.09.005 |
| [8] |
Yu H T,Chen J T,Bobet A,et al. Damage observation and assessment of the Longxi tunnel during the Wenchuan Earthquake[J]. Tunnelling and Underground Space Technology, 2016, 54: 102-116. DOI:10.1016/j.tust.2016.02.008 |
| [9] |
张令心,徐梓洋,刘洁平,等. 基于增量动力分析的超高层混合结构地震易损性分析[J]. 建筑结构学报, 2016, 37(9): 19-25. DOI:10.14006/j.jzjgxb.2016.09.003 |
| [10] |
Argyroudis S A,Pitilakis K D. Seismic fragility curves of shallow tunnels in alluvial deposits[J]. Soil Dynamics and Earthquake Engineering, 2012, 35: 1-12. DOI:10.1016/j.soildyn.2011.11.004 |
| [11] |
Qiu W G,Huang G,Zhou H C,et al. Seismic vulnerability analysis of rock mountain tunnel[J]. International Journal of Geomechanics, 2018, 18(3): 1-16. DOI:10.1061/(ASCE)GM.1943-5622.0001080 |
| [12] |
Bertero V V.Strength and deformation capacities of buildings under extreme environments[C]//Pister K S.Structural Engineering and Structural Mechanics.New Jersey:Prentice-Hall Englewood Cliffs,1977:211–215.
|
| [13] |
Vamvatsikos D,Cornell C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514. DOI:10.1002/eqe.141 |
| [14] |
周奎,李伟,余金鑫. 地震易损性分析方法研究综述[J]. 地震工程与工程振动, 2011, 31(1): 106-113. DOI:10.13197/j.eeev.2011.01.022 |
| [15] |
Karim K R,Yamazaki F. Effect of earthquake ground motions on fragility curves of highway bridge piers based on numerical simulation[J]. Earthquake Engineering and Structural Dynamics, 2001, 30(12): 1839-1856. DOI:10.1002/eqe.97 |
| [16] |
吕西林,苏宁粉,周颖. 复杂高层结构基于增量动力分析法的地震易损性分析[J]. 地震工程与工程振动, 2012, 32(5): 19-25. DOI:10.13197/j.eeev.2012.05.017 |
| [17] |
刘国庆,肖明,陈俊涛,等. 强震区隧洞洞口段地震响应数值模拟研究[J]. 中南大学学报(自然科学版), 2018, 49(11): 2804-2812. DOI:10.11817/j.issn.1672-7207.2018.11.022 |
| [18] |
赵宝友,马震岳,梁冰,等. 基于损伤塑性模型的地下洞室结构地震作用分析[J]. 岩土力学, 2009, 30(5): 1515-1521. DOI:10.16285/j.rsm.2009.05.057 |
| [19] |
张志国,肖明,陈俊涛. 大型地下洞室地震灾变过程三维动力有限元模拟[J]. 岩石力学与工程学报, 2011, 30(3): 509-523. DOI:10.3969/j.issn.1000-6915.2011.03.010 |
| [20] |
Yu H T,Chen J T,Yuan Y,et al. Seismic damage of mountain tunnels during the " 5·12” Wenchuan Earthquake[J]. Journal of Mountain Science, 2016, 13(11): 1958-1972. DOI:10.1007/s11629-016-3878-6 |
| [21] |
王超,张社荣,黎曼,等. 基于损伤指数模型的重力坝地震破坏等级划分[J]. 地震工程与工程振动, 2014, 34(6): 218-226. DOI:10.13197/j.eeev.2014.06.218.wangc.027 |
| [22] |
Wang Jinghe.Seismic response analysis for mountain tunnel portals in high steep slope based on wave theory[D].Chengdu:Southwest Jiaotong University,2016. 汪精河.基于波动理论的高陡边坡山岭隧道洞口地震响应分析[D].成都:西南交通大学,2016. |
| [23] |
中华人民共和国国家标准编写组.GB50011—2010:建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.
|
 2019, Vol. 51
2019, Vol. 51


