2. 华东师范大学 河口海岸学国家重点实验室,上海 200241;
3. 中国水利水电科学研究院 泥沙研究所,北京 100048
2. State Key Lab. of Estuarine and Coastal Research, East China Normal Univ., Shanghai 200241;
3. China Inst. of Water Resources and Hydropower Research, Beijing 100048, China
长期以来,众多学者通过水槽试验、实测资料、数值模拟等方法研究河流交汇区的水流运动规律。水槽试验研究方面,Brion等[1]指出了干支流河床高差对汇流区的水流运动结构和掺混过程的影响;Guillén-Ludeña等[2]认为在干流以泄洪为主,而支流以挟沙为主的山区河流中,汇流比、入汇角及支流的强挟沙能力是水动力学特性的主要控制因素;王平等[3]研究了交汇角对黄河上游高含沙交汇区的水流分区特性及沙坝淤坝规模特性的影响;贾猛[4]提出了干流的流速、环流强度、水面比降等水力特性在支流入汇弯道干流时,随入汇角和汇流比的变化情况;Wuppukondur等[5]指出如何控制由于交汇区二次环流导致的河床侵蚀。实测资料方面,兰波[6]分析了山区河流交汇口干支流的来水来沙特性以及交汇口处江心洲的形式;候志强等[7]利用伯努利方程推导出了水位随汇流比变化的规律;Riley等[8]研究了干流凹岸一侧汇入支流时交汇区的3维水流结构,以及动量比对河床地形的影响;黄莉等[9]分析了三峡水库蓄水后关洲河段的河势变化及其对松滋口分流的影响。数值模拟方面,王协康等[10]研究了交汇区的分离区、剪切层及交汇口下游的螺旋流的变化特性;张光碧等[11]利用VOF模型模拟计算了大渡河与楠桠河交汇处的流场,并根据数模计算结果和原位试验提出了固岸护堤措施;刘盛赟等[12]利用水气两相流模型分析了交汇角、动量比及能量比对交汇区水动力学参数的影响;Schindfessel等[13]利用大涡模拟的方法比较了直角交汇中,支流流量占总流量的75%、95%和100%时的3维水动力特征,发现支流对入汇对岸的撞击使得交汇区上游产生循环涡流,而下游的螺旋流和上升流也因此增强;付中敏[14]通过3维数学模型,研究了长江与沱江交汇区在不同流量组合条件下的水流运动特性,并建立了弯曲干流交汇河道中分离区的长和宽与汇流比和入汇角之间的关系;周苏芬[15]基于数值模拟技术提出了针对入汇角为90°的交汇河道中的分离区的堤线优化整流方案;Penna等[16]研究了入汇角对交汇河道内的水流停滞区、流向偏转区、分离区和顺流向速度的影响。
岷江都江堰河段的来水来沙取决于岷江上游和支流白沙河的水沙特性。岷江都江堰河段突出的河床形态特征主要表现在岷江出关口河道急剧展宽,且白沙河入汇岷江,交汇区水流运动复杂多变,河床形态演变极为复杂。当岷江出现较大洪水时,常给都江堰水利工程和成都平原带来巨大灾害。2006年紫坪铺水库建成后,岷江干流的洪水得到了有效的控制,但白沙河的洪水仍会对都江堰枢纽区及下游的水安全造成极大的威胁。白沙河属典型山区河流,洪枯流量变化大,实测年最大洪峰流量1 450 m3/s(1972年8月),调查历史洪水流量1 710 m3/s(1923年),2010年8月18日20时至8月19日16时,都江堰市白沙河流域普降暴雨至大暴雨,白沙河发生特大洪水,河口杨柳坪水文站洪峰流量达1 510 m3/s,引发洪水灾害,导致成都市饮用水源中断数天。岷江都江堰河段交汇区,河道平均宽度由75 m增加至400 m,平均比降从0.82%降低为0.4%,河道展宽突出、比降大,水深相对较浅,属于典型的山区河流,为此采用平面二维数值模拟方法,对岷江干流与支流白沙河交汇区水流运动规律进行探讨,以揭示白沙河入汇岷江交汇区的水流运动特点,可为该河段防洪、河道整治等提供一定的科学依据。
1 模型的建立本文计算区域共包含4个开边界(见图1):上边界1选在紫坪铺水库下游的顺直河段,位于岷江与白沙河交汇口以上1.0 km左右;上边界2选在白沙河上,距离岷江与白沙河交汇口也约1.0 km;两个下边界分别位于内、外江河口水文站。数学模型的基本控制方程包括:
 |
| 图1 计算区域与网格划分 Fig. 1 Calculated region and grid partition |
水流连续方程:
| $ \frac{\partial h}{\partial t}+\frac{\partial h\bar{u}}{\partial x}+\frac{\partial h\bar{v}}{\partial y}=hs $ | (1) |
动量方程:
| $ \begin{aligned}[b] \frac{\partial h\bar{u}}{\partial t} & +\frac{\partial h{{{\bar{u}}}^{2}}}{\partial x}+\frac{\partial h{\overline v}\,{\overline u}}{\partial y}=f\bar{v}h-gh\frac{\partial \eta }{\partial x}-\frac{h}{{{\rho }_{0}}}\frac{\partial {{p}_{\rm a}}}{\partial x}\\ &-\frac{g{{h}^{2}}}{2{{\rho }_{0}}}\frac{\partial \rho }{\partial x}+ \frac{{{\tau }_{{\rm s}x}}}{{{\rho }_{0}}}-\frac{{{\tau }_{{\rm b}x}}}{{{\rho }_{0}}}-\frac{1}{{{\rho }_{0}}}\left( \frac{\partial {{s}_{xx}}}{\partial x}+\frac{\partial {{s}_{xy}}}{\partial y} \right)\\ &+\frac{\partial }{\partial x}\left( h{{T}_{xx}} \right)+\frac{\partial }{\partial y}\left( h{{T}_{xy}} \right)+h{{u}_{{\rm s}}}S \end{aligned} $ | (2) |
| $ \begin{aligned}[b] \frac{{\partial h\bar v}}{{\partial t}} & + \frac{{\partial h{\overline u}\,{\overline v} }}{{\partial x}} + \frac{{\partial h{{\bar v}^2}}}{{\partial y}} = - f\bar uh - gh\frac{{\partial \eta }}{{\partial y}} - \frac{h}{{{\rho _0}}}\frac{{\partial {p_{\rm a}}}}{{\partial y}} \\ & - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial y}} + \frac{{{\tau _{{\rm s}y}}}}{{{\rho _0}}} - \frac{{{\tau _{{\rm b}y}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{yy}}}}{{\partial y}} + \frac{{\partial {s_{yx}}}}{{\partial x}}} \right) \\ &+ \frac{\partial }{{\partial x}}\left( {h{T_{xy}}} \right) + \frac{\partial }{{\partial y}}\left( {h{T_{yy}}} \right) + h{v_{\rm s}}S \end{aligned} $ | (3) |
式中:x、y为直角坐标系坐标;t为时间变量;
模型基于Mike21软件建立,利用有限体积法求解基本方程的数值解。采用无结构三角形网格对研究河段进行网格划分,并对岷江与白沙河交汇区进行了网格加密,同时也加密了鱼嘴附近区域。最后共生成网格5 905个,计算节点3 174个,加密部分的最大网格面积为300 m2,其他地方的最大网格面积为600 m2。利用实测天然地形,对网格地形进行插值,并利用紫坪铺和杨柳坪水文站的流量作为上边界的控制条件,而下边界则分别采用内、外江河口水文站所测的水位流量关系控制。
2 模型的验证文献[17]指出都江堰河段的河床质主要为不均匀砂卵石,最大粒径可达0.51 m,文献[18]利用3维激光扫描系统测量了都江堰外江3 m×3 m范围内的糙率,认为该河段的糙率在0.030~0.035之间。基于河段的河床质特性和实测资料,选择0.033作为模型糙率,并结合水位及流量资料,选择了1969—1973年这5年中的6—9月的汛期实测资料验证模型。
点绘实测及计算流量关系,如图2和3所示,其中内、外江实测流量分别为1969—1973年内6—9月这20个月的内、外江月平均流量实测值Q1、Q2,对应的计算流量为Q1′、Q2′。将内、外江各20个月的流量误差值取了平均,再将两个平均误差再取平均可得n=0.033时对应的流量平均误差值为10.52%。
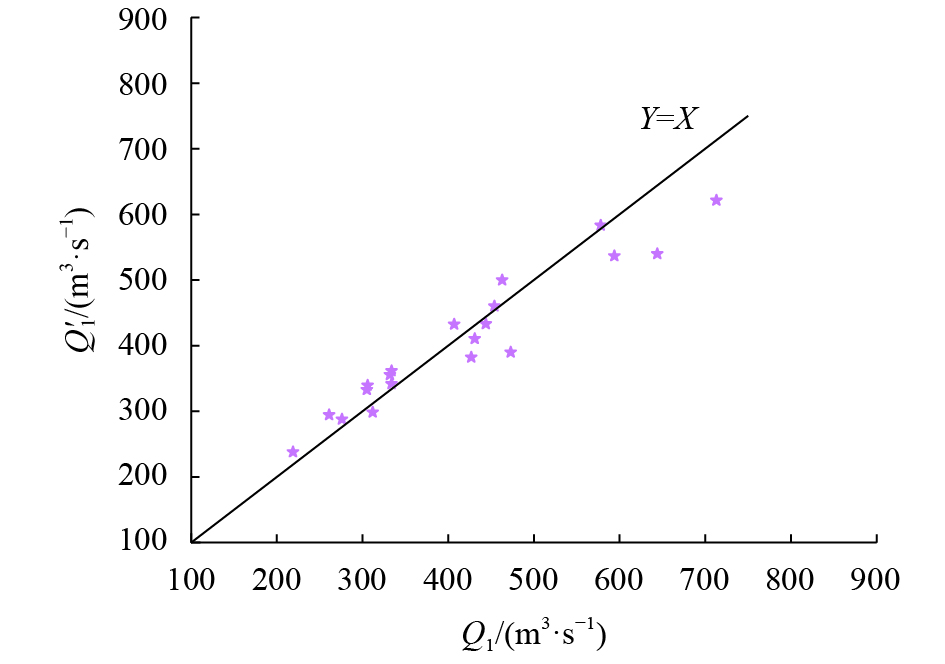 |
| 图2 内江河口站实测及计算流量关系 Fig. 2 Measured-calculated discharge of inner river station |
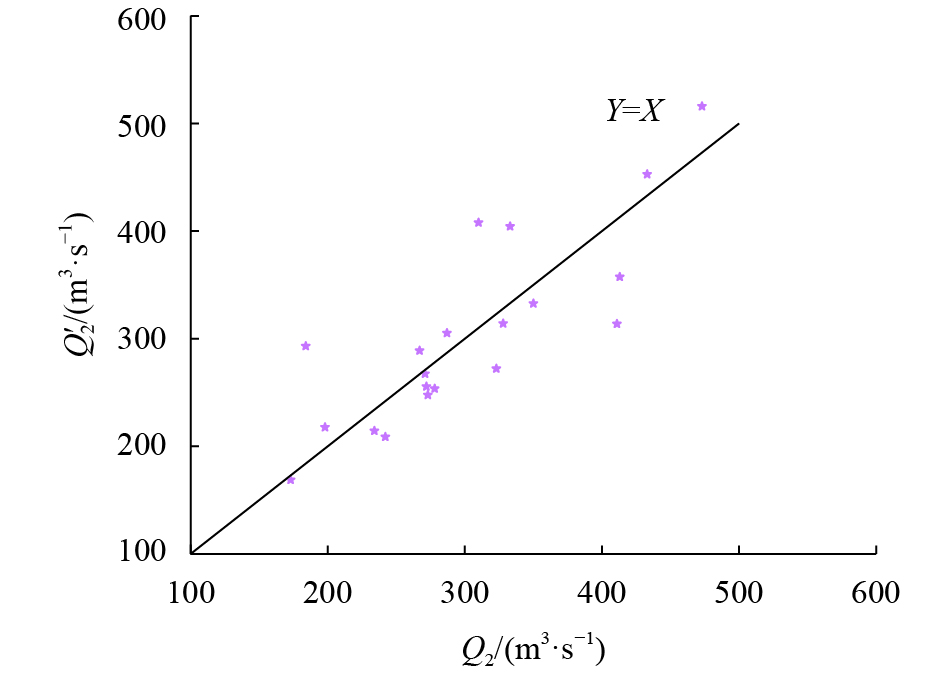 |
| 图3 外江河口站实测及计算流量关系 Fig. 3 Measured-calculated discharge of outer river station |
此外,将内、外江水文站断面的模拟水位与实测水位比较,将20个月对应的内、外江水位模拟值与实际值的差值分别取平均,再将所得的两个平均值再平均可得n=0.033时对应的水位差值为0.20 m。综上所述,模型糙率为0.033时,流量平均误差10.52%,水位平均差值0.20 m,误差基本能满足模型验证的要求,因而以此为基础进行之后的模拟计算。
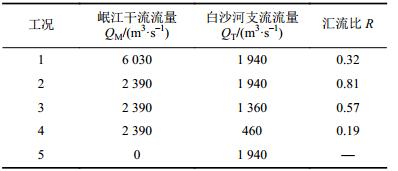
3 计算成果分析2006年,紫坪铺水库建成后,可充分利用库容进行调峰补枯,对百年一遇(洪峰流量为6 030 m3/s)及以下的洪水均采用限制泄流的方式进行调洪,即频率不超过百年一遇的洪水经过紫坪铺水库的调节,最大下泄流量均为2 390 m3/s。而白沙河支流的百年一遇、二十年一遇、两年一遇洪水的洪峰流量分别为1 940、1 360、460 m3/s。考虑岷江干流与白沙河支流的洪水组合效应,初步讨论如下模拟工况(见表1),其中汇流比R为支流白沙河流量QT与岷江干流流量QM的比值,即R=QT/QM。
| 表1 模拟工况 Tab. 1 Simulated cases |
 |
取LS1、LS2、LS3这3个纵断面和CS1~CS10 10个横断面,如图4所示,其中LS1从岷江干流入口(上边界1)直到内江出口断面,全长约3.68 km;LS2从上边界1到外江出口断面,全长约3.67 km;LS3从白沙河支流入口(上边界2)开始,到与LS2相交的点为止,全长0.73 km;CS1为入汇前岷江干流的关口区域(最窄断面),CS2则位于白沙河支流,CS3~CS10这8个断面之间的距离均为20 m。
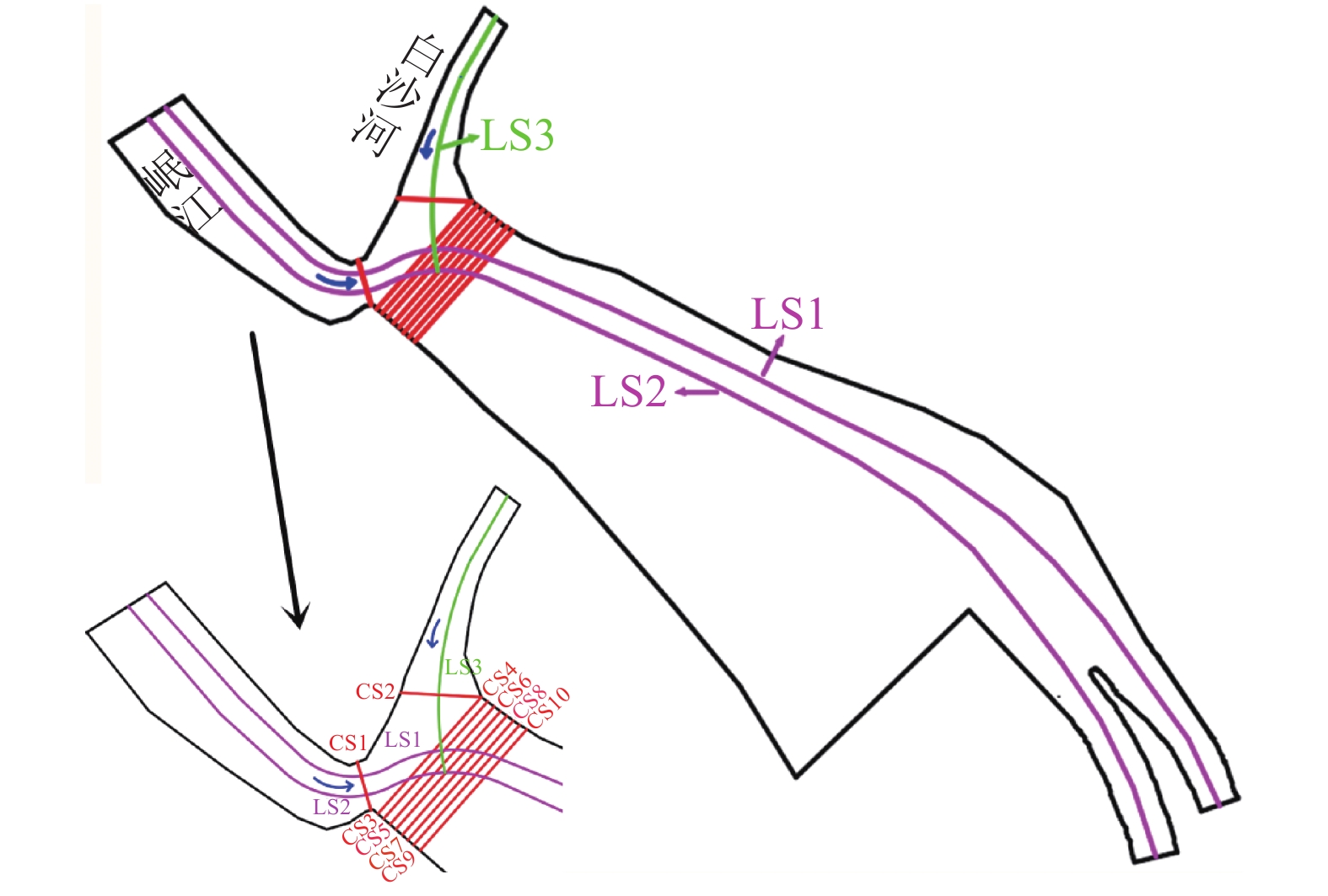 |
| 图4 断面布置 Fig. 4 Layout of section |
3.1 交汇区水流运动特性
LS1处于岷江干流左侧深泓线,LS2处于右侧深泓线,两者受到干支水流交汇的挤压作用不同。点绘干支流交汇区上下游一定范围内的水位、流速变化,如图5~8所示。受河道展宽、河床高程降低及干支水流相互作用影响,图5和7中CS1断面之后的一段距离内水位均沿程先增后降,干支流顶托壅水区和掺混区范围存在较大差异,LS1 和LS2掺混区纵向范围从约300 m减少到约100 m,而LS2的干流壅水范围比LS1更大。LS1和LS2流速变化,在掺混区均呈先减小后增加的特点,在干流来流恒定时,支流来流越小,受支流挤压作用减小,沿程流速变得越大。
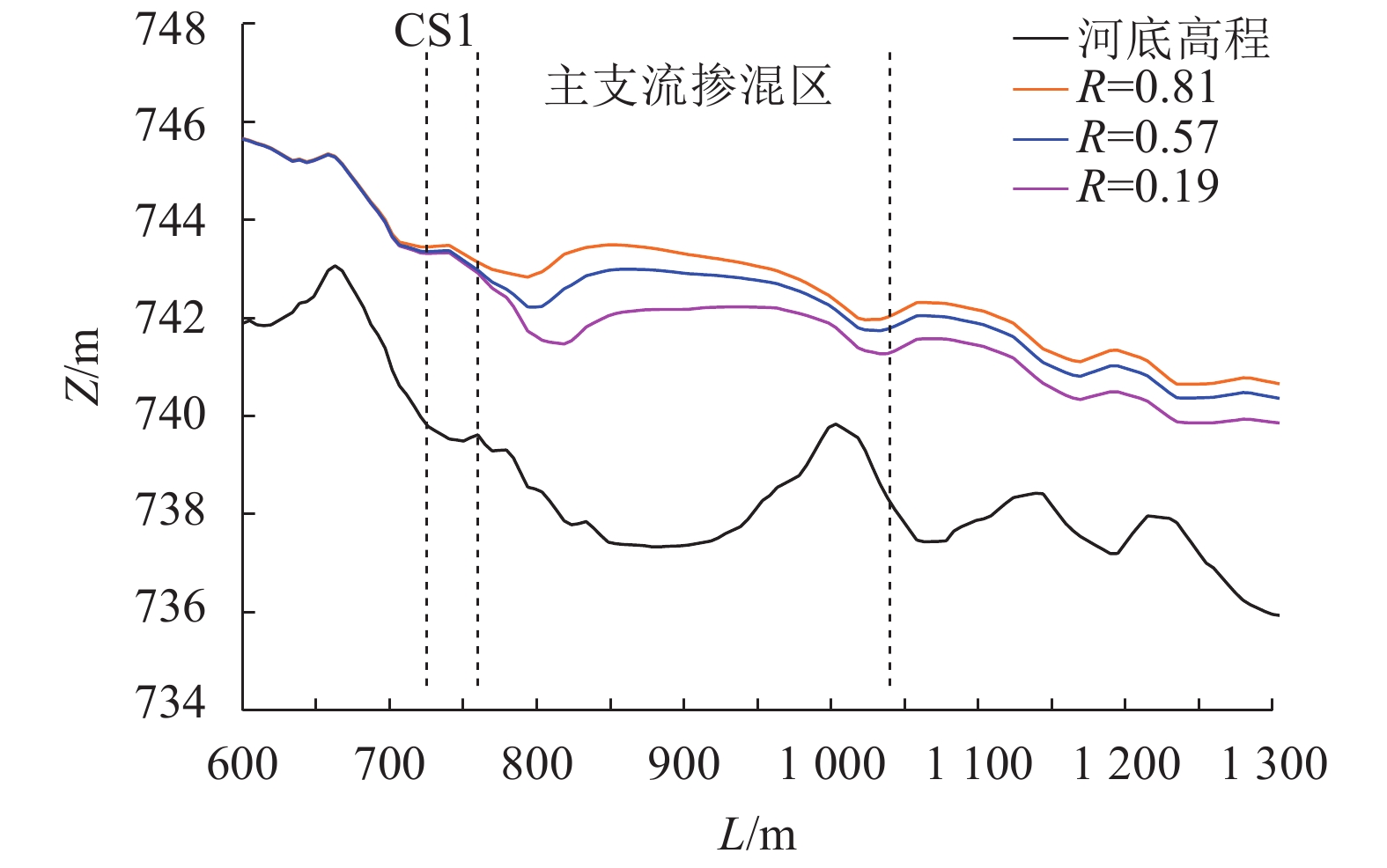 |
| 图5 LS1交汇区沿程水位 Fig. 5 Water level of LS1 at confluence zone |
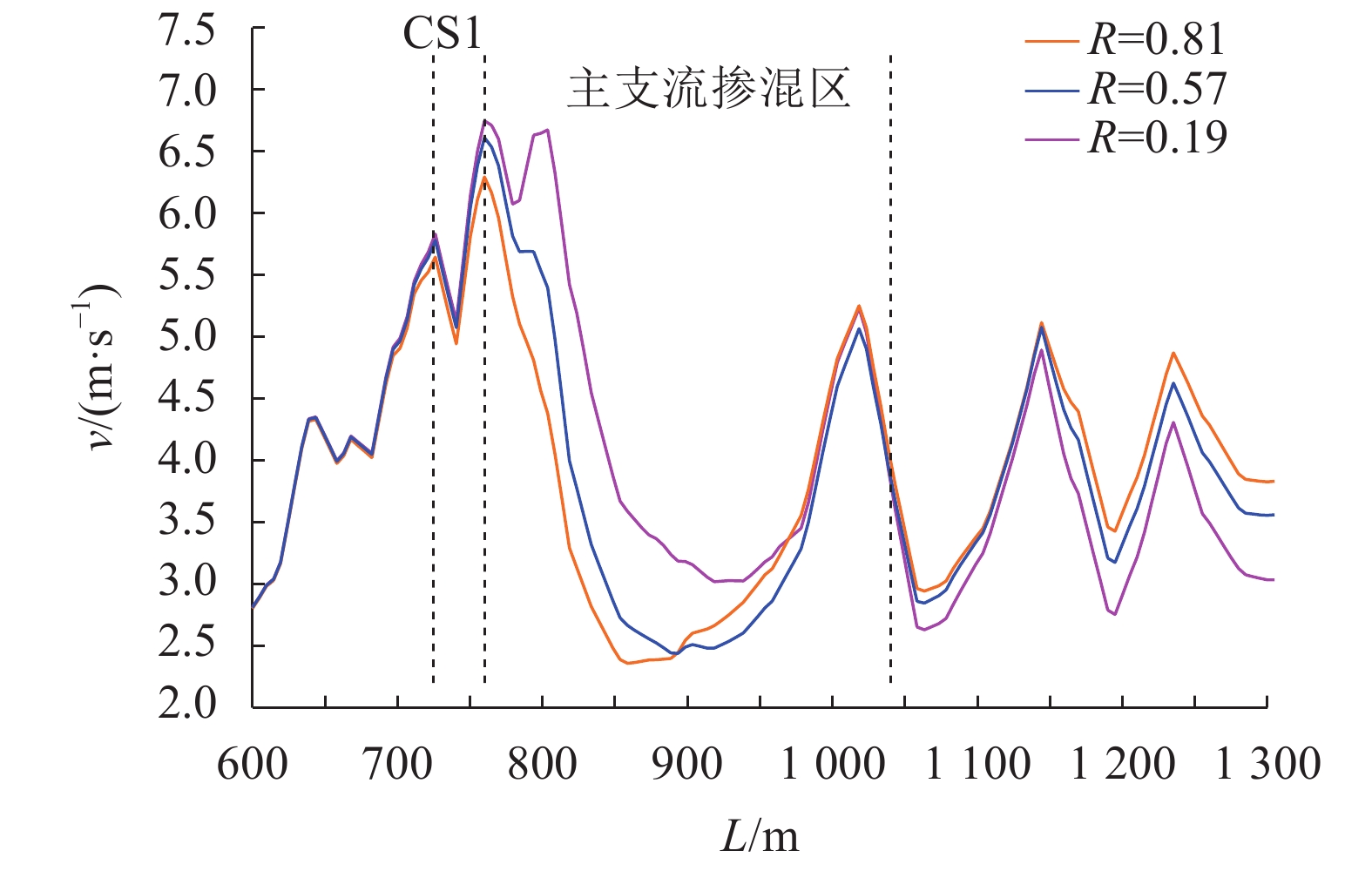 |
| 图6 LS1交汇区沿程流速 Fig. 6 Velocity of LS1 at confluence zone |
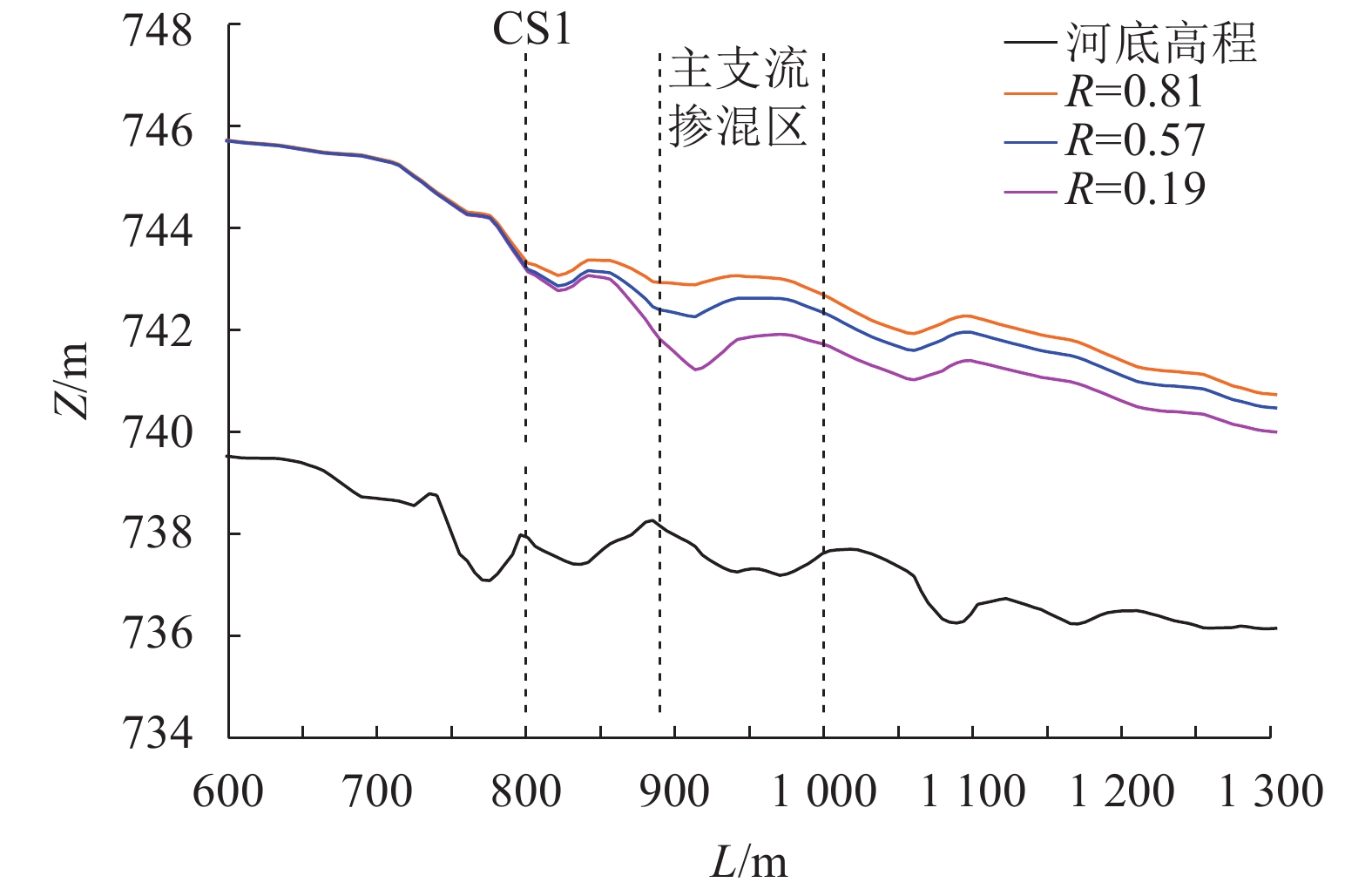 |
| 图7 LS2交汇区沿程水位 Fig. 7 Water level of LS2 at confluence zone |
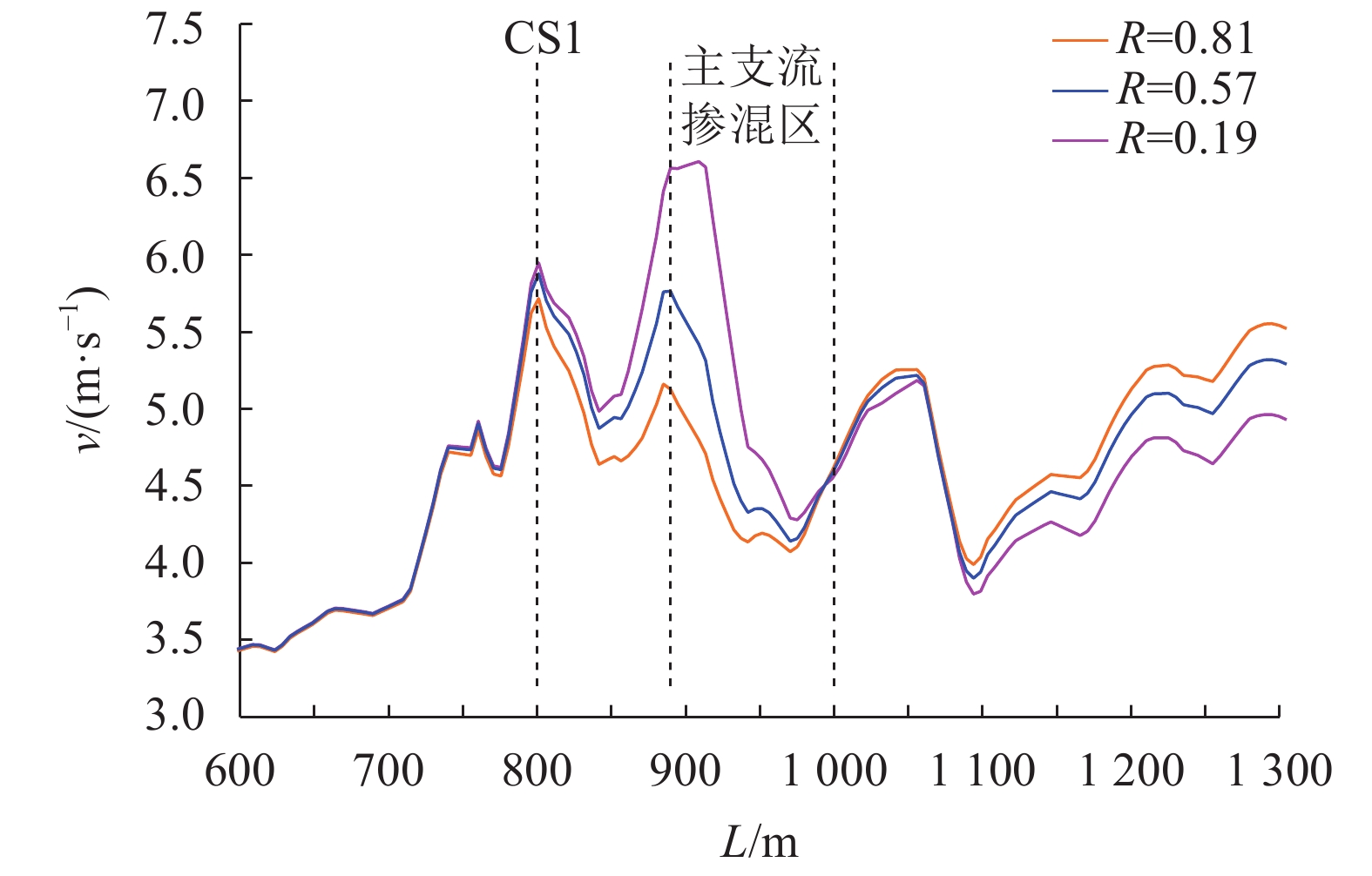 |
| 图8 LS2交汇区沿程流速 Fig. 8 Velocity of LS2 at confluence zone |
以横断面CS3、CS5、CS7、CS9的流速分析为例(图9),CS3和CS5的水流运动受支流挤压作用,水流高速区偏向右岸,流速在右岸一侧达到最大值,从而产生挤压高速区。汇流比R越大,最高流速出现的位置越靠右岸,支流对干流的挤压越强,高速带越窄。而CS7及CS9的最大流速则逐渐移到断面中部,且干支流汇合后总流量越大的流速也越大,说明该区域受干支水流交汇挤压作用减小。
 |
| 图9 典型断面的横向流速分布(横向距离:河道右岸至左岸) Fig. 9 Velocity distribution at typical cross section |
3.2 交汇区的水流分区特征
结合交汇区纵、横断面的水位及流速变化,可知白沙河入汇岷江交汇区时水流运动存在明显的分区特征,如图10所示,根据不同位置的特征点(A~H)便可确定不同分区:壅水低速区、挤压高速区、干支流掺混区,如A、B点之间为干支流掺混区,流速随QT的减小而增大。图10的各特征点在干支来流变化时会随之变化,即汇流比R不同,掺混区的位置也会有所改变,当R较小时,干流向支流方向顶冲的较多,位置就会更靠近支流,而掺混范围则会略小一些。
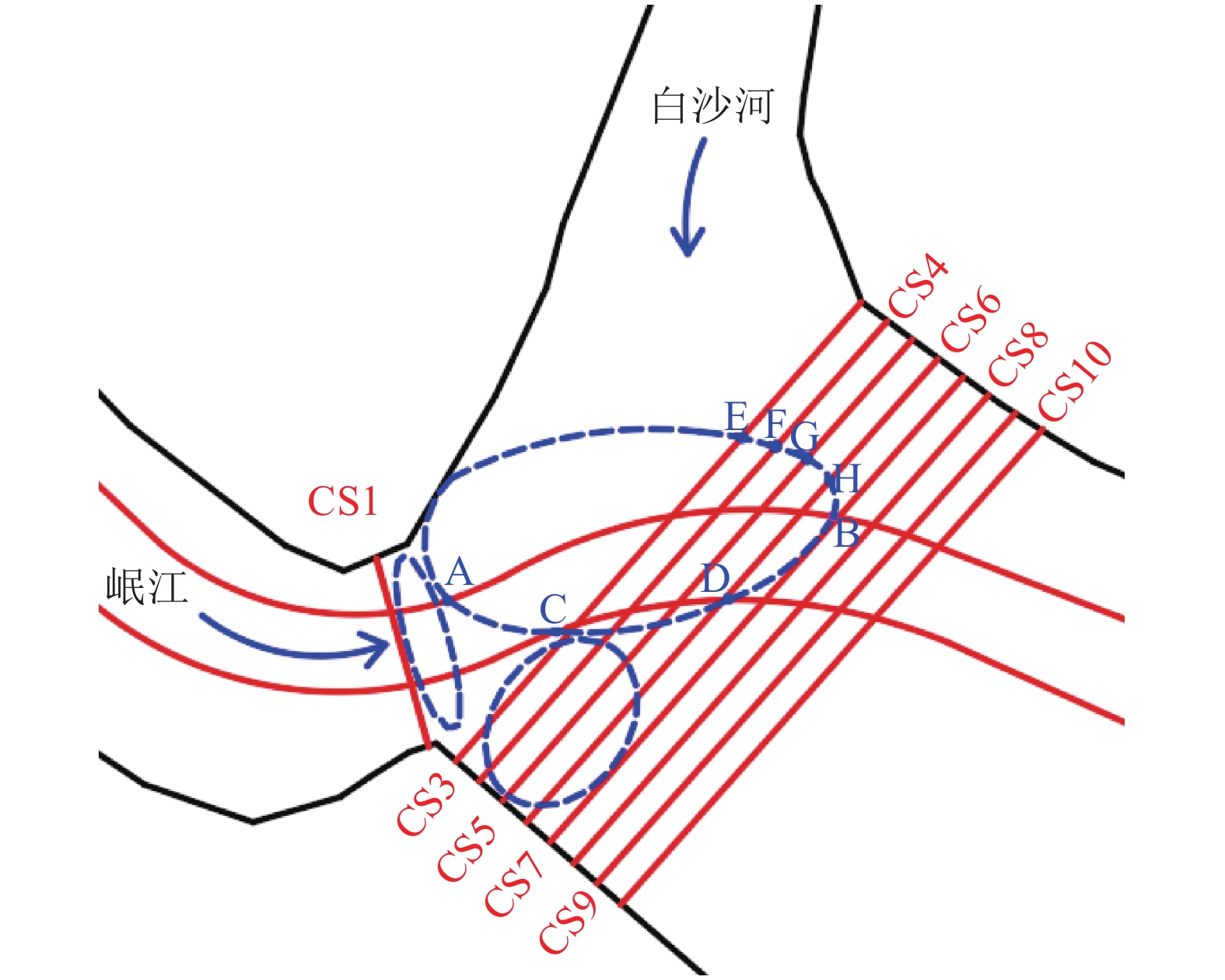 |
| 图10 交汇区分区示意图 Fig. 10 Subregion of confluence zone |
除了上述的3个典型分区外,河流交汇还会在支流入汇侧的干流下游一段距离内出现流速低、紊动强度低、压强低的分离区。有学者认为水流从交汇河道的内壁分离之后,它的重新贴壁流动将会延伸到下游,所以会在水流脱壁处产生具有水平环流的分离区[19]。支流汇入干流时,受到干流的顶冲,流向改变,但是由于惯性,流向并不能立刻改变成与干流一致而继续顺着干流河道贴壁流动,而是会形成流向改变的弧线,弧线与干流河岸之间便会产生分离区。
以分流比R分别为0.81、0.57和0.19的工况2、3、4的交汇区流场图为例来探讨其分区规律,见图11~13。结果表明,白沙河入汇岷江,支流汇入的左岸区域回流分离区较小,究其原因,主要是白沙河的弧形左岸使得支流流向改变的弧形能很好地契合于岸线,让流向自然得到调整,这便极大地降低了与其产生脱离的可能性,即有效地减小了分离区产生的可能与范围。
 |
| 图11 工况2(R=0.81)交汇部分流场 Fig. 11 Flow field of case 2 at confluence zone |
 |
| 图12 工况3(R=0.57)交汇部分流场 Fig. 12 Flow field of case 3 at confluence zone |
 |
| 图13 工况4(R=0.19)交汇部分流场 Fig. 13 Flow field of case 4 at confluence zone |
3.3 干流对支流的顶托作用
干流受到支流的顶托产生壅水的同时,支流也会被干流顶托。图14、15分别为工况1(R=0.32)和2(R=0.81)的水位等值线图,它们的QT均为1 940 m3/s,不同的是QM分别为6 030、2 390 m3/s。由图14、15可知,在支流入口之后的一定距离内,两个工况对应位置处的水位相同,说明干流没有影响到这一范围内水流,而再往下游,水位就开始出现较大差距,QM越大的,相同位置的水位也越高。
 |
| 图14 工况1(R=0.32)水位等值线 Fig. 14 Water level isoline of case 1 |
 |
| 图15 工况2(R=0.81)水位等值线 Fig. 15 Water level isoline of case 2 |
为了更直观地分析支流受到顶托而产生壅水的情况,点绘LS3(白沙河支流深泓线)在各工况下的沿程水位及流速变化,如图16和17所示,为突出白沙河来流未受顶托影响,特讨论了QM为0的工况5,其QT和工况1、2(R=0.32、R=0.81)相同,均为1 940 m3/s。
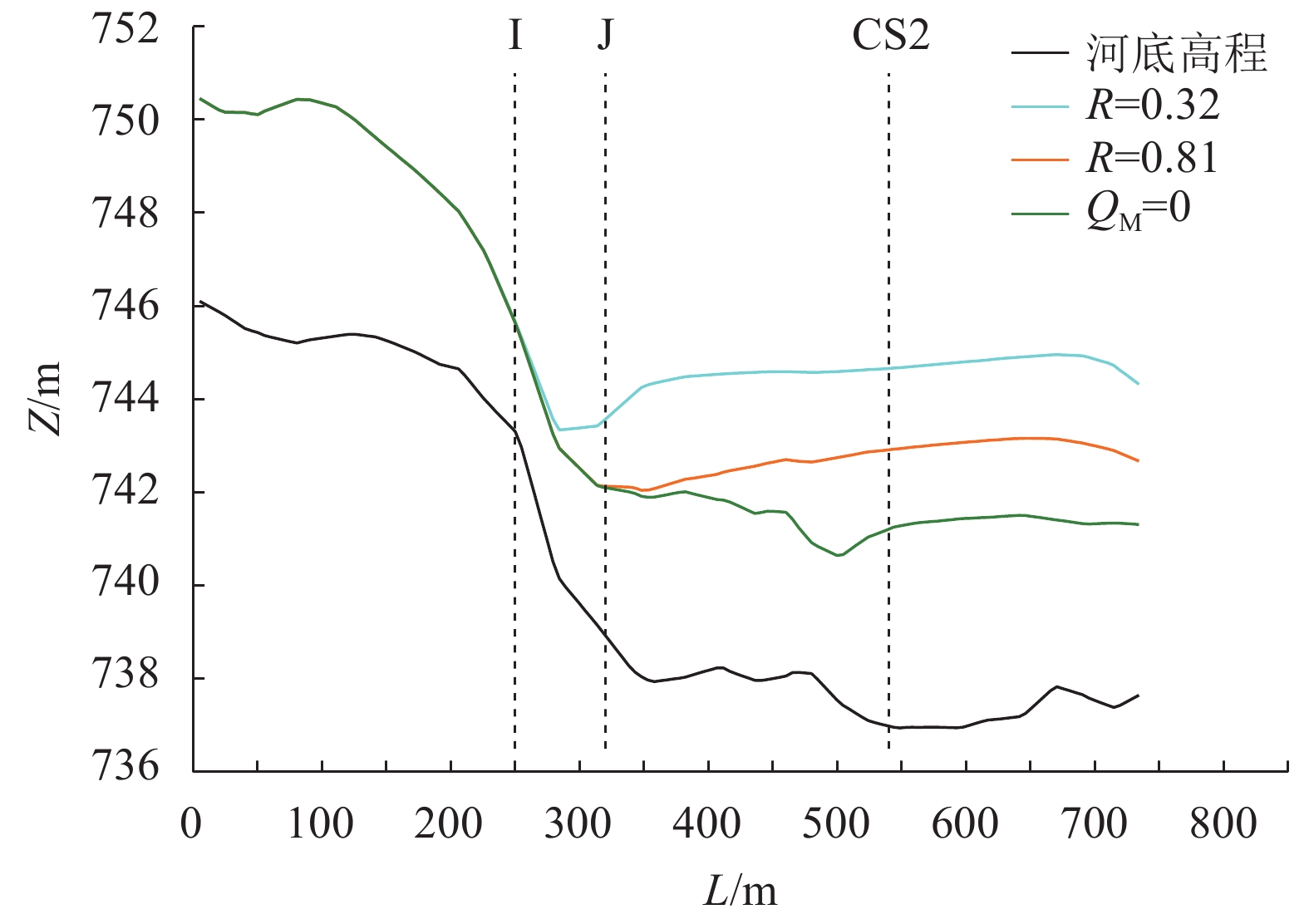 |
| 图16 LS3水位 Fig. 16 Water level along LS3 section of case 1, 2 and 5 |
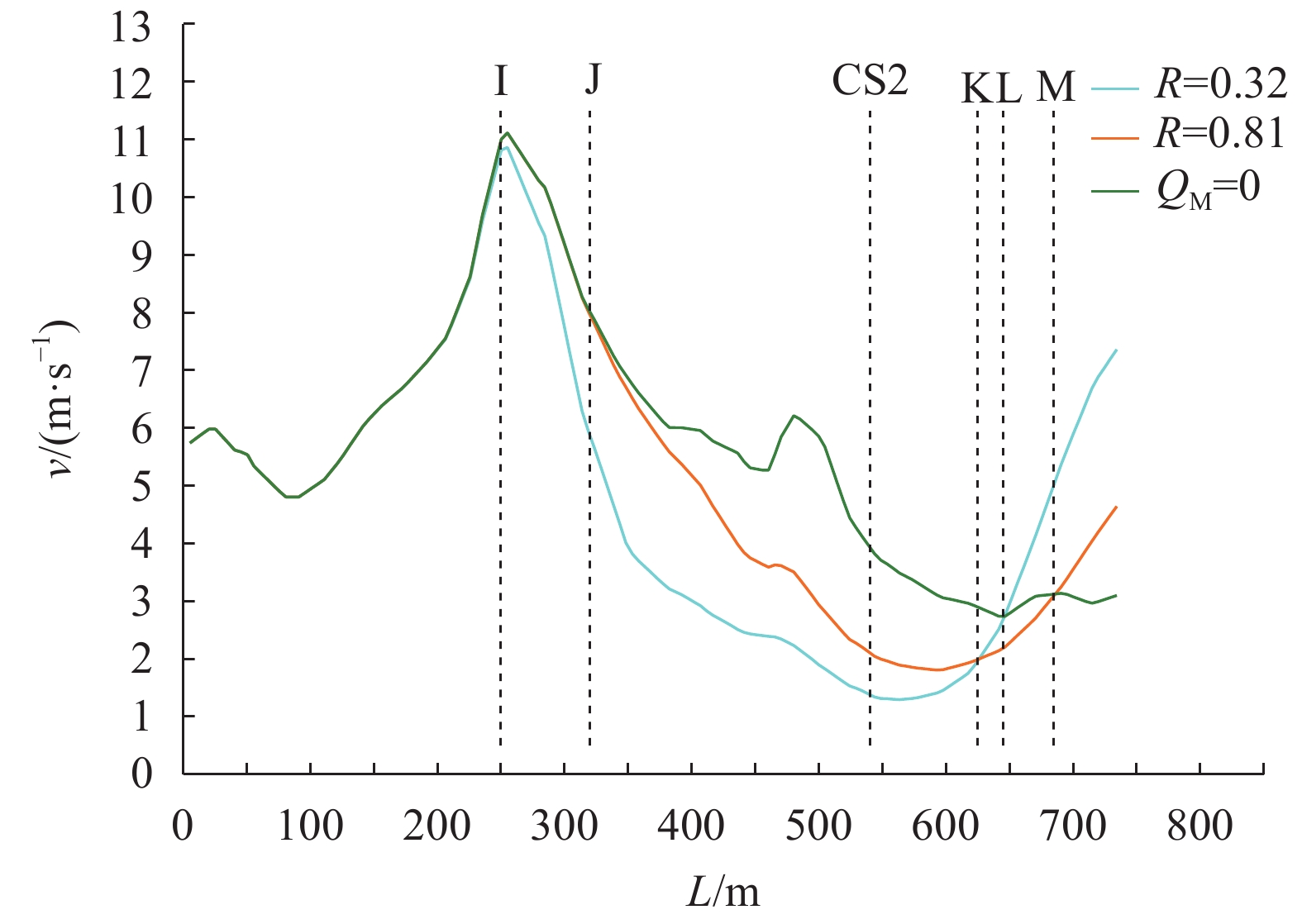 |
| 图17 LS3流速 Fig. 17 Velocity distribution along LS3 section of case 1, 2 and 5 |
图16水位变化表明:工况1的干支流流量相差较多,干流对支流的顶冲作用更强,水位更高,且顶冲到了I点,而工况2顶冲到了J点,I、J相距70 m。图17的流速沿程变化可知:3种工况条件下流速的变化趋势存在较大差异,相应特征点位置标记为I、J、K、L、M,其中,工况1和工况2的等流速位置为K,工况1和工况5的等流速位置为L,工况2和工况5的等流速位置为M。在J、K河段,工况5仅白沙河来流,未受岷江干流来水的顶托,支流流速值最大,而工况1和工况2岷江来流分别为6 030、2 390 m3/s,前者对支流产生顶托壅水、降低流速的作用更为明显。此外,与工况5相比,工况1和工况2对支流的顶托效应在L和M位置以后基本消失,流速显著增大。
4 结 论基于实测资料和数值模拟方法,分析了岷江干流与白沙河支流交汇区水流运动特性,主要成果有:
1)岷江干流与白沙河支流交汇易形成壅水低速区、干支流掺混区和挤压高速区。在岷江干流调峰来流2 390 m3/s,白沙河支流来流量为1 940和460 m3/s时,即当汇流比R分别为0.81和0.19时,前者比后者在壅水低速区内的最大壅水高度高0.31 m(LS2),在掺混区内的平均流速小0.78 m/s(LS2),在挤压高速区内,与右岸的距离近19.95 m(CS5),故QM相同,QT越大,即汇流比R越大时,壅水低速区的顶托壅水作用越强,掺混区内干支来流的相互顶冲作用越强,流速越小,而挤压高速区内支流对干流的挤压越强,最高流速出现的位置越靠右岸,高速带越窄。
2)支流受到干流的作用,入汇后流向会发生改变,而支流白沙河的弧形左岸能使支流在沿岸线流动的同时不断调整流向,可以降低支流脱壁流动的可能性,有效地抑制分离区的形成,对岸线保护具有较好的参考价值。
3)支流在顶托干流的同时,也受到干流的作用,且干支流流量差越大,干流对支流的顶托作用越强,支流产生的壅水范围也越大。
| [1] |
Biron P,Best J L,Roy A G. Effects of bed discordance on flow dynamics at open channel confluences[J]. Journal of Hydraulic Engineering, 1996, 122(12): 676-682. DOI:10.1061/(ASCE)0733-9429(1996)122:12(676) |
| [2] |
Guillén-Ludeña S,Franca M J,Cardoso A H,et al. Evolution of the hydromorphodynamics of mountain river confluences for varying discharge ratios and junction angles[J]. Geomorphology, 2016, 255: 1-15. DOI:10.1016/j.geomorph.2015.12.006 |
| [3] |
王平,胡恬,郭秀吉,等. 交汇角度对黄河上游高含沙交汇区淤堵影响的试验研究[J]. 工程科学与技术, 2017, 49(3): 44-53. |
| [4] |
Jia Meng.Bend flow under the conditions of curve intersection study on hydraulic characteristics of the curve[D].Handan:Hebei University of Engineering,2016. 贾猛.曲线交汇条件下弯道水流水力特性试验研究[D].邯郸:河北工程大学,2016. |
| [5] |
Wuppukondur A,Chandra V. Control of bed erosion at 60° river confluence using vanes and piles[J]. International Journal of Civil Engineering, 2018, 16(6): 619-627. |
| [6] |
兰波. 山区河流交汇河口的综合特性分析[J]. 重庆交通大学学报(自然科学版), 1998, 17(4): 91-96. |
| [7] |
侯志强,王义安,陈一梅. 支流入汇对干流航道影响分析[J]. 现代交通技术, 2006, 3(4): 70-73. DOI:10.3969/j.issn.1672-9889.2006.04.019 |
| [8] |
Riley J D,Rhoads B L. Flow structure and channel morphology at a natural confluent meander bend[J]. Geomorphology, 2012, 163/164: 84-98. DOI:10.1016/j.geomorph.2011.06.011 |
| [9] |
黄莉,刘士和. 三峡水库蓄水后关洲河段河势调整对松滋口分流影响[J]. 工程科学与技术, 2018, 50(1): 22-27. |
| [10] |
王协康,周苏芬,叶龙,等. 长江与嘉陵江交汇区水流结构的数值模拟[J]. 水科学进展, 2015, 26(3): 372-377. |
| [11] |
张光碧,邓军,张法星,等. VOF模型在有支流汇入的河道复杂流场中的应用[J]. 河海大学学报(自然科学版), 2007, 35(5): 592-595. |
| [12] |
刘盛赟,康鹏,李然,等. 水流交汇区的水动力学特性数值模拟[J]. 水利水电科技进展, 2012, 32(4): 14-18. |
| [13] |
Schindfessel L,Creëlle S,Mulder T D. Flow patterns in an open channel confluence with increasingly dominant tributary inflow[J]. Water, 2015, 7(9): 4724-4751. |
| [14] |
Fu Zhongmin.Experimental study and numerical simulation of water and sediment movement in mountain-bend river confluences[D].Chongqing:Chongqing Jiaotong Institute,2012. 付中敏.山区河流弯曲干流型汇合口水沙运动试验及数值模拟研究[D].重庆:重庆交通大学,2012. |
| [15] |
Zhou Sufen.Study on flow pattern and disaster reduction method in River confluences[D].Chengdu:Sichuan University,2014. 周苏芬.河流交汇区顶托特征及整流方法研究[D].成都:四川大学,2014. |
| [16] |
Penna N,Marchis M D,Canelas O B,et al. Effect of the junction angle on turbulent flow at a hydraulic confluence[J]. Water, 2018, 10(4): 1-23. |
| [17] |
陈远信. 都江堰卵石推移质输沙率问题[J]. 成都科技大学学报, 1980(1): 81-86. |
| [18] |
罗茂盛,刘兴年,罗宪,等. 山区小流域坡面、沟道床面粗糙度与糙率测量方法探讨[J]. 四川大学学报(工程科学版), 2008, 40(6): 57-62. |
| [19] |
Best J L. Separation zone at open-channel junctions[J]. Journal of Hydraulic Engineering, 2015, 110(11): 1588-1594. |
 2019, Vol. 51
2019, Vol. 51


