2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074
2. Key Lab. of Hydraulic and Waterway Eng. of the Ministry of Education, Chongqing Jiaotong Univ., Chongqing 400074, China
天然河道中的水流多属明渠紊流,受水流质点运动速度随机脉动的影响,紊流瞬时流速也随时间变化。根据水流流速的雷诺分解方法,瞬时流速可分解为时均流速和脉动流速,其中时均流速结构决定着水流造床作用,而脉动流速结构与水流动量交换、泥沙颗粒悬浮及污染物质扩散等问题密切相关。迄今为止,明渠紊流时均流速结构已有较多研究[1–8],在纵向流速垂线分布规律方面也取得了较为一致的认识。相对而言,明渠紊流脉动流速结构的研究却仍较薄弱,但因其与紊流形成机理及诸多工程实际问题关系密切,相关研究也日益受到重视。明渠紊流脉动流速结构研究多采用象限分析方法[9],并按脉动流场(
综上所述,目前粗糙床面明渠紊流脉动流速结构的研究仍不充分,缺乏基于全场瞬时流速资料的光滑及粗糙床面明渠紊流脉动流速结构对比分析,而现有初步研究[14–16]发现,床面粗糙对明渠紊流的脉动流速结构具有较大影响。鉴于此,作者在PIV水槽中开展了不同类型床面明渠均匀紊流试验,基于瞬态流场资料,探讨不同类型床面明渠紊流脉动流速的分布特征,研究各象限紊流事件概率和紊动参数(雷诺应力、紊动能)的垂线分布规律,并建立相关参数的内在联系,研究结果可从定量角度阐明床面粗糙对明渠紊流脉动流速结构的影响规律,并对进一步揭示加糙阻力的形成机理具有科学意义。
1 水槽试验 1.1 试验装置与流场测试试验在重庆交通大学国家内河航道整治工程技术研究中心进行,高精度整体变坡水槽长12 m、宽0.25 m、高0.25 m,水槽侧面和底面均由3.6 m长有机玻璃板组成,玻璃安装误差小于0.2 mm,水槽结构变形小于0.3 mm。水槽入口放置整流格栅,出口设置合页式尾门。试验中采用了光滑床面和密排加糙床面,光滑床面为有机玻璃床面(床面B0),密排加糙床面为直径3、6和9 mm的圆形玻璃珠铺制床面(床面B1、B2和B3)。
试验水流为均匀流,流量采用电磁流量计测量,采样频率10 Hz,测量精度0.4%;水深采用精度0.1 mm的水位测针测量;底坡采用水槽进、出口断面的调坡测针控制,根据试验段水面比降与底坡一致的原则判断均匀流。流场采集窗口中部距水槽入口8 m,满足Dong等[17–18]建议的紊流充分发展所需进口段长度要求;距水槽出口4 m,可消除尾门对水流的扰动。应用2维高频PIV系统沿位于两排颗粒间的水槽纵向中轴面进行流场采集(图1),该系统主要由高频CMOS相机、8 W半导体连续激光和PIV流场计算软件组成;CMOS相机最高像素为2 560×1 920,满幅最高帧频为800 Hz;激光束经棱镜转变为45°角的片光,厚度约为1 mm;片光源从水槽玻璃底板进光,可穿透床面玻璃珠颗粒。示踪粒子采用直径8~12 μm、密度1.03 g/mm3的空心玻璃球。PIV流场计算采用WIDIM多重网格迭代图像变形算法,最小诊断窗口为16×16像素,
 |
| 图1 PIV流场采集 Fig. 1 PIV flow field acquisition |
研究共进行了4组试验,保持各组试验的流量和底坡不变,流量
| 表1 试验工况参数 Tab. 1 Summary data of experimental runs |
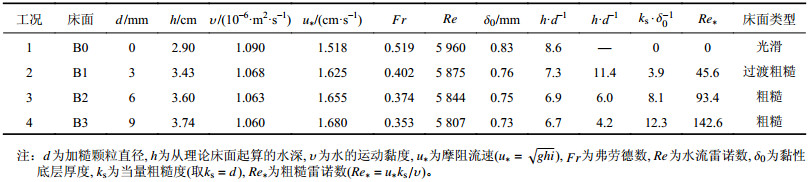 |
1.2 试验数据可靠性分析
为分析PIV流场采集数据的可靠性,图2给出了无量纲化后的纵向流速
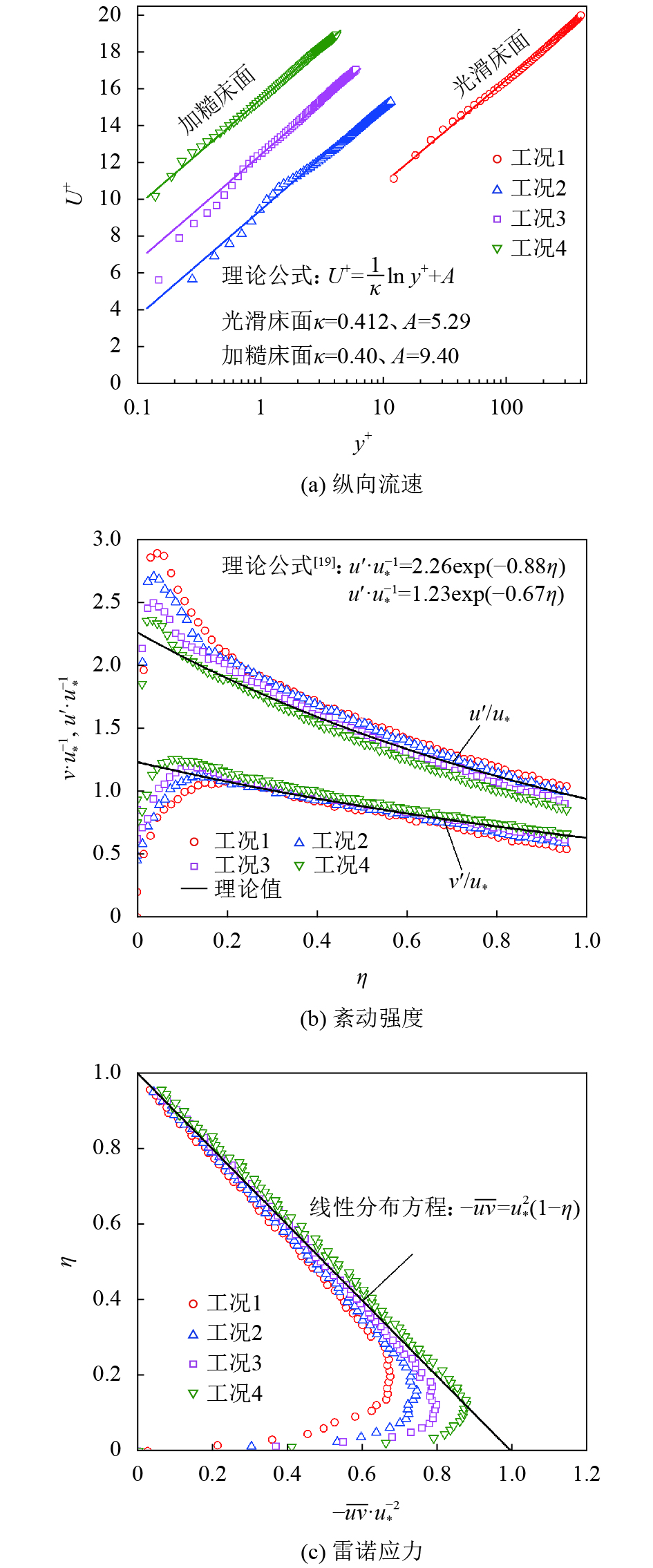 |
| 图2 时均紊流参数的垂线分布 Fig. 2 Vertical distribution of time-averaged turbulence parameters |
纵向流速垂线分布公式为:
| ${U^ + } = \frac{1}{\kappa }\ln\;{y^ + } + A$ | (1) |
式中:
根据Nezu[20]的研究,明渠紊流垂线上可分为3个区,即近壁区(0≤
从不同方向脉动流速及其组合特性两方面进行研究,前者主要分析脉动流速
根据前文的分析,床面加糙后基于脉动流速计算的紊动参数变化主要体现在近壁区(内区),外区变化相对较小,因此,这里重点探讨近壁区脉动流速
 |
| 图3 近壁区脉动流速的概率分布 Fig. 3 Probability distribution of velocity fluctuations in the inner region |
床面加糙改变近壁区脉动流速概率分布的同时,脉动流速的组织结构也将发生改变。条带结构是光滑床面明渠紊流近壁区脉动流速空间分布的典型特征,通常指黏性底层和缓冲层中存在的高、低速相间流带。图4给出了各工况近壁2 cm范围内纵向脉动流速
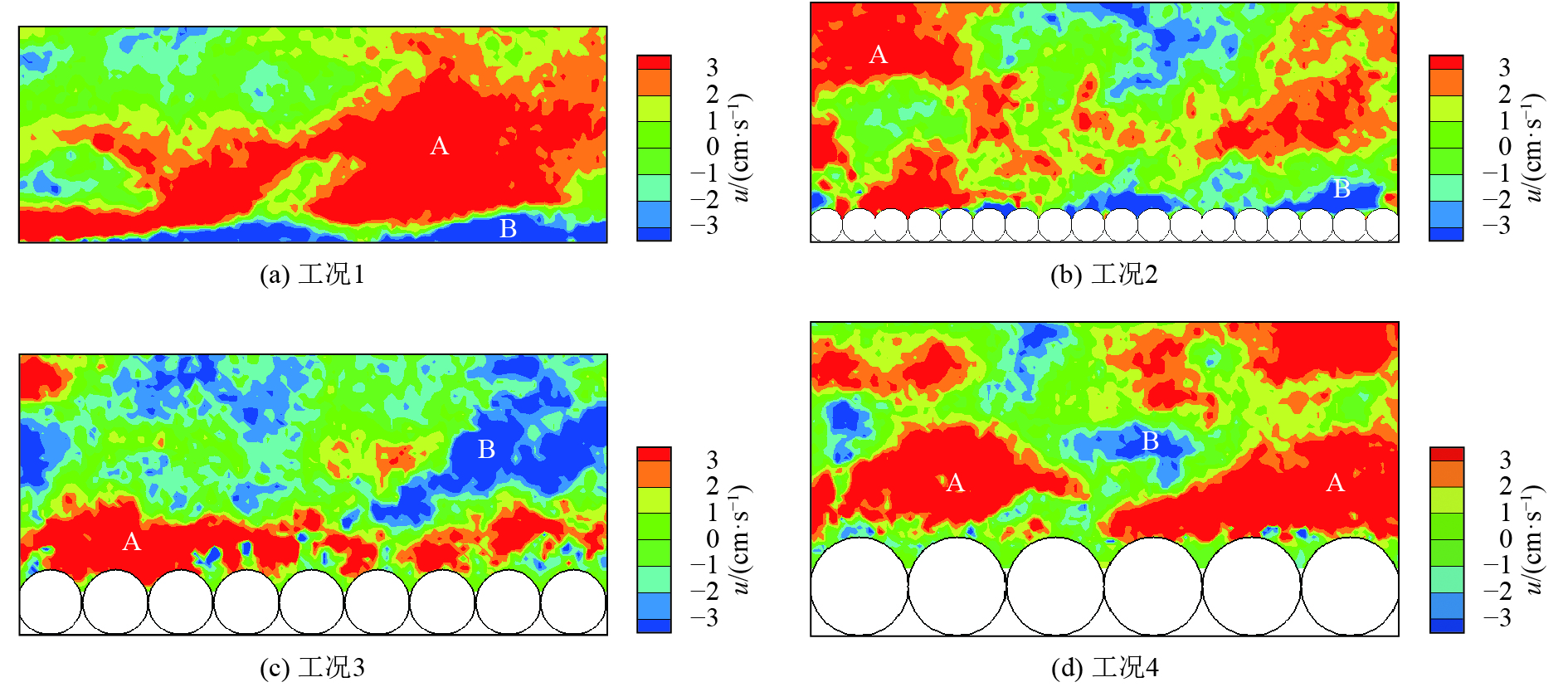 |
| 图4 纵向脉动流速的典型分布 Fig. 4 Typical distribution of longitudinal velocity fluctuations |
2.2 脉动流速的象限分析
脉动流速的象限分析可用于识别紊流相干结构并量化其对紊动参数(雷诺应力、紊动能)的作用贡献[9]。明渠紊流床面附近最重要的相干结构是条带结构与猝发现象;条带结构并不稳定,在向下游移动过程中将逐渐抬升,并突然振荡破碎;条带结构的破坏过程称为猝发现象,猝发现象包括Q2、Q4两类紊流事件,控制着壁面附近紊流的产生与维持[12]。紊动参数体现不同方向脉动流速的组合效应,其象限分布特征反映了不同类型紊流事件对紊流各向异性的影响。
表2给出了各象限紊动参数的计算公式。其中:上标+、–表示流速的正负,下标1、2、3、4分别表示第1~4象限代号;
| 表2 各象限紊动参数计算公式 Tab. 2 Calculating formulas of turbulence parameters in each quadrant |
 |
2.2.1 事件概率
脉动流速的象限分布概率体现了各类紊流事件的出现频次。对于采样窗口中的各点,通过对瞬时流速各次采样数据进行雷诺分解可获得相应的脉动流速(
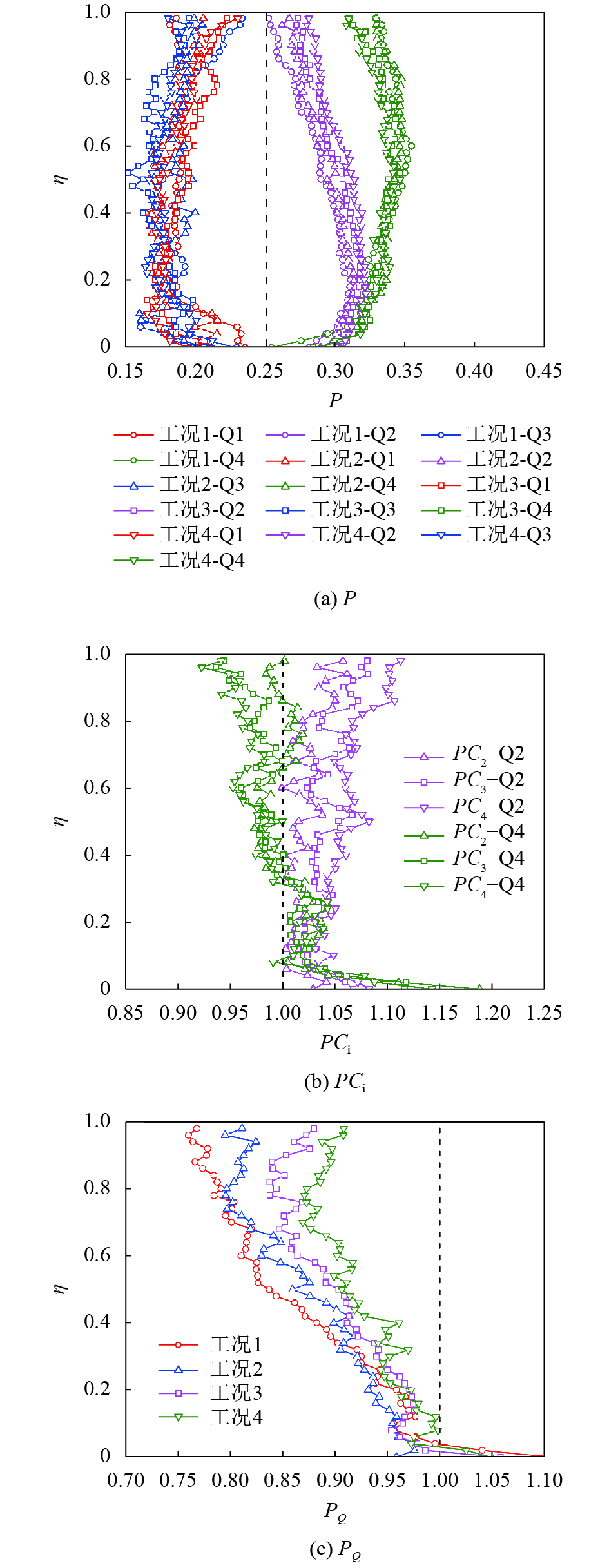 |
| 图5 紊流事件概率及其比值的垂线分布 Fig. 5 Vertical distribution of turbulence event probability and its ratio |
图5结果表明:
1)全水深范围内,各工况的Q2、Q4事件概率总体大于Q1、Q3事件,Q4事件沿水深占主导地位,Q2事件次于Q4事件,与杨胜发等[13]基于光滑床面的相关研究结论基本一致。
2)床面附近各工况的紊流事件概率
3)床面加糙后,Q2事件概率在全水深范围内总体增大,工况2~工况4的
4)各工况第2、4象限紊流事件概率的比值
5)图4呈现的加糙后低速条带完全消失,可能是Q2事件概率增加,内区低速流体喷射作用增强,质点混掺加剧,低速条带向下游抬升过程中发生破坏所致。
2.2.2 雷诺应力由表2可知,第1、3象限的雷诺应力为负值,第2、4象限的雷诺应力为正值,为便于比较,此处各象限雷诺应力均取绝对值。图6分别给出了无量纲雷诺应力
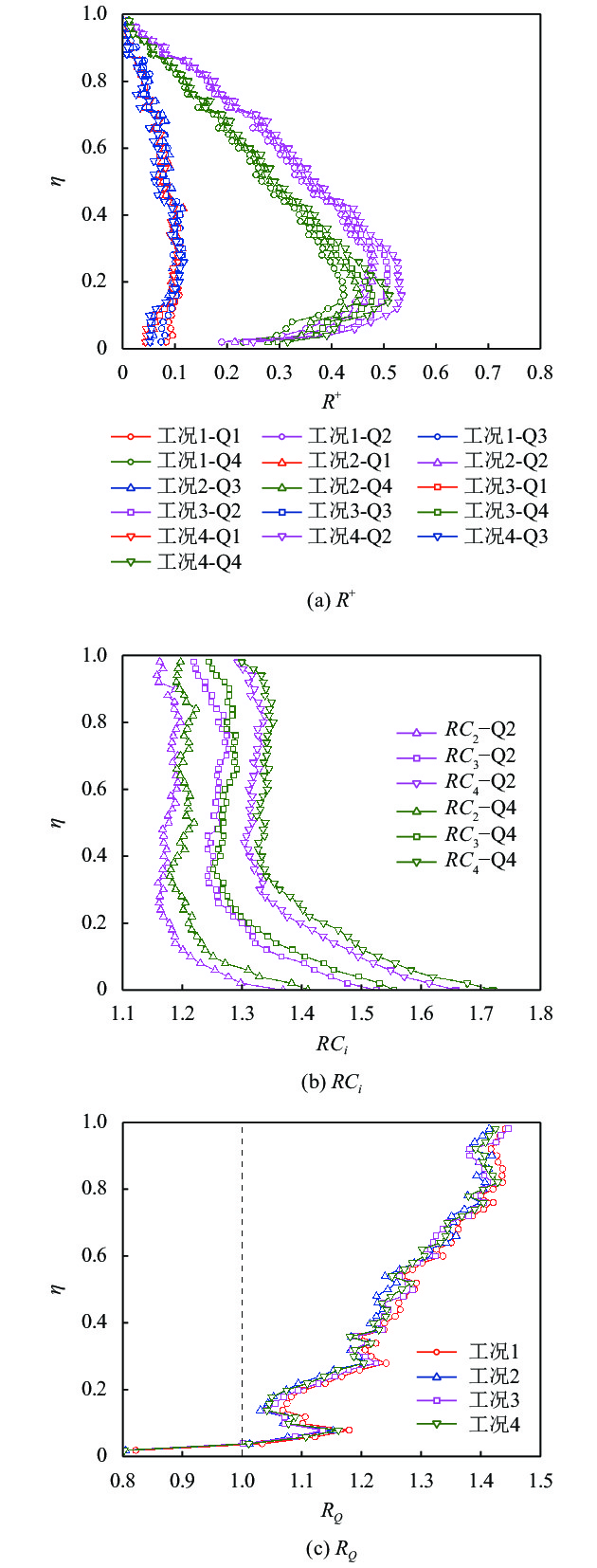 |
| 图6 雷诺应力及其比值的垂线分布 Fig. 6 Vertical distribution of Reynolds stress and its ratio |
1)第2、4象限的雷诺应力总体大于第1、3象限,第2象限的雷诺应力大于第4象限,符合光滑床面明渠紊流“Q2和Q4事件产生了大部分雷诺应力”的现有认识[12],也与Hong等[22]粗糙床面槽道流“第2、4象限雷诺应力占主要地位”的研究结论吻合。
2)第1、3象限雷诺应力垂线分布较均匀,第2、4象限雷诺应力随水深的增加呈先增大后减小的变化趋势,曲线拐点位于内区,外区雷诺应力沿水深总体呈线性递减变化。
3)第2、4象限的
4)各工况第2、4象限雷诺应力的比值
图7分别给出了各象限无量纲紊动能
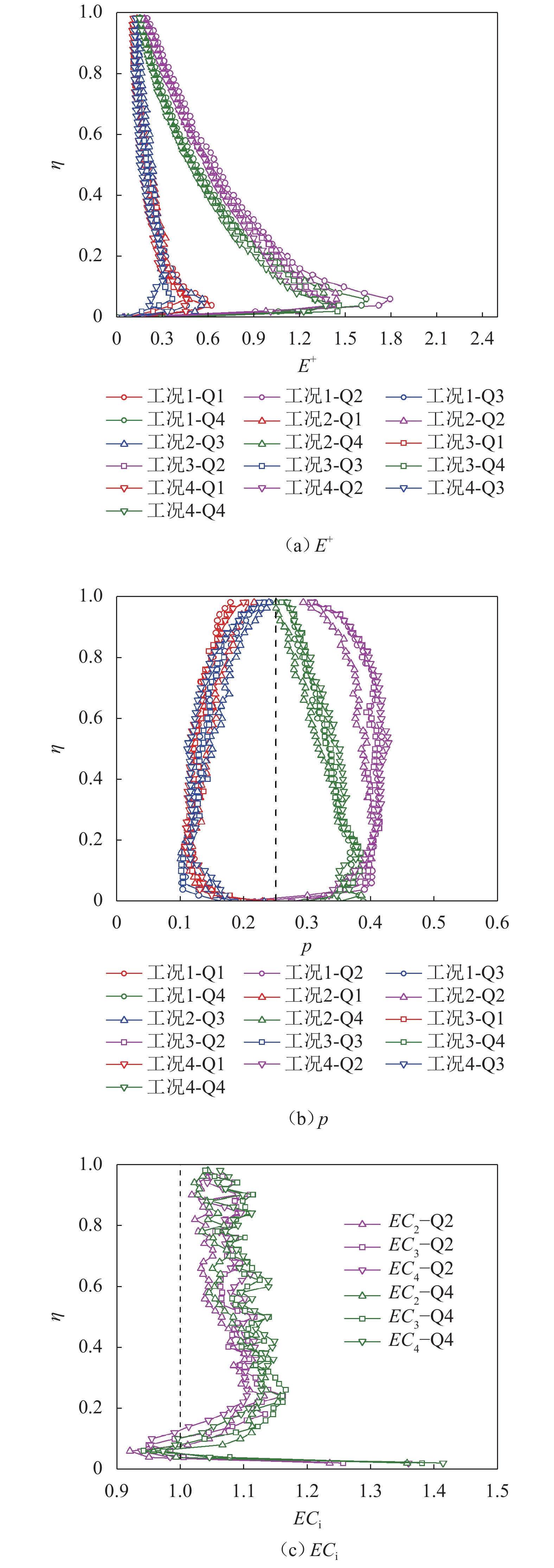 |
| 图7 紊动能及其比值的垂线分布 Fig. 7 Vertical distribution of turbulent kinetic energy and its ratio |
1)与各象限雷诺应力垂线分布规律相似,第1、3象限紊动能垂线分布曲线相互交织,相对均匀,第2、4象限紊动能随水深的增加呈先增大后减小的变化趋势,曲线拐点位于
2)比较而言,第2、4象限的紊动能总体大于第1、3象限,尤以第2象限紊动能所占百分比最大(
3)内区不同工况第2象限的
4)床面粗糙首先直接影响内区紊流结构,由于内、外区水流存在相互作用[14],因此进而会影响外区紊流结构,这可初步解释床面加糙后第2、4象限雷诺应力及紊动能沿整个水深均有变化的原因。
5)根据现有研究[12],Q2(Q4)事件是明渠紊动能量的主要来源,是明渠紊流除平均流动外从壁面到自由水面含能最多、最主要的大尺度结构;床面加糙可增大水流阻力,这与加糙后Q2、Q4紊流事件概率增大,高速流体清扫作用和低速流体喷射作用加剧,质点动量交换和能量传递增强,第2、4象限雷诺应力及紊动能绝对值增大有关,也是加糙阻力形成的内在机制。
2.2.4 参数关系第2、4象限紊流事件(Q2喷射事件和Q4清扫事件)对明渠紊流的形成与发展具有重要作用,前文分析表明,床面加糙后这2类事件将使质点混掺作用增强,并产生更大的雷诺应力和紊动能。为探讨紊流事件概率
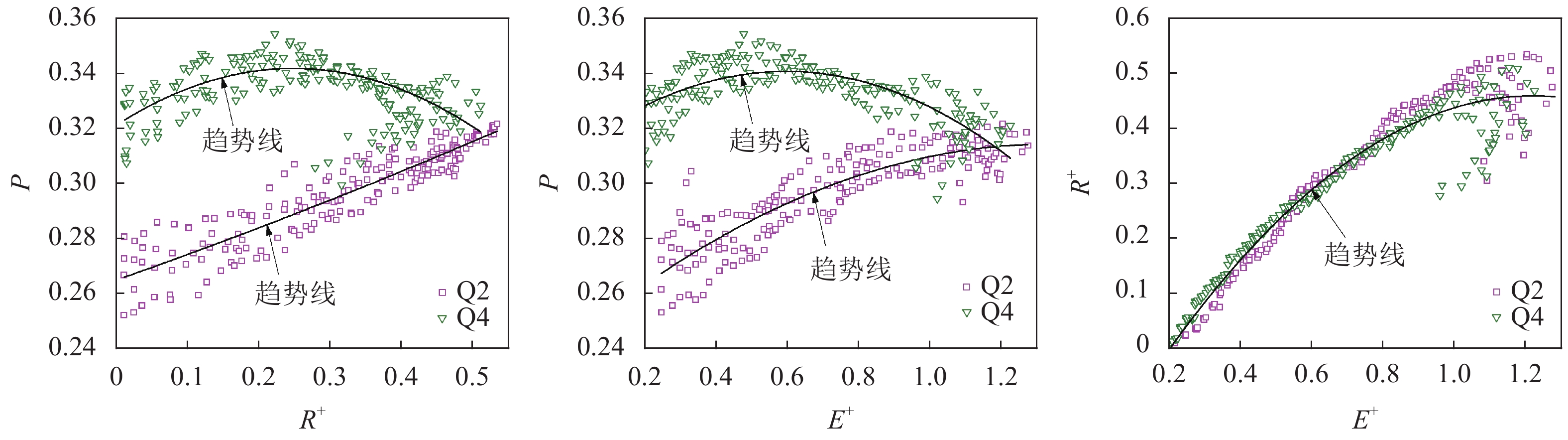 |
| 图8 P、R+及E+的相互关系 Fig. 8 Relationship among P、R+ and E+ |
1)第2象限的
2)第4象限
3)
表3给出了图8中各参数关系的拟合公式,可见第2、4象限
| 表3 参数关系拟合公式 Tab. 3 Parameters relation fitting formulas |
 |
3 结 论
1)床面加糙会改变近壁脉动流速
2)各象限脉动流速分别对应一类紊流事件,第2、4象限紊流事件是紊流产生和维持的关键过程。床面加糙不会改变第2、4象限紊流事件的主导地位,但会改变事件概率
3)无论对于光滑床面还是加糙床面,第2、4象限的雷诺应力及紊动能总体大于第1、3象限,尤以第2象限最大,该象限紊动能可占总紊动能的39.3%;床面加糙后,第2、4象限雷诺应力及紊动能的绝对值均增大,内区雷诺应力增加尤为明显,平均增幅24.0%~56.1%,内、外区紊动能增加较为接近,平均增幅3.4%~11.0%。
4)紊流事件概率、雷诺应力和紊动能变化具有较强的关联性,床面加糙后内区第2、4象限紊流事件概率增大,高速流体清扫作用和低速流体喷射作用加剧,质点动量交换和能量传递增强,雷诺应力和紊动能增大,水流阻力增大,为从紊流结构角度揭示加糙阻力的形成机理提供了帮助。
5)本文研究主要针对雷诺数较小时的情况,今后可进一步探讨雷诺数变化对明渠紊流脉动流速结构的影响规律,并分析不同床面粗糙下的纵横剖面动量及能量传递特性,以完善和丰富相关研究成果。
| [1] |
Sarma K V N,Lakshminarayana P,Rao N S L. Velocity distribution in smooth rectangular open channels[J]. Journal of Hydraulic Engineering, 1983, 109(2): 270-289. DOI:10.1061/(ASCE)0733-9429(1983)109:2(270) |
| [2] |
Kirkgöz M S. Turbulent velocity profiles for smooth and rough open channel flow[J]. Journal of Hydraulic Engineering, 1989, 115(11): 1543-1561. DOI:10.1061/(ASCE)0733-9429(1989)115:11(1543) |
| [3] |
Kirkgöz M S,Ardıçhoğlu M. Velocity profiles of developing and developed open channel flow[J]. Journal of Hydraulic Engineering, 1997, 123(12): 1099-1105. DOI:10.1061/(ASCE)0733-9429(1997)123:12(1099) |
| [4] |
Cheng N S. Power-law index for velocity profiles in open channel flows[J]. Advances in Water Resources, 2007, 30(8): 1775-1784. DOI:10.1016/j.advwatres.2007.02.001 |
| [5] |
Han Y,Yang S Q,Dharmasiri N,et al. Experimental study of smooth channel flow division based on velocity distribution[J]. Journal of Hydraulic Engineering, 2015, 141(4): 06014025. DOI:10.1061/(ASCE)HY.1943-7900.0000937 |
| [6] |
刘亚坤,倪汉根. 水力光滑明渠流流速分布的新公式[J]. 水利学报, 2007, 38(11): 1336-1340. DOI:10.13243/j.cnki.slxb.2007.11.017 |
| [7] |
王协康,杨青远,王宪业,等. 卵砾石床面时均流速分布的试验研究[J]. 四川大学学报(工程科学版), 2007, 39(2): 14-19. DOI:10.15961/j.jsuese.2007.02.003 |
| [8] |
梁越,曹叔尤,杨奉广,等. 光滑宽浅明渠流动垂线流速分布公式研究[J]. 水力发电学报, 2013, 32(5): 147-152. |
| [9] |
Lu S S,Willmarth W W. Measurements of the structure of the Reynolds stress in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1973, 60(3): 481-511. DOI:10.1017/S0022112073000315 |
| [10] |
Kim H T,Kline S J,Reynolds W C. The production of turbulence near a smooth wall in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1971, 50(1): 133-160. DOI:10.1017/S0022112071002490 |
| [11] |
王浩,李丹勋,陈启刚,等. 基于图像处理的明渠紊流近壁区条带结构试验[J]. 水科学进展, 2015, 26(2): 257-264. DOI:10.14042/j.cnki.32.1309.2015.02.014 |
| [12] |
钟强,李丹勋,陈启刚,等. 明渠湍流中的主要相干结构模式[J]. 清华大学学报(自然科学版), 2012, 52(6): 730-737. DOI:10.16511/j.cnki.qhdxxb.2012.06.001 |
| [13] |
杨胜发,张鹏,胡江,等. 明渠均匀流Q结构分布及运动特性[J]. 水科学进展, 2016, 27(3): 430-438. DOI:10.14042/j.cnki.32.1309.2016.03.011 |
| [14] |
Bhaganagar K,Kim J,Coleman G. Effect of roughness on wall-bounded turbulence[J]. Flow,Turbulence and Combustion, 2004, 72(2/3/4): 463-492. DOI:10.1023/B:APPL.0000044407.34121.64 |
| [15] |
Bomminayuni S,Stoesser T. Turbulence statistics in an open-channel flow over a rough bed[J]. Journal of Hydraulic Engineering, 2011, 137(11): 1347-1358. DOI:10.1061/(ASCE)HY.1943-7900.0000454 |
| [16] |
Grass A J. Structural features of turbulent flow over smooth and rough boundaries[J]. Journal of Fluid Mechanics, 1971, 50(2): 233-255. DOI:10.1017/S0022112071002556 |
| [17] |
Dong Z N,Wang J J,Chen C Z,et al. Hydraulic characteristics of open channel flows over rough beds[J]. Science in China(Ser A), 1992, 35(8): 1007-1016. |
| [18] |
董曾南,陈长植,李新宇. 明槽均匀紊流的水力特性[J]. 水动力学研究与进展, 1994, 9(1): 8-22. DOI:10.16076/j.cnki.cjhd.1994.01.002 |
| [19] |
Nezu I,Rodi W. Open-channel flow measurements with a laser Doppler anemometer[J]. Journal of Hydraulic Engineering, 1986, 112(5): 335-355. DOI:10.1061/(ASCE)0733-9429(1986)112:5(335) |
| [20] |
Nezu I. Turbulence intensities in open channel flows[J]. Proceedings of the Japan Society of Civil Engineers, 1977, 261: 67-76. DOI:10.2208/jscej1969.1977.261_67 |
| [21] |
梁在潮,刘士和. 边壁加糙对切变湍流相干结构的作用[J]. 水动力学研究与进展, 1987, 2(2): 50-56. DOI:10.16076/j.cnki.cjhd.1987.02.006 |
| [22] |
Hong J,Joseph K,Schultz M P. Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow[J]. Journal of Fluid Mechanics, 2011, 667: 1-37. DOI:10.1017/S0022112010003988 |
 2019, Vol. 51
2019, Vol. 51

