阴影的生成是3维虚拟场景绘制的重要部分,不仅可以增强虚拟场景的真实感,还可以帮助人们理解场景中物体之间的空间关系。
阴影可分为硬阴影和软阴影,前者在点光源下产生,后者则在面光源下产生,考虑了光源的大小,因而更加真实。软阴影生成算法可分为基于阴影图[1]的算法和基于阴影体[2]的算法,前者的运行时间相对较低,成为研究的热门。基于阴影图的算法主要有3种,面光源采样[3]、反投影[4–6]和PCSS[7],前两种算法虽然可以生成物理真实的软阴影,但是计算量较大,运行速度较慢。百分比靠近算法可以模拟出柔和的软阴影,并且运行速度相对较快,但该算法在特定的场景下,为了避免出现走样现象,会使用较大的过滤区域,从而严重影响了运行性能。
为了解决这一问题,文献[8–10]通过使用预计算数据来对阴影测试函数进行重构,因而对于较大的过滤区域,也能够快速地生成软阴影,但这些算法会降低软阴影的质量,例如,出现“漏光”现象。袁昱纬等[11]利用四叉树结构,对过滤操作进行优化,降低了计算量。其基于原始的PCSS算法框架,并未引入阴影测试函的重构,因而生成的软阴影拥有较高的质量。但使用四叉树结构进行遍历需要保存额外的信息,增加了算法的空间开销。沈笠等[12]提出了高质量快速百分比靠近软阴影(high quality and efficient percentage closer soft shadows,HQEPCSS)算法,其利用多尺度阴影图对过滤区域进行精练,使用线性四叉树结构[13]节省遍历时的空间开销,并通过与阴影测试函数重构方法进行比较,说明该算法可以生成高质量的软阴影,但该方法在待定场景下的运行速度仍然不够理想。
针对这一问题,作者沿用HQEPCSS算法的研究思路,并对其中的关键步骤进行改进,目标是在保证软阴影质量的条件下,进一步提升算法的性能。主要工作包括以下3个方面:首先是缩减式多尺度阴影图,对多尺度阴影图进行精炼,降低生成开销;然后是使用采样信息的快速遍历,提高快速遍历结果的准确性;最后是计算结果复用方案,通过复用部分计算结果,降低总的计算量,提高算法的运行速度。
1 算法概览为了便于理解作者提出的方法,首先介绍基本的PCSS算法:
Step 1 以面光源中心为视点绘制阴影图。
Step 2 对于屏幕上各像素
Step 3 设面光源
| ${s_L} \times \left( {{{{d_P}} / {{d_{\textit{Z}}} - 1}}} \right)$ | (1) |
Step 4 对于各像素
PCSS算法的瓶颈是Step 2和Step 4中的遍历操作,如果搜索区域过大,会导致算法性能的急剧下降。
HQEPCSS算法在一定程度上提高了PCSS算法的效率,其具体步骤如下:
Step 1 以面光源中心为视点绘制阴影图及相应的多尺度阴影图。
Step 2 进行延迟渲染,生成G-Buffer。
Step 3 对于G-Buffer中的每个像素,利用多尺度阴影图,精炼初始搜索区域,并使用线性四叉树对最终的搜索区域进行快速遍历,得到遮挡物的平均深度的估计值,据此计算过滤区域的范围。
Step 4 进行PCSS中的Step 3和Step 4,计算软阴影值。
该算法在很大程度上减少了PCSS算法Step 2中的遍历代价,但并没有对PCSS中的Step 4进行优化,如果新构造的搜索区域仍然很大,则运行效率仍然不能得到保障。
为了在合理的时间开销下得到较为真实的软阴影,使用以下步骤生成软阴影:
Step 1 以面光源中心为视点绘制阴影图及相应的缩减式多尺度阴影图。
Step 2 进行延迟渲染,生成G-Buffer。
Step 3 对于G-Buffer中的每个像素,利用缩减式多尺度阴影图,精炼初始搜索区域,并将结果保存到搜索区域图中。
Step 4 对于搜索区域图中的每个像素,利用线性四叉树结构遍历对应的区域,并使用采样信息和复用方案,得到遮挡物的平均深度,据此计算过滤区域的范围,并将结果保存到过滤区域图中。
Step 5 对于过滤区域图中的每个像素,采用同样的方法进行遍历,得到软阴影值,并将其保存到软阴影图中。
Step 6 对软阴影图进行模糊处理。
该算法与HQEPCSS算法的不同之处如下:
1)在Step 1中对多尺度阴影图的构造方式进行了改进,减少预处理的开销。
2)在Step 5中加入了对PCSS算法Step 4的优化,并且在Step 4和Step 5中利用采样信息,防止计算结果与真实值差距过大。
3)在Step 4和Step 5中使用复用方案,进一步提高算法的运行速度。
4)在Step 6中对软阴影图进行模糊处理,使软阴影更加平滑。
2 缩减式多尺度阴影图多尺度阴影图是对阴影图进行预处理而得到的一个层级结构,它保存的是阴影图不同区域内的最大深度和最小深度,其中高层数据由低一层的4个取样数据进行计算得到,保存了更大区域的信息。因而对阴影图进行查询时,如果使用较高层数据可以得到计算结果,就无需对较低层进行开销巨大的逐像素操作,大幅度降低了计算量。
HQEPCSS算法在多尺度阴影图中融入了区域内平均深度,但是其边缘像素对应的区域与阴影图部分相交,因而在构造过程中会出现取样数据的缺失,如图1所示。
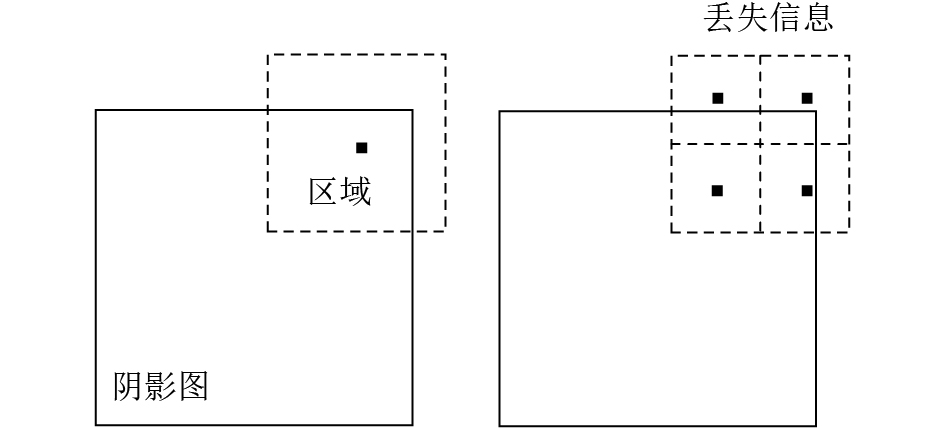 |
| 图1 取样数据缺失 Fig. 1 Lack of sampling data |
通过分析可以发现,边缘像素保存的是较小区域的信息。虽然可以通过较为复杂的方式对这些像素进行精确的计算,但是计算开销与其对阴影图查询的贡献不成正比,因此可以考虑去掉这些像素,只处理对应区域全部位于阴影图的像素。
2.1 构造方式设阴影图的大小为
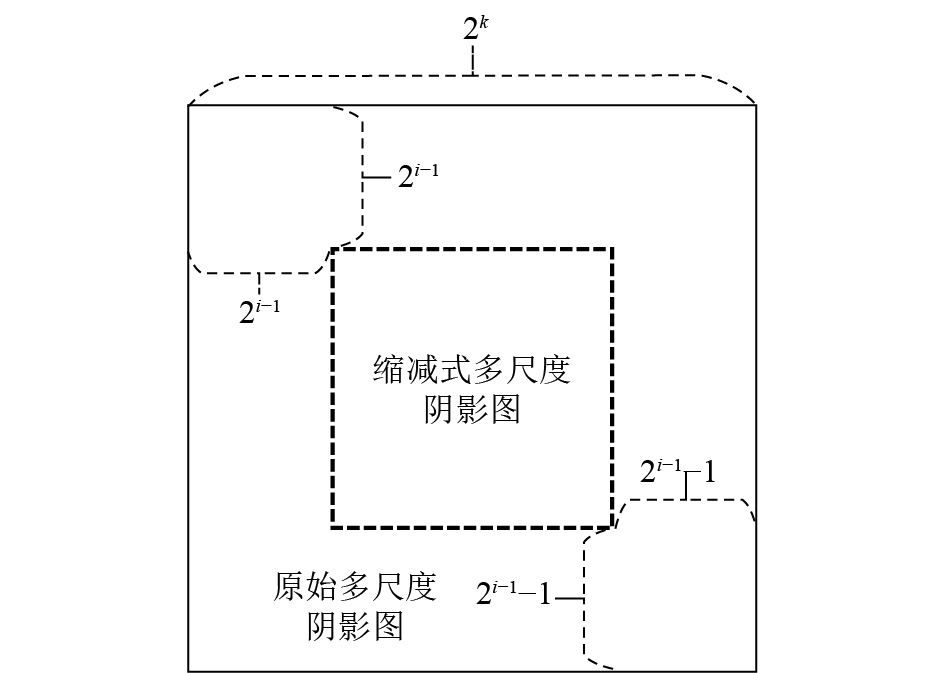 |
| 图2 缩减式多尺度阴影图 Fig. 2 Decreased multi-scale shadow map |
缩减式多尺度阴影图的第
| 表1 不同数据结构的构造时间对比 Tab. 1 Comparison of construction time of different data structures |
 |
2.2 使用方式
对阴影图的某区域进行查询时,如果查询区域的大小不是
Step 1 计算原区域的左边界
| $\left\{ \begin{gathered} l = \left\lfloor{x - {s / 2}}\right\rfloor, \\ r = \left\lceil {x + {s / 2}}\right\rceil, \\ t = \left\lfloor{y - {s / 2}}\right\rfloor, \\ b = \left\lceil {y + {s / 2}} \right\rceil \end{gathered} \right.$ | (2) |
Step 2 将区域的边界限制在阴影图内,设阴影图的大小为
| $\left\{ \begin{aligned} & l = \max \left( {l,0} \right),\\ & r = \min \left( {l,e - 1} \right),\\ & t = \max \left( {l,0} \right),\\ & b = \min \left( {l,e - 1} \right) \end{aligned} \right.$ | (3) |
Step 3 设
Step 4 将
Step 5 如果
Step 6 计算限制后的区域的中心
| $\left\{ \begin{aligned} & x' = l + {{s'} / 2},\\ & y' = t + {{s'} / 2} \end{aligned} \right.$ | (4) |
Step 7 如果
其中Step 1和Step 2的作用是将原区域限制在阴影图内;Step 3~Step 5的作用是确定近似区域的大小;Step 6和Step 7的作用是确定近似区域的中心点。
使用缩减式多尺度阴影图,本文算法在进行Step 3时可类比HQEPCSS算法Step 3中初始搜索区域的精练方法,只是在每一次迭代前需要对上一次得到的区域进行近似。
3 利用采样信息的快速遍历软阴影生成算法的瓶颈是区域的遍历操作。使用线性四叉树,并结合多尺度阴影图可以对搜索区域进行快速遍历,得到遮挡物的平均深度。
对于屏幕上某像素
如果访问到线性四叉树的叶子节点时,
作者使用了多重抖动采样[14],可以生成较为均匀的采样点。但在实现时还需考虑一些问题。首先,如果在运行时动态计算各个区域的采样点信息,会造成性能的下降。因此可以预先计算好采样点信息,一组采样点信息称为一个采样点组。
其次,如果对于大小不同的区域采用相同数量的采样点,则对于较小区域,浪费了计算资源,对于较大区域,采样信息不充分,计算结果较为粗糙。为了对不同大小的区域使用不同数量的采样点,需要保存采样点数量不同的采样点组。
最后,如果对所有大小相似区域采用同一采样点组,可能会造成相邻像素的计算结果基本相同,生成的软阴影不够平滑,因此,需要为每一种采样点数量生成多个采样点组,以便对大小相似的不同区域采用不同的采样点组[15]。
采样点组的最终组织方式如图3所示。
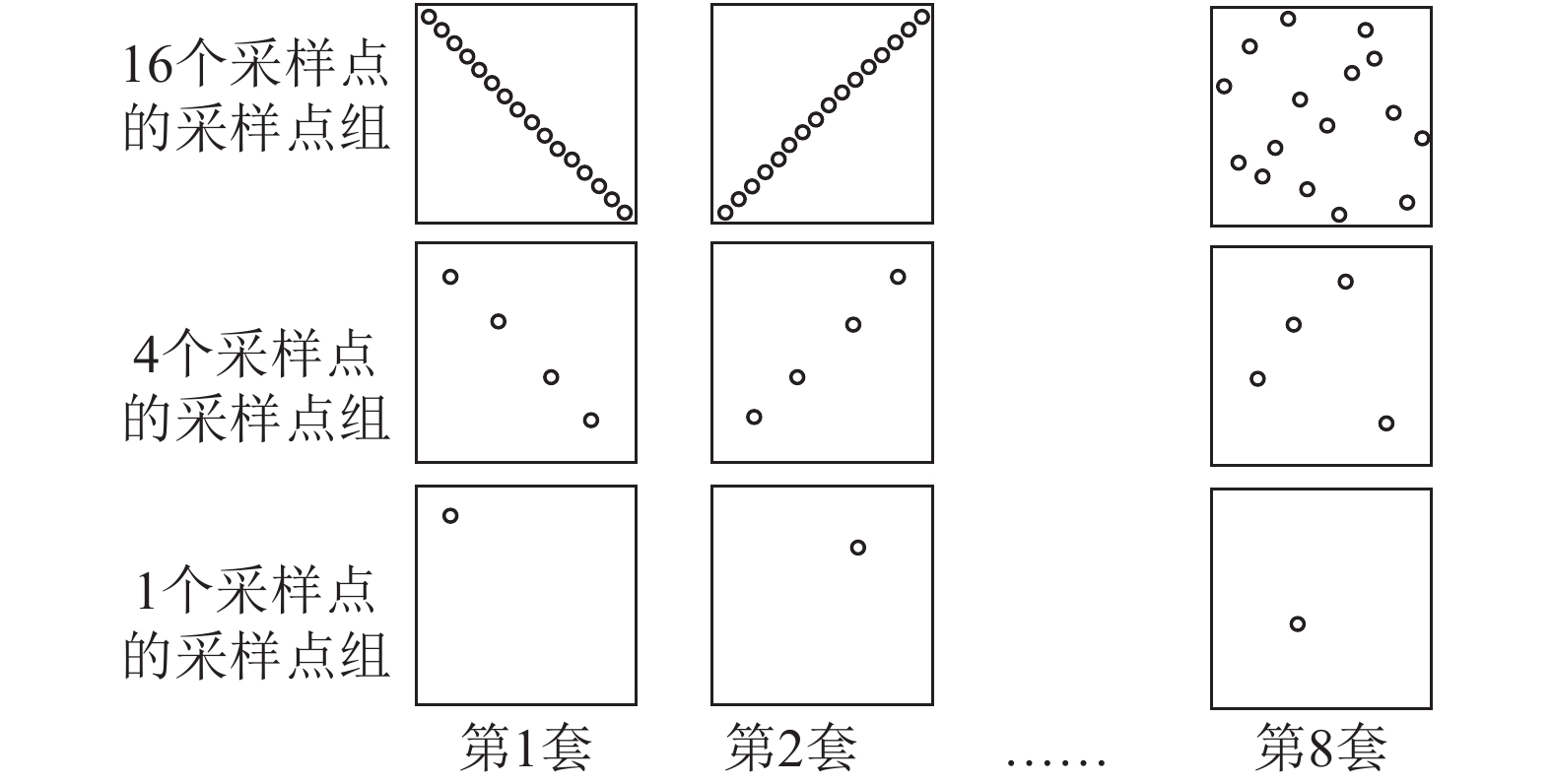 |
| 图3 采样点组织方式 Fig. 3 Organization of samples |
其使用了数量为1、4以及16的采样点组,而且对于每种数量,生成8套不同的采样点组,将采样点的位置标准化到0~1之间,并将所有的采样点组保存为一幅大小为21×8的图像。
3.2 采样信息使用方式对于中心为
Step 1 设
Step 2 设
Step 3 对所有标准化的采样点位置按区域大小进行放缩,并进行采样。
其中Step 1的作用是计算采样点数量;Step 2的作用是使相邻像素尽量使用不同的采样点组。
设采样点个数为
| ${{\sum\limits_{{d_i} < {d_P}} {{d_i}} }\Bigg/ {\sum\limits_{{d_i} < {d_P}} 1 }}$ | (5) |
在Step 5中,估算软阴影值的方法如式(6)所示:
| ${{\sum\limits_{{d_i} < {d_P}} 1 }\Bigg/ m}$ | (6) |
其本质上是用采样点的计算结果来替代真实的计算结果。
4 复用方案对于本文算法Step4中的搜索区域图和Step5中的过滤区域图来说,其中某些像素存储着相近的值,对这些像素进行计算得到的结果也近乎相同。因此,对于相近像素构成的相似像素组,只需对其中的一个代表像素进行较为耗时的计算,剩下的像素直接复用计算结果即可。
复用方案中的关键问题有两点:一是差异性的度量方式,用来判断两个像素是否相似;二是关联信息的存储方式,用来对相似像素进行关联。
4.1 差异性度量方式搜索区域图和过滤区域图的像素拥有相同的数据项,分别是深度值、搜索区域中心坐标(2个分量)以及搜索区域的大小。
设搜索区域图和过滤区域图中某像素
| $\left\{ \begin{gathered} \left| {{{\left( {{s_1} - {s_2}} \right)}/ {{s_2}}}} \right| \le {\sigma _1}, \\ \left| {{{\left( {{x_1} - {x_2}} \right)} / {{x_2}}}} \right| \le {\sigma _2}, \\ \left| {{{\left( {{y_1} - {y_2}} \right)}/ {{y_2}}}} \right| \le {\sigma _2}, \\ \left| {{{\left( {{d_1} - {d_2}} \right)}/ {{d_2}}}} \right| \le {\sigma _3} \\ \end{gathered} \right.$ | (7) |
就认为
对于每个像素,若其左边像素和上边像素与当前像素相似,则将其与当前像素关联起来。当所有的像素都计算完成后,相似的像素就会关联到一起,形成多个相似像素组。
为了描述像素之间的关联性,可以将一个像素看作另一个像素的父亲像素或者孩子像素。关联信息可以存储在孩子像素中(在孩子像素中保存父亲的位置信息),也可以存储在父亲像素中(在父亲像素中保存孩子的位置信息)。对于前一种方式,代表像素的值计算完毕后,其它像素需要找到其祖先,然后将祖先像素的值赋值给自身,这种做法会增加总的计算量,因为不同像素查找祖先时经过的路径可能会重复,因而本文使用后一种方式。在这种方式下,一个像素如果不是任何像素的孩子,它就是代表像素。代表像素需要负责其子孙像素的赋值工作。
4.3 局部区域上述方法可以达到复用计算结果的目的,但是会出现两方面的问题:一是误差累积现象。若像素
为了解决这两方面的问题,引入局部区域这一概念,只对位于同一局部区域中的像素执行复用方案。局部区域变相限制了相似像素组的大小,一方面,两像素间的最大误差有了上界,减轻了误差累积现象的影响;另一方面,形成的层次结构深度较低,减轻了代表像素的负担。
使用简单有效的局部区域实现方式,即将搜索区域图和过滤区域图均匀地划分为
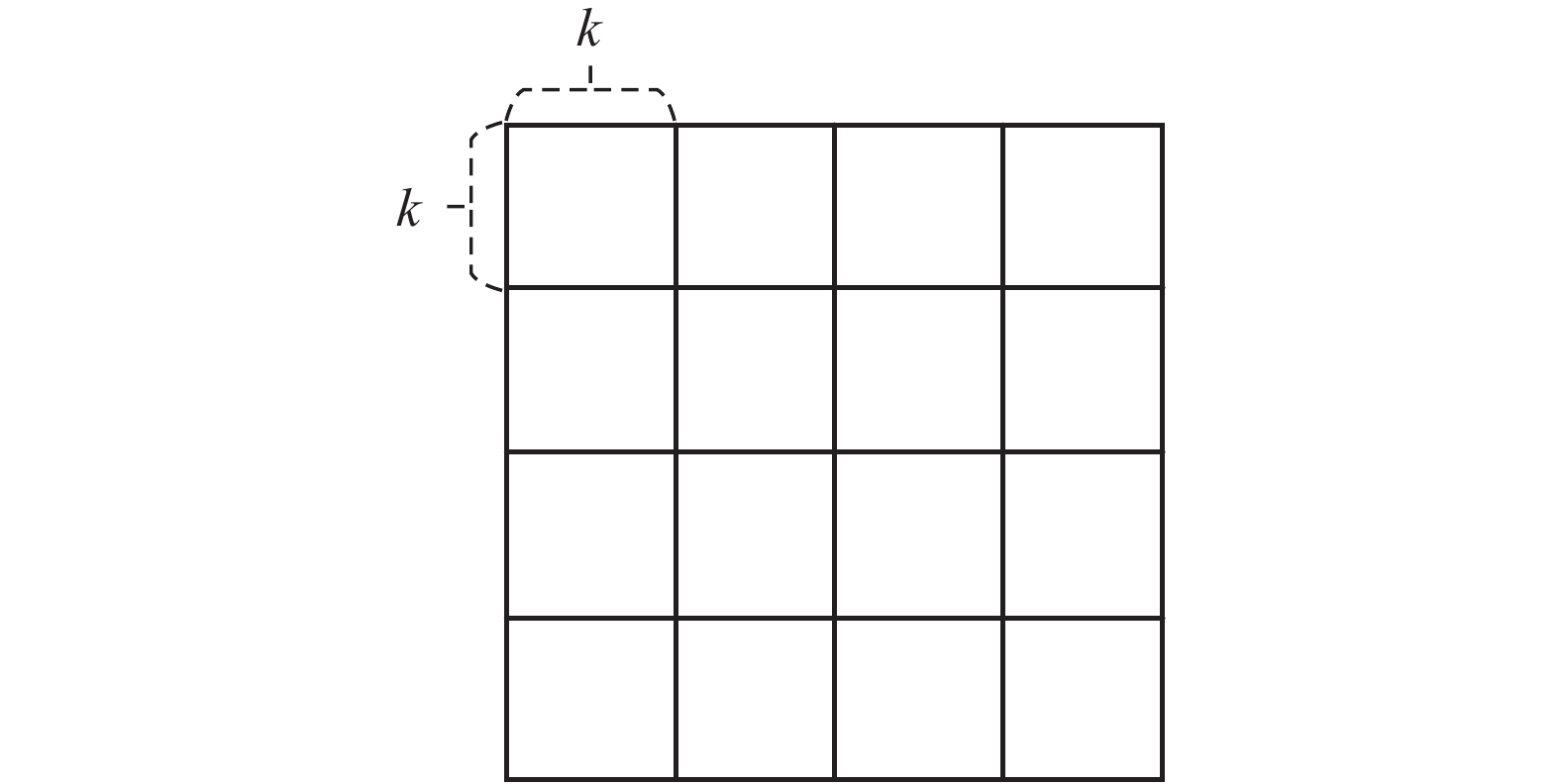 |
| 图4 图像划分方式 Fig. 4 Split mode of images |
在计算关联信息时,设当前处理像素的坐标为
实验使用OpenGL 4.5,GLSL对算法进行实现。硬件环境是CPU i7/内存8GB/显卡GTX970M。实验使用的基本参数设置如下:阴影图分辨率为1 024×1 024,绘制窗口分辨率为1 024×1 024。使用两个测试场景对算法进行测试,如图5所示。两个场景的复杂度不同,而且为了测试算法的通用性,场景图5(b)利用简单几何形体随机生成。
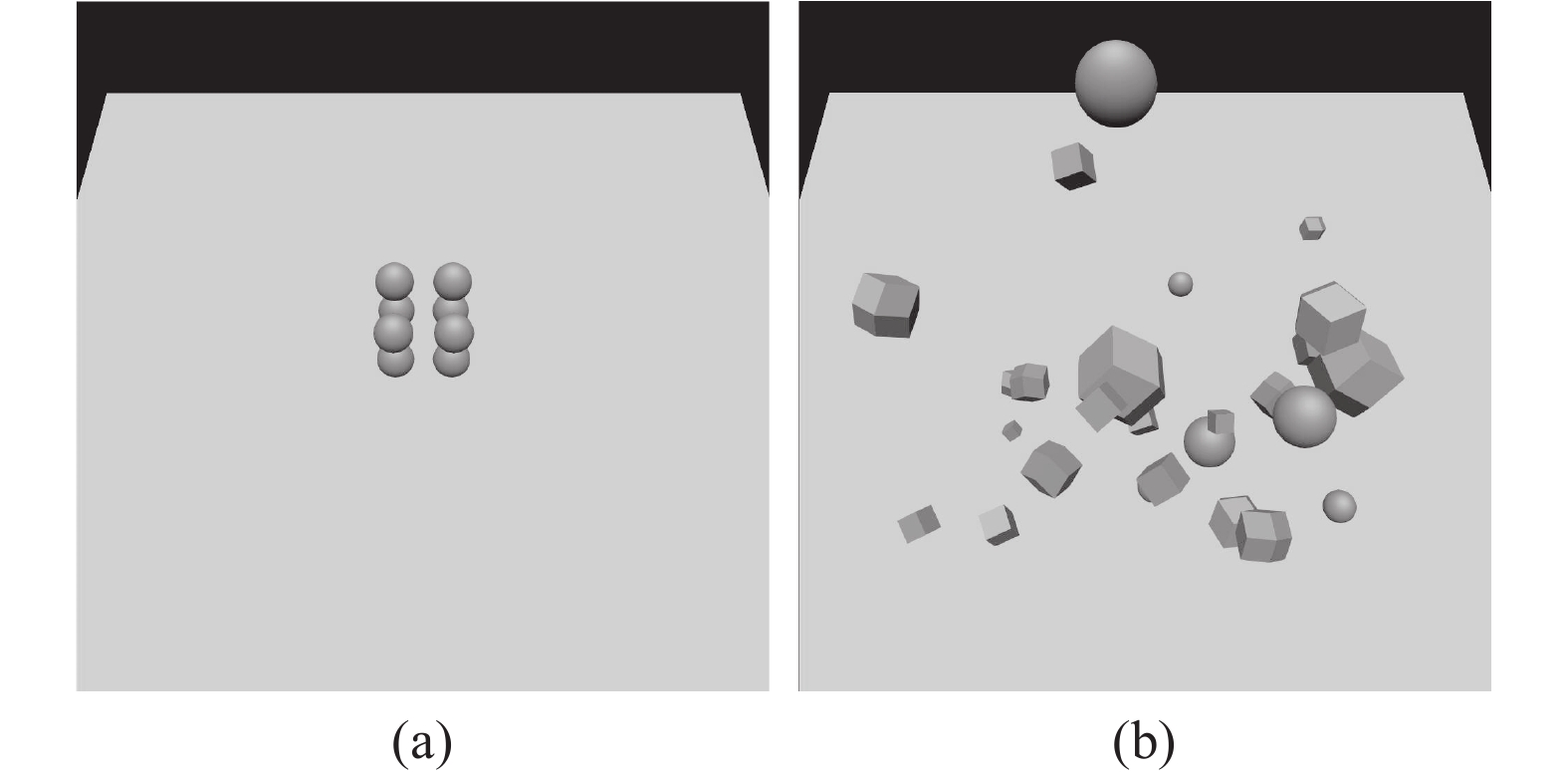 |
| 图5 测试场景 Fig. 5 Scenarios for test |
5.2 复用方案设置
算法对搜索区域大小进行了近似,看似相同的搜索区域实际上已经包含了一定的差异性,所以差异性度量中的
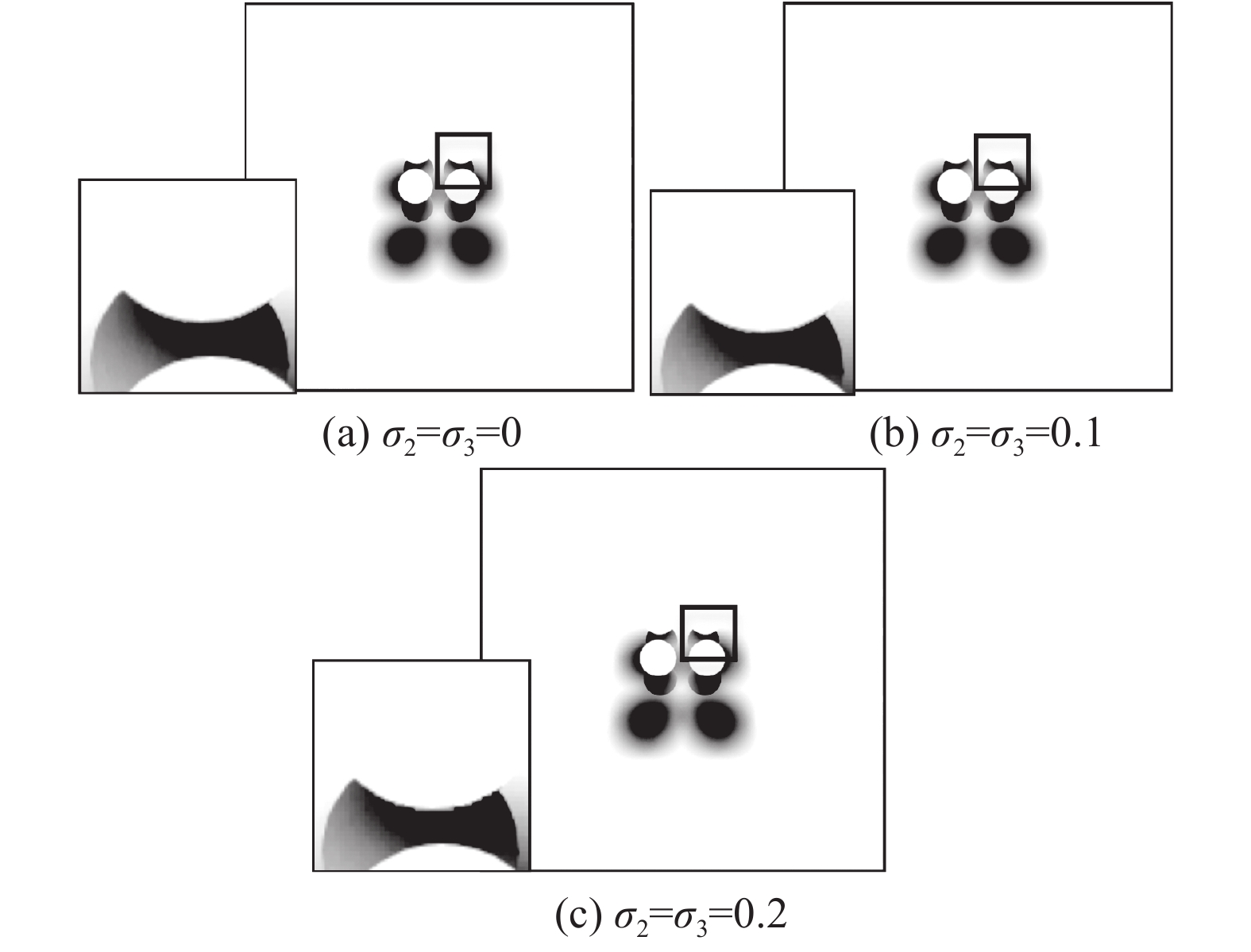 |
| 图6 不同差异性上界软阴影质量比较 Fig. 6 Comparison of the quality of soft shadows with different upper bound settings |
通过对比可以发现,差异性上界取0.1时,生成的软阴影质量受到的影响较小,因此设置
复用方案的另一个问题是确定合适的局部区域大小。以场景图5(a)为例,在使用缩减式阴影图和利用采样信息的快速遍历的情况下,不同局部区域设置下生成的软阴影如图7所示。
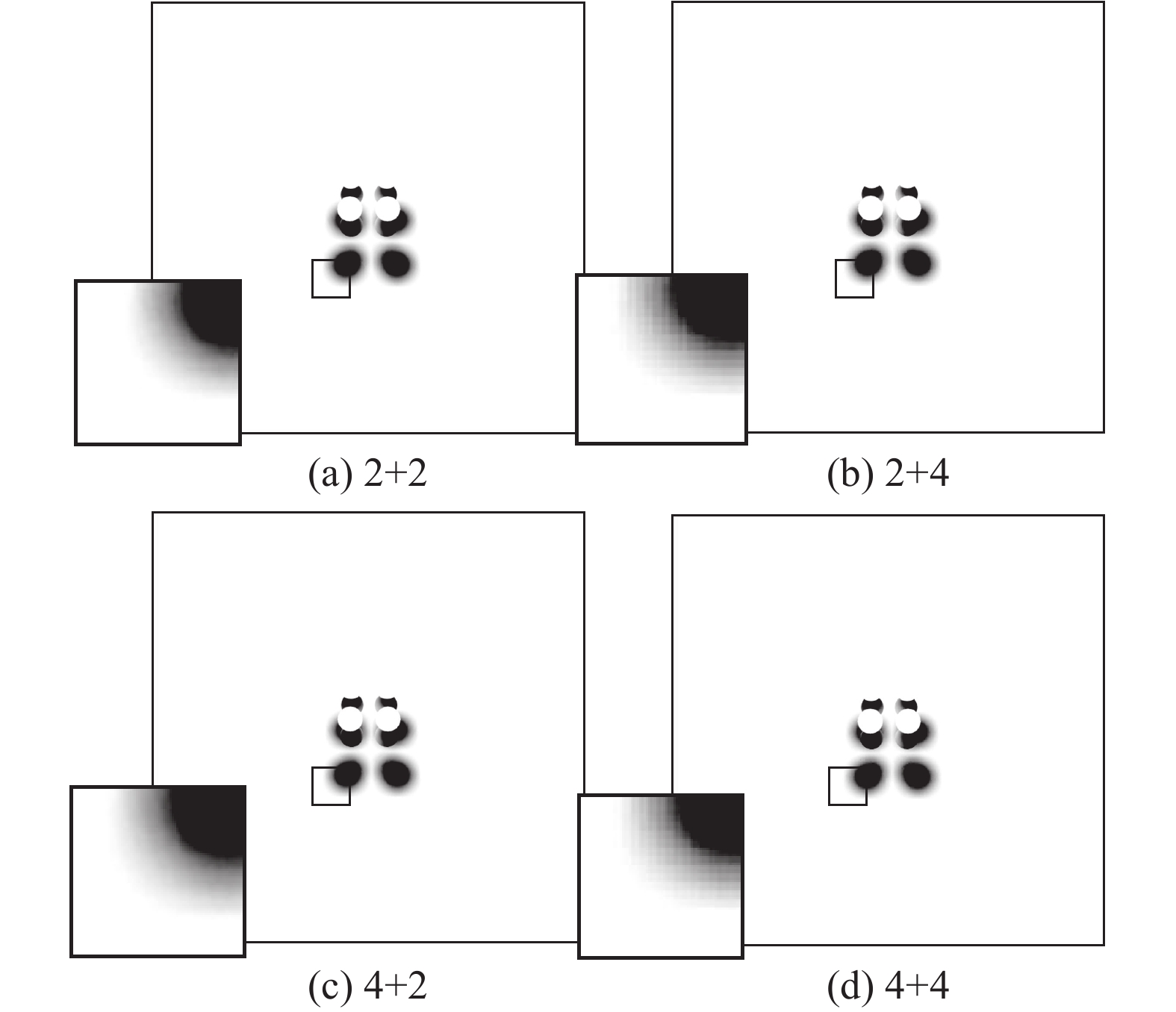 |
| 图7 不同划分方式软阴影质量比较 Fig. 7 Comparison of the quality of soft shadows with different split modes |
其中
通过比较图7(a)和7(b)以及7(c)和7(d),可知在Step5中,使用
| 表2 不同划分方式运行时间比较 Tab. 2 Comparison of running time with different split modes |
 |
在不同的场景下,
为了减轻走样现象的影响,对生成的软阴影还需进行模糊处理。作者采用高斯模糊,因为2维高斯函数具有可分离的特性,先在水平方向上用1维高斯函数进行处理,之后对处理后的结果再进行竖直方向的处理,这使得计算量随模糊半径成线性增长而不是成平方增长,提高了计算效率。由于算法已经考虑了像素计算结果的相似性,因而使用较小的模糊半径,具体设置为3。
5.4 对比原有算法为了说明改进算法不会降低软阴影质量,对其与PCSS算法和HQEPCSS算法生成软阴影的质量进行对比。以场景图5(b)为例,3种算法生成的软阴影如图8所示。
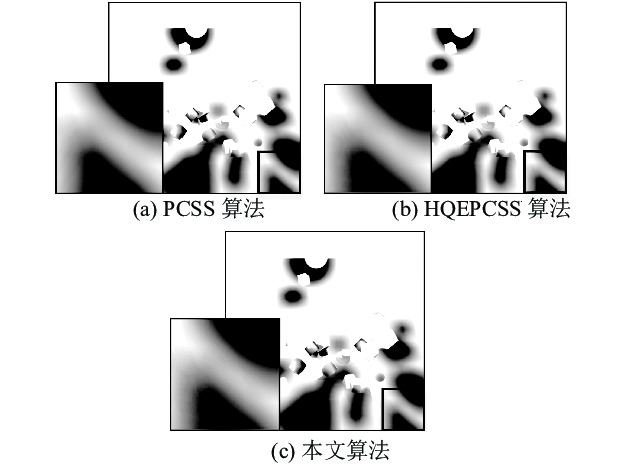 |
| 图8 不同算法软阴影质量比较 Fig. 8 Comparison of the quality of soft shadows with different algorithms |
以SSIM(structural similarity index,结构相似性)[16]为指标分别计算图8(a)与8(b)和8(c)的相似度,其中图8(a)与8(b)的相似度为0.986 6,图8(a)与8(c)的相似度为0.970 5,说明改进算法并没有显著降低软阴影的质量。接着对3种算法生成软阴影的时间进行对比,如表3所示。
| 表3 不同算法运行时间比较 Tab. 3 Comparison of running time with different algorithms |
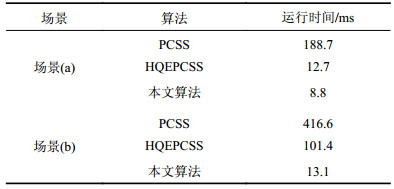 |
本文算法比PCSS算法和HQEPCSS算法的运行时间更低,而且场景中阴影部分越多,取得的提升效果就会越大,这是因为当阴影部分较少时,在使用复用方案时,存储的关联信息很多都是与软阴影计算无关的,因而浪费了计算资源,这部分浪费会与产生的加速效果相抵消。
6 结 论为了在较低的运行开销下生成质量较好的软阴影,提出了一种基于PCSS的软阴影生成算法。相对于已有方法,作者方法具有以下优点:1)对多尺度阴影图进行精炼,降低了生成开销;2)在快速遍历使用采样信息,提高快速遍历结果的准确性;3)设计了一种计算结果复用方案,降低总的计算量,进一步提高了算法的效率。
但作者算法仍然存在一些不足,主要体现在复用方案的自适应调整上,主要有以下两点:1)复用方案中使用的差异性上界是固定的,由于实验具有一定的局限性,该上界可能不适用于所有的场景;2)复用方案中局部区域的实现方式比较简单,可能会将相似程度较低但满足差异性指标的像素分到一组中,而将相似程度更高的像素分到不同的组中。
| [1] |
Williams L. Casting curved shadows on curved surfaces[J]. ACM Siggraph Computer Graphics, 1978, 12(3): 270-274. DOI:10.1145/965139.807402 |
| [2] |
Crow F C. Shadow algorithms for computer graphics[J]. ACM Siggraph Computer Graphics, 1977, 11(2): 242-248. DOI:10.1145/563858.563901 |
| [3] |
Schwärzler M. Real-time soft shadows with adaptive light source sampling[J]. Applied Optics, 2009, 24(18): 19-26. |
| [4] |
Guennebaud G,Barthe L,Paulin M.Real-time soft shadow mapping by backprojection[C]//Proceedings of the Eurographics Symposium on Rendering Techniques.Aire-la-Ville: Eurographics Association Press, 2006:227–234.
|
| [5] |
Schwarz M,Stamminger M. Bitmask soft shadows[J]. Computer Graphics Forum, 2007, 26(3): 515-524. DOI:10.1111/cgf.2007.26.issue-3 |
| [6] |
Guennebaud G,Barthe L,Paulin M. High-quality adaptive soft shadow mapping[J]. Computer Graphics Forum, 2010, 26(3): 525-533. |
| [7] |
Fernando R.Percentage-closer soft shadows[C]//ACM Siggraph 2005 Sketches.New York:ACM Press,2005:35.
|
| [8] |
Yang B,Dong Z,Feng J,et al. Variance soft shadow mapping[J]. Computer Graphics Forum, 2010, 29(7): 2127-2134. DOI:10.1111/cgf.2010.29.issue-7 |
| [9] |
Annen T,Dong Z,Mertens T,et al. Real-time,all-frequency shadows in dynamic scenes[J]. ACM Transactions on Graphics, 2008, 27(3): 1-8. DOI:10.1145/1360612.1360633 |
| [10] |
Shen L,Feng J,Yang B. Exponential soft shadow mapping[J]. Computer Graphics Forum, 2013, 32(4): 107-116. DOI:10.1111/cgf.12156 |
| [11] |
袁昱纬,刘传辉,全吉成. 大规模场景的百分比近邻软阴影绘制算法[J]. 海军航空工程学院学报, 2017, 32(4): 341-346. DOI:10.7682/j.issn.1673-1522.2017.04.001 |
| [12] |
沈笠,杨宝光,冯结青. 高质量快速百分比邻近滤波软影算法[J]. 计算机辅助设计与图形学学报, 2014, 26(3): 329-338. |
| [13] |
Bunnell M.Dynamic ambient occlusion and indirect lighting[M]//Fernando R.GPU Gems.New Jersey:Addison-Wesley,2004:223–233.
|
| [14] |
Chiu K,Shirley P,Wang C.Multi-jittered sampling[M]//Heckbert P S.Graphics gems IV.San Diego:Academic Press,1994:370–374.
|
| [15] |
Uralsky Y.Efficient soft-edged shadows using pixel shader branching[M]// Pharr M,Fernando R.GPU Gems 2.New Jersey:Addison-Wesley,2005:269–282.
|
| [16] |
Wang Z,Bovik A C,Sheikh H R,et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
 2019, Vol. 51
2019, Vol. 51


