2. 四川大学 水利水电学院,四川 成都 610065;
3. 四川省水利科学研究院,四川 成都 610072
2. College of Water Resource & Hydropower, Sichuan Univ., Chengdu 610065, China;
3. Sichuan Academy of Water Conservancy, Chengdu 610072, China
跌流通常作为明渠上下游衔接的设施,如没有被下游水流淹没,则称为自由跌流。受跌流影响,明渠水流流态存在从缓流到急流、均匀流到非均匀流的流态转变,出现临界水流,此时跌坎处水深与明渠流量间存在定量关系,这使得利用自由跌流测量明渠流量成为可能。
Rouse[1]早在1936年就注意到了明渠末端跌坎自由跌落水流的这种重要特征并提出了EDR的概念,即EDR为跌坎水深he与临界水深hc的比值,并通过试验给出了明渠水流为临界流时EDR值为0.715,通过此值即可计算明渠流量。自那以后,众多研究者又对明渠自由跌流进行了大量研究(Rajaratnam和Muralidhar[2-3]、Dey[4]、Ferro[5]、Vatankhah[6]、Amhad[7]、Castro-Orgaz和Mateos[8]、Chen[9]、Ahmad和Azamathulla[10]、Noori和Ibrahim[11]等),如明渠底坡S和边壁曼宁糙率n对EDR的影响,不同断面形式明渠(矩形、梯形、圆形、抛物线型等)的EDR值,并依据试验值得出了明渠流量的计算公式。之前的研究主要关注于EDR值与跌坎流量之间的的关系,很少有报道涉及在不同底坡和边壁糙率下的明渠自由跌流水力特性,如跌坎水深、受跌流影响的上游长度、来流弗洛德数和跌坎弗洛德数。并且,大多数试验是在光滑矩形明渠上进行的,而且明渠底坡较小,来流弗洛德数也较小。例如,Rajaratnam和Muralidhar[2],Davis[12]及Sahnaz和 Firat[13]的试验中,明渠底坡最大分别为0.028 8,0.033和0.039 4,弗洛德数最大值分别为2.78,1.97和3.68。基于无量纲和回归分析分析的方法,Davis[12]及Sahnaz和Firat[13]提出了EDR与底坡S和边壁糙率n的经验公式,但其边壁糙率n仅为0.009 1和0.001 47,而且渠道底坡很小,因此其应用受到限制。
本文采用模型试验的方法,针对不同底坡S和不同边壁糙率n的矩形明渠的自由跌流水力特性进行研究,这将为推求明渠跌水测流流量公式提供良好的研究基础。试验中,底坡S在0.002 6到0.097 3之间,在此底坡范围内,各工况条件下,跌坎上游水流皆为急流流态,边壁糙率n在0.009 3到0.019 3之间变化,共计5个糙率,弗洛德数Fr0在1.0到6.62之间,这远大于前人研究范围。根据明渠水流流态,明渠水流为缓流时,其表现出的跌坎水流水力特征性与急流不同,因此本文只针对明渠水流为急流,即明渠底坡S大于临界底坡Sc的工况进行了分析与研究,而缓流则需进一步试验后再行研究。
1 试验装置与工况试验装置如图1所示,矩形试验水槽由玻璃制作,长25.00 m,宽0.30 m,高0.40 m。跌坎下游渠道长10.00 m,宽0.60 m,为保证跌落水流为自由跌流,跌坎高度为0.60 m。在明渠下游出口末端安装矩形薄壁堰,以用于测量渠道流量。
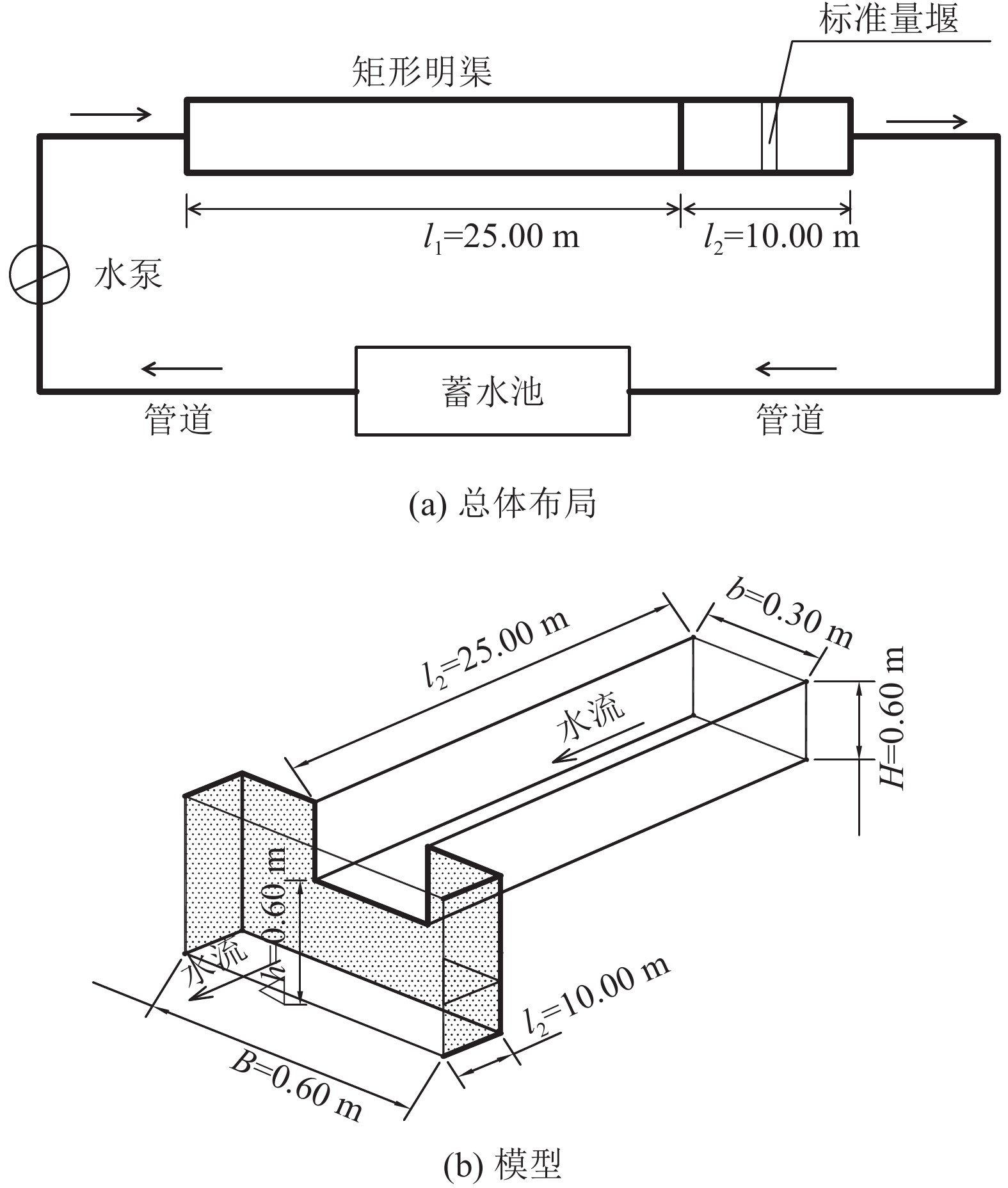 |
| 图1 试验装置 Fig. 1 Experimental installation |
在试验中,利用不同粒径的石英砂颗粒粘贴在渠道边壁上而获得不同的边壁糙率值,石英砂粒径分别为0.5~1.0 mm,1~2 mm,2~3 mm,和3~5 mm。利用渠道末端设置的标准矩形薄壁堰来标定渠道的曼宁糙率系数n,对应不同粒径的石英砂,光滑明渠和贴砂明渠的平均曼宁糙率系数n值分别为0.009 3、0.012 5、0.014 8、0.017 1和0.019 3。
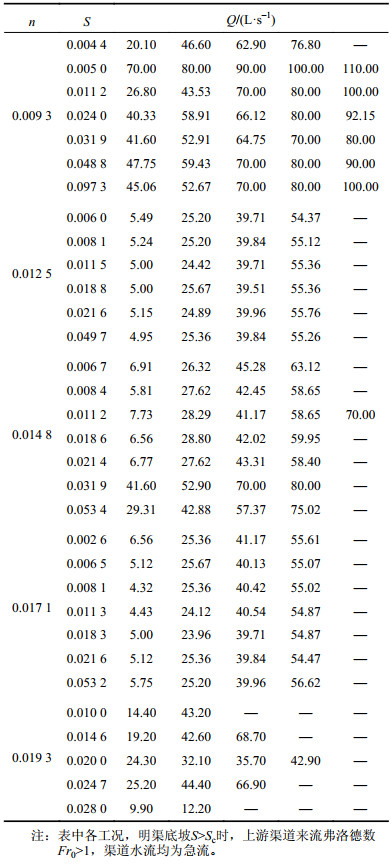
试验中改变流量Q和渠道底坡S,总共129个试验工况(表1)。明渠底坡S分别为陡坡(S>Sc,Sc为明渠水流为临界流时的底坡值)。水深采用探针测定,其精度为0.1 mm。
| 表1 数值模拟与试验工况 Tab. 1 Numerical simulation and test conditions |
 |
2 结果与讨论 2.1 坎末水深he
图2表示了一个典型的自由跌流过程,包括水力学剖面和流线曲率变化示意图[4]。在跌坎附近,水流受到重力加速度垂向的影响。在跌坎断面e–e上游一定距离(x=–L)的O–O断面,渠道水流为均匀流,其压力分布符合静水压力分布规律。但在跌坎处(x=0),跌落水舌的上部和下部压力都为大气压,即压力为0,这使得其压力分布相对于明渠水流中的静水压力分布规律而产生剧烈偏离。从断面O–O到跌坎断面e–e,水流垂向流速快速增加,水深则急剧减小。
 |
| 图2 自由跌流示意图 Fig. 2 Sketch of a rectangular free overall |
对矩形明渠而言,定义hc为临界水深,he为跌坎处水深,Vc为临界流速。通过设置水位测针可方便测得跌坎水深he。则对于临界水深hc,其与渠道流量Q存在如下关系:
| ${h_{\rm c}} = \sqrt[3]{{\frac{{\alpha {Q^2}}}{{gb}}}} = \frac{{\sqrt[3]{{aq}}}}{g}$ | (1) |
式中:q为单宽流量,q=Q/b;α为动能修正系数,α=1;g为重力加速度,g=9.81 m/s2;b为试验中的明渠水槽宽度,b=0.30 m。
在试验中可测得he,并通过式(1)可计算临界水深hc。当渠道底坡S和边壁糙率n变化时,he和hc的关系如图3所示。
 |
| 图3 S和n变化时,he和hc之间关系 Fig. 3 Relationship between he and hc as S and n changed |
由图3可知,随着明渠底坡S和糙率n变化,对于每个明渠底坡S,尽管其曼宁糙率系数n不同,但
取he/hc为无量纲量,文献[13]采用
| ${h_{\rm e}}/{h_{\rm c}} = f(F{r_0},S,n)$ | (2) |
式中:Fr0为跌坎上游刚刚受到跌流影响的断面的水流弗洛德数,即图2(a)中的O–O断面处的水流弗洛德数;对陡坡渠道而言(S>Sc),Fr0为渠道水流为均匀流处断面的水流弗洛德数。
对于急流(Fr>1),文献[12-13]通过大量试验证实,he/hc值只与明渠底坡S和曼宁糙率系数n有关。而对于缓流(Fr<1),he/hc值为常数。
试验中,当糙率n变化时,明渠来流弗洛德数Fr0和其底坡S之间关系见图4。
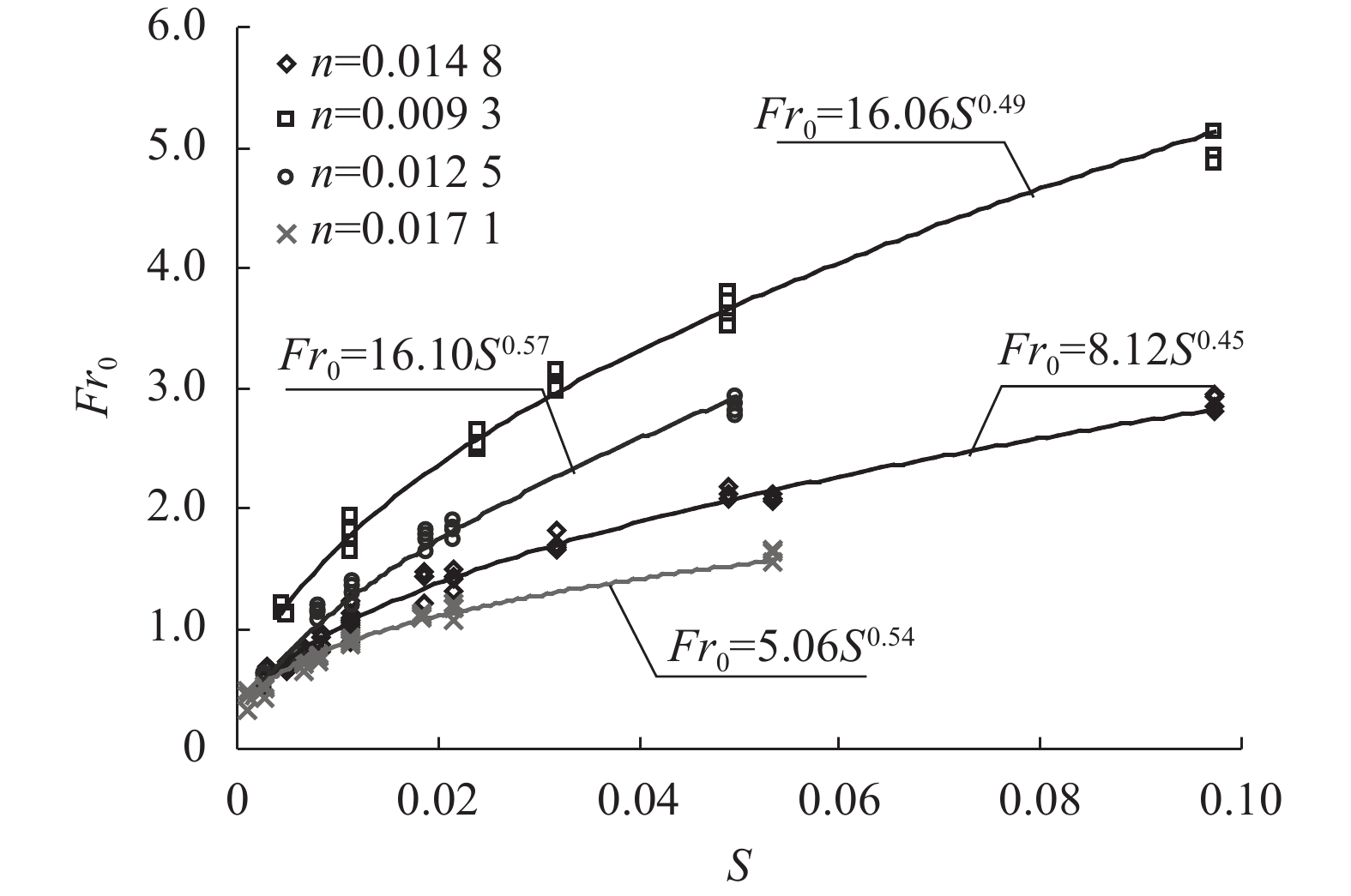 |
| 图4 n变化时Fr0和底坡S之间关系 Fig. 4 Relationship between Fr0 and S as n changes |
由图4可知,在不同的边壁粗糙条件下,Fr0随着底坡S的变化而呈指数变化,相关系数R2大于0.95,这表明二者之间存在良好的相关性。另外,流量Q并不影响来流弗洛德数Fr0。因此,对明渠均匀流而言,
| ${h_{\rm e}}/{h_{\rm c}} = f(S,n)$ | (3) |
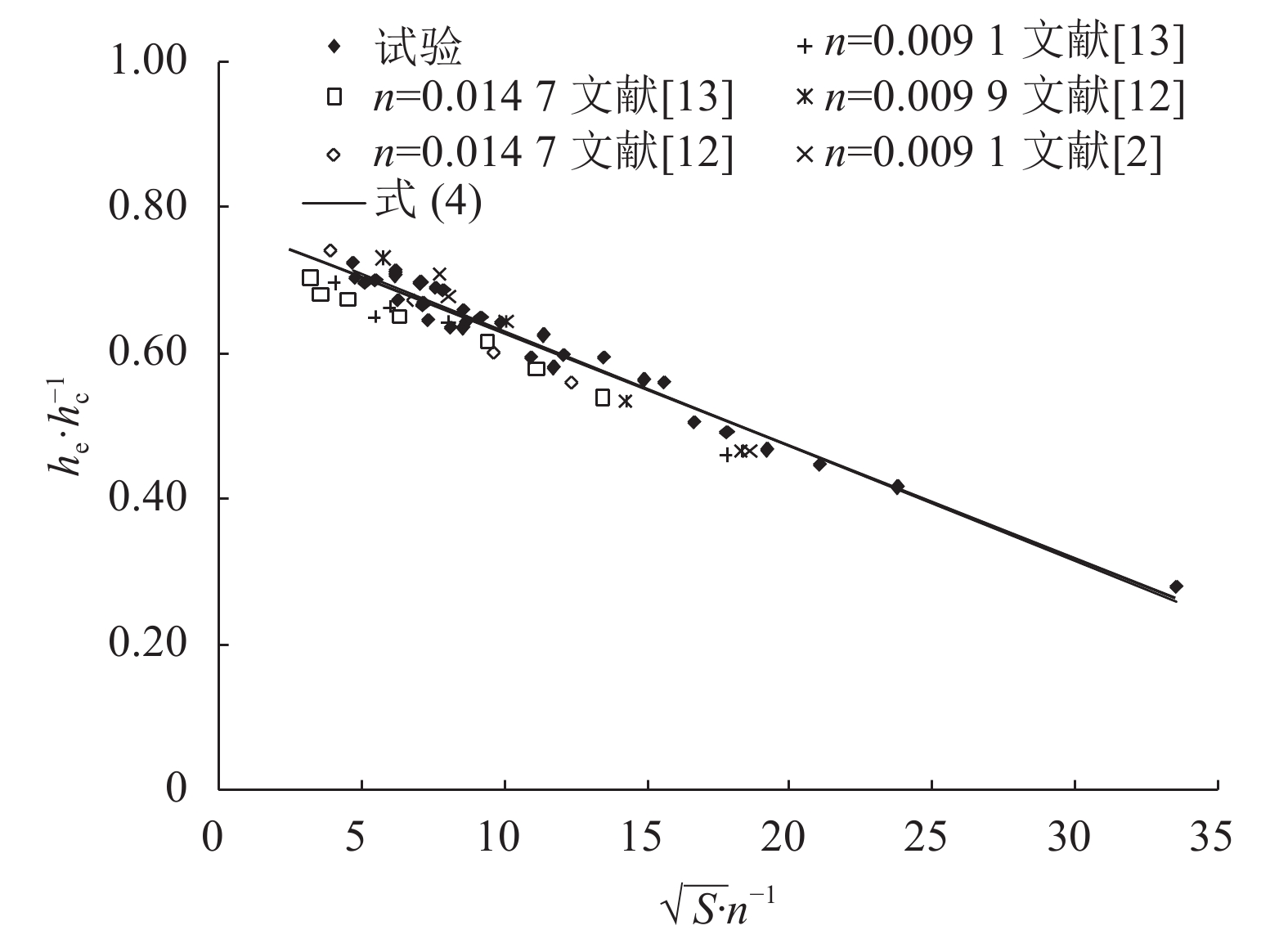
根据式(3),本文采用无量纲参数he/hc和
 |
|
图5 he/hc和
|
从图5可知,当底坡S为陡坡时,在从0.002 6变化至0.097的范围内,n从0.009 1变化至0.019 3时,he/hc和
| $ {h_{\rm e}}/{h_{\rm c}} = 0.783 - 0.015\;5\sqrt S /n,\;\;\;S>S_{\rm{c}} $ | (4) |
线性回归相关系数:R2 = 0.974。
本文结果与文献[2]、[12]及文献[13]的试验结果吻合良好。并且当底坡S和糙率n值较大时,
文献[13]针对糙率n分别为0.009 1和0.014 7,底坡S在0.008和0.038 5之间变化的矩形明渠进行了试验研究,得出如下
| ${h_{\rm e}}/{h_{\rm c}} = 0.773 - 0.018\sqrt S /n$ | (5) |
对陡坡渠道而言(S>Sc),本文结果与式(5)吻合良好,两个公式形式完全一样,系数大小也基本一致。
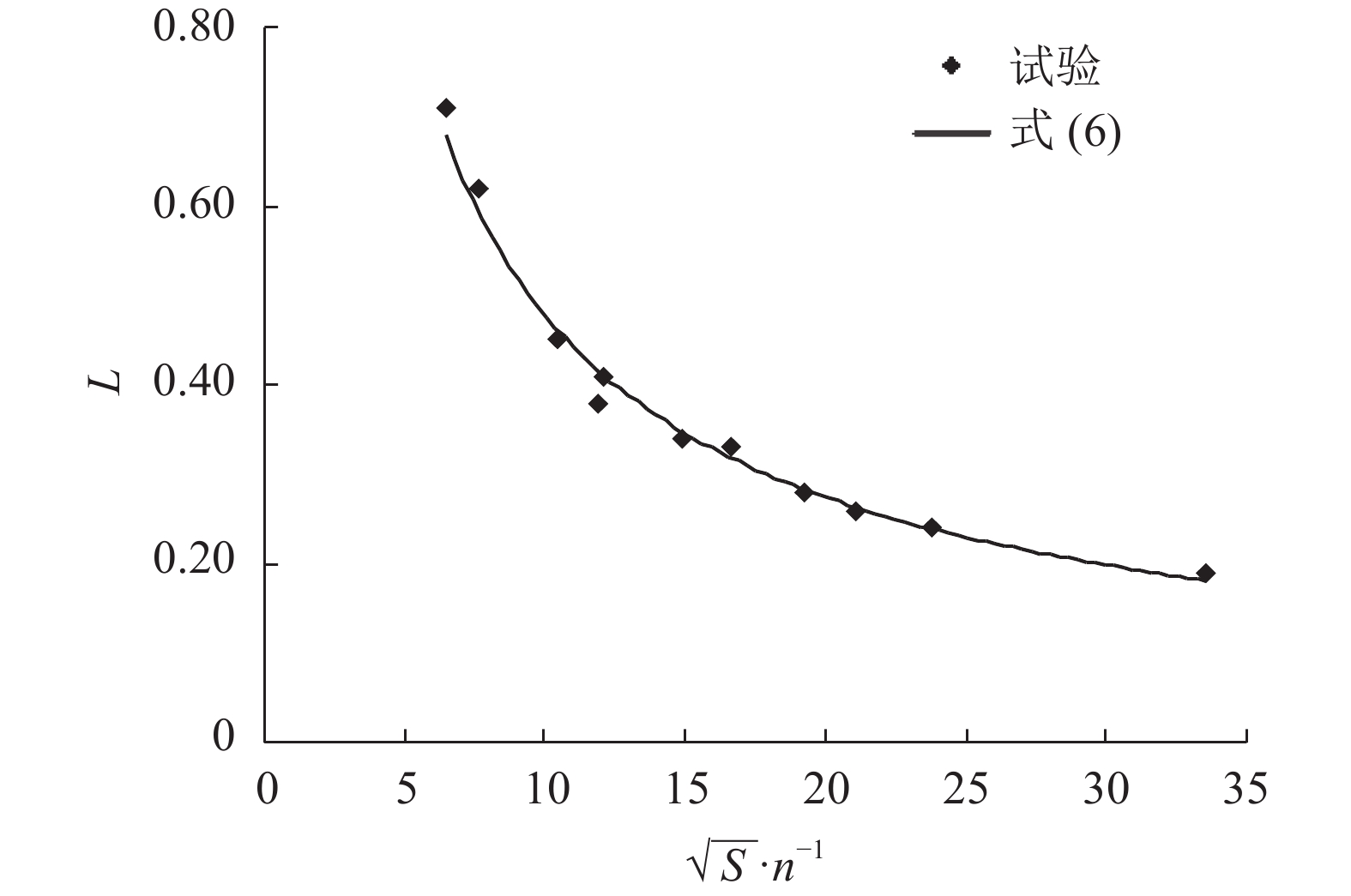
2.2 上游来流长度L跌坎上游水深随着临近跌坎而急剧减小。对于陡坡渠道而言(S>Sc),跌坎上游渠道为均匀流。如图2所示,跌落水流开始在上游断面O–O影响水流。因此,上游断面O–O和跌坎断面e–e为跌流影响区域,其断面之间距离为L。从试验可知,在一定的明渠底坡S和糙率n的条件下,L值不受流量Q的变化影响。换句话而言,L值仅与底坡S和糙率n有关。L值与无量纲参数
 |
|
图6 L和
|
从图6可得如下:
| $L = 3.01{\left( {\frac{{\sqrt S }}{n}} \right)^{ - 0.80}}$ | (6) |
回归相关系数:R2 = 0.989。
根据式(6),当渠道底坡S接近0时,受跌流影响距离L趋向与无限大。因此,对底坡S = 0的渠道而言,水流受跌流影响,其上游不可能出现均匀流。而当渠道底坡S无限大时,水流为垂直跌流,类似于瀑布水流,则对上游影响距离L趋近于0。这同实际水流在渠道底坡为0和垂直时相符合。因此,根据渠道底坡S的极端情况分析可知,式(6)显示了L随底坡S和糙率n的变化规律。
2.3 跌坎断面流速VeVe为跌坎断面的平均流速,则有:
| ${V_{\rm e}} = \frac{Q}{{b{h_{\rm e}}}}$ | (7) |
因此,对于无量纲参数Ve/Vc值,则有:
| $\frac{{{V_{\rm e}}}}{{{V_{\rm c}}}} = \frac{{{h_{\rm c}}}}{{{h_{\rm e}}}}$ | (8) |
根据第2.1节分析,he/hc值仅为明渠底坡S和边壁曼宁糙率系数n的函数。因此,从式(8)可知,Ve/Vc值也仅为底坡S和糙率系数n的函数。以Ve/Vc值为Y轴,
 |
|
图7 Ve/Vc and
|
根据图7,对于陡坡渠道而言(S>Sc),当渠道流量Q变化时,Ve/Vc值与
通过线性回归分析可得:
| $\frac{{{V_{\rm e}}}}{{{V_{\rm c}}}} = 0.051\;9\sqrt S /n + 1.102$ | (9) |
线性回归相关系数:R2=0.969。
本文研究结果同文献[2,13]的研究结果也是一致的,这从图7中二者研究的数据点与本文数据点较一致就可以判断。
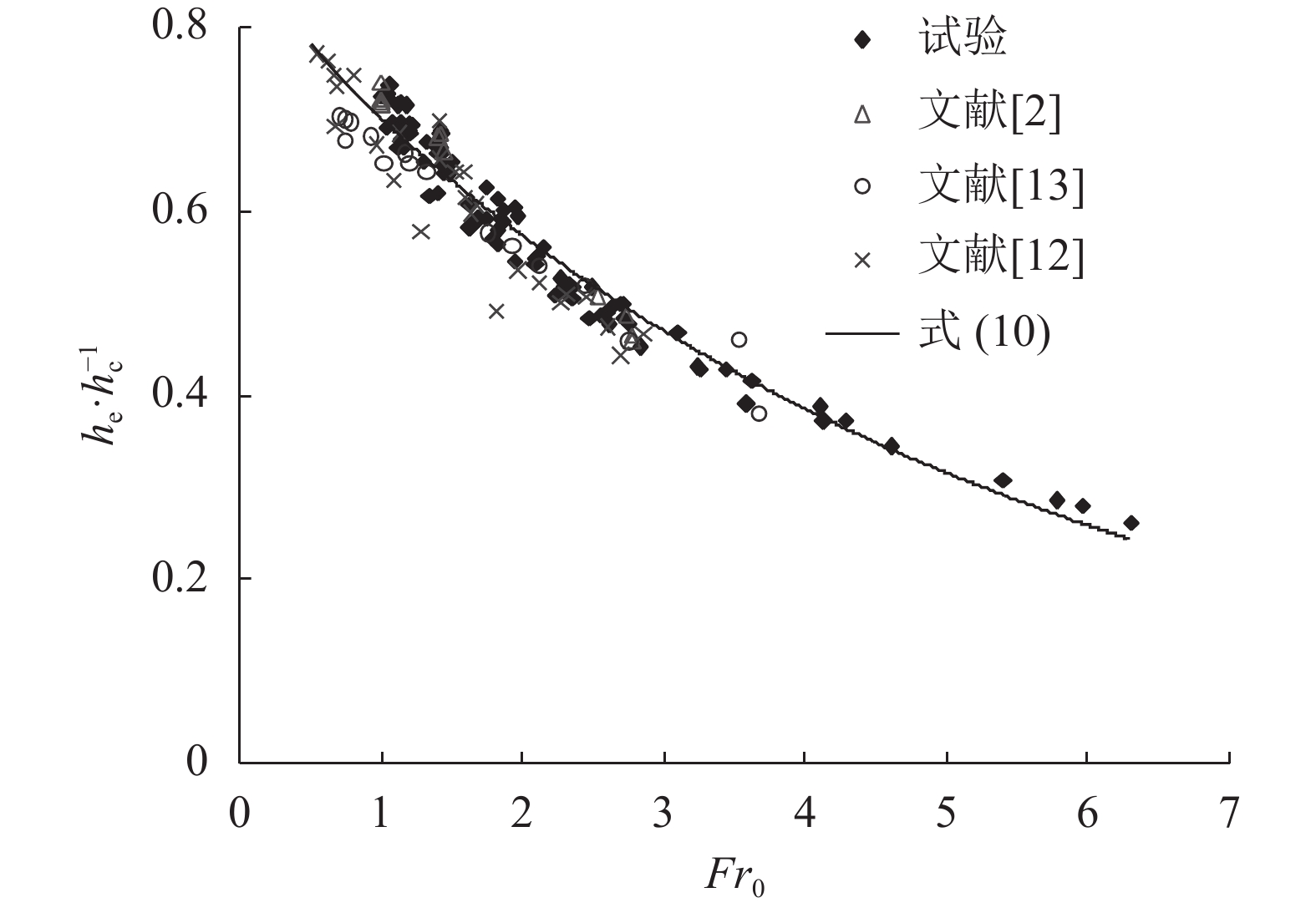
2.4 he/hc与水流弗洛德数Fr之间关系 2.4.1 he/hc与来流弗洛德数Fr0当明渠流量Q变化时,不同底坡S和糙率n的渠道,其临界底坡Sc在0.003 42到0.004 87范围内变化。根据临界底坡Sc计算公式,本试验中的正坡矩形明渠皆为陡坡渠道,渠道内水流为急流。在跌坎上游,急坡渠道内的水流流态为均匀流。定义在断面O–O处(图2所示)的水流弗洛德数为Fr0。在断面O–O处,水流刚好受到自由跌流的影响。根据试验数据,he/hc值和Fr0值间关系见图8。
 |
| 图8 he/hc和Fr0之间关系 Fig. 8 Relationship between he/hc and Fr0 |
由图8数据,经回归分析,得:
| $\frac{{{h_{\rm e}}}}{{{h_{\rm c}}}} = - 0.25\ln \;F{r_0} + 0.733$ | (10) |
相关系数:R2 =0.979。
本文试验结果同文献[2,12]及文献[13]的试验结果非常一致。并且,在更大的来流弗洛德数Fr0的范围内,he/hc值仍然与Fr0值之间存在非常良好的对数关系。
2.4.2 he/hc与跌坎弗洛德数Fre定义跌坎断面的水流弗洛德数为Fre,则有:
| $F{r_{\rm e}} = \frac{{{V_{\rm e}}}}{{\sqrt {g{h_{\rm e}}} }} = \frac{q}{{{h_{\rm e}}\sqrt {g{h_{\rm e}}} }}$ | (11) |
可得:
| $h_{\rm e}^3 = \frac{{{q^2}}}{{gFr_{\rm e}^2}}$ | (12) |
根据式(1),可计算其临界水深hc,即:
| $h_{\rm c}^3 = \frac{{{q^2}}}{g}$ | (13) |
则由式(12)~(13)可得:
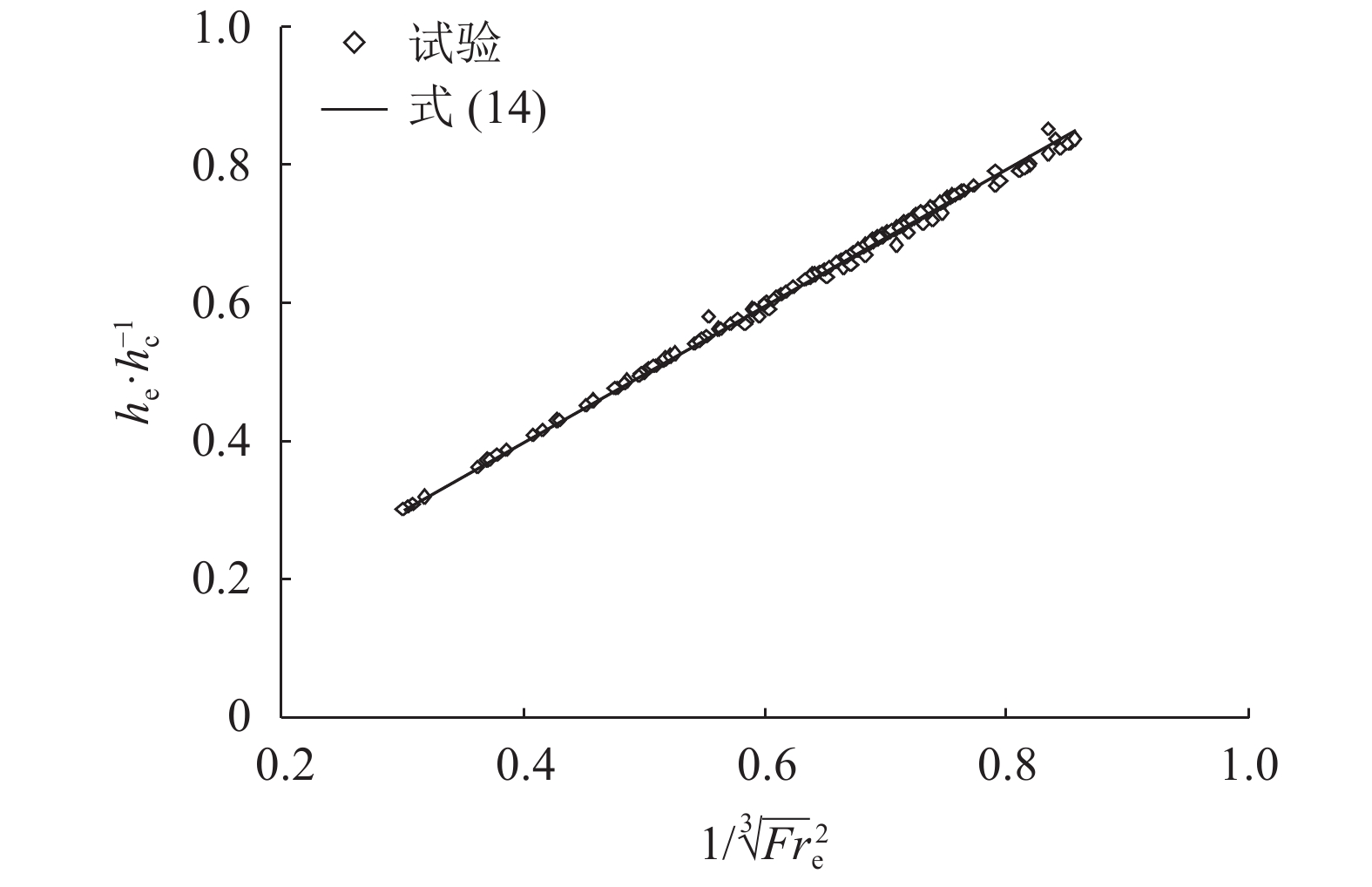
| $\frac{{{h_{\rm e}}}}{{{h_{\rm c}}}} = \frac{1}{{\sqrt[3]{{Fr_{\rm e}^2}}}}$ | (14) |
因此,在he/hc值和
 |
| 图9 he/hc和Fre之间关系 Fig. 9 Relationship between he/hc and Fre |
2.4.3 跌坎弗洛德数Fre与来流弗洛德数Fr0之间关系
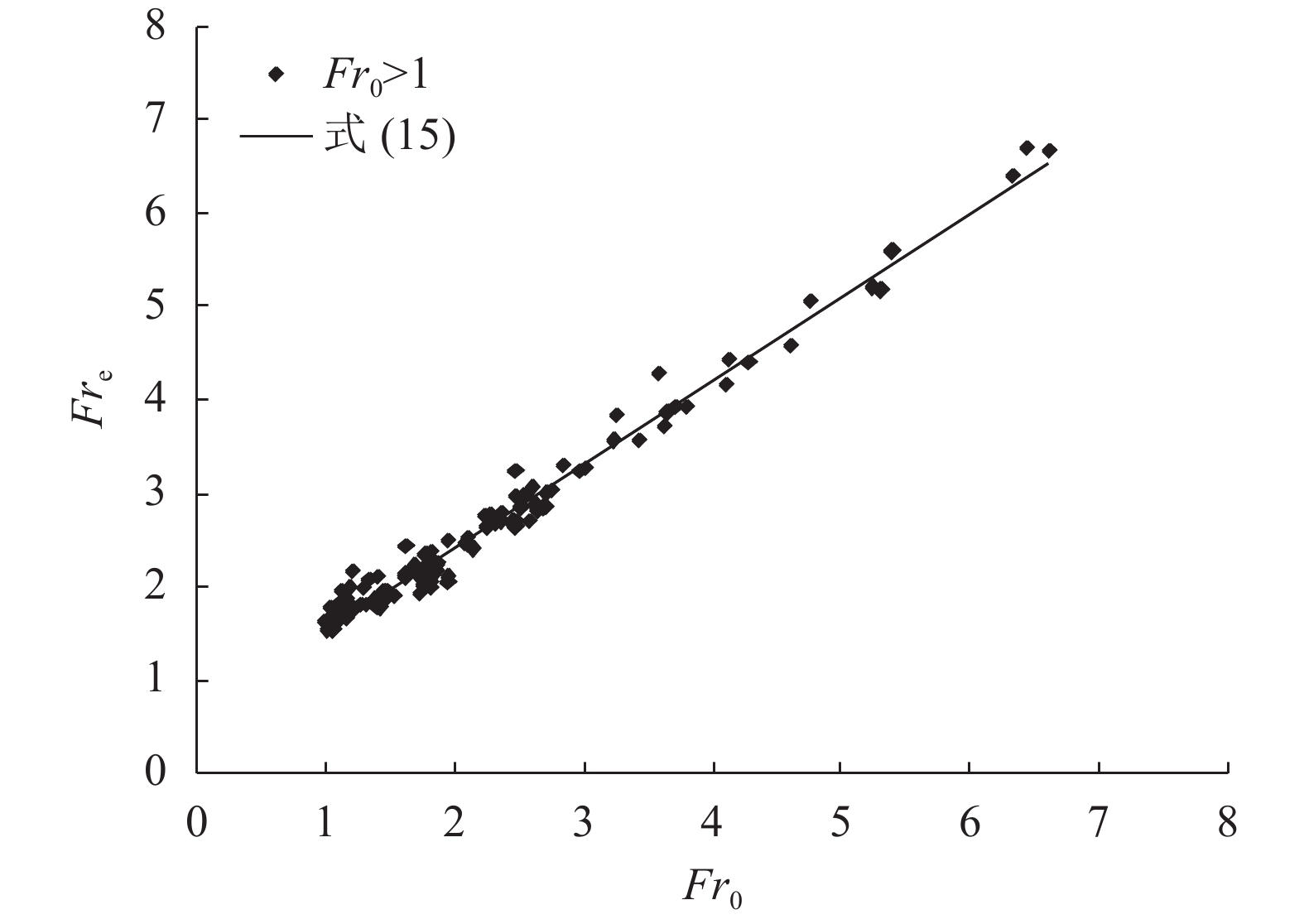
对不同底坡S和糙率n的矩形明渠而言,在流量Q变化的情况下,跌坎断面弗洛德数Fre与上游断面O–O弗洛德数Fr0之间关系见图10。可见,在来流弗洛德数Fr0大于1时,Fre值和Fr0值之间存在良好的线性相关性。通过线性回归分析,可得:
 |
| 图10 Fre和Fr0之间关系 Fig. 10 Relationship between Fre and Fr0 |
| $F{r_{\rm e}} = 0.887F{r_0} + 0.648$ | (15) |
相关系数:R2 = 0.981。
当来流弗洛德数Fr0等于1时,由式(15)计算得Fre值为1.535。另外,根据式(10)和式(14),可得:
| $F{r_{\rm e}} = \frac{1}{{[ - 0.25\ln \;F{r_0} + 0.733]^{1.5}}}$ | (16) |
当来流弗洛德数Fr0等于1时,由式(16)得Fre值为1.593,同式(15)计算结果基本一致。式(15)计算值
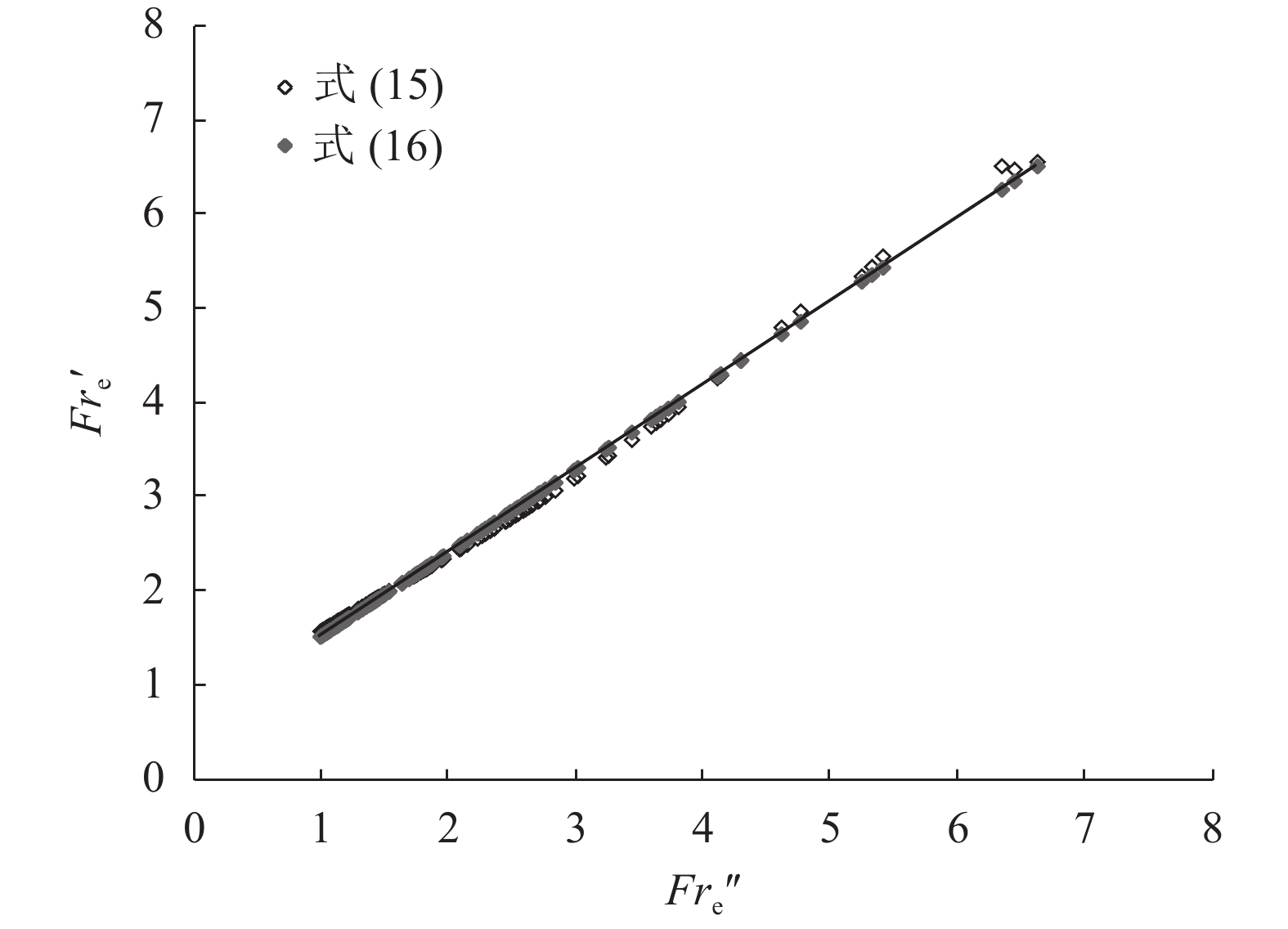 |
| 图11 式(15)与式(16)计算值的对比 Fig. 11 Comparison of Fre calculated by Eqs.15 and 16 |
3 结 论
本文通过试验的方法对不同底坡S和边壁糙率n的矩形明渠的自由跌流进行了研究。在试验中,明渠底坡S范围为0.002 6~0.097 3,糙率n范围为0.009 3~0.019 3,来流弗洛德数Fr0范围为1.0~6.62,研究范围远大于前人相应的研究范围。主要结论如下:
1)在试验条件下,当明渠底坡S>Sc,即陡坡明渠时,无量纲参数he/hc值和Ve/Vc值都与
2)跌流对上游的影响距离L与明渠流量Q无关,但与底坡S和糙率n有关,并给出了L与S和n之间的关系式。
3)对陡坡渠道,he/hc值随着来流弗洛德数Fr0的增加而呈对数规律减小,且与跌坎弗洛德数
4)本文提出了he/hc值与
本文通过扩大明渠底坡S和糙率n的研究应用范围,进一步完善和扩展了前人的研究成果,这对于应用跌流进行明渠流量计量具有重要应用价值。
| [1] |
Rouse H. Discharge characteristics of the free overfall[J]. Civil Engineering, 1936, 6(4): 257-260. |
| [2] |
Rajaratnam N,Muralidhar D. Characteristics of the rectangular free overfall[J]. Journal Hydraulic Research, 1968, 6(3): 233-258. DOI:10.1080/00221686809500236 |
| [3] |
Rajaratnam N,Muralidhar D. The trapezoidal free overfall[J]. Journal Hydraulic Research, 1970, 8(4): 419-447. DOI:10.1080/00221687009500324 |
| [4] |
Dey S. Free overall in open channels:State-of-art review[J]. Flow Measurement Instrument, 2002, 13(1): 247-264. DOI:10.1016/S0955-5986(03)00013-X |
| [5] |
Ferro V. Theoretical end-depth-discharge relationship for free overfall[J]. Journal of Irrigation & Drainage Engineering, 1999, 125(1): 40-44. DOI:10.1061/(ASCE)0733-9437(1999)125:1(40) |
| [6] |
Vatankhah A R. Direct solution for discharge in generalized trapezoidal free overfall[J]. Flow Measurement Instrument, 2013, 29: 61-64. DOI:10.1016/j.flowmeasinst.2012.09.006 |
| [7] |
Ahmad Z. Quasi-theoretical end-depth-discharge relationship for rectangular channels[J]. Journal of Irrigation & Drainage Engineering, 2003, 129(2): 138-141. DOI:10.1061/(ASCE)0733-9437(2003)129:2(138) |
| [8] |
Castro-Orgaz O,Mateos L. Water discharge measurement in agricultural catchments using critical depth flumes affected by sediment deposition[J]. Journal of Irrigation & Drainage Engineering, 2014, 140(3): 1-6. DOI:10.1061/(ASCE)IR.1943-4774.0000672 |
| [9] |
Chen Xiaopan,Li Naiwen,Liu Chao,et al.Experiment on free overfall measuring flume in rectangular channel [J].Journal of Sichuan University (Engineering Science Edition),2015,47(Supp1):1–6. 陈小攀,李乃稳,刘超,等.矩形明渠跌水量水试验研究[J].四川大学学报(工程科学版),2015,47(增刊1):1–6. |
| [10] |
Ahmad Z,Azamathulla H M. Quasi-theoretical end-depth-discharge relationship for trapezoidal channels[J]. Journal of Hydrology, 2012, 456–457: 151-155. DOI:10.1016/j.jhydrol.2012.06.025 |
| [11] |
Noori B M A,Ibrahim,S S. Effect of bed and side slopes on flow measurements in trapezoidal free overfall channels[J]. Arab Journal of Science Engineering, 2016, 41: 4187-4194. DOI:10.1007/s13369-016-2129-z |
| [12] |
Davis A C,Ellet B G S,Jacob R P. Flow measurement in sloping channels with rectangular free overfall[J]. Journal of Hydraulic Engineering ASCE, 1998, 124(7): 760-763. DOI:10.1061/(ASCE)0733-9429(1998)124:7(760) |
| [13] |
Sahnaz T,Firat C E,Ger M. Use of brink depth in discharge measurement[J]. Journal of Irrigation and Drainage Engineering ASCE, 2008, 134(1): 89-95. DOI:10.1061/(ASCE)0733-9437(2008)134:1(89) |
 2019, Vol. 51
2019, Vol. 51


